Local Path Planner for Mobile Robot Considering Future Positions of Obstacles
Abstract
:1. Introduction
- A multi-obstacle velocities detection algorithm through 2D lidar and Kalman filter is proposed.
- An improved TEB local planner that combines the TEB poses and obstacle velocities is designed to improve the robot’s dynamic obstacle avoidance efficiency.
- A series of simulations and experiments are performed to verify the effectiveness of the proposed method.
2. Related Work
3. Methodology
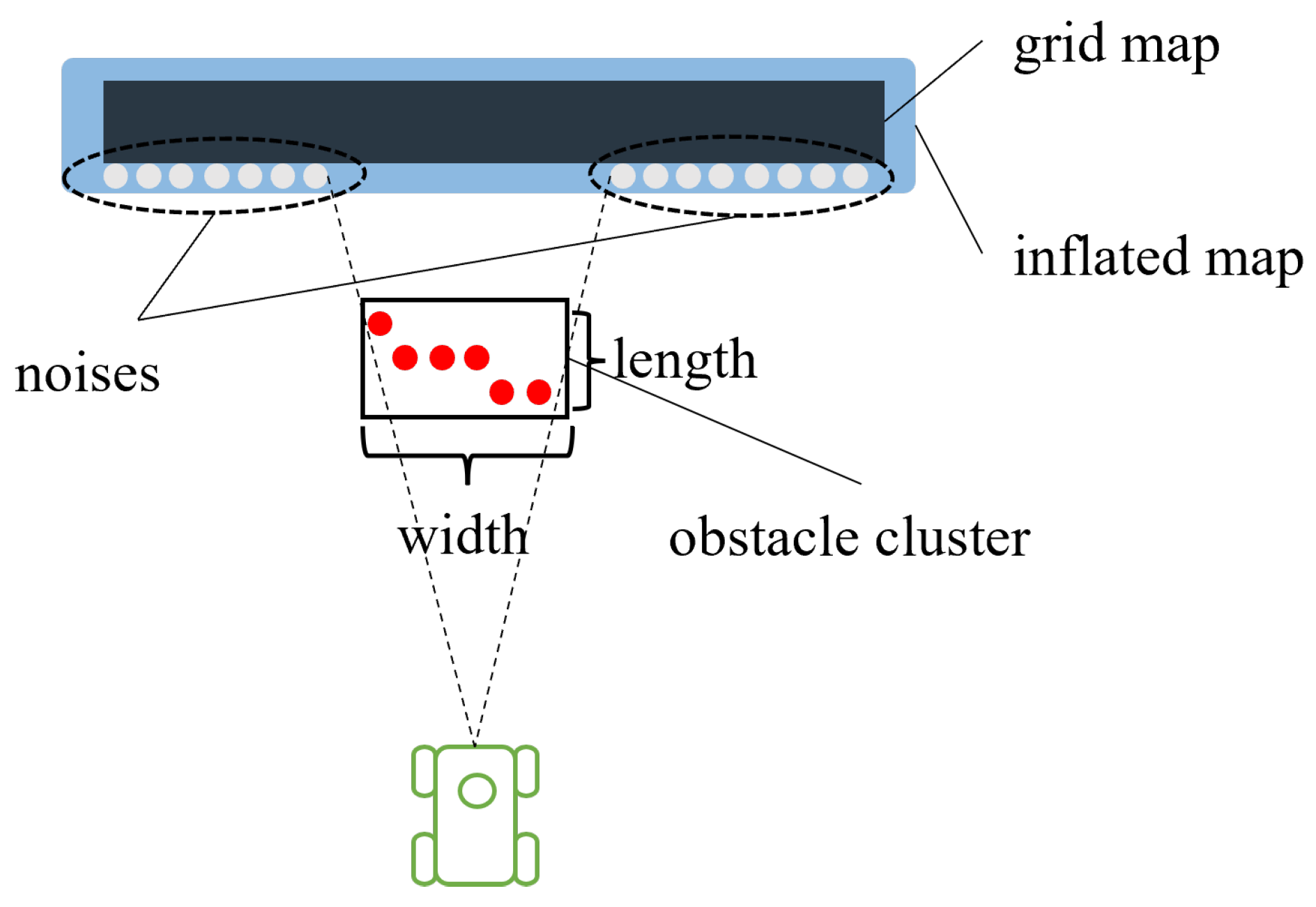
3.1. Obstacle Detection
3.1.1. Clustering
3.1.2. Data Association Matrix
3.1.3. Kalman Filter Tracking
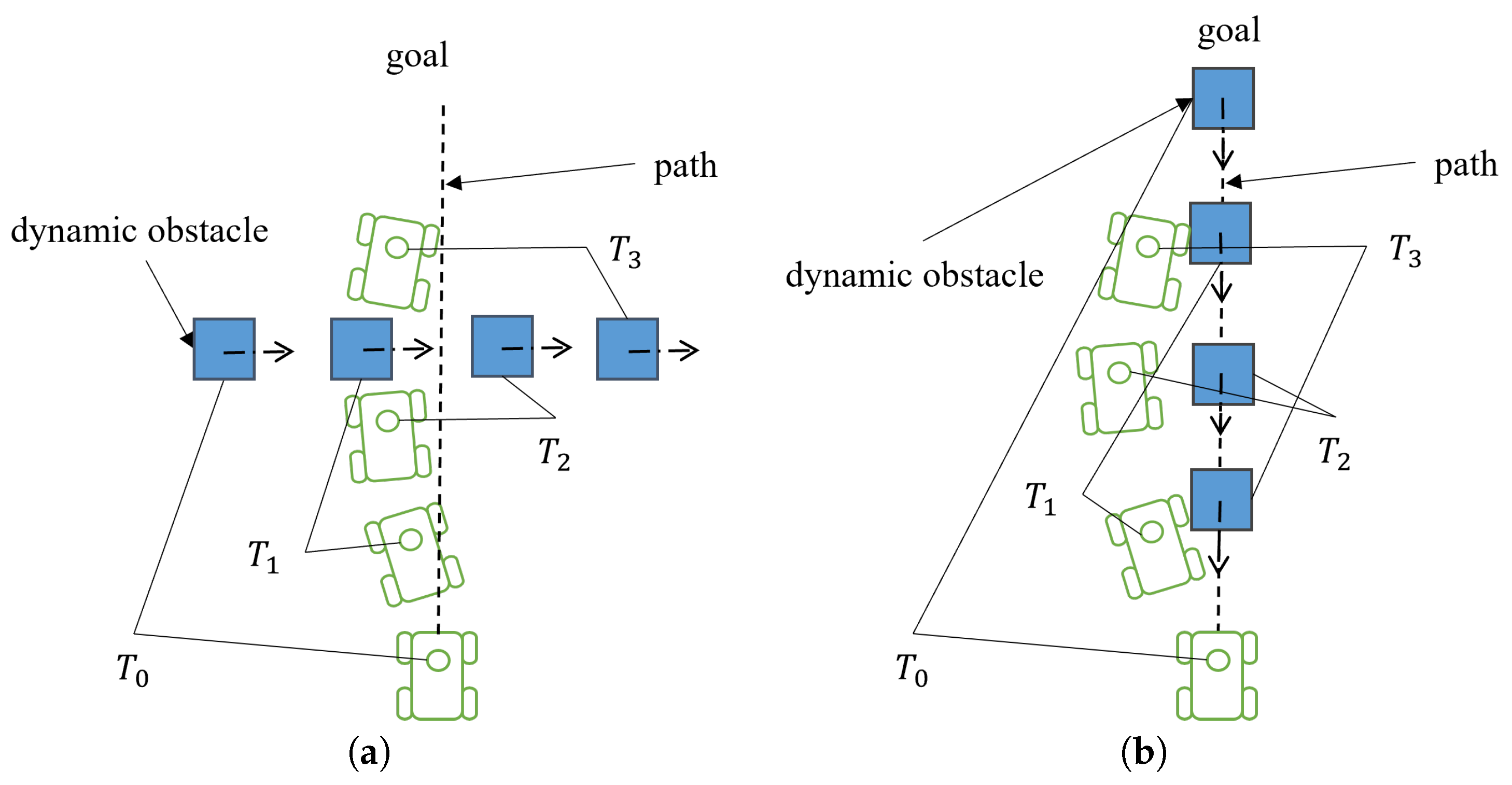
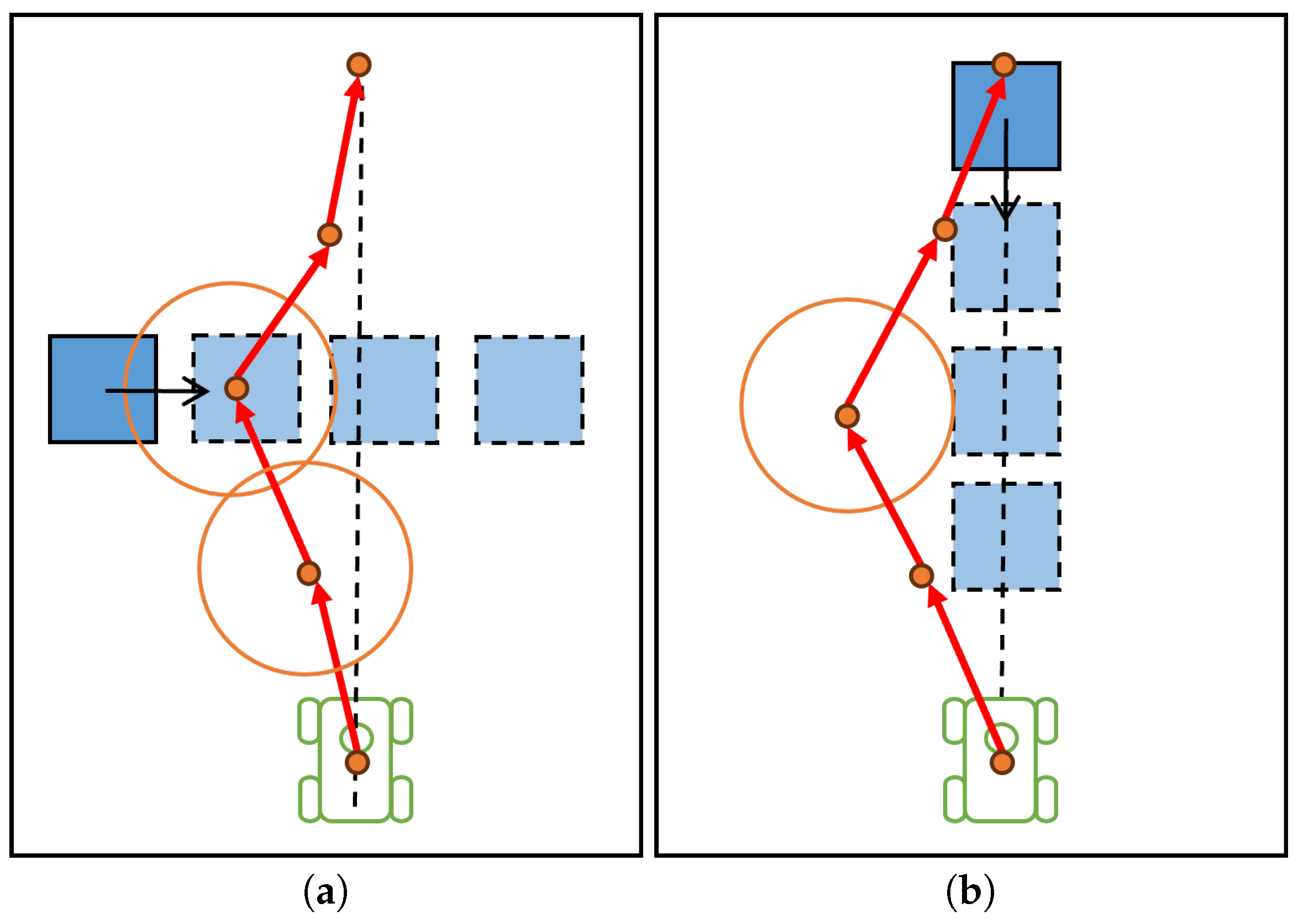
3.2. Improved TEB Algorithm
4. Simulations and Experiments
4.1. Simulations
4.1.1. Obstacle Ahead of the Robot
4.1.2. Obstacle Approaching from the Side of the Robot
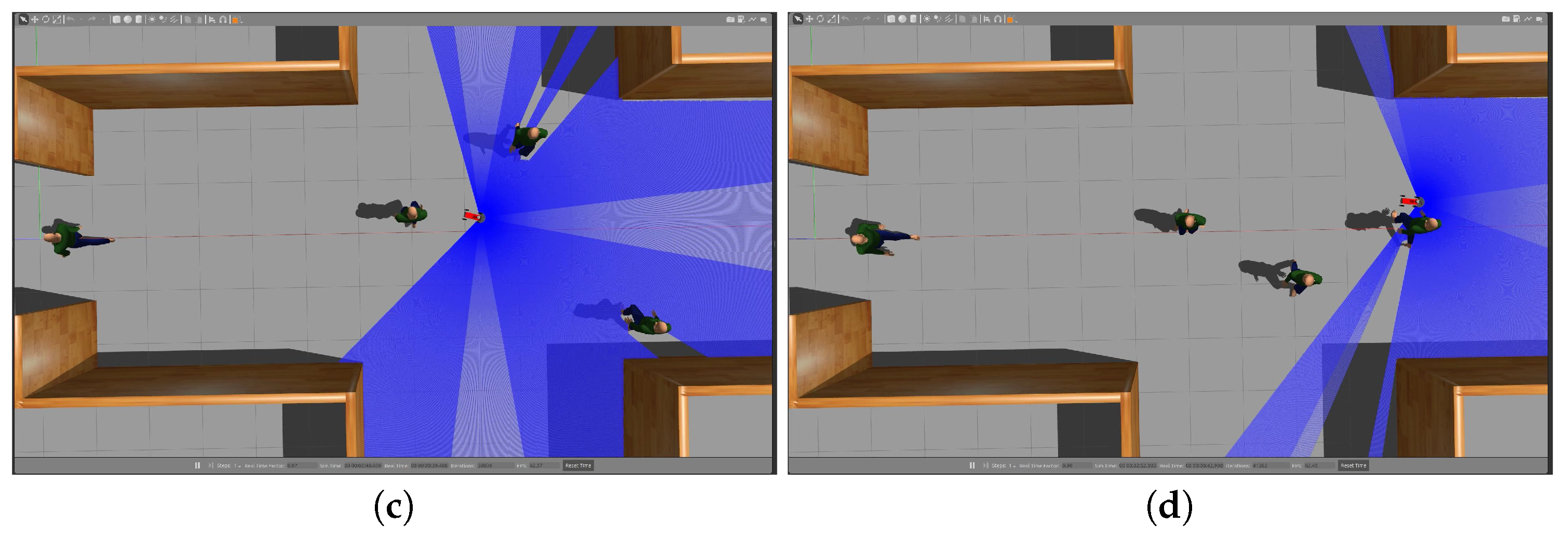
4.1.3. Navigation in Complex Environments
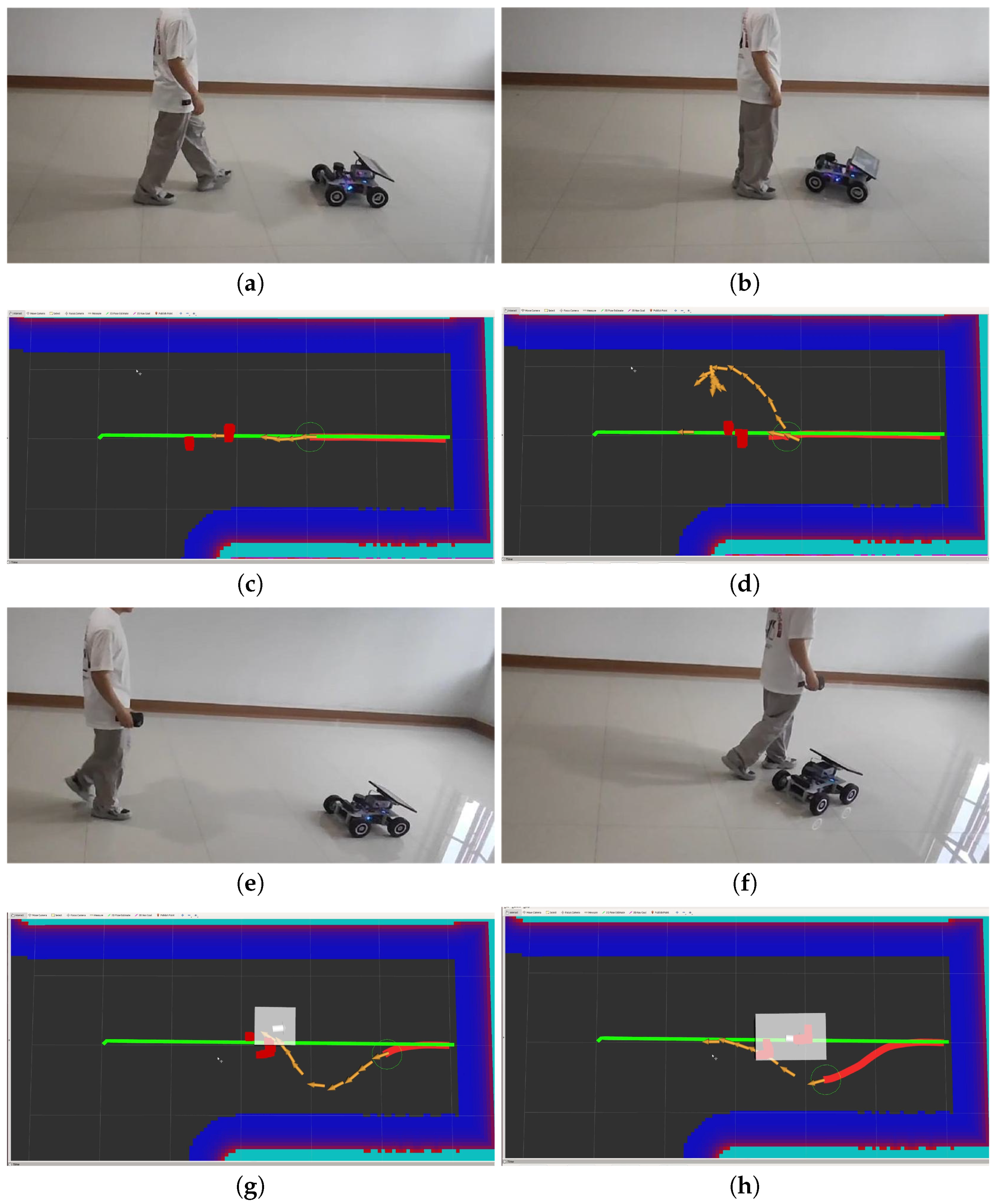
4.2. Experiments
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qi, J.; Yang, H.; Sun, H. MOD-RRT*: A sampling-based algorithm for robot path planning in dynamic environment. IEEE Trans. Ind. Electron. 2020, 68, 7244–7251. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S. LSPP: A novel path planning algorithm based on perceiving line segment feature. IEEE Sens. J. 2021, 22, 720–731. [Google Scholar] [CrossRef]
- Kim, B.; Pineau, J. Socially adaptive path planning in human environments using inverse reinforcement learning. Int. J. Soc. Robot. 2016, 8, 51–66. [Google Scholar] [CrossRef]
- Sun, T.; Pan, W.; Wang, Y.; Liu, Y. Region of interest constrained negative obstacle detection and tracking with a stereo camera. IEEE Sens. J. 2022, 22, 3616–3625. [Google Scholar] [CrossRef]
- Almasri, M.M.; Alajlan, A.M.; Elleithy, K.M. Trajectory planning and collision avoidance algorithm for mobile robotics system. IEEE Sens. J. 2016, 16, 5021–5028. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Sugimoto, T.; Tanaka, K.; Shimomura, Y.; Arjonilla Garcia, F.J.; Kim, C.H.; Yabushita, H.; Toda, T. Robot navigation based on predicting of human interaction and its reproducible evaluation in a densely crowded environment. Int. J. Soc. Robot. 2022, 14, 373–387. [Google Scholar] [CrossRef]
- Duong, H.T.; Suh, Y.S. Human gait tracking for normal people and walker users using a 2D LiDAR. IEEE Sens. J. 2020, 20, 6191–6199. [Google Scholar] [CrossRef]
- Lee, H.; Lee, H.; Shin, D.; Yi, K. Moving objects tracking based on geometric model-free approach with particle filter using automotive LiDAR. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17863–17872. [Google Scholar] [CrossRef]
- Wei, C.; Wang, Y.; Shen, Z.; Xiao, D.; Bai, X.; Chen, H. AUQ–ADMM algorithm-based peer-to-peer trading strategy in large-scale interconnected microgrid systems considering carbon trading. IEEE Syst. J. 2023, 17, 6248–6259. [Google Scholar] [CrossRef]
- Chen, Q.; Li, Y.; Hong, Y.; Shi, H. Prescribed-Time Robust Repetitive Learning Control for PMSM Servo Systems. IEEE Trans. Ind. Electron. 2024; in press. [Google Scholar] [CrossRef]
- Shim, I.; Choi, D.G.; Shin, S.; Kweon, I.S. Multi lidar system for fast obstacle detection. In Proceedings of the 2012 9th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Daejeon, Republic of Korea, 26–28 November 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 557–558. [Google Scholar]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Rösmann, C.; Feiten, W.; Wösch, T.; Hoffmann, F.; Bertram, T. Trajectory modification considering dynamic constraints of autonomous robots. In Proceedings of the ROBOTIK 2012: 7th German Conference on Robotics, VDE, Munich, Germany, 21–22 May 2012; pp. 1–6. [Google Scholar]
- Rösmann, C.; Hoffmann, F.; Bertram, T. Planning of multiple robot trajectories in distinctive topologies. In Proceedings of the 2015 European Conference on Mobile Robots (ECMR), Lincoln, UK, 2–4 September 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Rösmann, C.; Hoffmann, F.; Bertram, T. Kinodynamic trajectory optimization and control for car-like robots. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 5681–5686. [Google Scholar]
- Rösmann, C.; Oeljeklaus, M.; Hoffmann, F.; Bertram, T. Online trajectory prediction and planning for social robot navigation. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1255–1260. [Google Scholar]
- Rösmann, C.; Feiten, W.; Wösch, T.; Hoffmann, F.; Bertram, T. Efficient trajectory optimization using a sparse model. In Proceedings of the 2013 European Conference on Mobile Robots, Barcelona, Spain, 25–27 September 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 138–143. [Google Scholar]
- Hwang, C.L.; Huang, H.H. Experimental validation of a car-like automated guided vehicle with trajectory tracking, obstacle avoidance, and target approach. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2858–2863. [Google Scholar]
- Ding, Z.; Liu, J.; Chi, W.; Wang, J.; Chen, G.; Sun, L. PRTIRL based socially adaptive path planning for mobile robots. Int. J. Soc. Robot. 2023, 15, 129–142. [Google Scholar] [CrossRef]
- Zhou, Y.; Tuzel, O. Voxelnet: End-to-end learning for point cloud based 3D object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 19–23 June 2018; pp. 4490–4499. [Google Scholar]
- Ren, W.; Wang, X.; Tian, J.; Tang, Y.; Chan, A.B. Tracking-by-counting: Using network flows on crowd density maps for tracking multiple targets. IEEE Trans. Image Process. 2020, 30, 1439–1452. [Google Scholar] [CrossRef]
- Li, C.; Guo, S.; Guo, J. Study on obstacle avoidance strategy using multiple ultrasonic sensors for spherical underwater robots. IEEE Sens. J. 2022, 22, 24458–24470. [Google Scholar] [CrossRef]
- Jha, B.; Turetsky, V.; Shima, T. Robust path tracking by a Dubins ground vehicle. IEEE Trans. Control Syst. Technol. 2018, 27, 2614–2621. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, X.; Zhou, Q.; Tian, Y. A model predictive controller with switched tracking error for autonomous vehicle path tracking. IEEE Access 2019, 7, 53103–53114. [Google Scholar] [CrossRef]
- Qu, P.; Li, S.; Zhang, J.; Duan, Z.; Mei, K. A Low-cost and Robust Mapping and Relocalization Method Base on Lidar Inertial Odometry. In Proceedings of the 2021 IEEE International Conference on Real-time Computing and Robotics (RCAR), Xining, China, 15–19 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 257–262. [Google Scholar]
- Wang, E.; Chen, D.; Fu, T.; Ma, L. A Robot Relocalization Method Based on Laser and Visual Features. In Proceedings of the 2022 IEEE 11th Data Driven Control and Learning Systems Conference (DDCLS), Chengdu, China, 3–5 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 519–524. [Google Scholar]
- Chen, X.; Vizzo, I.; Läbe, T.; Behley, J.; Stachniss, C. Range image-based LiDAR localization for autonomous vehicles. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xian, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 5802–5808. [Google Scholar]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter. 1995. Available online: https://perso.crans.org/club-krobot/doc/kalman.pdf (accessed on 20 April 2024).
- Huang, Y.; Ding, H.; Zhang, Y.; Wang, H.; Cao, D.; Xu, N.; Hu, C. A motion planning and tracking framework for autonomous vehicles based on artificial potential field elaborated resistance network approach. IEEE Trans. Ind. Electron. 2019, 67, 1376–1386. [Google Scholar] [CrossRef]
- Fiorini, P.; Shiller, Z. Motion planning in dynamic environments using velocity obstacles. Int. J. Robot. Res. 1998, 17, 760–772. [Google Scholar] [CrossRef]
- Bharath, G.; Singh, A.; Kaushik, M.; Krishna, K.; Manocha, D. Prvo: Probabilistic reciprocal velocity obstacle for multi robot navigation under uncertainty. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 24–28. [Google Scholar]
- Van den Berg, J.; Lin, M.; Manocha, D. Reciprocal velocity obstacles for real-time multi-agent navigation. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1928–1935. [Google Scholar]
- Guo, K.; Wang, D.; Fan, T.; Pan, J. VR-ORCA: Variable responsibility optimal reciprocal collision avoidance. IEEE Robot. Autom. Lett. 2021, 6, 4520–4527. [Google Scholar] [CrossRef]
- Guo, B.; Guo, N.; Cen, Z. Obstacle avoidance with dynamic avoidance risk region for mobile robots in dynamic environments. IEEE Robot. Autom. Lett. 2022, 7, 5850–5857. [Google Scholar] [CrossRef]
- Reddy, A.K.; Malviya, V.; Kala, R. Social cues in the autonomous navigation of indoor mobile robots. Int. J. Soc. Robot. 2021, 13, 1335–1358. [Google Scholar] [CrossRef]
- Smith, T.; Chen, Y.; Hewitt, N.; Hu, B.; Gu, Y. Socially aware robot obstacle avoidance considering human intention and preferences. Int. J. Soc. Robot. 2021, 15, 661–678. [Google Scholar] [CrossRef]
- Chen, C.S.; Lin, S.Y. Costmap generation based on dynamic obstacle detection and velocity obstacle estimation for autonomous mobile robot. In Proceedings of the 2021 21st International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 12–15 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1963–1968. [Google Scholar]
- Lu, D.V.; Hershberger, D.; Smart, W.D. Layered costmaps for context-sensitive navigation. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 709–715. [Google Scholar]
- Wojke, N.; Bewley, A.; Paulus, D. Simple online and realtime tracking with a deep association metric. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3645–3649. [Google Scholar]
- Dong, H.; Weng, C.Y.; Guo, C.; Yu, H.; Chen, I.M. Real-time avoidance strategy of dynamic obstacles via half model-free detection and tracking with 2d lidar for mobile robots. IEEE/ASME Trans. Mechatronics 2020, 26, 2215–2225. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.; Li, C.; Song, R.; Li, Y.; Meng, M.Q.H. Chase and track: Toward safe and smooth trajectory planning for robotic navigation in dynamic environments. IEEE Trans. Ind. Electron. 2022, 70, 604–613. [Google Scholar] [CrossRef]









| Pedestrian Velocity | TEB | Ours |
|---|---|---|
| 0.8 m/s | 2.998 m | 3.110 m |
| 1.0 m/s | 2.732 m | 4.618 m |
| 1.2 m/s | 2.258 m | 5.180 m |
| Algorithm | Success | Running Distance | Time |
|---|---|---|---|
| TEB local planner | 75% | 18.61 m | 21.81 s |
| MPC local planner | 80% | 17.54 m | 21.62 s |
| State lattice | 90% | 16.33 m | 18.82 s |
| Ours | 95% | 15.03 m | 16.82 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, X.; You, Z.; He, X. Local Path Planner for Mobile Robot Considering Future Positions of Obstacles. Processes 2024, 12, 984. https://doi.org/10.3390/pr12050984
Ou X, You Z, He X. Local Path Planner for Mobile Robot Considering Future Positions of Obstacles. Processes. 2024; 12(5):984. https://doi.org/10.3390/pr12050984
Chicago/Turabian StyleOu, Xianhua, Zhongnan You, and Xiongxiong He. 2024. "Local Path Planner for Mobile Robot Considering Future Positions of Obstacles" Processes 12, no. 5: 984. https://doi.org/10.3390/pr12050984
APA StyleOu, X., You, Z., & He, X. (2024). Local Path Planner for Mobile Robot Considering Future Positions of Obstacles. Processes, 12(5), 984. https://doi.org/10.3390/pr12050984







