Research of the Influence of Lateral Inflow Angles on the Cavitation Flow and Movement Characteristics of Underwater Moving Objects
Abstract
1. Introduction
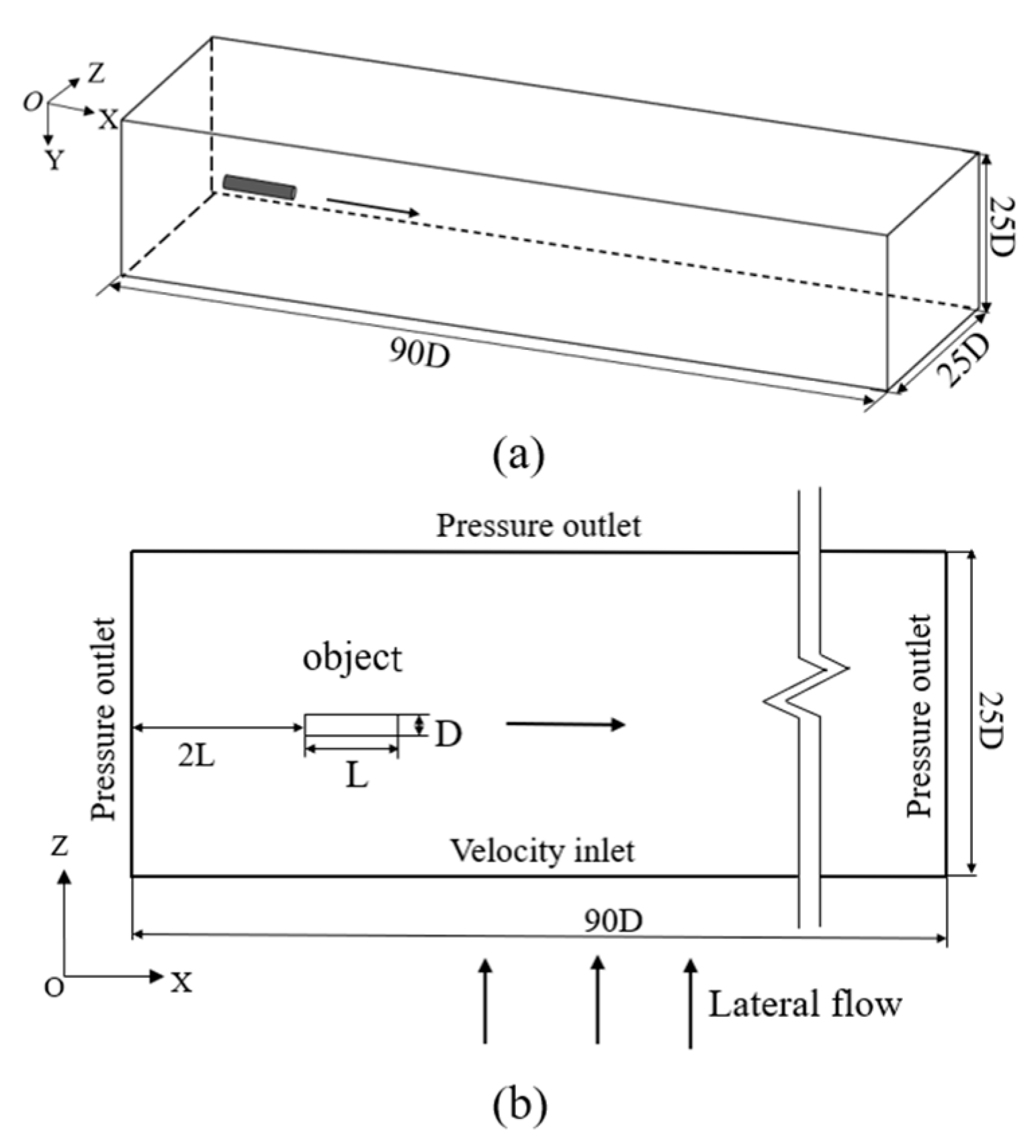
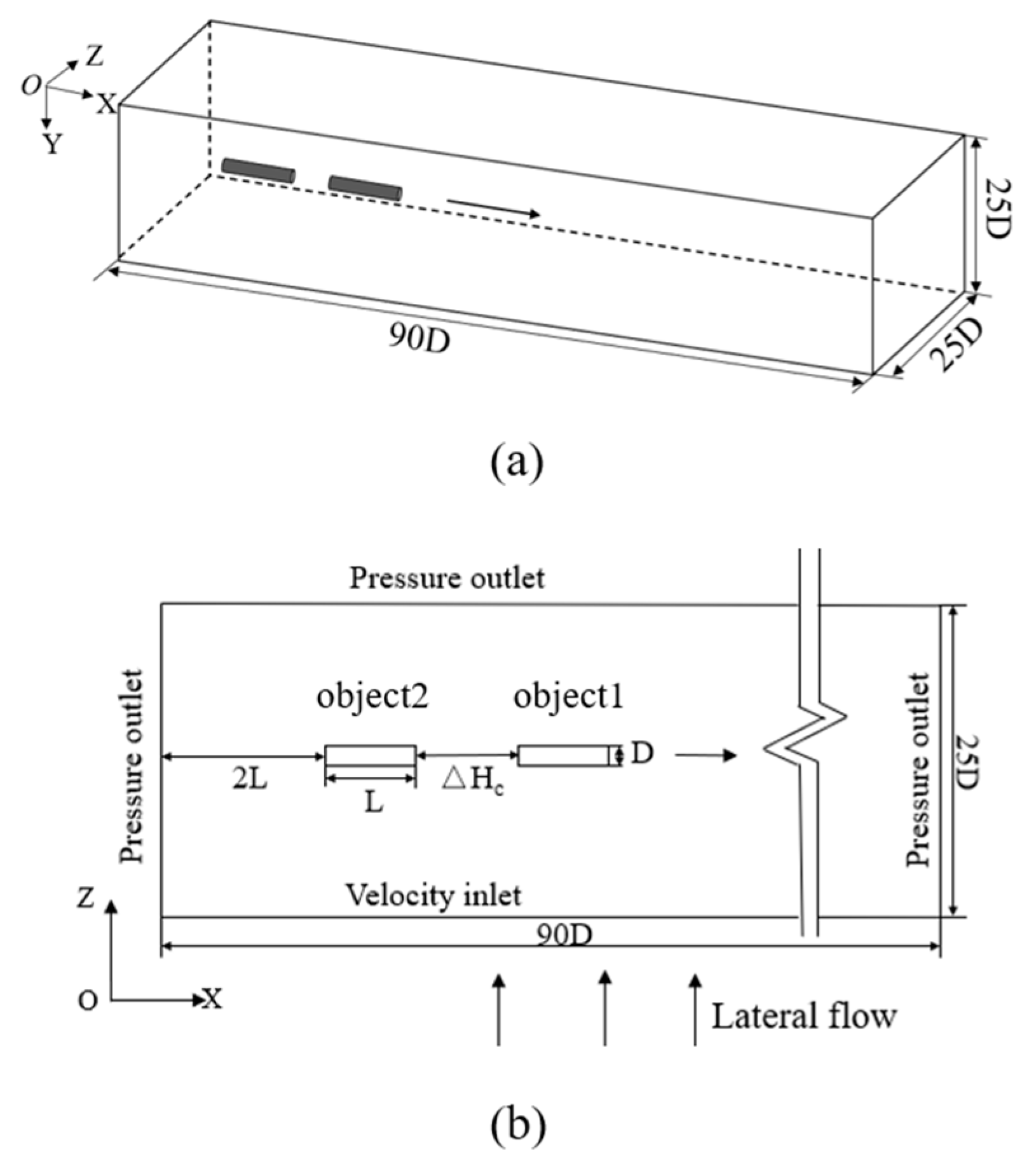
2. Governing Equations and Numerical Methods
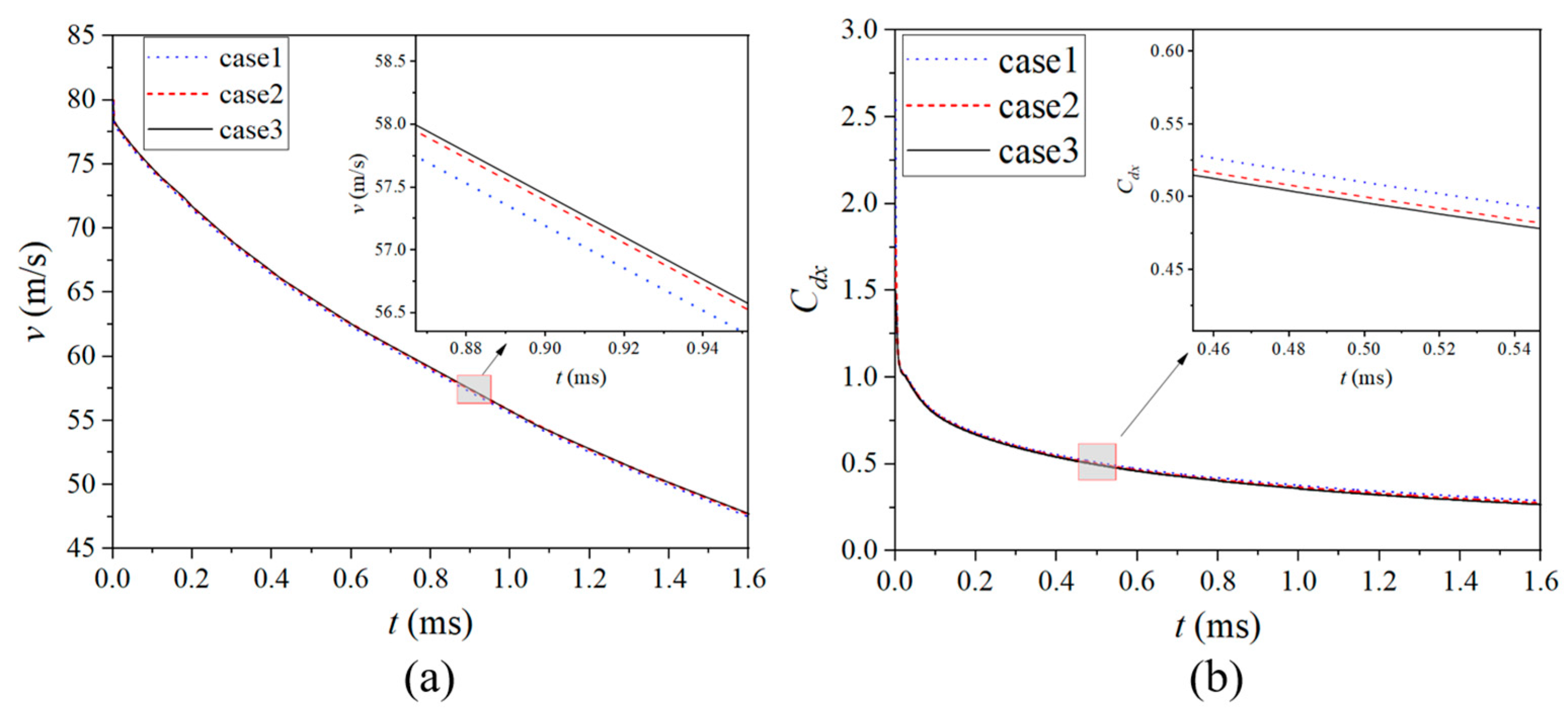
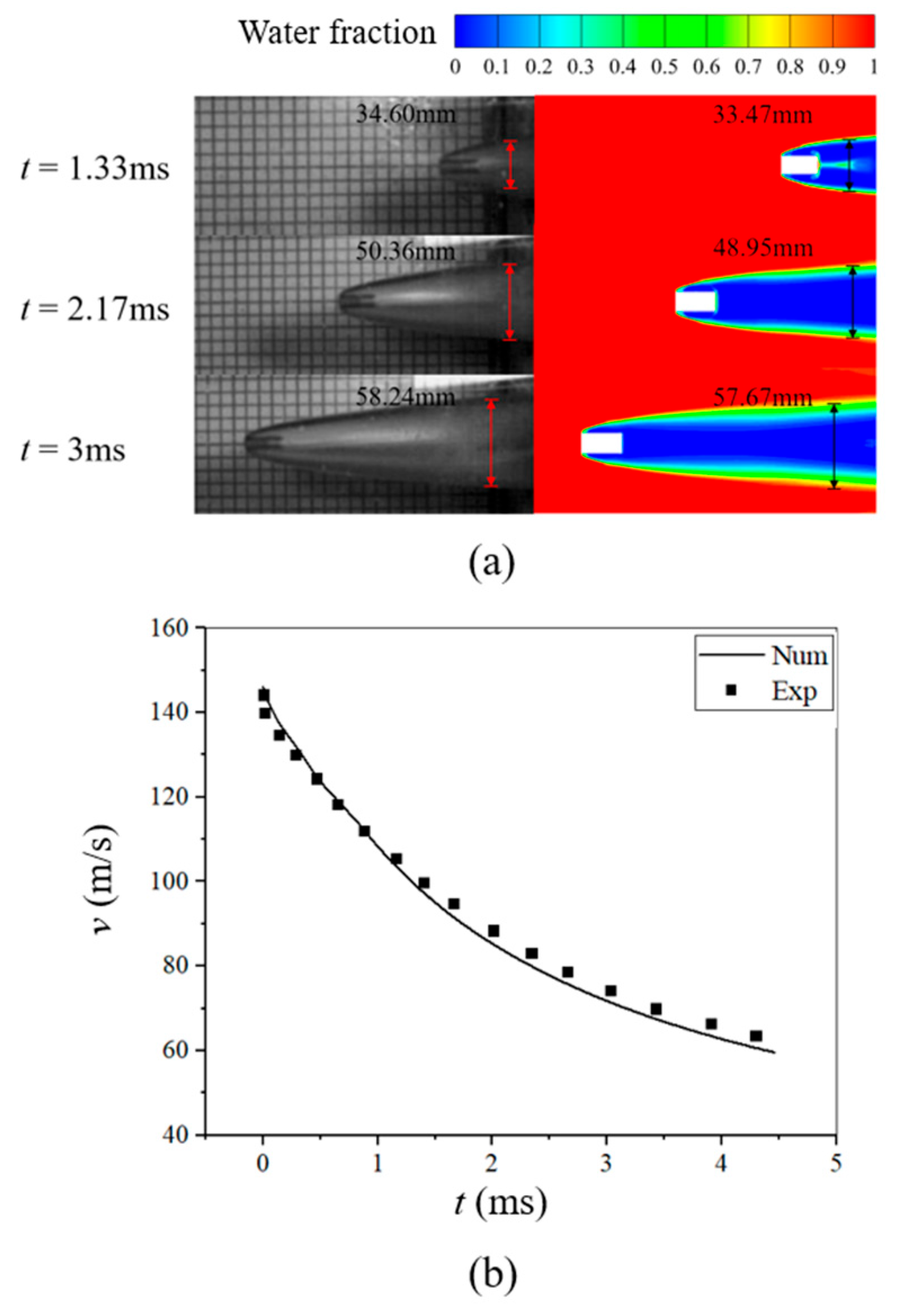
3. Verification of Mesh Independence and Numerical Models
4. Results and Discussion
4.1. Effect of the Lateral Flow on a Single Object
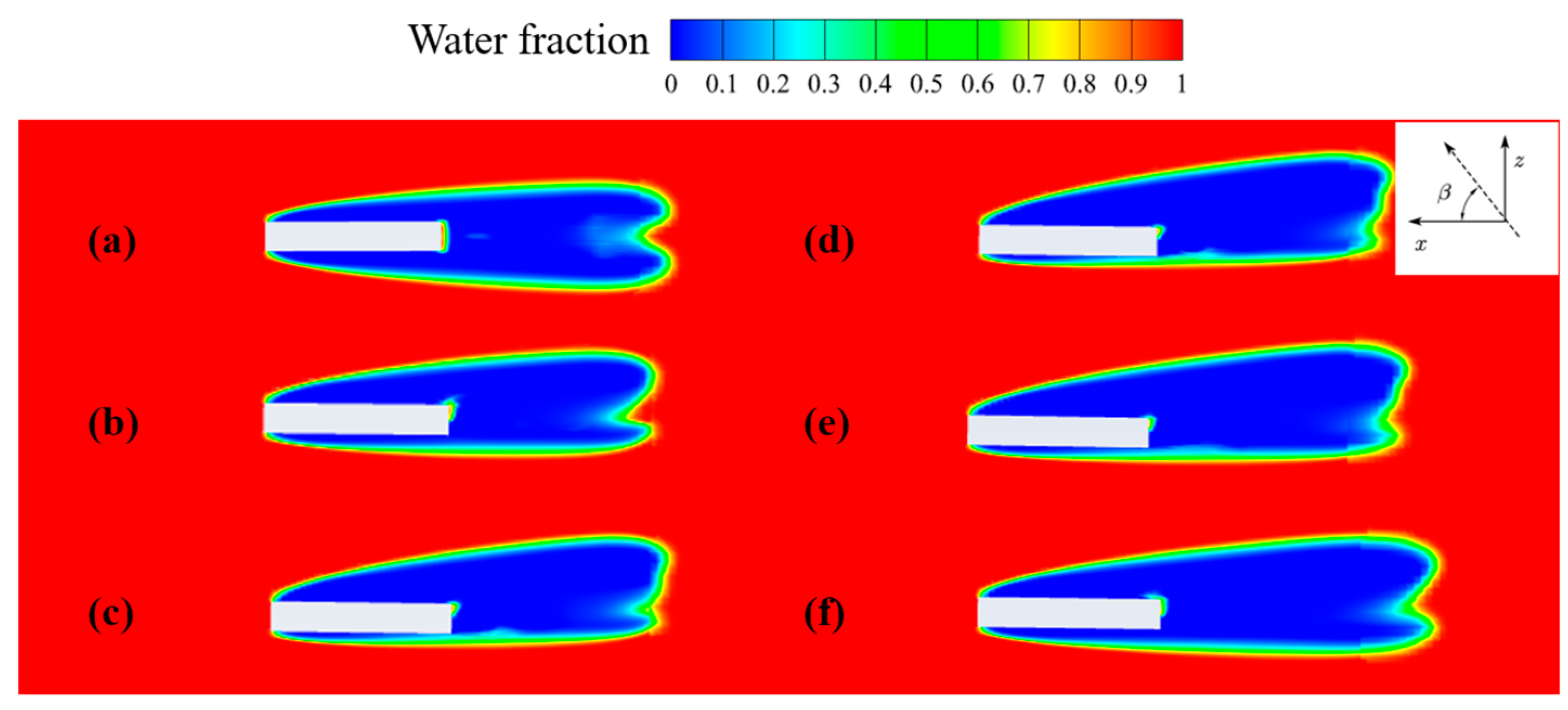
4.1.1. Effect on the Supercavitation Profile and the Size of a Single Object
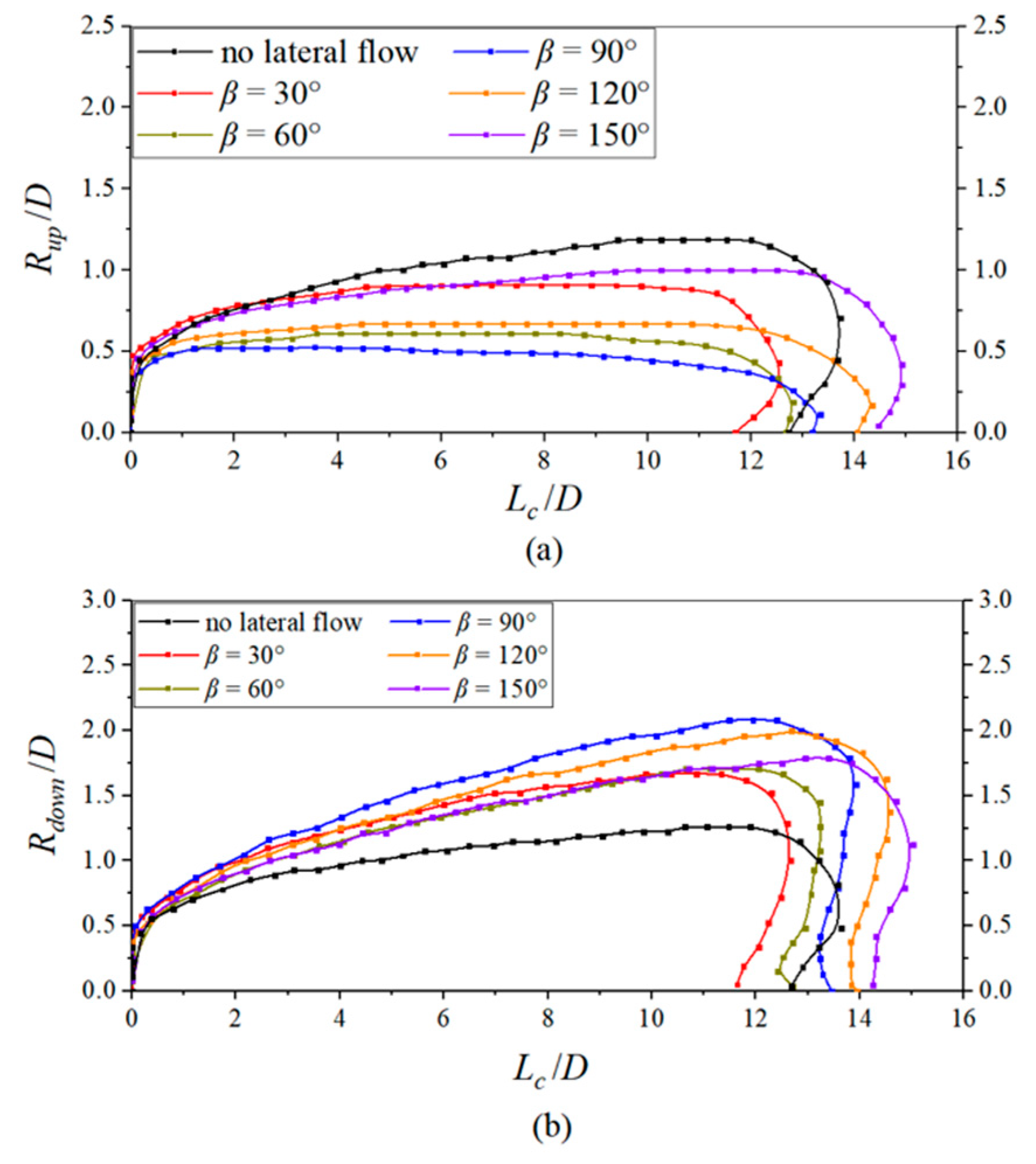
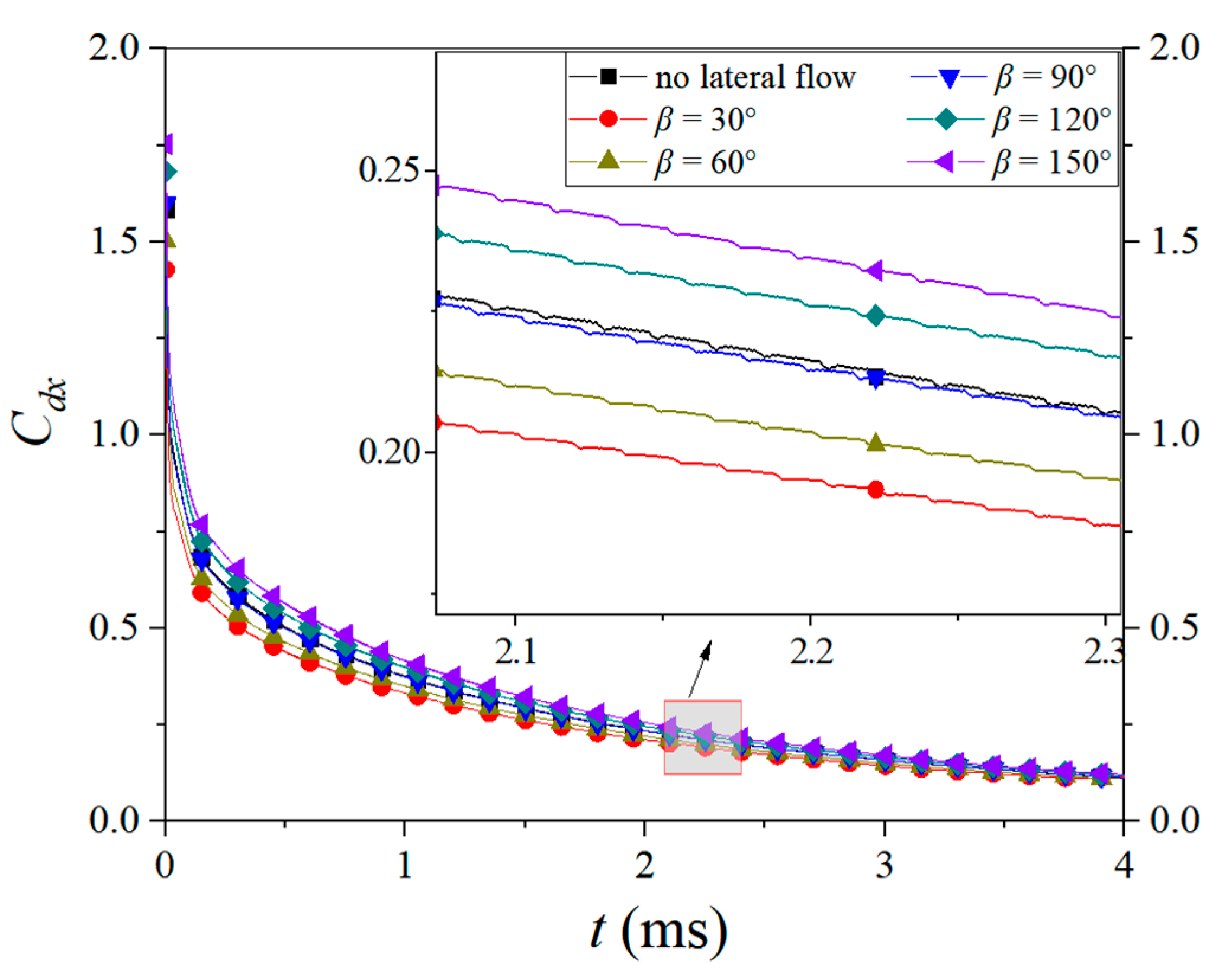
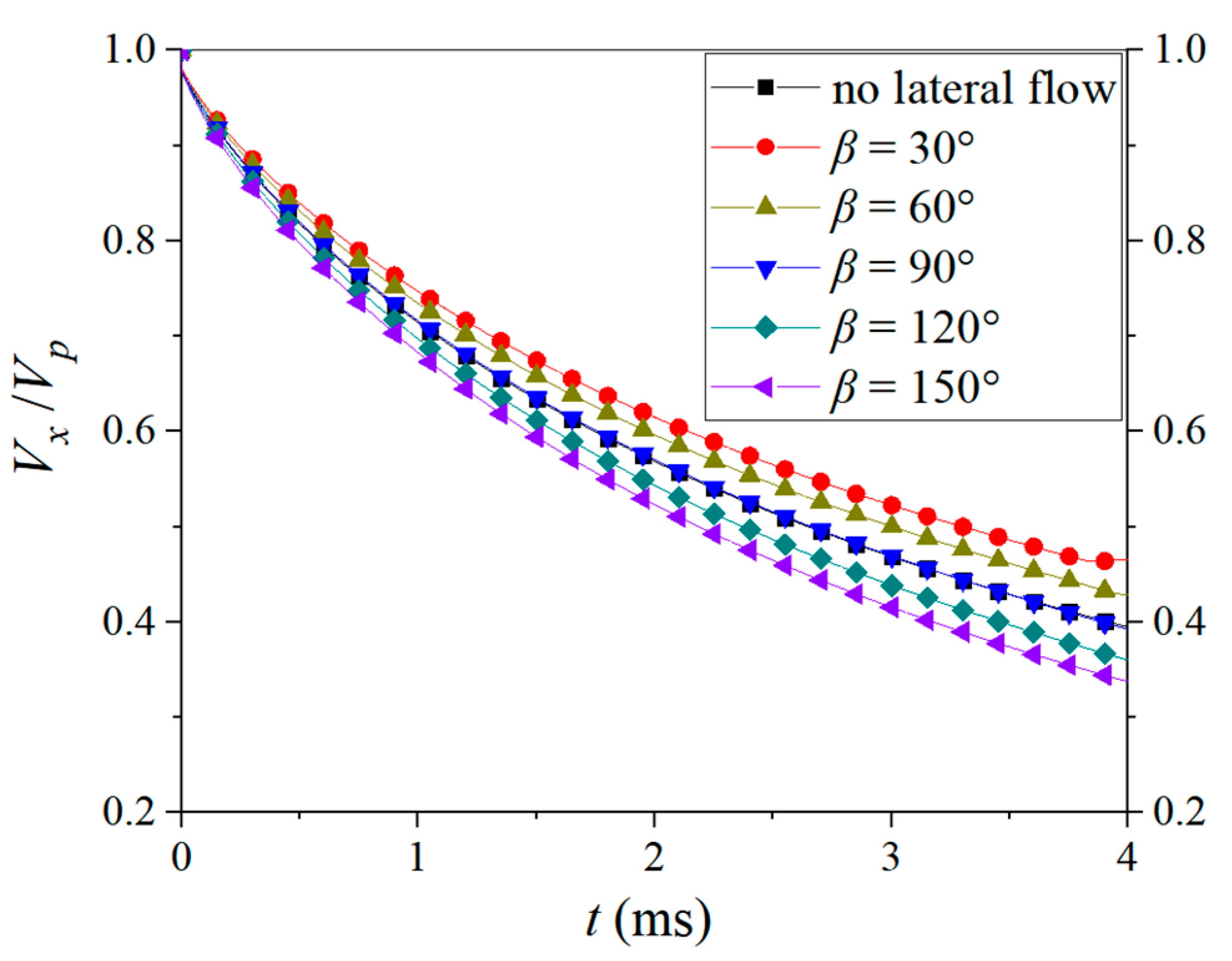
4.1.2. Effect on the Hydrodynamic Characteristics and Trajectory of a Single Object
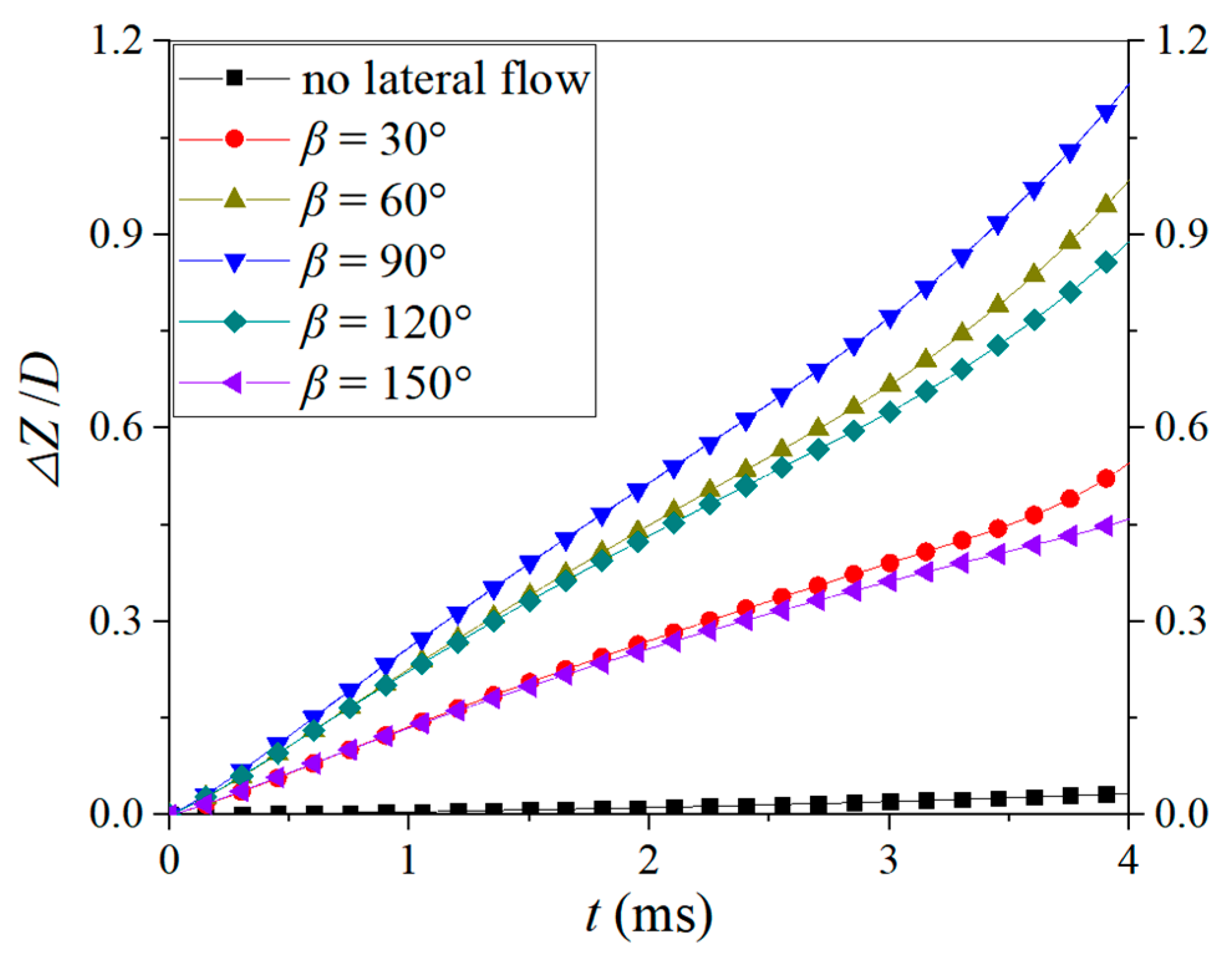
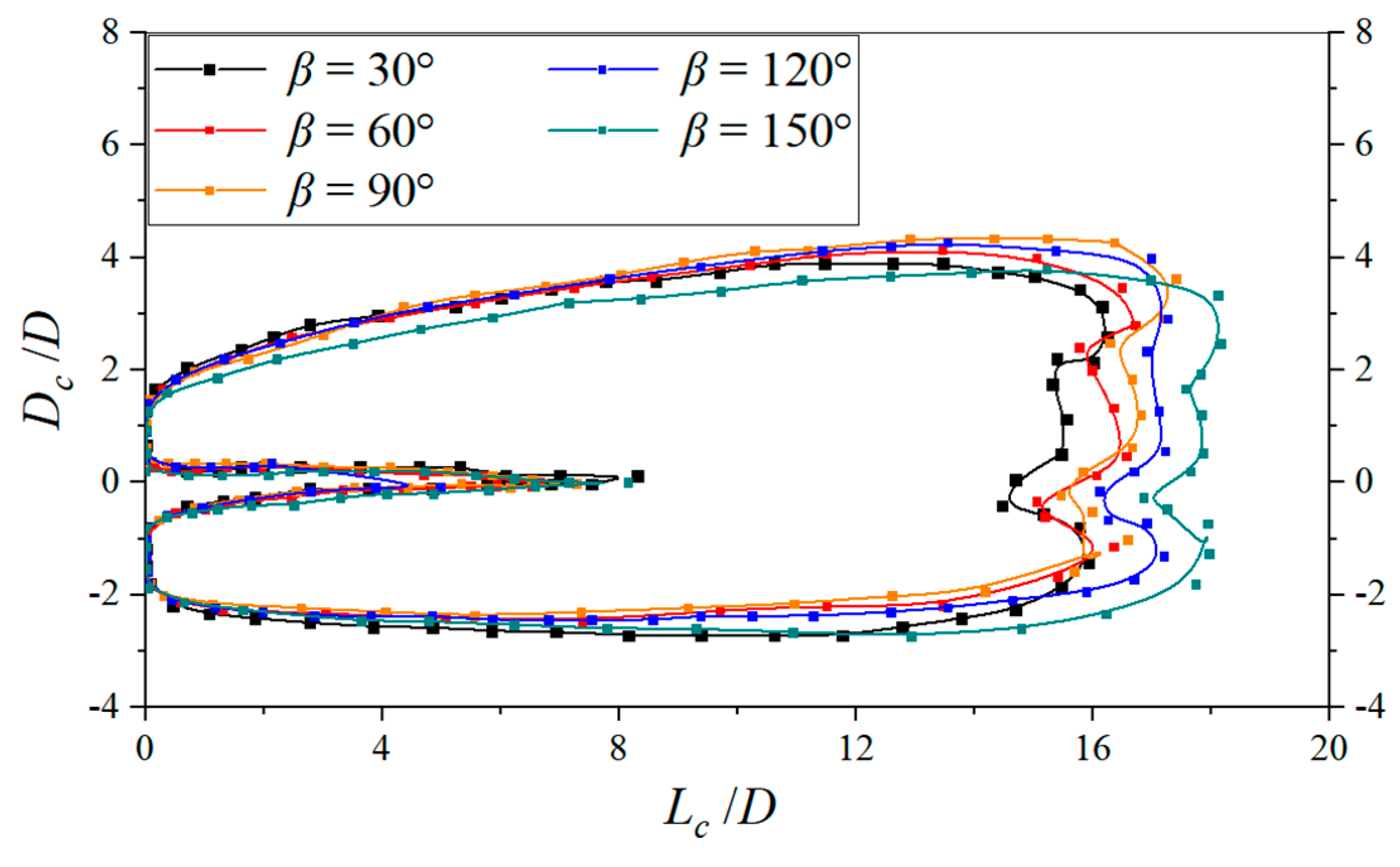
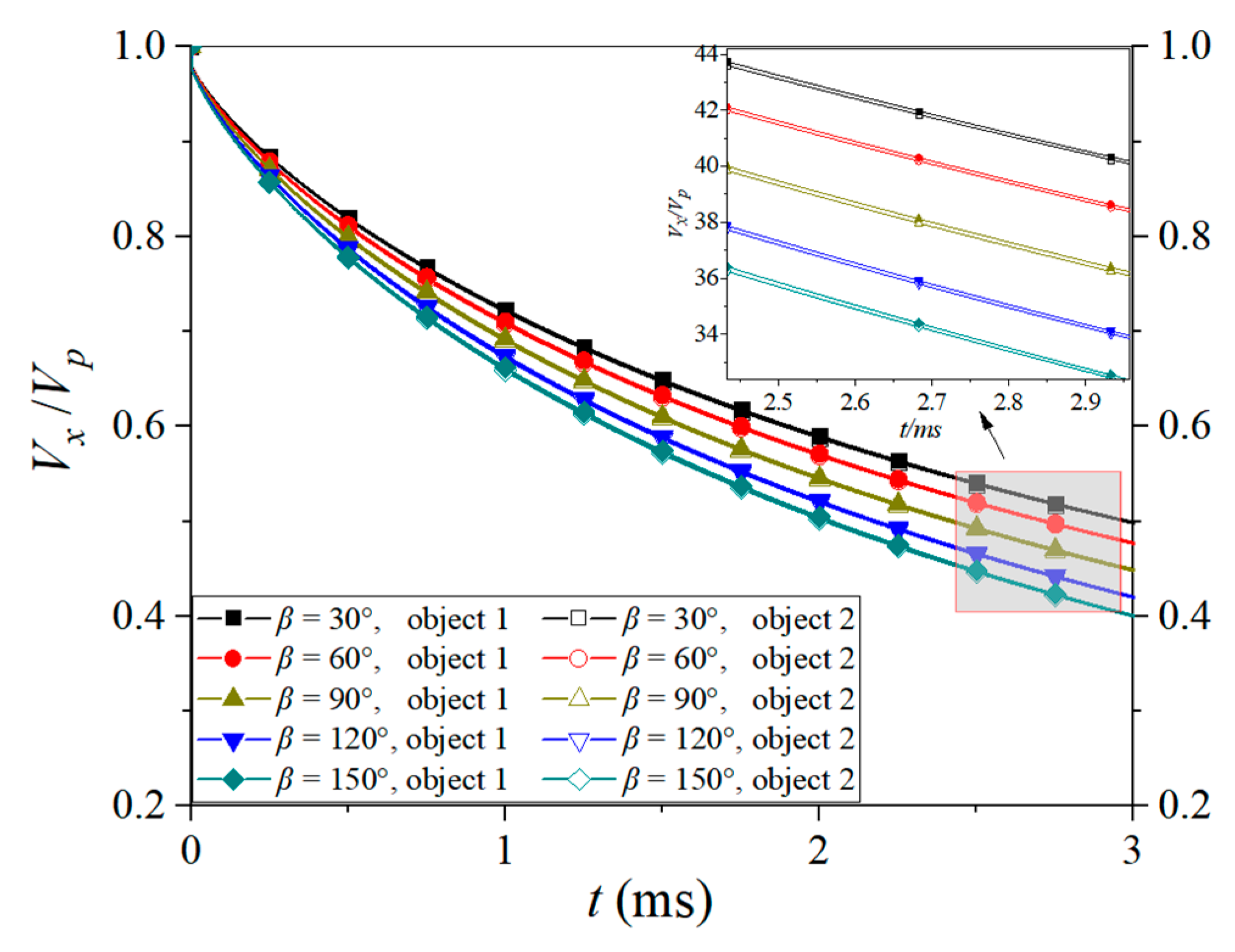
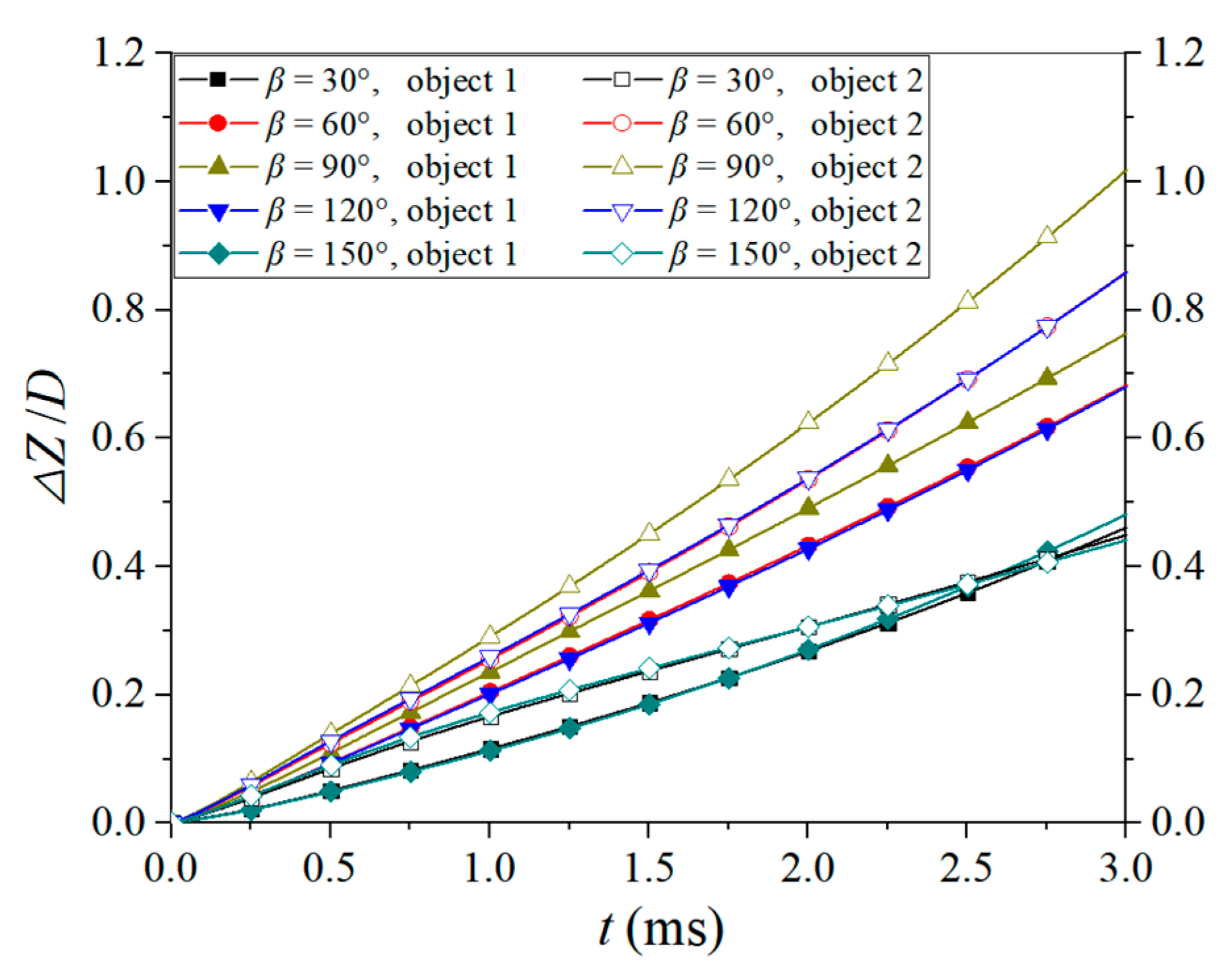
4.2. Effect of Lateral Inflow Angle on Parallel Objects
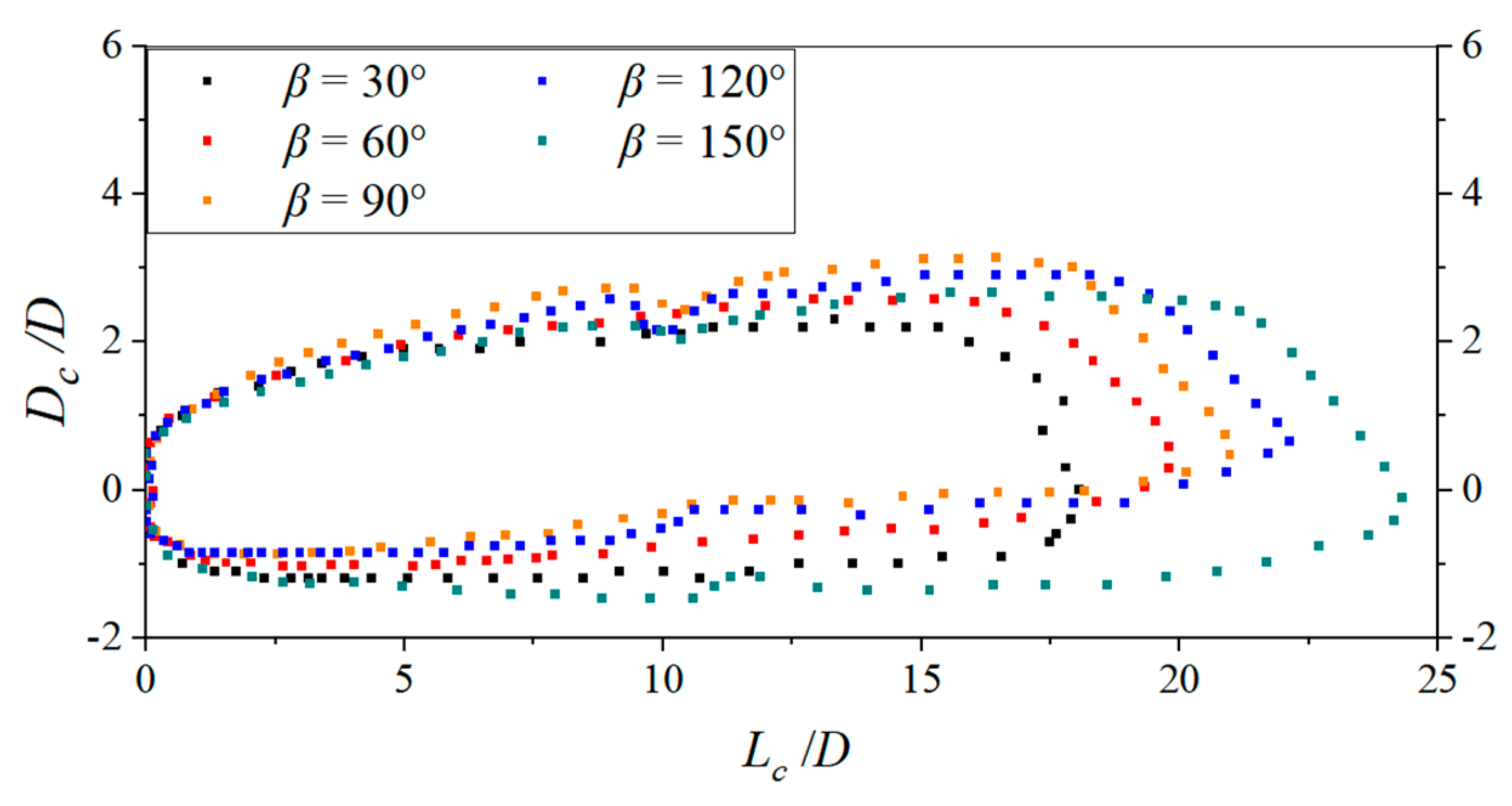
4.2.1. Effect on the Supercavitation Profile and Size of Parallel Objects
4.2.2. Effect on the Hydrodynamic Characteristics and Trajectories of Parallel Objects
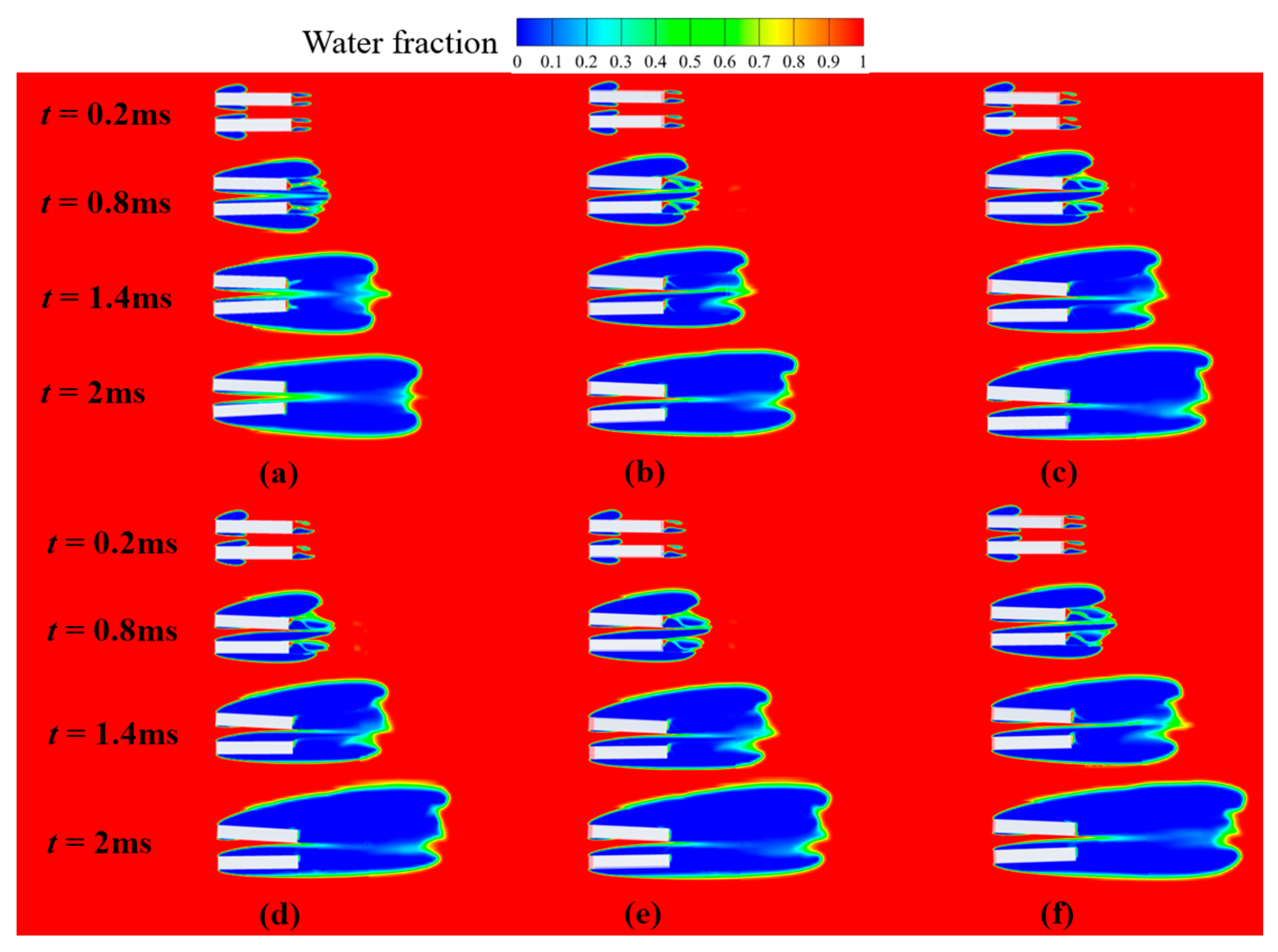
4.3. Effect of Lateral Inflow Angles on Tandem Objects
4.3.1. Effect on the Supercavitation Profile and Size of Tandem Objects
4.3.2. Effect on the Hydrodynamic Characteristics and Trajectories of Series Objects
5. Conclusions
- (1)
- The cavitation profile exhibits asymmetry because of the effect of the lateral flow. As the z-component of the lateral flow increases, the cavity profile’s asymmetry also increases. The cavity length is related to the relative axial speed between the object(s) and the water.
- (2)
- In the investigated cases for the parallel objects, the cavity profile is determined by the superimposed influence of the lateral flow and the nearby object. For object 1, the influence of the lateral flow and the nearby object is opposite in the inner zone, and thus the cavity asymmetry is weakened. However, the influence of the lateral flow and the nearby object is superimposed on the incoming side of object 2, and the cavity asymmetry is enhanced. Compared to object 2, the trajectory stability of object 1 is better. As the lateral incoming angle increases, the decay rate of the axial speed for the two objects decreases.
- (3)
- For the series objects, the supercavity length increases as the lateral incoming angle increases after object 2 enters the front cavity. As the z-component of the lateral flow velocity increases, the deviation speed increases. During the process of object 2 entering the front cavity, the increase in the deviation speed is obvious.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ceccio, S.L. Friction drag reduction of external flows with bubble and gas injection. Annu. Rev. Fluid Mech. 2010, 42, 183–203. [Google Scholar] [CrossRef]
- Logvinovich, G.V. Hydrodynamics of Free-Boundary Flows (Gidrodinamika Techenii so Svobodnymigranitsami); IPST Press: Jersualem, Israel, 1972. [Google Scholar]
- Vasin, A.D. The Principle of Independence of the Cavity Sections Expansion (Principle of Logvinovich) as the Basis for Investigation on Cavitation Flows; National Tax Association—Tax Institute of America: Washington DC, USA, 2001. [Google Scholar]
- Aristoff, J.M.; Bush, J.W.M. Water entry of small hydrophobic spheres. J. Fluid Mech. 2009, 619, 45–78. [Google Scholar] [CrossRef]
- Savchenko, Y.N.; Vlasenko, Y.D.; Semenenko, V.N. Experimental studies of high-speed cavitated flows. Int. J. Fluid Mech. Res. 1999, 26, 365–374. [Google Scholar] [CrossRef]
- Hrubes, J.D. High-speed imaging of supercavitating underwater projectiles. Exp. Fluids 2001, 30, 57–64. [Google Scholar] [CrossRef]
- Burkin, V.; Akinshin, R.N.; Afanaseva, S.A.; Borisenkov, I.L.; Ishchenko, A.N.; Khabibullin, M.V.; Chupashev, A.V.; Yugov, N.T. Features of high-velocity penetration and motion of supercavitating kinetic strikers in water. J. Eng. Phys. Thermophys. 2018, 91, 655–662. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Vu, D.T.; Park, W.G.; Jung, C.M. Navier–stokes solver for water entry bodies with moving chimera grid method in 6dof motions. Comput. Fluids 2016, 140, 19–38. [Google Scholar] [CrossRef]
- Zhang, Q.; Zong, Z.; Sun, T.Z.; Chen, Z.; Li, H.T. Experimental study of the evolution of water-entry cavity bubbles behind a hydrophobic sphere. Phys. Fluids 2020, 32, 062109. [Google Scholar] [CrossRef]
- Güzel, B.; Korkmaz, F.C. Experimental investigation of water entry of bodies with constant deadrise angles under hydrophobic effects. Exp. Fluids 2021, 62, 107–128. [Google Scholar] [CrossRef]
- Watson, D.A.; Bom, J.M.; Weinberg, M.P.; Souchik, C.J.; Dickerson, A.K. Water entry dynamics of spheres with heterogeneous wetting properties. Phys. Rev. Fluids 2021, 6, 044003. [Google Scholar] [CrossRef]
- Jia, H.; Xie, R.; Zhou, Y. Experimental investigation of the supercavitation and hydrodynamic characteristics of high-speed projectiles with hydrophobic and hydrophilic coatings. Fluids 2022, 7, 363. [Google Scholar] [CrossRef]
- Yun, H.; Lyu, X.; Wei, Z. Experimental study on oblique water entry of two tandem spheres with collision effect. J. Vis. 2020, 23, 49–59. [Google Scholar] [CrossRef]
- Mnasri, C.; Hafsia, Z.; Omri, M.; Maalel, K. A moving grid model for simulation of free surface behavior induced by horizontal cylinders exit and entry. Eng. Appl. Comput. Fluid Mech. 2010, 4, 260–275. [Google Scholar] [CrossRef][Green Version]
- Lu, L.; Yan, X.; Li, Q.; Wang, C.; Shen, K.C. Numerical study on the water-entry of asynchronous parallel projectiles at a high vertical entry speed. Ocean Eng. 2022, 250, 111026. [Google Scholar] [CrossRef]
- Xu, H.; Wei, Y.; Wang, C.; Lu, J. On wake vortex encounter of axial-symmetric projectiles launched successively underwater. Ocean Eng. 2019, 189, 106382. [Google Scholar] [CrossRef]
- Ishchenko, A.N.; Afanaseva, S.A.; Burkin, V.; Dyachkovskii, A.S.; Chupashev, A.V. Studying the mutual influence of a set of strikers during simultaneous high-velocity entry into water. Tech. Phys. Lett. 2019, 45, 1059–1062. [Google Scholar] [CrossRef]
- Yun, H.; Lyu, X.; Wei, Z. Experimental study on vertical water entry of two tandem spheres. Ocean Eng. 2020, 201, 107143. [Google Scholar] [CrossRef]
- Zhou, D.; Shi, H.; Jia, H. Characteristics of the multiphase flow field with super-cavitation induced by successively fired projectiles under-water and cross-medium. J. Mech. Sci. Technol. 2022, 36, 247–258. [Google Scholar] [CrossRef]
- Qi, C.; Wang, X.; Lyu, X. On the flow characteristics of two supercavitating projectiles moving in water side-by-side. Phys. Fluids 2023, 35, 017127. [Google Scholar] [CrossRef]
- Yu, D.; Wang, C.; He, C. Numerical simulation of cavitation and motion characteristics during parallel water entry of rotating bodies. J. Harbin Inst. Technol. 2021, 53, 23–32. [Google Scholar]
- Wang, M.; Fan, C.; Hou, G. Numerical research of lateral flow influence on supercavitating flow. AIP Adv. 2022, 12, 045214. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, C.; Jia, H.; Dong, R.L. Effects of lateral flows on the super- cavitation and hydrodynamic characteristics of underwater series and parallel high-speed projectiles. J. Mar. Sci. Eng. 2023, 11, 878. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, Z. Numerical simulation of cavitation around a hydrofoil and evaluation of a rng k-ε model. J. Fluids Eng. Trans. Asme 2008, 130, 011302. [Google Scholar] [CrossRef]
- Schnerr, G.H.; Sauer, J. Physical and numerical modeling of unsteady cavitation dynamics. In Fourth International Conference on Multiphase Flow; ICMF New Orleans: New Orleans, LO, USA, 2001; Volume 1. [Google Scholar]
- Patankar, S. Numerical Heat Transfer and Fluid Flow, 1st ed.; CRC Press: Washington, DC, USA, 1980. [Google Scholar]
- Muzaferija, S.; Peric, M.; Sames, P.C.; Schellin, T.E. A two-fluid navier-stokes solver to simulate water entry. In Symposium on Naval Hydrodynamics; National Academy Press: Washington, DC, USA, 1988; pp. 277–289. [Google Scholar]
- Guo, Z.; Zhang, W.; Xiao, X.; Wei, G.; Ren, P. An investigation into horizontal water entry behaviors of projectiles with different nose shapes. Int. J. Impact Eng. 2012, 49, 43–60. [Google Scholar] [CrossRef]













Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, R.; Jia, H.; Chen, J.; Zhang, L.; Zhang, C. Research of the Influence of Lateral Inflow Angles on the Cavitation Flow and Movement Characteristics of Underwater Moving Objects. Processes 2024, 12, 1051. https://doi.org/10.3390/pr12061051
Xie R, Jia H, Chen J, Zhang L, Zhang C. Research of the Influence of Lateral Inflow Angles on the Cavitation Flow and Movement Characteristics of Underwater Moving Objects. Processes. 2024; 12(6):1051. https://doi.org/10.3390/pr12061051
Chicago/Turabian StyleXie, Rishan, Huixia Jia, Jiawei Chen, Lite Zhang, and Chengwei Zhang. 2024. "Research of the Influence of Lateral Inflow Angles on the Cavitation Flow and Movement Characteristics of Underwater Moving Objects" Processes 12, no. 6: 1051. https://doi.org/10.3390/pr12061051
APA StyleXie, R., Jia, H., Chen, J., Zhang, L., & Zhang, C. (2024). Research of the Influence of Lateral Inflow Angles on the Cavitation Flow and Movement Characteristics of Underwater Moving Objects. Processes, 12(6), 1051. https://doi.org/10.3390/pr12061051




