Recent Progress in Design and Performance Analysis of Vertical-Axis Wind Turbines—A Comprehensive Review
Abstract
1. Introduction
- A comprehensive examination of numerous operational parameters is conducted to gain an enhanced understanding of how these parameters influence turbine efficiency.
- Unlike existing work, this study covers the geographical aspects of wind power harvesting, such as proper site siting and the flow dynamic effects over various terrains and flow structures in wind power applications.
- The present review offers a wider range of VAWT designs by focusing on the most recent developments in VAWT design, which are the Darrieus and Savonius rotors, as most of the existing works focus on only a single VAWT design and/or narrowly focus on too specific performance parameters.
2. Fundamental Physical Principle of VAWTs
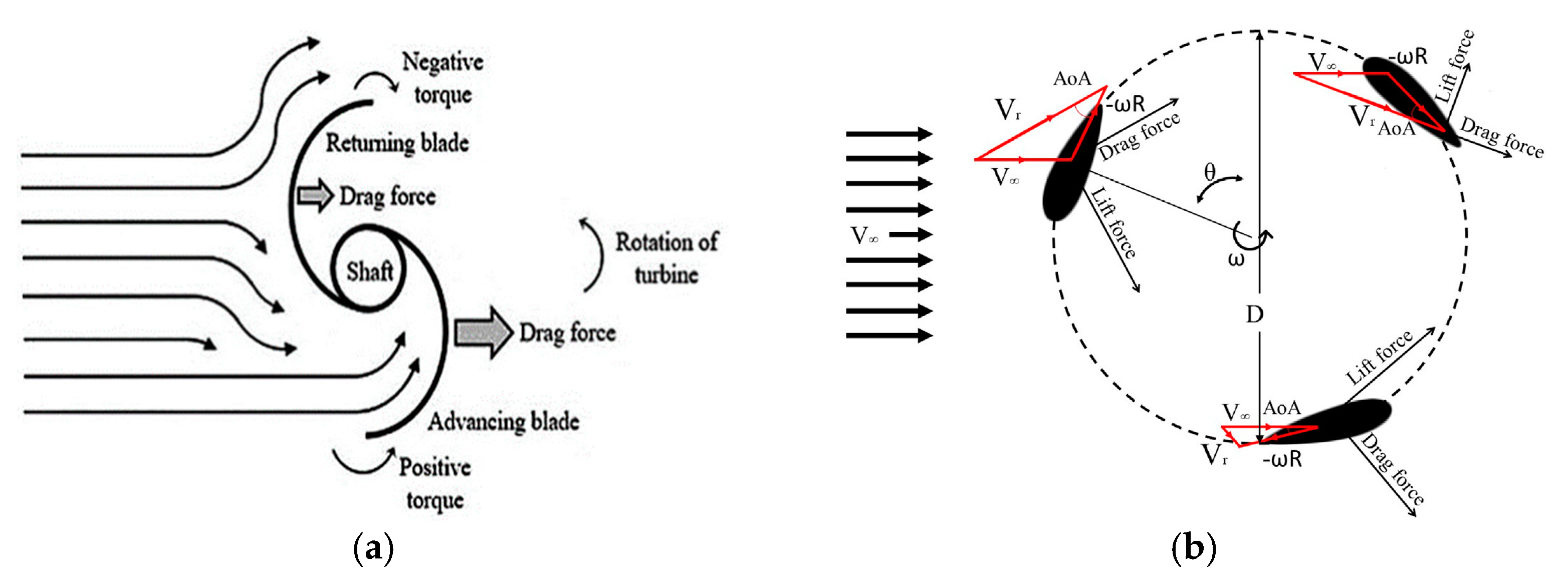
Performance Parameters of VAWTs
3. Mechanism of Wind Power Harvesting: Active Techniques
3.1. Counter-Rotating Technique
3.2. Design Parameters Affecting the Performance of VAWTs
3.2.1. Aspect Ratio (AR) Effect
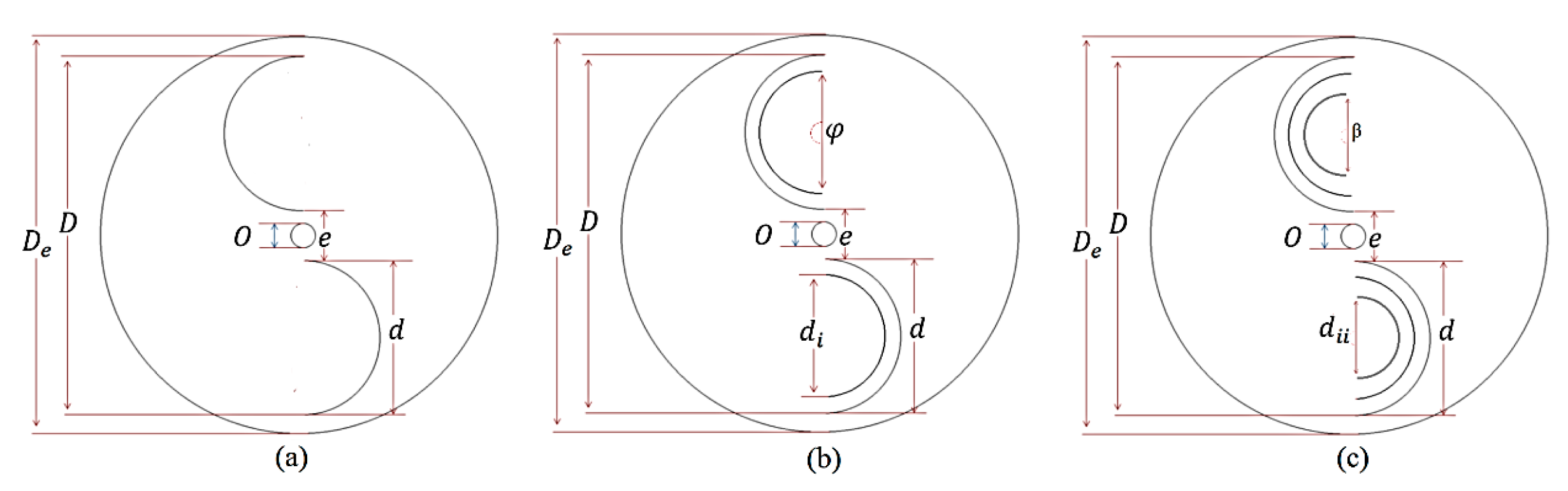
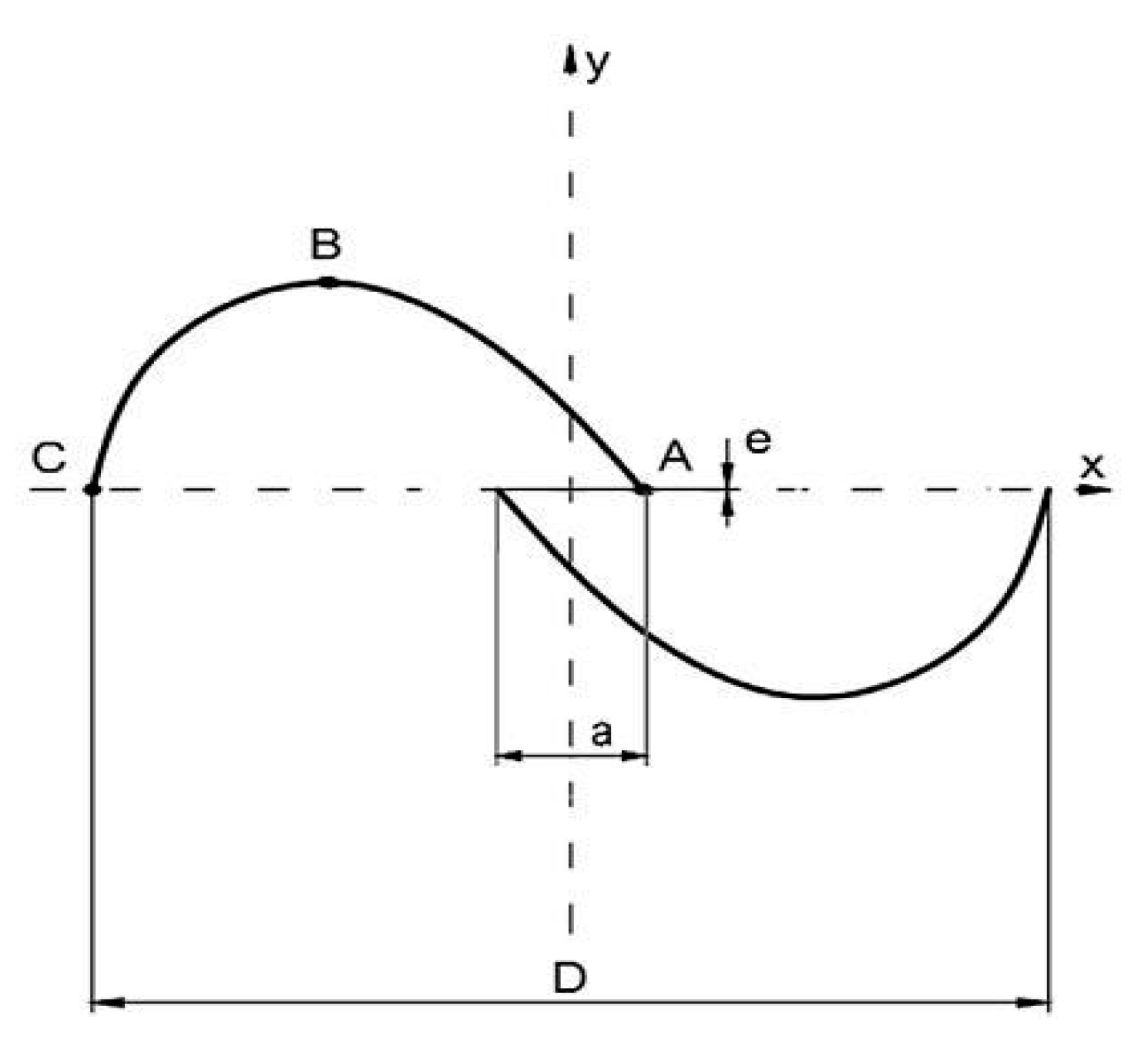
3.2.2. Overlap Ratio Effect
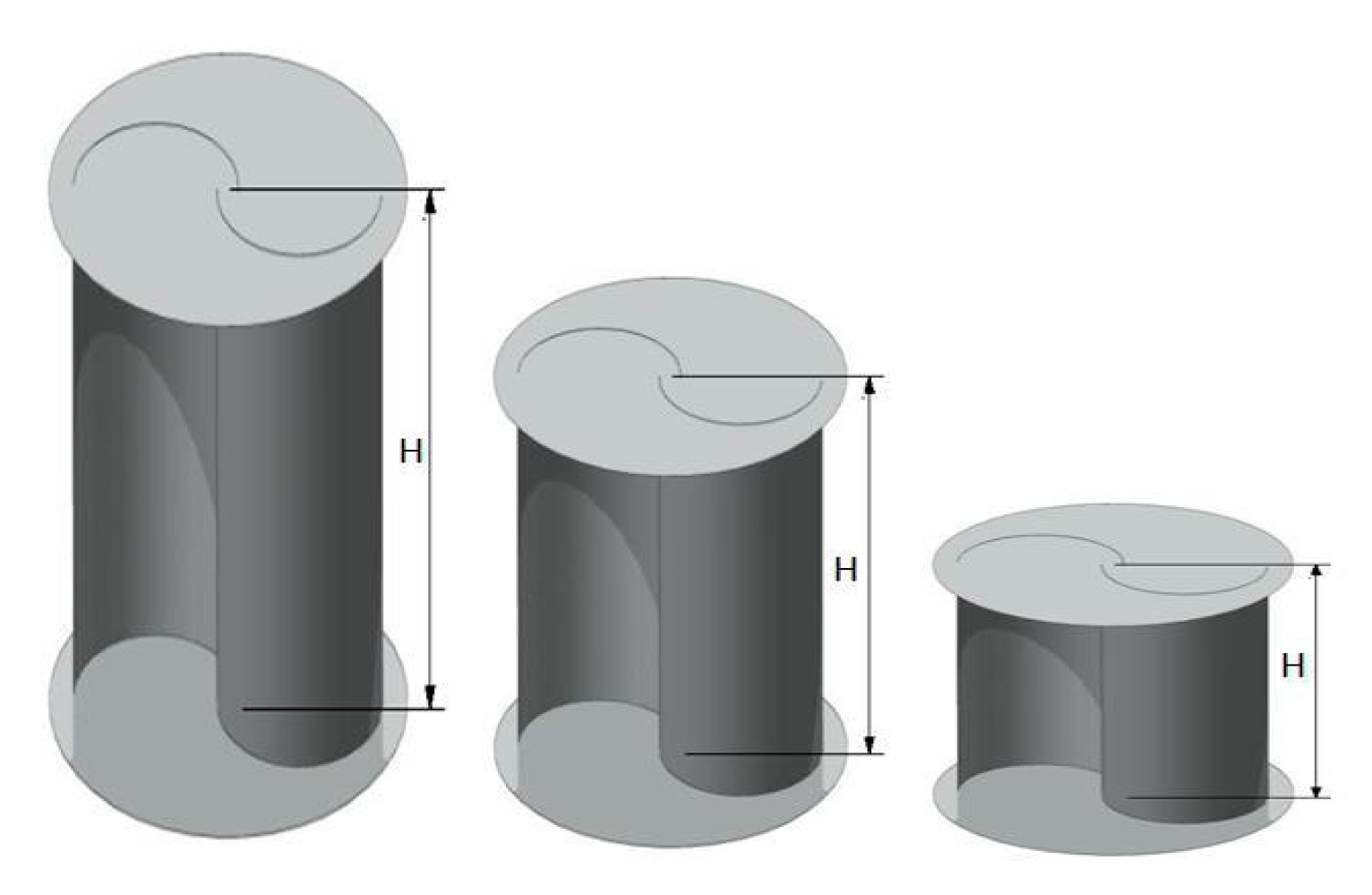
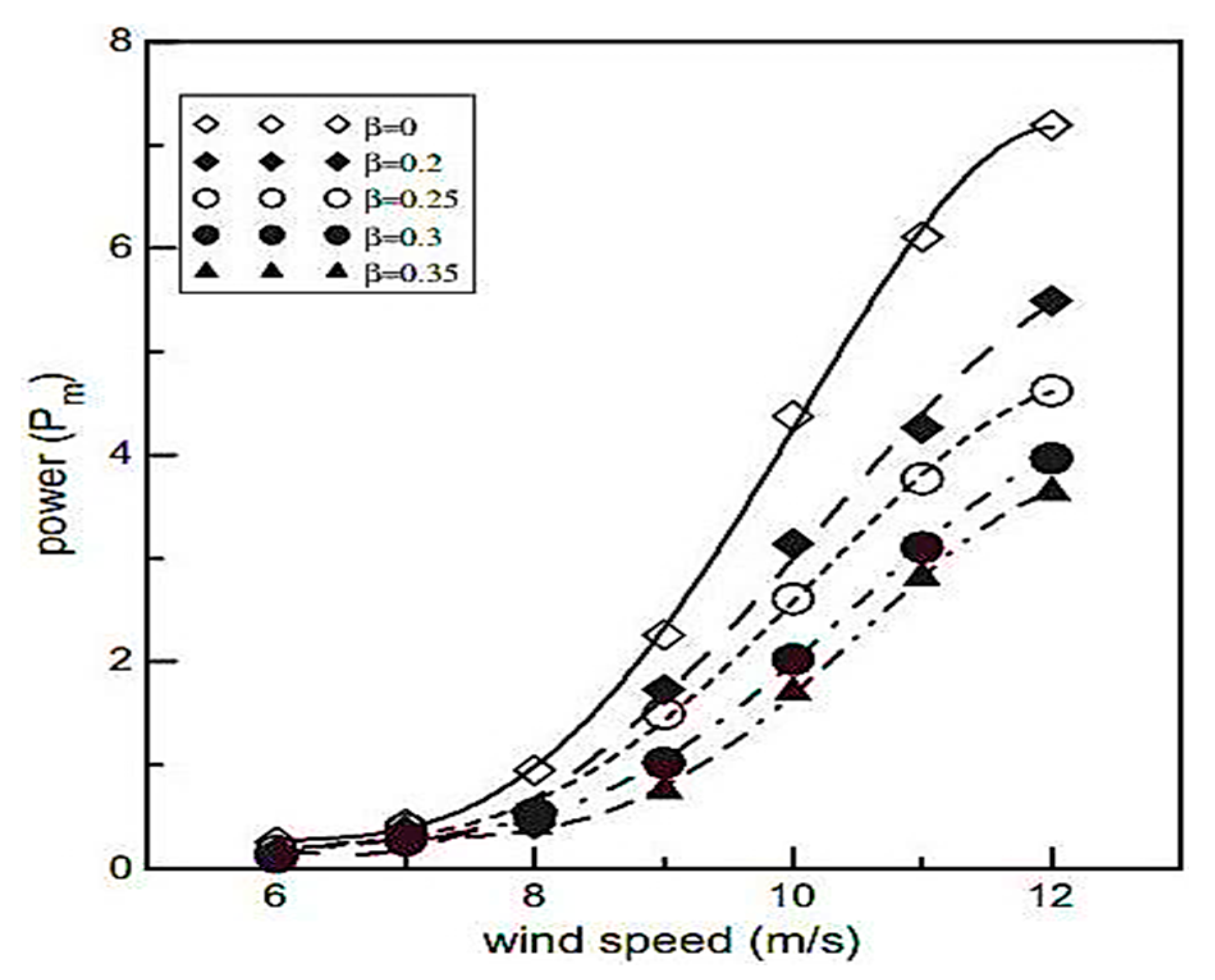
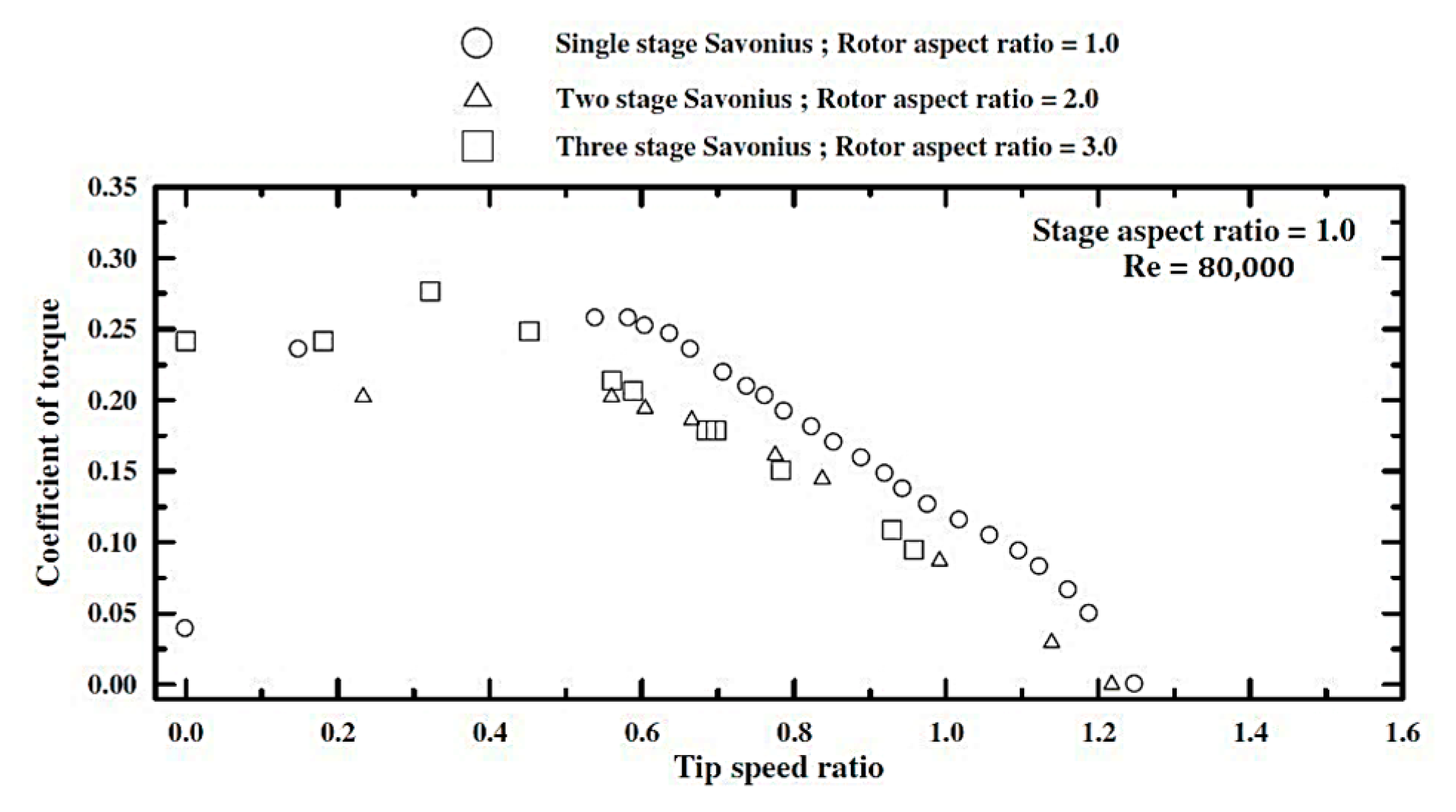
3.2.3. Multi-Staging Effect
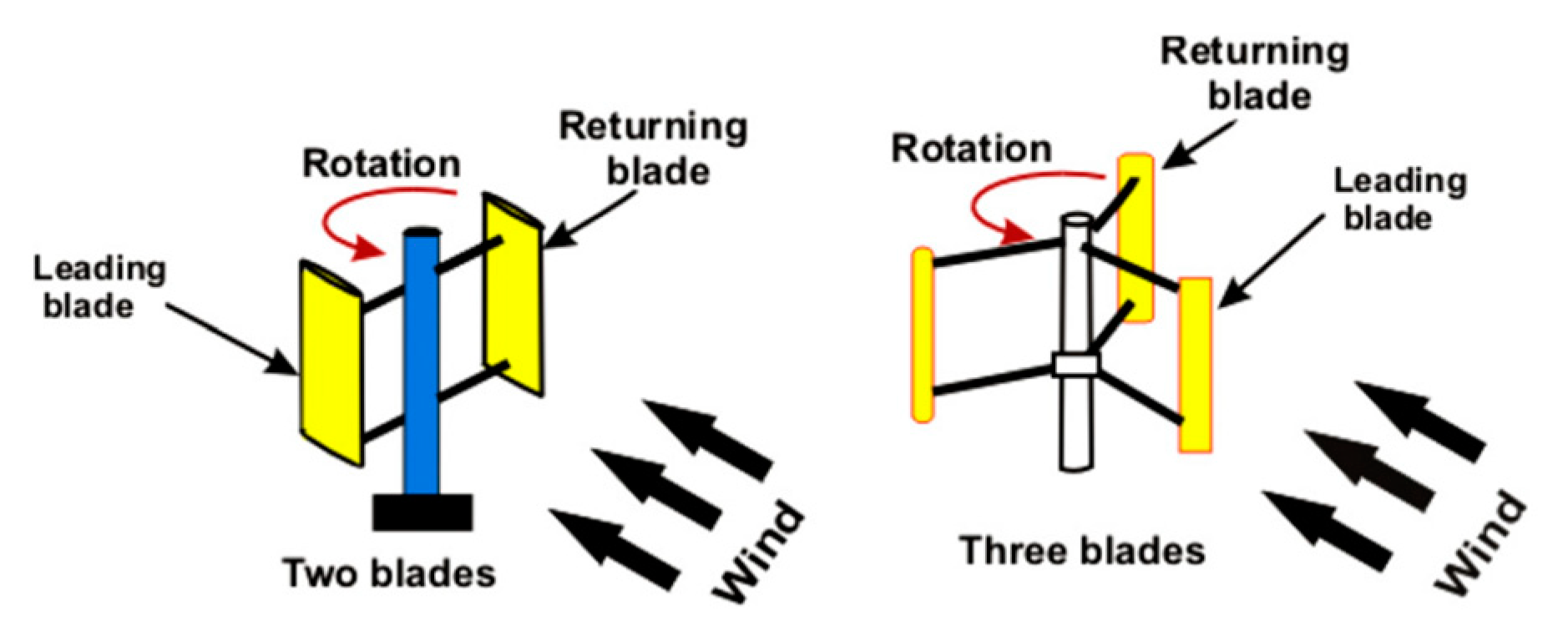
3.2.4. Effect of Number of Blades
3.2.5. Effect of Inner Blades
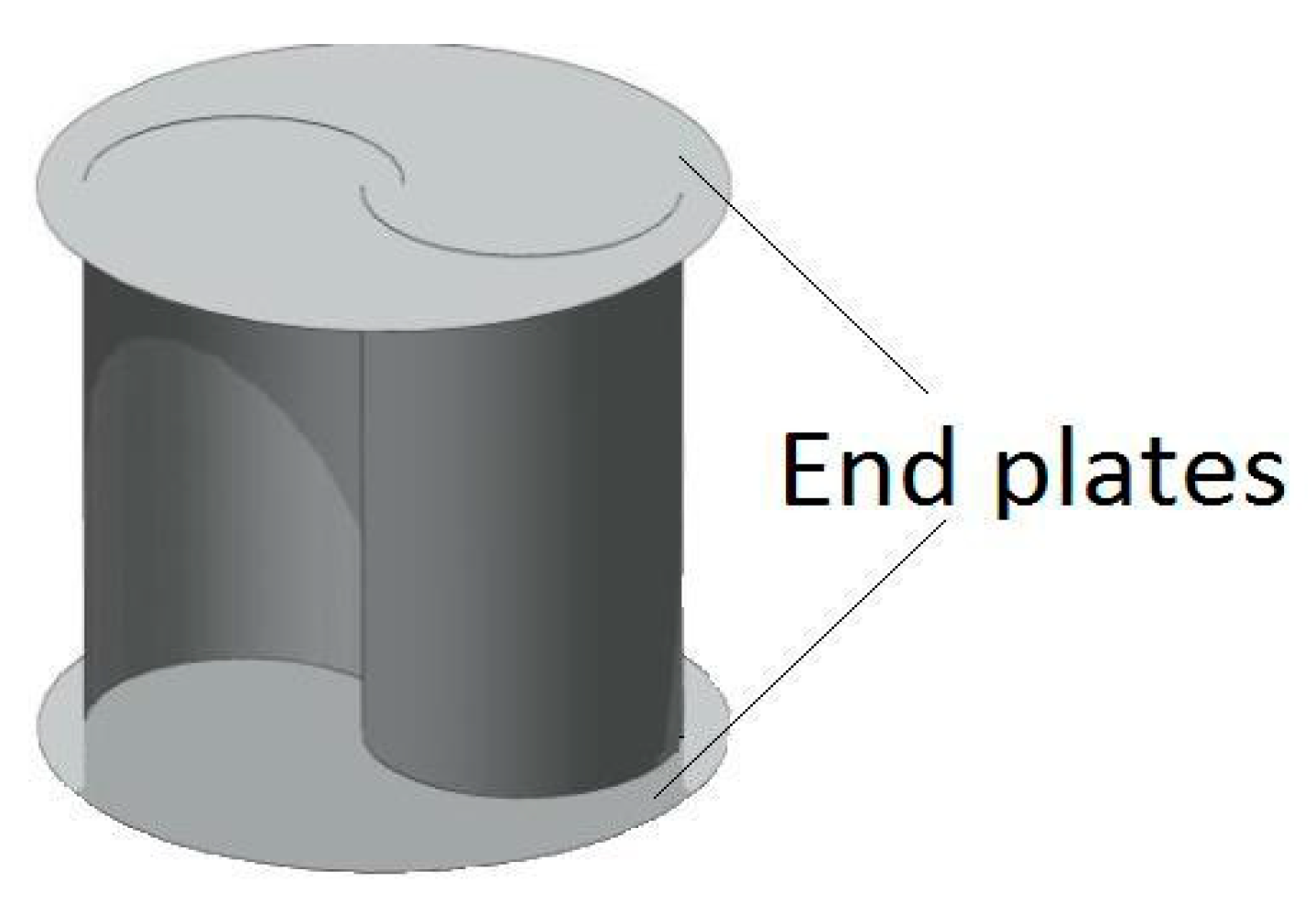
3.2.6. Effect of Endplates
3.2.7. Tip Speed Ratio (TSR) Effect
3.2.8. Effect of Reynolds Number
3.2.9. Effect of Blade Shape and Profile
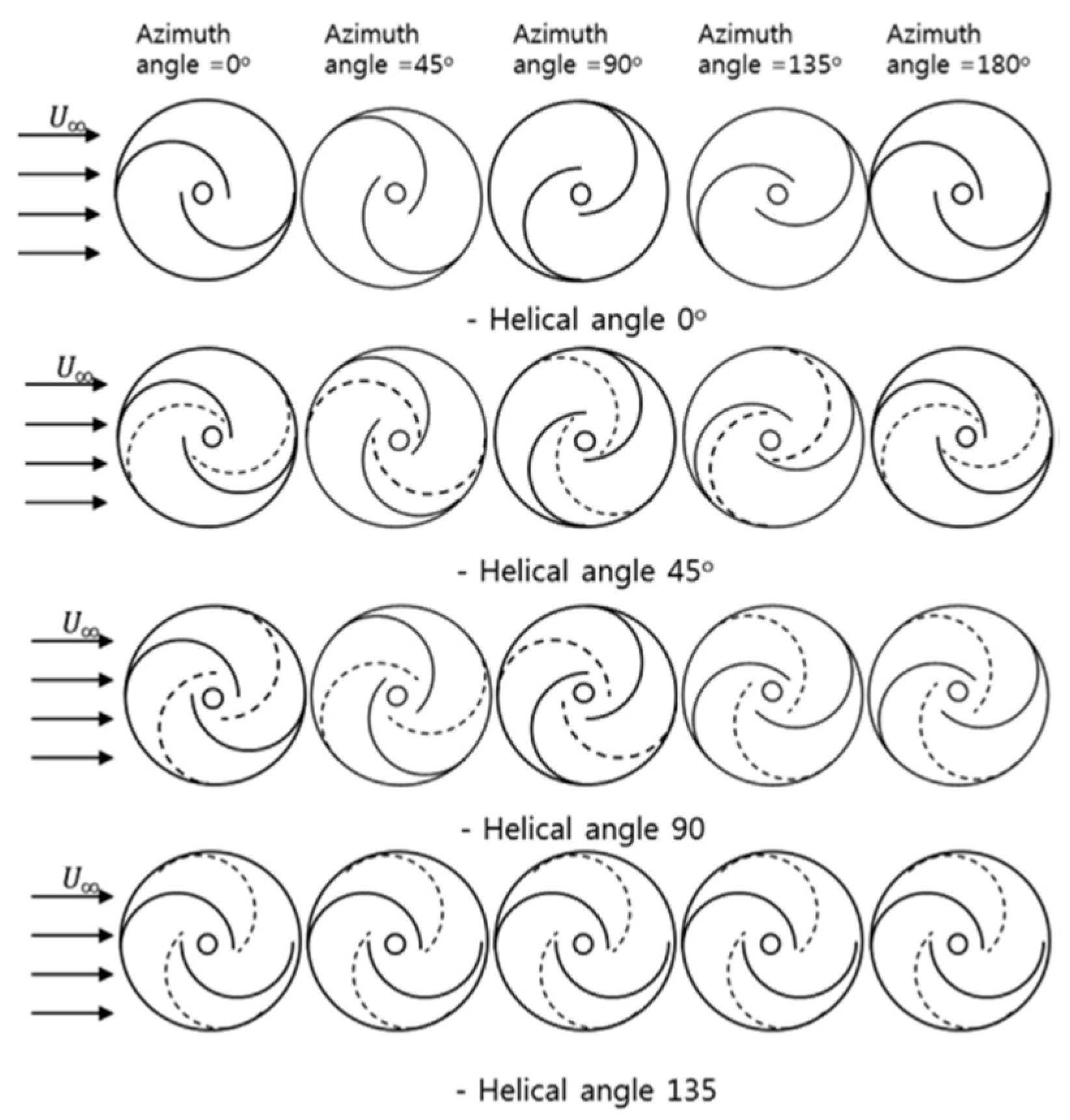
3.2.10. Angle of Twist
4. Mechanism of Wind Power Harvesting: Passive Techniques
4.1. Guided-Vane Technique
4.2. Wind Deflectors
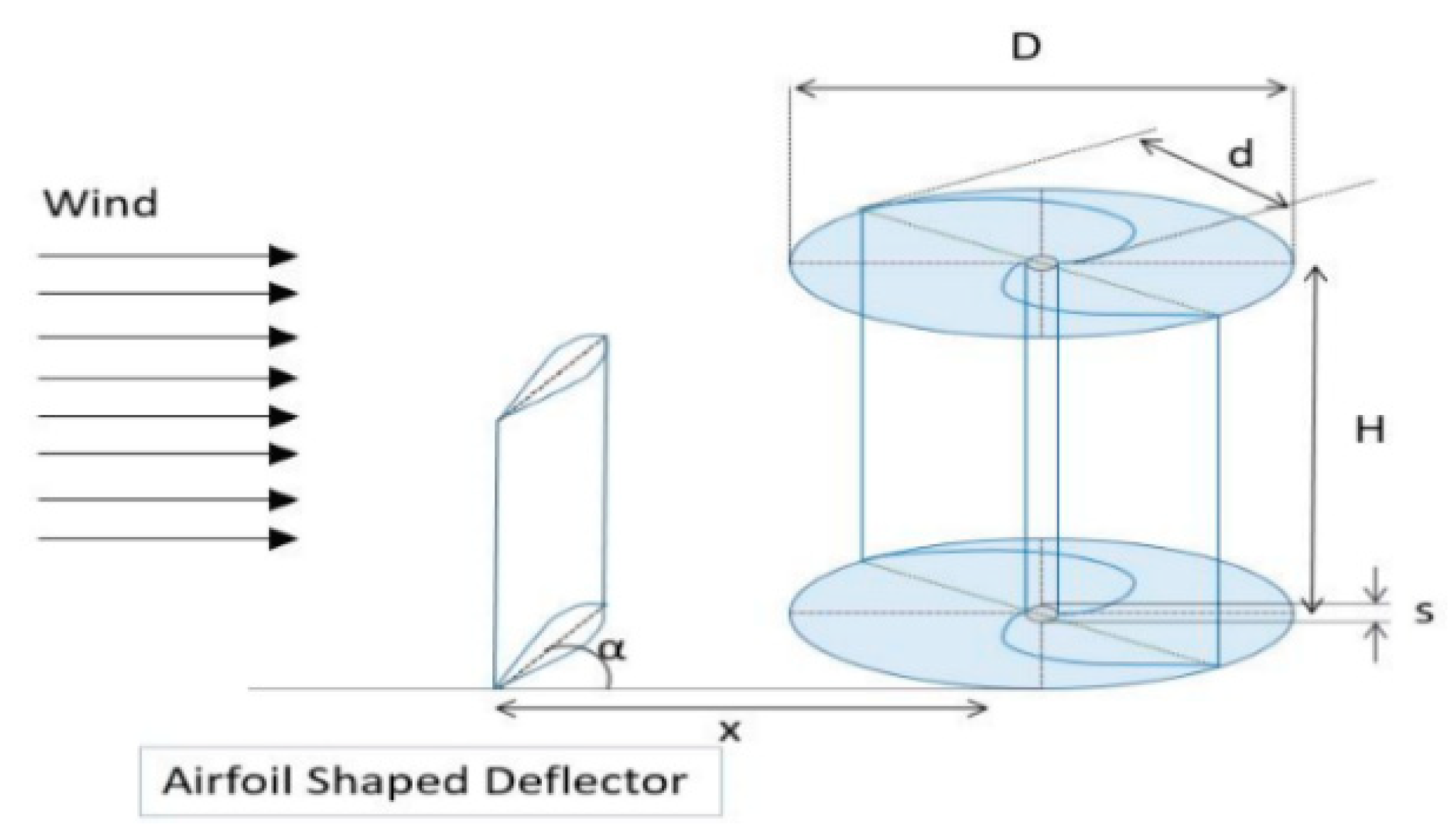
4.2.1. Airfoil-Shaped Wind Deflectors
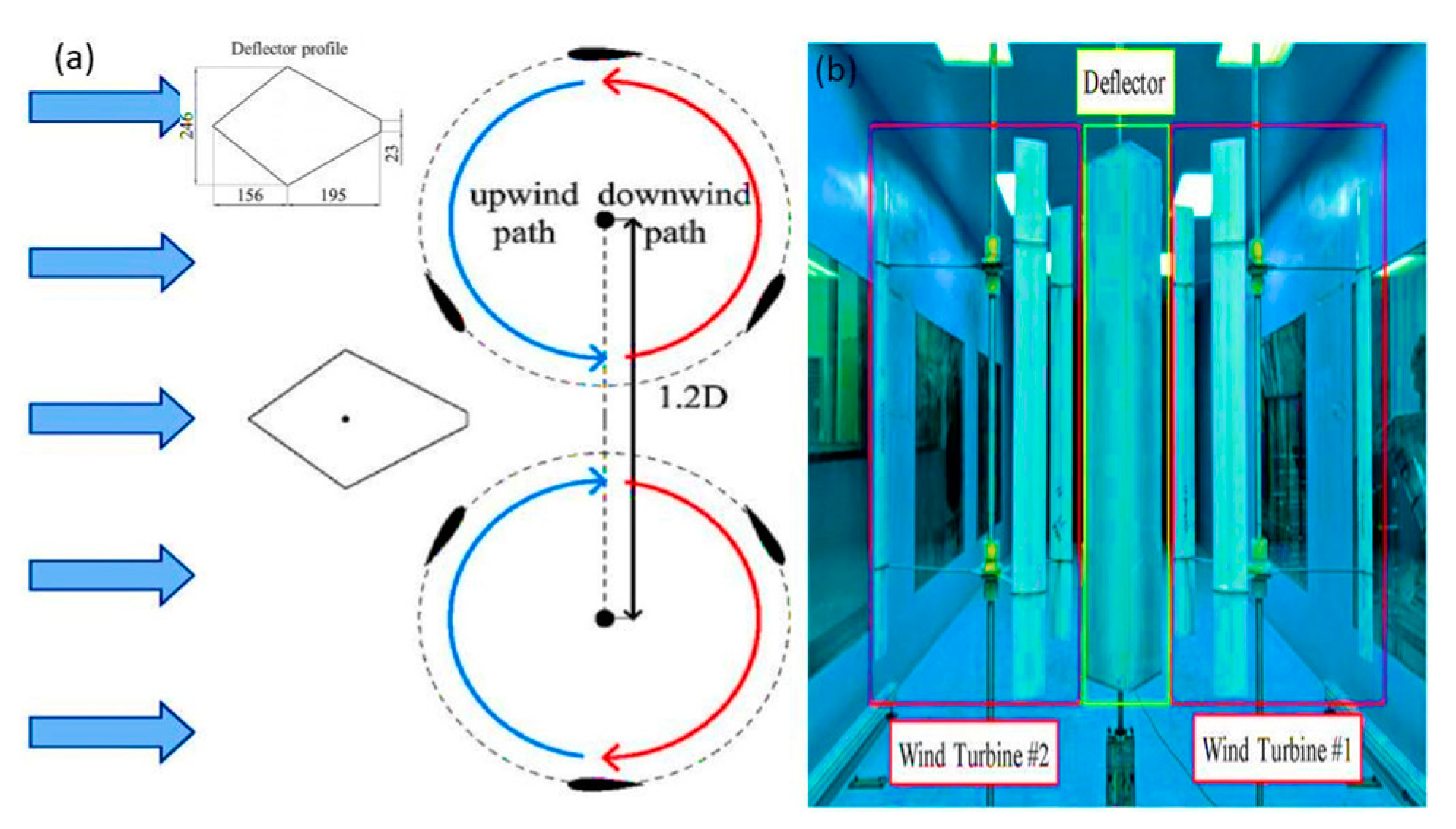
4.2.2. Compound Structured Wind Deflectors
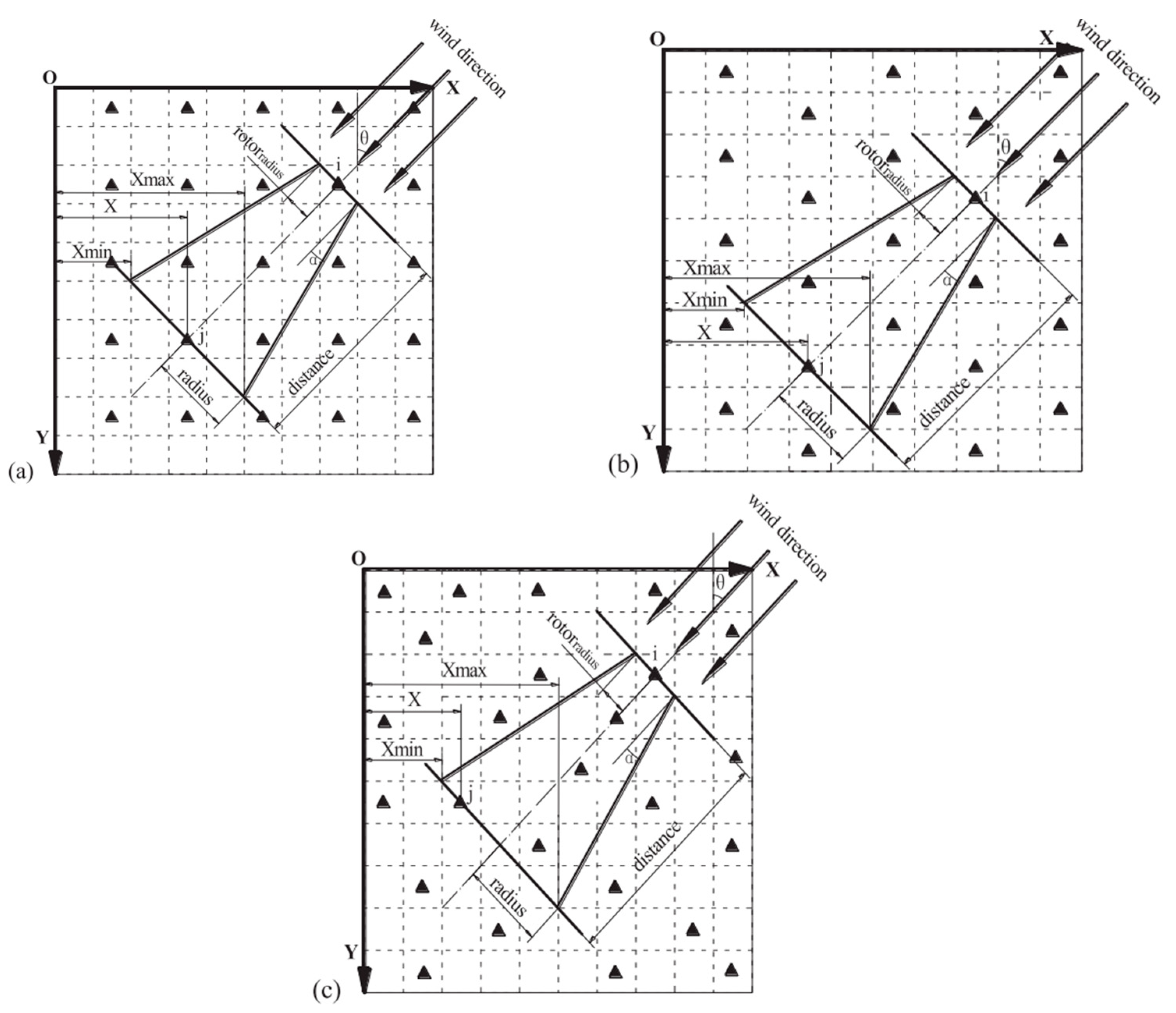
5. Geographical Aspect of Wind Power Harvesting
5.1. Flow Structure
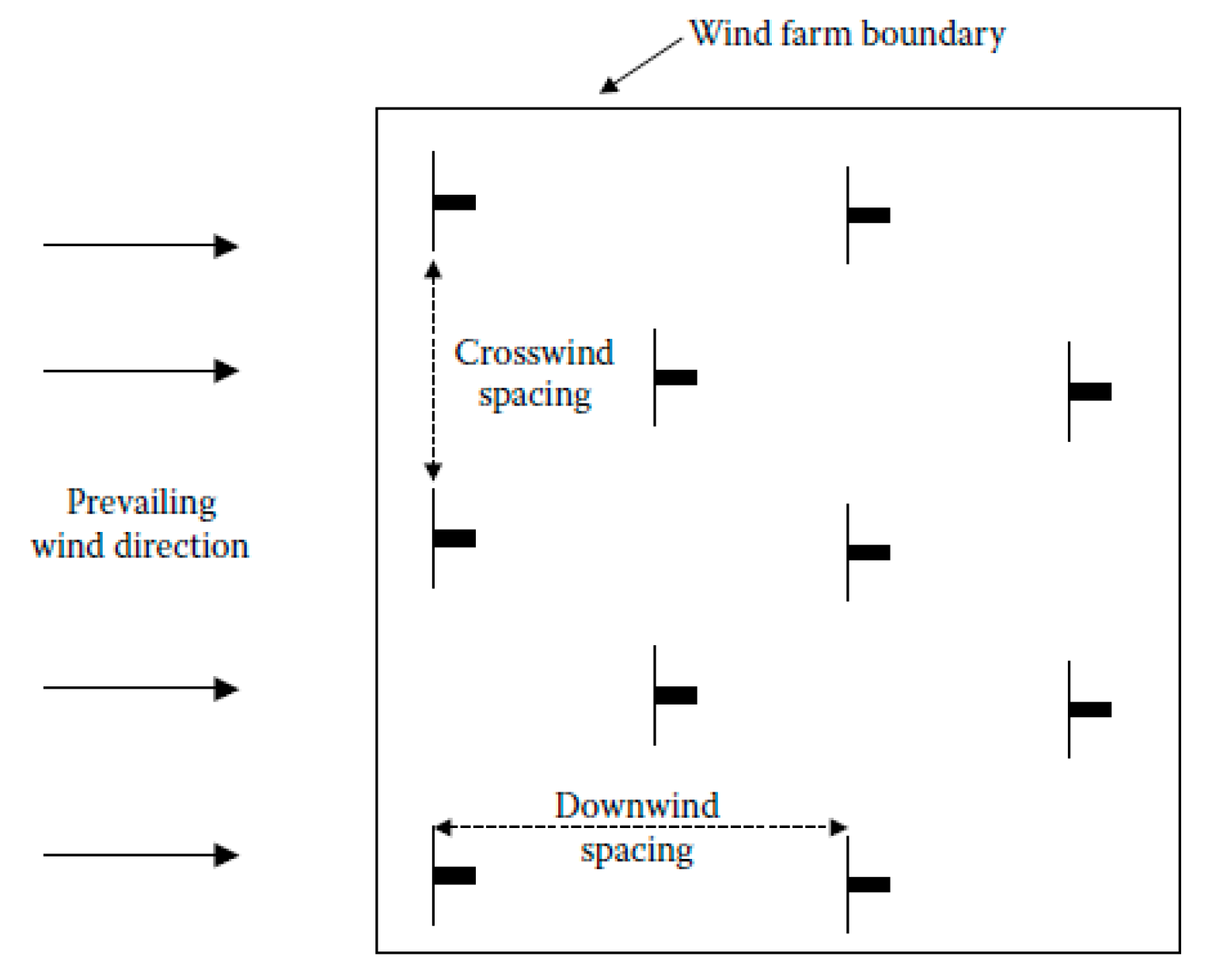
5.2. Micro-Siting
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Didane, D.H.; Ab Wahab, A.; Shamsudin, S.S.; Rosly, N. Wind as a sustainable alternative energy source in Malaysia—A review. ARPN J. Eng. Appl. Sci. 2016, 11, 6442–6449. [Google Scholar]
- Hau, E. Wind Turbines: Fundamentals, Technologies, Application, Economics; Springer: Berlin/Heidelberg, Germany, 2013; p. 9783642271. [Google Scholar]
- Syahmy, M.; Halmy, M.; Didane, D.H.; Afolabi, L.O.; Al-Alimi, S. Computational Fluid Dynamics (CFD) Study on the Effect of the Number of Blades on the Performance of Double-Stage Savonius Rotor. CFD Lett. 2021, 13, 1–10. [Google Scholar]
- Loutun, M.J.T.; Didane, D.H.; Batcha, M.F.M.; Abdullah, K.; Ali, M.F.M.; Mohammed, A.N.; Afolabi, L.O. 2D CFD Simulation Study on the Performance of Various NACA Airfoils. CFD Lett. 2021, 13, 38–50. [Google Scholar] [CrossRef]
- Didane, D.H.; Anuar, M.A.Z.S.; Batcha, M.F.M.; Abdullah, K.; Ali, M.F.M.; Mohammed, A.N. Simulation study on the performance of a counter-rotating savonius vertical axis wind turbine. CFD Lett. 2020, 12, 1–11. [Google Scholar] [CrossRef]
- Mcgowan, J.G.; Manwell, J.F. Wind Energy Explained; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2002. [Google Scholar]
- GWEC. Global Offshore Wind Report 2023-Global Wind Energy Council. 2023. Available online: https://gwec.net/globalwindreport2023/ (accessed on 26 February 2024).
- TAKASHI TSUJI. Renewable Energy Capacity on Track to Rival Fossil Fuels in 2024-Nikkei Asia. 2023. Available online: https://asia.nikkei.com/Spotlight/Environment/Climate-Change/Renewable-energy-capacity-on-track-to-rival-fossil-fuels-in-2024 (accessed on 26 February 2024).
- Global Wind Energy Council. Global Wind Energy Report 2022; Goblal Wind Energy Council: Brussels, Belgium, 2022. [Google Scholar]
- Renewable Energy Policy Network for the 21st Century (REN21). Renewables 2022 Global Status Report. 2022. Available online: https://www.ren21.net/gsr-2022 (accessed on 10 April 2024).
- International Energy Agency. Variability of Wind Power and Other Renewables: Management Options and Strategies; International Energy Agency: Paris, France, 2005. [Google Scholar]
- Didane, D.H.; Mohd, S.; Subari, Z.; Rosly, N.; Ghafir, M.F.A.; Masrom, M.F.M. An aerodynamic performance analysis of a perforated wind turbine blade. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; Volume 160. [Google Scholar] [CrossRef]
- Alquraishi, B.A.; Asmuin, N.Z.; Mohd, S.; Abd Al-Wahid, W.A.; Mohammed, A.N. Review on Diffuser Augmented Wind Turbine (DAWT). Int. J. Integr. Eng. 2019, 11, 178–206. [Google Scholar] [CrossRef]
- Mathew, S.; Philip, G.S. 2.05-Wind Turbines: Evolution, Basic Principles, and Classifications. In Comprehensive Renewable Energy; Elsevier: Amsterdam, The Netherlands, 2012; pp. 93–111. [Google Scholar]
- Muljadi, E.; Nelms, R.M.; Gevorgian, V. Wind Plant Electrical Systems: Electrical Generation, Machines, Power Electronics, and Collector Systems; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2019.
- Sutherland, H.J.; Berg, D.E.; Ashwill, T.D. A Retrospective of VAWT Technology. Security 2012, 1, 1–64. [Google Scholar] [CrossRef]
- Dewan, A.; Gautam, A.; Goyal, R. Savonius wind turbines: A review of recent advances in design and performance enhancements. Mater. Today Proc. 2021, 47, 2976–2983. [Google Scholar] [CrossRef]
- Dincer, I. (Ed.) Comprehensive Energy Systems; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Akwa, J.V.; Vielmo, H.A.; Petry, A.P. A review on the performance of Savonius wind turbines. Renew. Sustain. Energy Rev. 2012, 16, 3054–3064. [Google Scholar] [CrossRef]
- Al-Gburi KA, H.; Alnaimi FB, I.; Al-quraishi, B.A.; Tan, E.S.; Maseer, M.M. A comparative study review: The performance of Savonius-type rotors. Mater. Today Proc. 2022, 57, 343–349. [Google Scholar] [CrossRef]
- Maldar, N.R.; Ng, C.Y.; Oguz, E. A review of the optimization studies for Savonius turbine considering hydrokinetic applications. Energy Convers. Manag. 2020, 226, 113495. [Google Scholar] [CrossRef]
- Zemamou, M.; Aggour, M.; Toumi, A. Review of savonius wind turbine design and performance. Energy Procedia 2017, 141, 383–388. [Google Scholar] [CrossRef]
- Savonius, S.J. The S-rotor and its applications. Mech. Eng. 1931, 53, 333–338. [Google Scholar]
- Rossetti, A.; Pavesi, G. Comparison of different numerical approaches to the study of the H-Darrieus turbines start-up.pdf. Renew. Energy 2013, 50, 7–19. [Google Scholar] [CrossRef]
- Salleh, M.B.; Kamaruddin, N.M.; Mohamed-Kassim, Z. The effects of deflector longitudinal position and height on the power performance of a conventional Savonius turbine. Energy Convers. Manag. 2020, 226, 113584. [Google Scholar] [CrossRef]
- Mohamed, O.S.; Ibrahim, A.A.; Etman, A.K.; Abdelfatah, A.A.; Elbaz, A.M.R. Numerical investigation of Darrieus wind turbine with slotted airfoil blades. Energy Convers. Manag. X 2020, 5, 100026. [Google Scholar] [CrossRef]
- Appa, K. Energy Innovations Small Grant (EISG) Program (Counter Rotating wind Turbine System); EISG: Lake Forest, CA, USA, 2002. [Google Scholar]
- Nicolas, P.; Fuchs, R.; Immas, A.; Silvert, F.; Deglaire, P. Efficiency improvement of vertical-axis wind turbines with counter-rotating lay-out. Proc. EWEA 2016, 1–8. [Google Scholar]
- Neagoe, M.; Saulescu, R.; Jaliu, C.; Munteanu, O.; Cretescu, N. A Comparative Performance Analysis of Four Wind Turbines with Counter-Rotating Electric Generators. Appl. Sci. 2022, 12, 4233. [Google Scholar] [CrossRef]
- Oprina, G.; Chihaia, R.A.; El-Leathey, L.A.; Nicolaie, S.; Băbuţanu, C.; Voina, A. A Review on Counter-Rotating Wind Turbines Development. J. Sustain. Energy 2016, 7, 1–8. [Google Scholar]
- Habash, R.W.Y.; Groza, V.; Yang, Y.; Blouin, C.; Guillemette, P. Performance of a Contrarotating Small Wind Energy Converter. ISRN Mech. Eng. 2011, 2011, 828739. [Google Scholar] [CrossRef]
- Jung, S.N.; No, T.S.; Ryu, K.W. Aerodynamic performance prediction of a 30 kW counter-rotating wind turbine system. Renew. Energy 2005, 30, 631–644. [Google Scholar] [CrossRef]
- Didane, D.H.; Rosly, N.; Zulkafli, M.F.; Shamsudin, S.S. Performance evaluation of a novel vertical axis wind turbine with coaxial contra-rotating concept. Renew. Energy 2018, 115, 353–361. [Google Scholar] [CrossRef]
- Didane, D.H.; Rosly, N.; Zulkafli, M.F.; Shamsudin, S.S. Numerical investigation of a novel contra-rotating vertical axis wind turbine. Sustain. Energy Technol. Assess. 2019, 31, 43–53. [Google Scholar] [CrossRef]
- Wahab, A.A.; Mohd, S.; Dahalan, M.N.; Mat, S.; Chong, W.T.; Ismail, M.H.; Abas, M.F.; Muslimen, R. Eqwin Turbine–The Break through for Wind Energy Implementation in Malaysia. In Proceedings of the International Conference on Mechanical & Manufacturing Engineering, Johor Bahru, Malaysia, 1– 23 May 2008; pp. 21–23. Available online: http://eprints.uthm.edu.my/72/ (accessed on 12 April 2024).
- Didane, D.H.; Maksud, S.M.; Zulkafli, M.F.; Rosly, N.; Shamsudin, S.S.; Khalid, A. Experimental Study on the Performance of a Savonius-Darrius Counter-Rotating Vertical Axis Wind Turbine. IOP Conf. Ser. Earth Environ. Sci. 2019, 268, 012060. [Google Scholar] [CrossRef]
- Didane, D.H.; Maksud, S.M.; Zulkafli, M.F.; Rosly, N.; Shamsudin, S.S.; Khalid, A. Performance investigation of a small Savonius-Darrius counter-rotating vertical-axis wind turbine. Int. J. Energy Res. 2020, 44, 9309–9316. [Google Scholar] [CrossRef]
- Didane, D.H.; Kudam, D.; Zulkafli, M.F.; Faizal, M.; Batcha, M.; Khalid, A. Development and Performance Investigation of a Unique Dual-rotor Savonius-type Counter-rotating Wind Turbine. Int. J. Integr. Eng. 2021, 6, 89–98. [Google Scholar] [CrossRef]
- Vance, W. Vertical axis wind rotors-status and potential. In Wind Energy Conversion Systems; NASA: Washington, DC, USA, 1973. [Google Scholar]
- Lin, C.H.; Klimina, L.A. CFD simulation and analysis for Savonius rotors with different blade configuration. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2014; Volume 1637, pp. 575–581. [Google Scholar] [CrossRef]
- Roy, S.; Saha, U.K. Review on the numerical investigations into the design and development of Savonius wind rotors. Renew. Sustain. Energy Rev. 2013, 24, 73–83. [Google Scholar] [CrossRef]
- Tjahjana, D.D.D.P.; Hadi, S.; Wicaksono, Y.A.; Kurniawati, D.M.; Utomo, I.S.; Cahyono, S.I.; Prasetyo, A. Study on Performance Improvement of the Savonius Wind Turbine for Urban Power System with Omni-directional Guide Vane (ODGV). J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 55, 126–135. Available online: https://www.akademiabaru.com/arfmts.html (accessed on 27 May 2020).
- Kamoji, M.A.; Kedare, S.B.; Prabhu, S.V. Experimental investigations on single stage modified Savonius rotor. Appl. Energy 2009, 86, 1064–1073. [Google Scholar] [CrossRef]
- Modi, V.J.; Roth, N.J.; Fernando, M.S.U.K. Optimum-configuration studies and prototype design of a wind-energy-operated irrigation system. J. Wind Eng. Ind. Aerodyn. 1984, 16, 85–96. [Google Scholar] [CrossRef]
- Roy, S.; Saha, U.K. Review of experimental investigations into the design, performance and optimization of the Savonius rotor. Proceedings of the Institution of Mechanical Engineers. Part A J. Power Energy 2013, 227, 528–542. [Google Scholar] [CrossRef]
- Alit, I.B.; Andyani, I.A.S.; Mirmanto, M. Effect of Overlapping Ratio, Blade Shape Factor, and Blade Arc Angle to modified Rotor Savonius performances. Int. J. Appl. Eng. Res. 2018, 13, 411–416. [Google Scholar] [PubMed]
- Altan, B.D.; Atılgan, M. An experimental and numerical study on the improvement of the performance of Savonius wind rotor. Energy Convers. Manag. 2008, 49, 3425–3432. [Google Scholar] [CrossRef]
- Akwa, J.V.; da Silva Júnior, G.A.; Petry, A.P. Discussion on the verification of the overlap ratio influence on performance coefficients of a Savonius wind rotor using computational fluid dynamics. Renew. Energy 2012, 38, 141–149. [Google Scholar] [CrossRef]
- Ramarajan, J.; Jayavel, S. Numerical Study on the Performance of Savonius Vertical Axis Wind Turbine with Guide Vanes. In Recent Advances in Computational and Experimental Mechanics, Vol—I: Select Proceedings of ICRACEM 2020; Springer: Singapore, 2022; pp. 287–298. [Google Scholar]
- Kudam, D. Performance Evaluation of a Savonius Type Counter-Rotating Wind Turbine. Master’s Thesis, Universiti Tun Hussein Onn Malaysia, Parit Raja, Malaysia, 2018. [Google Scholar]
- Nasef, M.H.; El-Askary, W.A.; Abdel-Hamid, A.A.; Gad, H.E. Evaluation of Savonius rotor performance: Static and dynamic studies. J. Wind Eng. Ind. Aerodyn. 2013, 123, 1–11. [Google Scholar] [CrossRef]
- Saha, U.K.; Thotla, S.; Maity, D. Optimum design configuration of Savonius rotor through wind tunnel experiments. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1359–1375. [Google Scholar] [CrossRef]
- Hayashi, T.; Li, Y.; Hara, Y. Wind Tunnel Tests on a Different Phase Three-Stage Savonius Rotor. JSME Int. J. Ser. B 2005, 48, 9–16. [Google Scholar] [CrossRef]
- Frikha, S.; Driss, Z.; Ayadi, E.; Masmoudi, Z.; Abid, M.S. Numerical and experimental characterization of multi-stage Savonius rotors. Energy 2016, 114, 382–404. [Google Scholar] [CrossRef]
- Jian, C.; Kumbernuss, J.; Linhua, Z.; Lin, L.; Hongxing, Y. Influence of Phase-Shift and Overlap Ratio on Savonius Wind Turbine’s Performance. J. Sol. Energy Eng. 2012, 134, 011016. [Google Scholar] [CrossRef]
- Kamoji, M.A.; Kedare, S.B.; Prabhu, S.V. Experimental investigations on single stage, two stage and three stage conventional Savonius rotor. Int. J. Energy Res. 2008, 32, 877–895. [Google Scholar] [CrossRef]
- Unsakul, S.; Sranpat, C.; Chaisiriroj, P.; Leephakpreeda, T. CFD-Based Performance Analysis and Experimental Investigation of Design Factors of Vertical Axis Wind Turbines under Low Wind Speed Conditions in Thailand. J. Flow Control Meas. Vis. 2017, 5, 86–98. [Google Scholar] [CrossRef][Green Version]
- Sheldahl, R.E.; Blackwell, B.F.; Feltz, L.V. Wind Tunnel Performance Data for Two-and Three-bucket Savonius Rotors. J. Energy 1977, 2, 160–164. [Google Scholar] [CrossRef]
- Emmanuel, B.; Jun, W. Numerical Study of a Six-Bladed Savonius Wind Turbine. J. Sol. Energy Eng. 2011, 133, 044503. [Google Scholar] [CrossRef]
- Bashar, M.M. Computational and Experimental Study on Vertical Axis Wind Turbine in Search for an Efficient Design. Master’s Thesis, Georgia Southern University, Statesboro, GA, USA, 2014. [Google Scholar]
- Bhayo, B.A.; Al-Kayiem, H.H.; Yahaya, N.Z. Performance investigation of the S-Rotors. IOP Conf. Ser. Mater. Sci. Eng. 2015, 100, 012043. [Google Scholar] [CrossRef]
- Mohamed, M.H. Performance investigation of H-rotor Darrieus turbine with new airfoil shapes. Energy 2012, 47, 522–530. [Google Scholar] [CrossRef]
- Wenehenubun, F.; Saputra, A.; Sutanto, H. An experimental study on the performance of Savonius wind turbines related with the number of blades. Energy Procedia 2015, 68, 297–304. [Google Scholar] [CrossRef]
- Kumar, A.; Saini, R. Performance parameters of Savonius type hydrokinetic turbine–A Review. Renew. Sustain. Energy Rev. 2016, 64, 289–310. [Google Scholar] [CrossRef]
- Al-Ghriybah, M.; Zulkafli, M.F.; Didane, D.H.; Mohd, S. The effect of inner blade position on the performance of the Savonius rotor. Sustain. Energy Technol. Assess. 2019, 36, 100534. [Google Scholar] [CrossRef]
- Al-Ghriybah, M.; Zulkafli, M.F.; Didane, D.H. Numerical investigation of inner blade effects on the conventional savonius rotor with external overlap. J. Sustain. Dev. Energy Water Environ. Syst. 2020, 8, 561–576. [Google Scholar] [CrossRef]
- Al-Ghriybah, M.; Fadhli, M.; Hissein, D.; Mohd, S. The effect of spacing between inner blades on the performance of the Savonius wind turbine. Sustain. Energy Technol. Assess. 2021, 43, 100988. [Google Scholar] [CrossRef]
- Al-Ghriybah, M.; Zulkafli, M.F.; Didane, D.H.; Mohd, S. Performance of Double Blade Savonius Rotor at Low Rotational Speed. J. Comput. Theor. Nanosci. 2020, 17, 1–7. [Google Scholar] [CrossRef]
- Abraham, J.P.; Plourde, B.D.; Mowry, G.S.; Minkowycz, W.J.; Sparrow, E.M. Summary of Savonius wind turbine development and future applications for small-scale power generation. J. Renew. Sustain. Energy 2012, 4, 042703. [Google Scholar] [CrossRef]
- Plourde, B.D.; Abraham, J.P.; Mowry, G.S.; Minkowycz, W.J. Simulations of Three-Dimensional Vertical-Axis Turbines for Communications Applications. Wind Eng. 2012, 36, 443–453. [Google Scholar] [CrossRef]
- Fujisawa, N.; Gotoh, F. Pressure measurements and flow visualization study of a Savonius rotor. J. Wind Eng. Ind. Aerodyn. 1992, 39, 51–60. [Google Scholar] [CrossRef]
- Sivasegaram, S. Secondary parameters affecting the performance of resistance-type vertical-axis wind rotors. Wind Eng. 1978, 2, 49–58. [Google Scholar]
- Jeon, K.S.; Jeong, J.I.; Pan, K.J.; Ryu, W.K. Effects of end plates with various shapes and sizes on helical Savonius wind turbines. Renew. Energy 2015, 79, 167–176. [Google Scholar] [CrossRef]
- Roy, S.; Saha, U.K. Wind tunnel experiments of a newly developed two-bladed Savonius-style wind turbine. Appl. Energy 2014, 137, 117–125. [Google Scholar] [CrossRef]
- Kacprzak, K.; Liskiewicz, G.; Sobczak, K. Numerical investigation of conventional and modified Savonius wind turbines. Renew. Energy 2013, 60, 578–585. [Google Scholar] [CrossRef]
- Zhao, Z.; Zheng, Y.; Xu, X.; Liu, W.; Hu, G. Research on the improvement of the performance of Savonius rotor based on numerical study. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009; pp. 1–6. [Google Scholar]
- Golecha, K.; Eldho, T.I.; Prabhu, S.V. Influence of the deflector plate on the performance of modified Savonius water turbine. Appl. Energy 2011, 88, 3207–3217. [Google Scholar] [CrossRef]
- Ochieng, P.O.; Manyonge, A.W.; Oduor, A.O. Mathematical Analysis of Tip Speed Ratio of a Wind Turbine and its Effects on Power Coefficient. Int. J. Math. Soft Comput. 2014, 4, 61. [Google Scholar] [CrossRef]
- Hosseini, A.; Cannon, D.T.; Vasel-Be-Hagh, A. Tip speed ratio optimization: More energy production with reduced rotor speed. Wind 2022, 2, 691–711. [Google Scholar] [CrossRef]
- Haibo, J.; Yanru, L.; Zhongqing, C. Renewable Energy. In Performances of Ideal Wind Turbine; Elsevier: Amsterdam, The Netherlands, 2015; pp. 658–662. [Google Scholar]
- Damak, A.; Driss, Z.; Abid, M.S. Experimental investigation of helical Savonius rotor with a twist of 180°. Renew. Energy 2013, 52, 136–142. [Google Scholar] [CrossRef]
- Najib, A.A.; Didane, D.H.; Behery, M.R.; Kabrein, H.A. Comparison of 2D and 3D Simulations on Predicting the Performance of a Savonius Wind Turbine. CFD Lett. 2024, 16, 71–88. [Google Scholar] [CrossRef]
- Mrigua, K.; Toumi, A.; Zemamou, M.; Ouhmmou, B.; Lahlou, Y.; Aggour, M. CFD Investigation of A New Elliptical-Bladed Multistage Savonius Rotors. Int. J. Renew. Energy Dev. 2020, 9, 383–392. [Google Scholar] [CrossRef]
- Hadi Ali, M. Experimental Comparison Study for Savonius Wind Turbine of Two & Three Blades At Low Wind Speed. Int. J. Mod. Eng. Res. (IJMER) 2013, 3, 2978–2986. [Google Scholar]
- Tian, W.; Mao, Z.; Zhang, B.; Li, Y. Shape optimization of a Savonius wind rotor with different convex and concave sides. Renew. Energy 2018, 117, 287–299. [Google Scholar] [CrossRef]
- Kang, C.; Zhang, F.; Mao, X. Comparison Study of a Vertical-Axis Spiral Rotor and a Conventional Savonius Rotor. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Chan, C.M.; Bai, H.L.; He, D.Q. Blade shape optimization of the Savonius wind turbine using a genetic algorithm. Appl. Energy 2018, 213, 148–157. [Google Scholar] [CrossRef]
- Alom, N.; Saha, U.K. Influence of blade profiles on Savonius rotor performance: Numerical simulation and experimental validation. Energy Convers. Manag. 2019, 186, 267–277. [Google Scholar] [CrossRef]
- Alom, N. Influence of curtain plates on the aerodynamic performance of an elliptical bladed Savonius rotor (S-rotor). Energy Syst. 2021, 13, 1–16. [Google Scholar] [CrossRef]
- Alom, N.; Saha, U.K. Performance evaluation of vent-augmented elliptical-bladed Savonius rotors by numerical simulation and wind tunnel experiments. Energy 2018, 152, 277–290. [Google Scholar] [CrossRef]
- Tartuferi, M.; D’Alessandro, V.; Montelpare, S.; Ricci, R. Enhancement of Savonius wind rotor aerodynamic performance: A computational study of new blade shapes and curtain systems. Energy 2015, 79, 371–384. [Google Scholar] [CrossRef]
- Grinspan, A.; Saha, U.K.; Mahanta, P. Experimental investigation of twisted bladed Savonius wind turbine rotor. Int. Energy J. 2004, 5, 1–9. [Google Scholar]
- Deb, B.; Gupta, R.; Misra, R.D. Performance analysis of a helical savonius rotor without shaft at 45 twist angle using CFD. J. Urban Environ. Eng. 2013, 7, 126–133. [Google Scholar] [CrossRef]
- Anbarsooz, M. Aerodynamic performance of helical Savonius wind rotors with 30° and 45° twist angles: Experimental and numerical studies. Proceedings of the Institution of Mechanical Engineers. Part A J. Power Energy 2016, 230, 523–534. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, Y.T.; Lim, H.C. Effect of twist angle on the performance of Savonius wind turbine. Renew. Energy 2016, 89, 231–244. [Google Scholar] [CrossRef]
- Ghatage, S.V.; Joshi, J.B. Optimisation of vertical axis wind turbine: CFD simulations and experimental measurements. Can. J. Chem. Eng. 2012, 90, 1186–1201. [Google Scholar] [CrossRef]
- Ricci, R.; Romagnoli, R.; Montelpare, S.; Vitali, D. Experimental study on a Savonius wind rotor for street lighting systems. Appl. Energy 2016, 161, 143–152. [Google Scholar] [CrossRef]
- Saha, U.K.; Rajkumar, M.J. On the performance analysis of Savonius rotor with twisted blades. Renew. Energy 2006, 31, 1776–1788. [Google Scholar] [CrossRef]
- Frikha, S. Study of the Computational Domain Effect on the Aerodynamic Structure Around a Savonius Wind Rotor. Int. J. Fluid Mech. Therm. Sci. 2015, 1, 20. [Google Scholar] [CrossRef]
- Loganathan, B.; Mustary, I.; Chowdhury, H.; Alam, F. Effect of sizing of a Savonius type vertical axis micro wind turbine. Energy Procedia 2017, 110, 555–560. [Google Scholar] [CrossRef]
- Saad, A.S.; Ookawara, S.; Elwardany, A.; El-Sharkawy, I.I.; Ahmed, M. Effect of the Number of Stages on the Performance of Savonius Vertical Axis Wind Turbines: Part II—Using Twisted Blades. ASME Int. Mech. Eng. Congr. Expo. 2020, 84584, V010T10A059. [Google Scholar]
- Chong, W.T.; Fazlizan, A.; Poh, S.C.; Pan, K.C.; Hew, W.P.; Hsiao, F.B. The design, simulation and testing of an urban vertical axis wind turbine with the omni-direction-guide-vane. Appl. Energy 2013, 112, 601–609. [Google Scholar] [CrossRef]
- Van Bussel, G.J. The science of making more torque from wind: Diffuser experiments and theory revisited. J. Phys. Conf. Ser. 2007, 75, 012010. [Google Scholar] [CrossRef]
- Lilley, G.M.; Rainbird, W.J. A Preliminary Report on the Design and Performance of a Ducted Windmill; Report 102; College of Aeronautics: Cranfield, UK, 1956. [Google Scholar]
- Foreman, K. Preliminary Design and Economic Investigations of Diffuser Augmented Wind Turbines (DAWT); Grumman Aerospace Corp.: Bethpage, NY, USA, 1981. [Google Scholar]
- Gilbert, B.L.; Foreman, K.M. Experiments with a diffuseraugmented model wind turbine. J. Energy Resour. Technol. Trans. ASME 1983, 105, 46–53. [Google Scholar] [CrossRef]
- Igra, O. Research and Development for Shrouded Wind Turbines. Energy Convers. Manag. 1981, 21, 13–48. [Google Scholar] [CrossRef]
- Phillips, D.G.; Flay, R.G.J.; Richards, P.J. An Investigation on Diffuser Augmented Wind Turbine Design. Dep. Mech. Eng. 2003, 370. [Google Scholar]
- Abe, K.I.; Ohya, Y. An investigation of flow fields around flanged diffusers using CFD. J. Wind Eng. Ind. Aerodyn. 2004, 92, 315–330. [Google Scholar] [CrossRef]
- Ohya, Y.; Karasudani, T.; Sakurai, A.; Abe, K.I.; Inoue, M. Development of a shrouded wind turbine with a flanged diffuser. J. Wind Eng. Ind. Aerodyn. 2008, 96, 524–539. [Google Scholar] [CrossRef]
- Ohya, Y.; Karasudani, T. A shrouded wind turbine generating high output power with wind-lens technology. Energies 2010, 3, 634–649. [Google Scholar] [CrossRef]
- Kosasih, B.; Tondelli, A. Experimental study of shrouded micro-wind turbine. Procedia Eng. 2012, 49, 92–98. [Google Scholar] [CrossRef]
- Kishore, R.A.; Coudron, T.; Priya, S. Small-scale wind energy portable turbine (SWEPT). J. Wind Eng. Ind. Aerodyn. 2013, 116, 21–31. [Google Scholar] [CrossRef]
- Liu, J.; Song, M.; Chen, K.; Wu, B.; Zhang, X. An optimization methodology for wind lens profile using Computational Fluid Dynamics simulation. Energy 2016, 109, 602–611. [Google Scholar] [CrossRef]
- Khamlaj, T.A.; Rumpfkeil, M.P. Analysis and optimization of ducted wind turbines. Energy 2018, 162, 1234–1252. [Google Scholar] [CrossRef]
- Maw, Y.Y.; Tun, M.T. Sensitivity analysis of angle, length and brim height of the diffuser for the small diffuser augmented wind turbine using the numerical investigation. ASEAN Eng. J. 2021, 11, 280–291. [Google Scholar] [CrossRef]
- Elsayed, A.M. Design optimization of diffuser augmented wind turbine. CFD Lett. 2021, 13, 45–59. [Google Scholar] [CrossRef]
- Layeghmand, K.; Ghiasi Tabari, N.; Zarkesh, M. Improving efficiency of Savonius wind turbine by means of an airfoil-shaped deflector. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 528. [Google Scholar] [CrossRef]
- Rajpar, A.H.; Ali, I.; Eladwi, A.E.; Bashir, M.B.A. Recent development in the design of wind deflectors for vertical axis wind turbine: A review. Energies 2021, 14, 5140. [Google Scholar] [CrossRef]
- Yang, M.H.; Huang, G.M.; Yeh, R.H. Performance investigation of an innovative vertical axis turbine consisting of deflectable blades. Appl. Energy 2016, 179, 875–887. [Google Scholar] [CrossRef]
- Yan, Y.; Avital, E.; Williams, J.; Cui, J. CFD analysis for the performance of micro-vortex generator on aerofoil and vertical axis turbine. J. Renew. Sustain. Energy 2019, 11, 043302. [Google Scholar] [CrossRef]
- Yuwono, T.; Sakti, G.; Aulia, F.N.; Wijaya, A.C. Improving the performance of Savonius wind turbine by installation of a circular cylinder upstream of returning turbine blade. Alex. Eng. J. 2020, 59, 4923–4932. [Google Scholar] [CrossRef]
- Al-Ghriybah, M.; Zulkafli, M.F.; Didane, D.H.; Mohd, S. Performance of the savonius wind rotor with two inner blades at low tip speed ratio. CFD Lett. 2020, 12, 11–21. [Google Scholar] [CrossRef]
- Aboujaoude, H.; Beaumont, F.; Murer, S.; Polidori, G.; Bogard, F. Aerodynamic performance enhancement of a Savonius wind turbine using an axisymmetric deflector. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104882. [Google Scholar] [CrossRef]
- Nimvari, M.E.; Fatahian, H.; Fatahian, E. Performance improvement of a Savonius vertical axis wind turbine using a porous deflector. Energy Convers. Manag. 2020, 220, 113062. [Google Scholar] [CrossRef]
- Majid, A.A. Accurate and efficient forecasted wind energy using selected temporal metrological variables and wind direction. Energy Convers. Manag. X 2022, 16, 100286. [Google Scholar]
- Huang, C.; Yan, J.; Zhang, D.; Zhong, Y. Analysis of the effect of slope on the power characteristics of wind turbines in hillside terrain. Energy Rep. 2022, 8, 352–361. [Google Scholar] [CrossRef]
- Liu, J.; Bao, B.; Chen, J.; Wu, Y.; Wang, Q. Passively adaptive wind energy harvester featuring a double-airfoil bluff body with adjustable attack angles. Mech. Syst. Signal Process. 2023, 185, 109814. [Google Scholar] [CrossRef]
- Hasan, M.E.; Eltayesh, A.; Awaad, M.I.; El-Batsh, H.M. Experimental Examination for the Electric Power Generation of a Commercial Small-scale Wind Turbine with Modified Aerodynamic Design. Alex. Eng. J. 2023, 64, 25–39. [Google Scholar] [CrossRef]
- Zhang, W.; Markfort, C.D.; Porté-Agel, F. Near-wake flow structure downwind of a wind turbine in a turbulent boundary layer. Exp. Fluids 2012, 52, 1219–1235. [Google Scholar] [CrossRef]
- Kazacoks, R.; Amos, L.; Leithead, W. Effect of wind flow direction on the loads at wind farm. J. Phys. Conf. Ser. 2019, 1356, 12005. [Google Scholar] [CrossRef]
- Uchida, T.; Li, G. Comparison of RANS and LES in the prediction of airflow field over steep complex terrain. Open J. Fluid Dyn. 2018, 8, 286–307. [Google Scholar] [CrossRef]
- Nelson, V.; Starcher, K. Wind Energy: Renewable Energy and the Environment, 3rd ed.; CRC Press: Boca Raton, MA, USA, 2018. [Google Scholar]
- Didane, D.H.; Rosly, N.; Zulkafli, M.F.; Shamsudin, S.S. Evaluation of wind energy potential as a power generation source in Chad. Int. J. Rotating Mach. 2017, 2017, 3121875. [Google Scholar] [CrossRef]
- Dabiri, J.O. Potential order-of-magnitude enhancement of wind farm power density via counter-rotating vertical-axis wind turbine arrays. J. Renew. Sustain. Energy 2011, 3, 043104. [Google Scholar] [CrossRef]
- Nelson, V. Wind Energy: Renewable Energy and the Environment; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Gao, X.; Yang, H.; Lu, L. Investigation into the optimal wind turbine layout patterns for a Hong Kong offshore wind farm. Energy 2014, 73, 430–442. [Google Scholar] [CrossRef]
- Gualtieri, G. A novel method for wind farm layout optimization based on wind turbine selection. Energy Convers. Manag. 2019, 193, 106–123. [Google Scholar] [CrossRef]


















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Didane, D.H.; Behery, M.R.; Al-Ghriybah, M.; Manshoor, B. Recent Progress in Design and Performance Analysis of Vertical-Axis Wind Turbines—A Comprehensive Review. Processes 2024, 12, 1094. https://doi.org/10.3390/pr12061094
Didane DH, Behery MR, Al-Ghriybah M, Manshoor B. Recent Progress in Design and Performance Analysis of Vertical-Axis Wind Turbines—A Comprehensive Review. Processes. 2024; 12(6):1094. https://doi.org/10.3390/pr12061094
Chicago/Turabian StyleDidane, Djamal Hissein, Mostafa Radwan Behery, Mohanad Al-Ghriybah, and Bukhari Manshoor. 2024. "Recent Progress in Design and Performance Analysis of Vertical-Axis Wind Turbines—A Comprehensive Review" Processes 12, no. 6: 1094. https://doi.org/10.3390/pr12061094
APA StyleDidane, D. H., Behery, M. R., Al-Ghriybah, M., & Manshoor, B. (2024). Recent Progress in Design and Performance Analysis of Vertical-Axis Wind Turbines—A Comprehensive Review. Processes, 12(6), 1094. https://doi.org/10.3390/pr12061094








