Signal Decomposition for Monitoring Systems of Processes
Abstract
1. Introduction
2. Materials and Methods
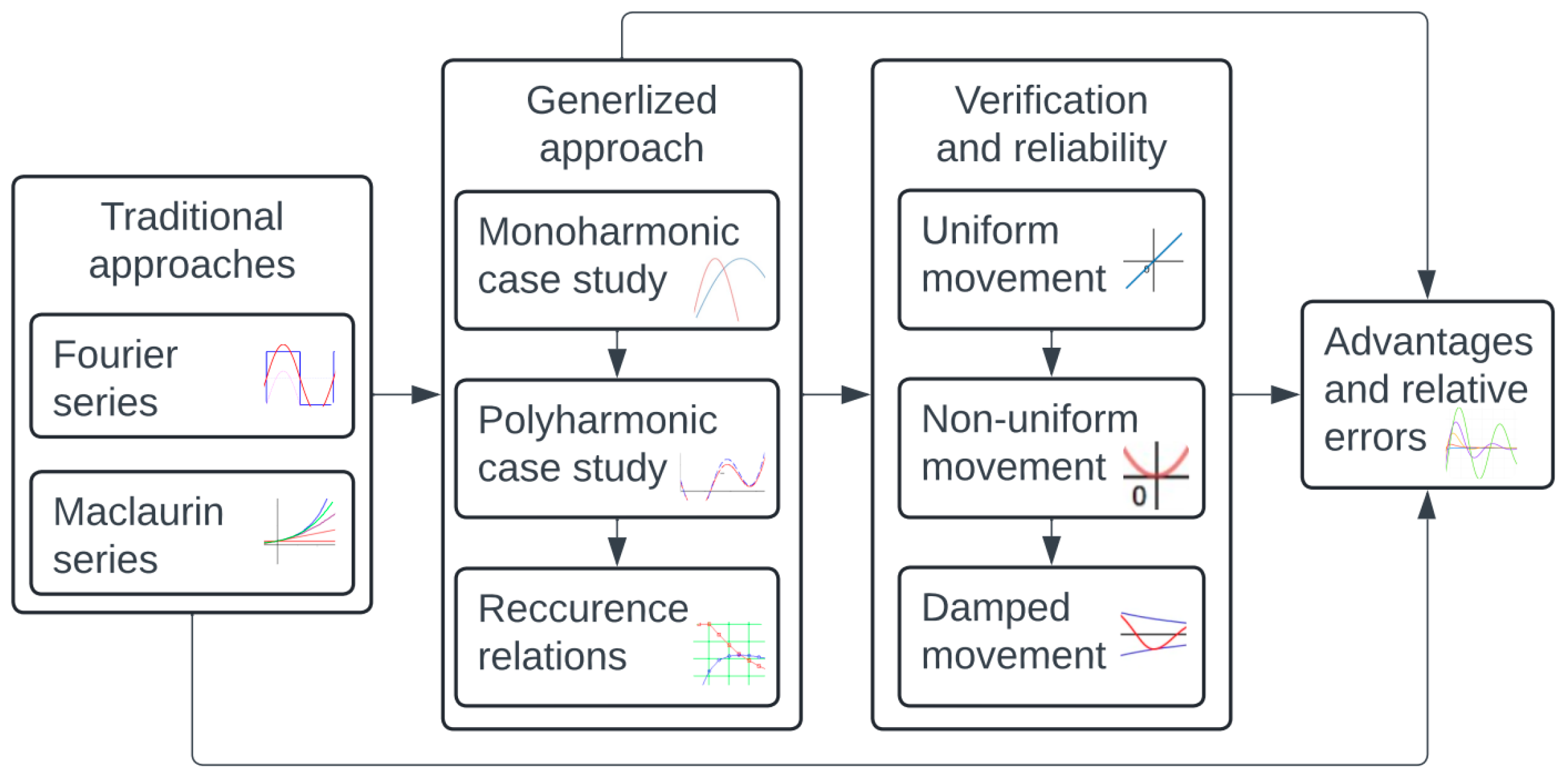
2.1. The Research Stages
2.2. The Monoharmonic Case Study
2.3. The Polyharmonic Case Study
3. Results
3.1. Recurrence Relations
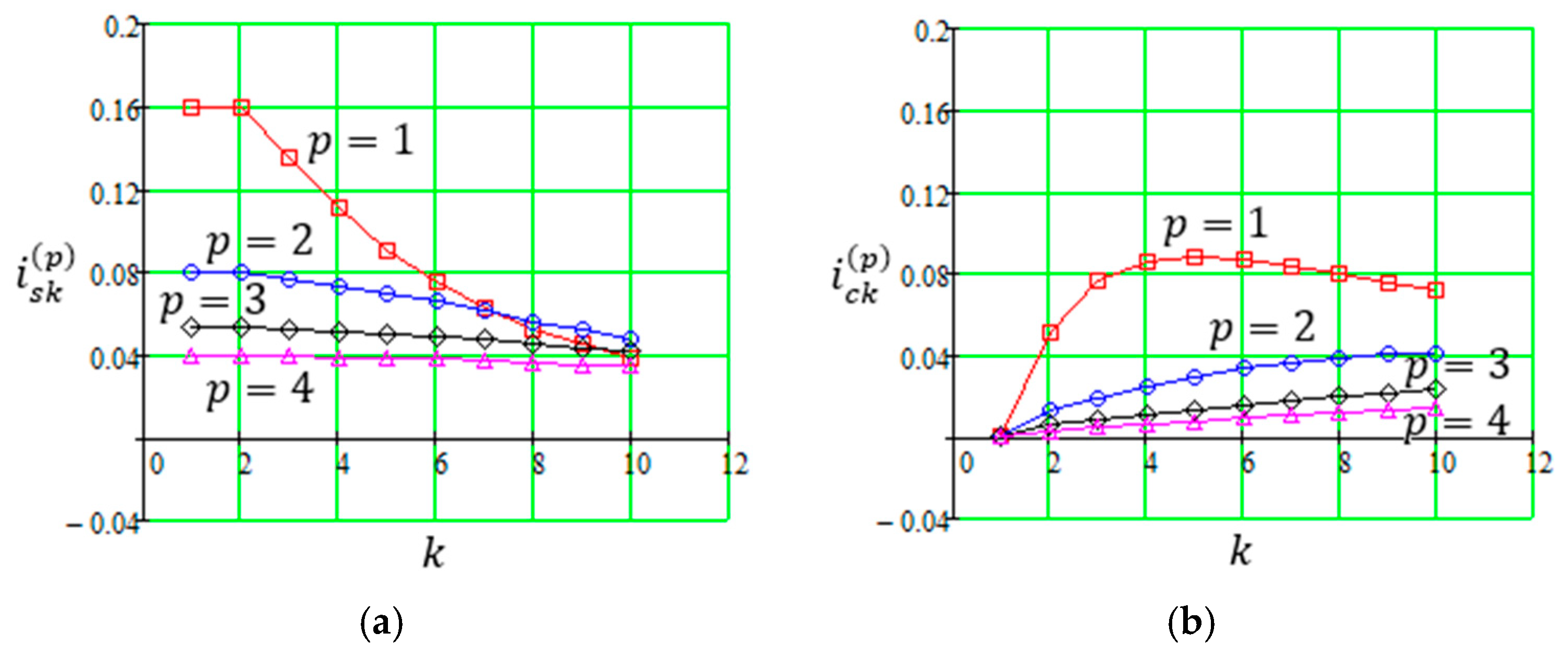
3.2. Numerical Calculation of Integrals
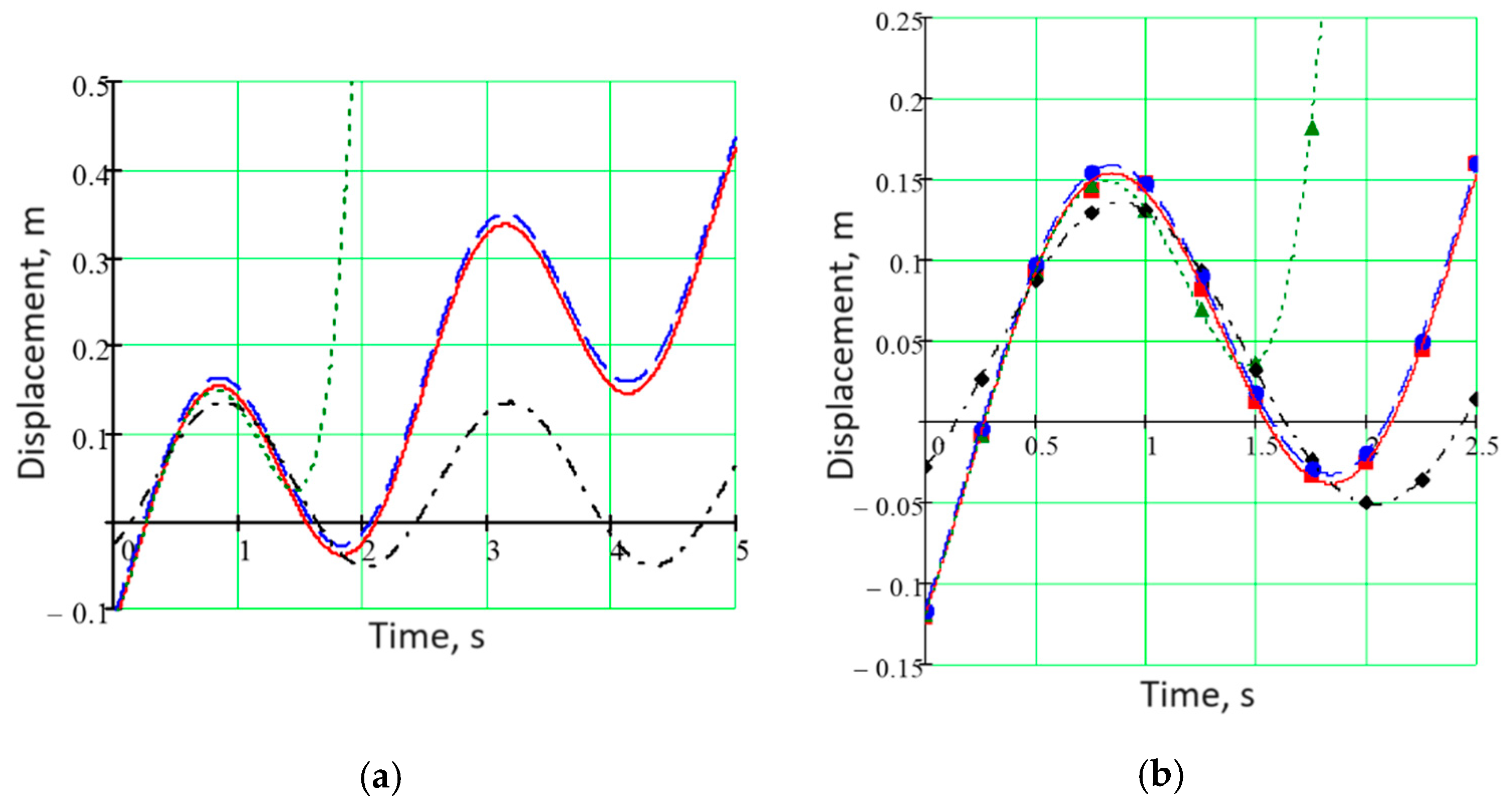
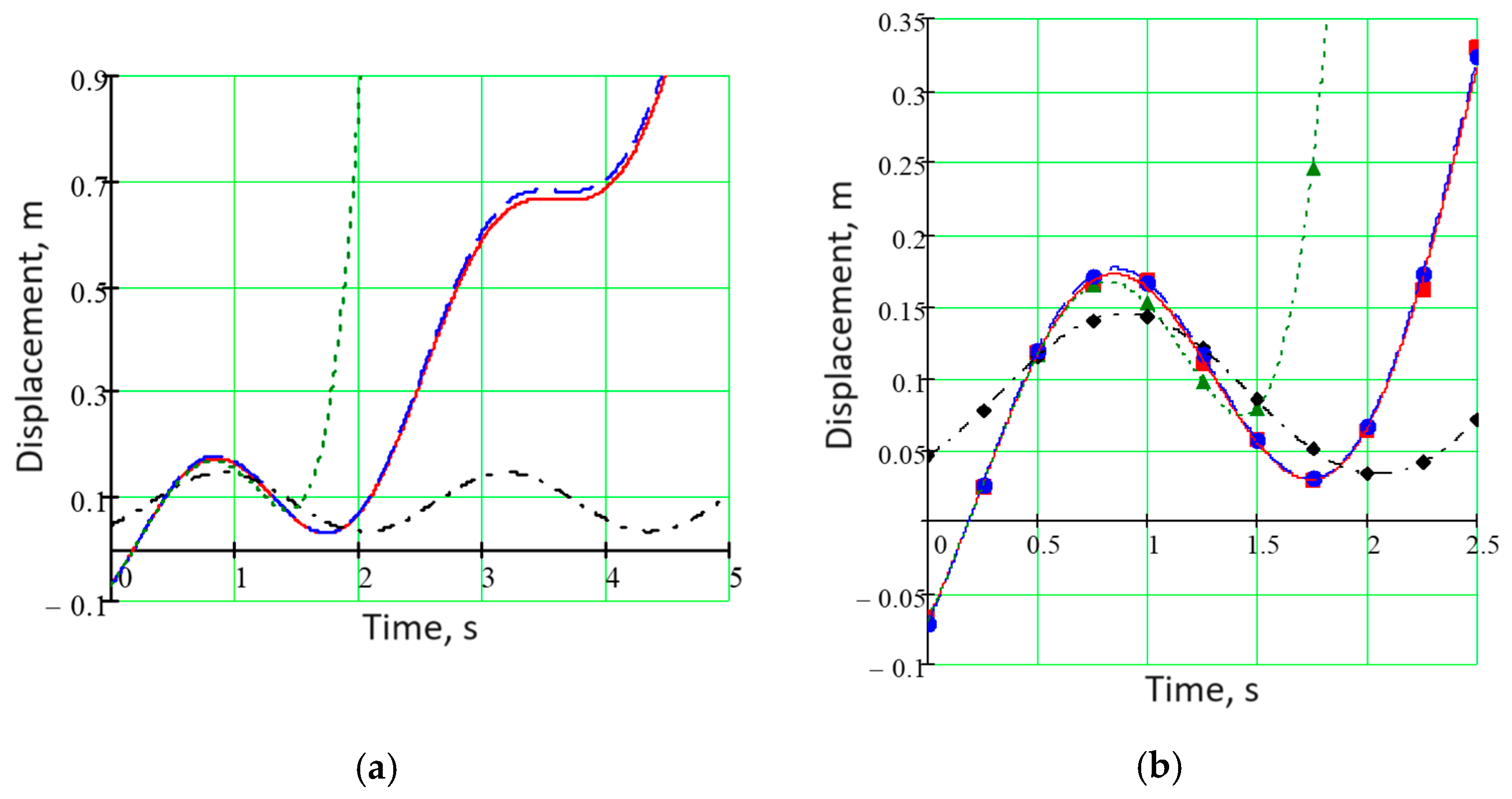
3.3. Examples of Numerical Calculations
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yegnanarayana, B.; D’Alessandro, C.; Darsinos, V. An iterative algorithm for decomposition of speech. IEEE Trans. Speech Audio Process. 1998, 6, 1–11. [Google Scholar] [CrossRef]
- D’Alessandro, C.; Darsinos, V.; Yegnanarayana, B. Effectiveness of a periodic and aperiodic decomposition method for analysis of voice sources. IEEE Trans. Speech Audio Process. 1998, 6, 12–23. [Google Scholar] [CrossRef]
- Barszcz, T. Decomposition of vibration signals into deterministic and non-deterministic components and its capabilities of fault detection and identification. Int. J. Appl. Math. Comput. Sci. 2009, 19, 327–335. [Google Scholar] [CrossRef]
- Lyons, R.; Zumbrun, K. A calculus proof of the Cramer–Wold theorem. Proc. Am. Math. Soc. 2018, 146, 1331–1334. [Google Scholar] [CrossRef]
- Zubrycki, P.; Petrovsky, A. Accurate speech decomposition into periodic and aperiodic components based on discrete harmonic transform. In Proceedings of the 15th European Signal Processing Conference (EUSIPCO 2007), Poznan, Poland, 3–7 September 2007; pp. 2336–2340. [Google Scholar]
- Prots’ko, I. The generalized technique of computation the discrete harmonic transforms. In Proceedings of the Perspective Technologies and Methods in MEMS Design (MEMSTECH 2008), Polyana, Ukraine, 21–24 May 2008; pp. 101–102. [Google Scholar] [CrossRef]
- Elie, B.; Chardon, G. Robust tonal and noise separation in presence of colored noise, and application to voiced fricatives. In Proceedings of the 22nd International Congress on Acoustics, Buenos Aires, Argentina, 5–9 September 2016. ICA2016-722. [Google Scholar]
- Pomme, S. Comparing significance criteria for cyclic modulations in time series. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 968, 163933. [Google Scholar] [CrossRef]
- Vijayan, K.; Dhiman, J.K.; Seelamantula, C.S. Time-frequency coherence for periodic-aperiodic decomposition of speech signals. In Proceedings of the Interspeech, Stockholm, Sweden, 20–24 August 2017; pp. 329–333. [Google Scholar] [CrossRef]
- Betancor, J.J.; Dalmasso, E.; Fariña, J.C.; Scotto, R. Bellman functions and dimension free Lp-estimates for the Riesz transforms in Bessel settings. Nonlinear Anal. Theory Methods Appl. 2020, 197, 111850. [Google Scholar] [CrossRef]
- Aczel, K.; Vajk, I. Separation of periodic and aperiodic sound components by employing frequency estimation. In Proceedings of the 16th European Signal Processing Conference (EUSIPCO 2008), Lausanne, Switzerland, 25–29 August 2008; pp. 1–5. [Google Scholar]
- Kaur, K.; Jindal, N.; Singh, K. Fractional fourier transform based Riesz fractional derivative approach for edge detection and its application in image enhancement. Signal Process. 2021, 180, 107852. [Google Scholar] [CrossRef]
- Hu, Q.; Huang, S.; Liang, M. Decomposition of speech signal into a periodic and an aperiodic part. In Proceedings of the First International Conference on Innovative Computing, Information and Control—Volume I (ICICI’06), Beijing, China, 30 August–1 September 2006; pp. 746–750. [Google Scholar] [CrossRef]
- Chaturvedi, G.K.; Thomas, D.W. Adaptive noise cancelling and condition monitoring. J. Sound Vib. 1981, 76, 391–405. [Google Scholar] [CrossRef]
- El-Sayed, A.A.; Agarwal, P. Numerical solution of multiterm variable-order fractional differential equations via shifted Legendre polynomials. Math. Methods Appl. Sci. 2019, 42, 3978–3991. [Google Scholar] [CrossRef]
- Luscinski, S.; Dobrowolski, D. System dynamics model for continuous review inventory system in demand shock conditions. In Advances in Design, Simulation and Manufacturing. DSMIE 2018. Lecture Notes in Mechanical Engineering; Ivanov, V., Rong, Y., Trojanowska, J., Venus, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; Springer: Cham, Switzerland, 2019; pp. 306–316. [Google Scholar] [CrossRef]
- Pavlenko, I.; Neamtu, C.; Verbovyi, A.; Pitel, J.; Ivanov, V.; Pop, G. Using computer modeling and artificial neural networks for ensuring the vibration reliability of rotors. CEUR Workshop Proc. 2019, 2353, 702–716. [Google Scholar] [CrossRef]
- Shao, Y.; Kang, R.; Li, R.; Liu, J. Reliability evaluation method of centrifugal compressor based on rotor vibration signal monitoring. In Proceedings of the 2021 3rd International Conference on System Reliability and Safety Engineering, SRSE 2021, Harbin, China, 26–28 November 2021; pp. 19–25. [Google Scholar] [CrossRef]
- Lishchenko, N.V.; Larshin, V.P.; Pitel, J. Vibrational impact on milled surface irregularities. J. Eng. Sci. 2020, 7, A8–A16. [Google Scholar] [CrossRef] [PubMed]
- Tarelnyk, V.; Konoplianchenko, I.; Martsynkovskyy, V.; Zhukov, A.; Kurp, P. Comparative tribological tests for face impulse seals sliding surfaces formed by various methods. In Advances in Design, Simulation and Manufacturing. DSMIE 2018. Lecture Notes in Mechanical Engineering; Ivanov, V., Ed.; Springer: Cham, Switzerland, 2019; pp. 382–391. [Google Scholar] [CrossRef]
- Vencl, A.; Vucetic, F.; Bobic, B.; Pitel, J.; Bobic, I. Tribological characterisation in dry sliding conditions of compocasted hybrid A356/SiCp/Grp composites with graphite macroparticles. Int. J. Adv. Manuf. Technol. 2019, 100, 2135–2146. [Google Scholar] [CrossRef]
- Ivanov, V.; Dehtiarov, I.; Denysenko, Y.; Malovana, N.; Martynova, N. Experimental diagnostic research of fixture. Diagnostyka 2018, 19, 3–9. [Google Scholar] [CrossRef]
- Olejárová, Š.; Krenický, T. Water Jet Technology: Experimental verification of the input factors variation influence on the generated vibration levels and frequency spectra. Materials 2021, 14, 4281. [Google Scholar] [CrossRef] [PubMed]
- Panda, A.; Prislupcak, M.; Jurko, J.; Pandova, I.; Mrkvica, I.; Luscinski, S. The impact of vibration on the technological head. Manuf. Technol. 2016, 16, 579–585. [Google Scholar] [CrossRef]
- Molitoris, M.; Piteľ, J.; Hošovský, A.; Tóthová, M.; Židek, K. A review of research on water jet with slurry injection. Procedia Eng. 2016, 149, 333–339. [Google Scholar] [CrossRef][Green Version]
- Orgiyan, A.; Tkachenko, B.; Oborskyi, G.; Balaniuk, A.; Iorgachov, V. Determining rational cutting modes for horizontal boring operation adjusted for the variable rigidity of the process system. In Advanced Manufacturing Processes. InterPartner 2019. Lecture Notes in Mechanical Engineering; Tonkonogyi, V., Rong, Y., Trojanowska, J., Venus, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; Springer: Cham, Switzerland, 2020; pp. 246–253. [Google Scholar] [CrossRef]
- Pavlenko, I.; Liaposhchenko, A.; Ochowiak, M.; Demyanenko, M. Solving the stationary hydroaeroelasticity problem for dynamic deflection elements of separation devices. Vib. Phys. Syst. 2018, 29, 2018026. [Google Scholar]
- Zavialov, V.; Mysiura, T.; Popova, N.; Sukmanov, V.; Chornyi, V. Regularities of solid-phase continuous vibration extraction and prospects for its industrial use. In Advances in Design, Simulation and Manufacturing. DSMIE 2019. Lecture Notes in Mechanical Engineering; Ivanov, V., Rong, Y., Trojanowska, J., Venus, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; Springer: Cham, Switzerland, 2020; pp. 920–930. [Google Scholar] [CrossRef]
- Sprung, D.W.L.; Betti, M.I.; Van Dijk, W. Finite Fourier transforms computed by a modified Filon-Euler-Maclaurin method. Comput. Phys. Commun. 2013, 184, 607–616. [Google Scholar] [CrossRef]
- Lian, P. Quaternion and fractional Fourier transform in higher dimension. Appl. Math. Comput. 2021, 389, 125585. [Google Scholar] [CrossRef]

| p | k | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 0.159 | 0.159 | 0.135 | 0.111 | 0.091 | 0.075 | 0.063 | 0.053 | 0.045 | 0.039 |
| 2 | 0.08 | 0.08 | 0.077 | 0.074 | 0.07 | 0.066 | 0.061 | 0.056 | 0.052 | 0.047 |
| 3 | 0.053 | 0.053 | 0.052 | 0.051 | 0.05 | 0.049 | 0.047 | 0.045 | 0.044 | 0.042 |
| 4 | 0.040 | 0.04 | 0.039 | 0.039 | 0.039 | 0.038 | 0.037 | 0.036 | 0.036 | 0.035 |
| 5 | 0.032 | 0.032 | 0.032 | 0.031 | 0.031 | 0.031 | 0.031 | 0.03 | 0.03 | 0.029 |
| 6 | 0.027 | 0.027 | 0.026 | 0.026 | 0.026 | 0.026 | 0.026 | 0.026 | 0.025 | 0.025 |
| 7 | 0.023 | 0.023 | 0.023 | 0.023 | 0.023 | 0.022 | 0.022 | 0.022 | 0.022 | 0.022 |
| 8 | 0.020 | 0.020 | 0.020 | 0.020 | 0.020 | 0.020 | 0.020 | 0.019 | 0.019 | 0.019 |
| 9 | 0.018 | 0.018 | 0.018 | 0.018 | 0.018 | 0.018 | 0.017 | 0.017 | 0.017 | 0.017 |
| 10 | 0.016 | 0.016 | 0.016 | 0.016 | 0.016 | 0.016 | 0.016 | 0.016 | 0.016 | 0.016 |
| p | k | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 0.000 | 0.051 | 0.076 | 0.086 | 0.088 | 0.087 | 0.084 | 0.08 | 0.076 | 0.072 |
| 2 | 0.000 | 0.013 | 0.019 | 0.024 | 0.029 | 0.033 | 0.037 | 0.039 | 0.04 | 0.041 |
| 3 | 0.000 | 0.006 | 0.008 | 0.011 | 0.014 | 0.016 | 0.018 | 0.02 | 0.022 | 0.023 |
| 4 | 0.000 | 0.003 | 0.005 | 0.006 | 0.008 | 0.009 | 0.011 | 0.012 | 0.013 | 0.014 |
| 5 | 0.000 | 0.002 | 0.003 | 0.004 | 0.005 | 0.006 | 0.007 | 0.008 | 0.009 | 0.009 |
| 6 | 0.000 | 0.001 | 0.002 | 0.003 | 0.003 | 0.004 | 0.005 | 0.005 | 0.006 | 0.007 |
| 7 | 0.000 | 0.001 | 0.002 | 0.002 | 0.003 | 0.003 | 0.004 | 0.004 | 0.005 | 0.005 |
| 8 | 0.000 | 0.001 | 0.001 | 0.002 | 0.002 | 0.002 | 0.003 | 0.003 | 0.003 | 0.004 |
| 9 | 0.000 | 0.001 | 0.001 | 0.001 | 0.002 | 0.002 | 0.002 | 0.002 | 0.003 | 0.003 |
| 10 | 0.000 | 0.001 | 0.001 | 0.001 | 0.001 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| Time, s | Actual Value, m | Evaluated Value, m | ||
|---|---|---|---|---|
| Fourier Series | Maclaurin Series | Proposed Approach | ||
| 0.0 | −0.121 | −0.028 | −0.120 | −0.121 |
| 0.2 | −0.008 | 0.026 | −0.009 | −0.009 |
| 0.4 | 0.093 | 0.088 | 0.093 | 0.093 |
| 0.6 | 0.143 | 0.129 | 0.145 | 0.149 |
| 0.8 | 0.148 | 0.131 | 0.131 | 0.142 |
| 1.0 | 0.082 | 0.093 | 0.069 | 0.085 |
| 1.2 | 0.013 | 0.032 | 0.036 | 0.013 |
| 1.4 | −0.033 | −0.024 | 0.182 | −0.034 |
| 1.6 | −0.025 | −0.051 | 0.748 | −0.024 |
| 1.8 | 0.044 | −0.036 | 2.086 | 0.046 |
| 2.0 | 0.159 | 0.014 | 4.674 | 0.154 |
| Time, s | Actual Value, m | Evaluated Value, m | ||
|---|---|---|---|---|
| Fourier Series | Maclaurin Series | Proposed Approach | ||
| 0.0 | −0.067 | 0.045 | −0.070 | −0.070 |
| 0.2 | 0.024 | 0.077 | 0.025 | 0.025 |
| 0.4 | 0.117 | 0.114 | 0.115 | 0.116 |
| 0.6 | 0.164 | 0.140 | 0.164 | 0.167 |
| 0.8 | 0.167 | 0.142 | 0.151 | 0.162 |
| 1.0 | 0.109 | 0.120 | 0.097 | 0.113 |
| 1.2 | 0.056 | 0.084 | 0.079 | 0.055 |
| 1.4 | 0.028 | 0.049 | 0.245 | 0.029 |
| 1.6 | 0.062 | 0.033 | 0.838 | 0.065 |
| 1.8 | 0.162 | 0.040 | 2.208 | 0.167 |
| 2.0 | 0.330 | 0.070 | 4.835 | 0.315 |
| Time, s | Actual Value, m | Evaluated Value, m | ||
|---|---|---|---|---|
| Fourier Series | Maclaurin Series | Proposed Approach | ||
| 0.0 | 0.010 | 0.285 | 0.010 | 0.010 |
| 0.2 | 0.060 | 0.295 | 0.060 | 0.060 |
| 0.4 | 0.127 | 0.321 | 0.133 | 0.123 |
| 0.6 | 0.206 | 0.370 | 0.576 | 0.206 |
| 0.8 | 0.297 | 0.423 | 4.520 | 0.290 |
| 1.0 | 0.287 | 0.393 | – | 0.288 |
| 1.2 | 0.121 | 0.196 | – | 0.118 |
| 1.4 | −0.002 | 0.052 | – | −0.002 |
| 1.6 | 0.118 | 0.147 | – | 0.115 |
| 1.8 | 0.265 | 0.274 | – | 0.263 |
| 2.0 | 0.292 | 0.297 | – | 0.302 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavlenko, I.; Trojanowska, J.; Ivanov, V.; Radchenko, S.; Husár, J.; Mižáková, J. Signal Decomposition for Monitoring Systems of Processes. Processes 2024, 12, 1188. https://doi.org/10.3390/pr12061188
Pavlenko I, Trojanowska J, Ivanov V, Radchenko S, Husár J, Mižáková J. Signal Decomposition for Monitoring Systems of Processes. Processes. 2024; 12(6):1188. https://doi.org/10.3390/pr12061188
Chicago/Turabian StylePavlenko, Ivan, Justyna Trojanowska, Vitalii Ivanov, Svetlana Radchenko, Jozef Husár, and Jana Mižáková. 2024. "Signal Decomposition for Monitoring Systems of Processes" Processes 12, no. 6: 1188. https://doi.org/10.3390/pr12061188
APA StylePavlenko, I., Trojanowska, J., Ivanov, V., Radchenko, S., Husár, J., & Mižáková, J. (2024). Signal Decomposition for Monitoring Systems of Processes. Processes, 12(6), 1188. https://doi.org/10.3390/pr12061188










