Simulation of Elbow Erosion of Gas–Liquid–Solid Three-Phase Shale Gas Gathering Pipeline Based on CFD-DEM
Abstract
:1. Introduction
2. Numerical Modeling
2.1. VOF-DEM Modeling
- (1)
- Continuity equation: Tracking the interface between phases is carried out by solving the continuity equation for the volume ratio of a single or multiphase fluid. For phase q, there is the following:
- (2)
- Momentum equation: By solving a single momentum equation for the entire region, the resulting velocity field is shared by the phases. The momentum equation depends on the volume ratio of all phases through the properties ρ and μ. The equation is as follows:
2.2. Turbulence Model
2.3. Fluid–Particle Force
2.4. Erosion Prediction Model
3. Physical Model and Solution Method
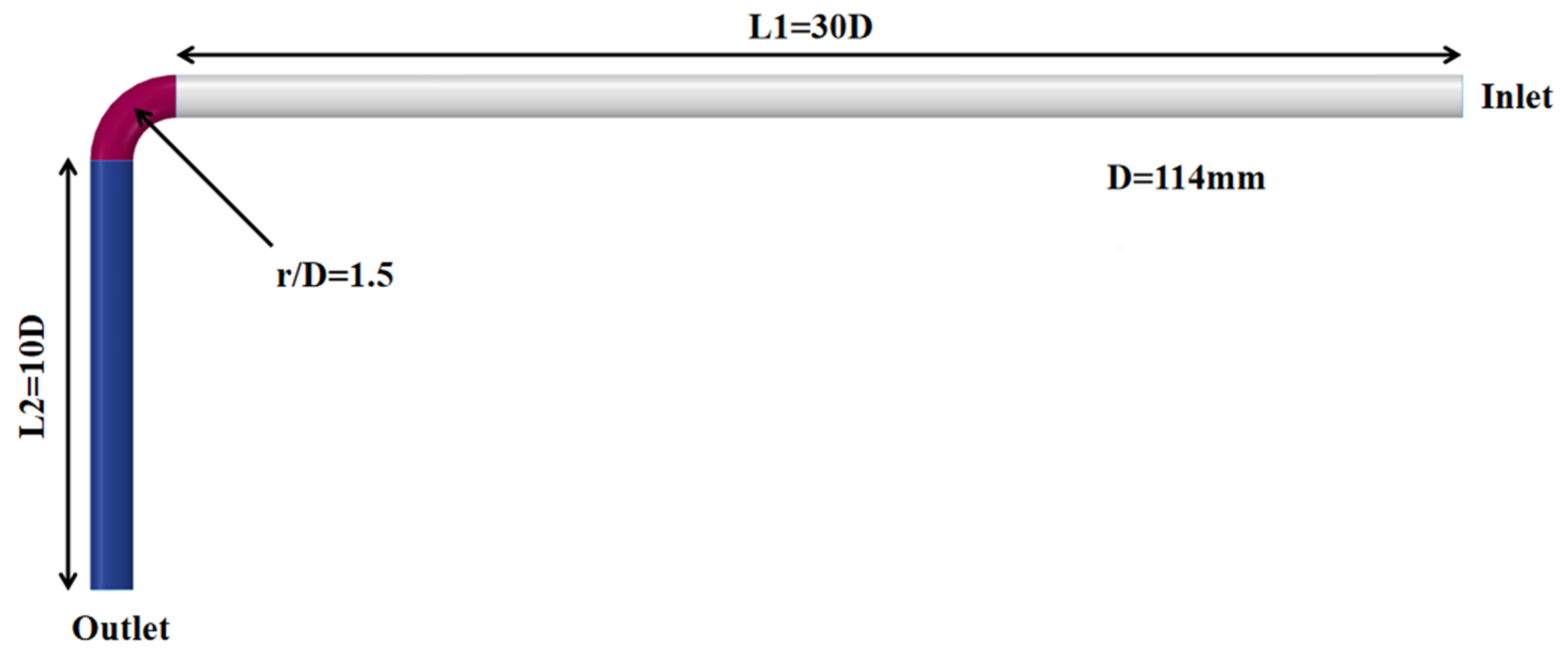
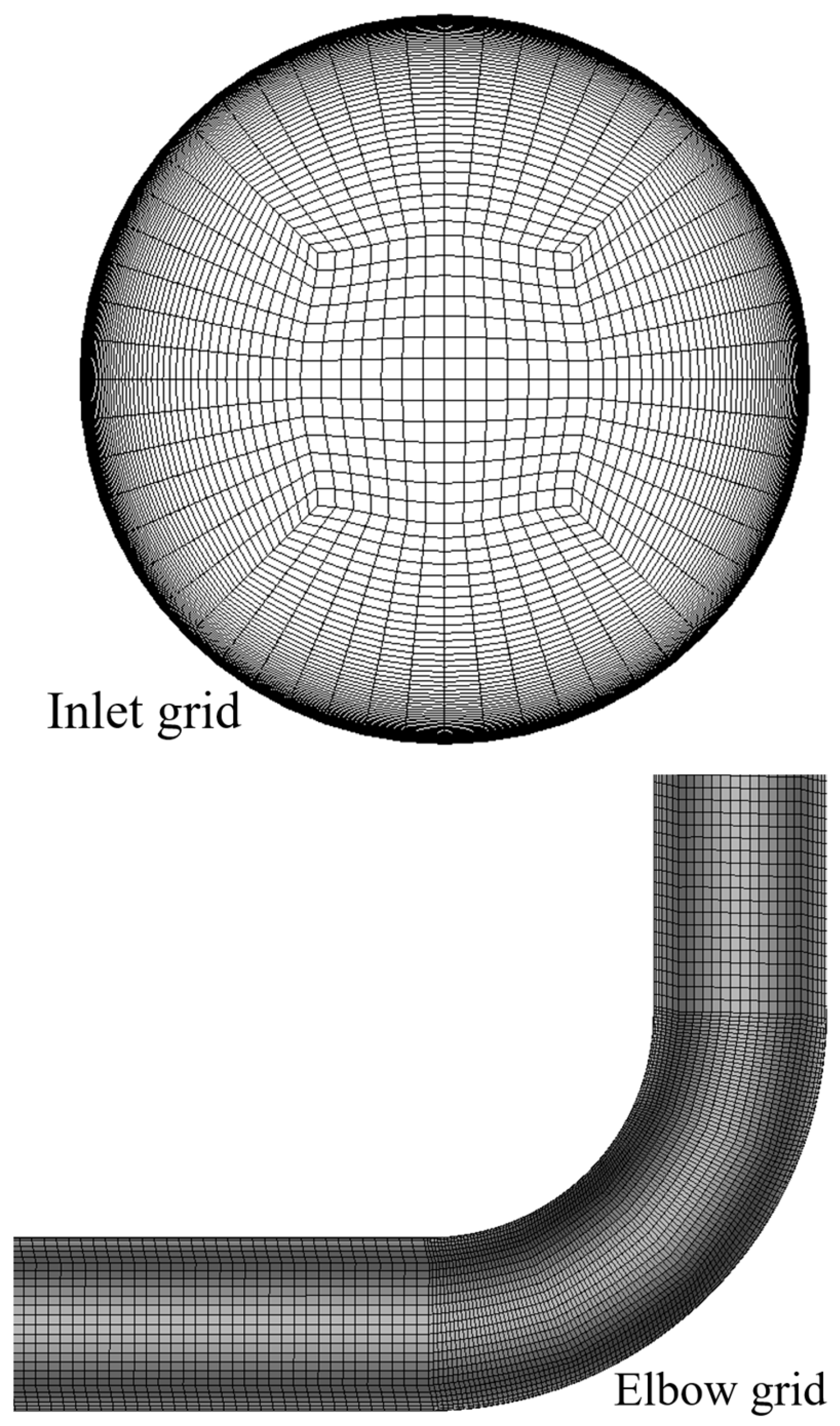
3.1. Geometry and Meshing
3.2. Simulation Parameter Settings
3.2.1. Basic Working Condition Parameter Setting
3.2.2. Particle Parameter Settings
3.3. Boundary Conditions and Simulation Procedure
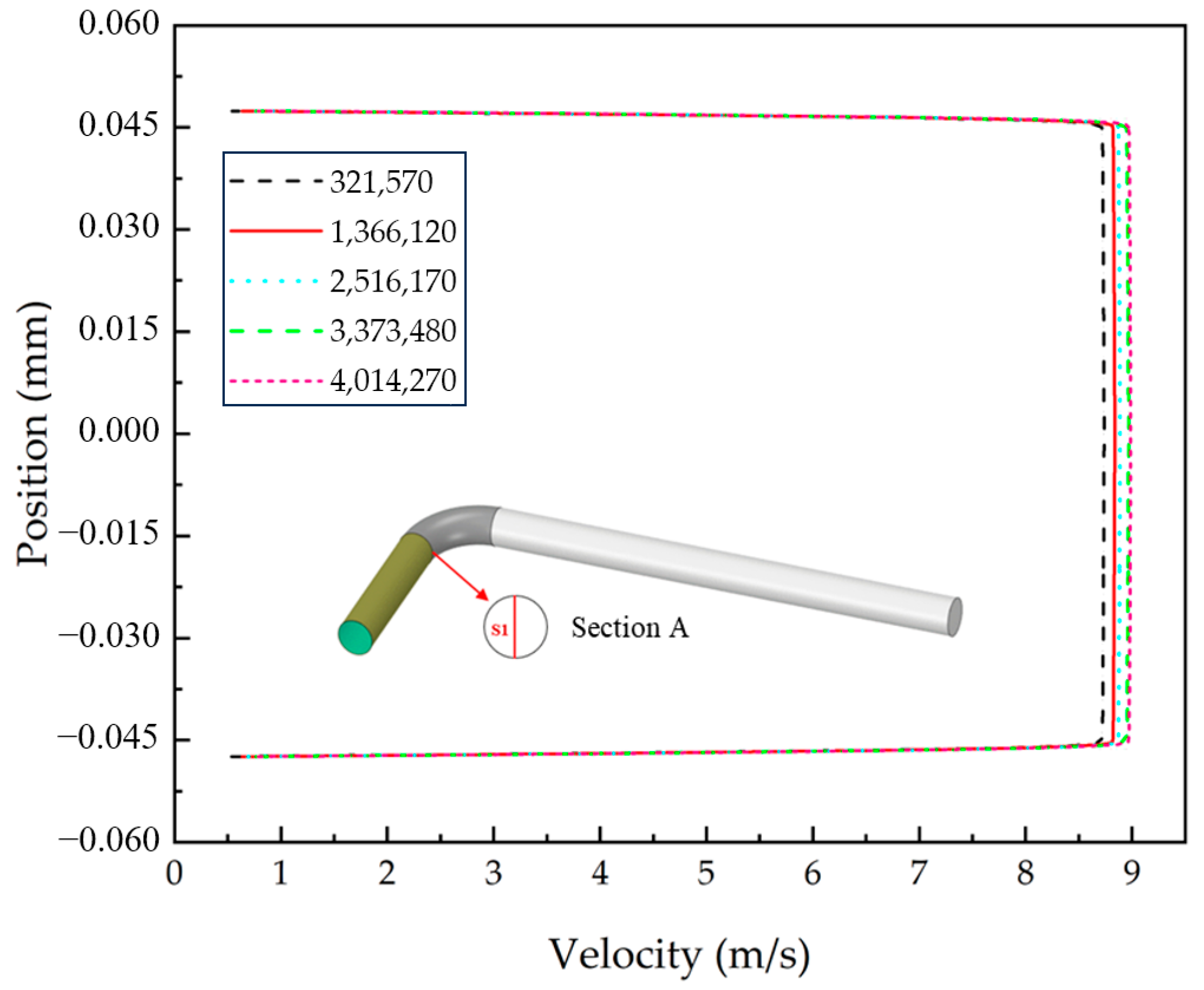
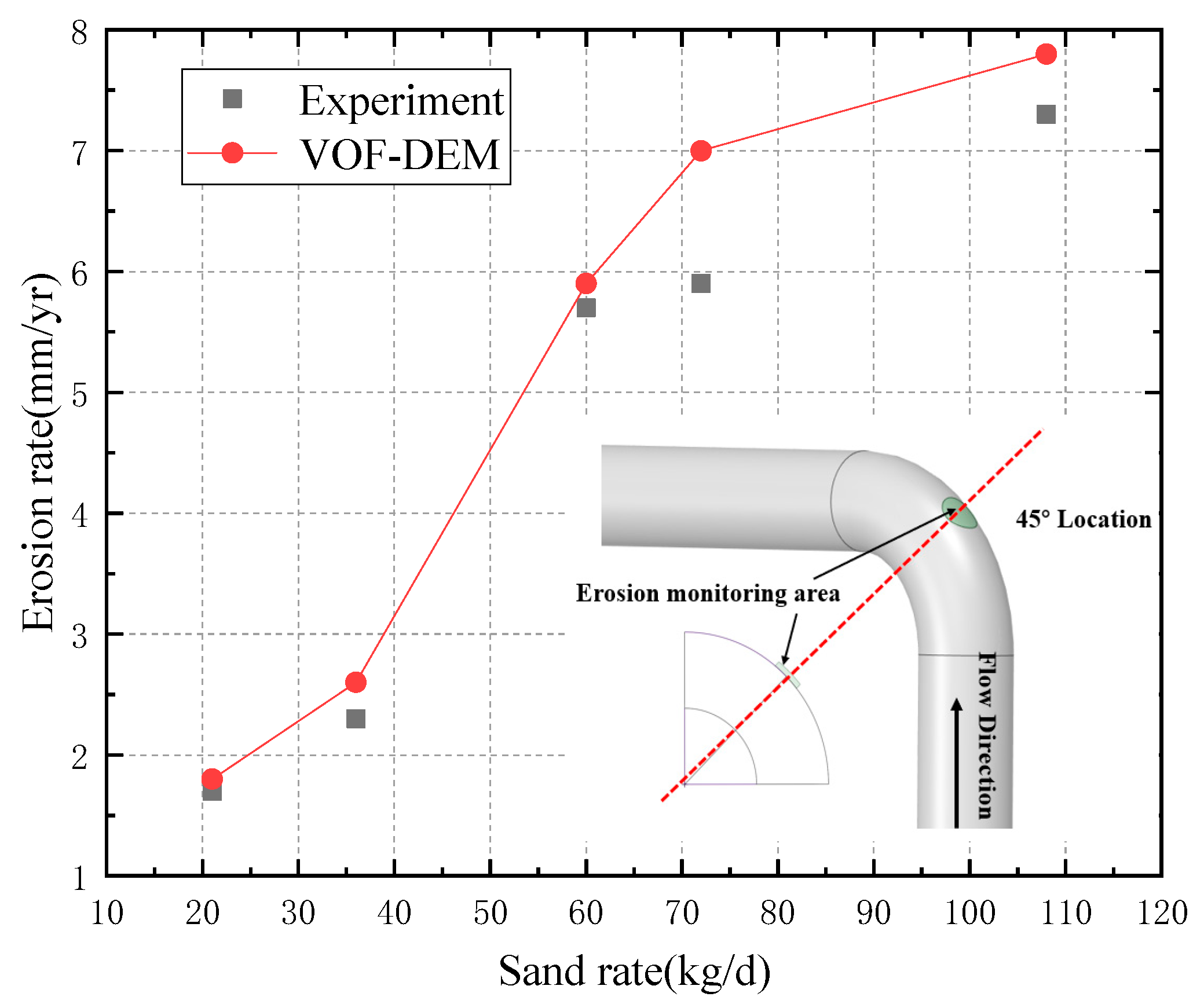
3.4. Model Validation
4. Results and Discussion
4.1. Three-Phase Flow Characteristic
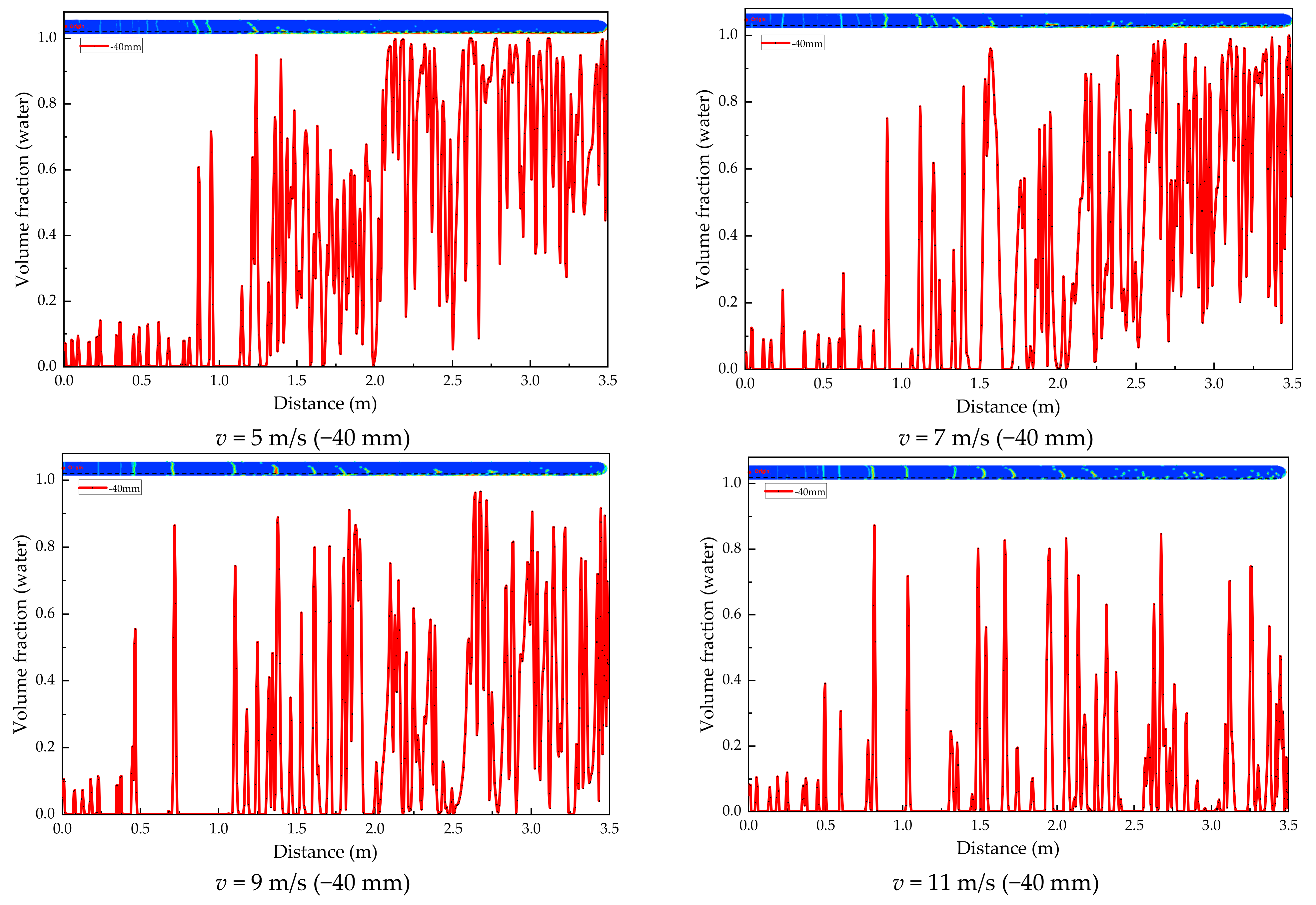
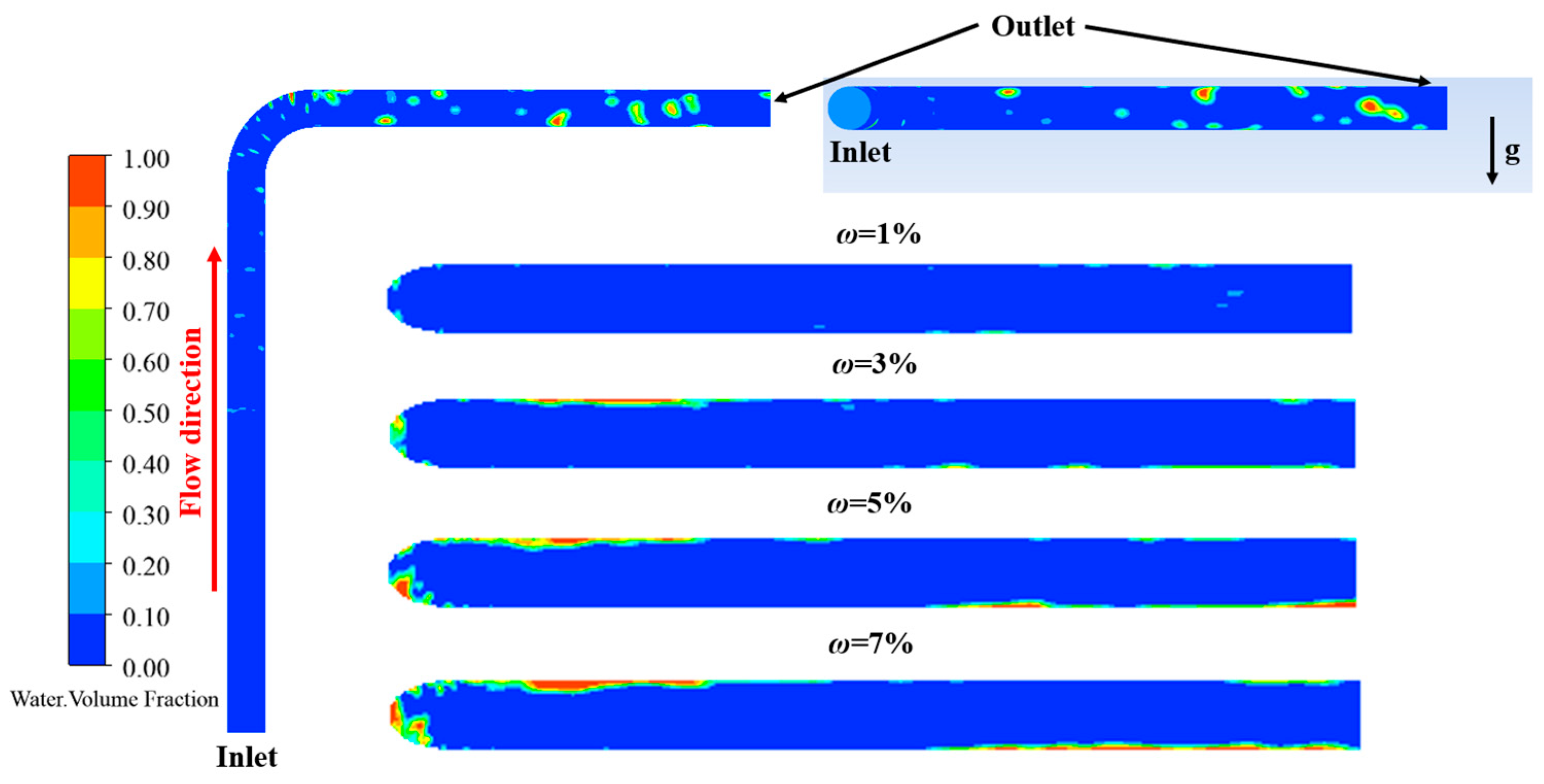
4.1.1. Analysis of Gas–Liquid Two-Phase Flow
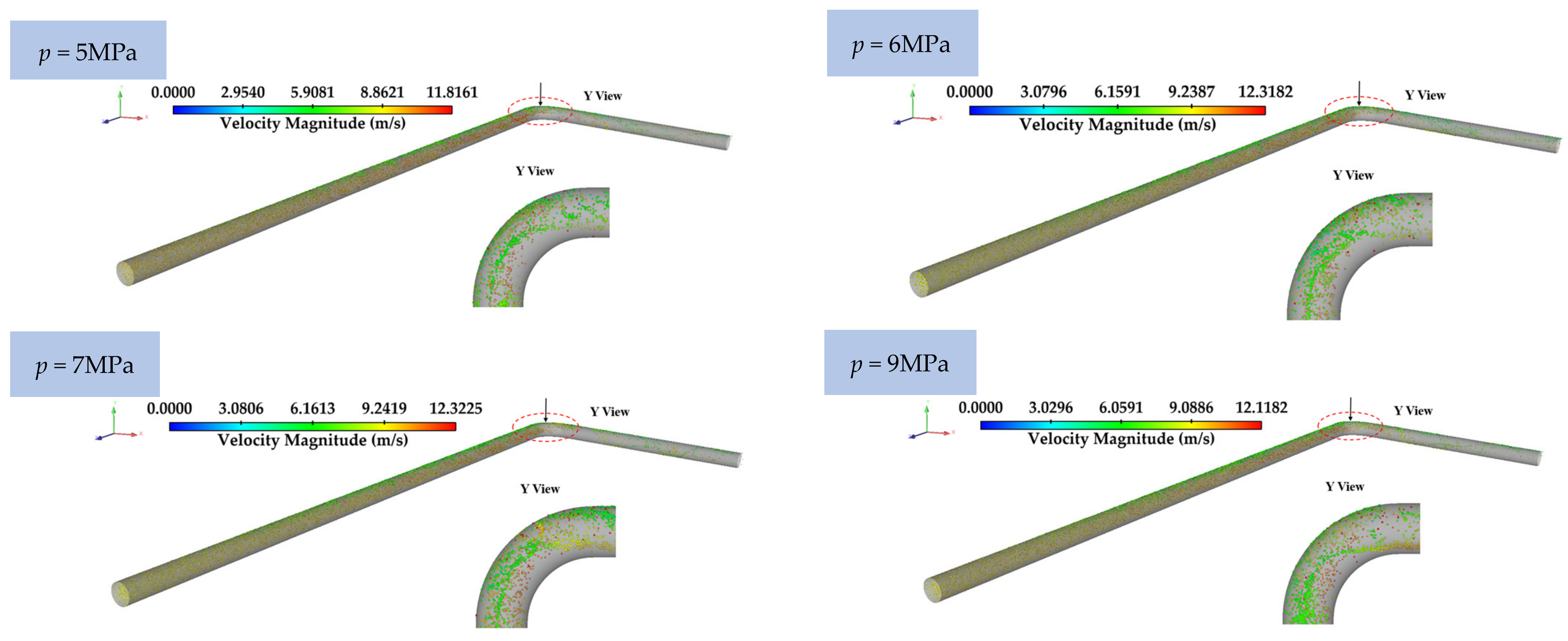
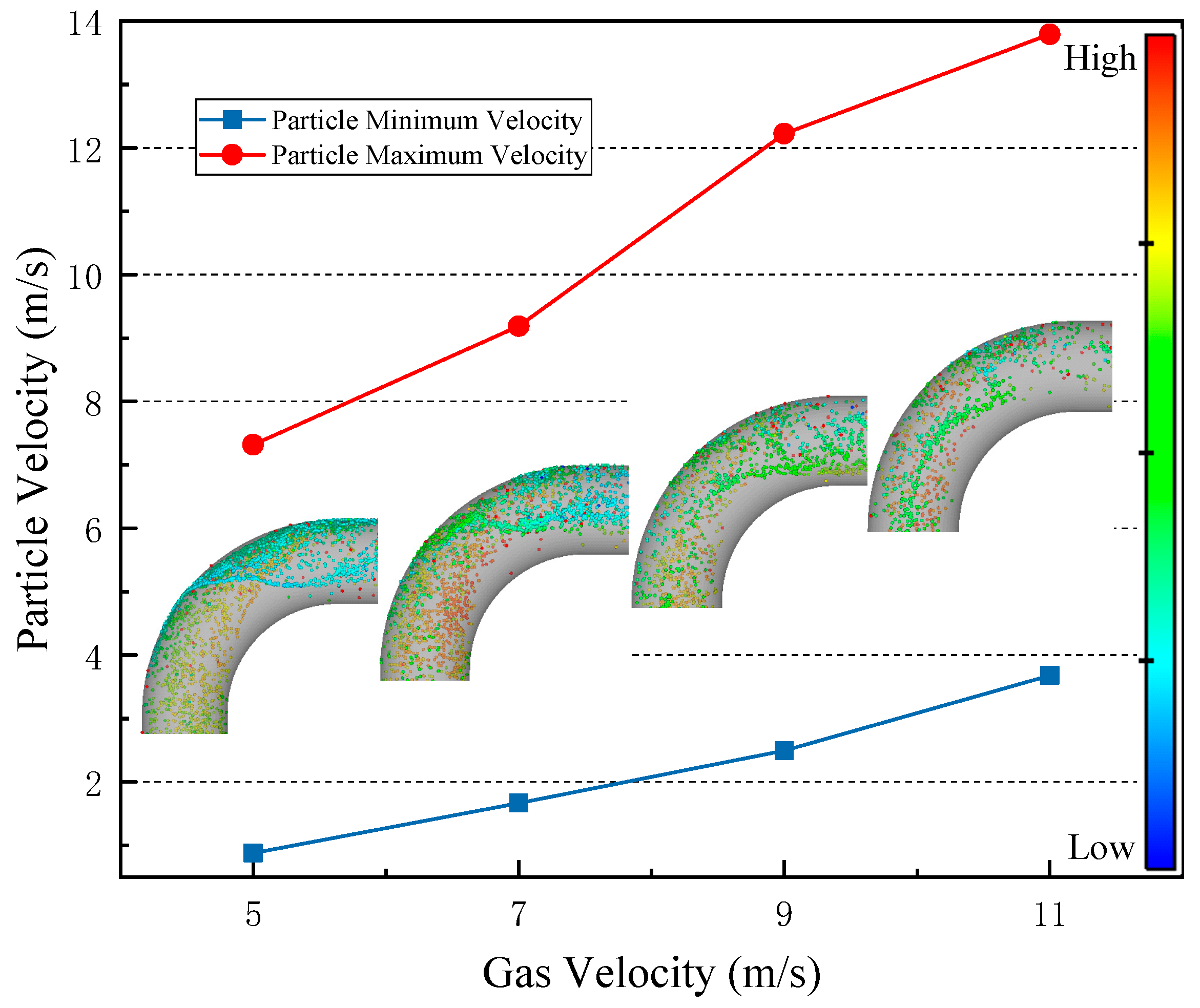
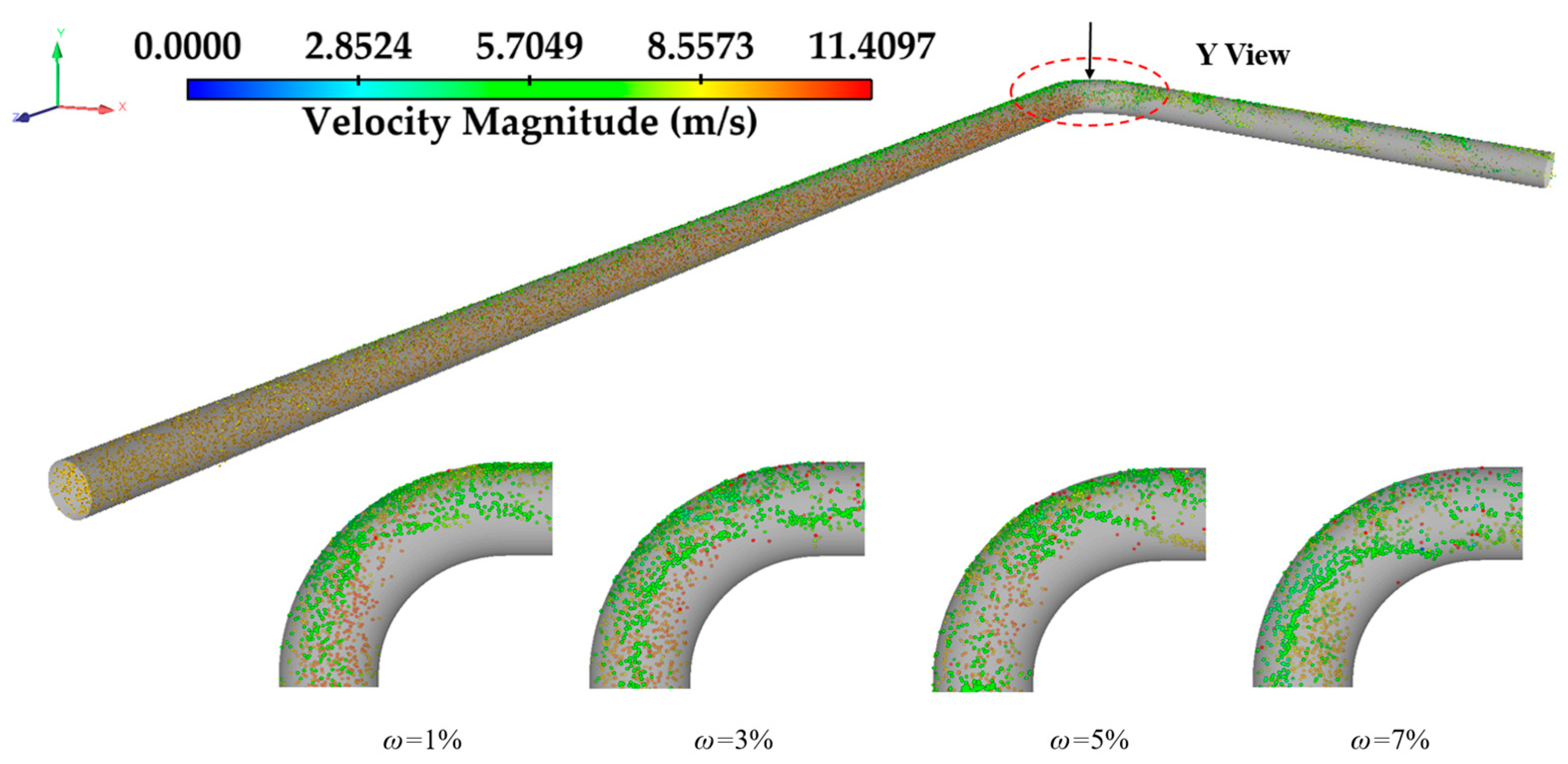
4.1.2. Particle Velocity Distribution and Trajectory
4.2. Analysis of Elbow Erosion
4.2.1. Elbow Wall Erosion
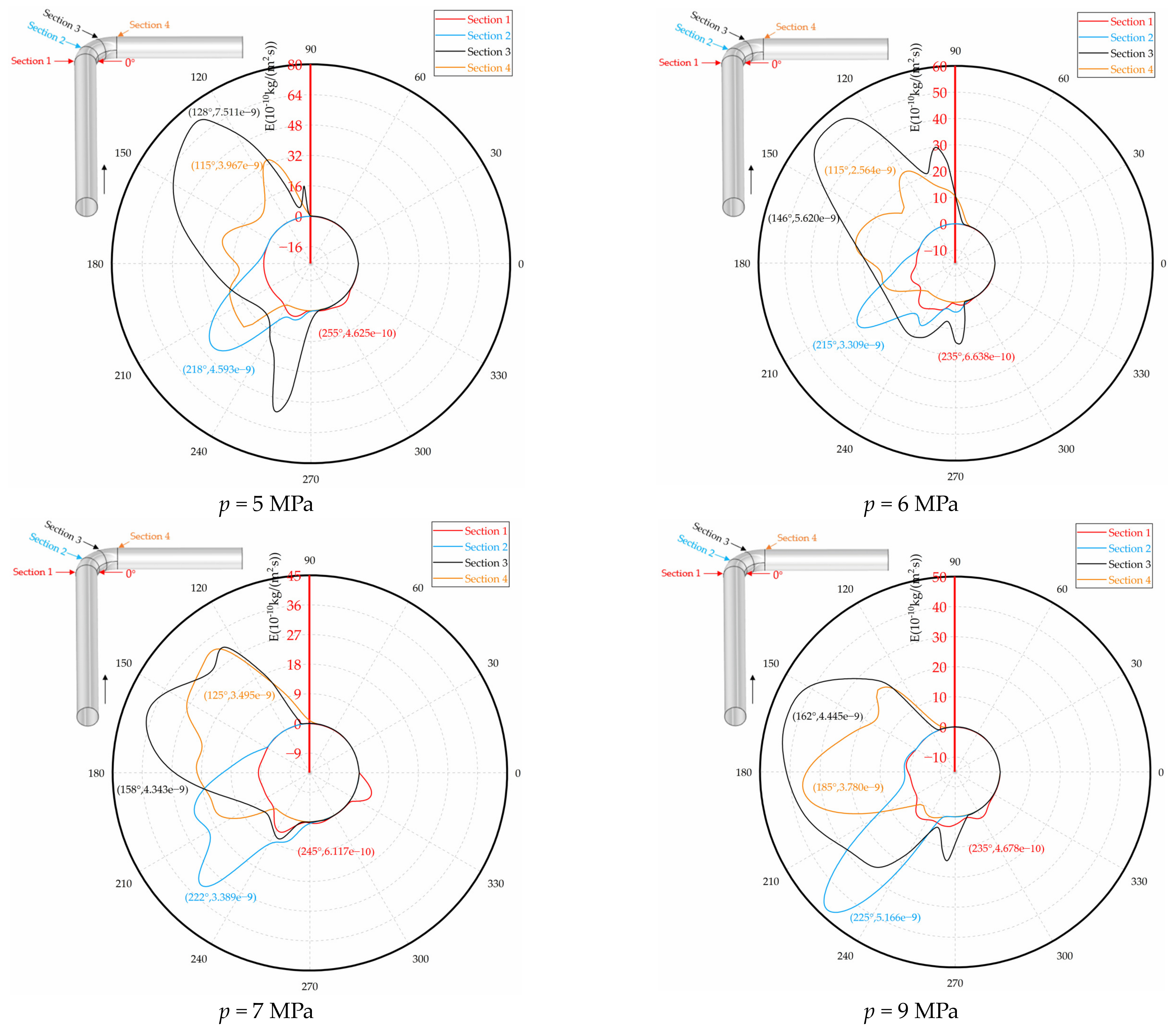
4.2.2. Circumferential Erosion of Elbow
5. Conclusions
- (1)
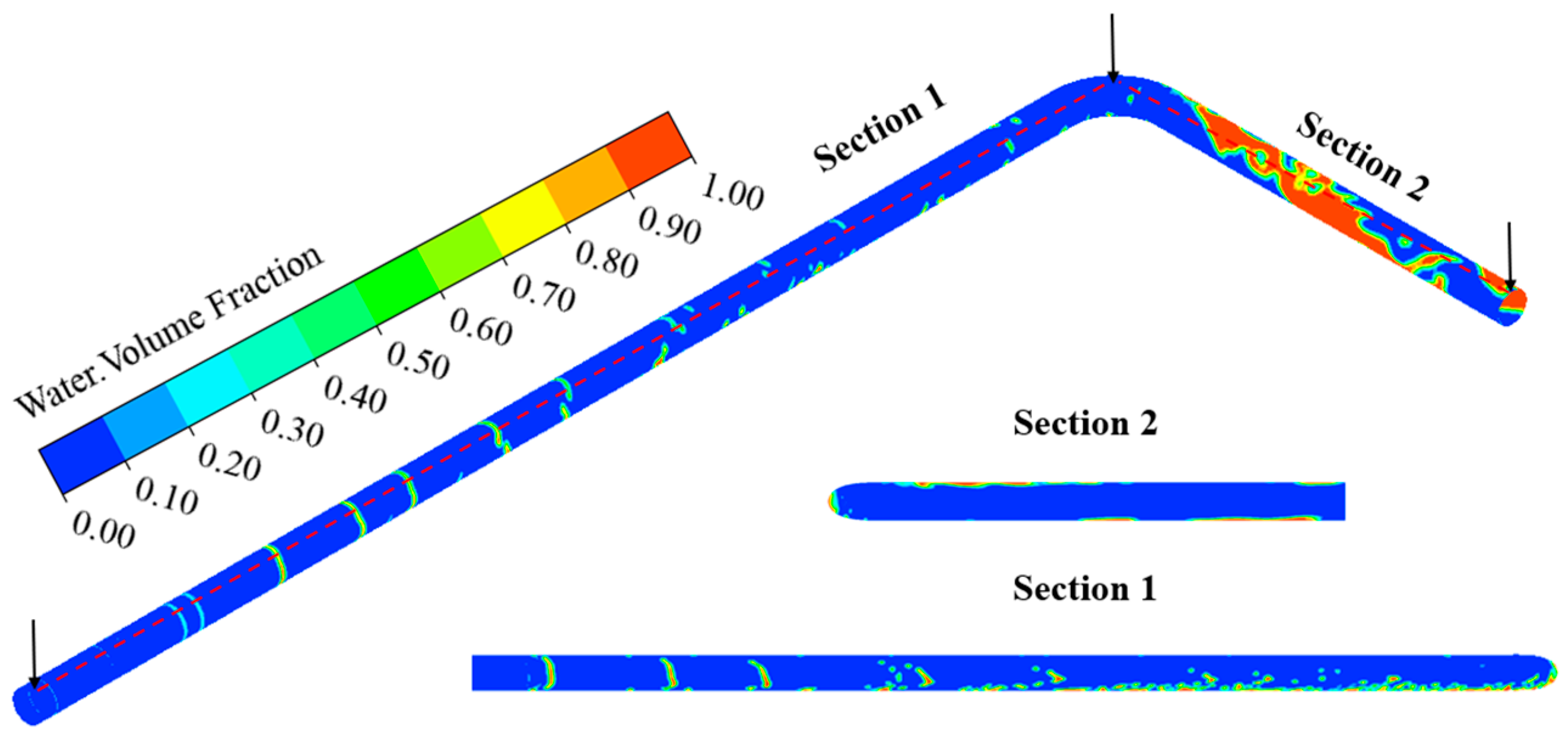
- When the gas flow rate is small, there is a certain amount of ponding at the bottom of the inlet pipe. When the gas flow rate increases, the volume of water in the horizontal section of the inlet is small and some water phase is dispersed. When the gathering pressure is small, there is a certain amount of ponding at the bottom of the inlet pipe. With the increase in gathering pressure, the water volume at the bottom of the inlet pipe decreases, while the water phase at the top of the outlet pipe changes from the state of aggregation to the state of dispersion. When the water content in the pipe is small, there is basically no ponding at the bottom of the inlet pipe. When the water content increases, the volume of water in the tube increases, and the height of the water increases. The water phase at the elbow mainly collects on the outer arch wall and the top area of the elbow outlet.
- (2)
- When the gas flow rate, gathering pressure, and water content in the pipe change, respectively, the particles move from the bottom of the pipe to the elbow after entering the inlet pipe and then collide with the outer arch wall of the elbow and rotate counterclockwise along the outer arch wall of the outlet pipe facing the top of the pipe. At the same time, the erosion area of the elbow is consistent with the movement track of particles at the elbow, mainly concentrated on the outer arch wall of the elbow and the inclined area between the outer arch wall of the elbow and the top of the outlet pipe.
- (3)
- When the gas flow rate increases, the particles at the elbow mainly gather at the bottom of the elbow and the outer wall, and the maximum particle velocity increases with the increase in the gas flow rate. When the gathering pressure is 4–8 MPa, most of the particles mainly collect at the bottom of the pipeline and the outer arch wall, and when the gathering pressure increases to 9 MPa, the particles gradually move to the top of the outlet pipeline. When the water content in the pipe is 1%, the particles mainly gather on the outer wall of the elbow. When the water content in the pipe increases gradually, the particles gathered on the outer wall of the elbow move along the outer wall of the elbow and face the inner arch surface.
- (4)
- The erosion position on the same section of the elbow remains consistent across varying gas flow rates. As the gas flow rate increases, the degree of erosion on the elbow section also increases. Moreover, an increase in the gathering pressure leads to a higher maximum erosion rate on the wall and a larger erosion area. Conversely, an increase in water content results in a decrease in the collision area between particles and the wall, leading to a relatively reduced erosion area. However, despite this reduction, the maximum erosion rate on the wall actually increases with higher water content. When the gas flow rate, gathering pressure, and water content in the pipe increase, respectively, the erosion zone from Sections 1 to 4 rotates clockwise from the outer arch wall of the elbow to the top of the pipe. The most serious erosion on the elbow is at Section 3.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, C.; Zhao, Q.; Dong, D.; Yang, Z.; Qiu, Z.; Liang, F.; Wang, N.; Huang, Y.; Duan, A.; Zhang, Q.; et al. Geological characteristics, main challenges and future prospect of shale gas. Nat. Gas Geosci. 2017, 28, 1781–1796. [Google Scholar] [CrossRef]
- Zou, C.; Zhao, Q.; Cong, L.; Wang, H.; Shi, Z.; Wu, J.; Pang, S. Development progress, potential and prospect of shale gas in China. Nat. Gas Geosci. 2021, 41, 1–14. [Google Scholar]
- Gui, S.; Xing, F.; Li, Q. Research of Pipe Erosion for Aqueous Natural Gas Based on CFD. Bull. Sci. Technol. 2017, 33, 89–92. [Google Scholar]
- Vieira, R.E.; Parsi, M.; Zahedi, P.; McLaury, B.S.; Shirazi, S.A. Sand erosion measurements under multiphase annular flow conditions in a horizontal-horizontal elbow. Powder Technol. 2017, 320, 625–636. [Google Scholar] [CrossRef]
- Li, J. Study on Influencing Factors of Erosion Failure of Large Diameter Pipeline; Northeast Petroleum University: Daqing, China, 2019. [Google Scholar]
- Xu, S. Simulation Research and Influencing Factors Analysis on Petroleum Pipeline Erosion. Pet. Tubul. Goods Instrum. 2019, 5, 25–27,32. [Google Scholar]
- Zahedi, P.; Parsi, M.; Asgharpour, A.; McLaury, B.S.; Shirazi, S.A. Experimental investigation of sand particle erosion in a 90° elbow in annular two-phase flows. Wear 2019, 438–439, 203048. [Google Scholar] [CrossRef]
- Peng, W.; Cao, X.; Hou, J.; Xu, K.; Fan, Y.; Xing, S. Experiment and numerical simulation of sand particle erosion under slug flow condition in a horizontal pipe bend. J. Nat. Gas Sci. Eng. 2020, 76, 103175. [Google Scholar] [CrossRef]
- Parsi, M.; Agrawal, M.; Srinivasan, V.; Vieira, R.E.; Torres, C.F.; McLaury, B.S.; Shirazi, S.A. CFD simulation of sand particle erosion in gas-dominant multiphase flow. J. Nat. Gas Sci. Eng. 2015, 27, 706–718. [Google Scholar] [CrossRef]
- Parsi, M.; Kara, M.; Agrawal, M.; Kesana, N.; Jatale, A.; Sharma, P.; Shirazi, S. CFD simulation of sand particle erosion under multiphase flow conditions. Wear 2017, 376–377, 1176–1184. [Google Scholar] [CrossRef]
- Wee, S.K.; Yap, Y.J. CFD study of sand erosion in pipeline. J. Pet. Sci. Eng. 2019, 176, 269–278. [Google Scholar] [CrossRef]
- Bilal, F.S.; Sedrez, T.A.; Shirazi, S.A. Experimental and CFD investigations of 45 and 90 degrees bends and various elbow curvature radii effects on solid particle erosion. Wear 2021, 476, 203646. [Google Scholar] [CrossRef]
- Bayareh, M.; Mortazavi, S. Equilibrium position of a buoyant drop in Couette and Poiseuille flows at finite Reynolds numbers. J. Mech. 2013, 29, 53–58. [Google Scholar] [CrossRef]
- Feng, Z.G.; Michaelides, E.E. Equilibrium position for a particle in a horizontal shear flow. Int. J. Multiph. Flow 2003, 29, 943–957. [Google Scholar] [CrossRef]
- Farokhipour, A.; Mansoori, Z.; Saffar-Avval, M.; Ahmadi, G. 3D computational modeling of sand erosion in gas-liquid-particle multiphase annular flows in bends. Wear 2020, 450–451, 203241. [Google Scholar] [CrossRef]
- Sedrez, T.A.; Shirazi, S.A.; Rajkumar, Y.R.; Sambath, K.; Subramani, H.J. Experiments and CFD simulations of erosion of a 90° elbow in liquid-dominated liquid-solid and dispersed-bubble-solid flows. Wear 2019, 426–427, 570–580. [Google Scholar] [CrossRef]
- Ogunsesan, O.A.; Hossain, M.; Iyi, D.; Dhroubi, M.G. CFD Modelling of Pipe Erosion Due to Sand Transport; Springer: Singapore, 2018; pp. 274–289. [Google Scholar]
- Zahedi, P.; Zhang, J.; Arabnejad, H.; McLaury, B.S.; Shirazi, S.A. CFD simulation of multiphase flows and erosion predictions under annular flow and low liquid loading conditions. Wear 2017, 376–377, 1260–1270. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Y.; Li, X.; He, R.; Han, S.; Chen, Y. Erosion prediction of liquid-particle two-phase flow in pipeline elbows via CFD–DEM coupling method. Powder Technol. 2015, 275, 182–187. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, Q.; Zheng, J.; Zhao, Y. Numerical prediction of erosion in elbow based on CFD-DEM simulation. Powder Technol. 2016, 302, 236–246. [Google Scholar] [CrossRef]
- Zeng, D.; Zhang, E.; Ding, Y.; Yi, Y.; Xian, Q.; Yao, G.; Zhu, H.; Shi, T. Investigation of erosion behaviors of sulfur-particle-laden gas flow in an elbow via a CFD-DEM coupling method. Powder Technol. 2018, 329, 115–128. [Google Scholar] [CrossRef]
- Farokhipour, A.; Mansoori, Z.; Rasteh, A.; Rasoulian, M.A.; Saffar-Avval, M.; Ahmadi, G. Study of erosion prediction of turbulent gas-solid flow in plugged tees via CFD-DEM. Powder Technol. 2019, 352, 136–150. [Google Scholar] [CrossRef]
- Lin, Z.; Sun, X.; Yu, T.; Zhang, Y.; Li, Y.; Zhu, Z. Gas–solid two-phase flow and erosion calculation of gate valve based on the CFD-DEM model. Powder Technol. 2020, 366, 395–407. [Google Scholar] [CrossRef]
- Malan, L.C.; Malan, A.G.; Zaleski, S.; Rousseau, P.G. A geometric VOF method for interface resolved phase change and conservative thermal energy advection. J. Comput. Phys. 2021, 426, 109920. [Google Scholar] [CrossRef]
- Torres, C.; Borman, D.; Sleigh, A.; Neeve, D. Application of Three-Dimensional CFD VOF to Characterize Free-Surface Flow over Trapezoidal Labyrinth Weir and Spillway. J. Hydraul. Eng. 2021, 147, 04021002. [Google Scholar] [CrossRef]
- Xia, C.; Zhao, R.; Shi, W.; Zhang, D.; Gao, X. Numerical Investigation of Particle Induced Erosion in a Mixed Pump by CFD-DEM Coupled Method. J. Eng. Thermophys. 2021, 42, 357–369. [Google Scholar]
- FU Chenbo. Improvement of Standard k-ε Turburnt Model in Plane Wakes; Harbin Institute of Technology: Shenzhen, China, 2018. [Google Scholar]
- Tomac, I.; Gutierrez, M. Micromechanics of proppant agglomeration during settling in hydraulic fractures. J. Pet. Explor. Prod. Technol. 2015, 5, 417–434. [Google Scholar] [CrossRef]
- Pereira, G.C.; de Souza, F.J.; de Moro Martins, D.A. Numerical prediction of the erosion due to particles in elbows. Powder Technol. 2014, 261, 105–117. [Google Scholar] [CrossRef]
- Oka, Y.I.; Yoshida, T. Practical Estimation of Erosion Damage Caused by Solid Particle Impact. Part 2: Mechanical Properties of Materials Directly Associated with Erosion Damage; Elsevier Science: Lausanne, Switzerland; Amsterdam, The Netherland; New York, NY, USA, 2005; pp. 102–109. [Google Scholar]
- Oka, Y.I.; Mihara, S.; Yoshida, T. Impact-angle dependence and estimation of erosion damage to ceramic materials caused by solid particle impact. Wear 2009, 267, 129–135. [Google Scholar] [CrossRef]
- Liu, Z.; Ji, Z.; Wu, X.; Xu, Q. Detection on particulate matters in gas pipeline and assessment on separator performance. Oil Gas Storage Transp. 2016, 35, 47–51. [Google Scholar]





| Well Number | Daily Gas (104 m3/d) | Pressure (MPa) | Sand Rate (kg/d) | Sand Size (mesh) |
|---|---|---|---|---|
| Well 1 | 21.6085 | 5.81 | 2.3 | 70~180 mesh |
| Well 2 | 21.6706 | 7.06 | 3.1 | 70~180 mesh |
| Well 3 | 37.9431 | 6.12 | 4.8 | 70~180 mesh |
| Well 4 | 44.0585 | 8.17 | 6.1 | 70~180 mesh |
| Well 5 | 50.3707 | 5.84 | 6.9 | 70~180 mesh |
| Well 6 | 62.2861 | 9.34 | 8.5 | 70~180 mesh |
| Influencing Factors | Specific Parameters |
|---|---|
| Gas Flow Rate (m/s) | 5, 7, 9, 11 |
| Pressure (MPa) | 4, 5, 6, 7, 8, 9 |
| Moisture Content (%) | 1, 3, 5, 7 |
| Coefficient of Restitution | Static Friction Coefficient | Rolling Friction Coefficient | Sand Density (kg/m3) | Poisson’s Ratio | Shear Modulus (Pa) |
|---|---|---|---|---|---|
| 0.9 | 0.1 | 0.005 | 2650 | 0.12 | 2.37 × 109 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Tan, R.; Chang, B.; Chen, B.; Li, J.; Lu, Q.; Zhang, T. Simulation of Elbow Erosion of Gas–Liquid–Solid Three-Phase Shale Gas Gathering Pipeline Based on CFD-DEM. Processes 2024, 12, 1231. https://doi.org/10.3390/pr12061231
Wang Y, Tan R, Chang B, Chen B, Li J, Lu Q, Zhang T. Simulation of Elbow Erosion of Gas–Liquid–Solid Three-Phase Shale Gas Gathering Pipeline Based on CFD-DEM. Processes. 2024; 12(6):1231. https://doi.org/10.3390/pr12061231
Chicago/Turabian StyleWang, Yixuan, Rui Tan, Bei Chang, Bin Chen, Junxiang Li, Qianli Lu, and Tao Zhang. 2024. "Simulation of Elbow Erosion of Gas–Liquid–Solid Three-Phase Shale Gas Gathering Pipeline Based on CFD-DEM" Processes 12, no. 6: 1231. https://doi.org/10.3390/pr12061231
APA StyleWang, Y., Tan, R., Chang, B., Chen, B., Li, J., Lu, Q., & Zhang, T. (2024). Simulation of Elbow Erosion of Gas–Liquid–Solid Three-Phase Shale Gas Gathering Pipeline Based on CFD-DEM. Processes, 12(6), 1231. https://doi.org/10.3390/pr12061231





