Scheduling of Automated Wet-Etch Stations with One Robot in Semiconductor Manufacturing via Constraint Answer Set Programming
Abstract
:1. Introduction
2. Literature Review
2.1. Automated Wet-Etch Scheduling Problem
2.2. ASP and CASP
3. Materials and Methods
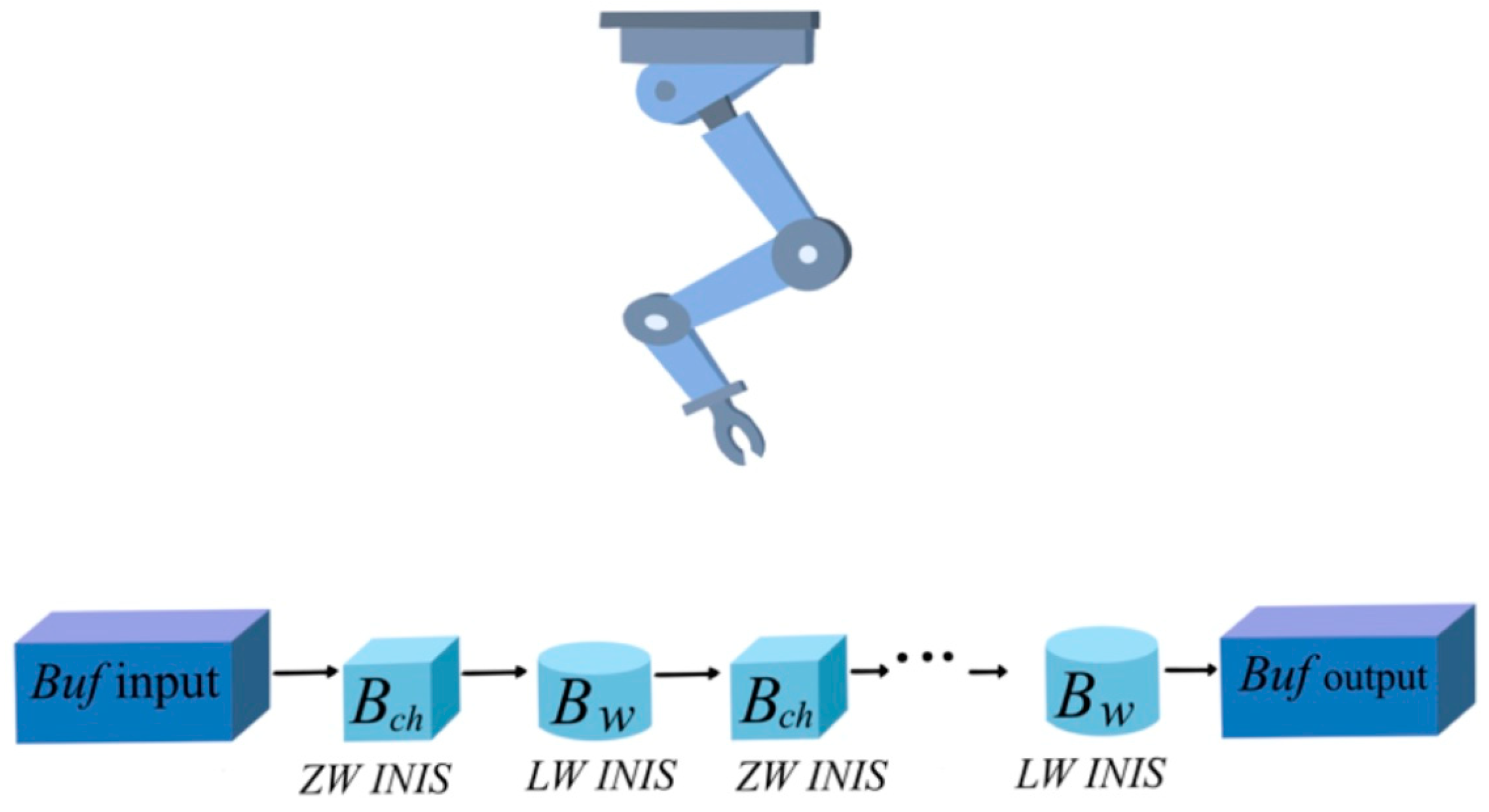
3.1. Production Model
- (a)
- The wafer is covered with a thin uniform layer of silicon oxide (SiO2) or gallium arsenide (GaAs).
- (b)
- Portions of the wafer are selected and marked to form the circuit configuration (photolithography or photo-masking).
- (c)
- Etching is applied; it is a key step in the manufacturing of the wafer. This process is performed by one or more highly automated stations:
- (d)
- At these stations, the excess film of SiO2 or AsGa is eliminated in a series of chemical and deionizing baths.
- (e)
- The batches of AWS wafers are all of the same type and come from previous processing.
- (f)
- The lots are subject to processing in chemical and water baths arranged alternatively.
- (g)
- The batches are transferred by one or more robots between the baths. In the case study of this research, only one robot is considered for material transfer. Lot transference is performed by a robot on the order of milliseconds and can be different for each pair of baths.
- (h)
- The chemical baths follow a zero-wait storage policy and can never be used as temporal buffering (Zero Wait/No Intermediate Storage, ZW/NIS) because chemical overexposure can damage the wafers.
- (i)
- The water baths are used for storage (LS).
- (j)
- The processing time for each lot depends on the lot and bath.
- (k)
- In each bath, one lot can only be processed at a time.
- (l)
- It is assumed that the baths and the robot are never out of order.
3.2. Problem Definition
3.3. Notations and Nomenclature
3.3.1. Indexes
3.3.2. Sets
- -
- the scheduled start time slot for j processing in bath b;
- -
- the scheduled completion time for j processing in bath b;
- -
- the bath assigned to job j;
- -
- the scheduled start time slot for robot r to transfer the job j from bath to bath
- -
- the scheduled completion time slot for robot r to finish the job transfer from bath to bath
- -
- the deadline for finishing the processing of all the jobs.
3.4. Constraints and Function Definitions
3.5. Encoding the Problem in CASP
(iniJob(P, M) $+ D $+ Tr).
$and iniJob(P, M) $+ D $+ Tr $> iniJob(P’,M).
iniJob(P, M) $<= iniJob(P, M’)
$and iniJob(P, M) $+ D $+ Tr $> iniJob(P, M’).
beginRobot(P, M) $!= (iniJob(P, M) $+ D).
: numBaths(Nb): moveBatch(P, M, Tr)}.
4. Results
4.1. Input Data
The Design of the Experiment
4.2. The Discussion of the Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oks, S.J.; Jalowski, M.; Lechner, M.; Mirschberger, S.; Merklein, M.; Vogel-Heuser, B.; Moeslein, K. Cyber-Physical Systems in the Context of Industry 4.0: A Review, Categorization and Outlook. Inf. Syst. Front. 2022, 1–42. [Google Scholar] [CrossRef]
- Wang, S.; Wan, J.; Li, D.; Liu, C. Knowledge reasoning with semantic data for real-time data processing in smart factory. Sensors 2018, 18, 471. [Google Scholar] [CrossRef] [PubMed]
- Negri, E.; Fumagalli, L.; Garetti, M.; Tanca, L. Requirements and languages for the semantic representation of manufacturing systems. Comput. Ind. 2015, 81, 55–66. [Google Scholar] [CrossRef]
- Zhong, R.Y.; Xu, X.; Klotz, E.; Newman, S.T. Intelligent manufacturing in the context of Industry 4.0: A review. Engineering 2017, 3, 616–630. [Google Scholar] [CrossRef]
- Estrada-Jimenez, L.A.; Pulikottil, T.; Nikghadam-Hojati, S.; Barata, J. Self-Organization in Smart Manufacturing—Background, Systematic Review, Challenges and Outlook. IEEE Access 2023, 11, 10107–10136. [Google Scholar] [CrossRef]
- Fang, J.; Cheang, B.; Lim, A. Problems and Solution Methods of Machine Scheduling in Semiconductor Manufacturing Operations: A Survey. Sustainability 2023, 15, 13012. [Google Scholar] [CrossRef]
- Lee, D.H.; Lee, C.H.; Choi, S.H.; Kim, K.J. A Method for Wafer Assignment in Semiconductor Wafer Fabrication Considerint Both Quality and Productivity Perspectives. J. Manuf. Syst. 2019, 52 Pt A, 23–31. [Google Scholar] [CrossRef]
- Wang, J.; Liu, C.; Zhou, M.; Leng, T.; Albeshri, A. Optimal Cyclic Scheduling of Wafer-Residency-Time-Constrained Dual-Arm Cluster Tools by Configuring Processing Modules and Robot Waiting Time. IEEE Trans. Semicond. Manuf. 2023, 36, 251–259. [Google Scholar] [CrossRef]
- Crama, Y.; van de Klundert, J. Robotic Flowshop Scheduling Is Strongly NP-Complete; METEOR, Maastricht University School of Business and Economics: Maastricht, The Netherlands, 1997; METEOR Research Memorandum No. 019. [Google Scholar] [CrossRef]
- Gelfond, M.; Lifschitz, V. The Stable Model Semantics for Logic Programming. In Logic Programming, Proceedings of the Fifth International Conference and Symposium, Volume 2; Kowalksi, R., Boween, K.A., Eds.; Series in Logic Programming; The MIT Press: Cambridge, MA, USA; London, UK, 1988; pp. 1070–1080. [Google Scholar]
- Gelfond, M.; Lifschitz, V. Classical negation in logic programs and disjunctive databases. New Gener. Comput. 1991, 9, 365–386. [Google Scholar] [CrossRef]
- Ostrowski, M.; Schaub, T. ASP modulo CSP: The clingcon system. Theory Pract. Log. Program. 2012, 12, 485–503. [Google Scholar] [CrossRef]
- Banbara, M.; Kaufmann, B.; Ostrowski, M.; Schaub, T. Clingcon: The next generation. Theory Pract. Log. Program. 2017, 17, 408–461. [Google Scholar] [CrossRef]
- Gebser, M.; Kaminski, R.; Kaufmann, B.; Schaub, T. Multi-shot asp solving with clingo. Theory Pract. Log. Program. 2018, 19, 27–82. [Google Scholar] [CrossRef]
- Nogueira, M.; Balduccini, M.; Gelfond, M.; Watson, R.; Barry, M. An A-prolog decision support system for the space shuttle. In Practical Aspects of Declarative Languages; Ramakrishnan, I.V., Ed.; PADL 2001; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2001; Volume 1990, pp. 169–183. [Google Scholar] [CrossRef]
- Ricca, F.; Grasso, G.; Alviano, M.; Manna, M.; Lio, V.; Liritano, S.; Leone, N. Team-building with answer set programming in the gioia-tauro seaport. Theory Pract. Log. Program. 2012, 12, 361–381. [Google Scholar] [CrossRef]
- Erdem, E. Applications of answer set programming in phylogenetic systematics. In Logic Programming, Knowledge Representation, and Nonmonotonic Reasoning: Essays Dedicated to Michael Gelfond on the Occasion of His 65th Birthday, Vol. 6565 of LNCS; Balduccini, M., Son, T.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 415–431. [Google Scholar] [CrossRef]
- Gebser, M.; Obermeier, P.; Schaub, T.; Ratsch-Heitmann, M.; Runge, M. Routing Driverless Transport Vehicles in Car Assembly with Answer Set Programming. Theory Pract. Log. Program. 2018, 18, 520–534. [Google Scholar] [CrossRef]
- Dodaro, C.; Galtat, G.; Khan, M.K.; Maratea, M.; Porro, I. Operating Room (Re)Scheduling with Bed Management via ASP. Theory Pract. Log. Program. 2021, 22, 220–253. [Google Scholar] [CrossRef]
- Wotawa, F.; Kaufmann, D. Model-based reasoning using answer set programming. Appl. Intell. 2022, 52, 16993–17011. [Google Scholar] [CrossRef]
- Cao-Tran, S.; Pontelli, E.; Balduccini, M.; Schaub, T. Answer Set Planning: A Survey. Theory Pract. Log. Program. 2023, 23, 226–298. [Google Scholar] [CrossRef]
- Lierler, Y.Y.; Susman, B. Constraint Answer Set Programming versus Satisfiability Modulo Theories. In Proceedings of the 25th International Joint Conference on Artificial Intelligence (IJCAI), New York, NY, USA, 9–15 July 2016; pp. 1181–1187. Available online: https://dl.acm.org/citation.cfm?id=3060785 (accessed on 19 June 2024).
- Gebser, M.; Ostrowski, M.; Schaub, T. Constraint answer set solving. In Proceedings of the International Conference on Logic Programming (ICLP), Pasadena, CA, USA, 14–17 July 2009; pp. 235–249. Available online: https://link.springer.com/chapter/10.1007/978-3-642-02846-5_22 (accessed on 19 June 2024).
- Balduccini Balduccini, M. Representing constraint satisfaction problems in answer set programming. In Proceedings of the Working Notes of the Workshop on Answer Set Programming and Other Computing Paradigms (ASPOCP), Pasadena, CA, USA, 14 July 2009. [Google Scholar]
- Lierler, Y. Constraint Answer Set Programming: Integrational and Translational (or SMT-based) Approaches. Theory Pract. Log. 2023, 23, 195–225. [Google Scholar] [CrossRef]
- Gebser, M.; Kaminski, R.; Kaufmann, B.; Ostrowski, M.; Schaub, T.; Thiele, S. A Users Guide to Gringo, Clasp, Clingo, and Iclingo. 2010. Available online: http://wp.doc.ic.ac.uk/arusso/wp-content/uploads/sites/47/2015/01/clingo_guide.pdf (accessed on 19 June 2024).
- Bhushan, S.; Karimi, I.A. Heuristic algorithms for scheduling an automated wet-etch station. Comput. Chem. Eng. 2004, 28, 363–379. [Google Scholar] [CrossRef]
- Ahn, G.; Park, M.; Park, Y.J.; Hur, S. Interactive Q-Learning Approach for Pick-and-Place Optimization of the Die Attach Process in the Semiconductor Industry. Math. Probl. Eng. 2019, 2019, 4602052. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhou, M.; Qiao, Y.; Wu, N. Close-down Process Scheduling of Wafer Residence Time-Constrained Multi-cluster Tools. In Proceedings of the IEEE International Conference of Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar]
- Li, P.Q.; Ma, H.H. Integrating Preventive Maintenance Planning and Production Scheduling under Reentrant Job Shop. Math. Probl. Eng. 2017, 2017, 6758417. [Google Scholar] [CrossRef]
- Ma, Y.; Qiao, F.; Zhao, F.; Sutherland, J. Dynamic Scheduling of a Semiconductor Production Line Based on a Composite Rule Set. Appl. Sci. 2017, 7, 1052. [Google Scholar] [CrossRef]
- Fuchigami, H.Y.; Rangel, S. A Survey of Case Studies in Production Scheduling: Analysis and perspectives. J. Comput. Sci. 2018, 25, 425–436. [Google Scholar] [CrossRef]
- Mönch, L.; Lars, L.; Fowler, J.W.; Dauzère-Pérès, S.; Mason, S.J.; Rose, O. A Survey of problems, solution techniques, and future challenges in scheduling semiconductor manufacturing operations. J. Sched. 2011, 14, 583–599. [Google Scholar] [CrossRef]
- García-Mata, C.L.; Márquez-Gutiérrez, P.R.; Burtseva, L. Rescheduling in Industrial Environments: Emerging Technologies and Forthcoming Trends. Int. J. Comb. Optim. Probl. Inform. 2015, 6, 34–48. [Google Scholar]
- Dequeant, K.; Vialletele, P.; Lemaire, P.; Espinouse, M.L.A. Literature review on variability in semiconductor manufacturing: The next forward leap to Industry 4.0. In Proceedings of the Winter Simulation Conference (WSC), Washington, DC, USA, 11–14 December 2016; pp. 2598–2609. [Google Scholar] [CrossRef]
- Khakifirooz, M.; Fathi, M.; Wu, K. Development of smart semiconductor manufacturing: Operations research and data science perspectives. IEEE Access 2019, 7, 108419–108430. [Google Scholar] [CrossRef]
- Suvra-Das, R. A Review of Artificial Intelligence Techniques for Quality Control in Semiconductor Production. Int. J. Comput. Eng. 2024, 5, 33–45. [Google Scholar]
- Aguirre, A.M.; Méndez, C.A.; Garcia Sánchez, A.; Ortega-Mier, M.; Castro, P.M. General framework for automated manufacturing systems: Multiple hoists scheduling solution. Chem. Eng. Trans. 2013, 32, 1381–1386. [Google Scholar] [CrossRef]
- Feng, J.; Che, A.; Chu, C. Dynamic Hoist Scheduling Problem with Multi-capacity Reentrant Machines: A Mixed Integer Programming Approach. Comput. Ind. Eng. 2015, 87, 611–620. [Google Scholar] [CrossRef]
- Yan, P.; Wang, G.; Che, A.; Li, Y. Hybrid discrete differential evolution algorithm for biobjective cyclic hoist scheduling with reentrance. Comput. Oper. Res. 2016, 76, 155–166. [Google Scholar] [CrossRef]
- Bhushan, S.; Karimi, I.A. An MILP approach to automated wet-etch scheduling. Ind. Eng. Chem. Res. 2003, 42, 1391–1399. [Google Scholar] [CrossRef]
- Karimi, I.A.; Tan, Z.Y.L.; Bhushan, S. An improved formulation for scheduling an automated wet-etch station. Comput. Chem. Eng. 2004, 29, 217–224. [Google Scholar] [CrossRef]
- Aguirre, A.M.; Méndez, C.A.; Castro, P.M. A novel optimization method to automated wet-etch station scheduling in semiconductor manufacturing systems. Comput. Chem. Eng. 2011, 28, 883–888. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2018, 52, 2191–2233. [Google Scholar] [CrossRef]
- Geiger, C.D.; Kempf, K.G.; Uzsoy, R. A Tabu search approach to scheduling an automated wet etch station. J. Manuf. Syst. 1997, 2, 102–116. [Google Scholar] [CrossRef]
- Rotondo, A.; Young, P.; Geraghty, J. Sequencing Optimisation for Makespan Improvement at Wet-Etch Tools. Comput. Oper. Res. 2015, 53, 261–274. [Google Scholar] [CrossRef]
- Zeballos, L.J.; Castro, P.M.; Méndez, C.A. Integrated constraint programming scheduling approach for automated wet-etch stations in semiconductor manufacturing. Ind. Eng. Chem. Res. 2011, 50, 1705–1715. [Google Scholar] [CrossRef]
- Novas, J.M.; Henning, G.P. Reactive scheduling framework based on domain knowledge and constraint programming. Comput. Chem. Eng. 2010, 34, 2129–2148. [Google Scholar] [CrossRef]
- Hegyháti, M.; Ösz, O.; Kovács, B. Combinatorial Approach for Scheduling Automated Wet-etch Stations. In Proceedings of the 5th International Conference on Recent Achievements in Mechatronics, Automation, Computer Science and Robotics, Tirgu Mures, Romania, 6–7 March 2015. [Google Scholar]
- Van Gelder, A.; Ross, A.K.; Schlipf, J.S. The well-founded semantics for general logic programs. J. ACM 1991, 38, 620–650. [Google Scholar] [CrossRef]
- Faber, W. An Introduction to Answer Set Programming and Some of its Extensions. In Reasoning Web. Declarative Artificial Intelligence, 16th International Summer School 2020, Oslo, Norway, 24–26 June 2020; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Brewka, G.; Eiter, T.; Truszczynski, M. Answer Set Programming at a Glance. Commun. ACM 2011, 54, 92–103. [Google Scholar] [CrossRef]
- Brain, M.; Cliffe, O.; De Vos, M. A pragmatic programmer’s guide to answer set programming. In Proceedings of the Software Engineering for Answer Set Programming (SEA09), Potsdam, Germany, 14 September 2009; pp. 49–63. [Google Scholar]
- Janhunen, T.; Niemelä, I. The Answer Set Programming Paradigm. AI Mag. 2016, 37, 13–24. [Google Scholar] [CrossRef]
- Vladimir, L. What is Answer Set Programming? Proc. Natl. Conf. Artif. Intell. 2008, 3, 1594–1597. [Google Scholar]
- Son, T.C.; Pontelli, E.; Le, T. Two applications of the ASP-prolog system: Decomposable programs and multi-context systems. In PADL 2014: Proceedings of the Sixteenth International Symposium on Practical Aspects of Declarative Languages, San Diego, CA, USA, 19–20 January 2014; pp. 87–103. [Google Scholar] [CrossRef]
- Cabalar, P.; Fandinno, J.; Schaub, T.; Wanko, P. On the Semantics of Hybrid ASP Systems Based on Clingo. Algorithms 2023, 16, 185. [Google Scholar] [CrossRef]
- Nieuwenhuis, R.; Oliveras, A.; Tinelli, C. Solving SAT and SAT modulo theories: From an abstract Davis-Putnam-Logemann-Loveland procedure to DPLL(T). J. ACM 2006, 53, 937–977. [Google Scholar] [CrossRef]
- Biere, A.; Heule, M.; Van Mareen, H.; Walsh, T. Handbook of Satisfiability. Frontiers in Artificial Intelligence and Applications; IOS Press: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Michel, R.; Hubaux, A.; Ganesh, V.; Heymans, P. An SMT-based approach to automated configuration. In Proceedings of the 10th International Workshop on Satisfiability Modulo Theories (SMT), Manchester, UK, 30 June–1 July 2012; pp. 107–117. [Google Scholar] [CrossRef]
- El-Kholany, M.M.S.; Ali, R.; Gebser, M. Hybrid ASP-Based Multi-objective Scheduling of Semiconductor Manufacturing Processes. In Logics in Artificial Intelligence—18th European Conference, JELIA 2023, Proceedings; Gaggl, S., Martinez, M.V., Ortiz, M., Ortiz, M., Eds.; (Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) Vol. 14281 LNAI); Springer Science and Business Media Deutschland GmbH: Berlin, Germany, 2023; pp. 243–252. [Google Scholar] [CrossRef]

| Job/Bath | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.3 | 6.7 | 11.3 | 6.3 | 2.5 | 6.9 | 8.1 | 7.5 | 4.2 | 7.1 | 3.9 | 6.8 |
| 2 | 5.8 | 6.7 | 8.2 | 6.5 | 4.9 | 6.5 | 12.8 | 6.8 | 10.4 | 6.7 | 11.8 | 6.7 |
| 3 | 10.6 | 6.7 | 2.6 | 6.4 | 2.7 | 7.3 | 13.0 | 6.6 | 11.4 | 6.8 | 9.2 | 6.6 |
| 4 | 2.7 | 6.9 | 6.9 | 7.6 | 3.5 | 7.4 | 3.9 | 6.6 | 7.2 | 6.7 | 3.9 | 6.8 |
| 5 | 4.1 | 6.7 | 11.0 | 6.8 | 7.4 | 6.2 | 3.1 | 6.3 | 3.7 | 6.2 | 9.4 | 6.9 |
| 6 | 3.7 | 6.9 | 2.5 | 6.4 | 6.5 | 6.6 | 2.5 | 6.6 | 2.6 | 6.5 | 2.7 | 6.3 |
| 7 | 10.5 | 6.7 | 3.7 | 6.6 | 11.9 | 6.6 | 2.6 | 6.2 | 6.9 | 6.5 | 3.9 | 6.8 |
| 8 | 3.9 | 6.8 | 6.6 | 6.4 | 3.3 | 6.9 | 3.4 | 6.4 | 11.3 | 6.7 | 5.8 | 7.5 |
| 9 | 2.5 | 7.5 | 1.4 | 7.6 | 6.6 | 6.8 | 11.0 | 6.9 | 12.9 | 6.5 | 5.2 | 7.8 |
| 10 | 10.8 | 6.7 | 10.1 | 6.5 | 2.5 | 6.6 | 2.7 | 7.1 | 4.6 | 6.5 | 11.4 | 6.3 |
| 11 | 8.7 | 6.2 | 4.2 | 7.2 | 6.1 | 6.2 | 5.9 | 6.5 | 4.6 | 6.7 | 8.8 | 6.6 |
| 12 | 7.0 | 6.3 | 7.2 | 6.6 | 2.7 | 6.7 | 8.9 | 7.1 | 2.9 | 6.7 | 6.4 | 6.8 |
| 13 | 9.1 | 6.8 | 2.8 | 6.4 | 5.9 | 6.4 | 5.9 | 6.9 | 10.4 | 6.9 | 8.8 | 6.5 |
| 14 | 2.7 | 6.1 | 11.4 | 6.9 | 7.7 | 6.4 | 5.1 | 6.2 | 4.7 | 6.9 | 10.0 | 6.8 |
| 15 | 2.8 | 6.8 | 6.8 | 6.3 | 4.2 | 6.7 | 8.5 | 6.6 | 5.7 | 6.5 | 4.3 | 6.9 |
| 16 | 5.7 | 6.9 | 2.8 | 7.1 | 4.7 | 6.1 | 3.9 | 6.9 | 4.4 | 6.4 | 2.7 | 6.3 |
| 17 | 2.5 | 7.6 | 6.7 | 6.5 | 2.6 | 6.4 | 3.4 | 7.2 | 2.9 | 6.7 | 7.8 | 6.4 |
| 18 | 3.9 | 6.8 | 12.1 | 6.8 | 2.7 | 6.3 | 9.3 | 6.2 | 4.7 | 6.3 | 2.6 | 6.8 |
| 19 | 9.7 | 6.7 | 7.6 | 6.4 | 10.9 | 6.9 | 2.6 | 6.7 | 4.6 | 6.6 | 10.1 | 6.3 |
| 20 | 2.6 | 6.7 | 2.9 | 6.5 | 10.4 | 6.9 | 2.6 | 6.7 | 11.5 | 6.6 | 3.7 | 6.2 |
| 21 | 4.7 | 6.6 | 4.9 | 6.9 | 2.6 | 6.8 | 12.7 | 6.2 | 2.6 | 6.7 | 6.9 | 6.4 |
| 22 | 2.5 | 6.3 | 2.6 | 6.6 | 7.9 | 6.8 | 12.5 | 6.8 | 2.6 | 6.5 | 7.8 | 6.4 |
| 23 | 11.4 | 6.4 | 8.9 | 6.6 | 2.7 | 6.4 | 11.4 | 7.4 | 11.3 | 6.8 | 2.9 | 6.9 |
| 24 | 6.8 | 6.5 | 2.8 | 7.5 | 3.9 | 7.2 | 9.8 | 6.5 | 8.6 | 6.3 | 11.8 | 6.2 |
| 25 | 8.8 | 6.9 | 8.8 | 6.8 | 11.3 | 6.8 | 11.3 | 6.1 | 6.7 | 6.5 | 2.6 | 6.4 |
| Lots | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| Baths | 1 | 11.1 | 8.47 | 9.19 | 10.8 | 7.4 | 10.8 | 3.48 | 2.51 |
| 2 | 6.68 | 6.35 | 6.35 | 7.12 | 7.05 | 6.76 | 6.67 | 6.23 | |
| 3 | 5.24 | 10.1 | 4.6 | 10.2 | 4.07 | 1.01 | 1.41 | 8 | |
| 4 | 6.92 | 7.02 | 6.71 | 6.83 | 6.58 | 6.37 | 6.46 | 6.23 |
| τ1 | τ2 | τ3 | τ4 | τ5 | τ6 | τ7 | τ8 | τ9 | τ10 | τ11 | τ12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.2 | 0.6 | 0.8 | 1.0 | 0.4 | 0.6 | 1.0 | 1.0 | 0.8 | 0.4 | 0.8 | 1.0 |
| Problem | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 |
|---|---|---|---|---|---|---|---|---|---|
| Baths | 6 | 6 | 6 | 12 | 12 | 12 | 4 | 4 | 12 |
| Jobs | 5 | 15 | 25 | 5 | 15 | 25 | 8 | 8 | 10 |
| Problem P[B × J] | First Solution | Best Solution | ||
|---|---|---|---|---|
| Makespan | CPU Time | Makespan | CPU Time | |
| P1 [6 × 5] | 89.6 | 0.040 | 89.6 | 0.140 |
| P2 [6 × 15] | 208.7 | 0.500 | 195.2 | 0.120 |
| P3 [6 × 25] | 316.0 | 1.090 | 316.0 | 2.94 |
| P4 [12 × 5] | 143.1 | 0.150 | 143.1 | 0.140 |
| P5 [12 × 15] | 250.0 | 1.780 | 250.0 | 1.770 |
| P6 [12 × 25] | 416.8 | 4.85 | 416.8 | 5.670 |
| P7 [4 × 8] | 106.8 | 0.040 | 106.8 | 0.1 |
| P9 [12 × 10] | 245.6 | 0.680 | 234.7 | 0.680 |
| P:[B × J] | First Solution | Best Solution | Approach | ||
|---|---|---|---|---|---|
| Makespan | CPU Time | Makespan | CPU Time | ||
| P1 [6 × 5] | 218.1 | 0.01 | 82.6 | 0.94 | MILP |
| 92.6 | 0.01 | 82.6 | 2.84 | CP+GVDR | |
| 89.6 | 0.040 | 89.6 | 0.140 | CASP | |
| P2 [6 × 15] | 196.1 | 1687 | 195.2 | 3600 a | MILP |
| 205.4 | 0.14 | 185 | 350 a | CP+GVDR | |
| 208.7 | 0.500 | 195.2 | 0.120 | CASP | |
| P3 [6 × 25] | NS | - | NS | 3600 a | MILP |
| 325.1 | 0.53 | 297.3 | 1346 a | CP+GVDR | |
| 316 | 1.090 | 316 | 2.94 | CASP | |
| P4 [12 × 5] | 154.4 | 2.38 | 144.1 | (7.39) 14.49 | MILP |
| 161.5 | 0.06 | 144.1 | 0.39 a | CP+GVDR | |
| 143.1 | 0.150 | 143.1 | 0.140 | CASP | |
| P5 [12 × 15] | NS | - | NS | 3600 a | MILP |
| 294.0 | 0.76 | 273.2 | 949 | CP+GVDR | |
| 250.0 | 1.780 | 250.0 | 1.770 | CASP | |
| P6 [12 × 25] | NS | -/ | NS | 3600 a | MILP |
| 497.5 | 17.29 | 443.4 | 493.37 | CP+GVDR | |
| 416.8 | 5.0 | 416.8 | 5.670 | CASP | |
| P7 [4 × 8] | 139.1 | 3.45 | 120.47 | (72.34) 152 | MILP |
| 128.20 | 0.05 | 120.47 (106.82) | 1.40 a | CP+GVDR | |
| 106.82 | 0.040 | 106.82 | 0.1 | CASP | |
| P9 [12 × 10] | 206.30 | 3452 | 206.30 | 3452 a | MILP |
| 232.8 | 0.38 | 199.0 | 3440 a | CP+GVDR | |
| 245.6 | 0.680 | 234.7 | 0.680 | CASP | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Mata, C.L.; Burtseva, L.; Werner, F. Scheduling of Automated Wet-Etch Stations with One Robot in Semiconductor Manufacturing via Constraint Answer Set Programming. Processes 2024, 12, 1315. https://doi.org/10.3390/pr12071315
García-Mata CL, Burtseva L, Werner F. Scheduling of Automated Wet-Etch Stations with One Robot in Semiconductor Manufacturing via Constraint Answer Set Programming. Processes. 2024; 12(7):1315. https://doi.org/10.3390/pr12071315
Chicago/Turabian StyleGarcía-Mata, Carmen L., Larysa Burtseva, and Frank Werner. 2024. "Scheduling of Automated Wet-Etch Stations with One Robot in Semiconductor Manufacturing via Constraint Answer Set Programming" Processes 12, no. 7: 1315. https://doi.org/10.3390/pr12071315
APA StyleGarcía-Mata, C. L., Burtseva, L., & Werner, F. (2024). Scheduling of Automated Wet-Etch Stations with One Robot in Semiconductor Manufacturing via Constraint Answer Set Programming. Processes, 12(7), 1315. https://doi.org/10.3390/pr12071315








