A Novel Data Mining Framework to Investigate Causes of Boiler Failures in Waste-to-Energy Plants
Abstract
1. Introduction
2. Overview of Umeå Waste-to-Energy Plant and Data Origin
3. Methodology
3.1. The Framework
3.2. Discrete Wavelet Transform
3.3. Principal Component Analysis
3.4. K-Means
- (1)
- Randomly generate k initial centroids within the dataset.
- (2)
- Generate new clusters by assigning every observation to its nearest centroid.
- (3)
- Calculate the centroids of the new clusters.
- (4)
- Repeat Steps 2 and 3 until convergence is reached.
3.5. Deep Embedded Clustering
- (1)
- Using a stacked autoencoder (SAE) to initialize the parameters .
- (2)
- Iterating the process of generating an auxiliary target distribution and minimizing the Kullback–Leibler (KL) divergence between the soft assignment and the auxiliary target distribution . By doing this, the parameters are optimized.
3.6. Key Hyperparameters of Models
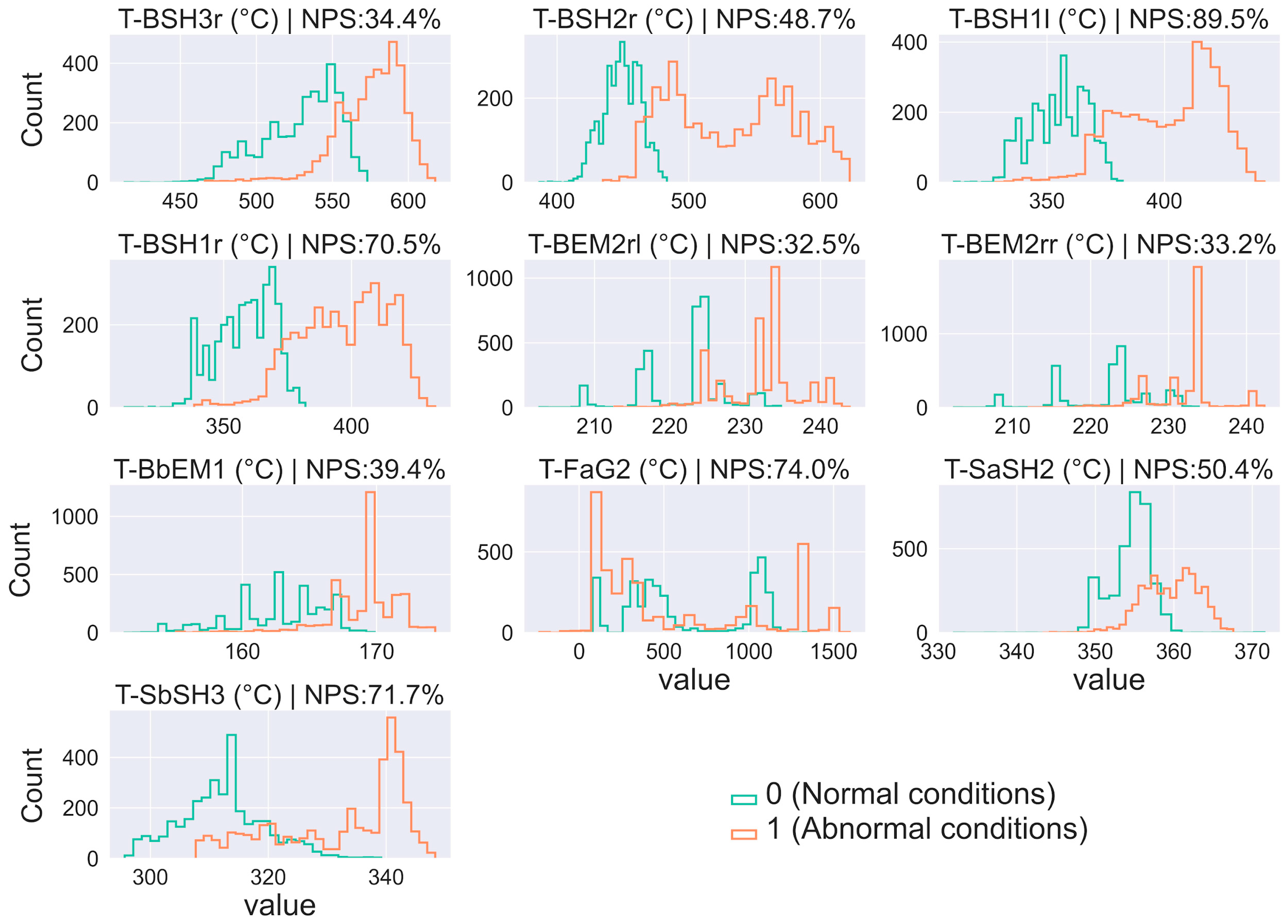
3.7. Normalized Peak Shift
4. Results and Discussion
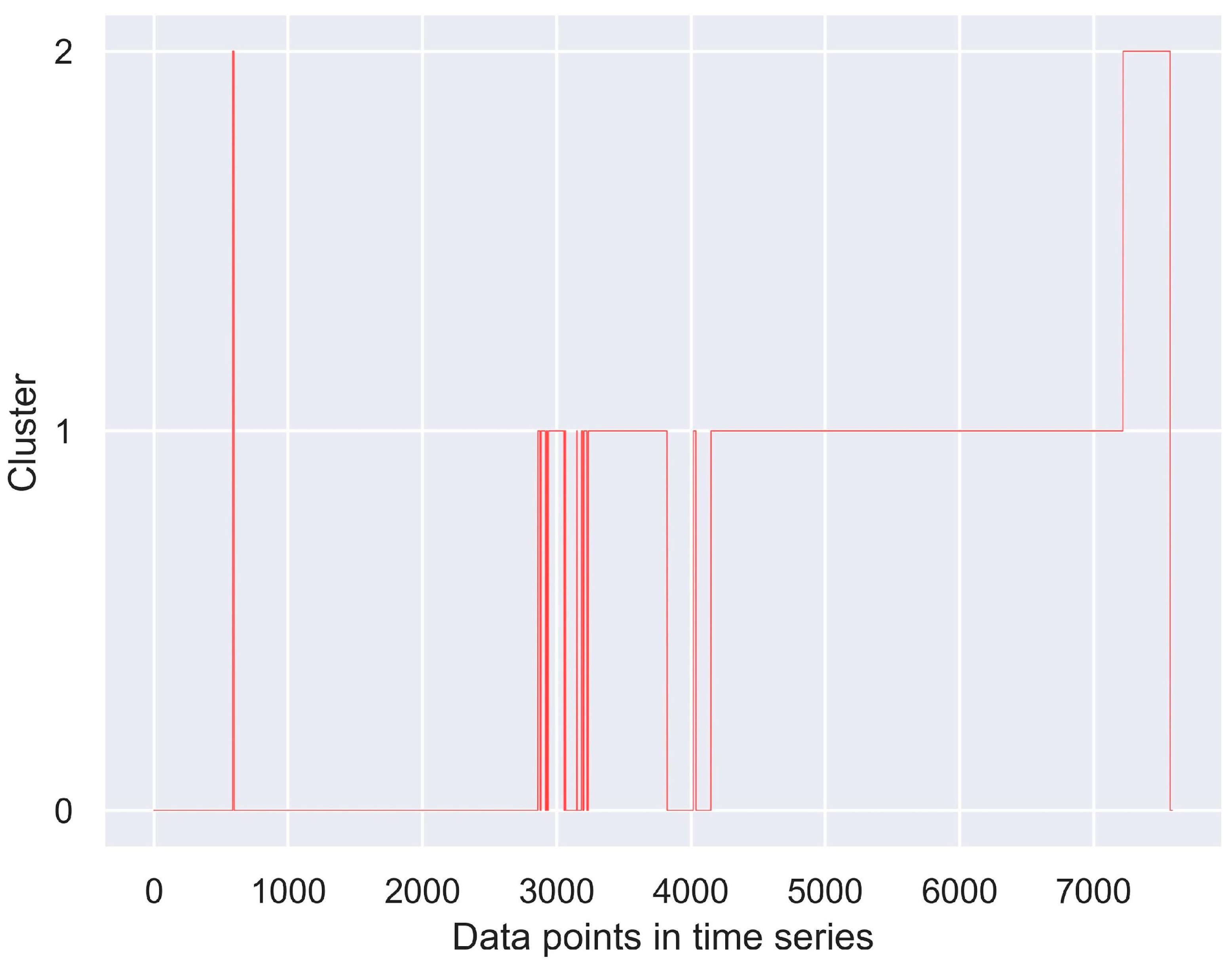
4.1. Results for Dataset A
4.2. Results for Dataset B
| Dataset ID | nhl | nn_hl | nn_el |
|---|---|---|---|
| A | 2 | 80 | 2 |
| B | 2 | 128 | 8 |
4.3. Discussion on the Results and Underlying Mechanisms
4.4. Factors Contributing to DEC’s Superior Performance over PCA + K-Means
4.5. Significance of Study and Limitations
5. Conclusions
- (1)
- The clustering outcomes of DEC consistently surpass those of PCA + K-means across nearly every dimension. This is attributed to DEC’s iterative refinement of the non-linearly embedded space and cluster centroids based on KL divergence feedback.
- (2)
- T-BSH3rm, T-BSH2l, T-BSH3r, T-BSH1l, T-SbSH3, and T-BSH1r emerged as the most significant contributors to the three failures recorded in the two datasets. This underscores the critical importance of vigilant monitoring and precise temperature control of the superheaters to ensure safe production.
- (3)
- It is advisable to maintain the operational levels of T-BSH3rm, T-BSH2l, T-BSH3r, T-BSH1l, T-SbSH3, and T-BSH1r around 527 °C, 432 °C, 482 °C, 338 °C, 313 °C, and 343°C, respectively. Additionally, it is crucial to prevent these values from reaching or exceeding 594 °C, 471 °C, 537 °C, 355 °C, 340 °C, and 359 °C for prolonged durations.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| API | Application Programming Interface |
| DEC | Deep Embedded Clustering |
| DM | Data Mining |
| DNN | Deep Neural Network |
| DWT | Discrete Wavelet Transform |
| HF | High-pass Filter |
| ID | Induced Draft |
| KL | Kullback–Leibler |
| LF | Low-pass Filter |
| nhl | number of hidden layers of the encoder |
| nn_el | number of neurons in the embedded layer of DEC |
| nn_hl | number of neurons in the hidden layer of DEC |
| npc | number of PCs |
| PC | Principal Component |
| PCA | Principal Component Analysis |
| PMF | Probability Mass Function |
| SAE | Stacked Autoencoder |
| WtE | Waste-to-Energy |
References
- Agarwal, S.; Suhane, A. Study of boiler maintenance for enhanced reliability of system A review. Mater. Today Proc. 2017, 4, 1542–1549. [Google Scholar] [CrossRef]
- Barma, M.; Saidur, R.; Rahman, S.; Allouhi, A.; Akash, B.; Sait, S.M. A review on boilers energy use, energy savings, and emissions reductions. Renew. Sustain. Energy Rev. 2017, 79, 970–983. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, J.; Zhu, Q.; Huo, D.; Li, Y.; Li, W. Methanol-based fuel boiler: Design, process, emission, energy consumption, and techno-economic analysis. Case Stud. Therm. Eng. 2024, 54, 103885. [Google Scholar] [CrossRef]
- Elwardany, M. Enhancing Steam Boiler Efficiency through Comprehensive Energy and Exergy Analysis: A Review. Process Saf. Environ. Prot. 2024, 184, 1222–1250. [Google Scholar] [CrossRef]
- Saha, A. Boiler tube failures: Some case studies. In Handbook of Materials Failure Analysis with Case Studies from the Chemicals, Concrete and Power Industries; Elsevier: Amsterdam, The Netherlands, 2016; pp. 49–68. [Google Scholar]
- Kumar, S.; Kumar, M.; Handa, A. Combating hot corrosion of boiler tubes—A study. Eng. Fail. Anal. 2018, 94, 379–395. [Google Scholar] [CrossRef]
- Shokouhmand, H.; Ghadimi, B.; Espanani, R. Failure analysis and retrofitting of superheater tubes in utility boiler. Eng. Fail. Anal. 2015, 50, 20–28. [Google Scholar] [CrossRef]
- Xue, S.; Guo, R.; Hu, F.; Ding, K.; Liu, L.; Zheng, L.; Yang, T. Analysis of the causes of leakages and preventive strategies of boiler water-wall tubes in a thermal power plant. Eng. Fail. Anal. 2020, 110, 104381. [Google Scholar] [CrossRef]
- Hu, W.; Xue, S.; Gao, H.; He, Q.; Deng, R.; He, S.; Xu, M.; Li, Z. Leakage failure analysis on water wall pipes of an ultra-supercritical boiler. Eng. Fail. Anal. 2023, 154, 107670. [Google Scholar] [CrossRef]
- Baglee, D.; Gorostegui, U.; Jantunen, E.; Sharma, P.; Campos, J. How can SMEs adopt a new method to advanced maintenance strategies? A Case study approach. In Proceedings of the COMADEM 2017 30th International Congress & Exhibition on Condition Monitoring and Diagnostic Engineering Management, Lancashire, UK, 10–13 July 2017. [Google Scholar]
- Ichihara, T.; Koike, R.; Watanabe, Y.; Amano, Y.; Machida, M. Hydrogen damage in a power boiler: Correlations between damage distribution and thermal-hydraulic properties. Eng. Fail. Anal. 2023, 146, 107120. [Google Scholar] [CrossRef]
- Haghighat-Shishavan, B.; Firouzi-Nerbin, H.; Nazarian-Samani, M.; Ashtari, P.; Nasirpouri, F. Failure analysis of a superheater tube ruptured in a power plant boiler: Main causes and preventive strategies. Eng. Fail. Anal. 2019, 98, 131–140. [Google Scholar] [CrossRef]
- Ding, Q.; Tang, X.-F.; Yang, Z.-G. Failure analysis on abnormal corrosion of economizer tubes in a waste heat boiler. Eng. Fail. Anal. 2017, 73, 129–138. [Google Scholar] [CrossRef]
- Mudgal, D.; Ahuja, L.; Bhatia, D.; Singh, S.; Prakash, S. High temperature corrosion behaviour of superalloys under actual waste incinerator environment. Eng. Fail. Anal. 2016, 63, 160–171. [Google Scholar] [CrossRef]
- Pal, U.; Kishore, K.; Mukhopadhyay, S.; Mukhopadhyay, G.; Bhattacharya, S. Failure analysis of boiler economizer tubes at power house. Eng. Fail. Anal. 2019, 104, 1203–1210. [Google Scholar] [CrossRef]
- Pramanick, A.; Das, G.; Das, S.K.; Ghosh, M. Failure investigation of super heater tubes of coal fired power plant. Case Stud. Eng. Fail. Anal. 2017, 9, 17–26. [Google Scholar] [CrossRef]
- Jones, D. Creep failures of overheated boiler, superheater and reformer tubes. Eng. Fail. Anal. 2004, 11, 873–893. [Google Scholar] [CrossRef]
- Kain, V.; Chandra, K.; Sharma, B. Failure of carbon steel tubes in a fluidized bed combustor. Eng. Fail. Anal. 2008, 15, 182–187. [Google Scholar] [CrossRef]
- Guo, H.; Fan, W.; Liu, Y.; Long, J. Experimental investigation on the high-temperature corrosion of 12Cr1MoVG boiler steel in waste-to-energy plants: Effects of superheater operating temperature and moisture. Process Saf. Environ. Prot. 2024. [Google Scholar] [CrossRef]
- Gu, B.; Jiang, S.; Wang, H.; Wang, Z.; Jia, R.; Yang, J.; He, S.; Cheng, R. Characterization, quantification and management of China’s municipal solid waste in spatiotemporal distributions: A review. Waste Manag. 2017, 61, 67–77. [Google Scholar] [CrossRef] [PubMed]
- Tsiliyannis, C.A. Enhanced waste to energy operability under feedstock uncertainty by synergistic flue gas recirculation and heat recuperation. Renew. Sustain. Energy Rev. 2015, 50, 1320–1337. [Google Scholar] [CrossRef]
- Paz, M.; Zhao, D.; Karlsson, S.; Liske, J.; Jonsson, T. Investigating corrosion memory: The influence of previous boiler operation on current corrosion rate. Fuel Process. Technol. 2017, 156, 348–356. [Google Scholar] [CrossRef]
- Sohaib, M.; Kim, J.-M. Data driven leakage detection and classification of a boiler tube. Appl. Sci. 2019, 9, 2450. [Google Scholar] [CrossRef]
- Jia, X.; Sang, Y.; Li, Y.; Du, W.; Zhang, G. Short-term forecasting for supercharged boiler safety performance based on advanced data-driven modelling framework. Energy 2022, 239, 122449. [Google Scholar] [CrossRef]
- Cui, Z.; Xu, J.; Liu, W.; Zhao, G.; Ma, S. Data-driven modeling-based digital twin of supercritical coal-fired boiler for metal temperature anomaly detection. Energy 2023, 278, 127959. [Google Scholar] [CrossRef]
- Khalid, S.; Hwang, H.; Kim, H.S. Real-world data-driven machine-learning-based optimal sensor selection approach for equipment fault detection in a thermal power plant. Mathematics 2021, 9, 2814. [Google Scholar] [CrossRef]
- Qin, H.; Yin, S.; Gao, T.; Luo, H. A data-driven fault prediction integrated design scheme based on ensemble learning for thermal boiler process. In Proceedings of the 2020 IEEE International Conference on Industrial Technology (ICIT), Buenos Aires, Argentina, 26–28 February 2020; pp. 639–644. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Verleysen, M.; François, D. The curse of dimensionality in data mining and time series prediction. In Proceedings of the International work-conference on artificial neural networks, Barcelona, Spain, 8–10 June 2005; pp. 758–770. [Google Scholar]
- Burrus, S.; Burrus, C.S.; Gopinath, R.A.; Guo, H.; Odegard, J.A.N.E.A.; Selesnick, I.W.A. Introduction to Wavelets and Wavelet Transforms: A Primer; Prentice Hall: Hoboken, NJ, USA, 1998. [Google Scholar]
- Lee, G.R.; Gommers, R.; Waselewski, F.; Wohlfahrt, K.; O’Leary, A. PyWavelets: A Python package for wavelet analysis. J. Open Source Softw. 2019, 4, 1237. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Xie, J.; Girshick, R.; Farhadi, A. Unsupervised deep embedding for clustering analysis. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 478–487. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Le, Q.V. Building high-level features using large scale unsupervised learning. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 8595–8598. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.-A. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Guo, X. DEC.py. Available online: https://github.com/XifengGuo/DEC-keras/blob/master/DEC.py (accessed on 25 February 2020).
- Gencoglu, O.; van Gils, M.; Guldogan, E.; Morikawa, C.; Süzen, M.; Gruber, M.; Leinonen, J.; Huttunen, H. HARK Side of Deep Learning—From Grad Student Descent to Automated Machine Learning. arXiv 2019, arXiv:1904.07633. [Google Scholar]
- Magnus, C.; Pardeshi, A. Investigation into the failure of a superheater tube in a power generation plant utilizing waste material combustion in a furnace. Eng. Fail. Anal. 2024, 156, 107838. [Google Scholar] [CrossRef]
- Ahmad, J.; Purbolaksono, J.; Beng, L. Thermal fatigue and corrosion fatigue in heat recovery area wall side tubes. Eng. Fail. Anal. 2010, 17, 334–343. [Google Scholar] [CrossRef]
- Lee, N.-H.; Kim, S.; Choe, B.-H.; Yoon, K.-B.; Kwon, D.-i. Failure analysis of a boiler tube in USC coal power plant. Eng. Fail. Anal. 2009, 16, 2031–2035. [Google Scholar] [CrossRef]
- Ahmad, J.; Rahman, M.M.; Zuhairi, M.; Ramesh, S.; Hassan, M.; Purbolaksono, J. High operating steam pressure and localized overheating of a primary superheater tube. Eng. Fail. Anal. 2012, 26, 344–348. [Google Scholar] [CrossRef]
- Hosseini, R.K.; Yareiee, S. Failure analysis of boiler tube at a petrochemical plant. Eng. Fail. Anal. 2019, 106, 104146. [Google Scholar] [CrossRef]
- Munda, P.; Husain, M.M.; Rajinikanth, V.; Metya, A. Evolution of microstructure during short-term overheating failure of a boiler water wall tube made of carbon steel. J. Fail. Anal. Prev. 2018, 18, 199–211. [Google Scholar] [CrossRef]
- Deshmukh, S.; Dhamangaonkar, P. A review paper on factors that causes the bulging failure of the metal tube. Mater. Today Proc. 2022, 62, 7610–7617. [Google Scholar] [CrossRef]
- Lobley, G.R.; Al-Otaibi, W.L. Diagnosing boiler tube failures related to overheating. Adv. Mater. Res. 2008, 41, 175–181. [Google Scholar] [CrossRef]
- Rahman, M.; Purbolaksono, J.; Ahmad, J. Root cause failure analysis of a division wall superheater tube of a coal-fired power station. Eng. Fail. Anal. 2010, 17, 1490–1494. [Google Scholar] [CrossRef]
- Hayazi, N.F.; Shamsudin, S.R.; Wardan, R.; Sanusi, M.S.M.; Zainal, F.F. Graphitization damage on seamless steel tube of pressurized closed-loop of steam boiler. IOP Conf. Ser. Mater. Sci. Eng. 2019, 701, 012042. [Google Scholar] [CrossRef]
- Nutal, N.; Gommes, C.J.; Blacher, S.; Pouteau, P.; Pirard, J.-P.; Boschini, F.; Traina, K.; Cloots, R. Image analysis of pearlite spheroidization based on the morphological characterization of cementite particles. Image Anal. Stereol. 2010, 29, 91–98. [Google Scholar] [CrossRef]
- Pérez, I.U.; Da Silveira, T.L.; Da Silveira, T.F.; Furtado, H.C. Graphitization in low alloy steel pressure vessels and piping. J. Fail. Anal. Prev. 2011, 11, 3–9. [Google Scholar] [CrossRef][Green Version]
- da Silveira, R.M.S.; Guimarães, A.V.; Oliveira, G.; dos Santos Queiroz, F.; Guzela, L.R.; Cardoso, B.R.; Araujo, L.S.; de Almeida, L.H. Failure of an ASTM A213 T12 steel tube of a circulating fluidized bed boiler. Eng. Fail. Anal. 2023, 148, 107188. [Google Scholar] [CrossRef]
- McIntyre, K.B. A review of the common causes of boiler failure in the sugar industry. Proc. S. Afr. Sug. Technol. Ass. 2002, 75, 355–364. [Google Scholar]
- Dooley, R.B.; Bursik, A. Hydrogen damage. PowerPlant Chem. 2010, 12, 122. [Google Scholar]
- Dooley, R.B.; Bursik, A. Caustic gouging. PowerPlant Chem. 2010, 12, 188–192. [Google Scholar]
- Kim, Y.-S.; Kim, W.-C.; Kim, J.-G. Bulging rupture and caustic corrosion of a boiler tube in a thermal power plant. Eng. Fail. Anal. 2019, 104, 560–567. [Google Scholar] [CrossRef]
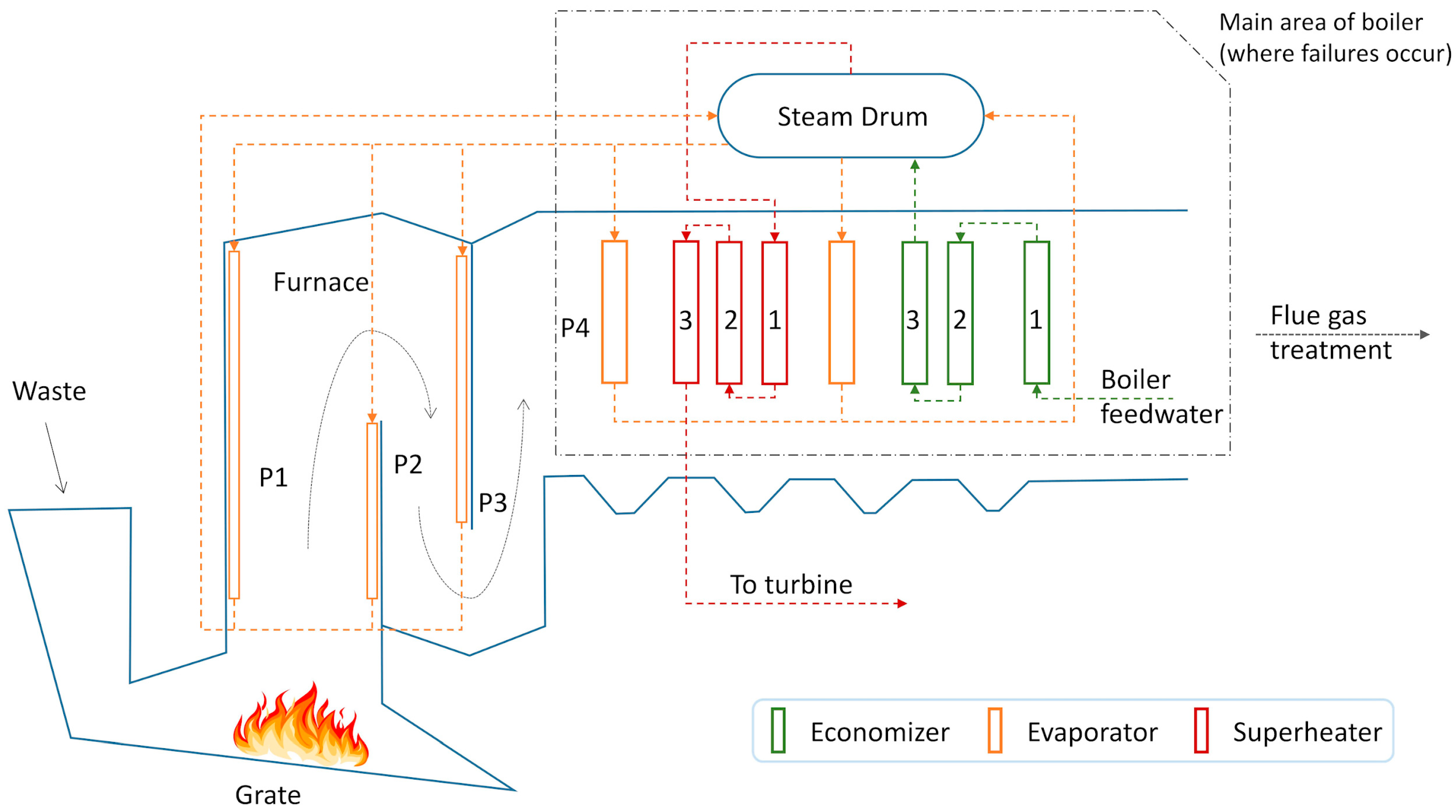



| Dataset ID | No. of Failures/Stoppages | Data Resolution | Dataset Size (Row × Column) |
|---|---|---|---|
| A | 2 | 30 min | 5808 × 66 |
| B | 1 | 30 min | 7856 × 66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Jiang, L.; Kjellander, M.; Weidemann, E.; Trygg, J.; Tysklind, M. A Novel Data Mining Framework to Investigate Causes of Boiler Failures in Waste-to-Energy Plants. Processes 2024, 12, 1346. https://doi.org/10.3390/pr12071346
Wang D, Jiang L, Kjellander M, Weidemann E, Trygg J, Tysklind M. A Novel Data Mining Framework to Investigate Causes of Boiler Failures in Waste-to-Energy Plants. Processes. 2024; 12(7):1346. https://doi.org/10.3390/pr12071346
Chicago/Turabian StyleWang, Dong, Lili Jiang, Måns Kjellander, Eva Weidemann, Johan Trygg, and Mats Tysklind. 2024. "A Novel Data Mining Framework to Investigate Causes of Boiler Failures in Waste-to-Energy Plants" Processes 12, no. 7: 1346. https://doi.org/10.3390/pr12071346
APA StyleWang, D., Jiang, L., Kjellander, M., Weidemann, E., Trygg, J., & Tysklind, M. (2024). A Novel Data Mining Framework to Investigate Causes of Boiler Failures in Waste-to-Energy Plants. Processes, 12(7), 1346. https://doi.org/10.3390/pr12071346






