Next Article in Journal
Epidermal and Blood Vessel Barrier Functions of Glucosylceramides and Digalactosyldiacylglycerols Isolated from Yellow Strawberry Guava
Previous Article in Journal
Network Traffic Anomaly Detection Based on Spatiotemporal Feature Extraction and Channel Attention
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Processes
Volume 12
Issue 7
10.3390/pr12071420
processes-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Modeling Study on Heat Capacity, Viscosity, and Density of Ionic Liquid–Organic Solvent–Organic Solvent Ternary Mixtures via Machine Learning

by
You Shu
1,
Lei Du
1,
Yang Lei
1,*,
Shaobin Hu
2,
Yongchao Kuang
2,
Hongming Fang
1,
Xinyan Liu
1 and
Yuqiu Chen
3,*
1
Hubei Key Laboratory of Coal Conversion and New Carbon Materials, School of Chemistry and Chemical Engineering, Wuhan University of Science and Technology, Wuhan 430081, China
2
Hubei Energy Group Jiangling Power Generation Co., Ltd., Jiangling 434100, China
3
Department of Chemical and Biomolecular Engineering, University of Delaware, 150 Academy Street, Newark, DE 19716, USA
*
Authors to whom correspondence should be addressed.
Processes 2024, 12(7), 1420; https://doi.org/10.3390/pr12071420
Submission received: 17 May 2024 / Revised: 12 June 2024 / Accepted: 14 June 2024 / Published: 7 July 2024
(This article belongs to the Special Issue Ionic Liquids: Modeling, Design and Applications)
Browse Figures
Versions Notes

Abstract

:
Physicochemical properties of ionic liquids (ILs) are essential in solvent screening and process design. However, due to their vast diversity, acquiring IL properties through experimentation alone is both time-consuming and costly. For this reason, the creation of prediction models that can accurately forecast the characteristics of IL and its mixtures is crucial to their application. This study proposes a model for predicting the three important parameters of the IL-organic solvent–organic solvent ternary system: density, viscosity, and heat capacity. The model incorporates group contribution (GC) and machine learning (ML) methods. A link between variables such as temperature, pressure, and molecular structure is established by the model. We gathered 2775 viscosity, 6515 density, and 1057 heat capacity data points to compare the prediction accuracy of three machine learning methods, namely, artificial neural networks (ANNs), extreme gradient boosting (XGBoost), and light gradient boosting machine (LightGBM). As can be observed from the findings, the ANN model produced the best results out of the three GC-based ML methods, even though all three produced dependable predictions. For heat capacity, the mean absolute error (MAE) of the ANN model is 1.7320 and the squared correlation coefficient (R2) is 0.9929. Regarding viscosity, the MAE of the ANN model is 0.0225 and the R2 is 0.9973. For density, the MAE of the ANN model is 7.3760 and the R2 is 0.9943. The Shapley additive explanatory (SHAP) approach was applied to the study to comprehend the significance of each feature in the prediction findings. The analysis results indicated that the R-CH3 group of the ILs, followed by the imidazolium (Im) group, had the highest impact on the heat capacity property of the ternary system. On the other hand, the Im group and the R-H group of ILs had the most effects on viscosity. In terms of density, the Im group of the ILs had the greatest effect on the ternary system, followed by the molar fraction of the organic solvent.

1. Introduction

Ionic liquids (ILs) are salts composed only of ions that remain in a liquid state at room temperature or low temperatures [1]. Many ILs have demonstrated significant potential as environmentally friendly solvents in different applications [2]. Compared to traditional organic solvents and electrolytes, ILs offer a range of unique properties, garnering considerable attention. These properties, including low vapor pressure, high solubility, recyclability, and environmental friendliness [3,4,5], enable ILs to be employed in a variety of processes, including absorption [6], distillation [7], and extraction [8]. Notably, ILs occupy a vital part in chemical industry applications due to their outstanding physical and chemical characteristics [9,10]. Therefore, understanding the properties of ILs and their combinations is crucial for their effective utilization.
One of the most important thermodynamic characteristics in the construction of chemical reactors and heat exchangers is heat capacity. This parameter is crucial for the design of chemical processes, commonly utilized in thermodynamic calculations, and necessary for evaluating the heat transfer efficiency of many important chemical equipment pieces (like heat exchangers and reactors) [11,12]. Viscosity, on the other hand, reflects the internal friction that occurs when a fluid is subjected to external forces or shear stresses [13]. This property appears essential in several fields, including engineering, medicine, and petroleum [14,15,16]. Additionally, density is another important IL physical characteristic, which serves as the foundation for determining other thermodynamic parameters like viscosity and heat capacity. It is essential for energy accounting, equipment selection, and other process steps [17,18].
Even though they are steadily growing, the available experimental data on the physical and chemical characteristics of ILs are still insufficient and typically pertain to only a limited number of extensively studied ILs. Additionally, there are instances where experimental results from different sources contradict one another, leading to inconsistencies in the available data. Given the vast variety of ILs, it would not be practical to determine all their physical and chemical properties experimentally. Therefore, obtaining data on the desired properties through theoretical or empirical methods is promising. Empirical or theoretical models that can reliably predict the nature of ILs are essential for their application. To address this need, some researchers have presented predictive models, including random forest (RF) models [19], group contribution (GC)-based models [20], molecular connectivity index (MCI) models [21], and support vector regression (SVR) models [22]. The best design of a molecule may frequently be achieved by manipulating its molecular characteristics, and this is the key to making significant scientific advancements and enhancing the efficiency of process systems [23]. GC models have gained wide application due to their ease of use and their ability to incorporate computer-aided molecular design (CAMD) techniques into the prediction process [24].
To date, most modeling studies on heat capacity [25,26,27], viscosity [28,29,30], density [31,32,33,34], and conductivity [35] have concentrated on IL in its pure form, whereas only a few studies have considered binary mixtures of IL [36,37,38,39]. Predictive models for IL ternary mixtures are even fewer [40], especially for the IL-organic solvent–organic solvent ternary hybrid system, which is ductile, tunable, thermally stable, and reusable, and can be widely used in energy, biomedicine, separation, and synthesis. The wide range of applications makes this mixture a very important solvent system with great application potential. Therefore, to predict the properties of these ternary IL combinations, it has become imperative to develop trustworthy models. Most attribute models created with the GC model utilize a linear regression algorithm to associate with group numbers [41]. However, linear model formulations are not sufficient to characterize hybrid systems. The nonlinear GC model could be a wise option in this respect. The application of machine learning (ML) and artificial intelligence (AI) [42] as computer-assisted techniques for building intricate nonlinear GC models to forecast various IL characteristics has been widespread. Nowadays, ML-based algorithms like artificial neural networks (ANNs) [43,44], extreme gradient boosting (XGboost) [45,46], and light gradient boosting machines (LightGBMs) [47,48] have become popular for predicting the viscosity, density, and heat capacity of ILs in industrial processes.
Inspired by previous studies, the goal of this study is to construct a model for predicting the density, viscosity, and heat capacity of the ternary system composed of IL-organic solvent–organic solvent by combining ML with GC. The GC method is utilized with three effective ML algorithms, ANN, XGboost, and LightGBM, to create nonlinear models that forecast the heat capacity, viscosity, and density of IL-organic solvent–organic solvent combinations. All three ML-GC models’ prediction efficacy is assessed and compared. Furthermore, the Shapley additive interpretation (SHAP) [49,50] approach was applied to clarify the characteristics of the model and comprehend the impact of these features on the heat capacity, viscosity, and density of the IL ternary system mixes.

2. Investigated Data

In this work, a total of 1057 heat capacity data points covering 8 IL-organic solvent–organic solvent blend systems and 2775 viscosity data points covering 34 IL-organic solvent–organic solvent blend systems with varying temperatures, pressures, and mole fractions were collected. Additionally, density data comprising 6515 data points covering 54 IL-organic solvent–organic solvent blend systems were collected. For heat capacity, the data points were randomly divided into 741 for training, 159 for validation, and 159 for testing. Likewise, viscosity data points were divided into 1949 for training, 414 for validation, and 414 for testing. Similarly, density data points were divided into 4555 for training, 981 for validation, and 981 for testing. Primary information about the collected heat capacity data is provided in Table 1, the collected viscosity data in Table 2, and the collected density data in Table 3. For details on heat capacity, viscosity, and density data points, please refer to Table S1.

3. Method

3.1. GC Method

For GC-based modeling studies, IL molecules are divided into three types of functional groups: cationic backbone, anionic, and side substituents on the cationic backbone. Using this decomposition method, a total of one cationic backbone, one anion, and four substituents were identified from the ILs associated with the heat capacity data. Organic solvents, on the other hand, are split into five functional groups. Similarly, one cationic backbone, nine anions, and four substituents were obtained from the ILs associated with the viscosity data. The organic solvent is divided into 22 functional groups. From the ILs associated with the density data, 3 cationic backbones, 12 anions, and 5 substituents are obtained. Likewise, we categorize organic solvents into 28 functional groups. It is worth noting that some of the groups split from ILs and organics in the IL-OS-OS ternary system are the same; however, they belong to different feature dimensions in the model input. More detailed information can be found in Table 4, Table 5 and Table 6.

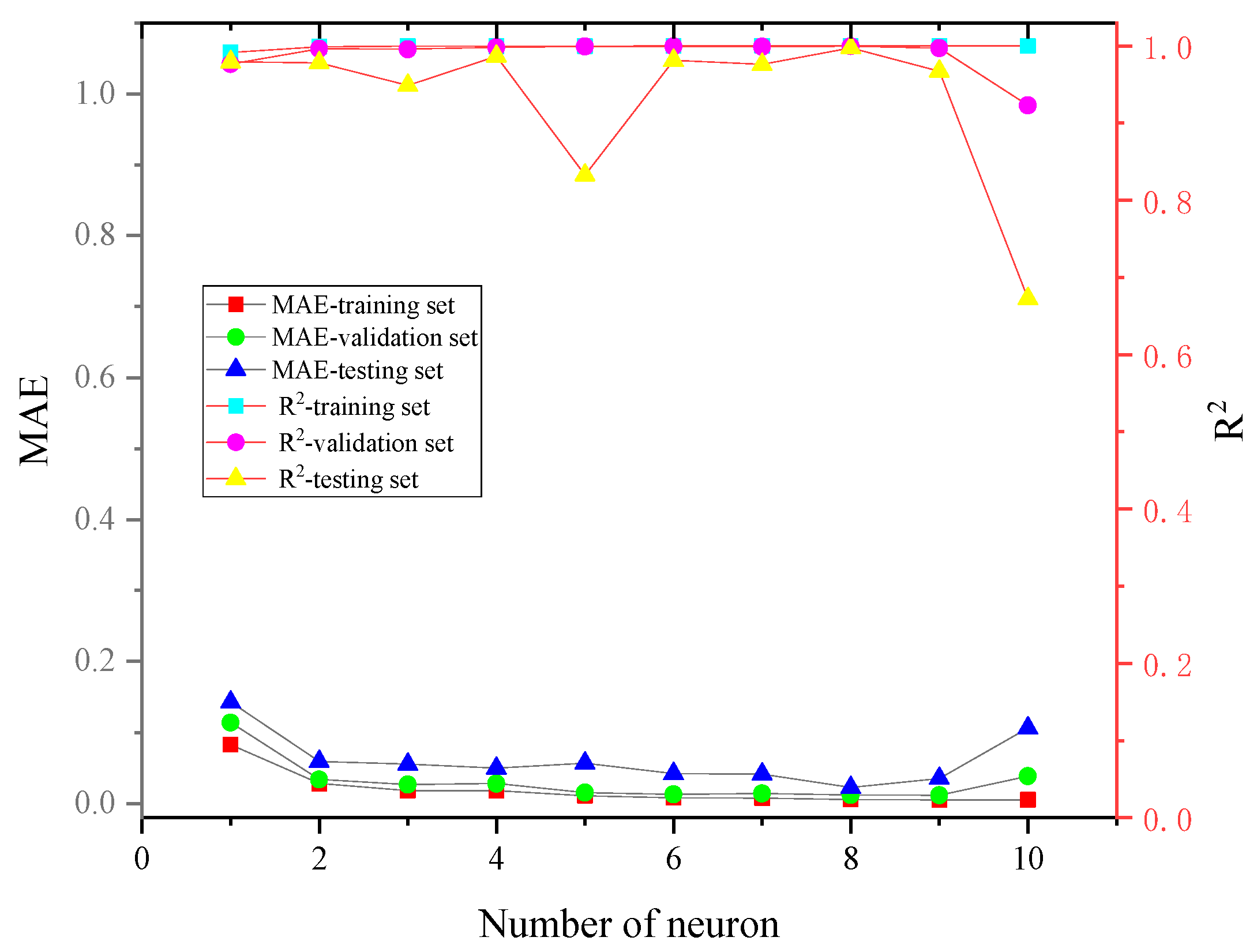
3.2. ANN Algorithm

Artificial neural networks (ANNs) are networks created to resemble the biological nervous system of the animal brain. This network mimics the functioning of brain neurons using nodes known as artificial neurons. As shown in Figure 1, it stands out due to its multi-layered structure, which typically consists of several nodes in each of the input, output, and hidden layers. The operation of ANN is mainly based on mathematical calculations between neurons, starting from the input layer and eventually passing to the output layer.
The data to be processed are received via the input layer, including temperature, pressure, and divided groups of organic solvents and IL. The hidden layer is denoted by W1 and the output layer by W2. B1 and B2 represent the bias parameters of the output layer and hidden layer, respectively. The input data are analyzed from the hidden layer and sent to the output layer after the weights and biases have been modified to fit the data. Improved predictions can be obtained by altering the neuron count of the hidden layer. Increasing the number of ANN neurons may result in overfitting, insufficient training data, neurons interfering with each other, and unreasonable structure. Therefore, when increasing the number of ANN neurons, it is necessary to consider the characteristics of the data, the complexity of the model, the amount of training data, and a reasonable structural setup to obtain the best performance and results. Equations (1) and (2) determine the output of Y and Z1.
Z 1 = f 1 W 1 P + B 1
  Y = f 2 W 2 Z 1 + B 2
In the ANN framework, P denotes the vector representation of each substance. The data are converted into P-vectors by the input layer, and these are further processed employing Equations (1) and (2) to propagate the outcomes via the output and hidden layers, respectively. The ANN estimates the difference between the predicted and actual outputs during training, dynamically adjusting the weights (W1, W2) and biases (B1, B2) of the neurons in the hidden and output layers.
In the hidden layer, every neuron has a corresponding activation function. The expectation value is calculated by optimizing the activation function and sent to later neurons for additional processing. In this study, the hidden layer utilizes the hyperbolic tangent function (tansig, Equation (3)) as the activation function, while the output layer employs the purelin transfer function (Equation (4)).
f 1 x = 2 1 + e − 2 x
f 2 x = x

3.3. XGBoost

XGBoost is a machine learning technique particularly adept at handling regression and classification tasks. It has become one of the most popular and powerful algorithms in the field of machine learning, progressively improving prediction performance by iteratively training a sequence of decision trees within a gradient-boosting framework. The objective of XGBoost is to minimize the error between anticipated and actual values by optimizing the loss function.
XGBoost combines multiple weak learners, typically decision trees, to create stronger predictive models. It achieves more accurate forecasts by weighting the predictions of each decision tree. The objective function of XGBoost comprises a regularization term and a loss function. As an additive model, the predicted value of the model for the T tree and the i sample is represented in Equation (5).
Y ^ i T = ∑ k = 1 T f k x i = y ^ T − 1 + f T x i
where y ^ i ( t ) is the prediction for sample i after the t iteration; y ^ i ( t − 1 ) is the prediction for the T − 1 tree; and f t x i is the model prediction for the T tree. For the i sample, the final predicted value is represented in Equation (6).
y ^ i ( T ) = ∑ j = 1 T f t x i
In step, the original objective function is obtained as follows.
O b j = ∑ n = 1 n l y i , y ^ i + ∑ j = 1 t Ω f j
In summary, XGBoost employs a similar approach to CART regression trees, utilizing a greedy algorithm that evaluates all possible feature splits at each node. However, it differs in its objective function. Instead of solely maximizing the gain of the objective function for each split, XGBoost considers the relative improvement in the objective function value compared to the gain of the singleton leaf child node. Additionally, to prevent overfitting and limit tree depth, a threshold is introduced, ensuring that splitting occurs only when the gain exceeds this threshold. The process iterates, forming a tree by recursively selecting optimal splits until a stopping criterion is met, thus optimizing the predictive performance of the model.
In this paper, parameter optimization is performed on the XGBoost model. A combination of classes and functions from the XGBoost and scikit-learn libraries were used for grid search and hyper-parameter tuning to tune the parameters and improve the fit for the three properties.

3.4. LightGBM

Combining decision trees and gradient boosting, the gradient boosting decision tree (GBDT) is an integrated classification algorithm known for its strong generalization capabilities and ease of visualization. However, it faces challenges of low efficiency and poor scalability when dealing with large datasets or high-dimensional features. In 2017, Microsoft proposed LightGBM as an approach to enhance the processing speed of GBDT for complex data. LightGBM represents an evolutionary iteration of GBDT, building upon its classic version. Notably, it incorporates optimization techniques such as the feature bundling algorithm (EFB), gradient-based, single-sided sampling method (GOSS), and growth strategy for tree building based on the leaf-wise algorithm.
By adopting the leaf-wise algorithm for tree growth strategy, unnecessary computations are avoided and errors minimized. The GOSS algorithm initially sorts the data based on the absolute value of the data gradient, preserving samples with significant gradients that contribute more to information gain, while randomly sampling the remaining less influential samples. This reduction in data volume maintains the original data distribution, ensuring accurate evaluation of information gain and enhancing model classification speed effectively. Through the combination of mutually exclusive features using the EFB algorithm, new features are generated, leading to reduced data feature dimensionality and improved operational efficiency of the model. The mathematical definition of LightGBM is represented in Equation (8), where f t x represents the regression tree.
Y t = ∑ h = 1 T f t x
The parameters of LightGBM model are also optimized in this paper. We use classes and functions from LightGBM and scikit-learn libraries for grid search and hyperparameter tuning to optimize parameters and enhance model fitting.

3.5. Model Evaluation Methods

Selecting the appropriate evaluation method is crucial for confirming the accuracy of the model. Evaluation techniques such as mean absolute error (MAE) and coefficient of determination (R2) are commonly used to precisely assess the accuracy and stability of regression models. In addition, the relative errors (REs) between the experimental values and the predicted values are calculated in the article and a comparison chart is made to compare the accuracy of the model more intuitively.
The MAE is determined by calculating the absolute deviation of all predicted values, providing an accurate reflection of the actual prediction error. The calculation process of MAE is shown in Equation (9):
M A E = 1 N ∑ I = 1 N σ I = 1 e x p − σ I = 1 c a l
where σ I = 1 e x p is the experimental value and σ I = 1 c a l is the predicted value.
R2 assesses how well the model explains changes in dependent variables based on changes in independent variables. It is calculated using Equation (10):
R 2 = 1 − ∑ I = 1 N σ I = 1 e x p − σ I = 1 c a l 2 ∑ I = 1 N σ I = 1 e x p − σ ¯ 2
where σ I = 1 e x p is the experimental value, σ I = 1 c a l is the predicted value, σ ¯ is the mean of the experimental value, ∑ I = 1 N σ I = 1 e x p − σ I = 1 c a l 2 is the error generated by the prediction, and ∑ I = 1 N σ I = 1 e x p − σ ¯ 2 is the error generated by the mean.
RE is the value of the error obtained by dividing the difference between the measured and exact values by the exact value, usually expressed as a percentage. It can be calculated using Equation (11).
R E = σ I = 1 e x p − σ I = 1 c a l σ I = 1 e x p
where σ I = 1 e x p is the experimental value and σ I = 1 c a l is the predicted value.

3.6. SHAP Interpretation

Using SHAP, a method for understanding model output that considers feature interactions and calculates each feature variable’s contribution to the overall projected outcome, enhances the interpretability of a machine learning model. By analyzing the SHAP value of each feature in each sample, we can determine the degree of contribution of each feature to the anticipated result. This is based on the understanding that the predicted value of the model results from the collaboration of input features. Equation (11) is utilized to compute the Shapley value.
∅ j ^ = 1 K ∑ K = 1 K g ^ x + j m − g ^ x − j m

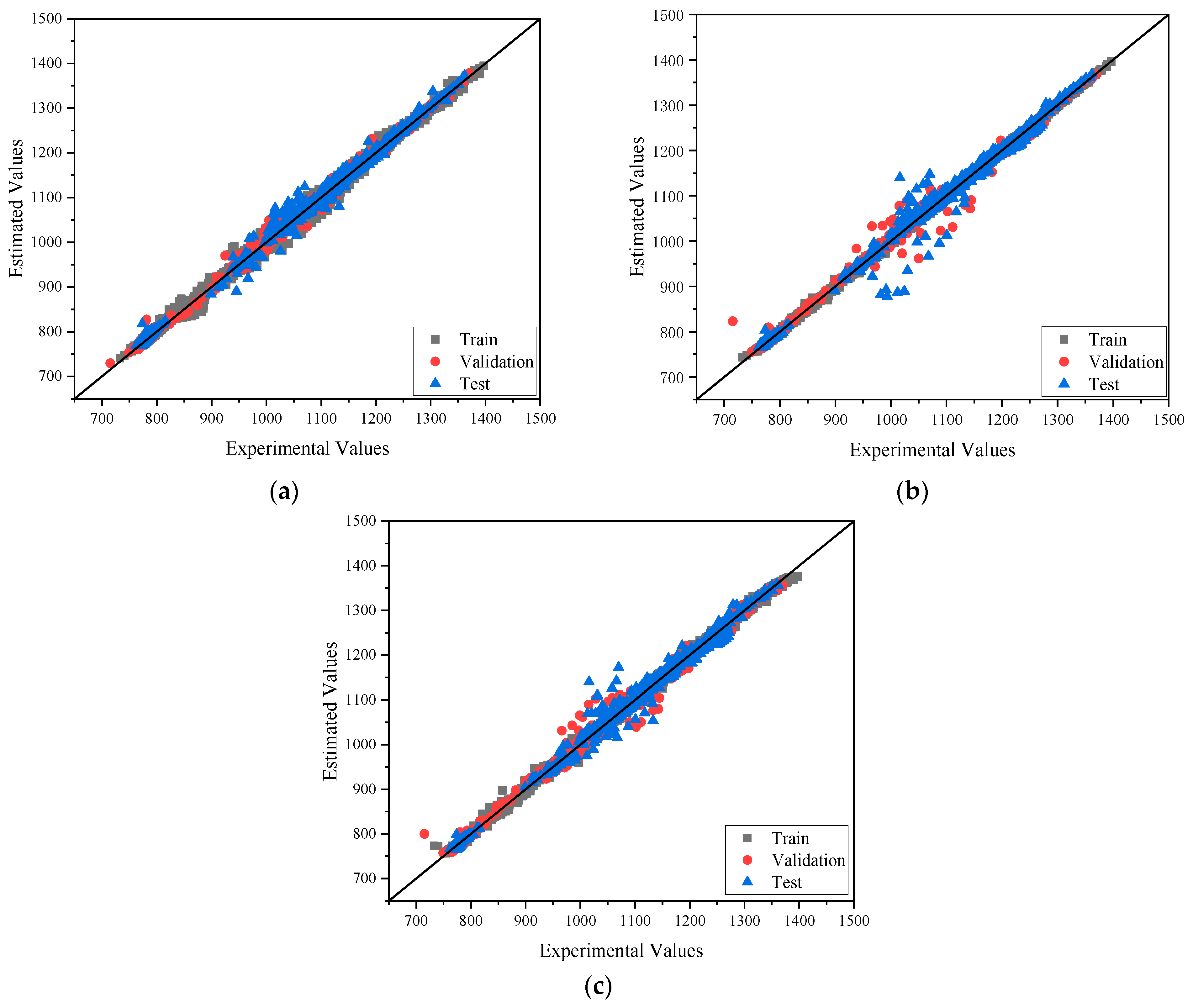
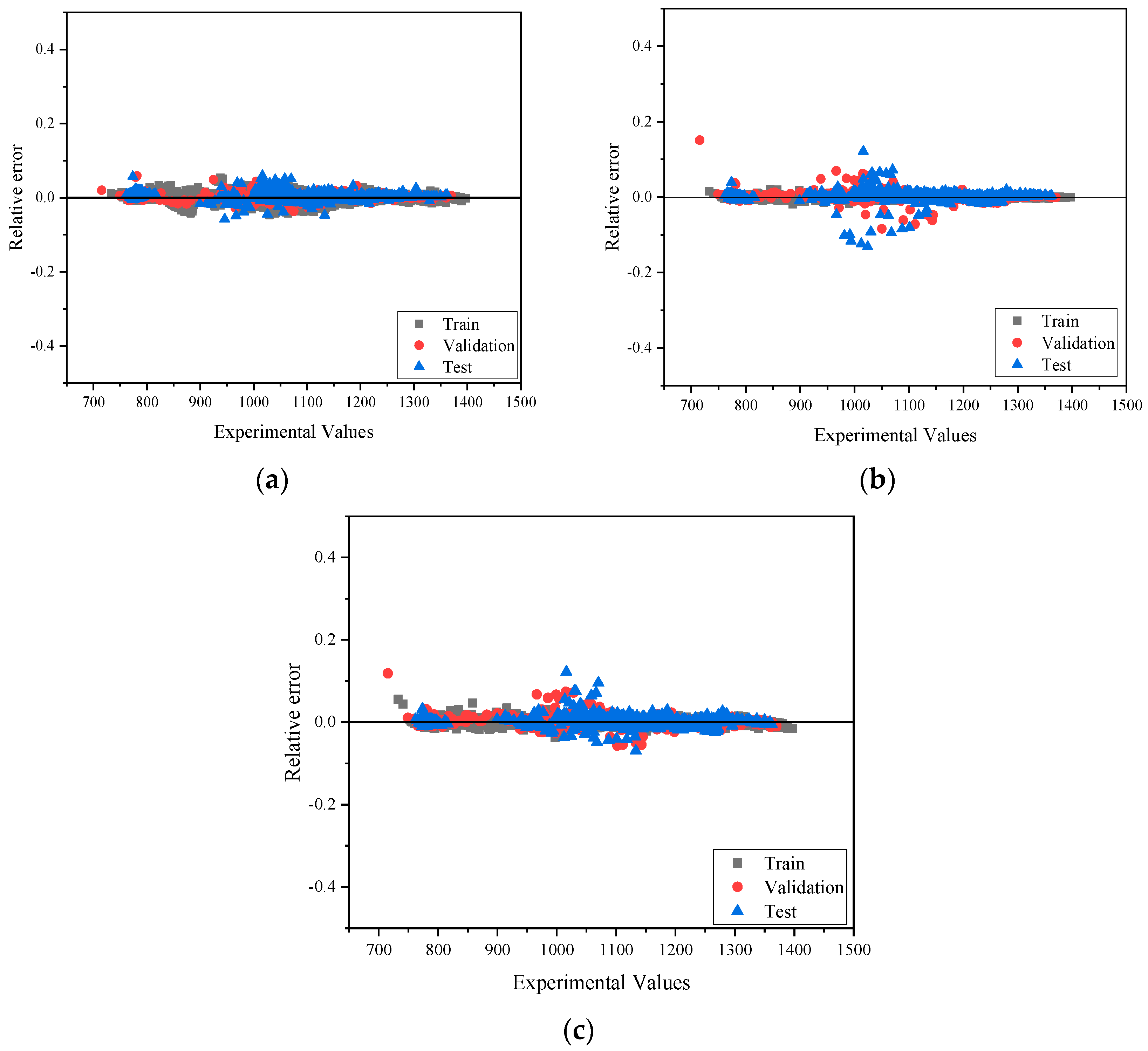
4. Results and Discussions

The collected data were divided into training, validation, and test sets at 75%, 15%, and 15%, respectively, before commencing the modeling study, and the three sets of data were subsequently normalized to mitigate any negative effects of certain data. Through this training process, a set of predicted data is generated, and their relative error values are calculated by comparing them with the experimental data. Data points with significant errors are eliminated to enhance the reliability of the dataset. Further details are provided in the subsequent subsections. In the present study, one method to optimize the ANN model involves increasing the number of neurons in the hidden layer from 1 to 20. Model performance is assessed using metrics such as MAE and R2, where a higher R2 and lower MAE indicate superior model performance.

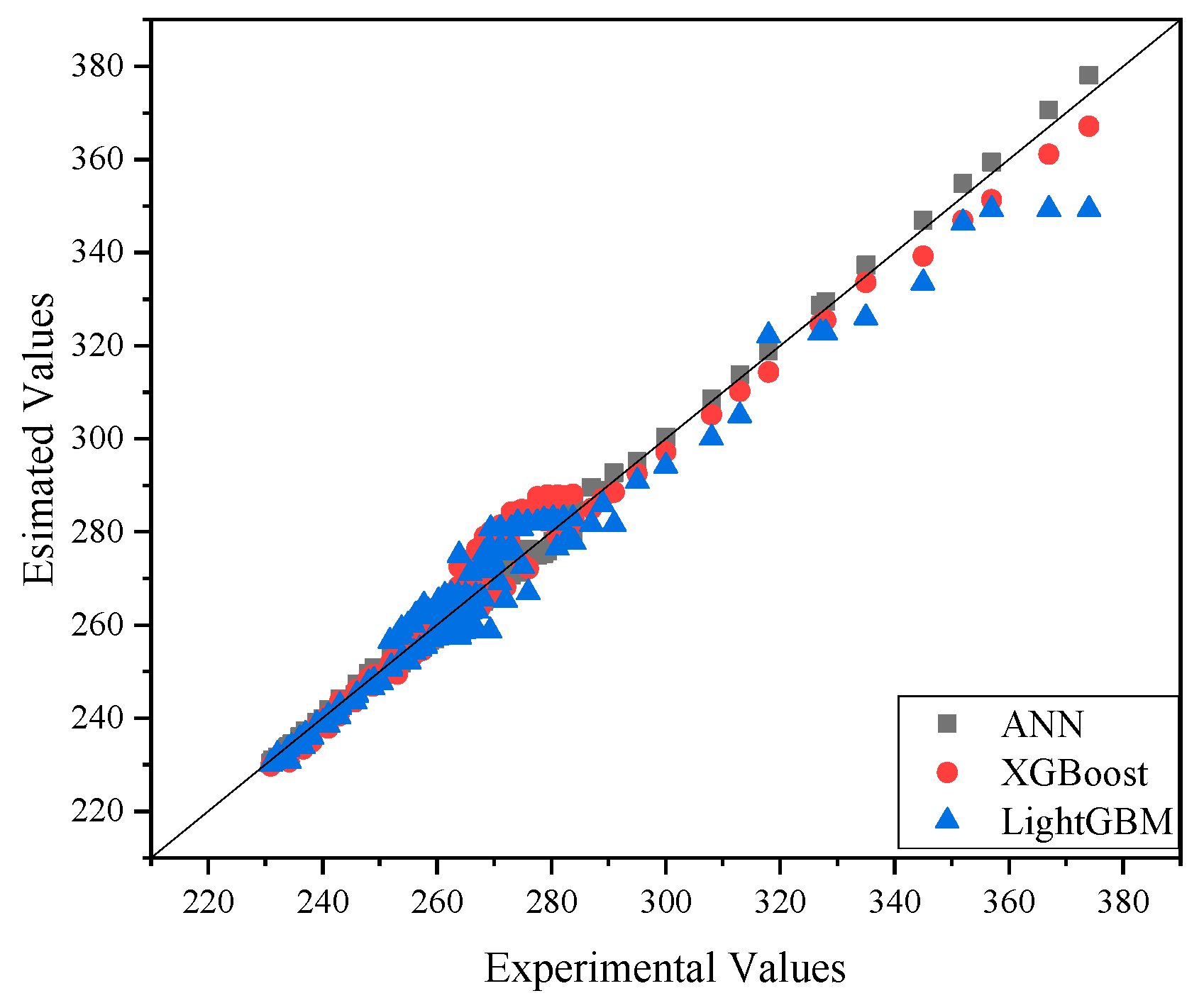
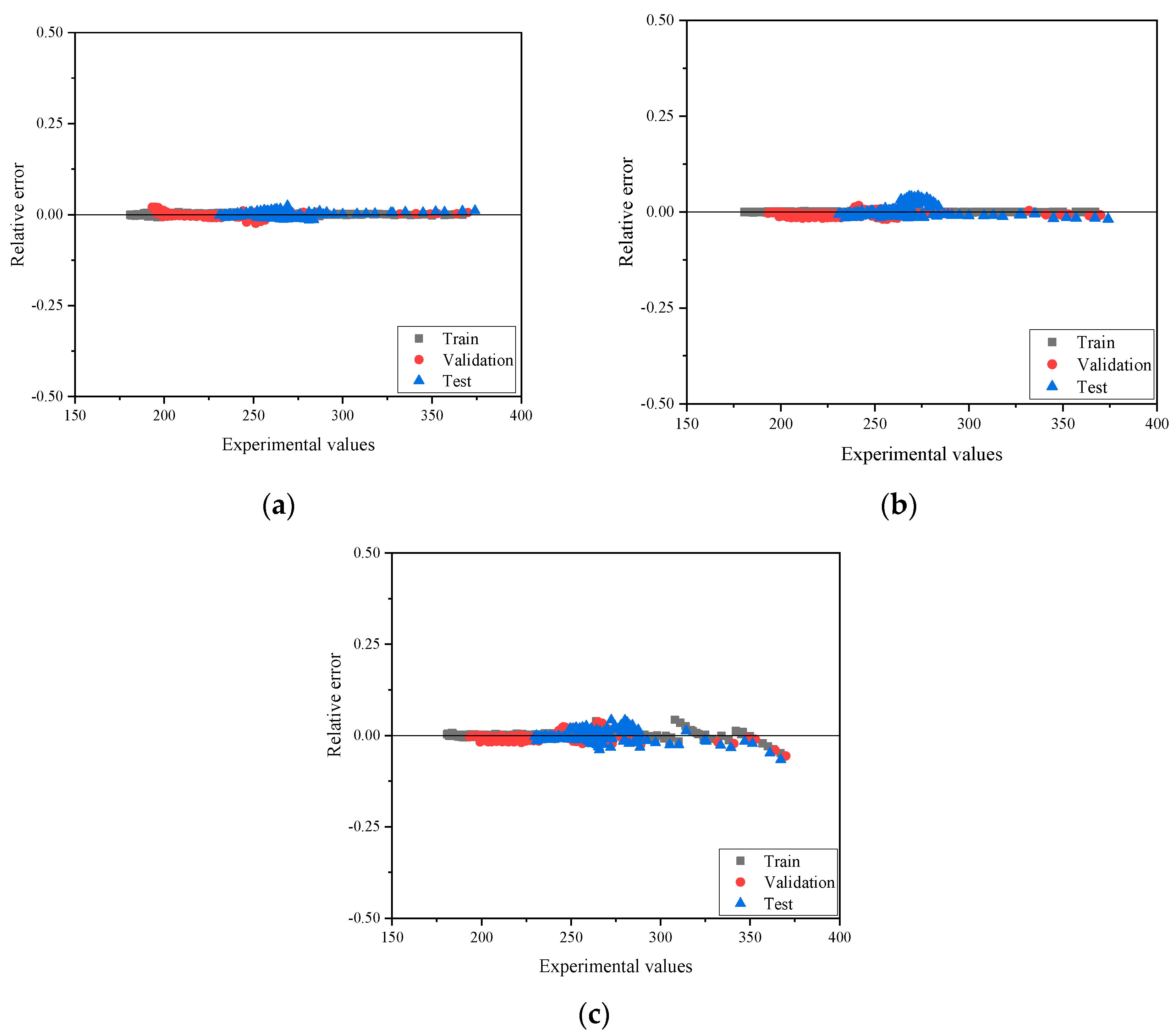
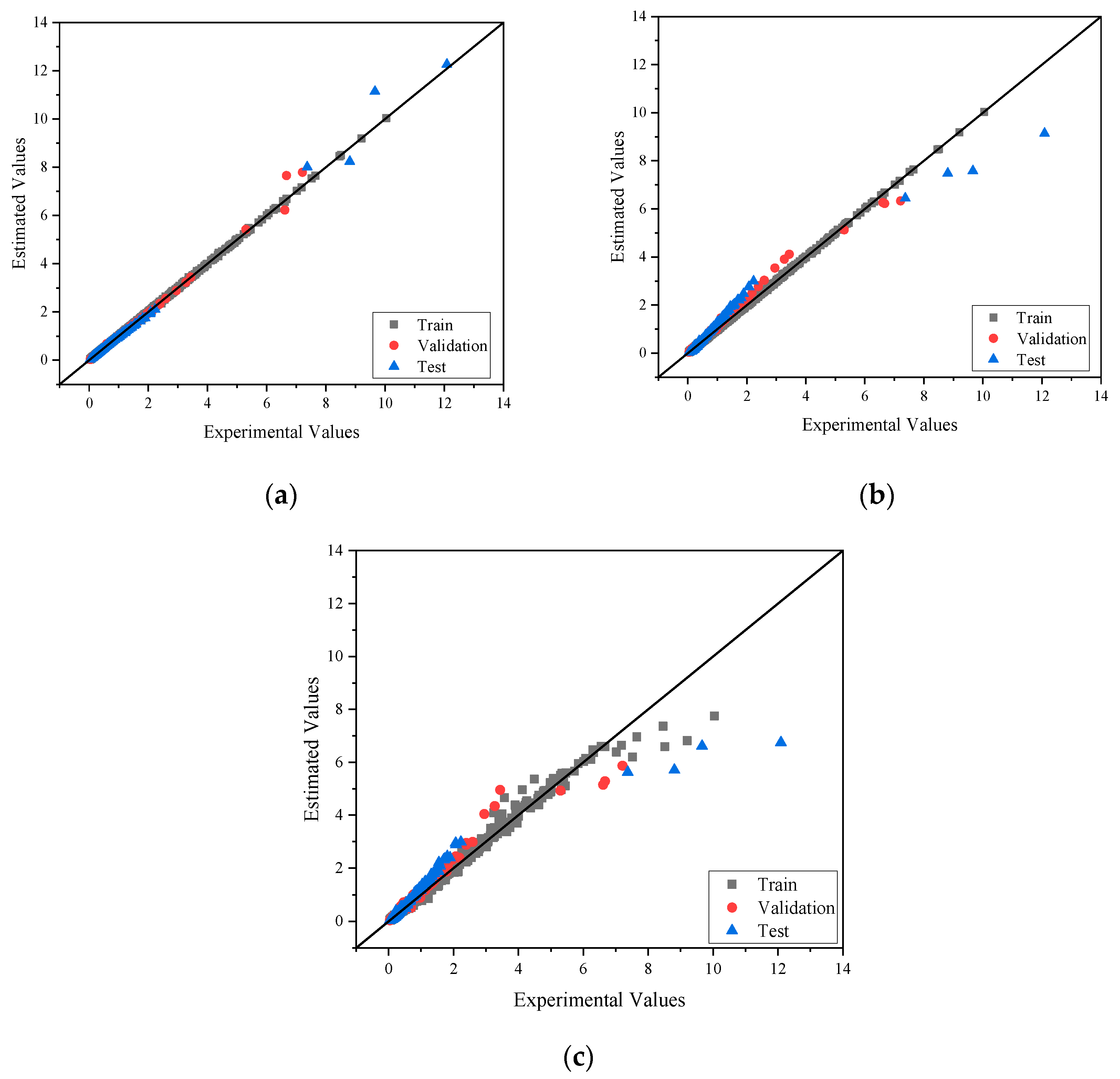
4.1. Heat Capacity

Table 7 demonstrates the predictive performance of the GC model for heat capacity in IL ternary mixtures using three different methods. Table 8 represents the comparison of prediction performance before and after XGBoost and lightGBM tuning parameters. All three models achieve R2 values of at least 0.9, indicating their ability to provide accurate predictions, as depicted in the table. From Table 8, it can be seen that the prediction accuracy of XGBoost and LightGBM has been improved after parameter tuning. Notably, ANN exhibits the highest accuracy in prediction both in comparison with XGBoost and LightGBM pre-tuning and post-tuning. Notably, the ANN exhibits the highest accuracy in forecasting, while XGBoost and LightGBM show slightly inferior performance. Further details on the computational time required for each algorithm are provided in Table 7. XGBoost requires the least amount of time, whereas ANN necessitates the most processing time. In addition, we compare the fit of the training set of the three ML methods with that calculated using the GC method of the linear model. The MAE and R2 calculated using the GC method with the linear model are 2.0908 and 0.9942. All three ML methods can be seen to be superior to the GC method calculations using a linear model.
When utilizing 19 neurons in the hidden layer, as illustrated in Figure 2, the ANN-based GC model provides the most accurate estimation of heat capacity. Figure 3a–c and Figure 4 provide a comprehensive overview of the predictions generated by the different algorithms, comparing the predicted and experimental values of the GC models using three distinct techniques. The data distribution reveals that most data points tend to cluster along a diagonal line, indicating the high accuracy of these nonlinear algorithms in predicting the heat capacity of IL ternary mixtures. In Figure 5a–c, the relative error between the experimental and predicted values of the GC model using the three approaches is depicted. For the majority of data points, particularly in the model employing the ANN algorithm, the relative errors are minimal. This underscores the effectiveness of ANN in predicting the heat capacity of ternary systems composed of IL-organic solvent–organic solvent.
A SHAP analysis was conducted for each feature to explore its effect on the heat capacity of the IL ternary mixture. The results of the SHAP analysis for heat capacity prediction are depicted in Figure 6a,b, while Figure 6c illustrates the degree of interaction between the influencing elements. According to the findings, the CH3 group has minimal impact on the heat capacity of these ternary mixtures, whereas the R-CH3 group of the ILs exerts the most significant influence. This underscores the importance of distinguishing between the CH3 and R-CH3 groups during group division. Additionally, the imidazolium (Im) group of Ils exhibits the second-largest effect after the R-CH3 group of Ils. These results suggest that the presence of Ils has a more pronounced impact on the total heat capacity in mixed systems, as Ils generally possess higher heat capacities than organic solvents.
These findings demonstrate the effectiveness of the GC approach in describing ILs and their heat capacity characteristics. The SHAP interaction value plot reveals the influence of combining two pairs of components on the prediction, with off-diagonal locations indicating this impact. Specifically, the presence of the R-CH3 and Im groups of the Ils had the most significant impact on the predictions, as indicated by the charts. Overall, the SHAP studies provide valuable insights into the independent and combined effects of various parameters on the heat capacity of IL-ternary mixtures.

4.2. Viscosity

During the iterations of the ANN hidden layer, the ANN achieves the most accurate viscosity prediction with eight neurons, as illustrated in Figure 7. Similar to heat capacity prediction, the ANN-based GC model outperforms XGBoost and LightGBM in viscosity prediction. Table 9 demonstrates the effectiveness of the GC model in predicting heat capacity for IL ternary mixtures using three different methods, confirming the accuracy of GC models in estimating viscosity for ternary mixtures. It is worth noting that ANN requires more computing time compared to the other two methods, despite its superior prediction performance. Table 10 shows the comparison results before and after the parameter tuning of the XGBoost and LightGBM models in viscosity prediction. It can be seen that after tuning, although the fit is improved, it is still not as good as the prediction accuracy of ANN. This further illustrates the superiority of ANN in predicting the viscosity properties of the IL-organic solvent–organic solvent ternary system. Additionally, the linear model-based GC method for predicting viscosity properties yields an MAE of 0.1180 and an R² of 0.8874. One can see that the prediction accuracy is much lower than that of the three ML-based models.
The projected values generated by the ANN, XGBoost, and LightGBM algorithms are compared with the experimental values in Figure 8a–c to illustrate the prediction outcomes of the models. Additionally, Figure 9 presents the comparison between the predicted and experimental results for each of the three algorithm test sets. In Figure 8a–c, the data points are mostly concentrated near the diagonal line, indicating a strong fit with these prediction algorithms. However, LightGBM shows slightly more dispersion. This suggests a high level of agreement between the predictions and observations, further validating the reliability of these prediction algorithms. Furthermore, Figure 10 clearly demonstrates that compared to the other two methods, the ANN approach yields the lowest error, indicating its capability to accurately predict the viscosity of the ternary mixing system. According to the viscosity SHAP plot in Figure 11, it is evident that the Im and R-H groups are the main factors influencing viscosity, with viscosity increasing with higher levels of the Im and R-H groups.

4.3. Density

The most accurate density predictions were achieved with the 16th neuron in the hidden layer, as demonstrated by iterative training in Figure 12. Table 11 provides a comparative analysis of prediction performance and computation time for each model. The table illustrates that the ANN model excels, surpassing the other two techniques with R2 values exceeding 0.99 for every dataset. The comparative results before and after parameter optimization in density prediction for the XGBoost and LightGBM models are shown in Table 12. After tuning, both XGBoost and LightGBM achieve R² values above 0.99 on each dataset, and LightGBM’s prediction accuracy slightly exceeds that of ANN, indicating their predictive potential. However, tuning XGBoost and LightGBM takes longer due to the larger density dataset. Therefore, the selection of algorithms should be based on specific requirements in real production scenarios. Meanwhile, the MAE and R² values of the linear model-based GC method for predicting the density properties are 27.9713 and 0.9109, respectively, and the prediction accuracies are likewise much lower than those of the three ML-based models.
Figure 13 and Figure 14 illustrate a comparison of the three algorithms in terms of their goodness of fit and prediction capabilities. Clearly, ANN provides a better prediction performance compared to the other algorithms. Figure 15 displays the relative error between the experimental and predicted values, revealing that most errors are within 10%, with only a few data points having errors beyond 10%. These figures demonstrate that the most accurate prediction outcomes are obtained from the ANN algorithm. Furthermore, Figure 16 presents the density SHAP diagram, revealing that the Im group within IL has the greatest influence on density. Moreover, it indicates that a higher concentration of Im leads to higher density, followed by the mole fraction of organic solvent, where a higher concentration results in lower density.

5. Conclusions

In this study, the GC approach is integrated with three machine learning methods (ANN, XGBoost, and LightGBM) to construct prediction models for density, viscosity, and the heat capacity of ternary IL-organic solvent–organic solvent mixtures. The modeling outcomes affirm the reliability and accuracy of the GC model, which leverages all three machine learning algorithms employed in this research. Particularly, the ANN-based GC model with optimized hidden layer neurons exhibits the best performance, achieving a density fit of 0.9998, a viscosity fit of 0.9999, and a heat capacity fit of 0.9989. These findings underscore the efficacy of ANN in predictive modeling of IL-organic solvent–organic solvent ternary mixture properties. Furthermore, SHAP analyses reveal that the functional groups R-CH3 and Im in IL exert the greatest influence on heat capacity, while viscosity is predominantly affected by the R-H and Im groups. Density, on the other hand, is most influenced by the Im groups and the molar fraction of the second organic solvent. These SHAP insights offer valuable guidance for understanding the key factors shaping the properties of IL-organic solvent mixtures. The machine learning-based GC models developed in this study hold promise for enhancing process calculations and equipment design accuracy in systems containing such mixtures. Additionally, the SHAP analysis results provide valuable insights for designing IL-organic solvent–organic solvent blends, which could find wide-ranging applications across various industries. In conclusion, this research contributes to advancing the understanding and optimization of IL-based processes and their diverse applications.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/pr12071420/s1, Table S1 presents the heat capacity, viscosity, and density data set for IL-organic solvent–organic solvent systems. Table S2 summarizes the abbreviations and names of all the ILs involved. Table S3 concludes the experimental data for the heat capacity of all IL-organic solvent–organic solvent mixtures. Table S4 shows the experimental data for the viscosity of all IL-organic solvent–organic solvent mixtures. Table S5 summarizes the experimental data for the density of all IL-organic solvent–organic solvent mixtures. Table S6 provides the dataset used for the ML-GC model of all IL-organic solvent–organic solvent mixtures in heat capacity. Table S7 summarizes the dataset used for the ML-GC model of all IL-organic solvent–organic solvent mixtures in viscosity. Table S8 concludes the dataset used for the ML-GC model of all IL-organic solvent–organic solvent mixtures in density. Table S9 summarizes the optimized parameters for the ANN-GC model in heat capacity prediction. Table S10 concludes the optimized parameters for the ANN-GC model in viscosity prediction. Table S11 provides the optimized parameters for the ANN-GC model in density prediction.

Author Contributions

Conceptualization, Y.C.; Methodology, Y.L. and Y.C.; Validation, L.D.; Formal analysis, Y.K.; Investigation, Y.L. and S.H.; Resources, H.F.; Data curation, X.L.; Writing—original draft, Y.S.; Writing—review & editing, Y.C.; Supervision, Y.L. and Y.C.; Funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.

Funding

The authors gratefully acknowledge the financial support from Science and Technology Major Project of Wuhan (2023020302020572) and the National Natural Science Foundation of China (21706198).

Data Availability Statement

The data used in this work are mainly obtained from the NIST standard reference database. The data supporting reported results can be found in Tables S6–S8.

Conflicts of Interest

Authors Shaobin Hu and Yongchao Kuang were employed by the company Hubei Energy Group Jiangling Power Generation Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. Greer, A.J.; Jacquemin, J.; Hardacre, C. Industrial applications of ionic liquids. Molecules 2020, 25, 5207. [Google Scholar] [CrossRef] [PubMed]
  2. Lei, Z.; Chen, B.; Koo, Y.M.; MacFarlane, D.R. Introduction: Ionic liquids. Chem. Rev. 2017, 117, 6633–6635. [Google Scholar] [CrossRef] [PubMed]
  3. MacFarlane, D.R.; Forsyth, M.; Izgorodina, E.I.; Abbott, A.P.; Annat, G.; Fraser, K. Industrial applications of ionic liqui liquids. Phys. Chem. Chem. Phys. 2009, 11, 4962–4967. [Google Scholar] [CrossRef] [PubMed]
  4. Hayes, R.; Warr, G.G.; Atkin, R. Structure and nanostructure in ionic liquids. Chem. Rev. 2015, 115, 6357–6426. [Google Scholar] [PubMed]
  5. Armstrong, J.P.; Hurst, C.; Jones, R.G.; Licence, P.; Lovelock, K.R.; Satterley, C.J.; Villar-Garcia, I.J. Vapourisation of ionic liquids. Phys. Chem. Chem. Phys. 2007, 9, 982–990. [Google Scholar] [CrossRef] [PubMed]
  6. Lei, Y.; Du, L.; Liu, X.; Yu, H.; Liang, X.; Kontogeorgis, G.M.; Chen, Y. Natural gas sweetening using tailored ionic liquid-methanol mixed solvent with selective removal of H2S and CO2. Chem. Eng. J. 2023, 476, 146424–146441. [Google Scholar] [CrossRef]
  7. Lei, Y.; Guo, Z.; Du, L.; Meng, X.; Liu, X.; Wu, X.; Chen, Y. Replacing DMF with ionic liquid in isoprene/n-pentane separation in C5 plants: Solvent design, process optimization, and industrial-scale assessment. Fuel 2024, 357, 130006–130019. [Google Scholar] [CrossRef]
  8. Lei, Y.; Yu, Z.; Wei, Z.; Liu, X.; Luo, H.; Chen, Y.; Liang, X.; Kontogeorgis, G.M. Energy-efficient separation of propylene/propane by introducing a tailor-made ionic liquid solvent. Fuel 2022, 326, 124930–124941. [Google Scholar] [CrossRef]
  9. Durga, G.; Mishra, A. Ionic liquids: Industrial applications. In Sustainable Inorganic Chemistry; Wiley: Hoboken, NJ, USA, 2016; pp. 221–234. [Google Scholar]
  10. Plechkova, N.V.; Seddon, K.R. Applications of ionic liquids in the chemical industry. Chem. Soc. Rev. 2008, 37, 123–150. [Google Scholar] [CrossRef]
  11. Müller, K.; Albert, J. Contribution of the individual ions to the heat capacity of ionic liquids. Ind. Eng. Chem. Res. 2014, 53, 10343–10346. [Google Scholar] [CrossRef]
  12. Dai, Z.; Chen, Y.; Liu, C.; Lu, X.; Liu, Y.; Ji, X. Prediction and verification of heat capacities for pure ionic liquids. Chin. J. Chem. Eng. 2021, 31, 169–176. [Google Scholar] [CrossRef]
  13. Bischoff, L.A.; Drisch, M.; Kerpen, C.; Hennig, P.T.; Landmann, J.; Sprenger, J.A.P.; Bertermann, R.; Grüne, M.; Yuan, Q.; Warneke, J.; et al. Cyanohydridoborate Anions: Synthesis, Salts, and Low-Viscosity Ionic Liquids. Chem.—A Eur. J. 2019, 25, 3560–3574. [Google Scholar] [CrossRef]
  14. Sepehrnia, M.; Shahsavar, A.; Maleki, H.; Moradi, A. Experimental study on the dynamic viscosity of hydraulic oil HLP 68-Fe3O4-TiO2-GO ternary hybrid nanofluid and modeling utilizing machine learning technique. J. Taiwan Inst. Chem. Eng. 2023, 145, 104841–104856. [Google Scholar] [CrossRef]
  15. Li, N.; Ma, H.; Wang, T.; Sun, C.; Xia, S. Effect of molecular weight on the properties of water-soluble terpolymers for heavy oil viscosity reduction. J. Taiwan Inst. Chem. Eng. 2023, 144, 104738–104751. [Google Scholar] [CrossRef]
  16. Amith, W.D.; Araque, J.C.; Margulis, C.J. A pictorial view of viscosity in ionic liquids and the link to nanostructural heterogeneity. J. Phys. Chem. Lett. 2020, 11, 2062–2066. [Google Scholar] [CrossRef]
  17. Alavianmehr, M.M.; Hosseini, S.M.; Moghadasi, J. Densities of ionic liquids from ion contribution-based equation of state: Electrolyte perturbation approach. J. Mol. Liq. 2014, 197, 287–294. [Google Scholar] [CrossRef]
  18. Amar, M.N.; Ghriga, M.A.; Hemmati-Sarapardeh, A. Application of gene expression programming for predicting density of binary and ternary mixtures of ionic liquids and molecular solvents. J. Taiwan Inst. Chem. Eng. 2020, 117, 63–74. [Google Scholar] [CrossRef]
  19. Speiser, J.L.; Miller, M.E.; Tooze, J.; Ip, E. A comparison of random forest variable selection methods for classification prediction modeling. Expert Syst. Appl. 2019, 134, 93–101. [Google Scholar] [CrossRef]
  20. Gani, R. Group contribution-based property estimation methods: Advances and perspectives. Curr. Opin. Chem. Eng. 2019, 23, 184–196. [Google Scholar] [CrossRef]
  21. Mjalli, F.S. Mass connectivity index-based density prediction of deep eutectic solvents. Fluid Phase Equilibria 2016, 409, 312–317. [Google Scholar] [CrossRef]
  22. Zhang, D.; Lin, J.; Peng, Q.; Wang, D.; Yang, T.; Sorooshian, S.; Liu, X.; Zhuang, J. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef]
  23. Alshehri, A.S.; Gani, R.; You, F. Deep learning and knowledge-based methods for computer-aided molecular design-toward a unified approach: State-of-the-art and future directions. Comput. Chem. Eng. 2020, 141, 107005–107063. [Google Scholar] [CrossRef]
  24. Liu, Q.; Zhang, L.; Liu, L.; Du, J.; Liang, X.; Mao, H.; Meng, Q. GC-COSMO based Reaction Solvent Design with New Kinetic Model using CAMD. Comput. Aided Chem. Eng. 2018, 44, 235–240. [Google Scholar]
  25. Oster, K.; Jacquemin, J.; Hardacre, C.; Ribeiro, A.; Elsinawi, A. Further development of the predictive models for physical properties of pure ionic liquids: Thermal conductivity and heat capacity. J. Chem. Thermodyn. 2018, 118, 1–15. [Google Scholar] [CrossRef]
  26. Shi, W.; Maginn E, J. Molecular simulation and regular solution theory modeling of pure and mixed gas absorption in the ionic liquid 1-n-hexyl-3-methylimidazolium bis (trifluoromethylsulfonyl) amide ([hmim][Tf2N]). J. Phys. Chem. B. 2008, 112, 16710–16720. [Google Scholar] [CrossRef] [PubMed]
  27. Azadfar, R.; Shaabanzadeh, M.; Hashemi-Moghaddam, H.; Mohammadi Nafchi, A. A new simple model to calculate the heat capacity of pure ionic liquids. Phys. Chem. Res. 2020, 8, 139–154. [Google Scholar]
  28. Macías-Salinas, R.; Gross, J. A viscosity model for pure ionic liquids via the use of a residual-entropy scaling. Fluid Phase Equilibria 2023, 574, 113897–113909. [Google Scholar] [CrossRef]
  29. Fatehi, M.R.; Raeissi, S.; Mowla, D. Estimation of viscosities of pure ionic liquids using an artificial neural network based on only structural characteristics. J. Mol. Liq. 2017, 227, 309–317. [Google Scholar] [CrossRef]
  30. Haghbakhsh, R.; Raeissi, S. Two simple correlations to predict viscosities of pure and aqueous solutions of ionic liquids. J. Mol. Liq. 2015, 211, 948–956. [Google Scholar] [CrossRef]
  31. Paduszynski, K.; Domanska, U. A new group contribution method for prediction of density of pure ionic liquids over a wide range of temperature and pressure. Ind. Eng. Chem. Res. 2012, 51, 591–604. [Google Scholar] [CrossRef]
  32. Wandschneider, A.; Lehmann, J.K.; Heintz, A. Surface tension and density of pure ionic liquids and some binary mixtures with 1-propanol and 1-butanol. J. Chem. Eng. Data 2008, 53, 596–599. [Google Scholar] [CrossRef]
  33. Jacquemin, J.; Husson, P.; Padua, A.A.H.; Majer, V. Density and viscosity of several pure and water-saturated ionic liquids. Green Chem. 2006, 8, 172–180. [Google Scholar] [CrossRef]
  34. Chen, Y.; Kontogeorgis, G.M.; Woodley, J.M. Group contribution based estimation method for properties of ionic liquids. Ind. Eng. Chem. Res. 2019, 58, 4277–4292. [Google Scholar] [CrossRef]
  35. Chen, Y.; Cai, Y.; Thomsen, K.; Kontogeorgis, G.M.; Woodley, J.M. A group contribution-based prediction method for the electrical conductivity of ionic liquids. Fluid Phase Equilibria 2020, 509, 112462–112478. [Google Scholar] [CrossRef]
  36. Jouyban, A.; Soleymani, J.; Jafari, F.; Khoubnasabjafari, M.; Acree, W.E. Mathematical representation of viscosity of ionic liquid+ molecular solvent mixtures at various temperatures using the Jouyban–Acree model. J. Chem. Eng. Data 2013, 58, 1523–1528. [Google Scholar] [CrossRef]
  37. Jouyban, A.; Mirheydari, S.N.; Barzegar-Jalali, M.; Shekaari, H.; Acree, W.E. Comprehensive models for density prediction of ionic liquid+ molecular solvent mixtures at different temperatures. Phys. Chem. Liq. 2020, 58, 309–324. [Google Scholar] [CrossRef]
  38. Jouyban, A.; Acree, W.E., Jr. A single model to represent physico-chemical properties of liquid mixtures at various temperatures. J. Mol. Liq. 2021, 323, 115054–115065. [Google Scholar] [CrossRef]
  39. Mirheydari, S.N.; Soleymani, J.; Jouyban-Gharamaleki, V.; Barzegar-Jalali, M.; Jouyban, A.; Shekaari, H. Viscosity prediction of ionic liquid+ molecular solvent mixtures at various temperatures. J. Mol. Liq. 2018, 263, 228–236. [Google Scholar] [CrossRef]
  40. Wan Normazlan, W.M.D.; Sairi, N.A.; Alias, Y.; Udaiyappan, A.F.; Jouyban, A.; Khoubnasabjafari, M. Composition and temperature dependence of density, surface tension, and viscosity of EMIM DEP/MMIM DMP+ water+ 1-propanol/2-propanol ternary mixtures and their mathematical representation using the Jouyban–acree model. J. Chem. Eng. Data 2014, 59, 2337–2348. [Google Scholar] [CrossRef]
  41. Gmehling, J. Present status and potential of group contribution methods for process development. J. Chem. Thermodyn. 2009, 41, 731–747. [Google Scholar] [CrossRef]
  42. Amar, M.N.; Ouaer, H.; Ghriga, M.A. Robust smart schemes for modeling carbon dioxide uptake in metal-organic frameworks. Fuel 2022, 311, 122545–122555. [Google Scholar] [CrossRef]
  43. Koutsoukos, S.; Philippi, F.; Malaret, F.; Welton, T. A review on machine learning algorithms for the ionic liquid chemical space. Chem. Sci. 2021, 12, 6820–6843. [Google Scholar] [CrossRef] [PubMed]
  44. Amar, M.N.; Ghriga, M.A.; Ouaer, H. On the evaluation of solubility of hydrogen sulfide in ionic liquids using advanced committee machine intelligent systems. J. Taiwan Inst. Chem. Eng. 2021, 118, 159–168. [Google Scholar] [CrossRef]
  45. Li, M.; Fu, X.; Li, D. Diabetes prediction based on XGBoost algorithm. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 768, pp. 072093–072101. [Google Scholar]
  46. Zhao, W.P.; Li, J.; Zhao, J.; Zhao, D.; Lu, J.; Wang, X. Xgb model: Research on evaporation duct height prediction based on XGboost algorithm. Radioengineering 2020, 29, 81–93. [Google Scholar] [CrossRef]
  47. Liang, W.; Luo, S.; Zhao, G.; Wu, H. Predicting hard rock pillar stability using GBDT, XGBoost, and LightGBM algorithms. Mathematics 2020, 8, 765. [Google Scholar] [CrossRef]
  48. Yan, J.; Xu, Y.; Cheng, Q.; Jiang, S.; Wang, Q.; Xiao, Y.; Ma, C.; Yan, J.; Wang, X. LightGBM: Accelerated genomically designed crop breeding through ensemble learning. Genome Biol. 2021, 22, 1–24. [Google Scholar] [CrossRef]
  49. Nohara, Y.; Matsumoto, K.; Soejima, H.; Nakashima, N. Explanation of machine learning models using improved shapley additive explanation. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, Niagara Falls, NY, USA, 7–10 September 2019; p. 546. [Google Scholar]
  50. Wang, D.; Thunéll, S.; Lindberg, U.; Jiang, L.; Trygg, J.; Tysklind, M. Towards better process management in wastewater treatment plants: Process analytics based on SHAP values for tree-based machine learning methods. J. Environ. Manag. 2022, 301, 113941–113953. [Google Scholar] [CrossRef]
  51. Sharma, V.K.; Bhagour, S.; Solanki, S.; Sharma, D. Excess heat capacities of (binary+ ternary) mixtures containing [emim][BF4] and organic liquids. J. Chem. Thermodyn. 2014, 79, 19–32. [Google Scholar] [CrossRef]
  52. Darolia, P.J.; Malik, S.; Garg, S.; Sharma, V.K. Molar heat capacities and excess molar heat capacities of mixtures containing ionic liquids and cyclic amides. Chem. Data Collect. 2022, 41, 100939–100955. [Google Scholar] [CrossRef]
  53. Sharma, V.K.; Kataria, J.; Sharma, D. Excess heat capacities of mixtures containing 1-ethyl-3-methylimidazolium tetrafluoroborate, lactams and cyclic alkanones. J. Therm. Anal. Calorim. 2015, 121, 777–796. [Google Scholar]
  54. Anwar, N.; Riyazuddeen. Excess molar volumes, excess molar isentropic compressibilities, viscosity deviations, and activation parameters for 1-ethyl-3-methyl-imidazolium trifluoro-methanesulfonate+ dimethyl sulfoxide and/or acetonitrile at T= 298.15 to 323.15 K and P= 0.1 MPa. J. Chem. Eng. Data. 2018, 63, 269–289. [Google Scholar] [CrossRef]
  55. Anwar, N. Effect of composition and temperature variations on thermophysical properties of binary and ternary mixtures of 1-ethyl-3-methylimidazolium ethylsulfate with 1-butanol and/or methanol. Fluid Phase Equil. 2017, 437, 127–139. [Google Scholar] [CrossRef]
  56. Kermanpour, F.; Sharifi, T. Measurement and correlation of the excess properties of ternary mixture of {x1 [Hmim][BF4]+ x21-propanol+ x32-propanol} at different temperatures. J. Chem. Eng. Data. 2014, 59, 1922–1929. [Google Scholar] [CrossRef]
  57. Shekaari, H.; Zafarani-Moattar M, T.; Mirheydari S, N. Density, viscosity, speed of sound, and refractive index of a ternary solution of aspirin, 1-butyl-3-methylimidazolium bromide, and acetonitrile at different temperatures T = (288.15 to 318.15) K. J. Chem. Eng. Data. 2015, 60, 1572–1583. [Google Scholar]
  58. Shekaari, H.; Zafarani-Moattar M, T.; Mirheydari S, N. Thermodynamic study of aspirin in the presence of ionic liquid, 1-hexyl-3-methylimidazolium bromide in acetonitrile at T = (288.15 to 318.15) K. J. Mol. Liq. 2015, 209, 138–148. [Google Scholar] [CrossRef]
  59. Anwar, N.; Urooj, F. Effect of co-solvent and temperature on interactions in 1-ethyl-3-methylimidazolium trifluoromethanesulfonate+ ethylene glycol or/and N, N-dimethylformamide, and ethylene glycol+ N, N-dimethylformamide mixtures: Measurement of thermophysical properties. J. Mol. Liq. 2018, 265, 121–134. [Google Scholar] [CrossRef]
  60. Fatima, U.; Riyazuddeen; Anwar, N. Effect of solvents and temperature on interactions in binary and ternary mixtures of 1-butyl-3-methylimidazolium trifluoromethanesulfonate with acetonitrile or/and N, N-dimethylformamide. J. Chem. Eng. Data 2018, 63, 4288–4305. [Google Scholar]
  61. Fatima, U.; Riyazuddeen ; Dhakal, P.; Shah, J.K. Comparative study of influence of ethanol and 2, 2, 2-trifluoroethanol on thermophysical properties of 1-ethyl-3-methylimidazolium dicyanamide in binary mixtures: Experimental and MD simulations. J. Chem. Eng. Data 2020, 66, 101–115. [Google Scholar]
  62. Andreatta, A.E.; Arce, A.; Rodil, E.; Soto, A. Physical properties of binary and ternary mixtures of ethyl acetate, ethanol, and 1-octyl-3-methyl-imidazolium bis (trifluoromethylsulfonyl) imide at 298.15 K. J. Chem. Eng. Data 2009, 54, 1022–1028. [Google Scholar] [CrossRef]
  63. Andreatta, A.E.; Arce, A.; Rodil, E.; Soto, A. Physical and excess properties of (methyl acetate+ methanol+ 1-octyl-3-methyl-imidazolium bis (trifluoromethylsulfonyl) imide) and its binary mixtures at T = 298.15 K and atmospheric pressure. J. Chem. Thermodyn. 2009, 41, 1317–1323. [Google Scholar]
  64. Andreatta, A.E.; Arce, A.; Rodil, E.; Soto, A. Physico-chemical properties of binary and ternary mixtures of ethyl acetate+ ethanol+ 1-butyl-3-methyl-imidazolium bis (trifluoromethylsulfonyl) imide at 298.15 K and atmospheric pressure. J. Solution Chem. 2010, 39, 371–383. [Google Scholar] [CrossRef]
  65. Andreatta, A.E.; Francisco, M.; Rodil, E.; Soto, A.; Arce, A. Isobaric vapour–liquid equilibria and physical properties for isopropyl acetate+ isopropanol+ 1-butyl-3-methyl-imidazolium bis (trifluoromethylsulfonyl) imide mixtures. Fluid Phase Equil. 2011, 300, 162–171. [Google Scholar] [CrossRef]
  66. Andreatta, A.E.; Arce, A.; Rodil, E.; Soto, A. Physical properties and phase equilibria of the system isopropyl acetate+ isopropanol+ 1-octyl-3-methyl-imidazolium bis (trifluoromethylsulfonyl) imide. Fluid Phase Equil. 2010, 287, 84–94. [Google Scholar] [CrossRef]
  67. Shekaari, H.; Bezaatpour, A.; Khoshalhan, M. Thermophysical properties of ionic liquid, 1-hexyl-3-methylimidazolum bromide + N-N′bis(2-pyridylmethylidene)-1,2-diiminoethane (BPIE) Schiff base + N,N-dimethylformamide solutions. Thermochim. Acta 2012, 52, 67–74. [Google Scholar] [CrossRef]
  68. Shekaari, H.; Kazempour, A.; Khoshalhan, M. Effect of N, N′-bis (2-pyridylmethylidene)-1, 2-diiminoethane Schiff base (BPIE) on the thermodynamic properties of the ionic liquid 1-hexyl-3-methylimidazolium chloride in N, N-dimethylacetamide solvent at T = 298.15 K. J. Chem. Thermodyn. 2015, 81, 131–135. [Google Scholar] [CrossRef]
  69. Shekaari, H.; Kazempour, A.; Khoshalhan, M. Densities and Viscosities of Ternary N, N′-Bis (2-pyridylmethylidene)-1, 2-diiminoethane Schiff Base+ Imidazolium Based Ionic Liquids+ Acetonitrile Solutions at T = (298.15 to 313.15) K. J. Chem. Eng. Data 2015, 60, 1106–1118. [Google Scholar] [CrossRef]
  70. Shekaari, H.; Bezaatpour, A.; Khoshalhan, M. Effect of N, N′-Bis (2-pyridylmethylidene)-1, 2-diiminoethane (BPIE) Schiff Base on the thermophysical properties of ionic liquids in N, N-dimethylformamide solutions at 298.15 K. J. Chem. Eng. Data 2011, 56, 4164–4172. [Google Scholar] [CrossRef]
  71. Arce, A.; Rodil, E.; Soto, A. Volumetric and viscosity study for the mixtures of 2-ethoxy-2-methylpropane, ethanol, and 1-ethyl-3-methylimidazolium ethyl sulfate ionic liquid. J. Chem. Eng. Data 2006, 51, 1453–1457. [Google Scholar] [CrossRef]
  72. Foo, C.K.; Leo, C.Y.; Aramesh, R.; Aroua, M.K.; Aghamohammadi, N.; Shafeeyan, M.S.; Shamiri, A. Density and viscosity of aqueous mixtures of N-methyldiethanolamines (MDEA), piperazine (PZ) and ionic liquids. J. Mol. Liq. 2015, 209, 596–602. [Google Scholar] [CrossRef]
  73. Shekaari, H.; Bezaatpour, A.; Elhami-Kalvanagh, R. Thermodynamic properties of salophen schiff base+ ionic liquid ([C n mIm][Br])+ dimethylformamide ternary mixtures at 298.15 K. J. Chem. Eng. Data 2012, 57, 345–351. [Google Scholar] [CrossRef]
  74. Shekaari, H.; Bezaatpour, A.; Elhami, R. Volumetric and Viscometric Studies of N, N′-Bis (salicylaldehyde)-1, 3-diaminopropane Schiff Base (Salpr) in Ionic Liquid+ DMF solutions. J. Solut. Chem. 2012, 41, 516–524. [Google Scholar] [CrossRef]
  75. Shekaari, H.; Elhami-Kalvanagh, R.; Bezaatpour, A. Effect of ionic liquid on the solvation behavior of nonaqueous N, N′-salicylidenephenylediamine Schiff base (Salophen) solutions at 298.15 K. J. Chem. Thermodyn. 2013, 64, 58–64. [Google Scholar] [CrossRef]
  76. Kermanpour, F.; Iloukhani, H.; Javanshad, M. Measurement and modeling the excess properties of binary and ternary mixtures containing [Hmim][BF4], 2-methyl-2-propanol, and propylamin compounds at 298.15 K using PFP theory. J. Mol. Liq. 2013, 188, 22–27. [Google Scholar] [CrossRef]
  77. Ebrahiminejadhasanabadi, M.; Nelson, W.M.; Naidoo, P.; Mohammadi, A.H.; Ramjugernath, D. Investigation of mixed MEA-based solvents featuring ionic liquids and NMP for CO2 capture: Experimental measurement of CO2 solubility and thermophysical properties. J. Chem. Eng. Data 2021, 66, 899–914. [Google Scholar] [CrossRef]
  78. Ebrahiminejadhasanabadi, M.; Nelson, W.M.; Naidoo, P.; Mohammadi, A.H.; Ramjugernath, D. Experimental measurements of CO2 solubility, viscosity, density, sound velocity and evaporation rate for 2-(2-aminoethoxy) ethanol (DGA)+ 1-methylpyrrolidin-2-one (NMP)/water+ ionic liquid systems. Fluid Phase Equil. 2022, 559, 113475–113488. [Google Scholar] [CrossRef]
  79. Malik, S.; Gupta, H.; Sharma V, K. Molecular interactions in ternary liquid mixtures containing alkyl imidazolium tetrafluroborates and cyclic ketones: Excess molar volumes and excess isentropic compressibilities. Chem. Data Collect. 2021, 31, 100603–100611. [Google Scholar] [CrossRef]
  80. Deenadayalu, N.; Bahadur, I.; Hofman, T. Ternary excess molar volumes of {methyltrioctylammonium bis (trifluoromethylsulfonyl) imide+ ethanol+ methyl acetate, or ethyl acetate} systems at T=(298.15, 303.15, and 313.15) K. J. Chem. Thermodyn. 2010, 42, 726–733. [Google Scholar] [CrossRef]
  81. Sharma, V.K.; Solanki, S.; Bhagour, S.; Sharma, D. Topological investigations of thermodynamic properties of ionic liquid mixtures: Excess molar volumes and excess isentropic compressibilities. J. Mol. Liq. 2013, 188, 258–271. [Google Scholar] [CrossRef]
  82. Fatima, U.; Montes-Campos, H.; Varela L, M. Experimental and MD simulation investigation on thermophysical properties of binary/ternary mixtures of 1-butyl-3-methylimidazolium trifluoromethanesulfonate with molecular solvents. J. Mol. Liq. 2020, 302, 112481–112537. [Google Scholar] [CrossRef]
  83. Rafiee H, R.; Frouzesh, F. Volumetric properties for binary and ternary mixtures of allyl alcohol, 1, 3-dichloro-2-propanol and 1-ethyl-3-methyl imidazolium ethyl sulfate [Emim][EtSO4] from T= 298.15 to 318.15 K at ambient pressure. Thermochim. Acta 2015, 611, 36–46. [Google Scholar] [CrossRef]
  84. Singh, S.; Bahadur, I.; Redhi, G.G.; Karlapudi, S.; Ramjugernath, D.; Hofman, T.; Ebenso, E.E. Cibulka correlation for ternary excess/deviation properties of {[C2mim][EtSO4](x1)+ acetic or propionic acid (x2)+ acetonitrile (x3)} systems at different temperatures. J. Chem. Thermodyn. 2017, 107, 153–162. [Google Scholar] [CrossRef]
  85. Masilo, K.; Bahadur, I.; Paredes M L, L. Measurement and Modeling of Thermodynamic Properties for Ternary Mixtures Containing 1-Butyl-3-methylimidazolium-Based Ionic Liquids with Acetophenone and Acetic or Propionic Acid. J. Chem. Eng. Data 2021, 66, 4368–4383. [Google Scholar] [CrossRef]
  86. Sharma, V.K.; Bhagour, S.; Solanki, S.; Rohilla, A. Thermodynamic properties of ternary mixtures containing ionic liquids and organic solvents. J. Chem. Eng. Data 2013, 58, 1939–1954. [Google Scholar] [CrossRef]
  87. Sharma V, K.; Solanki, S.; Bhagour, S. Thermodynamic properties of ternary mixtures containing ionic liquid and organic liquids: Excess molar volume and excess isentropic compressibility. J. Chem. Eng. Data 2014, 59, 1140–1157. [Google Scholar] [CrossRef]
  88. Singh, S.; Bahadur, I.; Ebenso E, E. Thermodynamic properties of ternary mixture {[C4mim][SCN]+ acetic or propionic acid+ acetonitrile} over the temperature range of (293.15–313.15) K. J. Chem. Thermodyn. 2019, 138, 321–331. [Google Scholar] [CrossRef]
  89. Bahadur, I.; Deenadayalu, N.; Tywabi, Z.; Sen, S.; Hofman, T. Volumetric properties of ternary (IL+ 2-propanol or 1-butanol or 2-butanol+ ethyl acetate) systems and binary (IL+ 2-propanol or 1-butanol or 2-butanol) and (1-butanol or 2-butanol+ ethyl acetate) systems. J. Chem. Thermodyn. 2012, 49, 24–38. [Google Scholar] [CrossRef]
  90. Sharma V, K.; Kataria, J.; Solanki, S. Thermodynamic properties of ternary mixtures containing 1-ethyl-3-methylimidazolium tetrafluoroborate with cyclic amides and cyclopentanone or cyclohexanone at T = (293.15, 298.15, 303.15 and 308.15) K. J. Chem. Thermodyn. 2015, 86, 43–56. [Google Scholar] [CrossRef]
  91. Zhu, Q.; Wang, C.; Yin, J.; Li, H.; Jiang, W.; Liu, J.; Zhu, W. Efficient and remarkable SO2 capture: A discovery of imidazole-based ternary deep eutectic solvents. J. Mol. Liq. 2021, 330, 11559–11568. [Google Scholar] [CrossRef]
  92. Abu-Eishah S, I.; Dowaidar A, M. Liquid− liquid equilibrium of ternary systems of cyclohexane+(benzene,+ toluene,+ ethylbenzene, or+ o-xylene)+ 4-methyl-N-butyl pyridinium tetrafluoroborate ionic liquid at 303.15 K. J. Chem. Eng. Data 2008, 53, 1708–1712. [Google Scholar] [CrossRef]
  93. Bastos, P.D.; Oliveira, F.S.; Rebelo, L.P.; Pereiro, A.B.; Marrucho, I.M. Separation of azeotropic mixtures using high ionicity ionic liquids based on 1-ethyl-3-methylimidazolium thiocyanate. Fluid Phase Equil. 2015, 389, 48–54. [Google Scholar] [CrossRef]
  94. Hu, X.; Li, Y.; Cui, D.; Chen, B. Separation of ethyl acetate and ethanol by room temperature ionic liquids with the tetrafluoroborate anion. J. Chem. Eng. Data 2008, 53, 427–433. [Google Scholar] [CrossRef]
Processes 12 01420 g001
Figure 1. Three-layer ANN structure with N × 1 input vector size.
Figure 1. Three-layer ANN structure with N × 1 input vector size.
Processes 12 01420 g001
Processes 12 01420 g002
Figure 2. Effect of hidden layer neuron numbers on ANN-GC model performance (heat capacity).
Figure 2. Effect of hidden layer neuron numbers on ANN-GC model performance (heat capacity).
Processes 12 01420 g002
Processes 12 01420 g003
Figure 3. Comparison of experimental and predicted heat capacities ((a) ANN; (b) XGBoost; (c) LightGBM).
Figure 3. Comparison of experimental and predicted heat capacities ((a) ANN; (b) XGBoost; (c) LightGBM).
Processes 12 01420 g003
Processes 12 01420 g004
Figure 4. Comparison of experimental and predicted values of test group heat capacities.
Figure 4. Comparison of experimental and predicted values of test group heat capacities.
Processes 12 01420 g004
Processes 12 01420 g005
Figure 5. Comparison of relative error between experimental and predicted heat capacities ((a) ANN; (b) XGBoost; (c) LightGBM).
Figure 5. Comparison of relative error between experimental and predicted heat capacities ((a) ANN; (b) XGBoost; (c) LightGBM).
Processes 12 01420 g005
Processes 12 01420 g006
Figure 6. Heat capacity prediction-based SHAP general map (a), SHAP feature importance map (b), and SHAP interaction map (c) prediction.
Figure 6. Heat capacity prediction-based SHAP general map (a), SHAP feature importance map (b), and SHAP interaction map (c) prediction.
Processes 12 01420 g006
Processes 12 01420 g007
Figure 7. Effect of hidden layer neuron numbers on ANN-GC model performance (viscosity).
Figure 7. Effect of hidden layer neuron numbers on ANN-GC model performance (viscosity).
Processes 12 01420 g007
Processes 12 01420 g008
Figure 8. Comparison of experimental and predicted viscosities ((a) ANN; (b) XGBoost; (c) LightGBM).
Figure 8. Comparison of experimental and predicted viscosities ((a) ANN; (b) XGBoost; (c) LightGBM).
Processes 12 01420 g008
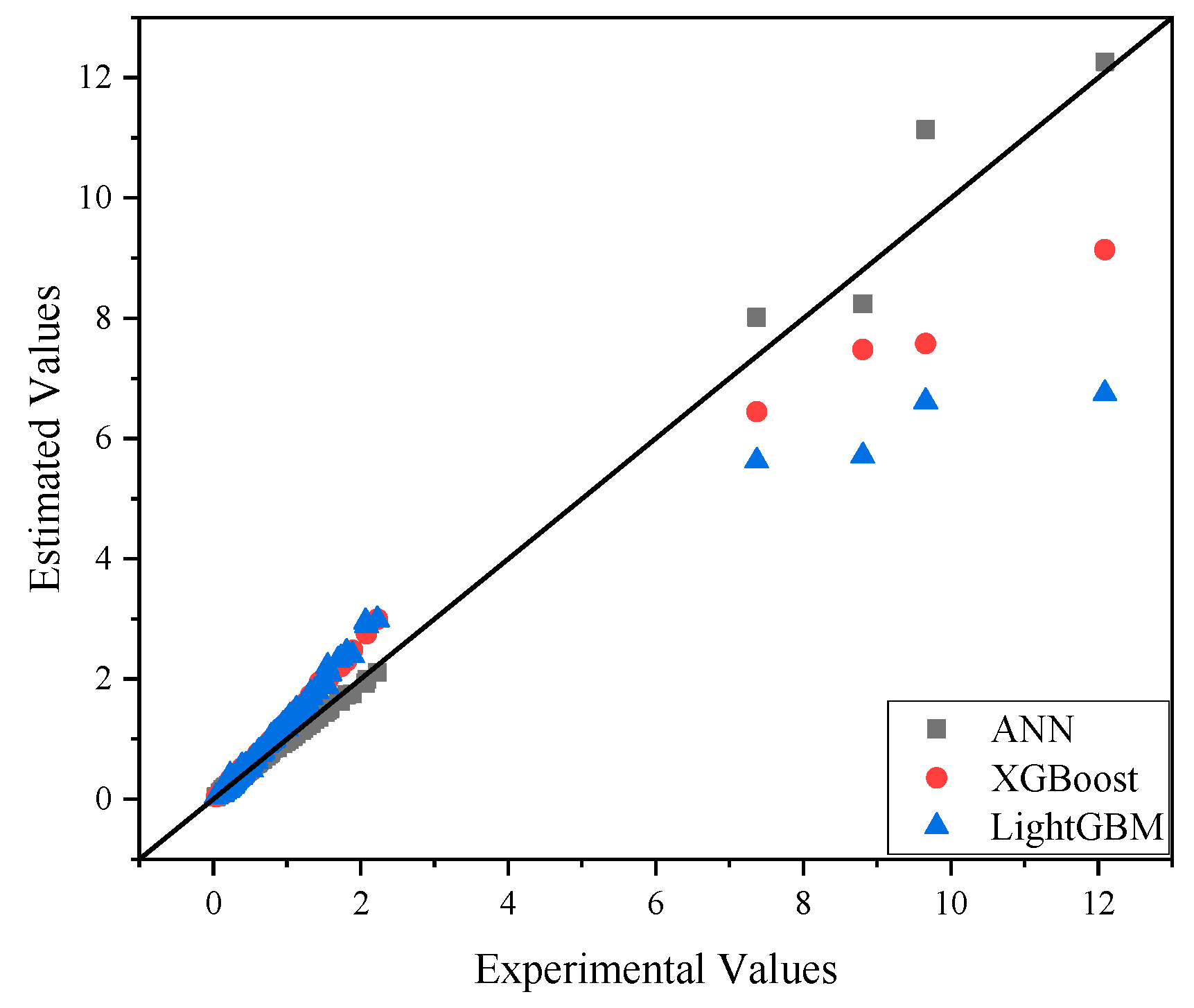
Processes 12 01420 g009
Figure 9. Comparison of experimental and predicted viscosities for the test dataset.
Figure 9. Comparison of experimental and predicted viscosities for the test dataset.
Processes 12 01420 g009
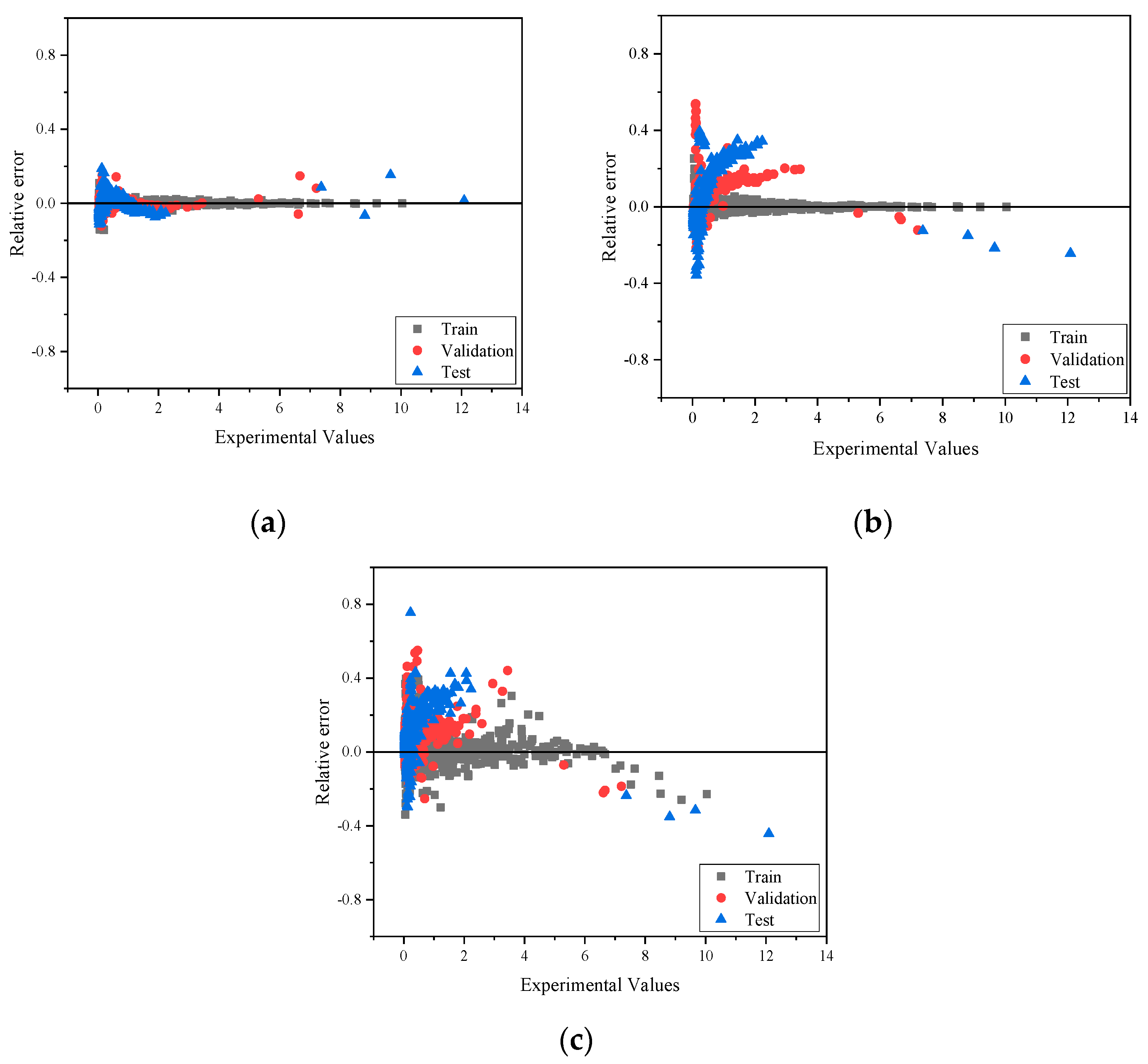
Processes 12 01420 g010
Figure 10. Comparison of relative error between experimental and predicted viscosities for the test dataset ((a) ANN; (b) XGBoost; (c) LightGBM).
Figure 10. Comparison of relative error between experimental and predicted viscosities for the test dataset ((a) ANN; (b) XGBoost; (c) LightGBM).
Processes 12 01420 g010
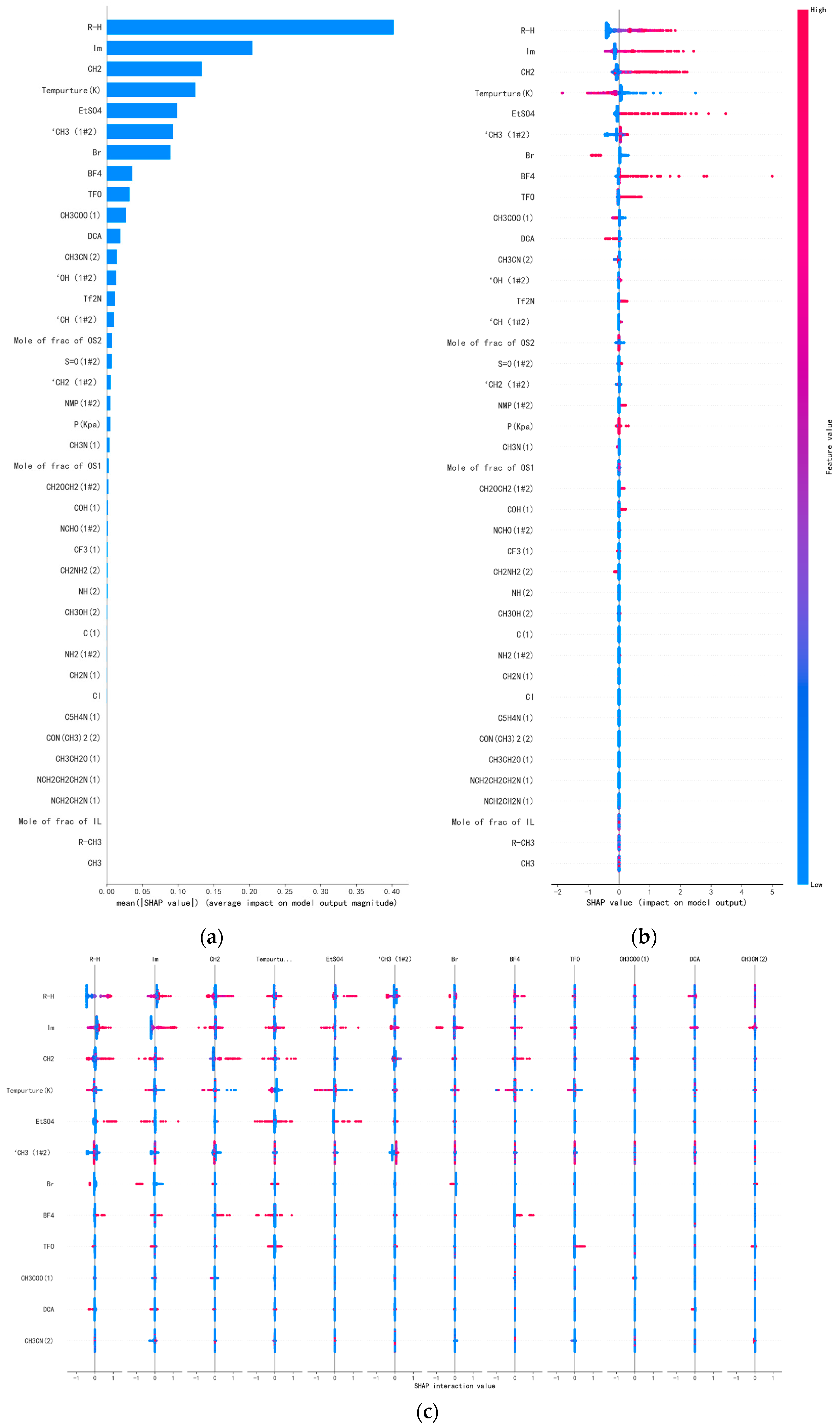
Processes 12 01420 g011
Figure 11. Viscosity prediction-based SHAP general map (a), SHAP feature importance map (b), and SHAP interaction map (c) prediction.
Figure 11. Viscosity prediction-based SHAP general map (a), SHAP feature importance map (b), and SHAP interaction map (c) prediction.
Processes 12 01420 g011
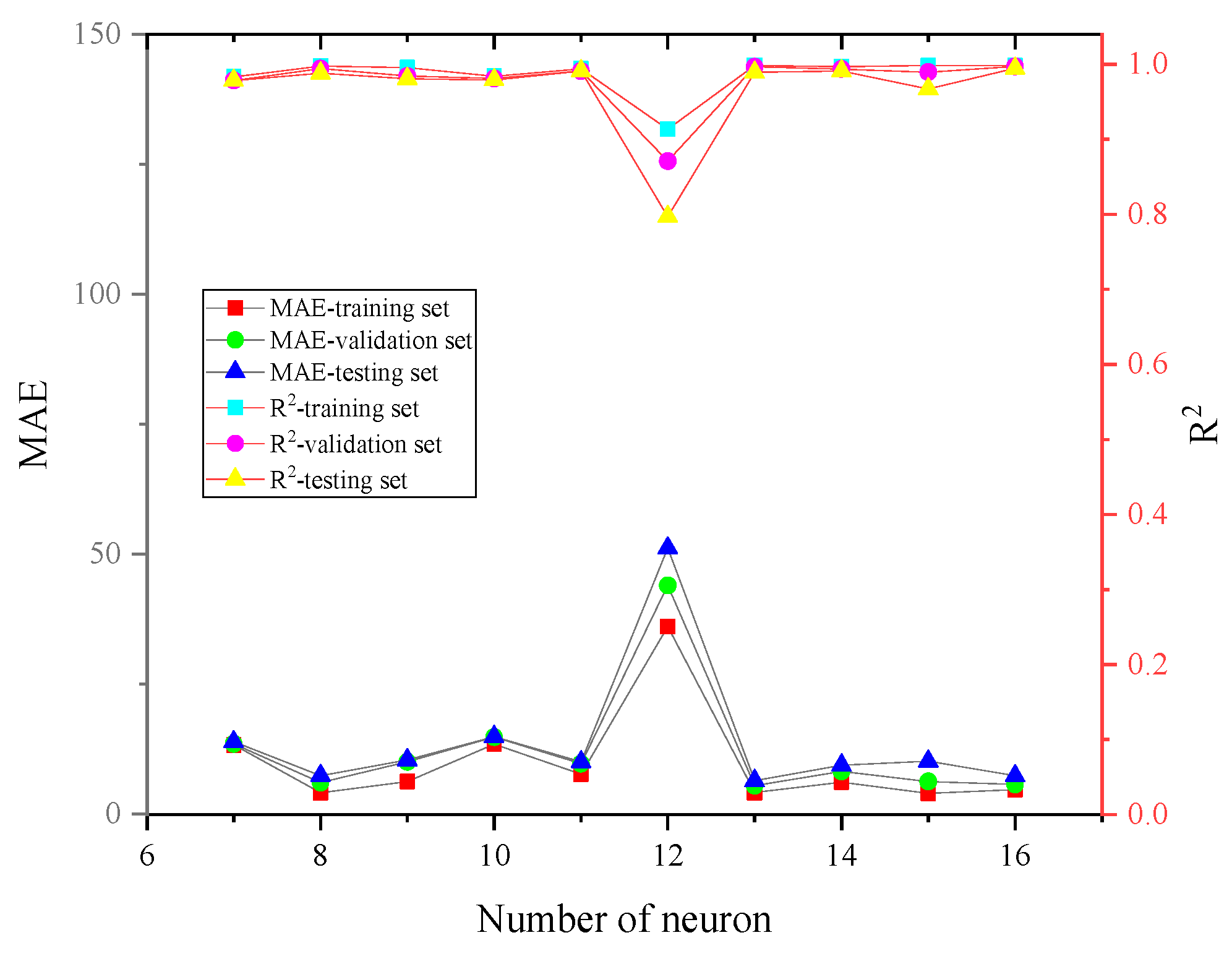
Processes 12 01420 g012
Figure 12. Effect of hidden layer neuron numbers on ANN-GC model performance (density).
Figure 12. Effect of hidden layer neuron numbers on ANN-GC model performance (density).
Processes 12 01420 g012
Processes 12 01420 g013
Figure 13. Comparison of experimental and predicted densities ((a) ANN; (b) XGBoost; (c) LightGBM).
Figure 13. Comparison of experimental and predicted densities ((a) ANN; (b) XGBoost; (c) LightGBM).
Processes 12 01420 g013
Processes 12 01420 g014
Figure 14. Comparison of experimental and predicted densities for the test dataset.
Figure 14. Comparison of experimental and predicted densities for the test dataset.
Processes 12 01420 g014
Processes 12 01420 g015
Figure 15. Comparison of relative error between experimental and predicted densities ((a) ANN; (b) XGBoost; (c) LightGBM).
Figure 15. Comparison of relative error between experimental and predicted densities ((a) ANN; (b) XGBoost; (c) LightGBM).
Processes 12 01420 g015
Processes 12 01420 g016
Figure 16. Density prediction-based SHAP general map (a), SHAP feature importance map (b), and SHAP interaction map (c).
Figure 16. Density prediction-based SHAP general map (a), SHAP feature importance map (b), and SHAP interaction map (c).
Processes 12 01420 g016
Table 1. ILs and organic solvents included in IL-OS-OS ternary systems (heat capacity).
Table 1. ILs and organic solvents included in IL-OS-OS ternary systems (heat capacity).
IL-OS (1)-OS (2)Temperature
(K)		Heat Capacity
(J·K−1·mol−1)
[EMIM][BF4]-(N-methylpyrrolidone)-pyridine [51]293.15–308.15189.9–270
[EMIM][BF4]-(2-pyrrolidinone)-pyridine [51]293.15–308.15190.6–269
[BMMIM][BF4]-(N-methylpyrrolidone)-(2-pyrrolidinone) [52]293.15–308.15196.1–374
[EMIM][BF4]-(N-methylpyrrolidone)-(2-pyrrolidinone) [52]293.15–308.15191–291
[EMIM][BF4]-(N-methylpyrrolidone)-cyclohexanone [53]293.15–308.15181.2–269.5
[EMIM][BF4]-(N-methylpyrrolidone)-cyclopentanone [53]293.15–308.15180.8–266.8
[EMIM][BF4]-cyclohexanone-(2-pyrrolidinone) [53]293.15–308.15184–272.7
[EMIM][BF4]-(2-pyrrolidinone)-cyclopentanone [53]293.15–308.15183.6–283.8
Table 2. ILs and organic solvents included in IL-OS-OS ternary systems (viscosity).
Table 2. ILs and organic solvents included in IL-OS-OS ternary systems (viscosity).
IL-OS (1)-OS (2)Temperature
(K)		Viscosity
(mPa·s)
[EMIM][TFO]-(dimethyl sulfoxide)-acetonitrile [54]298.15–323.150.28–46
[EMIM][EtSO4]-(butan-1-ol)-methanol [55]298.15–323.151.19–84.6
[HMIM][BF4]-(propan-2-ol)-(propan-1-ol) [56]298.15–333.151.06–153.8
[BMIM][Br]-(2-acetoxybenzoic acid)-acetonitrile [57]288.15–318.150.289–0.48
[HMIM][Br]-(2-acetoxybenzoic acid)-acetonitrile [58]288.15–318.150.292–0.462
[EMIM][TFO]-dimethylformamide-(1,2-ethanediol) [59]298.15–323.150.89–29.3
[BMIM][TFO]-dimethylformamide-(acetonitrile) [60]298.15–323.150.39–39.67
[EMIM][DCA]-(2,2,2-trifluoroethanol)-ethanol [61]298.15–323.150.1–8.84
[OMIM][Tf2N]-ethyl acetate-ethanol [62]298.15–323.150.498–60.11
[OMIM][Tf2N]-methyl ethanoate-methanol [63]298.15–323.150.456–70.2
[BMIM][TF2N]-ethyl acetate-ethanol [64]298.15–323.150.523–34.1
[BMIM][TF2N]-isopropyl acetate-(propan-2-ol) [65]298.150.674–34.77
[OMIM][TF2N]-isopropyl acetate-(propan-2-ol) [66]298.150.487–62.4
[HMIM][Br]-(1,2-Ethanediamine)-DMF [67]298.150.861–1.076
[HMIM][Cl]-(1,2-Ethanediamine)-(N,N-DMF) [68]298.150.989–1.234
[C3MIM][Br]-(1,2-Ethanediamine)-acetonitrile [69]298.150.343–0.4198
[C5MIM][Br]-(1,2-Ethanediamine)-acetonitrile [69]298.150.343–0.4391
[HMIM][Br]-(1,2-Ethanediamine)-acetonitrile [69]298.150.343–0.442
[HMIM][Cl]-(1,2-Ethanediamine)-acetonitrile [69]298.150.343–0.409
[C5MIM][Br]-(1,2-Ethanediamine)-DMF [70]298.150.877–1.05
[C3MIM][Br]-(1,2-Ethanediamine)-DMF [70]298.150.88–1.036
[EMIM][EtSO4]-(tert-amyl ethyl ether)-ethanol [71]298.150.878–100.4
[BMIM][BF4]-MDEA-piperazine [72]313.15–363.150.443–1.77
[BMIM][DCA]-MDEA-piperazine [72]313.15–363.150.5–1.97
[EMIM][TFO]-MDEA-piperazine [72]313.15–363.150.54–1.8
[C3MIM][Br]-bisphenol A-DMF [73]298.150.802–0.993
[C5MIM][Br]-H2pbp-DMF [74]298.150.831–1.179
[BMIM][Br]-bisphenol A-(N,N-DMF) [75]298.150.954–1.308
[BMIM][Br]-bisphenol A-dimethyl sulfoxide [75]298.151.998–2.53
[HMIM][BF4](tert-Butanol)-(propan-1-amine) [76]298.150.723–120.9
[BMIM][TF2N]-(N-methylpyrrolidone)-Olamine [77]293.15–333.151.848–6.416
[BMIM][TF2N]-DGA-(N-methylpyrrolidone) [78]293.152.335–12.21
[C5MIM][Br]-bisphenol A-(DMF) [79]298.150.827–0.962
Table 3. ILs and organic solvents included in IL-OS-OS ternary systems (density).
Table 3. ILs and organic solvents included in IL-OS-OS ternary systems (density).
IL-OS (1)-OS (2)Temperature
(K)		Specific Density Liquid
(kg·m−3)
[EMIM][TFA]-dimethyl sulfoxide-acetonitrile [54]298.15–323.15749.2–1379.9
[HMIM][Br]-(1,2-Ethanediamine)-DMF [67]298.15–313.15930.63–961.97
[HMIM][Br]-(1,2-Ethanediamine)-acetonitrile [69]298.15–313.15752.5–801.9
[C3MIM][Br]-(1,2-Ethanediamine)-acetonitrile [69]298.15–313.15755.4–802
[HMIM][Cl]-(1,2-Ethanediamine)-acetonitrile [69]298.15–313.15755.3–796.1
[C5MIM][Br]-(1,2-Ethanediamine)-acetonitrile [69]298.15–313.15752.5–805.2
[EMIM][EtSO4]-(butan-1-ol)(methanol [55]298.15–323.15824.2–1225.1
[HMIM][BF4]-(propan-1-ol)(propan-2-ol) [56]293.15–333.15846.62–1130.62
[BMIM][Br]-(2-acetoxybenzoic acid)-acetonitrile [57]288.15–318.15754.851–826.45
[HMIM][Br]-(2-acetoxybenzoic acid)-acetonitrile [58]288.15–318.15763.7–828.4
[BMIM][TFO]-DMF-(1,2-ethanediol) [59]298.15–323.15965.93–1356.6
[EMIM][TFO]-DMF-acetonitrile [60]298.15–323.15817.7–1263.9
[EMIM][DCA]-(2,2,2-trifluoroethanol)-ethanol [61]298.15–323.151103.4–1340.1
[EMIM][BF4]-cyclohexanone-cyclopentanone [79]293.15–308.151012.4–1283.9
[BMMIM][BF4]-cyclohexanone-cyclopentanone [79]293.15–308.15957.9–1193.5
[BMIM][BF4]-cyclohexanone-cyclopentanone [79]293.15–308.15995.6–1203.1
[N1,8,8,8][BEI]-methyl ethanoate-ethanol [80]298.15–313.15831.2–1104.6
[N1,8,8,8][BEI]-ethyl acetate-ethanol [80]298.15–313.15885.8–1105.1
[EMIM][BF4]-(2-methylaniline)-(N-methylaniline) [81]293.15–308.151038.77–1226
[EMIM][BF4]-(2-methylaniline)-aniline [81]293.15–308.151042.3–1243.7
[BMIM][TFO]-dimethyl sulfoxide-(1,2-ethanediol) [82]298.15–323.151092.9–1270.5
[EMIM][EtSO4]-(1,3-dichloro-2-propanol)-(2-propenol) [83]298.15–318.15899.6–1333
[EMIM][EtSO4]-acetic acid-acetonitrile [84]293.15–313.15962.8–1229.4
[BMIM][BF4]-propanoic acid-acetophenone [85]293.15–333.15974–1191
[EMIM][BF4]-(N-methylpyrrolidone)-pyridine [86]293.15–308.151085.8–1247.2
[EMIM][BF4]-(2-pyrrolidinone)-pyridine [86]293.15–308.151148.1–1253.8
[EMIM][BF4]-(2-methylaniline)-pyridine [87]293.15–308.151061.7–1238.3
[EMIM][BF4]-(2-methylaniline)-(4-methylpyridine) [87]293.15–308.151041.9–1241.2
[EMIM][BF4]-(2-methylaniline)-(3-methylpyridine) [87]293.15–308.151040.9–1234.1
[BMIM][SCN]-propanoic acid-acetonitrile [88]293.15–313.15908.9–1068.3
[BMIM][PF6]-acetophenone-acetic acid [85]293.15–333.151021–1397
[BMIM][BF4]-acetophenone-acetic acid [85]293.15–333.151004–1177
[BMIM][SCN]-acetic acid-acetonitrile [88]293.15–313.15924.8–1071.4
[N1,8,8,8][BEI]-(butan-1-ol)-ethyl acetate [89]298.15–313.15855–1105.4
[N1,8,8,8][BEI]-(butan-2-ol)-ethyl acetate [89]298.15–313.15855.3–1105.4
[EMIM][BF4]-(N-methylpyrrolidone)-cyclopentanone [90]293.15–308.151089.1–1241.4
[EMIM][BF4]-(2-pyrrolidinone)-cyclopentanone [91]293.15–308.151119.4–1249.5
[EMIM][BF4]-(2-pyrrolidinone)-cyclohexanone [90]293.15–308.151133.2–1245.7
[EMIM][BF4]-(N-methylpyrrolidone)-cyclohexanone [90]293.15–308.151036.4–1189.8
[N1,8,8,8][BEI]-ethyl acetate-(propan-2-ol) [89]298.15–313.15833.9–1102
[OMIM][BEI]-methyl ethanoate-methanol [63]298.15945.61–1313.39
[EMIM][EtSO4]-propanoic acid-acetonitrile [84]293.15–313.15958.4–1196.6
[N1,8,8,8][BEI]-methyl ethanoate-methanol [80]298.15–313.15926.7–1102.9
[EMIM][EtSO4]-(tert-amyl ethyl ether)-ethanol [71]298.15785.22–1238.8
[C5MIM][Br]-salnaph-DMF [73]298.15944.1–980.9
[EMIM][Cl]-(di(2-aminoethyl)amine)-(1,2-ethanediol) [91]293–3531013.4–1104.9
[BMPY][BF4]-(1,2-dimethylbenzene)-cyclohexane [92]303.157.652–11.634
[EMIM][SCN]-heptane-ethanol [93]298.15675.41–1113
[EMMIM][BF4]-ethyl acetate-ethanol [94]298.15822–1070
[HEMMIM][BF4]-ethyl acetate-ethanol [94]298.15817–1070
[HMIM][BF4]-(2-methylpropan-2-ol)-(propan-1-amine) [76]298774.36–1126.62
[HEMIM][BF4]-ethyl acetate-ethanol [94]298.15805–1205
[EMIM][BF4]-ethyl acetate-ethanol [94]298.15819–1112
Table 4. Functional groups of ILs and organic solvents involved in the studied IL-OS-OS ternary systems (heat capacity).
Table 4. Functional groups of ILs and organic solvents involved in the studied IL-OS-OS ternary systems (heat capacity).
NamesAbbreviationsNamesAbbreviations
IL-CationsIL-Anions
imidazolium[Im]tetrafluoroborate[BF4]
IL-SubstituentsOS-Functional groups
MethylCH3methyleneCH2
methyl attached to cation coresR-CH3carbon monoxideCO
methyleneCH2aminoNH2
hydrogen attached to cation cores R-Hn-methylpyrrolidoneNMP
pyridineC5H5N
Table 5. Functional groups of ILs and organic solvents involved in the studied IL-OS-OS ternary systems (viscosity).
Table 5. Functional groups of ILs and organic solvents involved in the studied IL-OS-OS ternary systems (viscosity).
NamesAbbreviationsNamesAbbreviations
IL-CationsIL-Anions
imidazolium[Im]trifluoromethanesulfonate[TFO]
IL-Substituentsethyl sulfate[EtSO4]
MethylCH3tetrafluoroborate[BF4]
methyl attached to cation coresR-CH3bromide[Br]
methyleneCH2dimethylphosphate[DMPO4]
hydrogen attached to cation coresR-Hethyl sulfate[EtSO4]
dicyanamide[DCA]
chloride[Cl]
OS-Functional groups
MethylCH3methylamineCH3N
methyleneCH2dimethylamineCH2N
methylidyneCHethyl groupCH3CH2O
hydrogen attached to cation coresOHn-methylpyrrolidoneNMP
sulfurous acidS=OaminoNH2
carbamoyl groupNCH2ethylene glycolCH2OCH2
trifluoromethyl-CF3acetonitrileCH3CN
acetate ionCH3COOmethanolCH3OH
pyrroleC5H4NN,N-dimethylformamideCON(CH3)2
ethylene diamineNCH2CH2N NH
1,3-diaminopropaneNCH2CH2CH2NformamideCH2NH2
Table 6. Functional groups of ILs and organic solvents involved in the studied IL-OS-OS ternary systems (density).
Table 6. Functional groups of ILs and organic solvents involved in the studied IL-OS-OS ternary systems (density).
NamesAbbreviationsNamesAbbreviations
IL-CationsIL-Anions
imidazolium[Im]trifluoroacetate[TFA]
ammonium[N]bromide[Br]
piperidinium[Pip]chloride[Cl]
IL-Substituentsethyl sulfate[EtSO4]
methylCH3tetrafluoroborate[BF4]
methyl attached to cation coresR-CH3ethyl sulfate[EtSO4]
methyleneCH2trifluoromethanesulfonate[TFO]
hydrogen attached to cation cores R-Hdicyanamide[DCA]
hydrogen attached to cation coresOHbis(trifluoromethylsulfonyl)-amide[BEI]
thiocyanate[SCN]
hexafluorophosphate[PF6]
thiocyanate[SCN]
OS-Functional groups
methylCH3carboxyl COOH
methyl attached to cation coresR-CH3acetyl CH3CO
methyleneCH2acetate ionCH3COO
methylidyneCHformamideNCHO
aminomethaneCNH2trifluoromethyl-CF3
hydrogen attached to cation coresOHchloromethylCH2Cl
pyridineC5H5Nn-methylpyrrolidoneNMP
carbon monoxideCO NH
pyrroleC5H4NaminoNH2
ethylene diamineNCH2CH2NmethoxymethylCH2OC
sulfurous acidS=OvinylCH2=CH
imineCH=Nhydrogen cyanideCNH
PhenylC6H5acetonitrileCH3CN
aryl moietyC6H4methanolCH3OH
Table 7. Performance of three models for predicting heat capacity of IL-OS-OS ternary systems.
Table 7. Performance of three models for predicting heat capacity of IL-OS-OS ternary systems.
ModelTraining SetValidation SetTest SetComputation
Time (s)
MAER2MAER2MAER2
ANN0.31950.99981.01380.99791.73200.992943
XGBoost0.07270.99991.82590.99392.79500.97313
LightGBM0.51880.99752.73750.98433.77720.95874
Table 8. XGBoost and lightGBM performance comparison before and after tuning (heat capacity).
Table 8. XGBoost and lightGBM performance comparison before and after tuning (heat capacity).
ModelTraining SetValidation SetTesting Set
MAER2MAER2MAER2
Original XGBoost0.07270.99991.82590.99392.79500.9731
XGBoost after parameter tuning0.04130.99991.61020.99502.66120.9756
Original LightGBM0.51880.99752.73750.98433.77720.9587
LightGBM after parameter tuning0.39910.99971.69710.99273.48830.9573
Table 9. Performance of three models for predicting the viscosity of IL-OS-OS ternary systems.
Table 9. Performance of three models for predicting the viscosity of IL-OS-OS ternary systems.
ModelTraining SetValidation SetTest SetComputation
Time (s)
MAER2MAER2MAER2
ANN0.00570.99990.01190.99950.02250.997374
XGBoost0.00830.99980.07000.97800.13330.94053
LightGBM0.03750.98840.09300.94000.17620.84394
Table 10. XGBoost and lightGBM performance comparison before and after tuning (viscosity).
Table 10. XGBoost and lightGBM performance comparison before and after tuning (viscosity).
ModelTraining SetValidation SetTesting Set
MAER2MAER2MAER2
Original XGBoost0.00830.99980.07000.97800.13330.9405
XGBoost after parameter tuning0.02630.99880.08210.97580.12880.9578
Original LightGBM0.03750.98840.09300.94000.17620.8439
LightGBM after parameter tuning0.04270.99560.07630.97370.13840.9198
Table 11. Performance of three models for predicting the density of IL-OS-OS ternary systems.
Table 11. Performance of three models for predicting the density of IL-OS-OS ternary systems.
ModelTraining SetValidation SetTest SetComputation
Time (s)
MAER2MAER2MAER2
ANN4.71600.99795.70160.99717.37600.9943426
XGBoost1.94440.99976.11190.99388.50780.98463
LightGBM3.31960.99916.76870.99447.32660.99254
Table 12. XGBoost and lightGBM performance comparison before and after tuning (density).
Table 12. XGBoost and lightGBM performance comparison before and after tuning (density).
ModelTraining SetValidation SetTesting Set
MAER2MAER2MAER2
Original XGBoost1.94440.99976.11190.99388.50780.9846
XGBoost after parameter tuning3.53630.99916.76870.99457.32660.9926
Original LightGBM3.31960.99916.76870.99447.32660.9925
LightGBM after parameter tuning2.56030.99954.76450.99785.58890.9957
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Shu, Y.; Du, L.; Lei, Y.; Hu, S.; Kuang, Y.; Fang, H.; Liu, X.; Chen, Y. Modeling Study on Heat Capacity, Viscosity, and Density of Ionic Liquid–Organic Solvent–Organic Solvent Ternary Mixtures via Machine Learning. Processes 2024, 12, 1420. https://doi.org/10.3390/pr12071420

AMA Style

Shu Y, Du L, Lei Y, Hu S, Kuang Y, Fang H, Liu X, Chen Y. Modeling Study on Heat Capacity, Viscosity, and Density of Ionic Liquid–Organic Solvent–Organic Solvent Ternary Mixtures via Machine Learning. Processes. 2024; 12(7):1420. https://doi.org/10.3390/pr12071420

Chicago/Turabian Style

Shu, You, Lei Du, Yang Lei, Shaobin Hu, Yongchao Kuang, Hongming Fang, Xinyan Liu, and Yuqiu Chen. 2024. "Modeling Study on Heat Capacity, Viscosity, and Density of Ionic Liquid–Organic Solvent–Organic Solvent Ternary Mixtures via Machine Learning" Processes 12, no. 7: 1420. https://doi.org/10.3390/pr12071420

APA Style

Shu, Y., Du, L., Lei, Y., Hu, S., Kuang, Y., Fang, H., Liu, X., & Chen, Y. (2024). Modeling Study on Heat Capacity, Viscosity, and Density of Ionic Liquid–Organic Solvent–Organic Solvent Ternary Mixtures via Machine Learning. Processes, 12(7), 1420. https://doi.org/10.3390/pr12071420

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop