Modeling and Optimizing Biocontrol in Wines: pH as a Modulator of Yeast Amensalism Interaction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Microorganisms and Pre-Fermentations
2.2. Model for Amensalism
2.3. Theoretical Methods: The Modeling Pipeline
2.4. Candidate Models Formulation
2.5. Parameter Estimation
2.6. Model Selection and Reduction
2.7. Numeric Tools
2.8. Optimization
2.8.1. Constant pH
2.8.2. Variable pH
- -
- Any piecewise continuous function can be approximated by a linear combination of the Fourier basis.
- -
- When the function to be approximated is smooth, only a few parameters are needed. Then, the first few terms of the series capture over 85% of the signal’s energy.
- -
- By adjusting the parameters, the signal can be bounded to handle constraints.
3. Results and Discussion
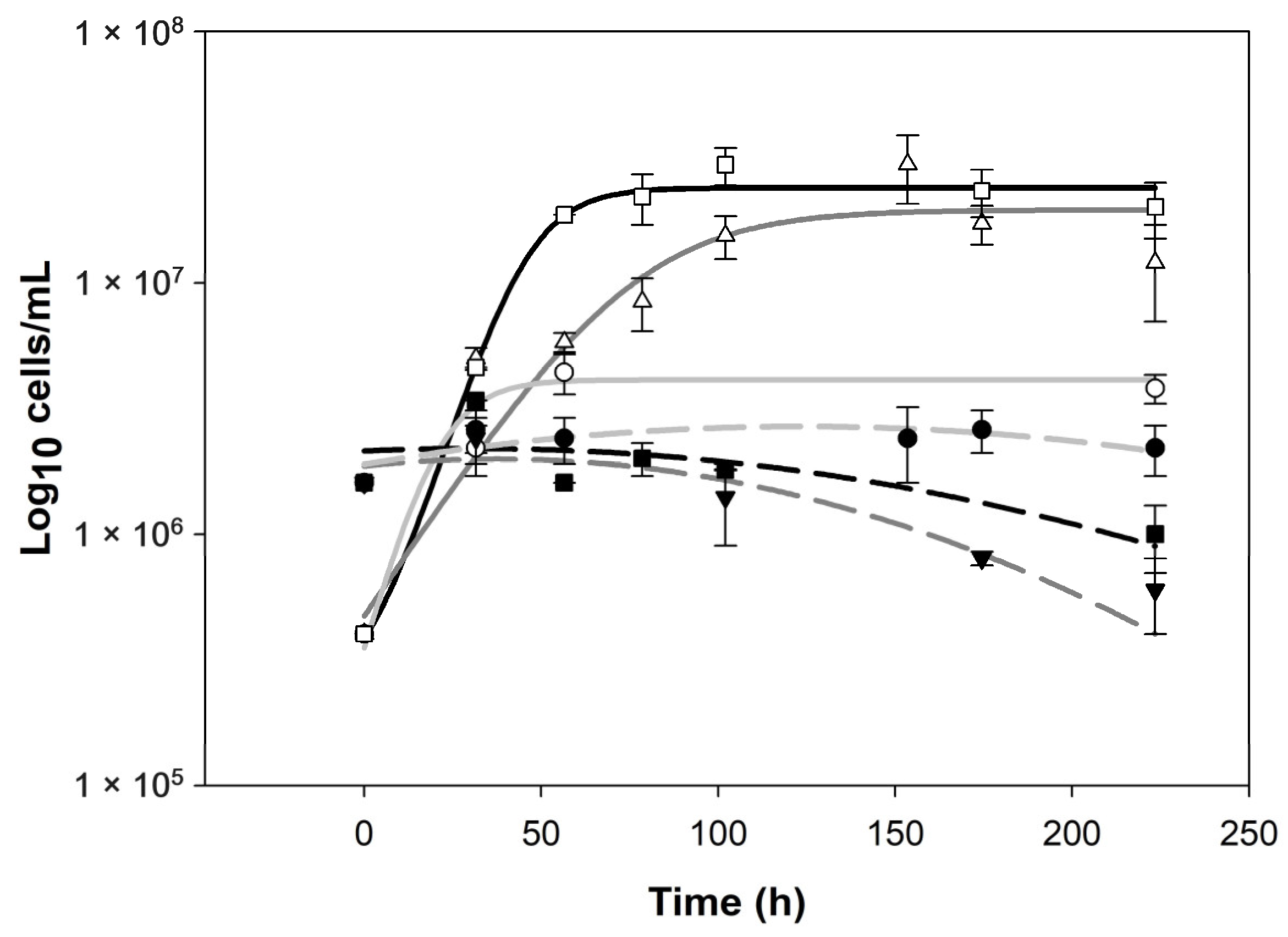
3.1. Data Obtained: Kinetic Behaviors Depend on pH
3.2. Model of Amensalism Improved, Best Fit: 0.68
3.3. Akaike Criterion: The Model with Five Quadratic Submodel Equations and One Linear Is the Reduced Model with Substantial Contribution
3.4. Kinetics and Parameters: The Growth Rates, Intraspecific Saturations, Toxin Production, and Toxin Toxicity Were Influenced by the pH
3.5. Correlation and Sensitivity Analysis: The Parametric Analyzes Were Consistent with the Model’s Behavior
3.6. Optimization at Constant and Variable pH: The Variable Profile Reduces 99% the Spoilage Population throughout the Process Compared to the Constant Profile
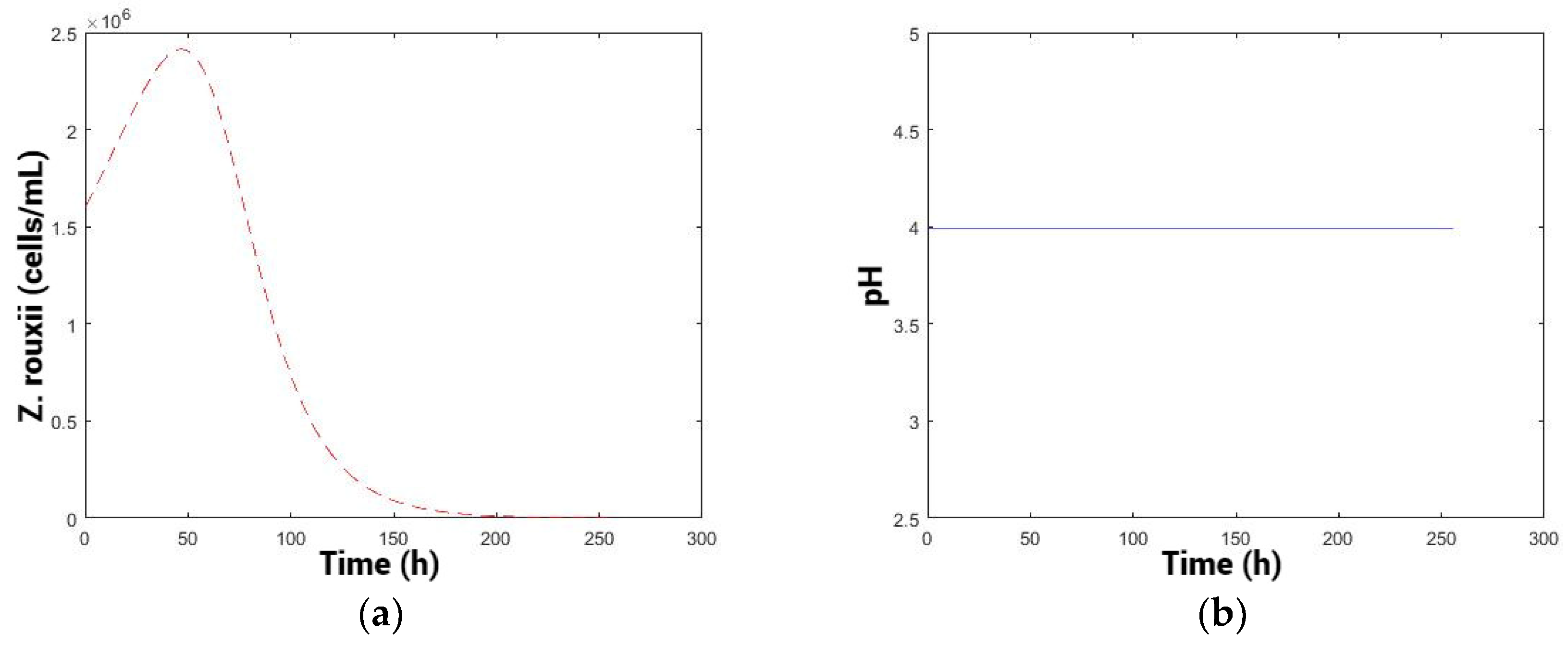
3.6.1. Optimization at Constant pH
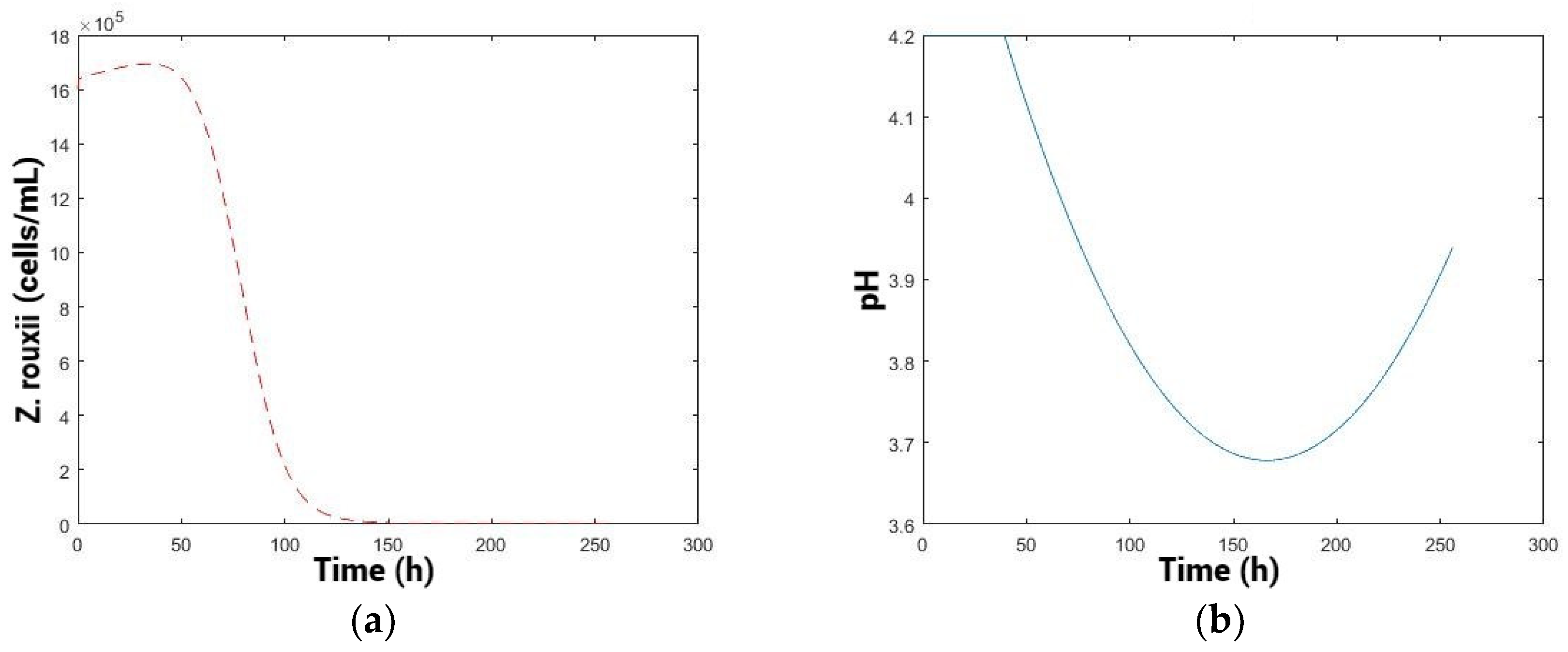
3.6.2. Optimization at Variable pH
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tafel, M.; Szolnoki, G. Estimating the economic impact of tourism in German wine regions. Int. J. Tour. Res. 2020, 22, 788–799. [Google Scholar] [CrossRef]
- Ciani, M.; Capece, A.; Comitini, F.; Canonico, L.; Siesto, G.; Romano, P. Yeast interactions in inoculated wine fermentation. Front. Microbiol. 2016, 7, 555. [Google Scholar] [CrossRef] [PubMed]
- Csoma, H.; Kállai, Z.; Antunovics, Z.; Czentye, K.; Sipiczki, M. Vinification without Saccharomyces: Interacting osmotolerant and “spoilage” yeast communities in fermenting and ageing botrytised high-sugar wines (tokaj essence). Microorganisms 2021, 9, 19. [Google Scholar] [CrossRef] [PubMed]
- Rojo, M.C.; Arroyo López, F.N.; Lerena, M.C.; Mercado, L.; Torres, A.; Combina, M. Evaluation of different chemical preservatives to control Zygosaccharomyces rouxii growth in high sugar culture media. Food Control 2015, 50, 349–355. [Google Scholar] [CrossRef]
- Cejudo-Bastante, M.J.; Sonni, F.; Chinnici, F.; Versari, A.; Perez-coello, M.S.; Riponi, C. Fermentation of sulphite-free white musts with added lysozyme and oenological tannins: Nitrogen consumption and biogenic amines composition of final wines. LWT-Food Sci. Technol. 2010, 43, 1501–1507. [Google Scholar] [CrossRef]
- Comitini, F.; Ciani, M. The zymocidial activity of Tetrapisispora phaffii in the control of Hanseniaspora uvarum during the early stages of winemaking. Lett. Appl. Microbiol. 2010, 50, 50–56. [Google Scholar] [CrossRef] [PubMed]
- Ferrer-Gallego, R.; Puxeu, M.; Martín, L.; Nart, E.; Hidalgo, C.; Andorrà, I. Microbiological, Physical, and Chemical Procedures to Elaborate High-Quality SO2-Free Wines. In Grapes and Wines-Advances in Production, Processing, Analysis and Valorization; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef]
- Lerena, M.C.; Rojo, M.C.; Sari, S.; Mercado, L.A.; Krieger-Weber, S.; Combina, M. Malolactic fermentation induced by Lactobacillus plantarum in Malbec wines from Argentina. S. Afr. J. Enol. Vitic. 2016, 37, 115–123. [Google Scholar] [CrossRef]
- Ribéreau-Gayon, P.; Dubourdieu, D.; Donèche, B.; Lonvaud, A. (Eds.) Handbook of Enology, Volume 2: The Microbiology of Wine and Vinifications; John Wiley & Sons Ltd.: Chichester, UK, 2006; Volume 2. [Google Scholar] [CrossRef]
- Baker, K.F.; Cook, R.J. Biological Control of Plant Pathogens; W.H. Freeman and Company: San Francisco, CA, USA, 1974. [Google Scholar]
- Canonico, L.; Agarbati, A.; Galli, E.; Comitini, F.; Ciani, M. Metschnikowia pulcherrima as biocontrol agent and wine aroma enhancer in combination with a native Saccharomyces cerevisiae. LWT 2023, 181, 114758. [Google Scholar] [CrossRef]
- Oro, L.; Ciani, M.; Comitini, F. Antimicrobial activity of Metschnikowia pulcherrima on wine yeasts. J. Appl. Microbiol. 2014, 116, 1209–1217. [Google Scholar] [CrossRef]
- Berbegal, C.; Garofalo, C.; Russo, P.; Pati, S.; Capozzi, V.; Spano, G. Use of autochthonous yeasts and bacteria in order to control Brettanomyces bruxellensis in wine. Fermentation 2017, 3, 65. [Google Scholar] [CrossRef]
- Simonin, S.; Roullier-Gall, C.; Ballester, J.; Schmitt-Kopplin, P.; Quintanilla-Casas, B.; Vichi, S.; Peyron, D.; Alexandre, H.; Tourdot-Maréchal, R. Bio-Protection as an Alternative to Sulphites: Impact on Chemical and Microbial Characteristics of Red Wines. Front. Microbiol. 2020, 11, 1308. [Google Scholar] [CrossRef] [PubMed]
- Boynton, P.J. The ecology of killer yeasts: Interference competition in natural habitats. Yeast 2019, 36, 473–485. [Google Scholar] [CrossRef] [PubMed]
- Kuchen, B.; Maturano, Y.P.; Gil, R.M.; Vazquez, F.; Scaglia, G.J.E. Kinetics and mathematical model of killer/sensitive interaction under different physicochemical conditions of must/wine: A study from a biological point of view. Lett. Appl. Microbiol. 2022, 74, 718–728. [Google Scholar] [CrossRef] [PubMed]
- Kuchen, B.; Maturano, Y.P.; Mestre, M.V.; Combina, M.; Toro, M.E.; Vazquez, F. Selection of native non-Saccharomyces yeasts with biocontrol activity against spoilage yeasts in order to produce healthy regional wines. Fermentation 2019, 5, 60. [Google Scholar] [CrossRef]
- Kuchen, B.; Vazquez, F.; Maturano, Y.P.; Scaglia, G.J.E.; Pera, L.; Vallejo, M.D. Toward application of biocontrol to inhibit wine spoilage yeasts: The use of statistical designs for screening and optimisation. Oeno One 2021, 55, 75–96. [Google Scholar] [CrossRef]
- Serra, A.; Strehaiano, P.; Taillandier, P. Influence of temperature and pH on Saccharomyces bayanus var. uvarum growth; impact of a wine yeast interspecific hybridization on these parameters. Int. J. Food Microbiol. 2005, 104, 257–265. [Google Scholar] [CrossRef] [PubMed]
- Comitini, F.; Ingeniis De, J.; Pepe, L.; Mannazzu, I.; Ciani, M. Pichia anomala and Kluyveromyces wickerhamii killer toxins as new tools against Dekkera/Brettanomyces spoilage yeasts. FEMS Microbiol. Lett. 2004, 238, 235–240. [Google Scholar] [CrossRef] [PubMed]
- Fanzone, M.L.; Sari, S.E.; Mestre, M.V.; Catania, A.A.; Catelén, M.J.; Jofré, V.P.; Maturano, Y.P. Combination of pre-fermentative and fermentative strategies to produce Malbec wines of lower alcohol and pH, with high chemical and sensory quality. OENO One 2020, 54, 1041–1058. [Google Scholar] [CrossRef]
- Comuzzo, P.; Battistutta, F. Acidification and pH control in red wines. In Red Wine Technology; Academic Press: Cambridge, MA, USA, 2019; Chapter 2; pp. 17–34. [Google Scholar]
- Hellweger, F.L.; Clegg, R.J.; Clark, J.R.; Plugge, C.M.; Kreft, J.U. Advancing microbial sciences by individual-based modelling. Nat. Rev. Microbiol. 2016, 14, 461–471. [Google Scholar] [CrossRef]
- Balsa-Canto, E.; Alonso-del-Real, J.; Querol, A. Temperature Shapes Ecological Dynamics in Mixed Culture Fermentations Driven by Two Species of the Saccharomyces Genus. Front. Bioeng. Biotechnol. 2020, 8, 915. [Google Scholar] [CrossRef] [PubMed]
- Narayanan, H.; Luna, M.F.; von Stosch, M.; Cruz Bournazou, M.N.; Polotti, G.; Morbidelli, M.; Butté, A.; Sokolov, M. Bioprocessing in the Digital Age: The Role of Process Models. Biotechnol. J. 2020, 15, e1900172. [Google Scholar] [CrossRef] [PubMed]
- Noll, P.; Lilge, L.; Hausmann, R.; Henkel, M. Modeling and Exploiting Microbial Temperature Response. Processes 2020, 8, 121. [Google Scholar] [CrossRef]
- Pantano, M.N.; Fernández, M.C.; Ortiz, O.A.; Scaglia, G.J.E.; Vega, J.R. A Fourier-based control vector parameterization for the optimization of nonlinear dynamic processes with a finite terminal time. Comput. Chem. Eng. 2020, 134, 106721. [Google Scholar] [CrossRef]
- Pantano, M.N.; Fernández, M.C.; Amicarelli, A.; Scaglia, G.J.E. Evolutionary Algorithms and Orthogonal Basis for Dynamic Optimization in L2 Space for Batch Biodiesel Production. Chem. Eng. Res. Des. 2022, 177, 354–364. [Google Scholar] [CrossRef]
- Groff, M.C.; Noriega, S.E.; Gil, R.M.; Pantano, N.; Scaglia, G. Dynamic Optimization of Lactic Acid Production from Grape Stalk Solid-State Fermentation with Rhizopus oryzae Applying a Variable Temperature Profile. Fermentation 2024, 10, 101. [Google Scholar] [CrossRef]
- Maturano, Y.P.; Mestre, M.V.; Combina, M.; Toro, M.E.; Vazquez, F.; Esteve-Zarzoso, B. Culture-dependent and independent techniques to monitor yeast species during cold soak carried out at different temperatures in winemaking. Int. J. Food Microbiol. 2016, 237, 142–149. [Google Scholar] [CrossRef] [PubMed]
- Ramon-Portugal, F.; Délia-Dupuy, M.L.; Pingaud, H.; Carrillo-leroux, G.A.; Riba, J.P. Kinetic study and mathematical modelling of killer and sensitive S. cerevisiae strains growing in mixed culture. Bioprocess Eng. 1997, 17, 375–381. [Google Scholar] [CrossRef]
- Pommier, S.; Strehaiano, P.; Délia, M.L. Modelling the growth dynamics of interacting mixed cultures: A case of amensalism. Int. J. Food Microbiol. 2005, 100, 131–139. [Google Scholar] [CrossRef] [PubMed]
- Hua, M.X.; Chi, Z.; Liu, G.L.; Aslam Buzdar, M.; Chi, Z.-M. Production of a novel and cold-active killer toxin by Mrakia frigida 2E00797 isolated from sea sediment in Antarctica. Extremophiles 2010, 14, 515–521. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel Inference: Understanding AIC and BIC in Model Selection. Soc. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. (TOMS) 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Egea, J.A.; Vazquez, E.; Banga, J.R.; Martí, R. Improved scatter search for the global optimization of computationally expensive dynamic models. J. Glob. Optim. 2009, 43, 175–190. [Google Scholar] [CrossRef]
- Solonen, A. Monte Carlo Methods in Parameter Estimation of Nonlinear Models. Master’s Thesis, Lappeenranta University of Technology, Lappeenranta, Finland, 2006. [Google Scholar]
- Kroese, D.P.; Brereton, T.; Taimre, T.; Botev, Z.I. Why the Monte Carlo method is so important today. Wiley Interdiscip. Rev. Comput. Stat. 2014, 6, 386–392. [Google Scholar] [CrossRef]
- Chaves de Resende, L.; Facion do Nascimento, R.; De Sousa Sales, W.; Aparecido de Assis, F.; Carlos do Nascimento, L. Well-Being Analysis Applied to the Study of Composite Systems Flexibility Considering Wind Energy Sources. IEEE Lat. Am. Trans. 2021, 19, 1640–1647. [Google Scholar] [CrossRef]
- Tempo, R.; Ishii, H. Monte Carlo and Las Vegas Randomized Algorithms for Systems and Control. Eur. J. Control 2007, 13, 189–203. [Google Scholar] [CrossRef]
- Nearing, J.C. Mathematical Tools for Physics; Dover Publications: New York, NY, USA, 2003. [Google Scholar]
- Kreyszig, E. Introductory Functional Analysis with Applications; John Wiley & Sons: Hoboken, NJ, USA, 1978. [Google Scholar]
- Arroyo-López, F.N.; Orlić, S.; Querol, A.; Barrio, E. Effects of temperature, pH and sugar concentration on the growth parameters of Saccharomyces cerevisiae, S. kudriavzevii and their interspecific hybrid. Int. J. Food Microbiol. 2009, 131, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Chase, J.; Leibold, M. Ecological Niches: Linking Classical and Contemporary Approaches, 2nd ed.; University of Chicago Press: Chicago, IL, USA, 2003. [Google Scholar] [CrossRef]
- Pirt, S.J. Parameters of growth and analysis of growth data. In Principles of Microbe and Cell Cultivation; Blackwell Scientific Publications: Hoboken, NJ, USA, 1975; pp. 4–14. [Google Scholar]
- Oztekin, S.; Dikmetas, D.N.; Devecioglu, D.; Acar, E.G.; Karbancioglu-Guler, F. Recent insights into the use of antagonistic yeasts for sustainable biomanagement of postharvest pathogenic and mycotoxigenic fungi in fruits with their prevention strategies against mycotoxins. J. Agric. Food Chem. 2023, 71, 9923–9950. [Google Scholar] [CrossRef] [PubMed]
- Martorell, P.; Stratford, M.; Steels, H.; Fernández-Espinar, M.T.; Querol, A. Physiological characterization of spoilage strains of Zygosaccharomyces bailii and Zygosaccharomyces rouxii isolated from high sugar environments. Int. J. Food Microbiol. 2007, 114, 234–242. [Google Scholar] [CrossRef] [PubMed]
- Johnson, D.B. Biodiversity and ecology of acidophilic microorganisms. FEMS Microbiol. Ecol. 1998, 27, 307–317. [Google Scholar] [CrossRef]
- Wang, H.; Hu, Z.; Long, F.; Guo, C.; Niu, C.; Yuan, Y.; Yue, T. Combined effect of sugar content and pH on the growth of a wild strain of Zygosaccharomyces rouxii and time for spoilage in concentrated apple juice. Food Control 2016, 59, 298–305. [Google Scholar] [CrossRef]
- Dantigny, P.; Bevilacqua, A. Fungal starters: An insight into the factors affecting the germination of conidia. In Starter Cultures in Food Production; Speranza, B., Bevilacqua, A., Corbo, R.M., Sinigaglia, M., Eds.; John Wiley and Sons: West Sussex, UK, 2017; pp. 50–63. [Google Scholar] [CrossRef]
- McBride, R.; Greig, D.; Travisano, M. Fungal viral mutualism moderated by ploidy. Evolution 2008, 62, 2372–2380. [Google Scholar] [CrossRef] [PubMed]
- Deschaine, B.M.; Heysel, A.R.; Lenhart, B.A.; Murphy, H.A. Biofilm formation and toxin production provide a fitness advantage in mixed colonies of environmental yeast isolates. Ecol. Evol. 2018, 8, 5541–5550. [Google Scholar] [CrossRef] [PubMed]
- Sinclair, R.M. Citation: Sinclair RM (2014) Persistence in the Shadow of Killers. Front. Microbiol. 2014, 5, 342. [Google Scholar] [CrossRef] [PubMed]
- Fernández de Ullivarri, M.; Mendoza, L.M.; Raya, R.R. Characterization of the killer toxin KTCf20 from Wickerhamomyces anomalus, a potential biocontrol agent against wine spoilage yeasts. Biol. Control 2018, 121, 223–228. [Google Scholar] [CrossRef]
- Károlyi, G.; Neufeld, Z.; Scheuring, I. Rock-scissors-paper game in a chaotic flow: The effect of dispersion on the cyclic competition of microorganisms. J. Theor. Biol. 2005, 236, 12–20. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.L.; Chi, Z.; Wang, G.Y.; Wang, Z.P.; Li, Y.; Chi, Z.M. Yeast killer toxins, molecular mechanisms of their action and their applications. Crit. Rev. Biotechnol. 2013, 35, 222–234. [Google Scholar] [CrossRef] [PubMed]
- Magliani, W.; Conti, S.; Gerloni, M.; Bertolotti, D.; Polonelli, L. Yeast killer systems. Clin. Microbiol. Rev. 1997, 10, 369–400. [Google Scholar] [CrossRef] [PubMed]
- Pieczynska, M.D.; Wloch-Salamon, D.; Korona, R.; de Visser, J.A.G.M. Rapid multiple-level coevolution in experimental populations of yeast killer and nonkiller strains. Evolution. Int. J. Org. Evol. 2016, 70, 1342–1353. [Google Scholar] [CrossRef]
- Zi, Z. Sensitivity analysis approaches applied to systems biology models. IET Syst. Biol. 2011, 5, 336–346. [Google Scholar] [CrossRef]
- Levine, J.; HilleRisLambers, J. The importance of niches for the maintenance of species diversity. Nature 2009, 461, 254–257. [Google Scholar] [CrossRef]
- Bianchi, A.; Taglieri, I.; Venturi, F.; Sanmartin, C.; Ferroni, G.; Macaluso, M.; Palla, F.; Flamini, G.; Zinnai, A. Technological Improvements on FML in the Chianti Classico Wine Production: Co-Inoculation or Sequential Inoculation? Foods 2022, 11, 1011. [Google Scholar] [CrossRef] [PubMed]
- Morata, A.; Loira, I.; Manuel del Fresno, J.; Escott, C.; Antonia Bañuelos, M.; Tesfaye, W.; González, C.; Palomero, F.; Antonio Suárez Lepe, J. Strategies to Improve the Freshness in Wines from Warm Areas. In Advances in Grape and Wine Biotechnology; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Feng, J.; Feng, N.; Zhang, J.S.; Yang, Y.; Jia, W.; Lin, C.C. A New Temperature Control Shifting Strategy for Enhanced Triterpene Production by Ganoderma Lucidum G0119 Based on Submerged Liquid Fermentation. Appl. Biochem. Biotechnol. 2016, 180, 740–752. [Google Scholar] [CrossRef] [PubMed]
- Cheng, K.K.; Zeng, J.; Jian, J.H.; Zhu, J.F.; Zhang, G.X.; Liu, D.H. Model-Based Temperature Control for Improving Lactic Acid Production from Glycerol. RSC Adv. 2019, 9, 11614–11620. [Google Scholar] [CrossRef] [PubMed]
- Maturano, Y.P.; Mestre, M.V.; Kuchen, B.; Toro, M.E.; Mercado, L.A.; Vazquez, F.; Combina, M. Optimization of fermentation-relevant factors: A strategy to reduce ethanol in red wine by sequential culture of native yeasts. Int. J. Food Microbiol. 2019, 289, 40–48. [Google Scholar] [CrossRef] [PubMed]



| Description | Variable | Value | Unit |
|---|---|---|---|
| Killer population | Xvk | 400,000 | cells/mL |
| Spoilage population | Xvs | 1,600,000 | cells/mL |
| Toxin concentration | T | 0 | g/L |
| Inhibitor concentration | I | 0 | g/L |
| The final time of reaction | tf | 225 | hours |
| Primary Model | Secondary Model | N° Parameter | AICM | ΔM | Merit |
|---|---|---|---|---|---|
| Kuchen | 10 Q | 30 | 132.843 | 67.371 | No support |
| Kuchen | 9 Q | 27 | 103.146 | 37.674 | No support |
| Kuchen | 8 Q | 24 | 90.474 | 25.002 | No support |
| Kuchen | 7 Q | 21 | 74.439 | 8.967 | No support |
| Kuchen | 6 Q | 18 | 68.105 | 2.633 | Considerably less support |
| Kuchen | 5 Q + 1 L | 17 | 65.471 | 0 | Reduced model |
| Parameter | Sub | Value | Submodel | pH | ||
|---|---|---|---|---|---|---|
| 3.2 | 3.7 | 4.2 | ||||
| mvk1 | 1.01 × 10−1 | mvk1 × pH2 − mvk2 × pH + mvk3 | 0.0897 | 0.0635 | 0.0878 | |
| mvk2 | 7.49 × 10−1 | |||||
| mvk3 | 1.45 | |||||
| mvs1 | 1.6 × 10−3 | −mvs1 × pH + mvs2 | 0.0139 | 0.0131 | 0.0123 | |
| mvs2 | 1.9 × 10−2 | |||||
| Ak1 | 3.59 × 102 | Ak1 × pH2 − Ak2 × pH + Ak3 | 257.49 | 58.30 | 38.39 | |
| Ak2 | 2.87 × 103 | |||||
| Ak3 | 5.78 × 103 | |||||
| As1 | 3.53 × 102 | As1 × pH2 − As2 × pH + As3 | 285.25 | 71.02 | 33.53 | |
| As2 | 2.87 × 103 | |||||
| As3 | 5.84 × 103 | |||||
| alfa1 | 1.51 × 10−3 | −alfa1 × pH2 + alfa2 × pH − alfa3 | 0.0016 | 0.0022 | 0.0020 | |
| alfa2 | 1.16 × 10−2 | |||||
| alfa3 | 1.16 × 10−2 | |||||
| K1 | 2.53 × 10−6 | −K1 × pH2 + K2 × pH − K3 | 1.31 × 10−7 | 4.97 × 10−7 | 2.45 × 10−7 | |
| K2 | 1.95 × 10−5 | |||||
| K3 | 3.7 × 10−5 | |||||
| µdk | 1.5 × 10−5 | cte | 1.5 × 10−5 | 1.5 × 10−5 | 1.5 × 10−5 | |
| µds | 1.5 × 10−5 | cte | 1.5 × 10−5 | 1.5 × 10−5 | 1.5 × 10−5 | |
| a | 1 × 10−9 | cte | 1 × 10−9 | 1 × 10−9 | 1 × 10−9 | |
| W | 3 × 10−9 | cte | 3 × 10−9 | 3 × 10−9 | 3 × 10−9 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuchen, B.; Groff, M.C.; Pantano, M.N.; Pedrozo, L.P.; Vazquez, F.; Scaglia, G. Modeling and Optimizing Biocontrol in Wines: pH as a Modulator of Yeast Amensalism Interaction. Processes 2024, 12, 1446. https://doi.org/10.3390/pr12071446
Kuchen B, Groff MC, Pantano MN, Pedrozo LP, Vazquez F, Scaglia G. Modeling and Optimizing Biocontrol in Wines: pH as a Modulator of Yeast Amensalism Interaction. Processes. 2024; 12(7):1446. https://doi.org/10.3390/pr12071446
Chicago/Turabian StyleKuchen, Benjamín, María Carla Groff, María Nadia Pantano, Lina Paula Pedrozo, Fabio Vazquez, and Gustavo Scaglia. 2024. "Modeling and Optimizing Biocontrol in Wines: pH as a Modulator of Yeast Amensalism Interaction" Processes 12, no. 7: 1446. https://doi.org/10.3390/pr12071446
APA StyleKuchen, B., Groff, M. C., Pantano, M. N., Pedrozo, L. P., Vazquez, F., & Scaglia, G. (2024). Modeling and Optimizing Biocontrol in Wines: pH as a Modulator of Yeast Amensalism Interaction. Processes, 12(7), 1446. https://doi.org/10.3390/pr12071446









