An Accurate Calculation Method on Blasingame Production Decline Model of Horizontal Well with Dumbbell-like Hydraulic Fracture in Tight Gas Reservoirs
Abstract
1. Introduction
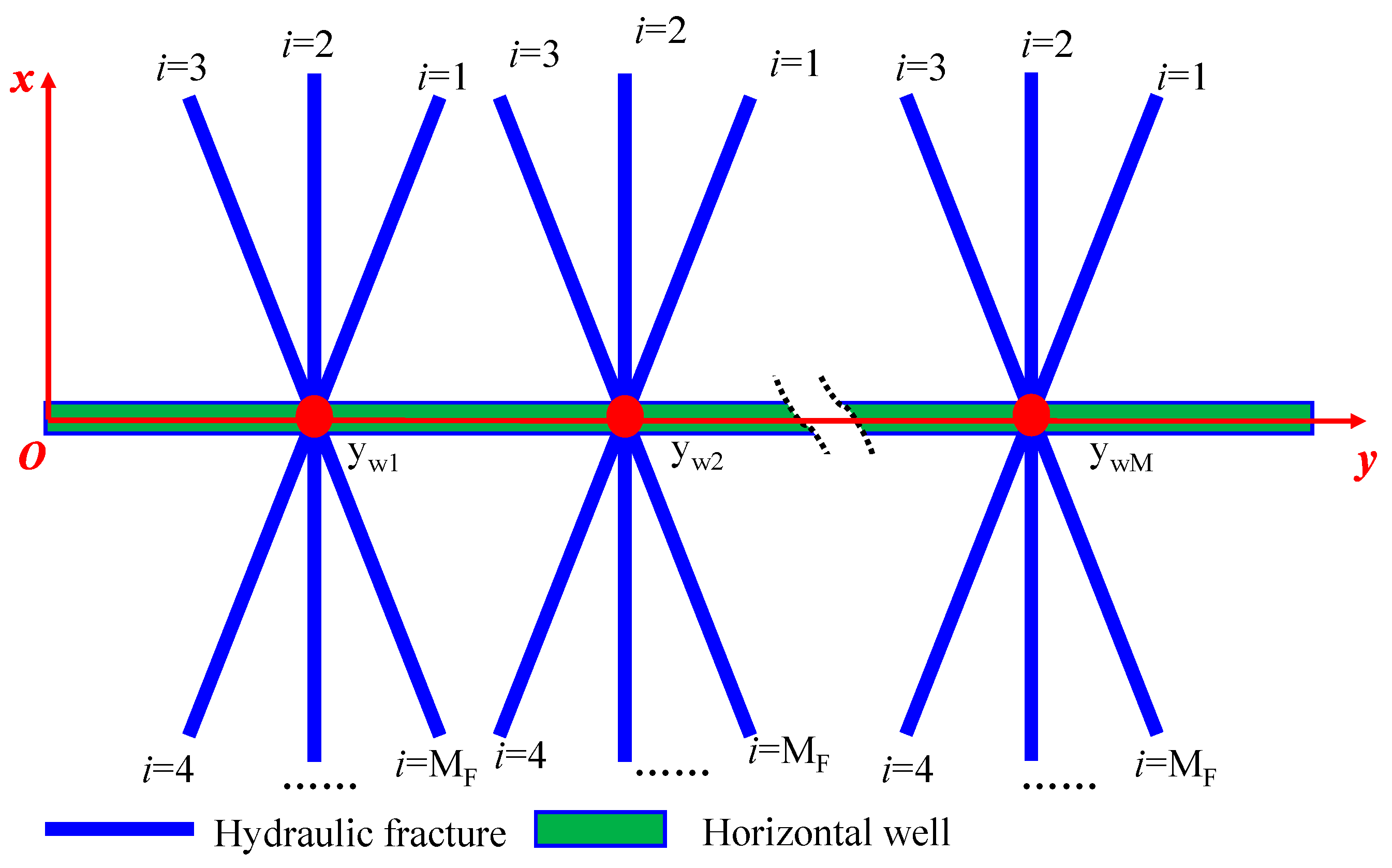
2. Physics Model
- (1)
- The total stage number of fractures is M. The height of the fractures is assumed to be equal to the formation thickness.
- (2)
- The total fracture number of each cluster is MF.
- (3)
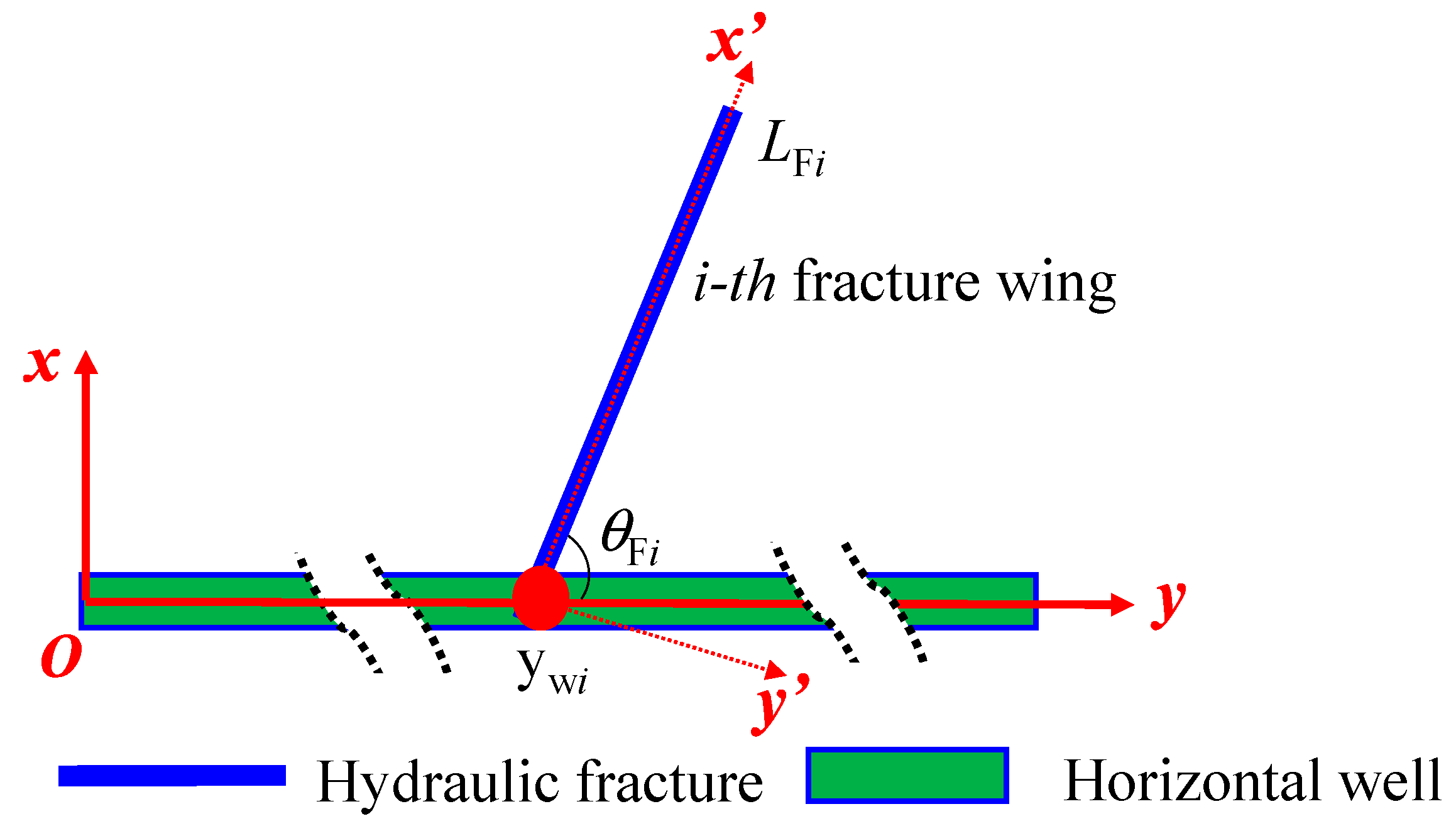
- The length, permeability, and width of the i-th fracture wings are represented by LFi, KFi, and wFi respectively.
- (4)
- The angle between each fracture wing and horizontal well is represented by θFi.
- (5)
- The gas flows into the horizontal wellbore mainly through the hydraulic fracture.
- (6)
- The total rate of the MFHWs is denoted by qsc for a constant-production gas well.
- (7)
- The top and bottom boundaries of gas reservoirs are considered as impermeable boundaries.
- (8)
- The gas flow meets Darcy’s law in formation and hydraulic fractures.
- (9)
- The influence of the gravity and capillary effect is ignored and gas flow meets isothermal seepage.
3. Mathematical Model and Solution
3.1. Reservoirs Model
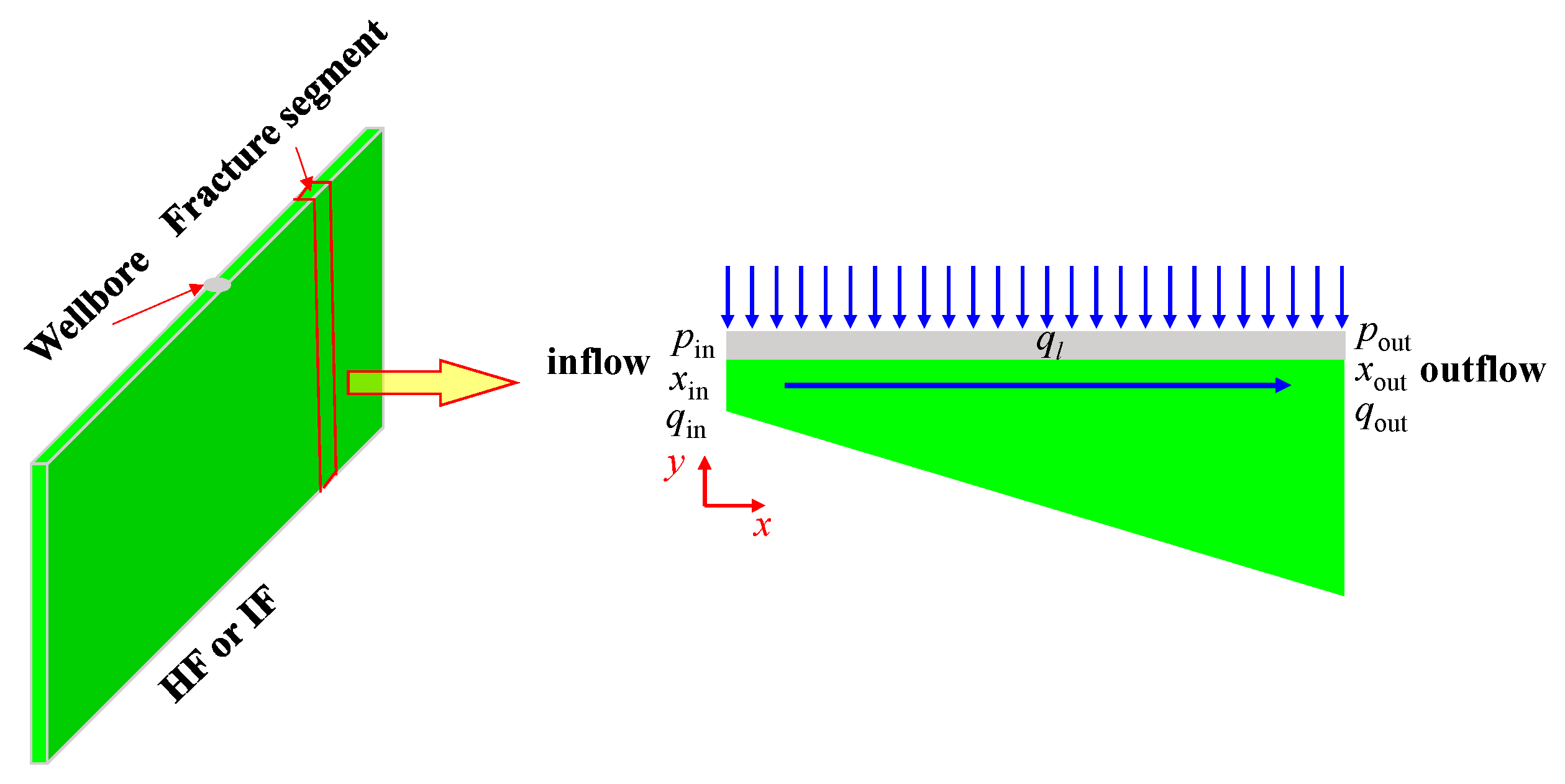
3.2. Fracture Wing Model
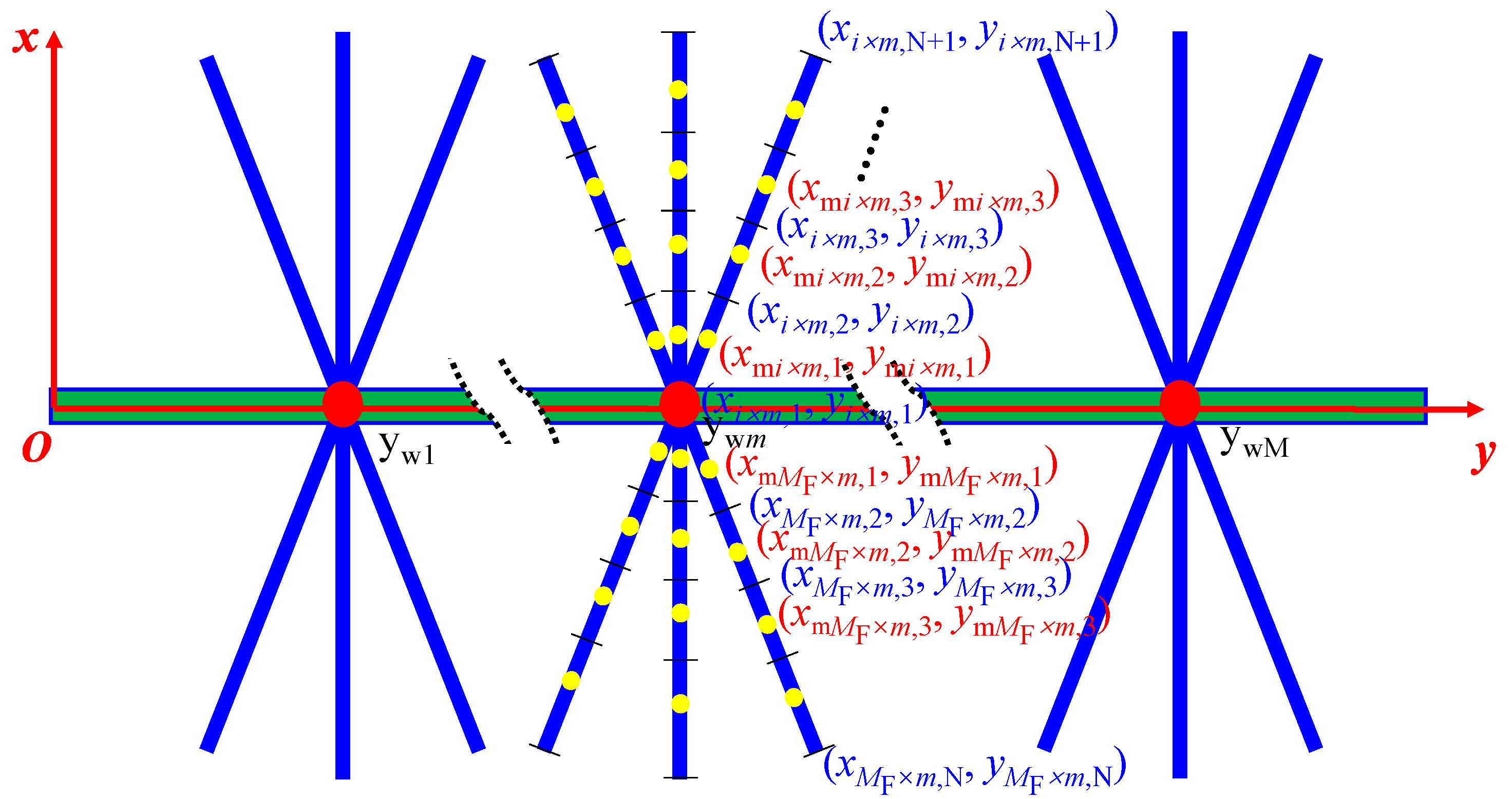
3.3. Coupling of Hydraulic and Reservoirs
- Dimensionless outflow vertice pseudo-pressure of every fracture segment in the Laplace domain, , i = 1, 2, …, MF × M × N.
- Dimensionless surface fluxes of the Laplace domain, , i = 1, 2, …, MF × M × N.
- Dimensionless inflow vertices flux of every fracture segment in the Laplace domain, , i = 1, 2, …, MF × N × M + M.
- Dimensionless wellbore pseudo-pressure of the Laplace domain, .
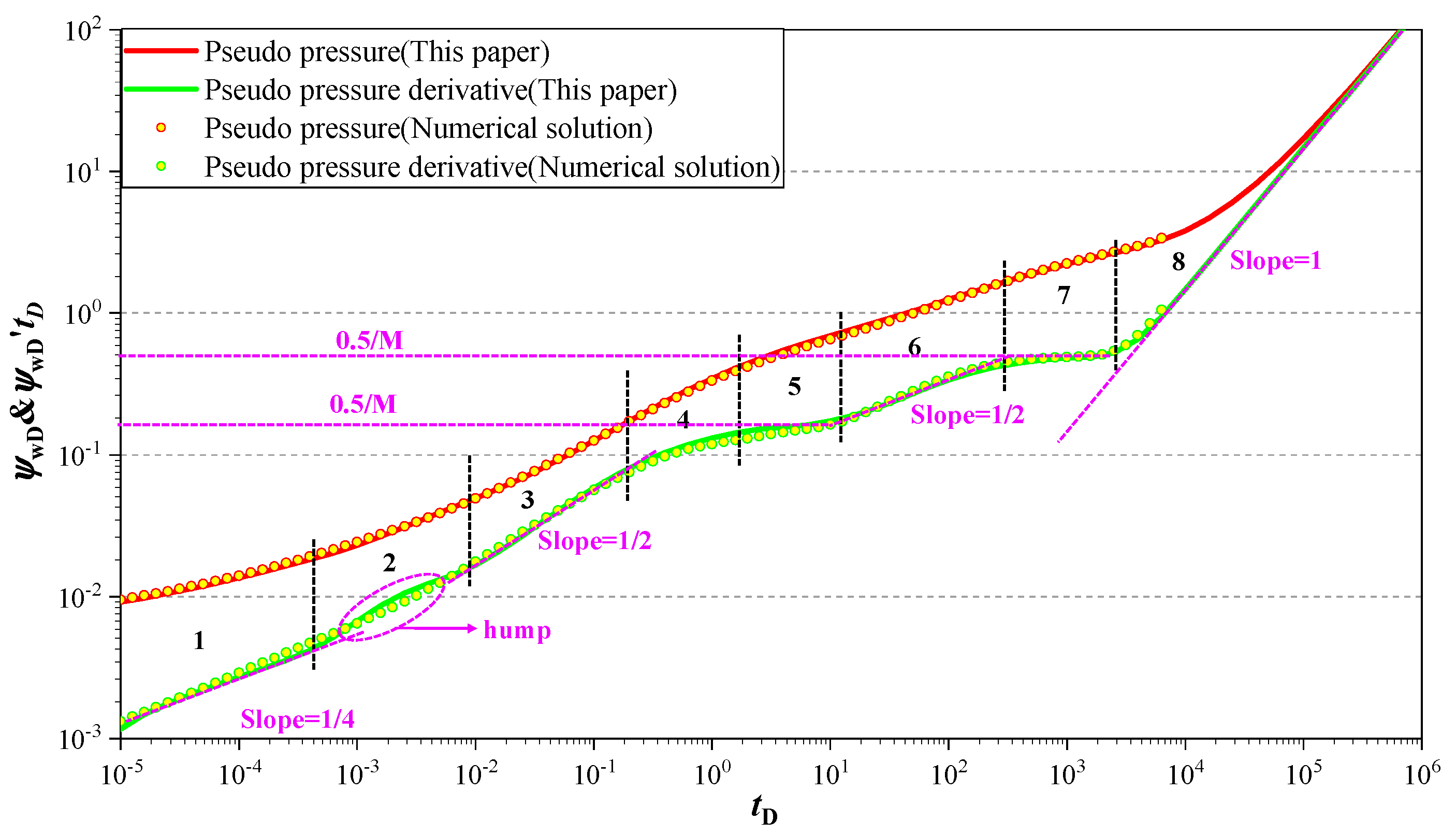
4. Wellbore Pressure Verification
5. Blasingame Production Decline and Verification
5.1. Blasingame Production Decline
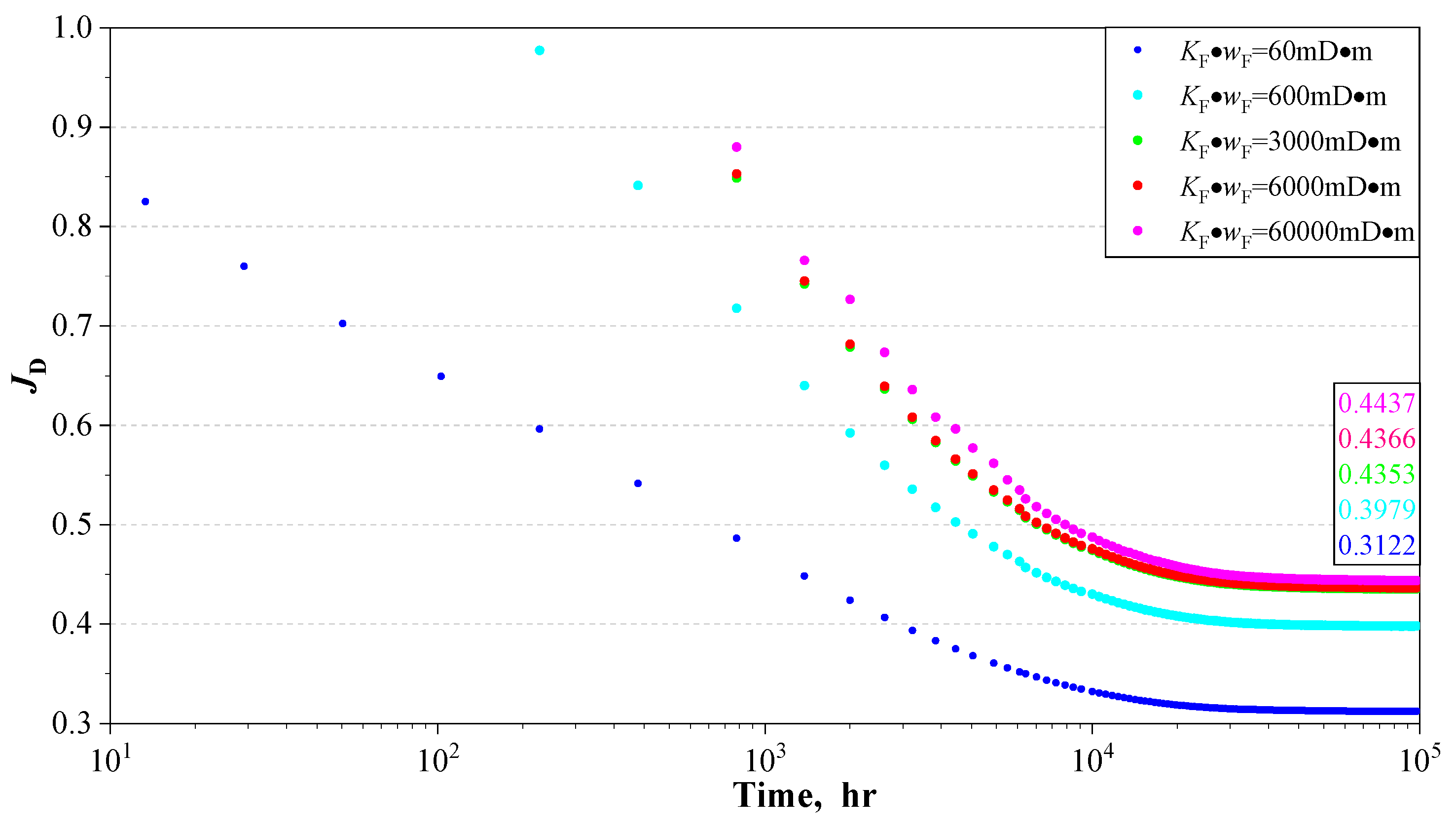
5.2. Model Verification by Productivity Index
6. Pressure Transient and Blasingame Production Decline Curve Analysis
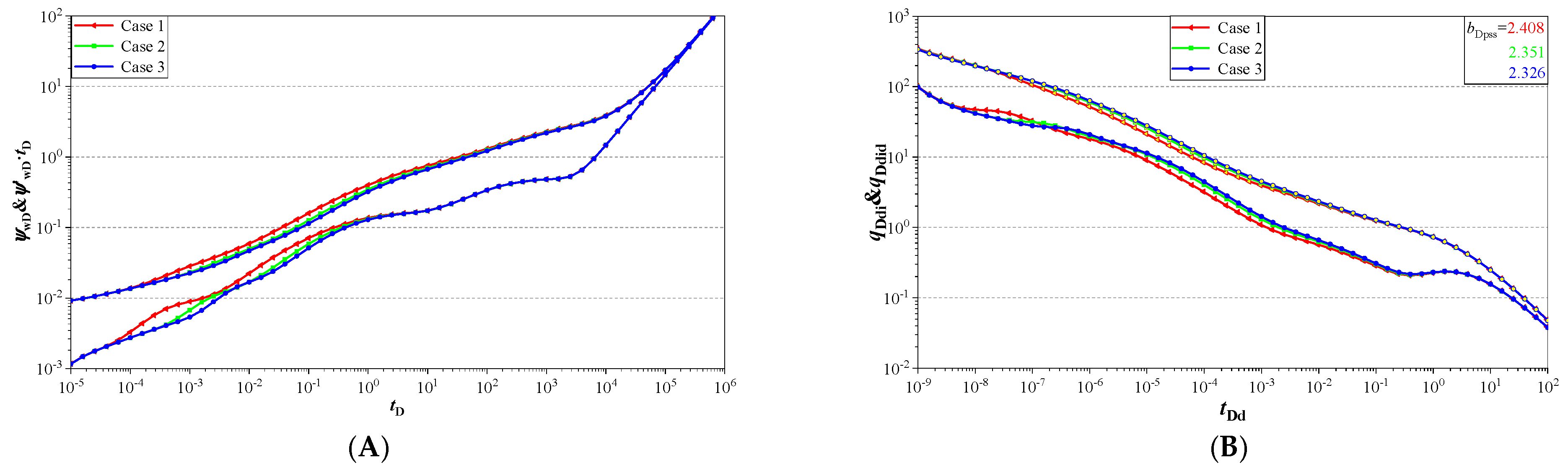
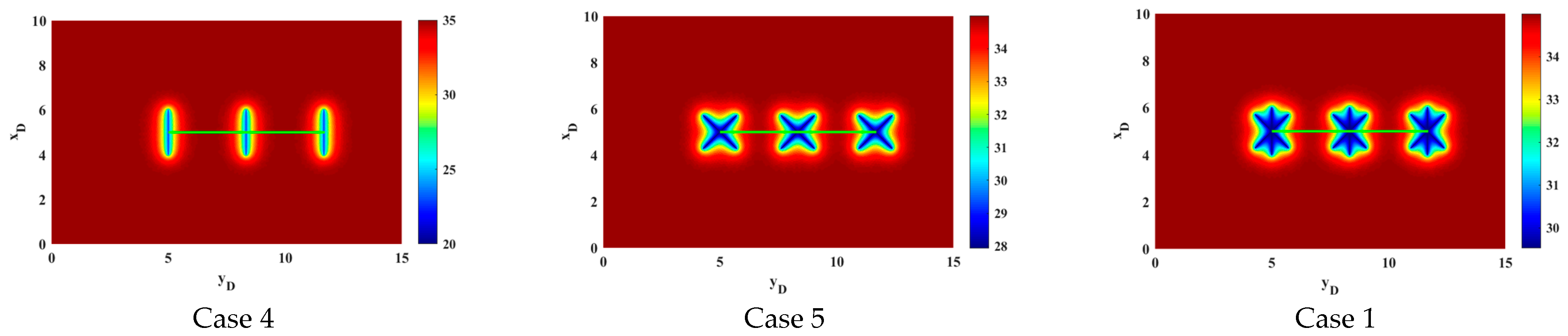
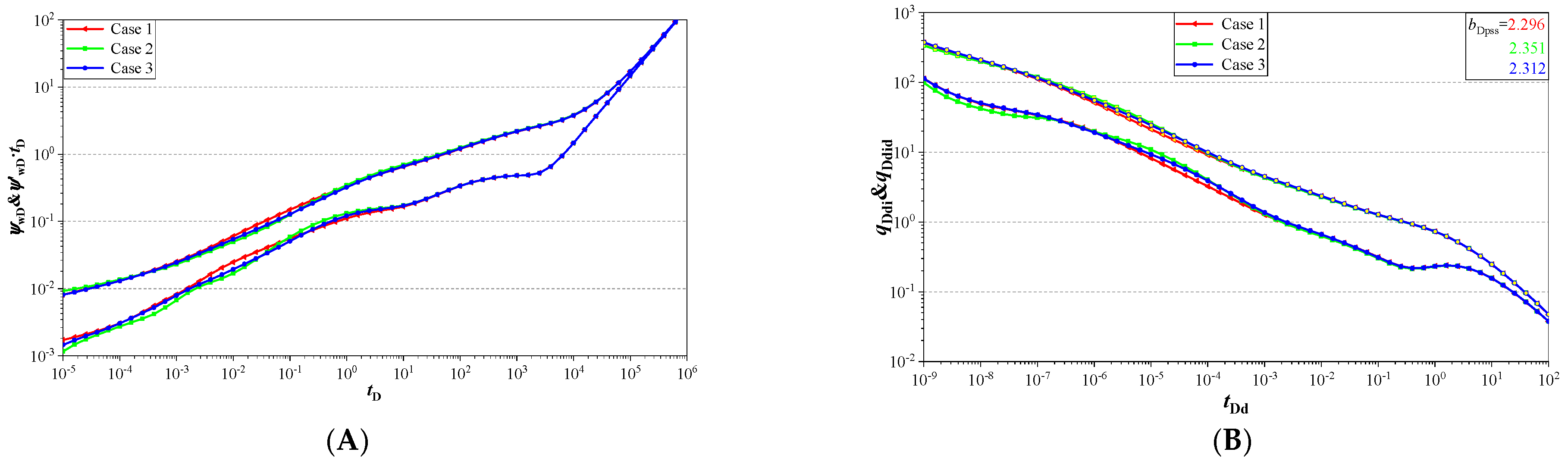
6.1. Fracture Distribution
6.2. Fracture Stages
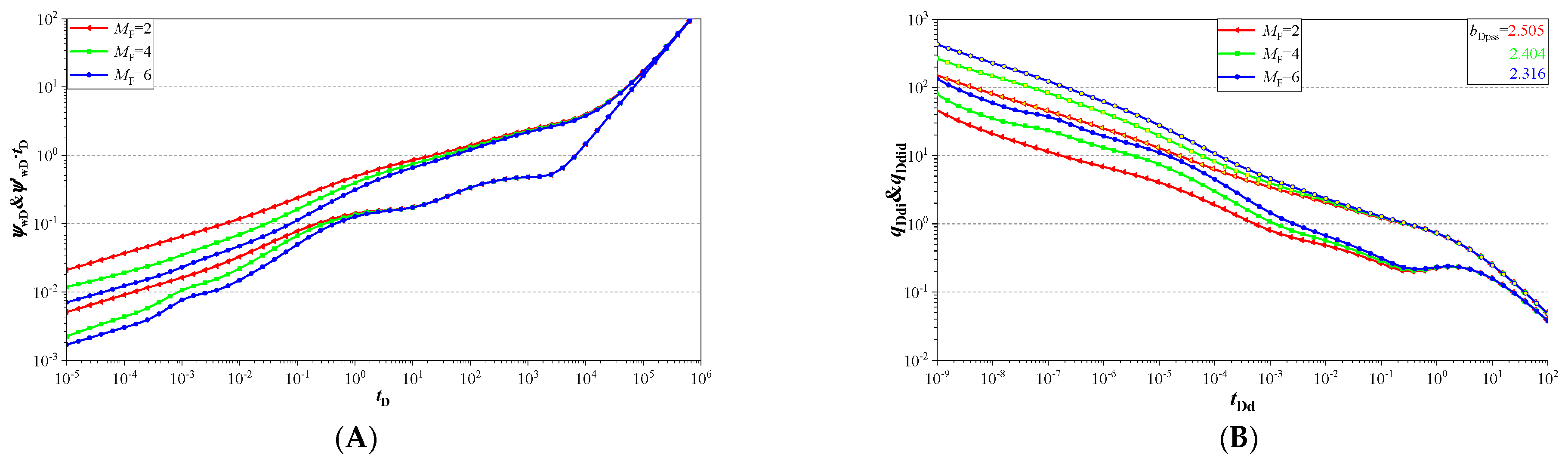
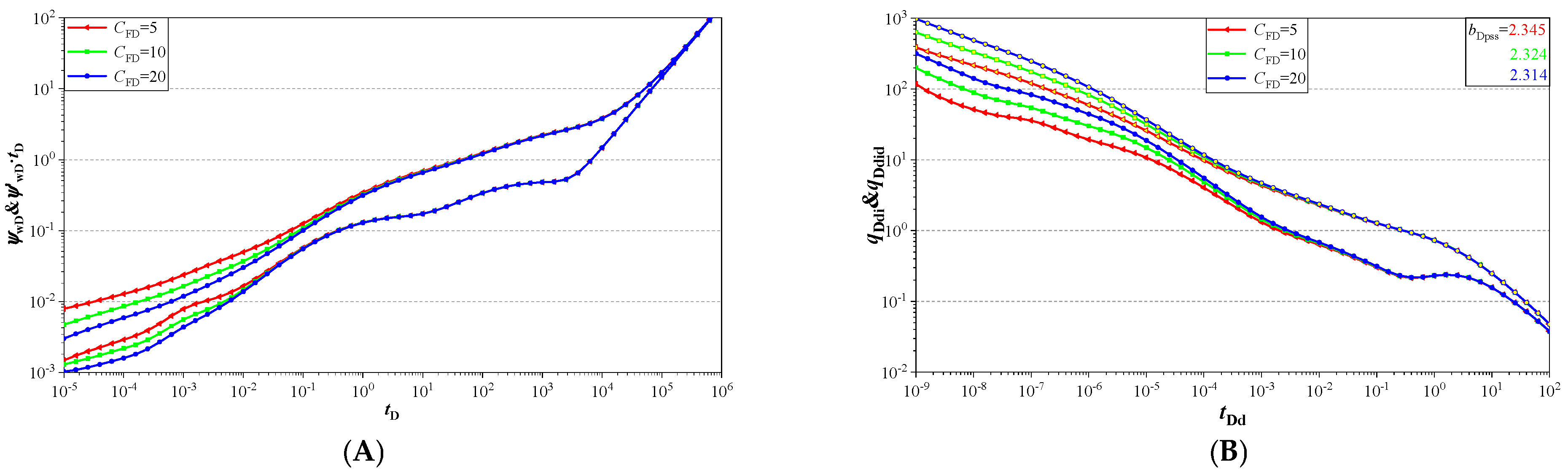
6.3. Fracture Conductivity
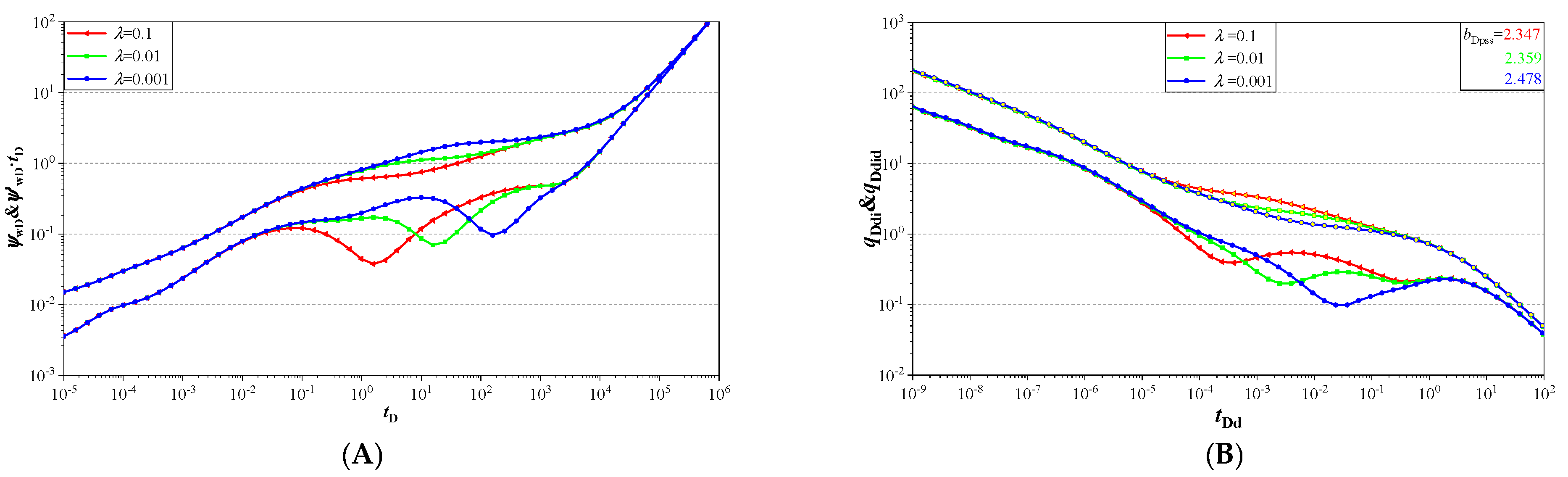
6.4. Inter-Porosity Flow Coefficient and Storativity Ratio
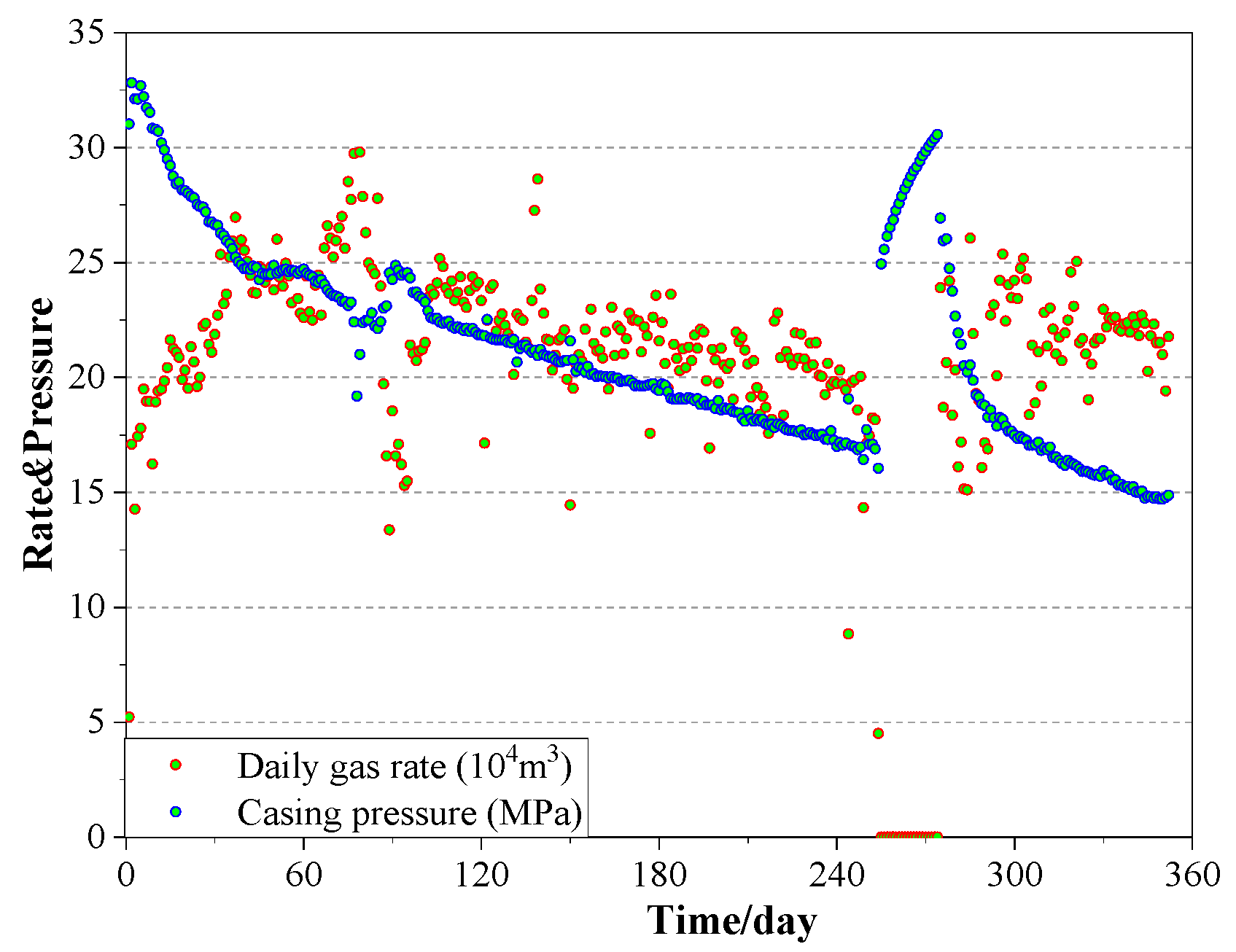
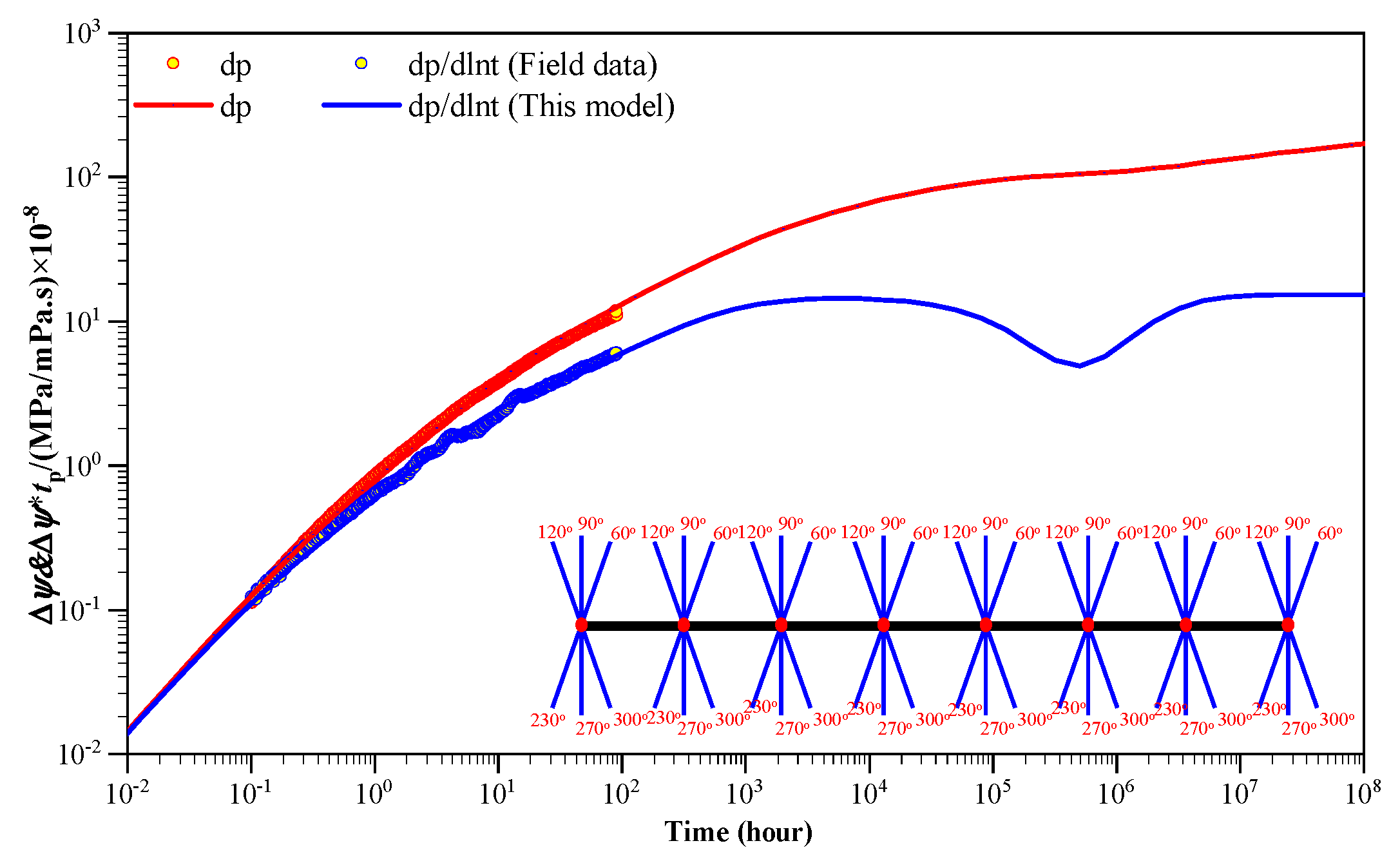
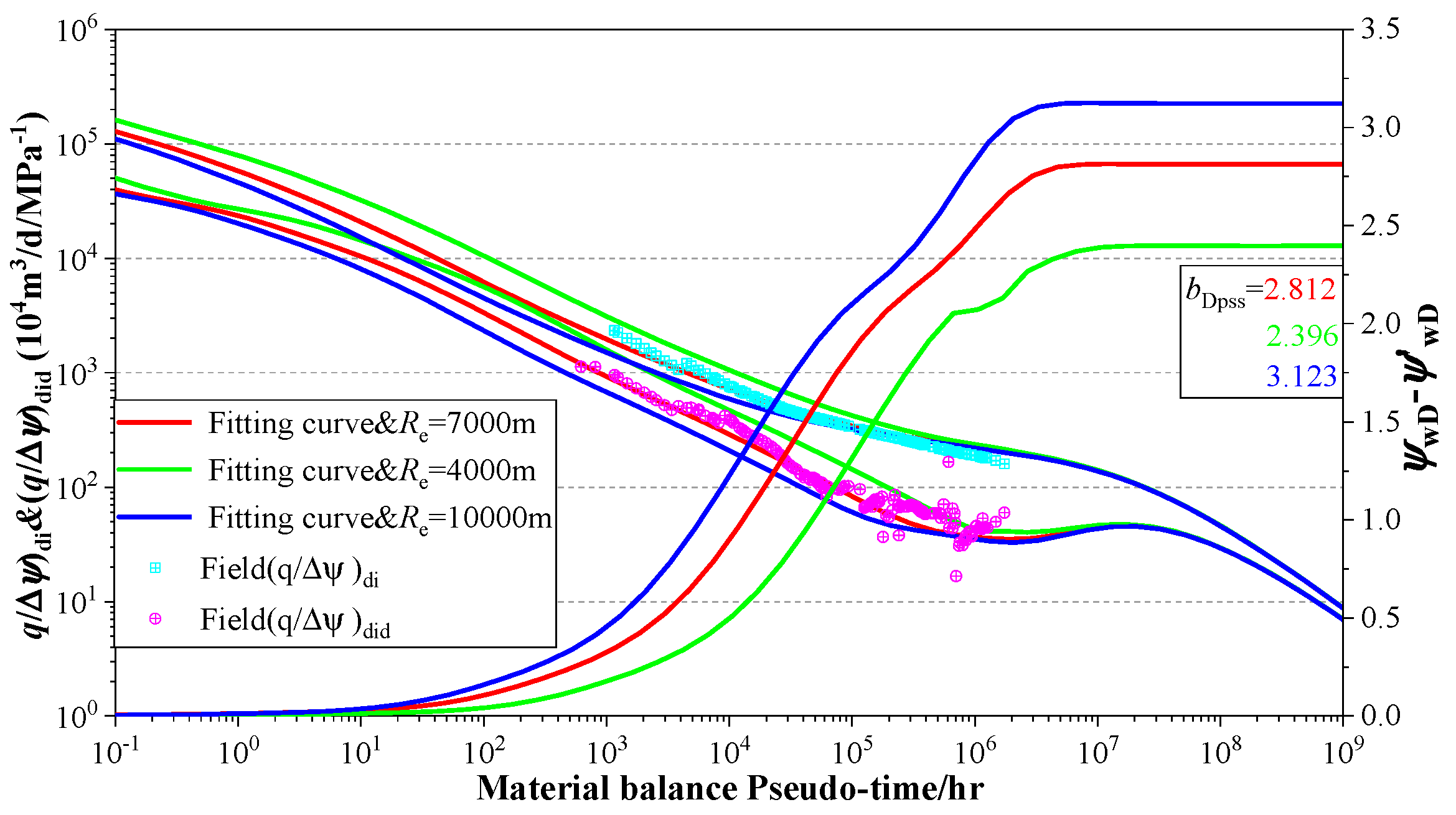
7. Field Application
8. Conclusions
- A semi-analytical model of MFHWs with a dumbbell-like hydraulic fracture in circle closed reservoirs is presented. The wellbore pressure transient is verified using a numerical solution. The comparison result reaches a good match. When comparing MFHWs with a bi-wing symmetrical fracture, there is an obvious ‘hump’ of the pressure derivative curve between the bilinear and early linear flow regimes. Compared with the numerical solution, the precision of the semi-analytical model is higher during the early flow regime.
- The wellbore pressure approximate solution of the pseudo-steady flow regime of MFHWs with a dumbbell-like hydraulic fracture is obtained and verified. The relative error of all comparison results is when the relative error is less than 1%.
- The smaller fracture wing angle leads to the higher pressure and its derivative curve before the early radial flow regime. The pressure derivative curve ‘hump’ of the fracture interferences regime appears earlier. The smaller the fracture wing number, the higher the pressure and its derivative curve before the early radial flow regime. A higher fracture cluster number leads to a small pressure curve before the radial flow regime and a shorter duration of the early radial flow regime.
- A smaller fracture wing angle, smaller fracture wing number, smaller dimensionless conductivity, and a smaller fracture cluster number lead to a smaller Blasingame integral curve and integral derivative curves before the pseudo-steady flow regime.
- When the crossflow from matrix to natural fracture appears after the pseudo-state flow regime, the value of the inter-porosity coefficient has an obvious influence on the pressure approximate solution of the pseudo-steady flow regime.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Gas well control area, m2 | The dimensionless pressure build-up time. | |
| bDpss | Wellbore pressure approximate solution coefficient | The dimensionless production time | |
| C | Wellbore storage coefficient, MPa/m3 | Re | Circle closed boundary radius, m |
| J | Productivity index, 104 m3/d/MPa | s | Laplace integration variables |
| CF | Conductivity of the hydraulic fracture wing, D·m | S | Skin factor, dimensionless |
| Ct | Total compressibility, MPa−1 | T | Temperature of shale gas reservoirs, K |
| I0(x) | The first-kind zero-order modified Bessel function | t | Production time, hr |
| I1(x) | The first-kind one-order modified Bessel function | x, y | Descartes coordinates, m |
| K | Permeability, D | xw, yw | x, y, z-coordinates of the line source, m |
| K0(x) | The second-kind zero-order modified Bessel function, | Z | Gas compression factor |
| K1(x) | The second-kind one-order modified Bessel function | θF | Angle between hydraulic fracture wing and horizontal well, degree |
| LF | Hydraulic fracture wing length, m | αm | Matrix shape factor, dimensionless |
| Lref | Reference length, m | ϕ | Formation porosity, decimal |
| ψ | Pseudo-pressure defined by Equation (1), MPa/(mPa·s) | λ | Inter-porosity coefficient, dimensionless |
| M | The hydraulic fracture cluster number, integer | μ | Shale gas viscosity, cp. |
| ψwD,pss | Wellbore pressure approximate solution during pseudo-state flowing regime | ω | Storativity ratio, dimensionless |
| N | The hydraulic fracture wing discrete element number, integer | Subscripts | |
| MF | The hydraulic fracture wing number of every hydraulic fracture cluster, integer | D | Dimensionless |
| w | Wellbore | ||
| p | Reservoirs pressure, MPa | E | Initial state |
| m | Matrix system | ||
| p0 | Reference pressure, MPa | f | Natural fracture system |
| Continuous unite length source strength, m3/d | in | Inflow vertices of every segment | |
| qsc | Total production, 104 m3/d | out | Outflow vertices of every segment |
| r | Radial distance in x-y plane, m | F | Hydraulic fracture |
| The dimensionless wellbore pressure during build-up test | Superscripts | ||
| The dimensionless wellbore pressure at the instant of falloff | - | Variables in the Laplace domain | |
| The dimensionless wellbore pressure build-up value from shut-in well time to | |||
| The dimensionless wellbore pressure drop value from production starting-time to | |||
References
- Mojid, M.R.; Negash, B.M.; Abdulelah, H.; Jufar, S.R.; Adewumi, B.K. A state-of-art review on waterless gas shale fracturing technologies. J. Pet. Sci. Eng. 2021, 196, 108048. [Google Scholar] [CrossRef]
- Liehui, Z.; Baochao, S.; Yulong, Z.; Zhaoli, G. Review of micro seepage mechanisms in shale gas reservoirs. Int. J. Heat Mass Transf. 2019, 139, 144–179. [Google Scholar] [CrossRef]
- King, G.E. Hydraulic Fracturing 101: What Every Representative, Environmentalist, Regulator, Reporter, Investor, University Researcher, Neighbor, and Engineer Should Know about Hydraulic Fracturing Risk. J. Pet. Technol. 2012, 64, 34–42. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, B.-R.; Zhao, Y.-L.; Zhang, L.-H.; Qiao, X.-Y.; Zhang, L.; Guo, J.-J.; Thanh, H.V. Inter-layer interference for multi-layered tight gas reservoir in the absence and presence of movable water. Pet. Sci. 2024, 21, 1751–1764. [Google Scholar] [CrossRef]
- Zhiming, C.; Xinwei, L.; Chenghui, H.; Xiaoliang, Z.; Langtao, Z.; Yizhou, C.; Heng, Y.; Zhenhua, C. Productivity estimations for vertically fractured wells with asymmetrical multiple fractures. J. Nat. Gas Sci. Eng. 2014, 21, 1048–1060. [Google Scholar] [CrossRef]
- Chen, Z.; Liao, X.; Zhao, X.; Dou, X.; Zhu, L. A semi-analytical mathematical model for transient pressure behavior of multiple fractured vertical well in coal reservoirs incorporating with diffusion, adsorption, and stress-sensitivity. J. Nat. Gas Sci. Eng. 2016, 29, 570–582. [Google Scholar] [CrossRef]
- Chen, Z.; Liao, X.; Zhao, X.; Lyu, S.; Zhu, L. A comprehensive productivity equation for multiple fractured vertical wells with non-linear effects under steady-state flow. J. Pet. Sci. Eng. 2017, 149, 9–24. [Google Scholar] [CrossRef]
- Liu, Q.-G.; Xu, Y.-J.; Peng, X.; Liu, Y.; Qi, S. Pressure transient analysis for multi-wing fractured wells in dual-permeability hydrocarbon reservoirs. J. Pet. Sci. Eng. 2019, 180, 278–288. [Google Scholar] [CrossRef]
- Luo, W.; Wang, X.; Tang, C.; Feng, Y.; Shi, E. Productivity of multiple fractures in a closed rectangular reservoir. J. Pet. Sci. Eng. 2017, 157, 232–247. [Google Scholar] [CrossRef]
- Ren, J.; Fang, N.; Zheng, Q.; Guo, P.; Wang, D.; Zhao, C. Semi-analytical model of a multi-wing fractured vertical well in linear composite reservoirs with a leaky fault. J. Pet. Sci. Eng. 2020, 191, 107143. [Google Scholar] [CrossRef]
- Wang, H.; Kou, Z.; Guo, J.; Chen, Z. A semi-analytical model for the transient pressure behaviors of a multiple fractured well in a coal seam gas reservoir. J. Pet. Sci. Eng. 2021, 198, 108159. [Google Scholar] [CrossRef]
- Wanjing, L.; Changfu, T. A Semianalytical Solution of a Vertical Fractured Well With Varying Conductivity Under Non-Darcy-Flow Condition. SPE J. 2015, 20, 1028–1040. [Google Scholar] [CrossRef]
- Chen, C.-C.; Raghavan, R. A Multiply-Fractured Horizontal Well in a Rectangular Drainage Region. SPE J. 1997, 2, 455–465. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramey, H.J.J. Unsteady-State Pressure Distributions Created by a Well with a Single Horizontal Fracture, Partial Penetration, or Restricted Entry. Soc. Pet. Eng. J. 1974, 14, 413–426. [Google Scholar] [CrossRef]
- Ozkan, E.; Raghavan, R. New Solutions for Well-Test-Analysis Problems: Part 1—Analytical Considerations (includes associated papers 28666 and 29213). SPE Form. Eval. 1991, 6, 359–368. [Google Scholar] [CrossRef]
- Cinco-Ley, H.; Meng, H.Z. Pressure Transient Analysis of Wells With Finite Conductivity Vertical Fractures in Double Porosity Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 2–5 October 1988. [Google Scholar]
- Hanyi, W. New Approaches to Model and Analyze Diagnostic Fracturing Injection Tests. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2019. [Google Scholar]
- He, J.; Teng, W.; Xu, J.; Jiang, R.; Sun, J. A quadruple-porosity model for shale gas reservoirs with multiple migration mechanisms. J. Nat. Gas Sci. Eng. 2016, 33, 918–933. [Google Scholar] [CrossRef]
- Wang, H.-T. Performance of multiple fractured horizontal wells in shale gas reservoirs with consideration of multiple mechanisms. J. Hydrol. 2014, 510, 299–312. [Google Scholar] [CrossRef]
- Zhao, Y.-L.; Zhang, L.-H.; Zhao, J.-Z.; Luo, J.-X.; Zhang, B.-N. “Triple porosity” modeling of transient well test and rate decline analysis for multi-fractured horizontal well in shale gas reservoirs. J. Pet. Sci. Eng. 2013, 110, 253–262. [Google Scholar] [CrossRef]
- Mayerhofer, M.J.; Lolon, E.P.; Warpinski, N.R.; Cipolla, C.L.; Walser, D.; Rightmire, C.M. What Is Stimulated Reservoir Volume? SPE Prod. Oper. 2010, 25, 89–98. [Google Scholar] [CrossRef]
- Sarvaramini, E.; Gracie, R.; Dusseault, M. Hydraulic Fracture Stimulated Zone Analysis with a FEM Upscaled Model. In Proceedings of the ISRM International Symposium-10th Asian Rock Mechanics Symposium, Singapore, 29 October–3 November 2018. [Google Scholar]
- Wang, H.; Ran, Q.; Liao, X. Pressure transient responses study on the hydraulic volume fracturing vertical well in stress-sensitive tight hydrocarbon reservoirs. Int. J. Hydrogen Energy 2017, 42, 18343–18349. [Google Scholar] [CrossRef]
- Zhu, Y.; Carr, T. Interpretation of Hydraulic Fractures Based on Microseismic Response in the Marcellus Shale, Monongalia County, West Virginia, USA: Implications for Shale Gas Production. SPE Reserv. Eval. Eng. 2020, 23, 1265–1278. [Google Scholar] [CrossRef]
- Chen, Z.; Liao, X.; Zhao, X.; Zhu, L. Influence of magnitude and permeability of fracture networks on behaviors of vertical shale gas wells by a free-simulator approach. J. Pet. Sci. Eng. 2016, 147, 261–272. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, J.; Liao, X.; Li, X.; Zhang, J.; Li, R.; Li, L. A Semi-Analytical Model for Complex Fracture Geometries with Fracture Hits. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2019. [Google Scholar]
- Jia, P.; Cheng, L.; Huang, S.; Wu, Y. A semi-analytical model for the flow behavior of naturally fractured formations with multi-scale fracture networks. J. Hydrol. 2016, 537, 208–220. [Google Scholar] [CrossRef]
- Luo, L.; Cheng, S.; Lee, J. Characterization of refracture orientation in poorly propped fractured wells by pressure transient analysis: Model, pitfall, and application. J. Nat. Gas Sci. Eng. 2020, 79, 103332. [Google Scholar] [CrossRef]
- Wang, L.; Xue, L. A Laplace-transform boundary element model for pumping tests in irregularly shaped double-porosity aquifers. J. Hydrol. 2018, 567, 712–720. [Google Scholar] [CrossRef]
- Xing, G.; Wang, M.; Wu, S.; Li, H.; Dong, J.; Zhao, W. Pseudo-Steady-State Parameters for a Well Penetrated by a Fracture with an Azimuth Angle in an Anisotropic Reservoir. Energies 2019, 12, 2449. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Q.; Li, X.; Meng, Z.; Yang, S.; Tan, X. Pressure transient and Blasingame production decline analysis of hydraulic fractured well with induced fractures in composite shale gas reservoirs. J. Nat. Gas Sci. Eng. 2021, 94, 104058. [Google Scholar] [CrossRef]
- Xu, C.; Li, P.; Lu, D. Production performance of horizontal wells with dendritic-like hydraulic fractures in tight gas reservoirs. J. Pet. Sci. Eng. 2017, 148, 64–72. [Google Scholar] [CrossRef]
- Cui, Y.; Jiang, R.; Gao, Y. Blasingame decline analysis for multi-fractured horizontal well in tight gas reservoir with irregularly distributed and stress-sensitive fractures. J. Nat. Gas Sci. Eng. 2021, 88, 103830. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, J.; Liu, T.; Yang, D. Semi-analytical modeling of transient rate behaviour of a horizontal well with multistage fractures in tight formations considering stress-sensitive effect. J. Nat. Gas Sci. Eng. 2020, 82, 103461. [Google Scholar] [CrossRef]
- Lu, T.; Li, Z.; Lai, F.; Meng, Y.; Ma, W.; Sun, Y.; Wei, M. Blasingame decline analysis for variable rate/variable pressure drop: A multiple fractured horizontal well case in shale gas reservoirs. J. Pet. Sci. Eng. 2019, 178, 193–204. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Dong, W. Rate decline curves analysis of multiple-fractured horizontal wells in heterogeneous reservoirs. J. Hydrol. 2017, 553, 527–539. [Google Scholar] [CrossRef]
- Hernandez, R.F.; Younes, A.; Fahs, M.; Hoteit, H. Pressure transient analysis for stress-sensitive fractured wells with fracture face damage. Geoenergy Sci. Eng. 2023, 221, 211406. [Google Scholar] [CrossRef]
- Zhang, Z.; He, S.; Liu, G.; Guo, X.; Mo, S. Pressure buildup behavior of vertically fractured wells with stress-sensitive conductivity. J. Pet. Sci. Eng. 2014, 122, 48–55. [Google Scholar] [CrossRef]
- Matthews, C.; Brons, F.; Hazebroek, P. A Method for Determination of Average Pressure in a Bounded Reservoir. Trans. AIME 1954, 201, 182–191. [Google Scholar] [CrossRef]
- Dietz, D. Determination of Average Reservoir Pressure From Build-Up Surveys. J. Pet. Technol. 1965, 17, 955–959. [Google Scholar] [CrossRef]
- Helmy, M.W.; Wattenbarger, R.A. New Shape Factors for Wells Produced at Constant Pressure. In Proceedings of the SPE Gas Technology Symposium, Calgary, AB, Canada, 15–18 March 1998. [Google Scholar]
- Haryanto, E. New Shape Factor for Vertically Fractured Well Produced at Constant Pressure. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005. [Google Scholar]
- Pratikno, H.; Rushing, J.A.; Blasingame, T.A. Decline Curve Analysis Using Type Curves—Fractured Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003. [Google Scholar] [CrossRef]
- van Kruysdijk, C.P.J.W. Semianalytical Modeling of Pressure Transients in Fractured Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 2–5 October 1988. [Google Scholar]
- Zhang, M.; Ayala, L.F. A General Boundary Integral Solution for Fluid Flow Analysis in Reservoirs With Complex Fracture Geometries. J. Energy Resour. Technol. 2018, 140, 052907. [Google Scholar] [CrossRef]
- Tang, X.; Chen, Z.; Chu, H.; Liao, X.; Chen, H.; Zhang, J. Well testing interpretation for horizontal well with hydraulic fractures and interconnected micro-fractures. J. Pet. Sci. Eng. 2019, 179, 546–557. [Google Scholar] [CrossRef]
- Zhou, W.; Banerjee, R.; Poe, B.D.; Spath, J.; Thambynayagam, M. Semianalytical Production Simulation of Complex Hydraulic-Fracture Networks. SPE J. 2013, 19, 6–18. [Google Scholar] [CrossRef]
- Jia, P.; Cheng, L.; Clarkson, C.R.; Williams-Kovacs, J.D. Flow behavior analysis of two-phase (gas/water) flowback and early-time production from hydraulically-fractured shale gas wells using a hybrid numerical/analytical model. Int. J. Coal Geol. 2017, 182, 14–31. [Google Scholar] [CrossRef]
- Van Everdingen, A.; Hurst, W. The Application of the Laplace Transformation to Flow Problems in Reservoirs. J. Pet. Technol. 1949, 1, 305–324. [Google Scholar] [CrossRef]
- Stehfest, H. Numerical inversion of Laplace transforms. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Xu, Y.; Tan, X.; Li, X.; Li, J.; Liu, Q. Blasingame production decline and production prediction model of inclined well in triple-porosity carbonate gas reservoir. J. Nat. Gas Sci. Eng. 2021, 92, 103983. [Google Scholar] [CrossRef]




| Dimensionless Variables | Definition | Dimensionless Variables | Definition |
|---|---|---|---|
| Dimensionless pseudo-pressure | Dimensionless coordinate | ||
| Dimensionless time (length) | Dimensionless source point coordinate | ; | |
| Dimensionless outer boundary radius | Dimensionless productivity index | ||
| Dimensionless hydraulic fracture wing length | Storage capacity ratio of natural fracture system | ||
| Crossflow coefficient from matrix to natural fracture | Dimensionless time (area) |
| Flowing Regime, | Regime Name, and Pseudo-Pressure Derivative Curve Characteristics | Sketch Map |
|---|---|---|
| Stage 1 | A bilinear flow regime perpendicular to every hydraulic fracture wing and parallel to the fracture wing. The pressure derivative curve is the 1/4-slope straight line during this regime in the log–log plot. |  |
| Stage 2 | The fracture interferences regime. The pressure derivative curve shows obvious “humps” in this regime, which reflect the interferences among multiple fracture wings at the intersection between the wellbore and hydraulic fracture wing (Chen, Z. et al. (2016) [6]). |  |
| Stage 3 | The early linear flow regime perpendicular to every hydraulic fracture wing. The pressure derivative curve is the 1/2-slope straight line during this regime in the log–log plot (Wang, H.-T. (2014) [19]). |  |
| Stage 4 | The transition flow period between the early-time linear flow regime and the early radial flow regime. After the end of the early linear flow regime, the radial flow around the fracture wing will last for a period. Therefore, compared with the bi-wing symmetrical fracture of the MFHW, this regime shows a long duration. |  |
| Stage 5 | The early radial flow regime around each fracture cluster. The pseudo-pressure derivative curve is a constant in this regime, and the value is a 0.5/M horizontal line. M is the hydraulic fracture cluster number consisting of the multi-fracture wing. Of course, when the hydraulic fracture cluster space is very small or the fracture wing is very long, the characteristics of the pseudo-pressure derivative curve may not be obvious in this regime. |  |
| Stage 6 | The intermediate-time linear flow period. The pressure wave has propagated to position away from the fractured horizontal well. During this flowing regime, formation fluid flows into the MFHW in the linear flowing style. Therefore, the pseudo-pressure derivative curve of this flow regime also shows an obvious 1/2-slope straight line. | 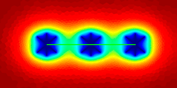 |
| Stage 7 | The radial flow regime around the MFHW pseudo-pressure derivative curve is a constant in this regime, and the value is a 0.5 horizontal line. Of course, when the outer boundary radius is very close to half the length of the horizontal well, the characteristics of the pseudo-pressure derivative curve may not be obvious in this regime. | 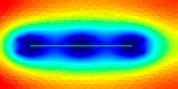 |
| Stage 8 | The pseudo-steady flow regime. The pressure wave has propagated to a circle closed boundary. The pseudo-pressure derivative curve is a unit-slope straight line. |
| CFD | JDpss (Numerical Solution) | JDpss (This Paper) | Relative Error/% |
|---|---|---|---|
| 0.1 | 0.3122 | 0.3127 | 0.16 |
| 1 | 0.3979 | 0.4006 | 0.67 |
| 5 | 0.4353 | 0.4342 | 0.25 |
| 10 | 0.4366 | 0.4379 | 0.30 |
| 100 | 0.4437 | 0.4427 | 0.23 |
| Stage | M = 1 | M = 2 | M = 3 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case | |||||||||||||||||||
| MF | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | |
| Case 1 | Length | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 |
| Angle | 65 | 90 | 115 | 245 | 270 | 295 | 65 | 90 | 115 | 245 | 270 | 295 | 65 | 90 | 115 | 245 | 270 | 295 | |
| Case 2 | Length | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 |
| Angle | 45 | 90 | 135 | 225 | 270 | 315 | 45 | 90 | 135 | 225 | 270 | 315 | 45 | 90 | 135 | 225 | 270 | 315 | |
| Case 3 | Length | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 |
| Angle | 30 | 90 | 150 | 210 | 270 | 330 | 30 | 90 | 150 | 210 | 270 | 330 | 30 | 90 | 150 | 210 | 270 | 330 | |
| Case 4 | Length | / | 60 | / | / | 60 | / | / | 60 | / | / | 60 | / | / | 60 | / | / | 60 | / |
| Angle | / | 90 | / | / | 270 | / | / | 90 | / | / | 270 | / | / | 90 | / | / | 270 | / | |
| Case 5 | Length | 60 | / | 60 | 60 | / | 60 | 60 | / | 60 | 60 | / | 60 | 60 | / | 60 | 60 | / | 60 |
| Angle | 45 | / | 135 | 225 | / | 315 | 45 | / | 135 | 225 | / | 315 | 45 | / | 135 | 225 | / | 315 | |
| Case 6 | Length | 30 | 120 | 30 | 30 | 120 | 30 | 30 | 120 | 30 | 30 | 120 | 30 | 30 | 120 | 30 | 30 | 120 | 30 |
| Angle | 45 | 90 | 135 | 225 | 270 | 315 | 45 | 90 | 135 | 225 | 270 | 315 | 45 | 90 | 135 | 225 | 270 | 315 | |
| Case 7 | Length | 75 | 30 | 75 | 75 | 30 | 75 | 75 | 30 | 75 | 75 | 30 | 75 | 75 | 30 | 75 | 75 | 30 | 75 |
| Angle | 45 | 90 | 135 | 225 | 270 | 315 | 45 | 90 | 135 | 225 | 270 | 315 | 45 | 90 | 135 | 225 | 270 | 315 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, Z.; Jia, Y.; Xu, Y.; Ao, X.; Liu, Z.; Zhu, S.; Chen, Z. An Accurate Calculation Method on Blasingame Production Decline Model of Horizontal Well with Dumbbell-like Hydraulic Fracture in Tight Gas Reservoirs. Processes 2024, 12, 1460. https://doi.org/10.3390/pr12071460
Xiang Z, Jia Y, Xu Y, Ao X, Liu Z, Zhu S, Chen Z. An Accurate Calculation Method on Blasingame Production Decline Model of Horizontal Well with Dumbbell-like Hydraulic Fracture in Tight Gas Reservoirs. Processes. 2024; 12(7):1460. https://doi.org/10.3390/pr12071460
Chicago/Turabian StyleXiang, Zuping, Ying Jia, Youjie Xu, Xiang Ao, Zhezhi Liu, Shijie Zhu, and Zhonghua Chen. 2024. "An Accurate Calculation Method on Blasingame Production Decline Model of Horizontal Well with Dumbbell-like Hydraulic Fracture in Tight Gas Reservoirs" Processes 12, no. 7: 1460. https://doi.org/10.3390/pr12071460
APA StyleXiang, Z., Jia, Y., Xu, Y., Ao, X., Liu, Z., Zhu, S., & Chen, Z. (2024). An Accurate Calculation Method on Blasingame Production Decline Model of Horizontal Well with Dumbbell-like Hydraulic Fracture in Tight Gas Reservoirs. Processes, 12(7), 1460. https://doi.org/10.3390/pr12071460






