Dynamics of Lagrangian Sensor Particles: The Effect of Non-Homogeneous Mass Distribution
Abstract
:1. Introduction
2. Materials and Methods
2.1. Lagrangian Sensor Particles
2.2. Lagrangian Particles
2.3. Buoyancy Calibration of Lagrangian Particles
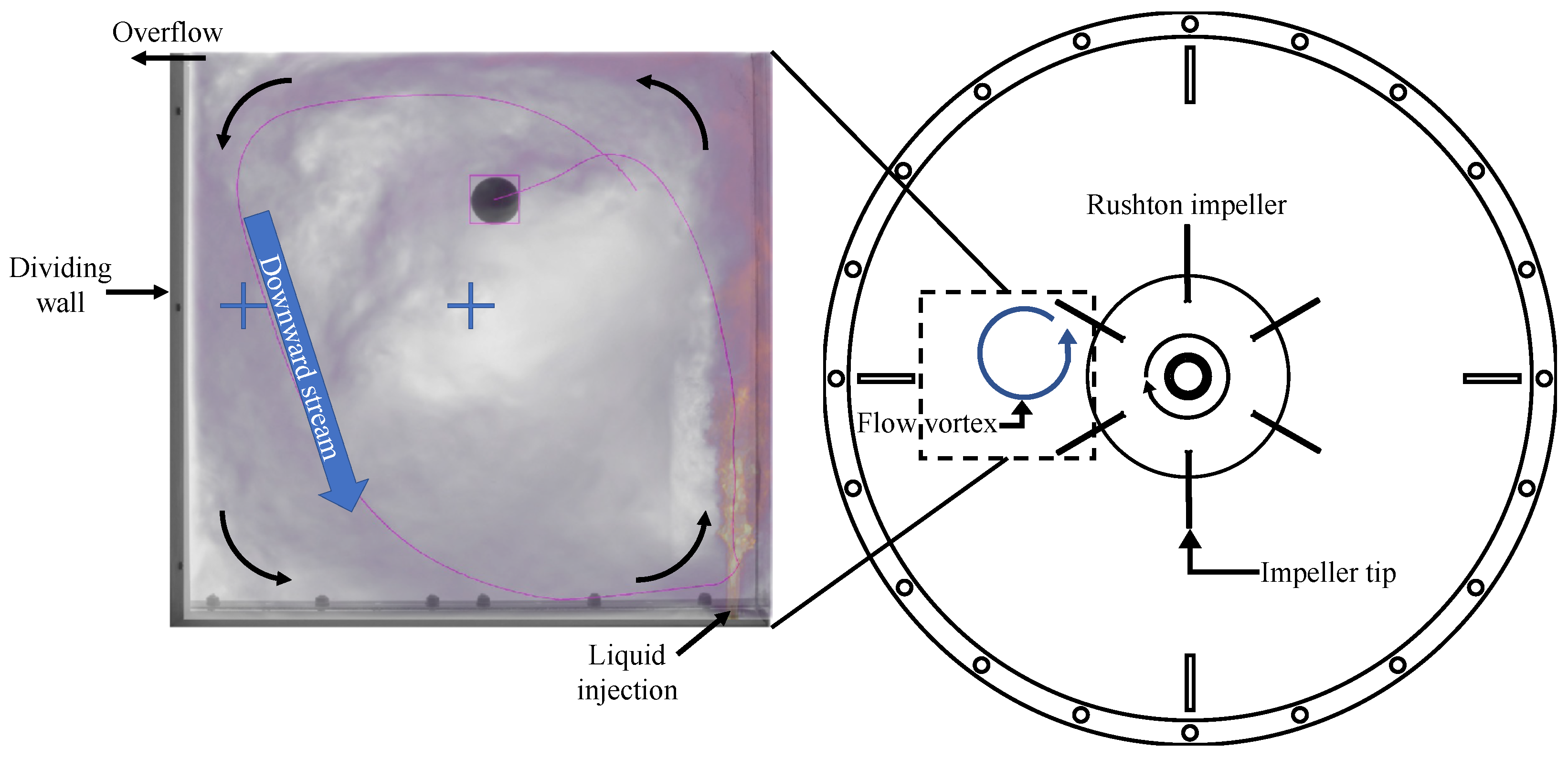
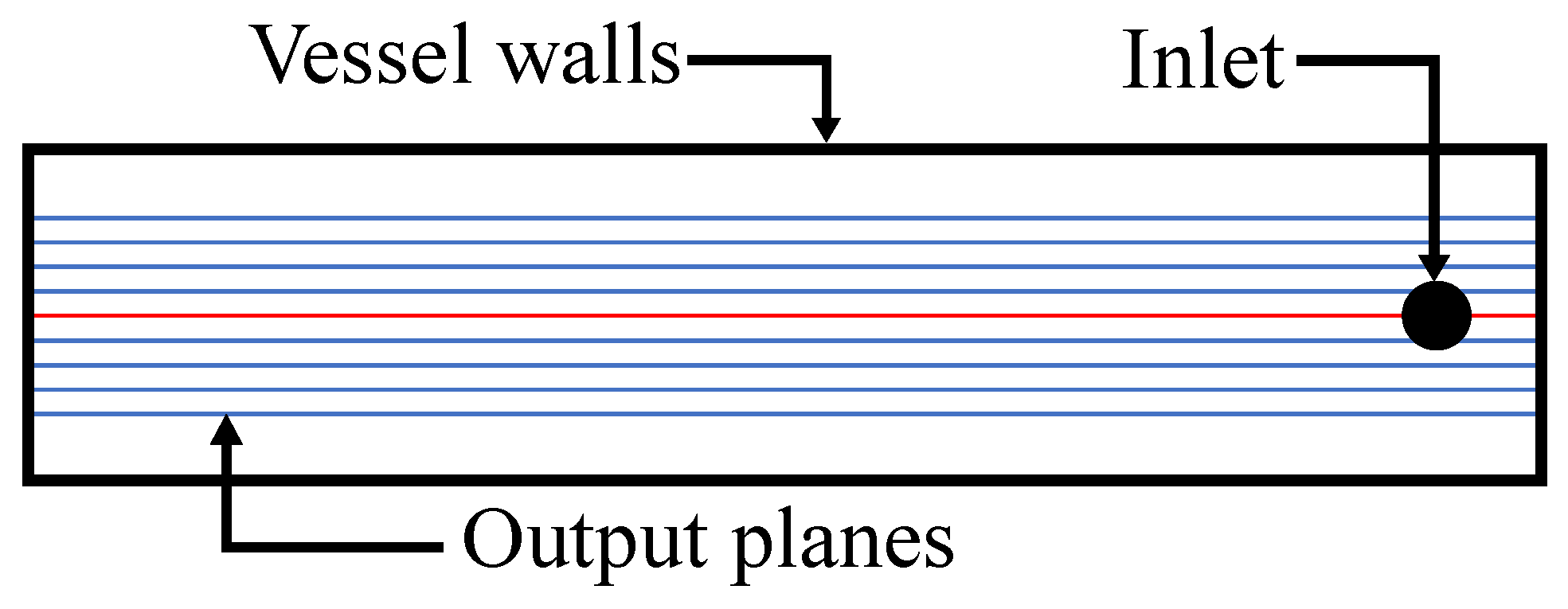
2.4. Experimental Procedure and Measurement of Flow-Following Capabilities
3. Experimental Evaluation and Tracking
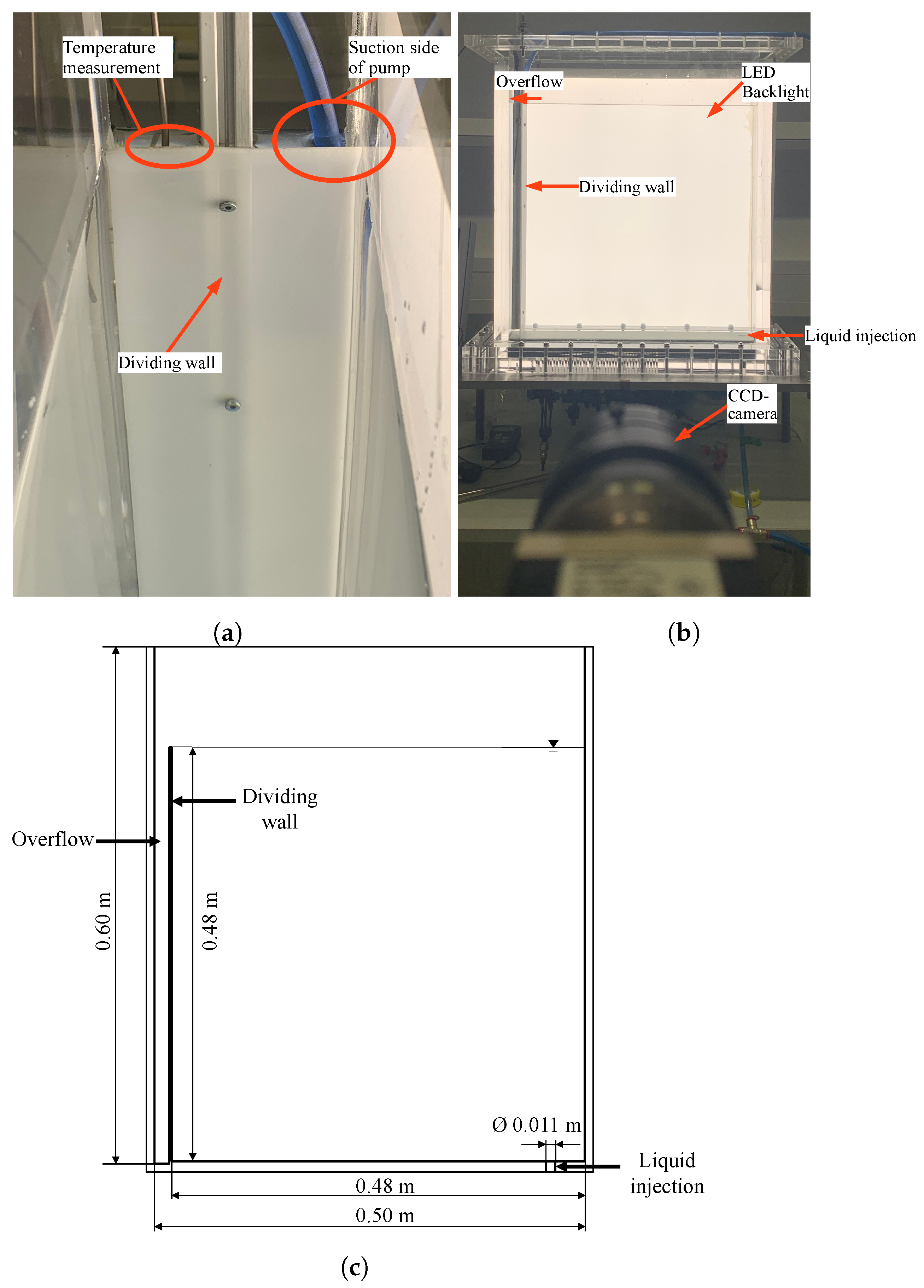
3.1. Camera and Capture Setup
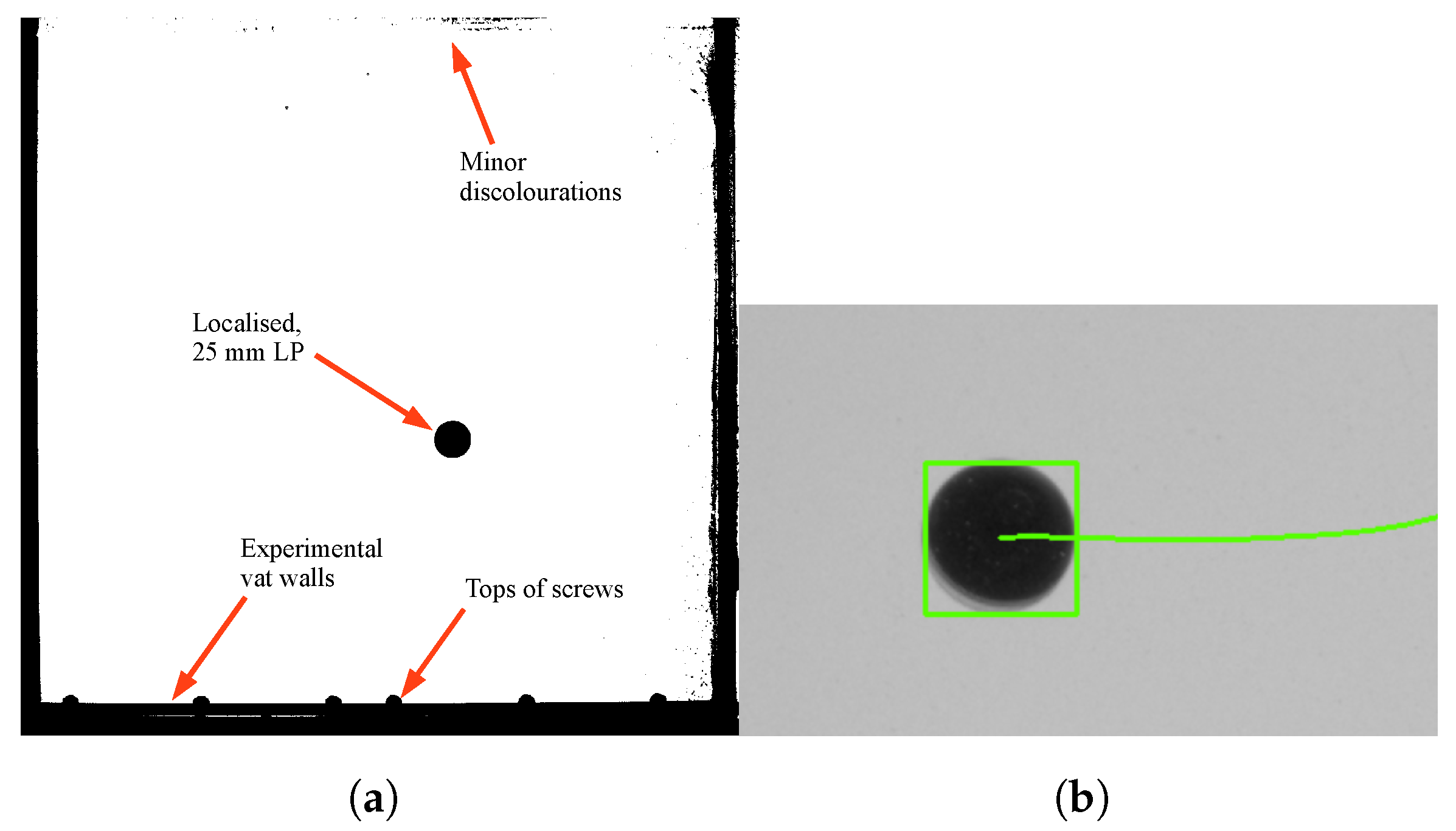
3.2. Tracking via OpenCV
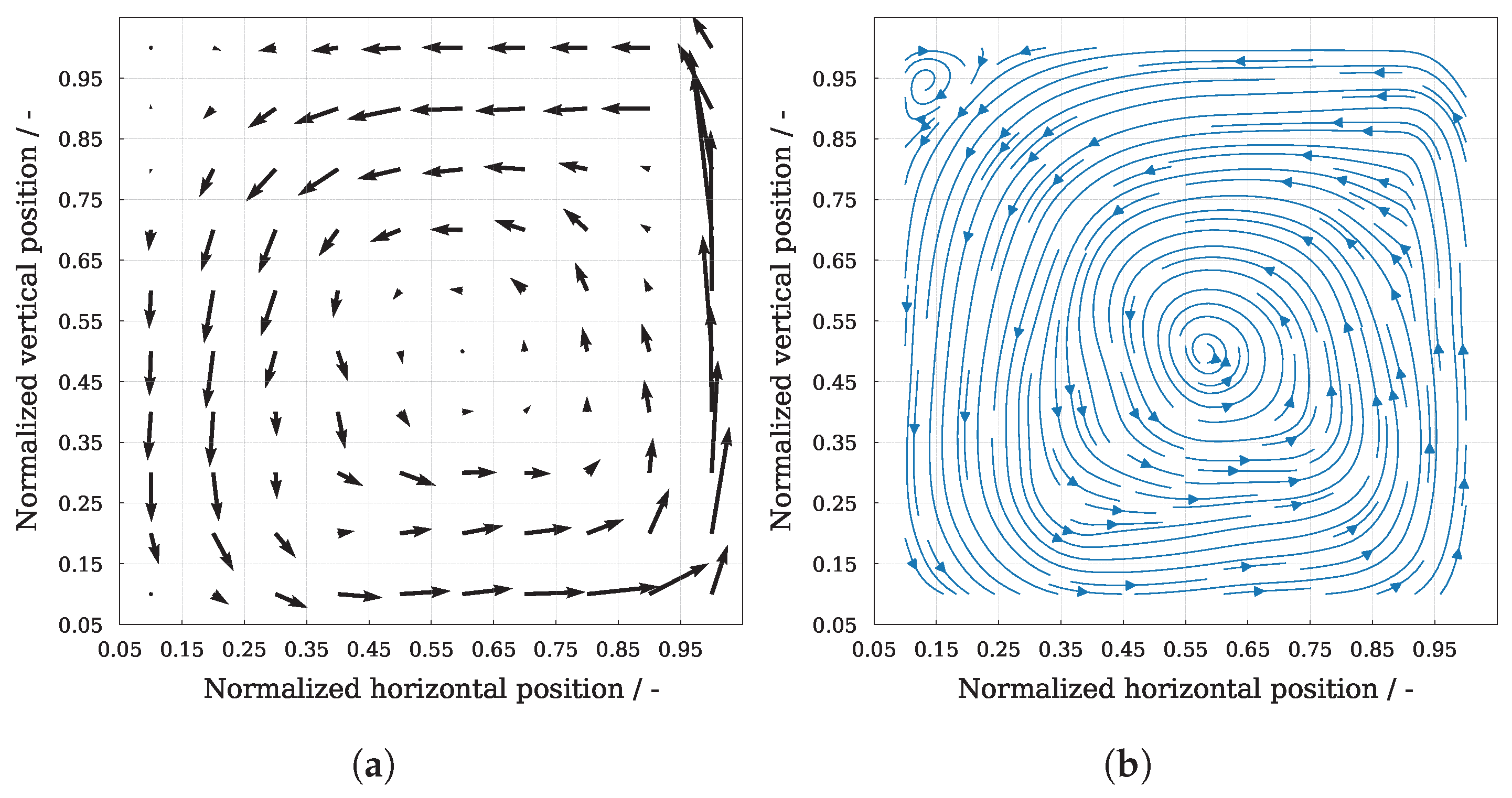
4. Lattice Boltzmann Simulations of Undisturbed Fluid Flow
5. Calculation and Characterization of Flow-Following Capabilities
6. Experimental Results
6.1. Evaluation of Flow Suspension Capability
6.2. Two-Dimensional Probability of Presence
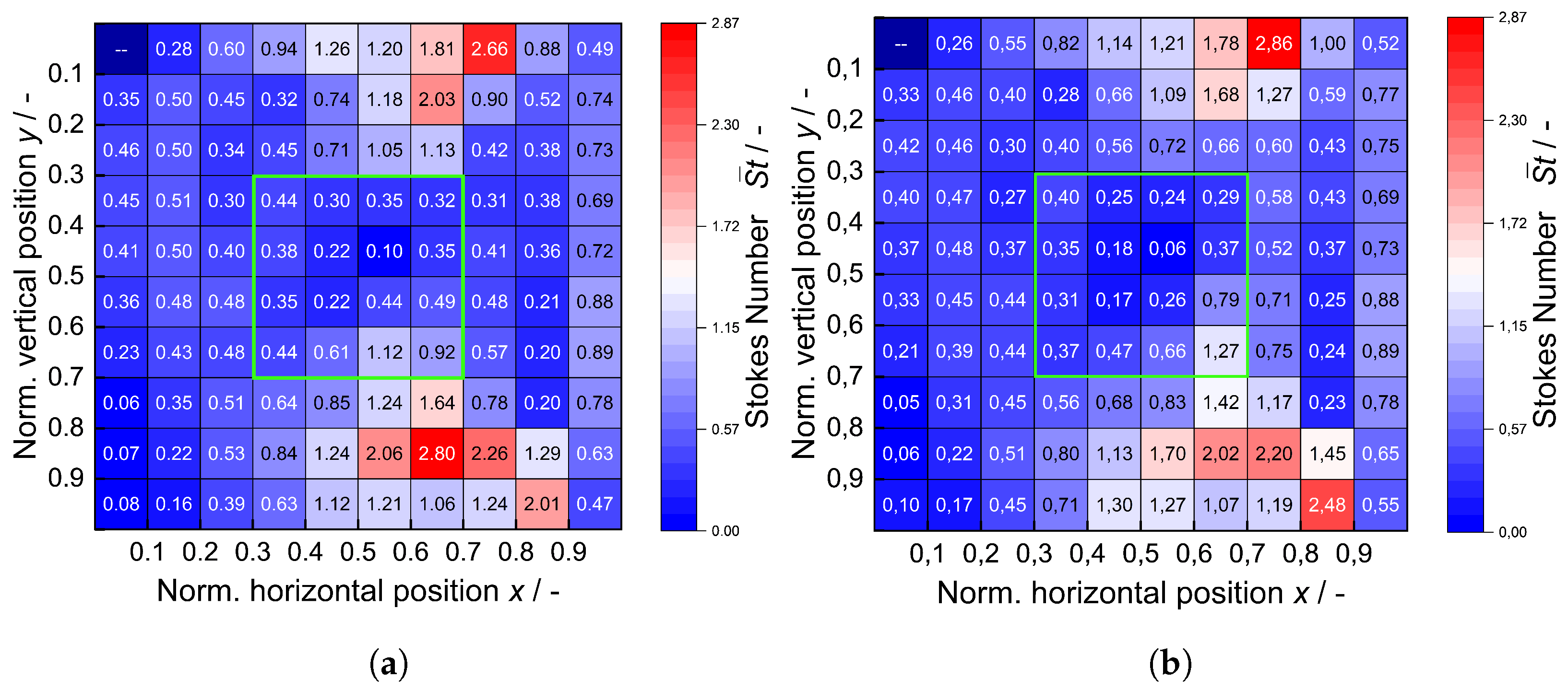
6.3. Stokes Number Grid
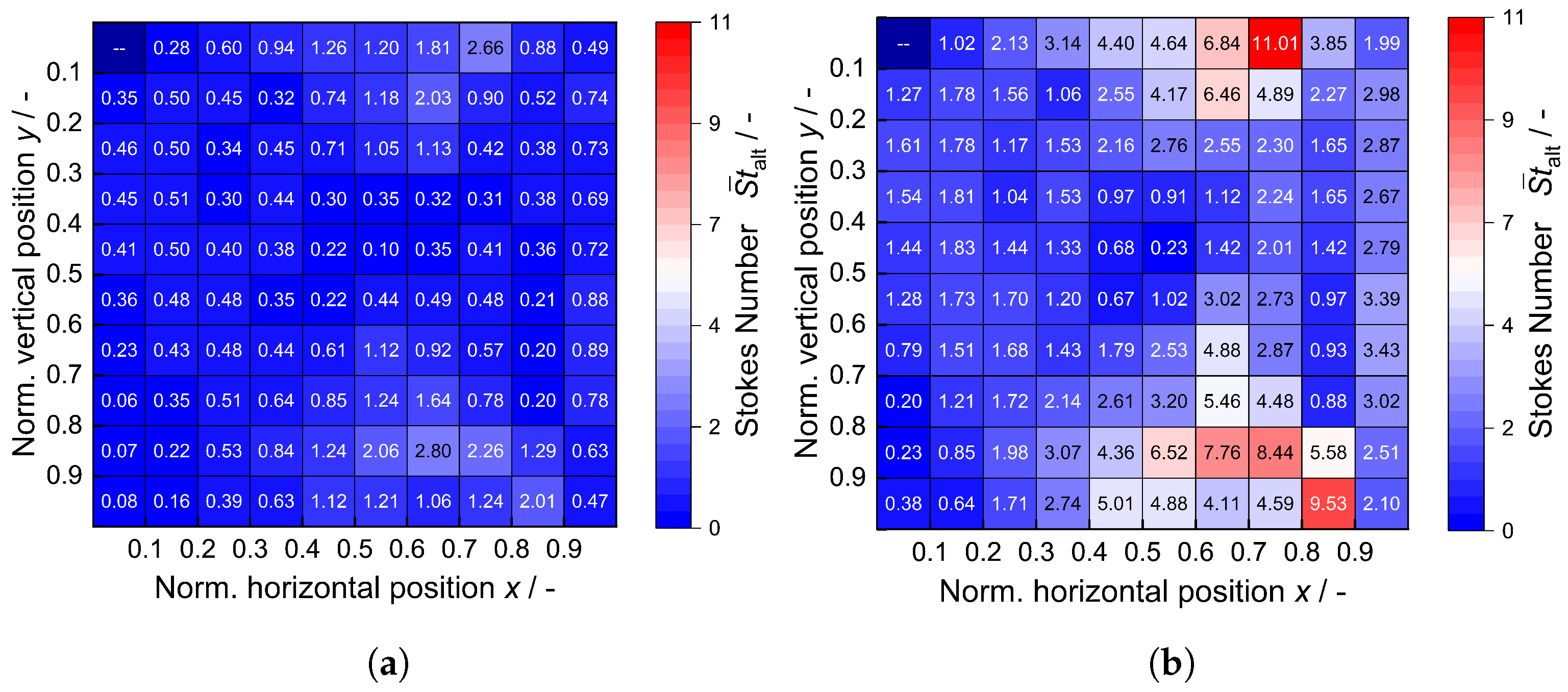
6.4. Alternative Stokes Number Approach
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haringa, C.; Deshmukh, A.T.; Mudde, R.F.; Noorman, H.J. Euler-Lagrange analysis towards representative down-scaling of a 22 m3 aerobic S. cerevisiae fermentation. Chem. Eng. Sci. 2017, 170, 653–669. [Google Scholar] [CrossRef]
- Bisgaard, J.; Muldbak, M.; Cornelissen, S.; Tajsoleiman, T.; Huusom, J.K.; Rasmussen, T.; Gernaey, K.V. Flow-following sensor devices: A tool for bridging data and model predictions in large-scale fermentations. Comput. Struct. Biotechnol. J. 2020, 18, 2908–2919. [Google Scholar] [CrossRef] [PubMed]
- Reinecke, S.F.; Hampel, U. Instrumented flow-following sensor particles with magnetic position detection and buoyancy control. J. Sens. Sens. Syst. 2016, 5, 213–220. [Google Scholar] [CrossRef]
- Lapin, A.; Müller, D.; Reuss, M. Dynamic Behavior of Microbial Populations in Stirred Bioreactors Simulated with Euler-Lagrange Methods: Traveling along the Lifelines of Single Cells. Ind. Eng. Chem. Res. 2004, 43, 4647–4656. [Google Scholar] [CrossRef]
- Blöbaum, L.; Haringa, C.; Grünberger, A. Microbial lifelines in bioprocesses: From concept to application. Biotechnol. Adv. 2023, 62, 108071. [Google Scholar] [CrossRef] [PubMed]
- Stine, J.M.; Beardslee, L.A.; Sathyam, R.M.; Bentley, W.E.; Ghodssi, R. Electrochemical Dissolved Oxygen Sensor-Integrated Platform for Wireless In Situ Bioprocess Monitoring. Sens. Actuators Chem. 2020, 320, 128381. [Google Scholar] [CrossRef]
- Todtenberg, N.; Klatt, J.; Schmitz-Hertzberg, S.T.; Jorde, F.; Schmalz, K. Wireless sensor capsule for bioreactors. In Proceedings of the 2013 IEEE MTT-S International Microwave Workshop Series on RF and Wireless Technologies for Biomedical and Healthcare Applications, IMWS-BIO 2013, Singapore, 9–11 December 2013. [Google Scholar] [CrossRef]
- Todtenberg, N.; Schmitz-Hertzberg, S.T.; Schmalz, K.; Klatt, J.; Jorde, F.; Jüttner, B.; Kraemer, R. Autonomous sensor capsule for usage in bioreactors. IEEE Sens. J. 2015, 15, 4093–4102. [Google Scholar] [CrossRef]
- Reinecke, S.; Deutschmann, A.; Jobst, K.; Kryk, H.; Friedrich, E.; Hampel, U. Flow following sensor particles-Validation and macro-mixing analysis in a stirred fermentation vessel with a highly viscous substrate. Biochem. Eng. J. 2012, 69, 159–171. [Google Scholar] [CrossRef]
- Reinecke, S.F.; Buntkiel, L.; Kipping, R.; Hampel, U. Process characterization in industrial vessels by flow-following sensor particles. Meas. Sci. Technol. 2022, 33, 12. [Google Scholar] [CrossRef]
- Duisterwinkel, E.; Demi, L.; Dubbelman, G.; Talnishnikh, E.; Wörtche, H.J.; Bergmans, J.W. Environment mapping and localization with an uncontrolled swarm of ultrasound sensor motes. Proc. Meet. Acoust. 2014, 20, 30001. [Google Scholar]
- Duisterwinkel, E.H.; Talnishnikh, E.; Krijnders, D.; Wortche, H.J. Sensor Motes for the Exploration and Monitoring of Operational Pipelines. IEEE Trans. Instrum. Meas. 2018, 67, 655–666. [Google Scholar] [CrossRef]
- Duisterwinkel, E.H.; Dubbelman, G.; Talnishnikh, E.; Bergmans, J.J.; Wortche, H.J.; Linnartz, J.P.M. Go-With-the-Flow Swarm Sensing in Inaccessible Viscous Media. IEEE Sens. J. 2020, 20, 4442–4452. [Google Scholar] [CrossRef]
- Bisgaard, J.; Zahn, J.A.; Tajsoleiman, T.; Rasmussen, T.; Huusom, J.K.; Gernaey, K.V. Data-based dynamic compartment model: Modeling of E. coli fed-batch fermentation in a 600 m3bubble column. J. Ind. Microbiol. Biotechnol. 2022, 49, kuac021. [Google Scholar] [CrossRef] [PubMed]
- Buntkiel, L.; Ma, Y.; Reinecke, S.F.; Hampel, U. Orientation resolved measurements of accelerations with sensor particles in bioreactors. Tech. Mess. 2023, 90, 835–845. [Google Scholar] [CrossRef]
- Hofmann, S.; Buntkiel, L.; Rautenbach, R.; Gaugler, L.; Ma, Y.; Haase, I.; Fitschen, J.; Wucherpfennig, T.; Reinecke, S.F.; Hoffmann, M.; et al. Experimental Analysis of Lifelines in a 15,000 L Bioreactor by Means of Lagrangian Sensor Particles. Chem. Eng. Res. Des. 2024, 205, 695–712. [Google Scholar] [CrossRef]
- Ascanio, G. Mixing time in stirred vessels: A review of experimental techniques. Chin. J. Chem. Eng. 2015, 23, 1065–1076. [Google Scholar] [CrossRef]
- Edwards, M.F.; Baker, M.R.; Godfrey, J.C. Chapter 8—Mixing of liquids in stirred tanks. In Mixing in the Process Industries; Harnby, N., Edwards, M.F., Nienow, A.W., Eds.; Butterworth-Heinemann: Oxford, UK, 1992; pp. 137–158. [Google Scholar] [CrossRef]
- Ascanio, G.; Brito-Bazán, M.; Fuente, E.B.D.L.; Carreau, P.J.; Tanguy, P.A. Unconventional Configuration Studies to Improve Mixing Times in Stirred Tanks. Can. J. Chem. Eng. 2002, 80, 558–565. [Google Scholar] [CrossRef]
- Carreau, P.J.; Patterson, I.; Yap, C.Y. Mixing of viscoelastic fluids with helical-ribbon agitators. I—Mixing time and flow patterns. Can. J. Chem. Eng. 1976, 54, 135–142. [Google Scholar] [CrossRef]
- Hoogendoorn, C.; den Hartog, A. Model studies on mixers in the viscous flow region. Chem. Eng. Sci. 1967, 22, 1689–1699. [Google Scholar] [CrossRef]
- Rosseburg, A.; Fitschen, J.; Wutz, J.; Wucherpfennig, T.; Schlüter, M. Hydrodynamic inhomogeneities in large scale stirred tanks—Influence on mixing time. Chem. Eng. Sci. 2018, 188, 208–220. [Google Scholar] [CrossRef]
- Kraume, M.; Zehner, P. Experience with Experimental Standards for Measurements of Various Parameters in Stirred Tanks: A Comparative Test. Chem. Eng. Res. Des. 2001, 79, 811–818. [Google Scholar] [CrossRef]
- Espinosa-Solares, T.; Fuente, E.B.D.L.; Tecante, A.; Medina-Torres, L.; Tanguy, P.A. Mixing Time in Rheologically Evolving Model Fluids by Hybrid Dual Mixing Systems. Chem. Eng. Res. Des. 2002, 80, 817–823. [Google Scholar] [CrossRef]
- Gaugler, L.; Mast, Y.; Fitschen, J.; Hofmann, S.; Schlüter, M.; Takors, R. Scaling-down biopharmaceutical production processes via a single multi-compartment bioreactor (SMCB). Eng. Life Sci. 2022, 23, e2100161. [Google Scholar] [CrossRef] [PubMed]
- Buntkiel, L.; Heller, A.; Budelmann, C.; Reinecke, S.; Hampel, U. 2.2—Mit UWB-Lokalisierung gekoppelte inertiale Lage- und Bewegungsverfolgung für instrumentierte Strömungsfolger. In Proceedings of the 15. Dresdner Sensor-Symposium 2021, Dresden, Germany, 6–8 December 2021; pp. 22–27. [Google Scholar] [CrossRef]
- Hofmann, S.; Weiland, C.; Fitschen, J.; von Kameke, A.; Hoffmann, M.; Schlüter, M. Lagrangian sensors in a stirred tank reactor: Comparing trajectories from 4D-Particle Tracking Velocimetry and Lattice-Boltzmann simulations. Chem. Eng. J. 2022, 449. [Google Scholar] [CrossRef]
- Will, J.B.; Krug, D. Dynamics of freely rising spheres: The effect of moment of inertia. J. Fluid Mech. 2021, 927, A7. [Google Scholar] [CrossRef]
- Will, J.B.; Krug, D. Rising and Sinking in Resonance: Mass Distribution Critically Affects Buoyancy-Driven Spheres via Rotational Dynamics. Phys. Rev. Lett. 2021, 126, 174502. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, R.; Fiabane, L.; Gasteuil, Y.; Volk, R.; Pinton, J.F. Characterizing flows with an instrumented particle measuring Lagrangian accelerations. New J. Phys. 2013, 15, 015018. [Google Scholar] [CrossRef]
- Rautenbach, R.; Buntkiel, L.; Schäfer, J.; Hofmann, S. Processes Data and Code for Dynamics of Lagrangian Sensor Particles; DARUS Repository of the University of Stuttgart; DaRUS: Stuttgart, Germany, 2024. [Google Scholar] [CrossRef]
- Lukežič, A.; Vojíř, T.; Luka, L.; Zajc, L.; Matas, J.; Kristan, M. Discriminative Correlation Filter with Channel and Spatial Reliability. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- M-Star. Theory and Implementation—M-Star CFD Documentation. Available online: https://docs.mstarcfd.com/ (accessed on 27 November 2022).
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Equation. In The Lattice Boltzmann Method: Principles and Practice; Springer International Publishing: Cham, Switzerland, 2017; pp. 61–104. [Google Scholar] [CrossRef]
- Guo, Z.; Shu, C. Lattice Boltzmann Method and Its Applications in Engineering; World Scientific: Singapore, 2013; Volume 3. [Google Scholar] [CrossRef]
- Mohamad, A.A. Lattice Boltzmann Method; Springer: London, UK, 2019. [Google Scholar] [CrossRef]
- Tropea, C. Springer Handbook of Experimental Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Ruzicka, M.C. On dimensionless numbers. Chem. Eng. Res. Des. 2008, 86, 835–868. [Google Scholar] [CrossRef]
- Maxey, M.R.; Riley, J.J. Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 1983, 26, 883–889. [Google Scholar] [CrossRef]
- Birch, D.M.; Martin, N. Tracer particle momentum effects in vortex flows. J. Fluid Mech. 2013, 723, 665–691. [Google Scholar] [CrossRef]
- Ouellette, N.T.; O’malley, P.J.J.; Gollub, J.P. Transport of Finite-Sized Particles in Chaotic Flow. Phys. Rev. Lett. 2008, 101, 174504. [Google Scholar] [CrossRef] [PubMed]
- Israel, R.; Rosner, D.E. Use of a Generalized Stokes Number to Determine the Aerodynamic Capture Efficiency of Non-Stokesian Particles from a Compressible Gas Flow. Aerosol Sci. Technol. 1982, 2, 45–51. [Google Scholar] [CrossRef]
- Crowe, C.T. Multiphase Flows with Droplets and Particles; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Fangary, Y.S.; Barigou, M.; Seville, J.P.; Parker, D.J. Fluid trajectories in a stirred vessel of non-newtonian liquid using positron emission particle tracking. Chem. Eng. Sci. 2000, 55, 5969–5979. [Google Scholar] [CrossRef]
- Bluemink, J.J.; Lohse, D.; Prosperetti, A.; Wijngaarden, L.V. Drag and lift forces on particles in a rotating flow. J. Fluid Mech. 2010, 643, 1–31. [Google Scholar] [CrossRef]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Zlokarnik, M. Stirring: Theory and Practice; Wiley-VCH: Hoboken, NJ, USA, 2001; 362p. [Google Scholar]
- Lewis, E.V. Principles of Naval Architecture; The Society of Naval Architects and Marine Engineering: Alexandria, VA, USA, 1988; Volume 1. [Google Scholar]

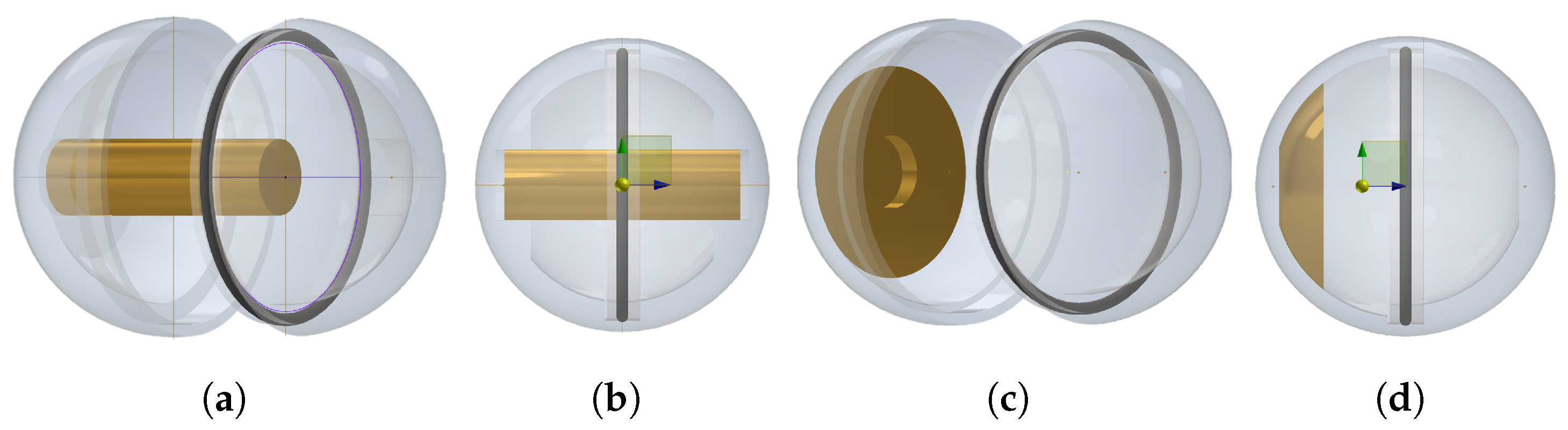







| LP Name | Diameter /mm | Internals | Position of Center of Mass |
|---|---|---|---|
| EQ-25 | 25 | Centered cylindrical brass weight | Center of sphere (equatorial) |
| OF-25 | 25 | Off-center brass weight | 3.6 mm offset from Center of sphere |
| EQ-40 | 40 | Centered cylindrical brass weight | Center of sphere (equatorial) |
| OF-40 | 40 | Off-center brass weight | 6.5 mm offset from Center of sphere |
| LP Name | Inlet Velocity vinlet/m s−1 | Total Runs nruns/- | Duration of Run trun/s |
|---|---|---|---|
| 0.77 | 24 | 300 | |
| OF-25 | 1.11 | 24 | 300 |
| 1.80 | 24 | 300 | |
| 0.77 | 24 | 300 | |
| EQ-25 | 1.11 | 24 | 300 |
| 1.80 | 24 | 300 | |
| 0.77 | 24 | 300 | |
| OF-40 | 1.11 | 24 | 300 |
| 1.80 | 24 | 300 | |
| 0.77 | 24 | 300 | |
| EQ-40 | 1.11 | 24 | 300 |
| 1.80 | 24 | 300 |
| Inlet velocity | LP Name | 0.77 | 1.11 | 1.80 |
| / | ||||
| LP velocity | EQ-25 | 5.3 ± 0.1 | 7.1 ± 0.3 | 8.6 ± 0.3 |
| /cm | OF-25 | 5.2 ± 0.1 | 7.1 ± 0.1 | 9.1 ± 0.2 |
| Total circulations | EQ-25 | 273 | 395 | 538 |
| /- | OF-25 | 266 | 407 | 565 |
| Total hits | EQ-25 | 100 | 30 | 81 |
| /- | OF-25 | 137 | 152 | 177 |
| Contacts per circulations | EQ-25 | 0.36 | 0.08 | 0.15 |
| /- | OF-25 | 0.52 | 0.37 | 0.31 |
| LP velocity | EQ-40 | 4.6 ± 0.1 | 6.2 ± 0.2 | 8.2 ± 0.3 |
| /cm | OF-40 | 5.2 ± 0.1 | 7.1 ± 0.1 | 8.9 ± 0.2 |
| Total circulations | EQ-40 | 273 | 370 | 534 |
| /- | OF-40 | 280 | 392 | 525 |
| Total hits | EQ-40 | 86 | 82 | 71 |
| /- | OF-40 | 185 | 230 | 163 |
| Contacts per circulations | EQ-40 | 0.31 | 0.22 | 0.13 |
| /- | OF-40 | 0.66 | 0.59 | 0.31 |
| LP Name | LP Radius /mm | CoM Shift /mm | CoM Shift /% | Shift Factor /- |
|---|---|---|---|---|
| EQ-25 | 12.50 | 0.00 | 0.00 | 1.00 |
| OF-25 | 12.50 | 3.61 | 28.89 | 0.55 |
| EQ-40 | 20.00 | 0.00 | 0.00 | 1.00 |
| OF-40 | 20.00 | 6.50 | 32.50 | 0.51 |
| LP Name | Stokes Number /- | Proposed Stokes Number /- | Difference in Stokes Number /- | Difference in Alternative Stokes Number /- |
|---|---|---|---|---|
| EQ-25 | 0.33 | 0.33 | 0.01 | 0.84 |
| OF-25 | 0.34 | 1.17 | ||
| EQ-40 | 0.78 | 0.78 | 0.13 | 2.72 |
| OF-40 | 0.91 | 3.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rautenbach, R.; Hofmann, S.; Buntkiel, L.; Schäfer, J.; Reinecke, S.F.; Hoffmann, M.; Hampel, U.; Schlüter, M. Dynamics of Lagrangian Sensor Particles: The Effect of Non-Homogeneous Mass Distribution. Processes 2024, 12, 1617. https://doi.org/10.3390/pr12081617
Rautenbach R, Hofmann S, Buntkiel L, Schäfer J, Reinecke SF, Hoffmann M, Hampel U, Schlüter M. Dynamics of Lagrangian Sensor Particles: The Effect of Non-Homogeneous Mass Distribution. Processes. 2024; 12(8):1617. https://doi.org/10.3390/pr12081617
Chicago/Turabian StyleRautenbach, Ryan, Sebastian Hofmann, Lukas Buntkiel, Jan Schäfer, Sebastian Felix Reinecke, Marko Hoffmann, Uwe Hampel, and Michael Schlüter. 2024. "Dynamics of Lagrangian Sensor Particles: The Effect of Non-Homogeneous Mass Distribution" Processes 12, no. 8: 1617. https://doi.org/10.3390/pr12081617
APA StyleRautenbach, R., Hofmann, S., Buntkiel, L., Schäfer, J., Reinecke, S. F., Hoffmann, M., Hampel, U., & Schlüter, M. (2024). Dynamics of Lagrangian Sensor Particles: The Effect of Non-Homogeneous Mass Distribution. Processes, 12(8), 1617. https://doi.org/10.3390/pr12081617








