Numerical Study to Optimize the Operating Parameters of a Real-Sized Industrial-Scale Micron Air Classifier Used for Manufacturing Fine Quartz Powder and a Comparison with the Prototype Model
Abstract
1. Introduction
2. Establishment of Computational Model
3. Mathematical Formulation
3.1. Discrete-Phase Model
3.2. Continuous-Phase Model
3.3. Boundary and Initial Conditions
- Structural parameters: In this study, the structural parameters of the device were fixed according to the dimensions shown in Figure 1b.
- According to [12,16], the results of previous studies related to the assessment of the effects of operating parameters on the classification performance of air classifiers show that classification performance is significantly influenced by the rotor speed, inlet air volume, and secondary air volume, but the impact of feed rate is relatively weak. Therefore, the rotor speed, inlet air volume, and secondary air volume were chosen, in this study, as the main factors influencing the industrial classifier’s the classification performance, and the feed rate was selected from the actual requirement of production.
- To partially optimize the outlet mass airflow rate for producing quartz fine powder (0–45 μm), the operating parameters including 2.44 kg/s for the feed flow rate, 290 rpm for the rotor speed, and the range of outlet mass airflow rate from 5.104 kg/s to 6.125 kg/s were set for the simulation (as shown in Table 2). These parameters were selected based on the partial optimization results [3] and the actual working conditions of quartz-based engineering stone production at the Vicostone Plant.
- Simulation parameters for investigating the influence of rotor speed: based on the results of the partial optimization of the outlet mass airflow rate and the actual working condition limits of the system, the operating parameters selected for studying the influence of rotor speed on the separation efficiency of the micron air classifier are shown in Table 3.
- Selecting simulation parameters for the study of the inlet secondary air velocity: The partial optimization results for outlet mass airflow rate and rotor speed were selected as input parameters. The secondary air velocity range was selected for the simulation based on the ratio of the secondary airflow volume to the primary airflow volume: 1:9, 2:8, 3:7, 4:6, and 5:5, respectively. The valve of the secondary inlet is 50% open (called “fresh air”), which was also considered in this study. The operating parameters selected for studying the influence of secondary inlet airflow velocity on the separation efficiency of the micron air classifier are shown in Table 4. In all computations, the densities of the particles and gas are, respectively, 2560 kg/m3 and 1.225 kg/m3 with the fixed particle–wall restitution coefficient (equal to 0.5).
4. Simulation Results
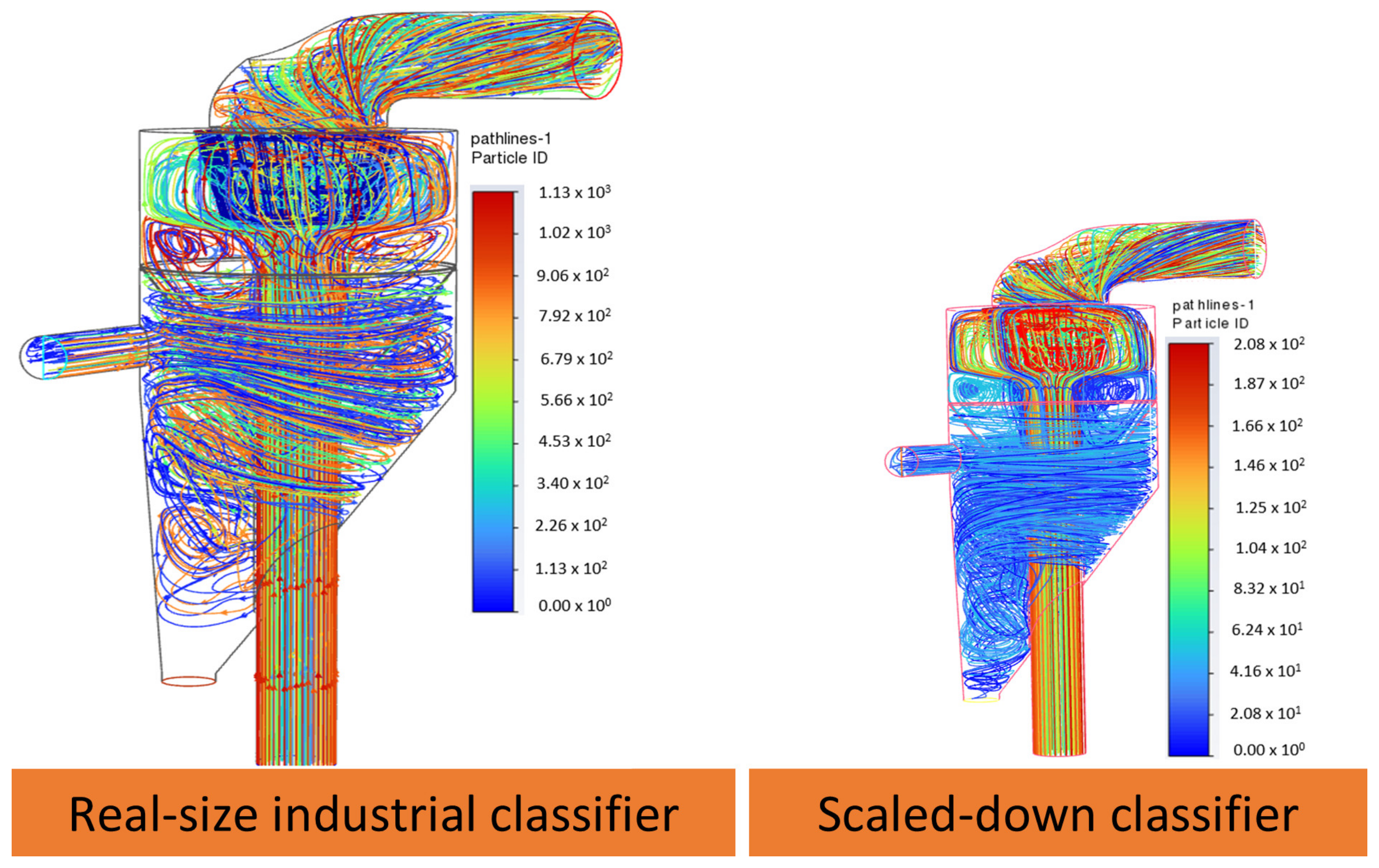
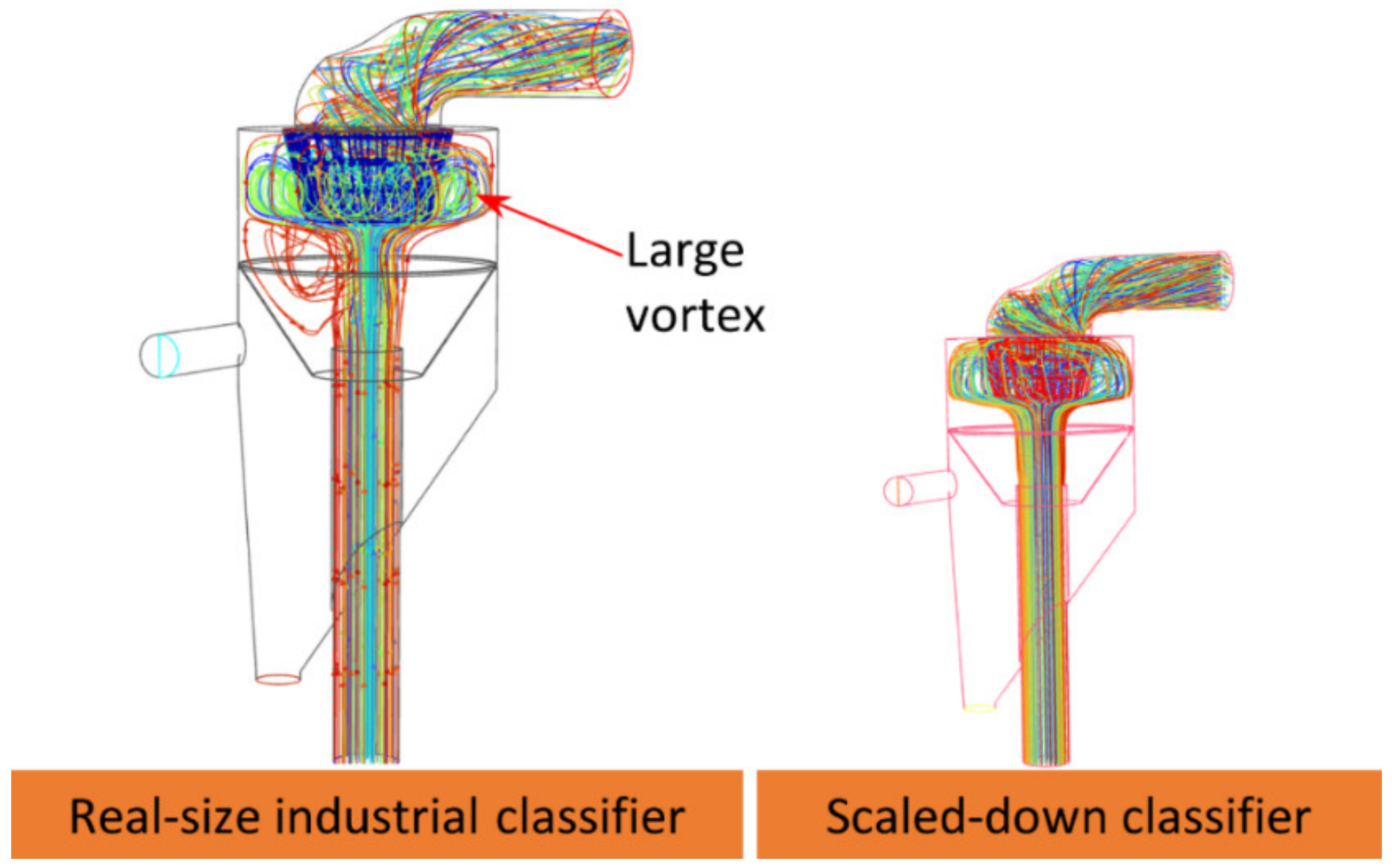
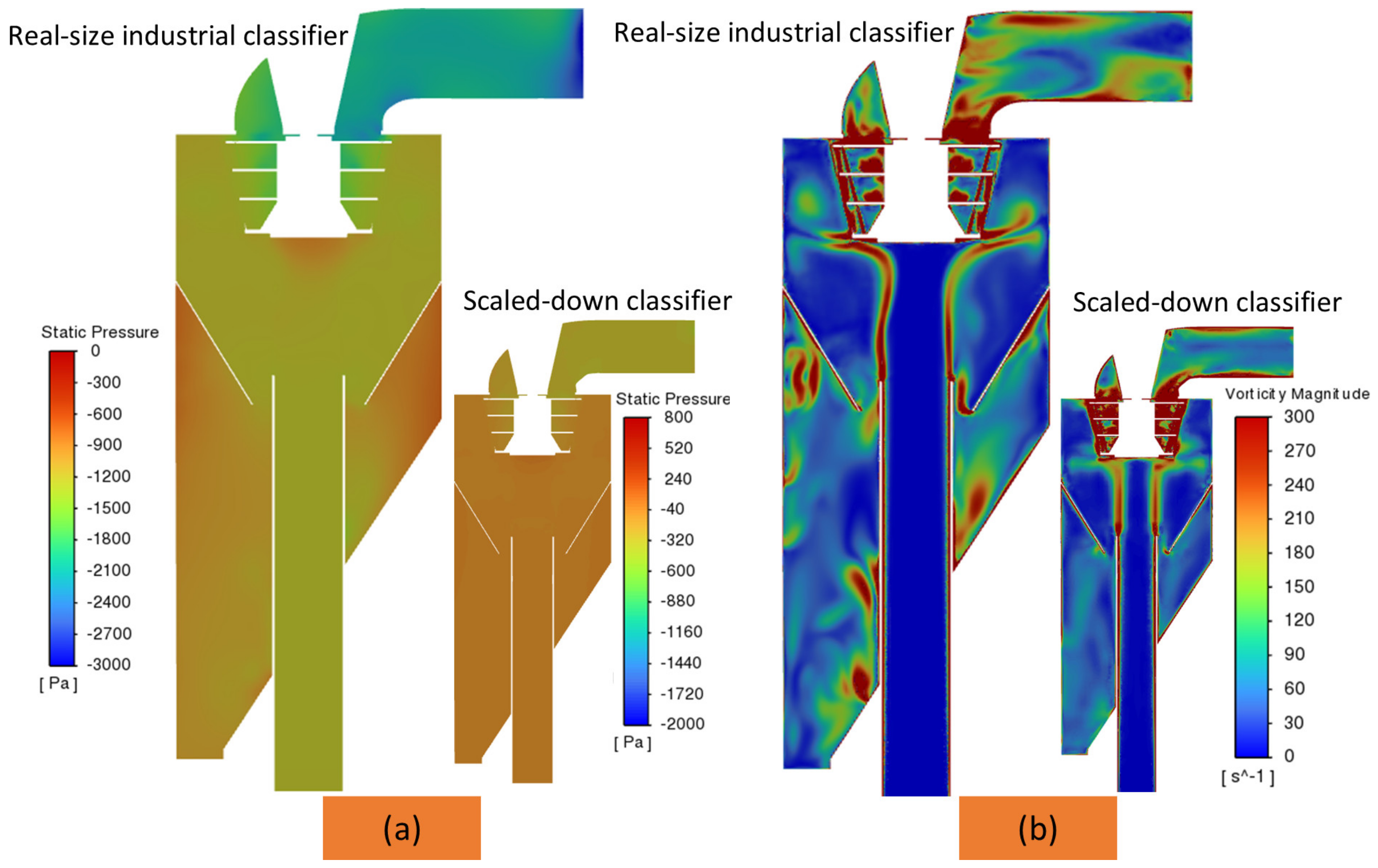
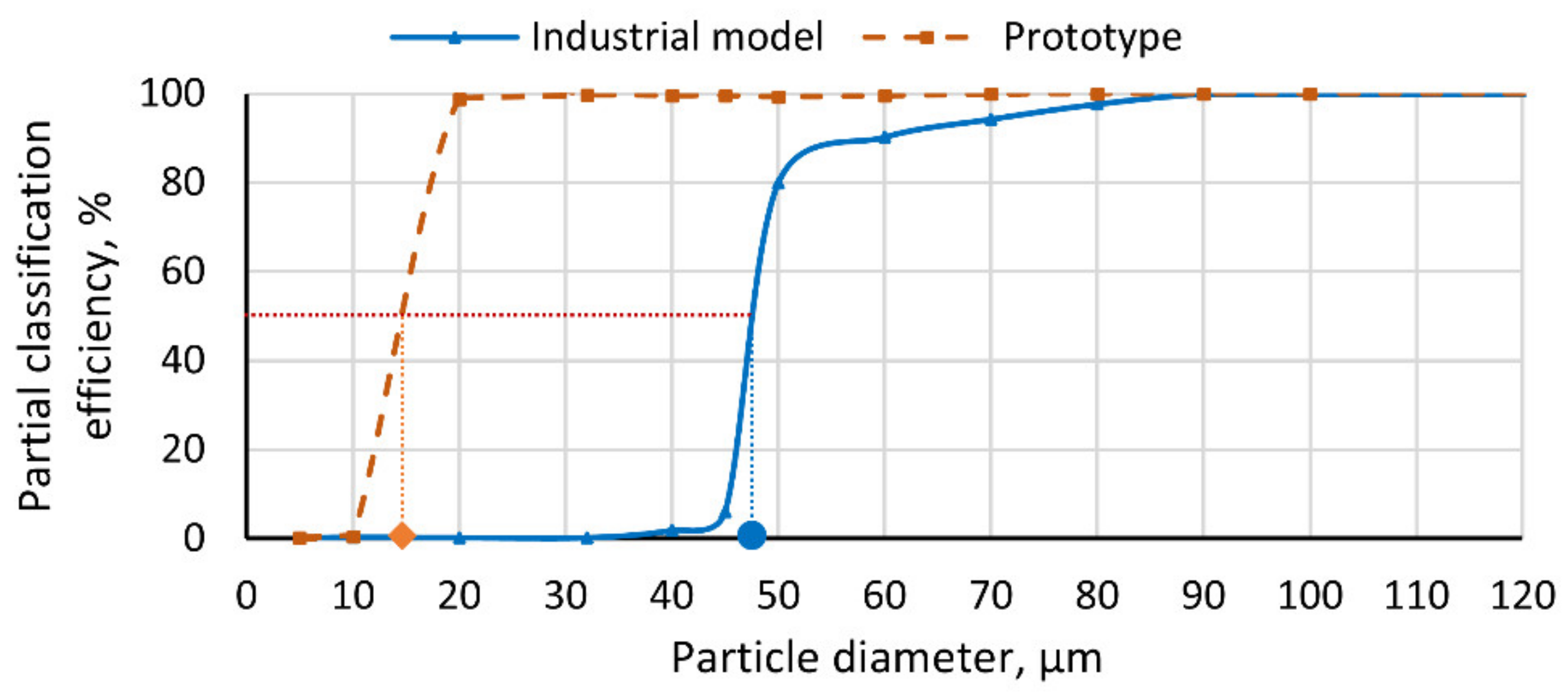
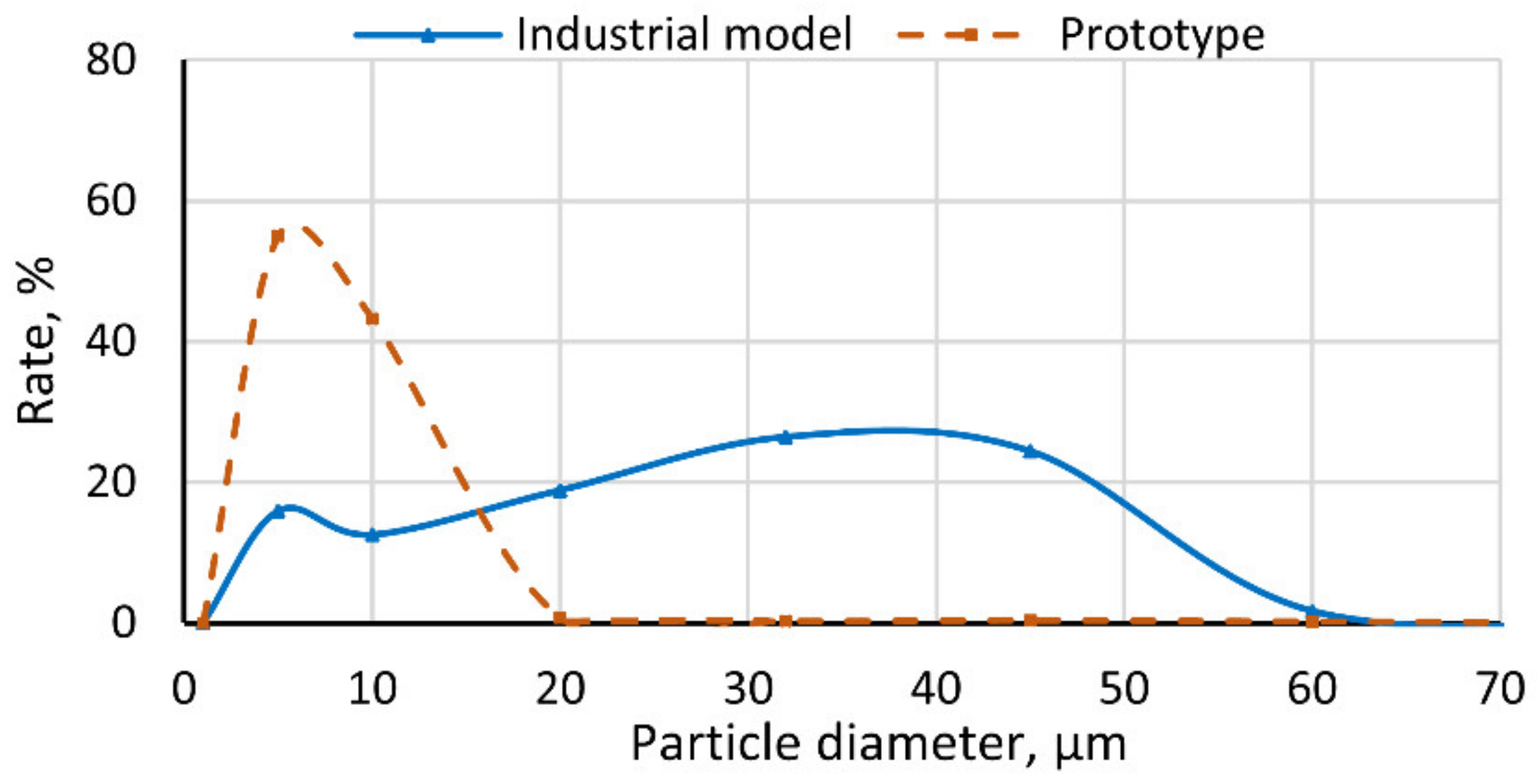
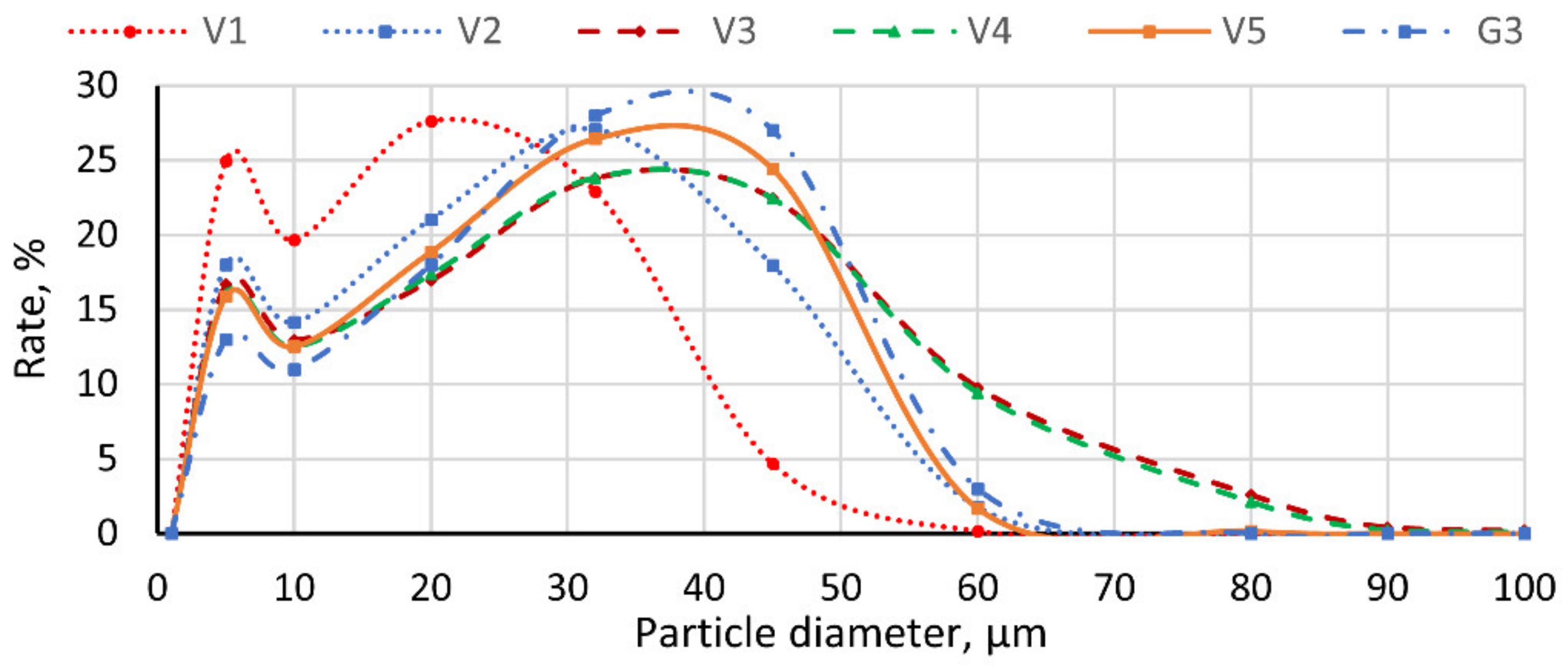
4.1. Investigation of the Real-Sized Industrial Classifier and the Scaled-Down Classifier
4.2. Influence of Outlet Mass Airflow Rate
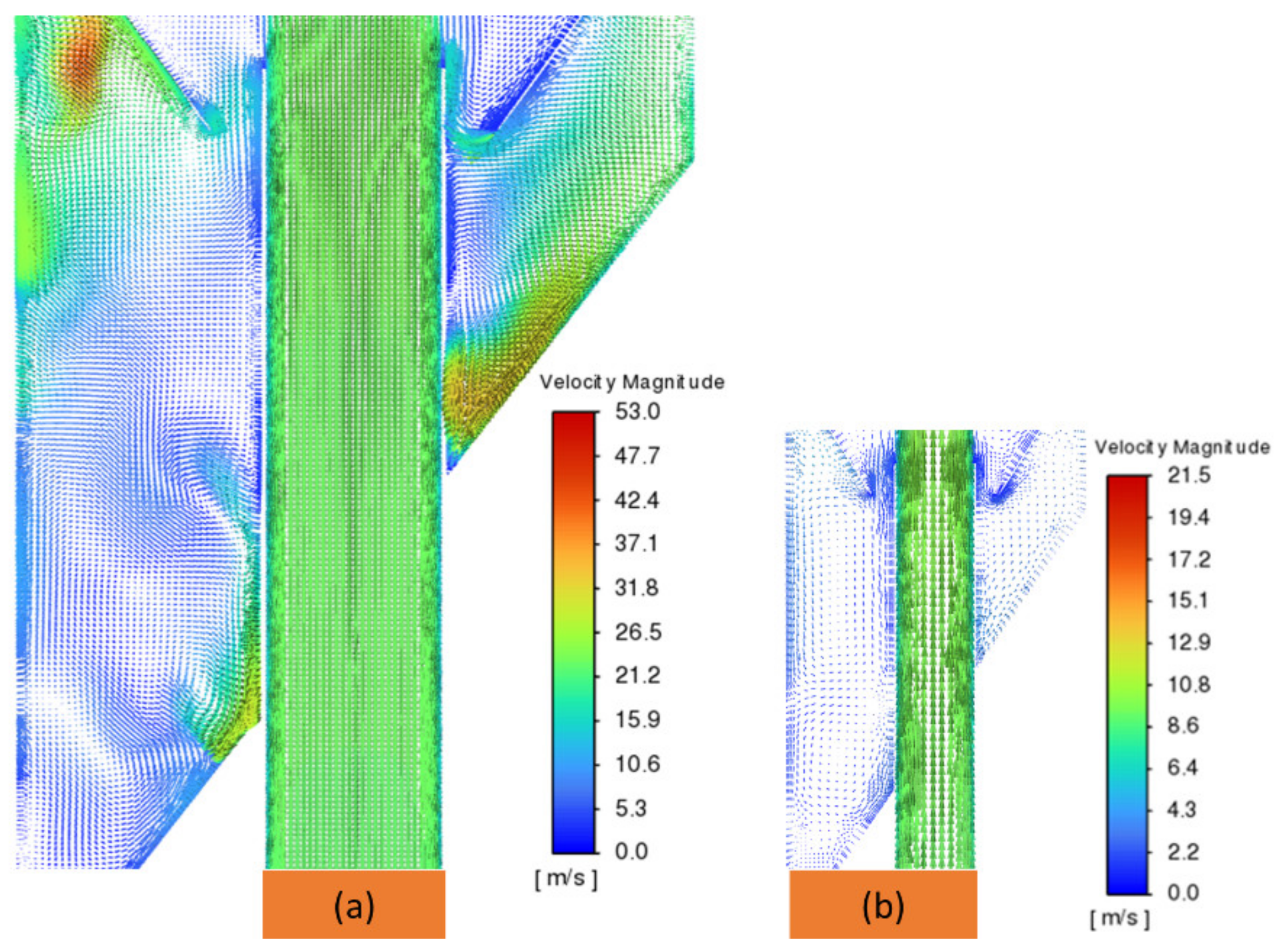
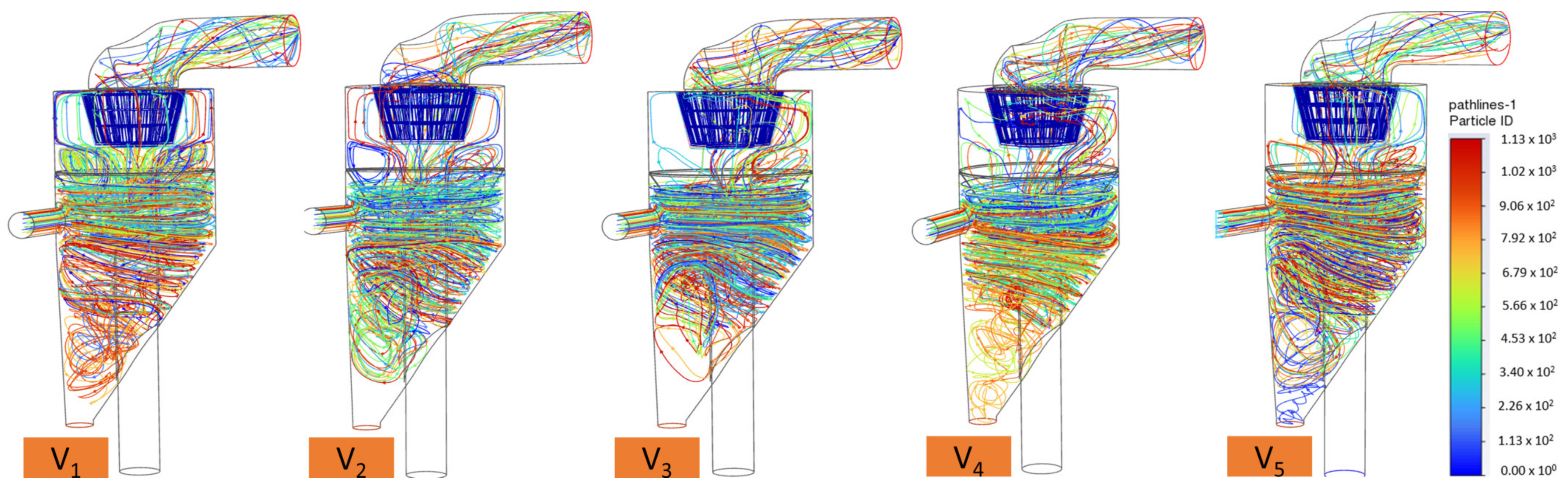
4.2.1. Influence of Outlet Mass Airflow Rate on Flow Field Within the Classifier
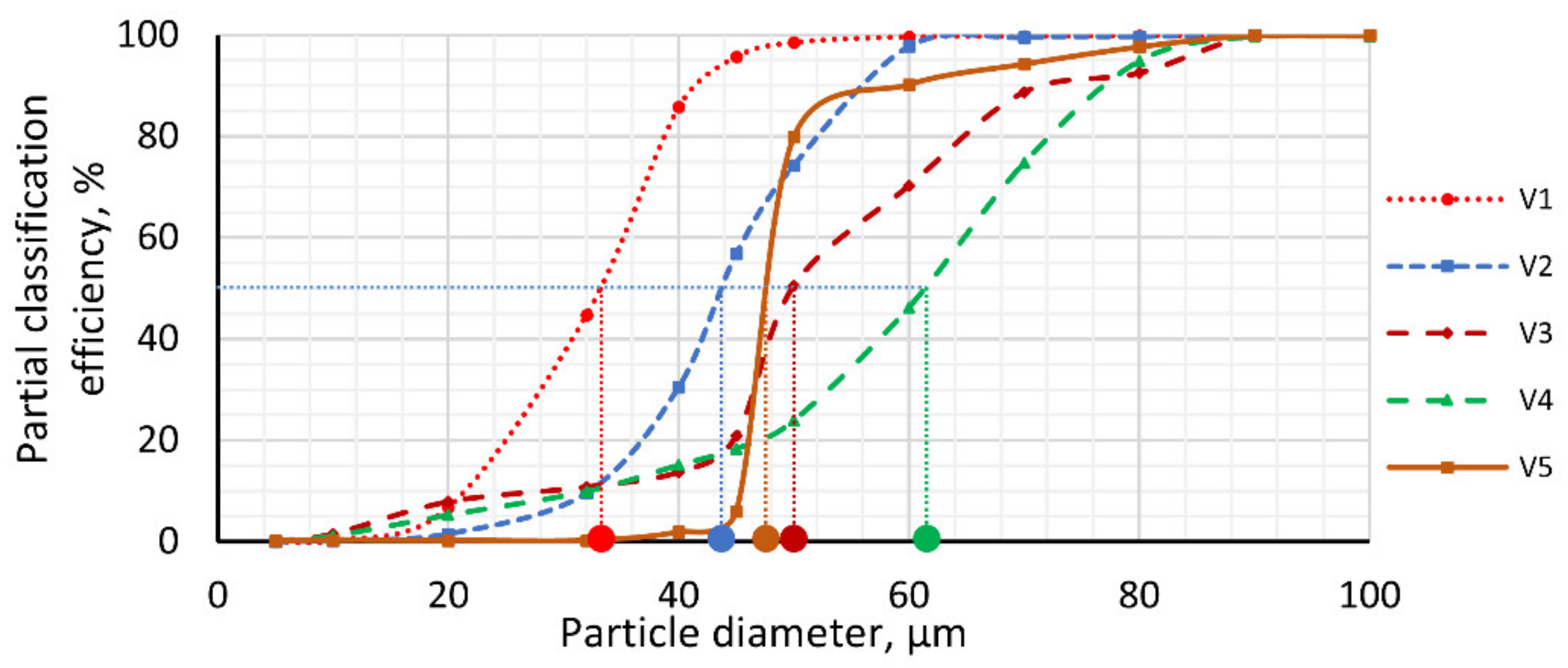
4.2.2. Influence of Outlet Mass Airflow Rate on Classification Efficiency
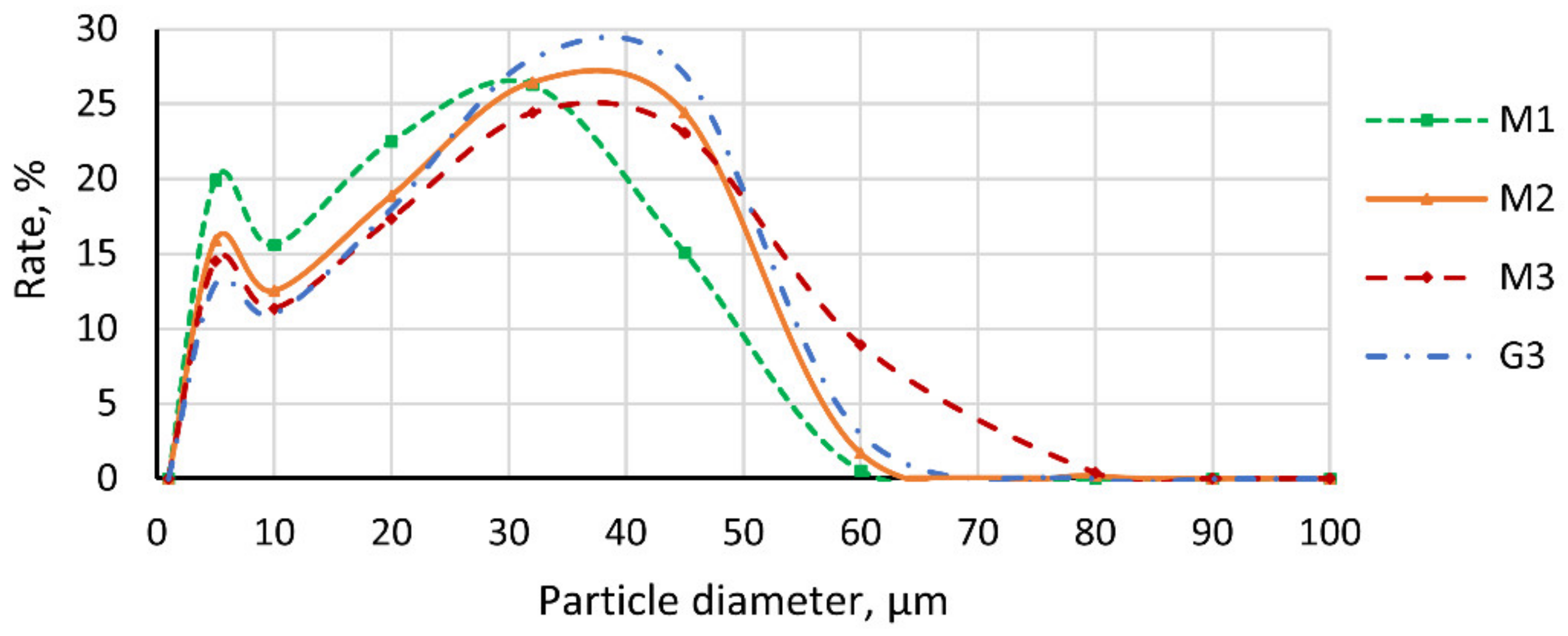
4.2.3. Influence of Outlet Mass Airflow Rate on Particle Size Distribution
4.3. Influence of Rotor Speed
4.3.1. Influence of Rotor Speed on the Flow Field Within the Classifier
4.3.2. Influence of Rotor Speed on Classification Efficiency
4.3.3. Influence of Rotor Speed on Particle Size Distribution
4.4. Influence of Secondary Inlet’s Airflow Velocity
4.4.1. Influence of Secondary Inlet’s Airflow Velocity on the Flow Field Within the Classifier
4.4.2. Influence of Secondary Inlet’s Airflow Velocity on Classification Efficiency
4.4.3. Influence of Secondary Inlet’s Airflow Velocity on Particle Size Distribution
4.5. Relationships Between Operating Parameters, Classification Performance, and Optimal Parameters
5. Experiment
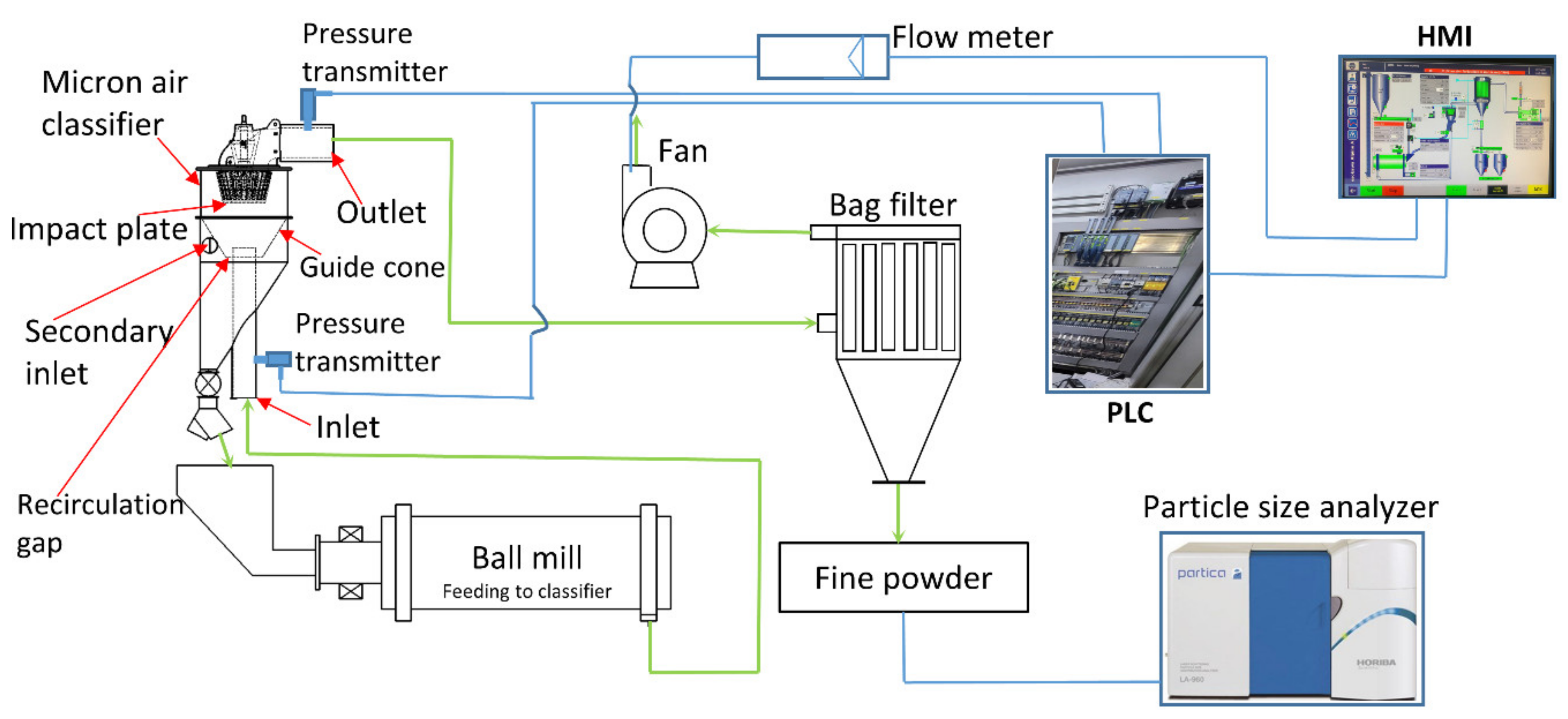
5.1. Experimental Setup
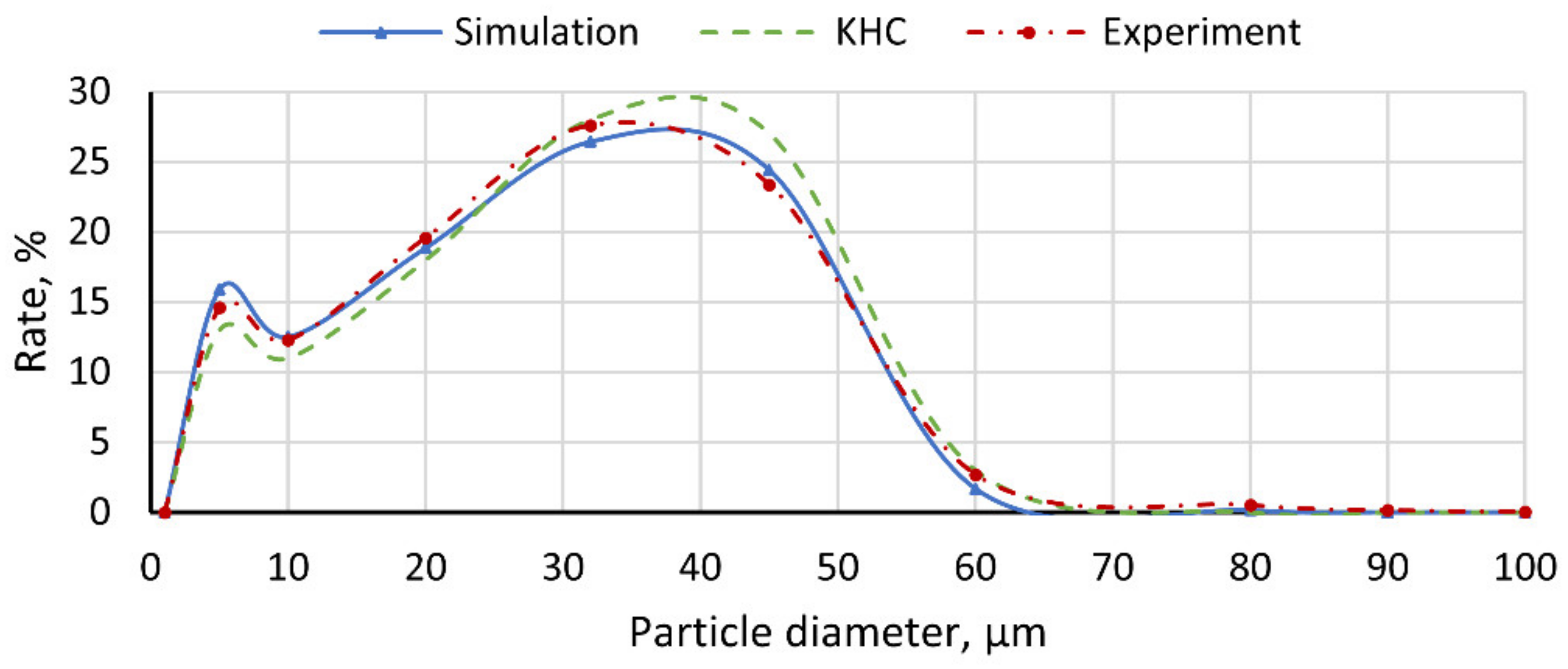
5.2. Experiment Results and Analysis
6. Conclusions
- The structure of the multiphase flow field within the industrial-scale micron gas classifier under different operating parameters was successfully identified and thoroughly analyzed. The results showed that the structure of the flow field, in terms of turbulence and the behaviors of the vortices, directly influences the classifier’s classification performance. There were significant differences in the flow field between the real-sized industrial-scale classifier and the prototype, highlighting the necessity of simulation studies on a real-size industrial-scale model for optimization purposes (as outlined in Section 4.1).
- The relationship between operating parameters and classification performance was addressed through partial optimization, and then the optimal set of operating parameters was examined and selected (as described in Section 4.5). The analysis showed that (i) an increase in the airflow rate results in higher yields for fine products; (ii) the higher the rotor speed, the higher the classification accuracy, but the lower the yields for fine products; and (iii) the higher the secondary inlet airflow velocity, the higher the Newton efficiency.
- Each operating parameter set had its own size distribution curve of particles. Each production process (of quartz-based engineering stone) may require a specific size distribution of particles, and thus one can choose a particular set to achieve the best corresponding classification performance.
- The experimental results, as measured using equipment and sensors certified by CE, showed good agreement with the simulated result, indicating the reliability of our computations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| CHL | Guide Cone |
| DPM | Discrete-Phase Model |
| HPC | High-Performance Computing |
| KHC | Know-How Curve |
| KPIs | Key Performance Indicators |
| PSDC | Particle Size Distribution Curve |
| QUICK | Quadratic Upwind Interpolation of Convective Kinematics |
| RSM | Reynolds Stress Model |
| SIMPLEC | Semi-Implicit Method for Pressure-Linked Equations Consistent |
| TWC | Two-Way Coupling |
| d50 | Cut Size |
| g | Gravitational Acceleration |
| K | Classification Sharpness Index |
| mp | Particle Mass |
| p | Pressure |
| t | Time |
| u | Average Fluid Velocity |
| u′ | Fluctuating Fluid Velocity |
| up | Particle Velocity |
| τr | Relaxation time |
| ε | Volume Fraction Locally Occupied by Fluid |
| η | Newton Classification Efficiency |
| ρ | Fluid Density |
| ρπ | Particle Density |
References
- Lagad, N.R.; Jadhav, S.M. Investigation into Effect of Rotor RPM on Degree of Separation in Air Classifier. Int. J. Sci. Res. (IJSR) 2015, 6, 539–544. [Google Scholar]
- Johansson, R. Air Classification of Fine Aggregates; Doktorsavhandlingar vid Chalmers Tekniska Högskola; Chalmers Univ. of Technology: Göteborg, Sweden, 2014; ISBN 978-91-7597-136-0. [Google Scholar]
- Ho, N.X.; Dinh, H.T.; Dau, N.T.; Nguyen, B.H. A Numerical Study on the Flow Field and Classification Performance of an Industrial-Scale Micron Air Classifier under Various Outlet Mass Airflow Rates. Processes 2024, 12, 2035. [Google Scholar] [CrossRef]
- Johansen, S.T.; Anderson, N.M.; De Silva, S.R. A two-phase model for particle local equilibrium applied to air classification of powders. Powder Technol. 1990, 63, 121–132. [Google Scholar] [CrossRef]
- Yang, Q.L.; Liu, J.X.; Zhou, Y.B. Flow Field Characteristic Analyses of a Turbo Air Classifier’s Rotor Cage and Its Structurally Improved Counterpart. AMR 2008, 58, 59–67. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, S.; Zhou, Y.; Li, M. Numerical Simulation of a Flow Field in a Turbo Air Classifier and Optimization of the Process Parameters. Processes 2020, 8, 237. [Google Scholar] [CrossRef]
- Guo, L.; Liu, J.; Liu, S.; Wang, J. Velocity Measurements and Flow Field Characteristic Analyses in a Turbo Air Classifier. Powder Technol. 2007, 178, 10–16. [Google Scholar] [CrossRef]
- Yu, Y.; Ren, W.; Liu, J. A New Volute Design Method for the Turbo Air Classifier. Powder Technol. 2019, 348, 65–69. [Google Scholar] [CrossRef]
- Sun, Z.; Sun, G.; Liu, J.; Yang, X. CFD Simulation and Optimization of the Flow Field in Horizontal Turbo Air Classifiers. Adv. Powder Technol. 2017, 28, 1474–1485. [Google Scholar] [CrossRef]
- Xia, B.; Chen, Y.; Chen, B. Numerical Simulation Analysis of Ultrafine Powder Centrifugal Classifier. In Proceedings of the 5th International Conference on Information Engineering for Mechanics and Materials, Hohhot, China, 25–26 July 2015; Atlantis Press: Paris, France, 2015; pp. 216–221. [Google Scholar]
- Denmud, N.; Baite, K.; Plookphol, T.; Janudom, S. Effects of Operating Parameters on the Cut Size of Turbo Air Classifier for Particle Size Classification of SAC305 Lead-Free Solder Powder. Processes 2019, 7, 427. [Google Scholar] [CrossRef]
- Peng, J.; Hui, C.; Zhao, Z.; Fang, Y. Research and Optimization of Operating Parameters of a Rotor Classifier for Calcined Petroleum Coke. Processes 2024, 12, 603. [Google Scholar] [CrossRef]
- Sun, Z.; Sun, G.; Yang, X.; Yuan, Y.; Wang, Q.; Liu, J. Effects of Fine Particle Outlet on Performance and Flow Field of a Centrifugal Air Classifier. Chem. Eng. Res. Des. 2017, 117, 139–148. [Google Scholar] [CrossRef]
- Braun, R.M.; Kolacz, J.; Hoyer, D.I. Fine Dry Comminution of Calcium Carbonate in a Hicom Mill with an Inprosys Air Classifier. Miner. Eng. 2002, 15, 123–129. [Google Scholar] [CrossRef]
- Zeng, C.; Liu, C.H.; Chen, H.Y.; Zhang, M.; Fu, Y.; Wang, X. Effects of secondary air on the classification performances of LNJ-36A air classifier. Chem. Ind. Eng. Prog. 2015, 11, 3859–3863. [Google Scholar] [CrossRef]
- Zhao, Z.; Hui, C.; Peng, J.; Fang, Y. Influence of Secondary Air on the Flow Field of NGZF Classifier. Therm. Sci. 2024, 28, 4637–4653. [Google Scholar] [CrossRef]
- Jia, F.; Mou, X.; Fang, Y.; Chen, C. A new rotor-type dynamic classifier: Structural optimization and industrial applications. Processes 2021, 9, 1033. [Google Scholar] [CrossRef]
- Li, Q.; Mou, X.; Fang, Y. Effects of a Guide Cone on the Flow Field and Performance of a New Dynamic Air Classifier. Processes 2022, 10, 874. [Google Scholar] [CrossRef]
- Kesseler, M.; Heller, V.; Turnbull, B. A Laboratory-Numerical Approach for Modelling Scale Effects in Dry Granular Slides. Landslides 2018, 15, 2145–2159. [Google Scholar] [CrossRef]
- Ahmad, T.; Plee, S.L.; Myers, J.P. Fluent Theory Guide; ANSYS: Canonsburg, PA, USA, 2021. [Google Scholar]
- Büttner, H. Dimensionless Representation of Particle Separation Characteristic of Cyclones. J. Aerosol Sci. 1999, 30, 1291–1302. [Google Scholar] [CrossRef]
- Frank, M.W. Fluid Mechanics, 7th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Pant, K.; Crowe, C.T.; Irving, P. On the Design of Miniature Cyclones for the Collection of Bioaerosols. Powder Technol. 2002, 125, 260–265. [Google Scholar] [CrossRef]
- Galletti, C.; Rum, A.; Turchi, V.; Nicolella, C. Numerical Analysis of Flow Field and Particle Motion in a Dynamic Cyclonic Selector. Adv. Powder Technol. 2020, 31, 1264–1273. [Google Scholar] [CrossRef]








| dp [µm] | Percentage [%] | dp [µm] | Percentage [%] |
|---|---|---|---|
| 5 | 12.8 | 60 | 4.6 |
| 10 | 10.1 | 70 | 1.9 |
| 20 | 15.2 | 80 | 1.1 |
| 32 | 21.3 | 90 | 0.6 |
| 40 | 15.4 | 100 | 0.4 |
| 45 | 4.8 | 300 | 5.8 |
| 50 | 4.5 | 600 | 1.5 |
| Boundary Name | Value | Unit |
|---|---|---|
| Outlet mass airflow rate | 5.104; 5.615; 6.125 | kg/s |
| Secondary air inlet | fresh air; open 50% | m/s |
| Rotor speed | 290 | rpm |
| Feed flow rate | 2.44 | kg/s |
| Boundary Name | Value | Unit |
|---|---|---|
| Outlet mass airflow rate | 5.615 | kg/s |
| Secondary air inlet | fresh air; open 50% | m/s |
| Rotor speed | 290; 310; 330 | rpm |
| Feed flow rate | 2.44 | kg/s |
| Boundary Name | Value | Unit |
|---|---|---|
| Outlet mass airflow rate | 5.615 | kg/s |
| Secondary air inlet | 14; 22; 29; 36; fresh air (open 50%); | m/s |
| Rotor speed | 290 | rpm |
| Feed flow rate | 2.44 | kg/s |
| Parameters | Simulation Result | Experiment | Deviation |
|---|---|---|---|
| Productivity (kg/h) | 7059 | 6480 | 8.2% |
| Pressure drop (Pa) | 2027 | 2200 | 8.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, N.X.; Dinh, H.T.; Dau, N.T. Numerical Study to Optimize the Operating Parameters of a Real-Sized Industrial-Scale Micron Air Classifier Used for Manufacturing Fine Quartz Powder and a Comparison with the Prototype Model. Processes 2025, 13, 106. https://doi.org/10.3390/pr13010106
Ho NX, Dinh HT, Dau NT. Numerical Study to Optimize the Operating Parameters of a Real-Sized Industrial-Scale Micron Air Classifier Used for Manufacturing Fine Quartz Powder and a Comparison with the Prototype Model. Processes. 2025; 13(1):106. https://doi.org/10.3390/pr13010106
Chicago/Turabian StyleHo, Nang Xuan, Hoi Thi Dinh, and Nhu The Dau. 2025. "Numerical Study to Optimize the Operating Parameters of a Real-Sized Industrial-Scale Micron Air Classifier Used for Manufacturing Fine Quartz Powder and a Comparison with the Prototype Model" Processes 13, no. 1: 106. https://doi.org/10.3390/pr13010106
APA StyleHo, N. X., Dinh, H. T., & Dau, N. T. (2025). Numerical Study to Optimize the Operating Parameters of a Real-Sized Industrial-Scale Micron Air Classifier Used for Manufacturing Fine Quartz Powder and a Comparison with the Prototype Model. Processes, 13(1), 106. https://doi.org/10.3390/pr13010106






