Low-Carbon Transformation of Polysilicon Park Energy Systems: Optimal Economic Strategy with TD3 Reinforcement Learning
Abstract
:1. Introduction
2. Dynamic Efficiency Model for Electrolyzer
2.1. Actual Engineering Model
2.2. Surrogate Model
2.3. Result Analysis
2.3.1. Actual Engineering Model Analysis
2.3.2. Surrogate Model Algorithm Comparison
3. Low-Carbon Economic Optimal Scheduling Model Based on TD3
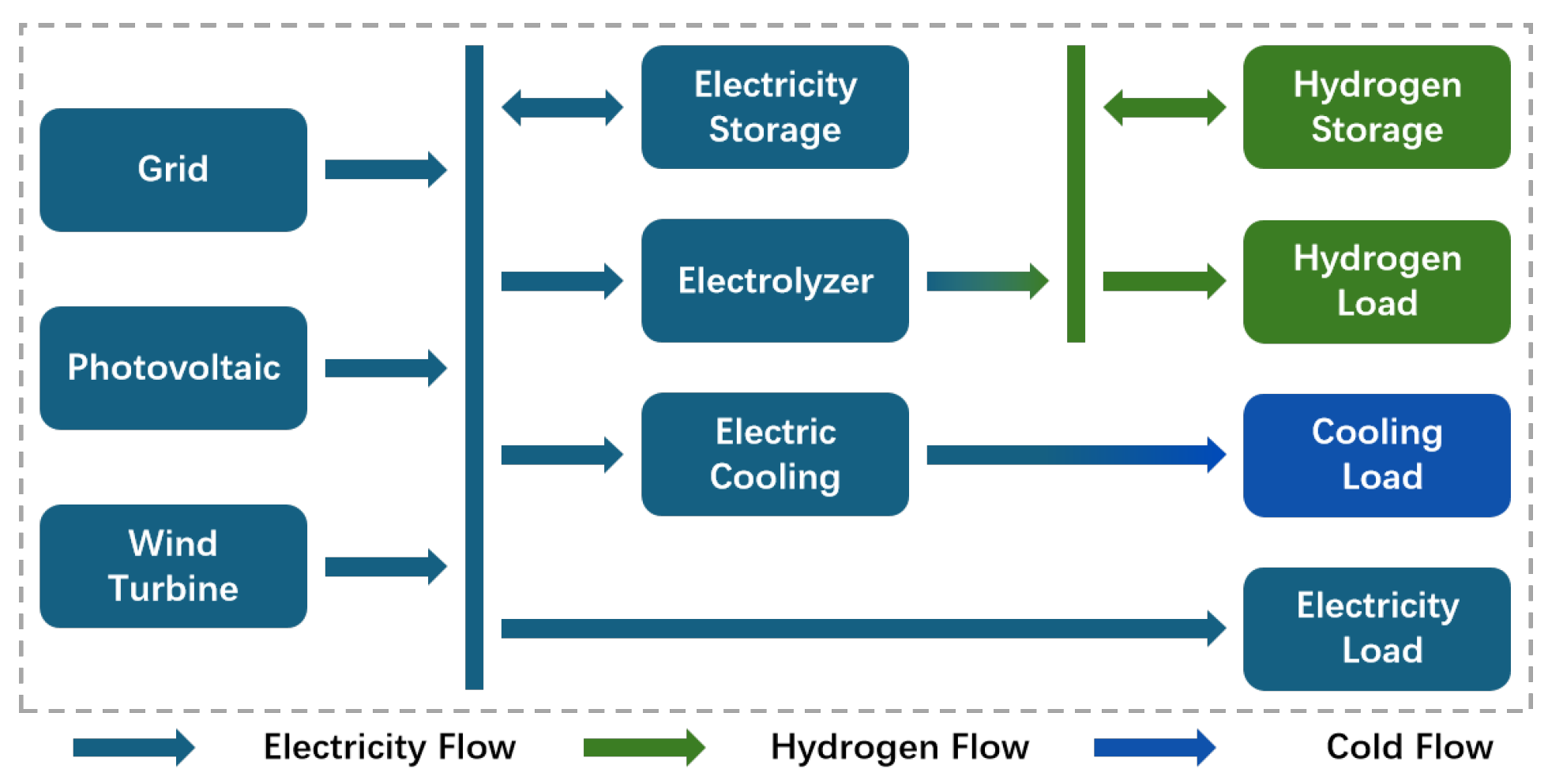
3.1. System Composition
3.2. Objective Function
3.3. Constraints
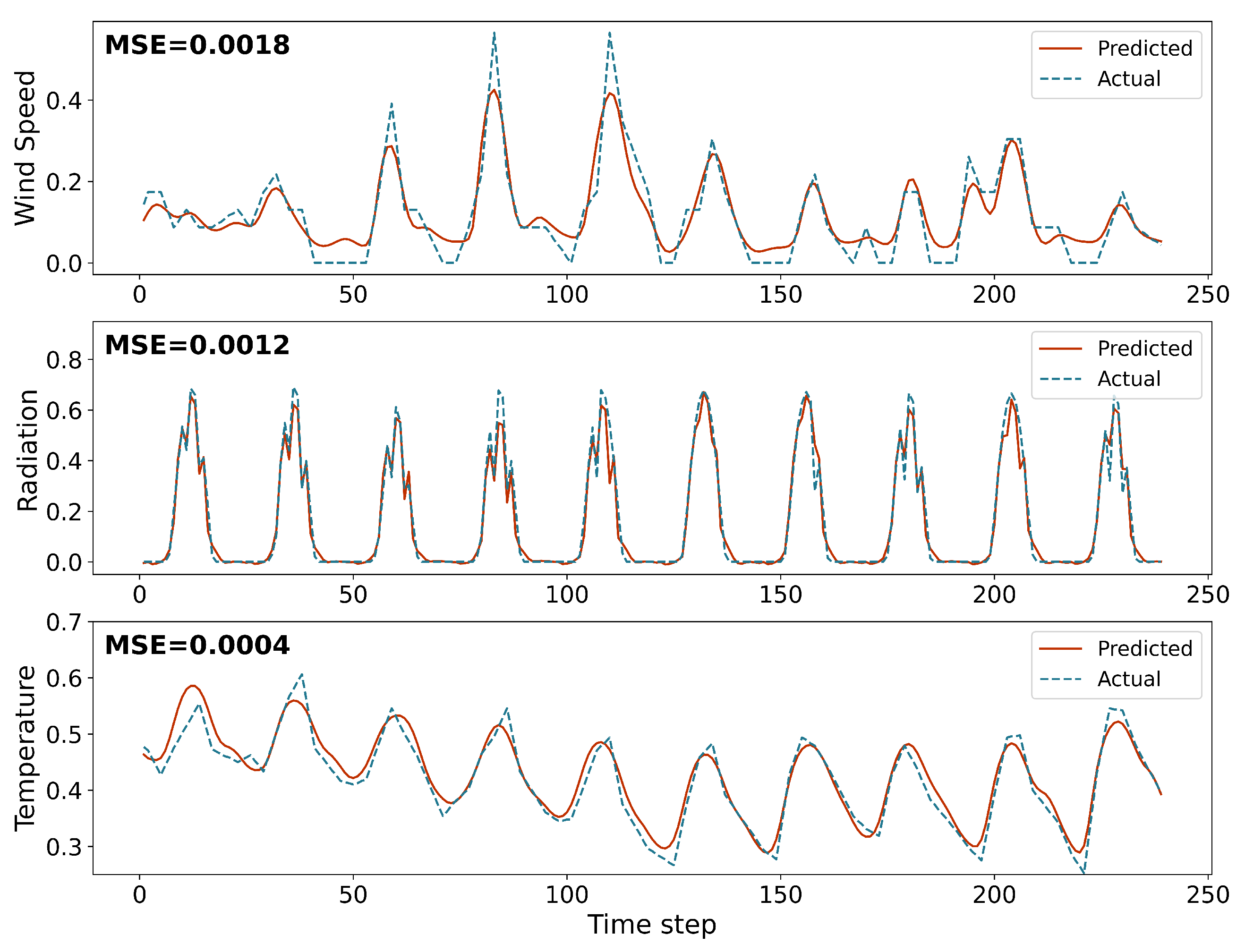
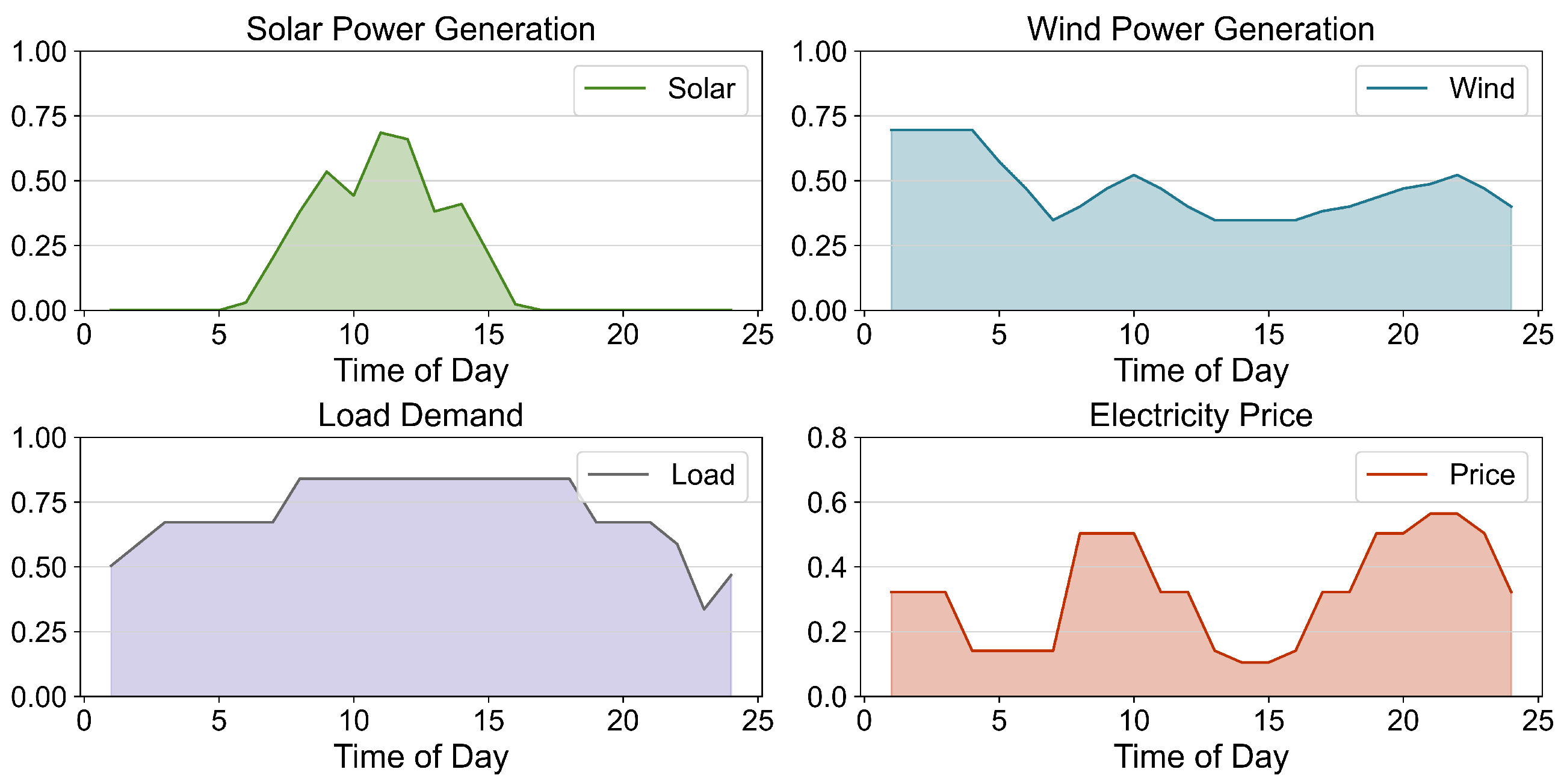
3.3.1. Photovoltaic Power Model
3.3.2. Wind Turbine Model
3.3.3. Energy Storage Model
3.3.4. Electric Chiller Model
3.3.5. Energy Balance
3.4. Theoretical Foundations of the TD3 Algorithm
- Network Structure Optimization: Truncated Double Q-Learning: TD3 employs two separate value estimation networks and target value networks, learning simultaneously by minimizing the mean squared error, as illustrated in Equation (26):where is the discount factor.
- Parameter Update Optimization: Target Policy Smoothing: TD3 incorporates truncated normal distribution noise into the target action, estimating the target Q-value using actions in the vicinity of the target policy, thereby smoothing the Q-value variation across different actions, as illustrated in Equation (27):where is the target policy, is the noise, and clip is the clipping function.
- Network Update Optimization: Delayed Policy Updates: The policy network updates less frequently than the value networks to ensure that the policy network stabilizes before reducing the estimation error of the value networks, typically updating the policy network once for every two updates of the value networks. The update formula and policy gradient are given by Equations (28) and (29):where is the learning rate for the policy network, is the policy gradient, and is the gradient of the policy with respect to the policy parameters.
3.5. Applying the TD3 Algorithm for Model Optimization
4. Results and Discussion
4.1. Parameter Settings
4.2. Convergence Analysis
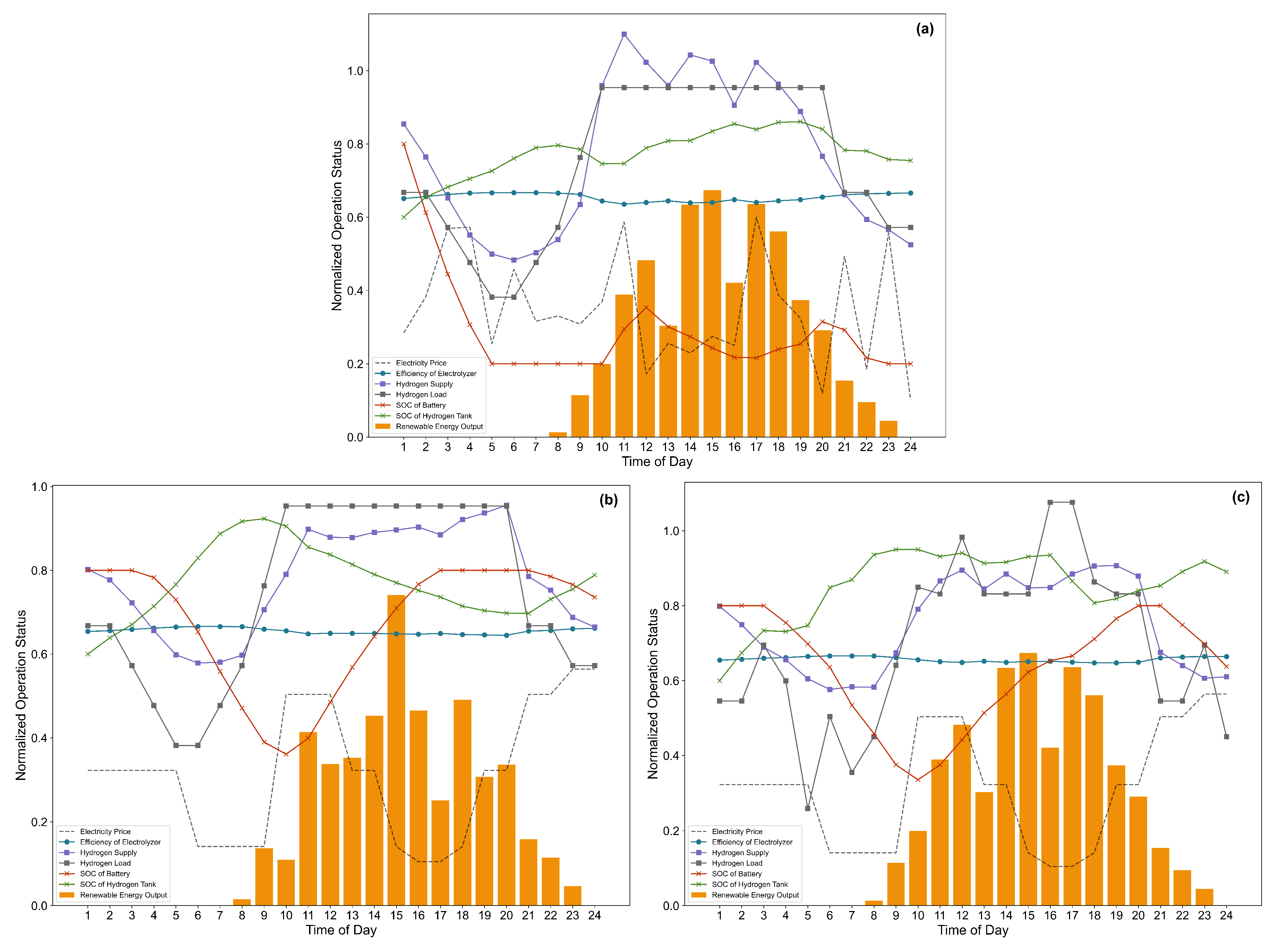
4.3. Cases Analysis
Analysis of Operational Strategies
4.4. Cost Analysis
4.5. Sensitivity Assessment
4.6. Comprehensive Benefits Analysis of Low-Carbon Transformation
4.7. Different Algorithm Contrast
5. Conclusions
- Equipment coupling and efficiency improvement: in this study, a dynamic physical model of electrolyzer with variable operating conditions is constructed and combined with the XGBoost agent model, which effectively improves the flexibility of system operation and energy utilization efficiency. The results of the study show that the total system cost decreases by about 0.027% after the introduction of the variable operating condition model. The energy storage device effectively reduces the cost of purchased electricity and improves the adaptability of the system to fluctuations in electricity prices. The synergy between the hydrogen storage device and the electrolyzer significantly improves the energy utilization efficiency, and the hydrogen storage device maintains the stability of its efficiency by smoothing the electrolyzer output.
- Performance advantages and disadvantages of the TD3 algorithm: the TD3 algorithm shows high efficiency and stability in this system. Compared with the DDPG and DQN algorithms, the TD3 algorithm reduces the average daily operation cost by about 0.6% and 1.2%, and the carbon emission cost by about 2.0% and 12.0%, respectively. Through the comparative analysis of five different operation scenarios and three environmental fluctuation cases, the adaptability of the TD3 algorithm in different environments and operation conditions is verified, showing strong robustness and generalization ability. However, at the same time, the convergence path of the model shows that it has problems such as many hyperparameters and hyperparameter sensitivity, which brings certain obstacles to the tuning in practical application.
- Evaluation of the low-carbon economy effect: the new energy transformation on the power supply side significantly reduces the carbon emission of the polysilicon reduction process, achieving a carbon reduction effect of 29.3%, but the high operating cost of renewable energy devices, especially solar cells, still makes the system less economical than direct power purchase. Optimizing the operation of the coupled part of electrolyzer and hydrogen storage tank is the most likely part of the system to achieve industrial applications, considering various dimensions, such as economy, energy saving and efficiency improvement, and equipment modification.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Zhao, X.; Huang, Y. Low-Carbon-Oriented Capacity Optimization Method for Electric–Thermal Integrated Energy System Considering Construction Time Sequence and Uncertainty. Processes 2024, 12, 648. [Google Scholar] [CrossRef]
- Yang, J.; Xie, L.; Song, X.; Ye, H.; Zhang, P.; Bian, Y. Optimal Configuration of PV-Fire-Hydrogen Polysilicon 787 Park Based on Multivariate Copula Function. Acta Energiae Solaris Sinica. Acta Energiae Solaris Sin. 2023, 44, 180–188. [Google Scholar] [CrossRef]
- Ramírez-Márquez, C.; Martín-Hernández, E.; Martín, M.; Segovia-Hernández, J.G. Surrogate based optimization of a process of polycrystalline silicon production. Comput. Chem. Eng. 2020, 140, 106870. [Google Scholar] [CrossRef]
- Saravanan, S.; Mahadevan, M.; Suratkar, P.; Gijo, E.V. Efficiency improvement on the multicrystalline silicon wafer through six sigma methodology. Int. J. Sustain. Energy 2012, 31, 143–153. [Google Scholar] [CrossRef]
- Mohammed, A.; Ghaithan, A.M.; Al-Hanbali, A.; Attia, A.M. A multi-objective optimization model based on mixed integer linear programming for sizing a hybrid PV-hydrogen storage system. Int. J. Hydrogen Energy 2023, 48, 9748–9761. [Google Scholar] [CrossRef]
- Ruiming, F. Multi-objective optimized operation of integrated energy system with hydrogen storage. Int. J. Hydrogen Energy 2019, 44, 29409–29417. [Google Scholar] [CrossRef]
- Hong, Z.; Wei, Z.; Han, X. Optimization scheduling control strategy of wind-hydrogen system considering hydrogen production efficiency. J. Energy Storage 2022, 47, 103609. [Google Scholar] [CrossRef]
- Kafetzis, A.; Ziogou, C.; Panopoulos, K.; Papadopoulou, S.; Seferlis, P.; Voutetakis, S. Energy management strategies based on hybrid automata for islanded microgrids with renewable sources, batteries and hydrogen. Renew. Sustain. Energy Rev. 2020, 134, 110118. [Google Scholar] [CrossRef]
- Pu, Y.; Li, Q.; Zou, X.; Li, R.; Li, L.; Chen, W.; Liu, H. Optimal sizing for an integrated energy system considering degradation and seasonal hydrogen storage. Appl. Energy 2021, 302, 117542. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, H.; He, Y.; Xu, B.; Zhang, M.; Ding, M. Optimal Scheduling Method for Integrated Energy Systems with Hydrogen Based on Deep Reinforcement Learning. Autom. Electr. Power Syst. 2024, 48, 132–141. [Google Scholar] [CrossRef]
- Perera, A.; Kamalaruban, P. Applications of reinforcement learning in energy systems. Renew. Sustain. Energy Rev. 2021, 137, 110618. [Google Scholar] [CrossRef]
- Shi, T.; Xu, C.; Dong, W.; Zhou, H.; Bokhari, A.; Klemeš, J.J.; Han, N. Research on energy management of hydrogen electric coupling system based on deep reinforcement learning. Energy 2023, 282, 128174. [Google Scholar] [CrossRef]
- Zhang, Z.; Qiu, C.; Zhang, D.; Xu, S.; He, X. A Coordinated Control Method for Hybrid Energy Storage System in Microgrid Based on Deep Reinforcement Learning. Power Syst. Technol. 2019, 43, 1914–1921. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Wang, X.; Zeng, J.; Huang, Q. Energy Management and Optimization of Multi-Energy Grid Based on Deep Reinforcement Learning. Power Syst. Technol. 2020, 44, 3794–3803. [Google Scholar] [CrossRef]
- Huang, W.; Li, Q.; Jiang, Y.; Lu, X. Parametric Dueling DQN- and DDPG-Based Approach for Optimal Operation of Microgrids. Processes 2024, 12, 1822. [Google Scholar] [CrossRef]
- Xu, B.; Xiang, Y. Optimal operation of regional integrated energy system based on multi-agent deep deterministic policy gradient algorithm. Energy Rep. 2022, 8, 932–939. [Google Scholar] [CrossRef]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Hou, S.; Salazar, E.M.; Vergara, P.P.; Palensky, P. Performance Comparison of Deep RL Algorithms for Energy Systems Optimal Scheduling. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Novi Sad, Serbia, 10–12 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Deng, J.; Jiang, F.; Wang, W.; He, G.; Zhang, X.; Liu, K. Low-carbon Optimized Operation of Integrated Energy System Considering Electric-Heat Flexible Load and Hydrogen Energy Refined Modeling. Power Syst. Technol. 2022, 46, 1692–1704. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, H.; Cao, F.; Cao, Y.; Liu, Q.; Tang, C.; Zhou, T. Study on the influence characteristics of multi-working condition parameters on membrane electrode type CO2 electrolyzer. Int. J. Electrochem. Sci. 2024, 19, 100870. [Google Scholar] [CrossRef]
- Ma, B.; Zheng, J.; Xian, Z.; Wang, B.; Ma, H. Optimal Operation Strategy for Wind–Photovoltaic Power-Based Hydrogen Production Systems Considering Electrolyzer Start-Up Characteristics. Processes 2024, 12, 1756. [Google Scholar] [CrossRef]
- Klyuev, R.; Madaeva, M.; Umarova, M. Mathematical Modeling of Specific Power Consumption of Electrolyzers. In Proceedings of the 2020 International Ural Conference on Electrical Power Engineering (UralCon), Chelyabinsk, Russia, 22–24 September 2020; pp. 356–361. [Google Scholar] [CrossRef]
- Wei, X.; Sharma, S.; Waeber, A.; Wen, D.; Sampathkumar, S.N.; Margni, M.; Maréchal, F.; Van Herle, J. Comparative life cycle analysis of electrolyzer technologies for hydrogen production: Manufacturing and operations. Joule 2024, 8, 3347–3372. [Google Scholar] [CrossRef]
- Scheepers, F.; Stähler, M.; Stähler, A.; Rauls, E.; Müller, M.; Carmo, M.; Lehnert, W. Improving the Efficiency of PEM Electrolyzers through Membrane-Specific Pressure Optimization. Energies 2020, 13, 612. [Google Scholar] [CrossRef]
- Scheepers, F.; Stähler, M.; Stähler, A.; Rauls, E.; Müller, M.; Carmo, M.; Lehnert, W. Temperature optimization for improving polymer electrolyte membrane-water electrolysis system efficiency. Appl. Energy 2021, 283, 116270. [Google Scholar] [CrossRef]
- Durisch, W.; Bitnar, B.; Mayor, J.C.; Kiess, H.; Lam, K.h.; Close, J. Efficiency model for photovoltaic modules and demonstration of its application to energy yield estimation. Sol. Energy Mater. Sol. Cells 2007, 91, 79–84. [Google Scholar] [CrossRef]
- Emrani, A.; Achour, Y.; Sanjari, M.J.; Berrada, A. Adaptive energy management strategy for optimal integration of wind/PV system with hybrid gravity/battery energy storage using forecast models. J. Energy Storage 2024, 96, 112613. [Google Scholar] [CrossRef]
- Elaouzy, Y.; El Fadar, A.; Achkari, O. Assessing the 3E performance of multiple energy supply scenarios based on photovoltaic, wind turbine, battery and hydrogen systems. J. Energy Storage 2024, 99, 113378. [Google Scholar] [CrossRef]

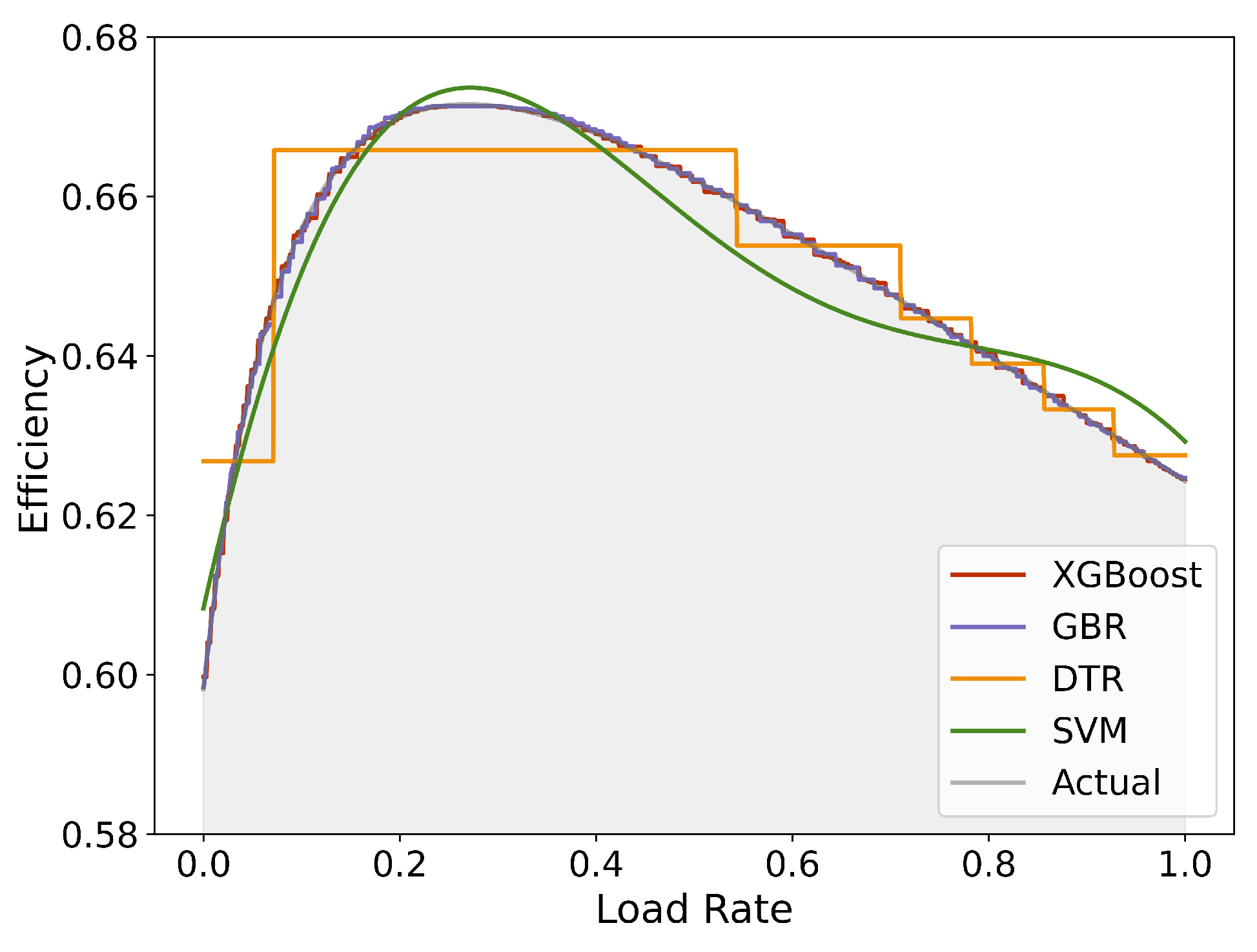



| Model | XGBoost | GBR | DTR | SVM |
|---|---|---|---|---|
| MSE | 6.27 × 10−7 | 8.388 × 10−7 | 7.46 × 10−5 | 5.10 × 10−5 |
| 0.999 | 0.998 | 0.824 | 0.880 |
| Equipment | Rated Power (MW) | Purchase Cost (CNY/kW) | Maintenance Cost (CNY/kW) | Expected Life (Years) | Mathematical Model Parameters |
|---|---|---|---|---|---|
| Wind Turbine | 160 | 8654 | 80 | 20 | , , |
| Photovoltaic | 240 | 2172 | 21 | 15 | , , , |
| Electrolyzer | 6 × 2 | 10738 | 375 | 15 | |
| Electric Cooling | 11 | 970 | 19 | 20 | , , , |
| Battery | 35 | 869 | 22 | 15 | , |
| Hydrogen Tank | 30 | 1256 | 18 | 20 | , |
| Scenario | Power Purchase Cost | Emission Cost | Operation and Maintenance Cost | Total Cost | Reward Value |
|---|---|---|---|---|---|
| Basic Model | 1,584,499.74 | 295,927.92 | 505,999.35 | 2,386,427.0 | −22.03 |
| Modified Reward Function | 1,587,993.84 | 295,941.43 | 501,338.00 | 2,385,273.3 | −21.84 |
| Modified Hydrogen Storage Capacity | 1,583,686.27 | 295,402.55 | 507,575.39 | 2,386,664.2 | −26.42 |
| Fixed Working Conditions | 1,579,777.19 | 295,189.11 | 512,174.31 | 2,387,140.6 | −32.75 |
| Scenario | Hydrogen Unsatisfaction Rate | Efficiency Average Value | Efficiency Range | Efficiency Variance |
|---|---|---|---|---|
| Electricity Price Fluctuation | 0 | 0.654 | 0.032 | 0.108 |
| Renewable Output Fluctuation | 0 | 0.655 | 0.021 | 0.007 |
| Demand Fluctuation | 0 | 0.657 | 0.018 | 0.007 |
| Algorithm | Emission Cost | Operation Cost | Total Cost | Reward Value |
|---|---|---|---|---|
| TD3 | 295,927.92 | 501,338 | 797,265.92 | −22.03 |
| DDPG | 307,173.18 | 504,362.15 | 811,535.33 | −28.08 |
| DQN | 321,377.72 | 507,153.67 | 828,531.39 | −43.12 |
| CPLEX | 291,489.00 | 500,221.39 | 791,710.39 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Zhao, C.; Wu, J.; Bian, H.; Liu, Y.; Li, M. Low-Carbon Transformation of Polysilicon Park Energy Systems: Optimal Economic Strategy with TD3 Reinforcement Learning. Processes 2025, 13, 268. https://doi.org/10.3390/pr13010268
Hu S, Zhao C, Wu J, Bian H, Liu Y, Li M. Low-Carbon Transformation of Polysilicon Park Energy Systems: Optimal Economic Strategy with TD3 Reinforcement Learning. Processes. 2025; 13(1):268. https://doi.org/10.3390/pr13010268
Chicago/Turabian StyleHu, Shurui, Chengwenxuan Zhao, Jialu Wu, Haiyang Bian, Yongkai Liu, and Mingtao Li. 2025. "Low-Carbon Transformation of Polysilicon Park Energy Systems: Optimal Economic Strategy with TD3 Reinforcement Learning" Processes 13, no. 1: 268. https://doi.org/10.3390/pr13010268
APA StyleHu, S., Zhao, C., Wu, J., Bian, H., Liu, Y., & Li, M. (2025). Low-Carbon Transformation of Polysilicon Park Energy Systems: Optimal Economic Strategy with TD3 Reinforcement Learning. Processes, 13(1), 268. https://doi.org/10.3390/pr13010268







