Adsorption Pore Volume Distribution Heterogeneity of Middle and High Rank Coal Reservoirs and Determination of Its Influencing Factors
Abstract
:1. Introduction
2. Experimental Methods and Related Theories
2.1. Geological Setting
2.2. Sample Preparation and Experimental Test
2.3. Fractal Theory
3. Results and Discussion
3.1. Microscopic Composition and Industrial Analysis
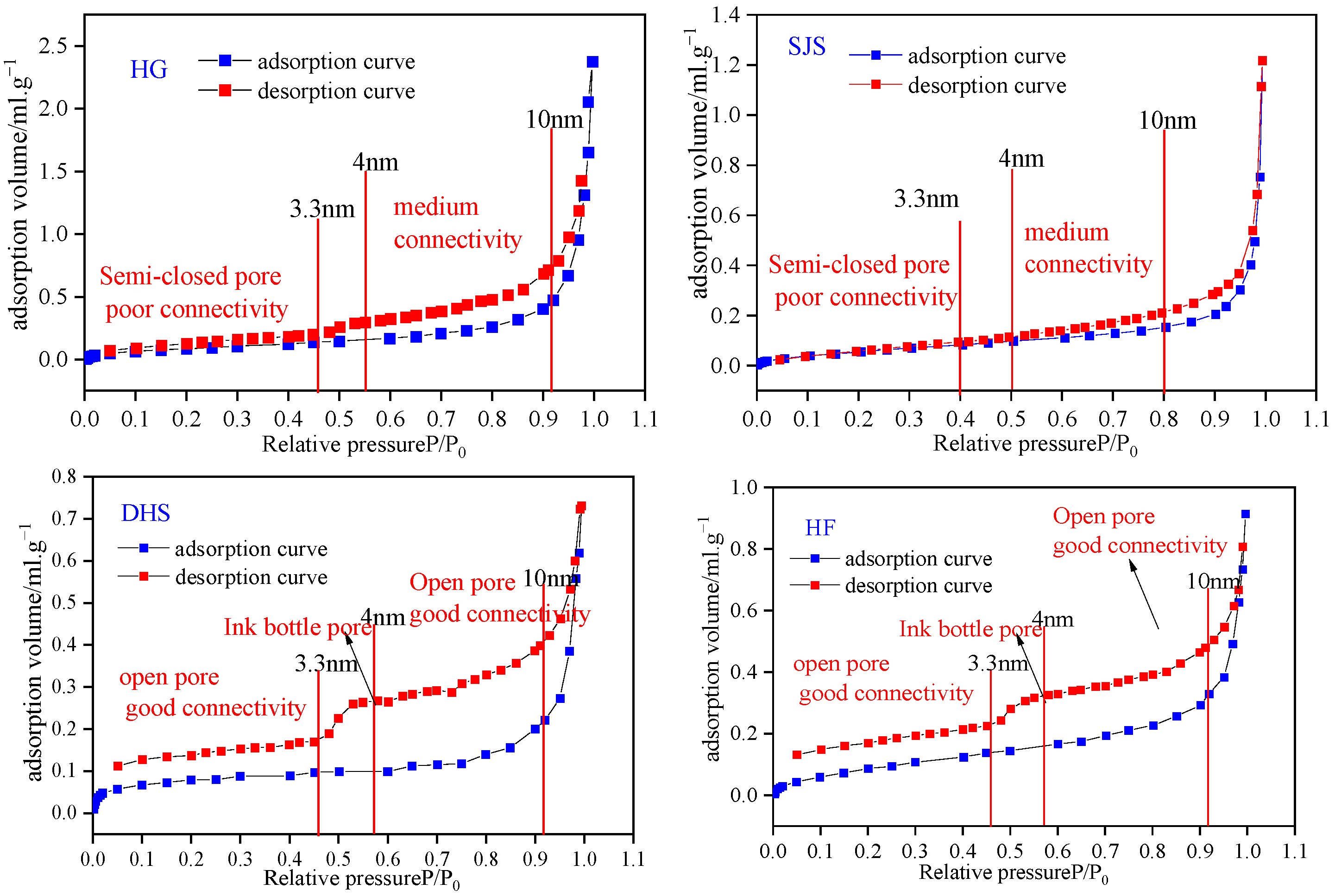
3.2. Pore Types and Connectivity of Adsorption Pores
3.3. Adsorption Pore Volume Distribution
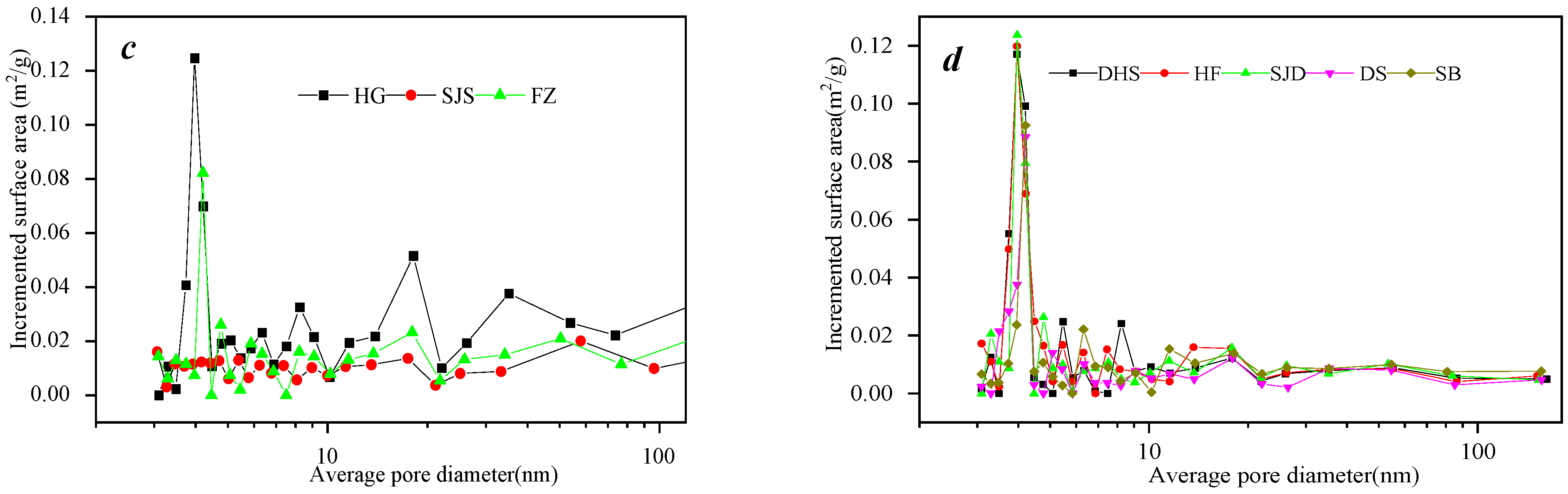
3.3.1. Pore Volume Distribution of 2~100 nm by Using LPN2 GA Tests
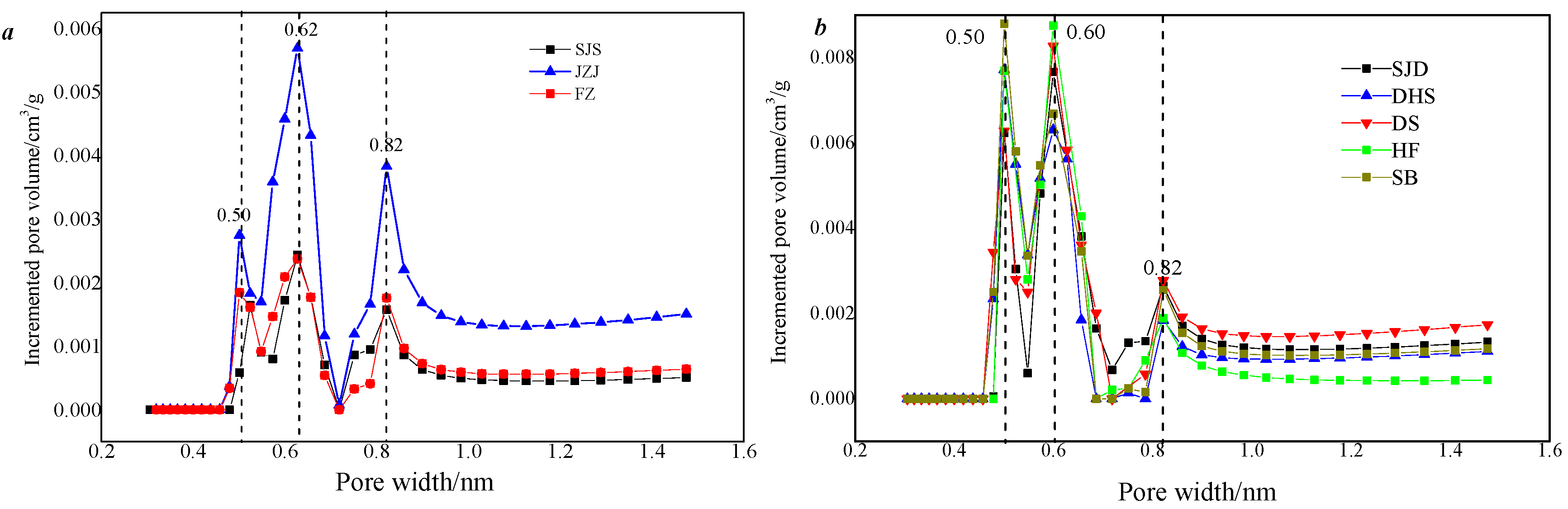
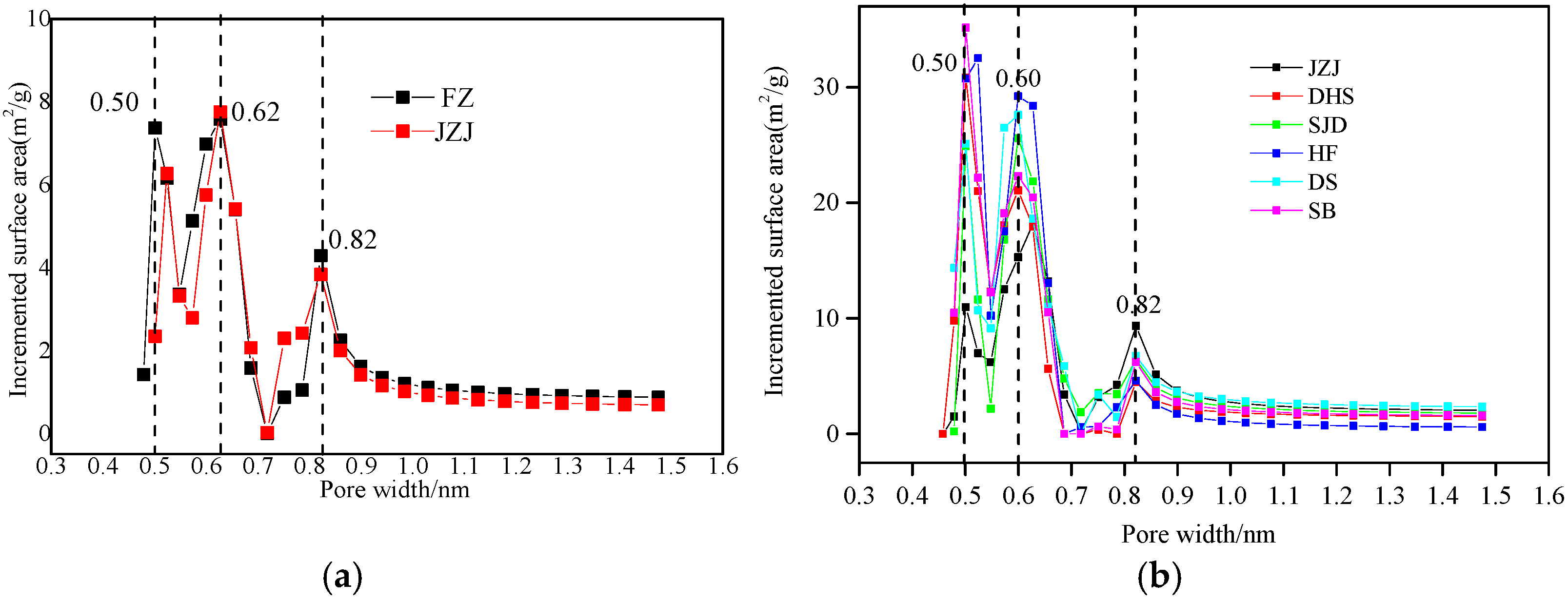
3.3.2. Micropore Distribution Characteristics Based on LPCO2 GA Test
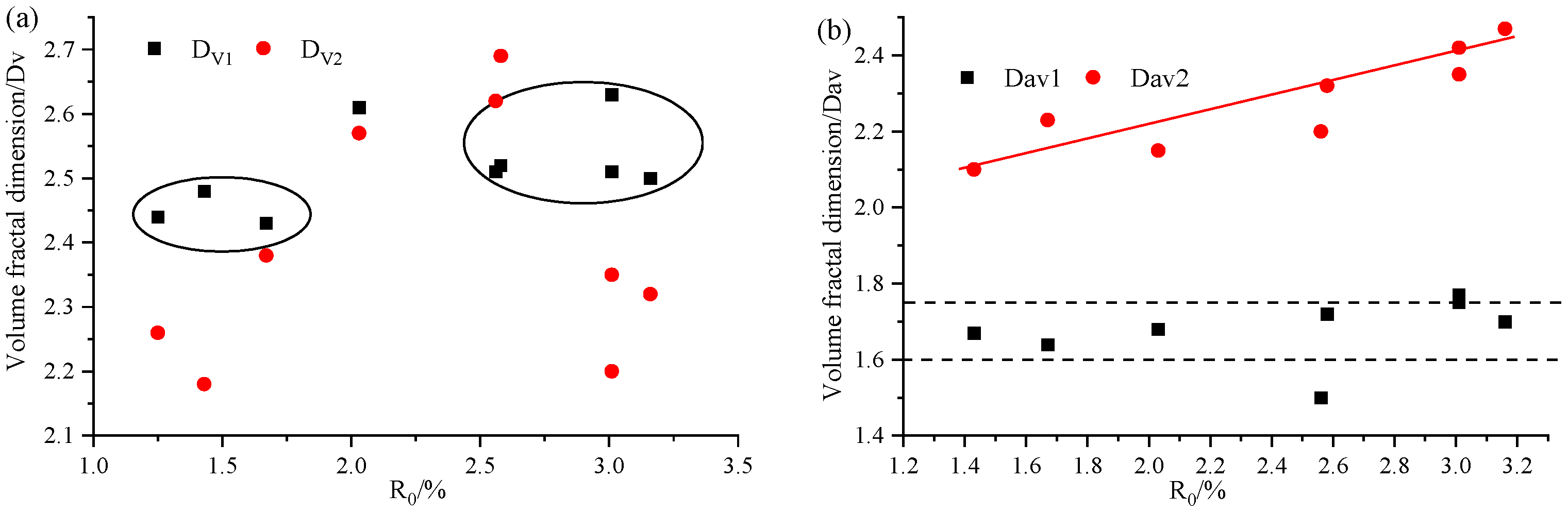
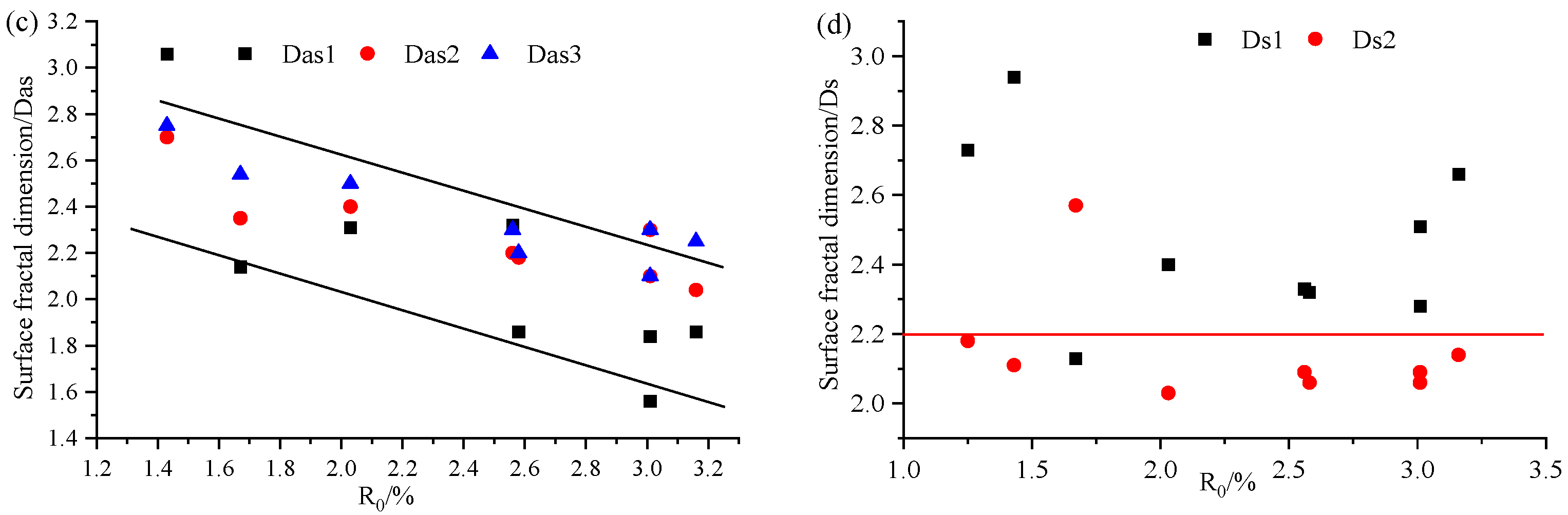
3.4. Pore Volume Distribution Heterogeneity of Adsorption Pore
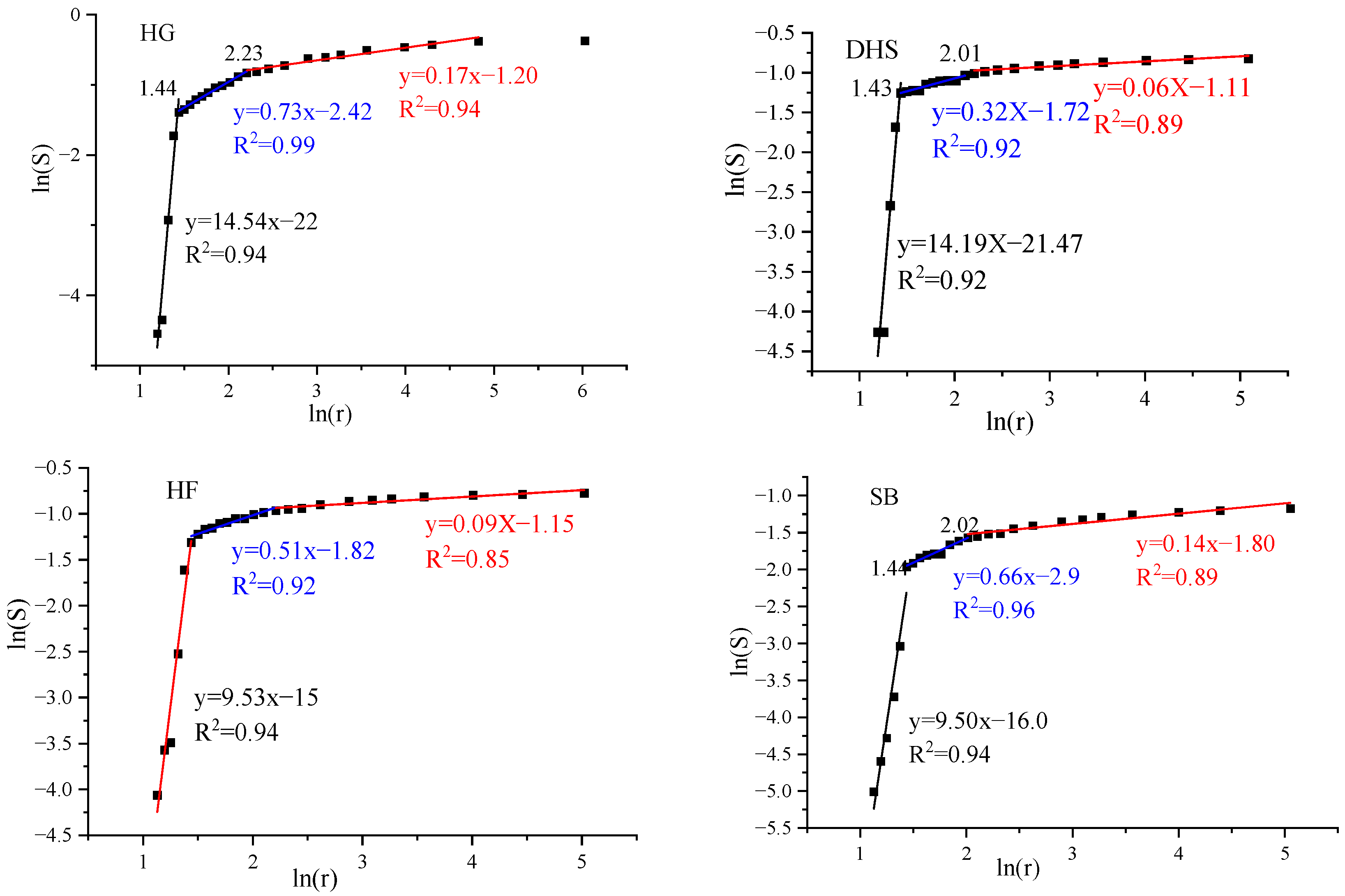
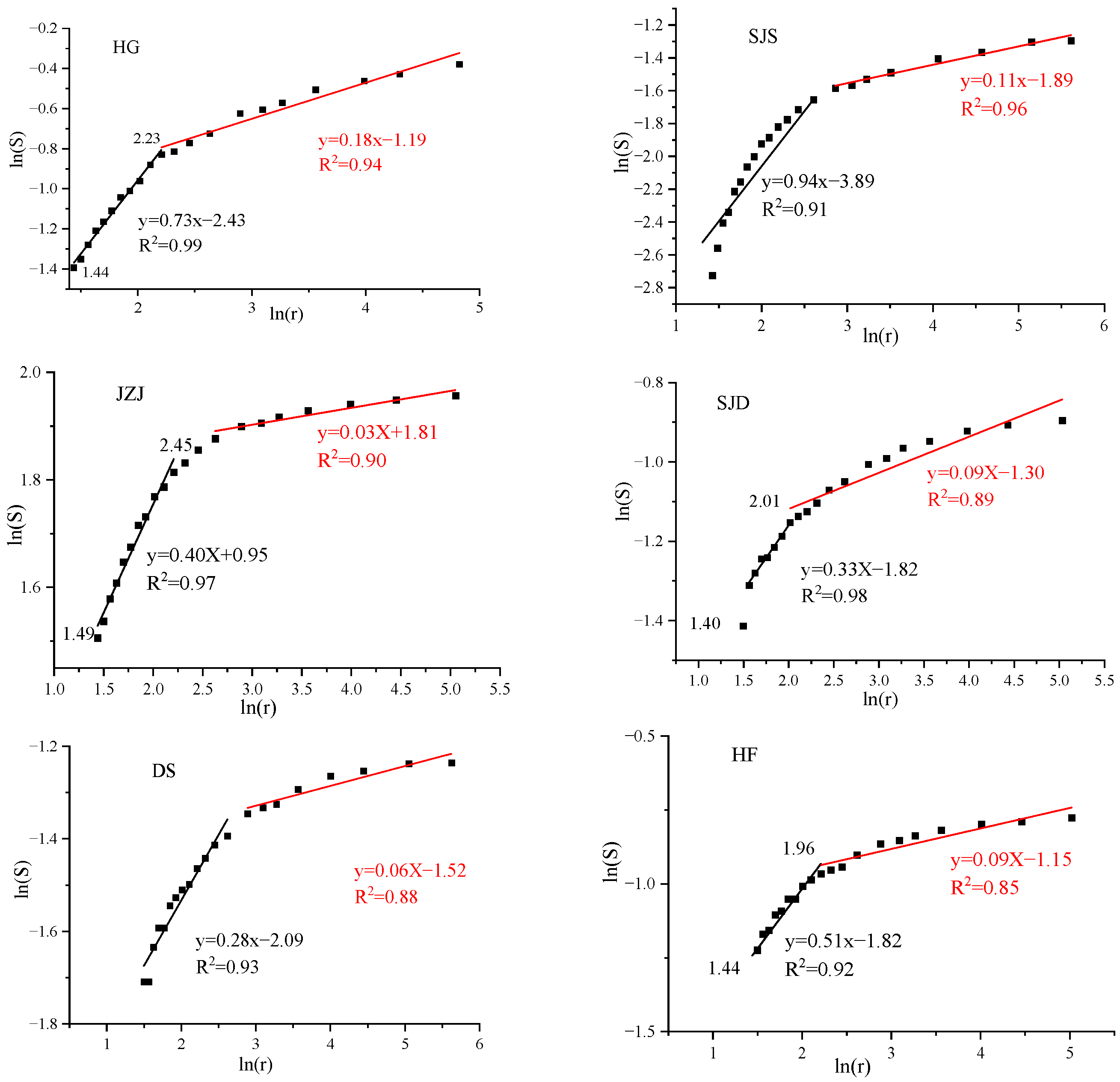
3.4.1. Fractal Dimension by Using LPN2 GA Data
3.4.2. Fractal Dimension by Using LPCO2 GA Data
3.5. Fractal Dimension Analysis
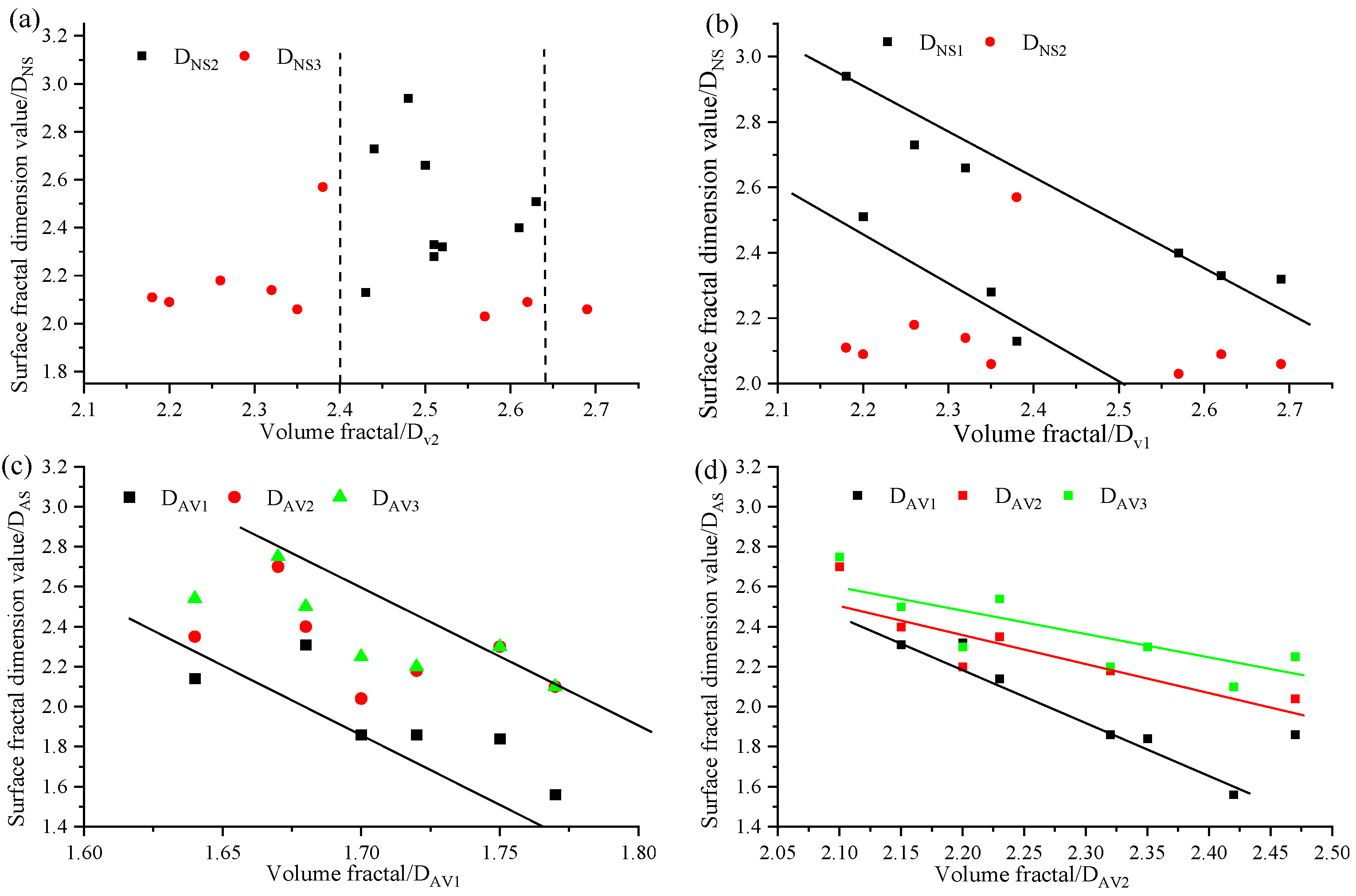
3.5.1. Relationships Between Volume Fractal and Surface Fractal Dimensions
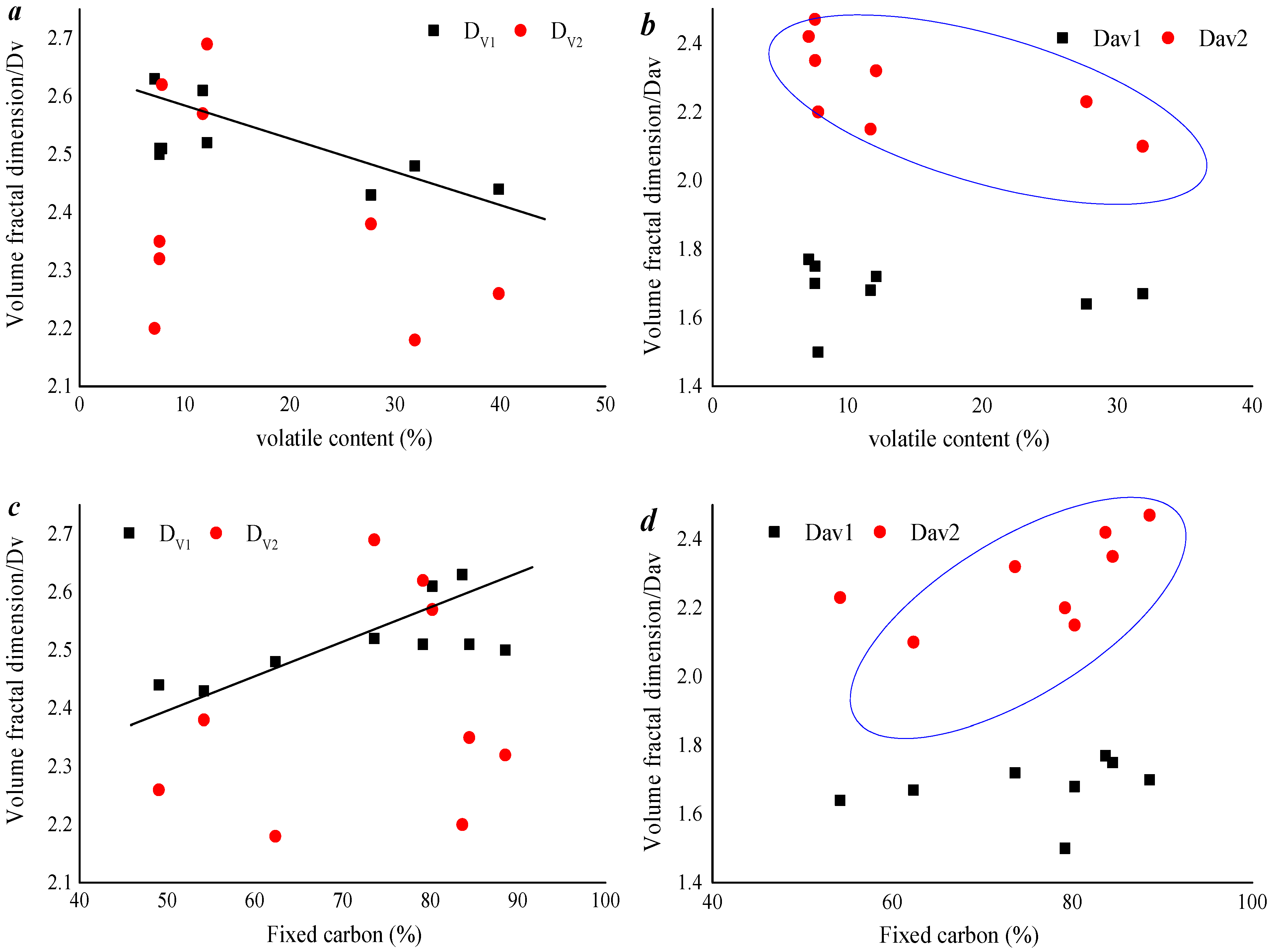
3.5.2. Effects of Coal Rank and Composition on Fractal Dimensions
4. Conclusions
- (1)
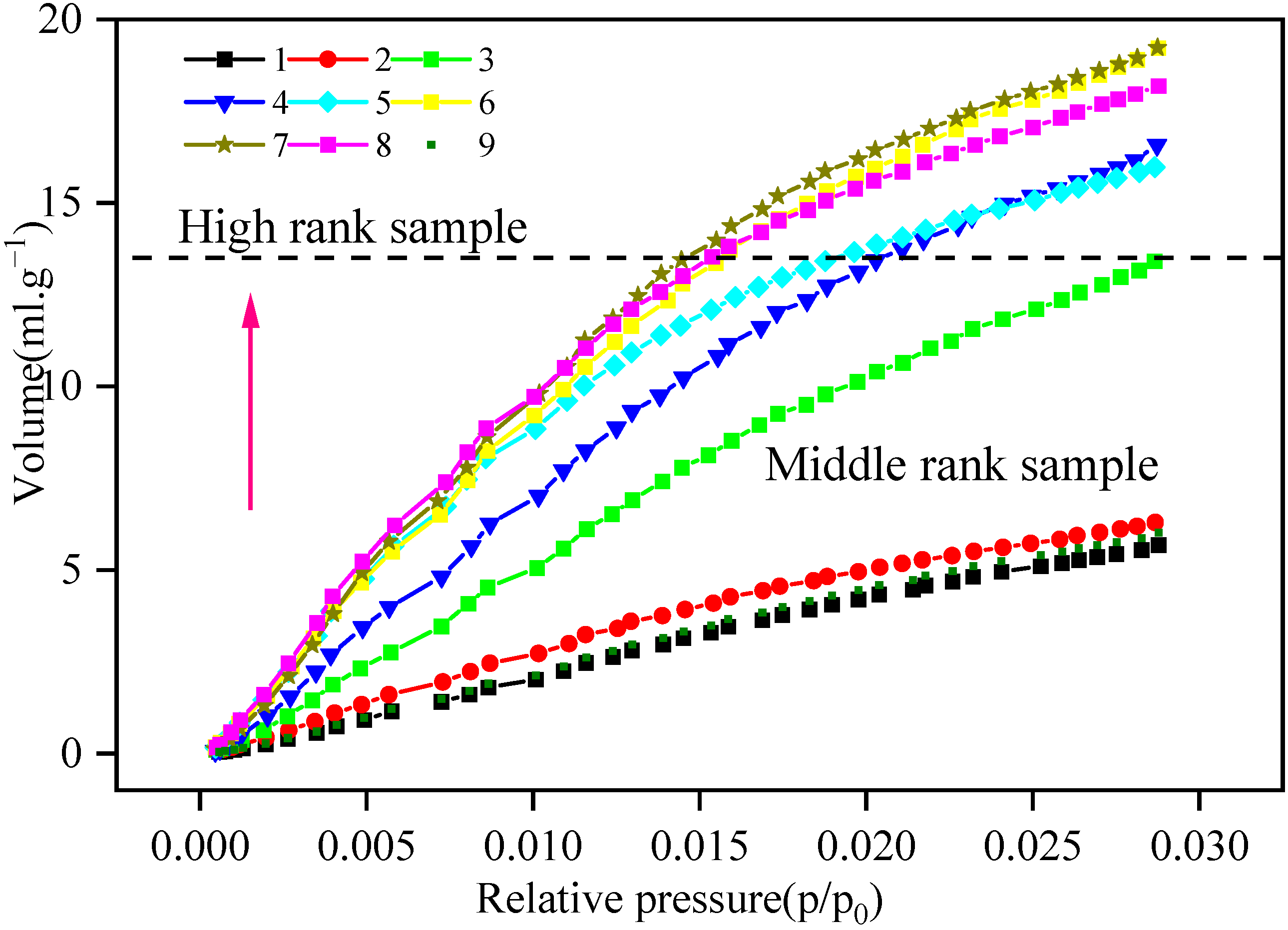
- Adsorption isotherms of the nine coal specimens exhibit a type IV with H3 type hysteresis loop by using the classification method proposed by IUPAC. Type A samples belong to the middle rank coal sample. The adsorption capacity of this type of sample is weak, but the good pore connectivity is conducive to the migration of bulk methane, which is beneficial for higher coalbed methane production capacity. The pore connectivity of this type of sample is stronger than that of types B and C.
- (2)
- The adsorption capacity of high rank coal samples (13.67~18.75 mL g−1) is much larger than that of medium rank coal samples (5.67~6.29 mL g−1), and the curve shape gradually changes from nearly linear to concave with the increase in coal metamorphic degree.
- (3)
- The volume complexity of 0.8~2 nm pores is stronger than that of <0.82 nm pores. tends to be stable within the same coal scale range, and the differences in different coal grades are more obvious. Volume homogeneity of the micropores is more sensitive to the degree of coal deterioration than that of the micropores of (r < 0.8 nm).
- (4)
- There is a significant negative correlation between/and the surface fractal dimension of each micropore stage, and the regularity of 0.8 nm < d < 2 nm pore segment is the best. It shows that the complexity of micropores increases, and the heterogeneity of pore surface area decreases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Quan, F.; Wei, C.; Li, R.; Hao, S.; Zhang, J.; Song, Y.; Yan, G. Reservoir damage in coalbed methane commingled drainage wells and its fatal impact on well recovery. Nat. Resour. Res. 2023, 32, 295–319. [Google Scholar] [CrossRef]
- Moosavi, N.; Bagheri, M.; Bidhendi, M. Fuzzy support vector regression for permeability estimation of petroleum reservoir using well logs. Acta Geophys. 2022, 70, 161–172. [Google Scholar] [CrossRef]
- Cai, Y.D.; Liu, D.M.; Pan, Z.J.; Yao, Y.B.; Li, J.Q.; Qiu, Y.K. Pore structure and its impact on CH4 adsorption capacity and flow capability of bituminous and subbituminous coals from Northeast China. Fuel 2013, 103, 258–268. [Google Scholar] [CrossRef]
- Liu, S.Q.; Sang, S.X.; Wang, G.; Ma, J.S.; Wang, X.; Wang, W.F.; Du, Y.; Wang, T. FIB-SEM and X-ray CT characterization of interconnected pores in high-rank coal formed from regional metamorphism. J. Pet. Sci. Eng. 2017, 148, 21–31. [Google Scholar] [CrossRef]
- Mehrabi, A.; Bagheri, M.; Bidhendi, M.N.; Delijani, E.B.; Behnoud, M. Improved porosity estimation in complex carbonate reservoirs using hybrid CRNN deep learning model. Earth Sci. Inform. 2024, 17, 4773–4790. [Google Scholar] [CrossRef]
- Zhou, Z.; Bouwman, W.G.; Schut, H.; Desert, S.; Jestin, J.; Hartmann, S.; Pappas, C. From nanopores to macropores: Fractal morphology of graphite. Carbon 2016, 96, 541–547. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, D.; Cai, Y.; Yao, Y.; Che, Y.; Liu, Z. Multi-scale fractal characterizations of lignite, subbituminous and high-volatile bituminous coals pores by mercury intrusion porosimetry. J. Nat. Gas. Sci. Eng. 2017, 44, 338–350. [Google Scholar] [CrossRef]
- Bagheri, M.; Rezaei, M. Reservoir rock permeability prediction using SVR based on radial basis function kernel. Carbonates Evaporites 2019, 34, 699–707. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, A.; Zhao, C.; Wang, W.; Jiang, Y.; Vandeginste, V.; Xue, Z.; Guo, Y.; Miao, H. A new parameter for characterizing pore-fracture structure heterogeneity: Fractal dimension based on the mercury extrusion curve. Front. Earth Sci. 2024. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D.; Tang, D.; Tang, S.; Huang, W. Fractal characterization of adsorption-pores of coals from North China: An investigation on CH4 adsorption capacity of coals. Int. J. Coal Geol. 2008, 73, 27–42. [Google Scholar] [CrossRef]
- Liu, W.; Yin, L.; Yang, Y.; Hu, J.; Zhou, S.; Tang, L. Study on the method of determining the lower limit of deep gas porosity in Qibei by porosity distribution trend curve. Logging Technol. 2015, 39, 68–71, 82. [Google Scholar]
- Zhao, J.; Xu, H.; Tang, D.; Mathews, J.P.; Li, S.; Tao, S. A comparative evaluation of coal specific surface area by CO2 and N2 adsorption and its influence on CH4 adsorption capacity at different pore sizes. Fuel 2016, 183, 420–431. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Tang, D.; Gan, Q.; Niu, X.; Wang, K.; Shen, R. Coal pore size distributions controlled by the coalification process: An experimental study of coals from the Junggar, Ordos and Qinshui basins in China. Fuel 2017, 206, 352–363. [Google Scholar] [CrossRef]
- Song, S. FLAC 3D-based simulation of the influence of faults in Jianyanhe Coal Mine in Songyi Mining Area on surface subsidence in golf. Miner. Explor. 2025, 1–6. [Google Scholar]
- Shen, Y.; Qin, Y.; Guo, Y.; Yi, T.; Yuan, X.; Shao, Y. Characteristics and sedimentary control of a coalbed methane-bearing system in lopingian (late permian) coal-bearing strata of western Guizhou Province. J. Nat. Gas Sci. Eng. 2016, 33, 8–17. [Google Scholar] [CrossRef]
- GB/T 19222-2003; Method for Taking Coal Rock Samples. Standards Press of China: Beijing, China, 2003.
- GB/T 18023-2000; Classification of Macrolithotype for Bituminouscoal. State Bureau of Quality and Technical Supervision: Beijing, China, 2000.
- GB/T 6948-1998; Microscopical Determination of the Reflectance of Vitrinite in Coal. AQSIQ: Beijing, China, 1998.
- GB/T 212-2001; Proximate Analysis of Coal. Standards Press of China: Beijing, China, 2001.
- Zhang, Y.; Sun, L.; Zhang, T.; Cheng, B.; Li, Y.; Ma, H.; Lu, C.; Yang, C.; Guo, J.; Zhou, X. Study on sequence stratigraphy and coal-uranium occurrence regularity of coal-uranium rock series in the northeastern margin of Ordos Basin. Geology 2016, 90, 17. [Google Scholar]
- Washburn, E.W. The Dynamics of Capillary Flow. Phys. Rev. J. Arch. 1921, 17, 273–283. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, S.; Tang, D.; Huang, W.; Pan, Z. Determining fractal dimensions of coal pores by FHH model: Problems and effects. J. Nat. Gas Sci. Eng. 2014, 21, 929–939. [Google Scholar] [CrossRef]
- Xu, H.; Tang, D.Z.; Liu, D.M.; Tang, S.H.; Yang, F.; Chen, X.Z.; He, W.; Deng, C.M. Study on coalbed methane accumulation characteristics and favorable areas in the Binchang area, southwestern Ordos Basin, China. Int. J. Coal Geol. 2012, 95, 1–11. [Google Scholar] [CrossRef]
- Zhao, J.L.; Xu, H.; Tang, D.Z.; Mathews, P.J.; Li, S.; Tao, S. Coal seam porosity and fracture heterogeneity of macrolithotypes in the Hancheng Block, eastern margin, Ordos Basin, China. Int. J. Coal Geol. 2016, 159, 18–29. [Google Scholar] [CrossRef]
- Gan, H.; Nandi, N.P.; Walker, P., Jr. Nature of the porosity in American coals. Fuel 1972, 51, 272–279. [Google Scholar] [CrossRef]
- Qu, T.; Wu, Z.S.; Shang, Q.C.; Li, Z.J.; Bai, L. Electromagnetic scattering by a uniaxial anisotropic sphere located in a stratified medium. J. Quant. Spectrosc. Radiat. Transf. 2015, 162, 103–113. [Google Scholar] [CrossRef]
- Zhu, H. Study on the Ultrastructure of Different Metamorphic Deformed Coal Based on AFM. Ph.D. Thesis, Henan Polytechnic University, Jiaozuo, China, 2014. [Google Scholar]
- Liu, Q.; Lu, Y.; Zhang, F. Qualitative analysis of micro-dissolution of limestone under temperature and hydrodynamic pressure. Geomechanics 2010, 31, 149–154. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, J.-Z.; Yang, Y.-M.; Cheng, J.; Zhou, J.-H.; Cen, K.-F. Fractal characteristics of pore structures in 13 coal specimens: Relationship among fractal dimension, pore structure parameter, and slurry ability of coal. Fuel Process. Technol. 2016, 149, 256–267. [Google Scholar] [CrossRef]
- Liu, X.; Kong, X.; Nie, B.; Song, D.; He, X.; Wang, L. Pore fractal dimensions of bituminous coal reservoirs in north China and their impact on gas adsorption capacity. Nat. Resour. Res. 2021, 30, 4585–4596. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D.; Tang, D.; Tang, S.; Huang, W.; Liu, Z.; Che, Y. Fractal characterization of seepage-pores of coals from China: An investigation on permeability of coals. Comput. Geosci. 2009, 35, 1159–1166. [Google Scholar] [CrossRef]
- Sun, W.J.; Feng, Y.Y.; Jiang, C.F.; Chu, W. Fractal characterization and methane adsorption features of coal particles taken from shallow and deep coalmine layers. Fuel 2015, 155, 7–13. [Google Scholar] [CrossRef]
- Yao, P.; Zhang, J.; Lv, D.; Vandeginste, V.; Chang, X.; Zhang, X.; Wang, D.; Han, S.; Liu, Y. Effect of water occurrence in coal reservoirs on the production capacity of coalbed methane by using NMR simulation technology and production capacity simulation. Geoenergy Sci. Eng. 2024, 243, 213353. [Google Scholar] [CrossRef]
- SPSS Version 26.0; IBM Corporation: Armonk, NY, USA, 2019.





| Type | Sample | BET SSA (m2/g) | BJH TPV (.10−3 cm3/g) | BJH APD (nm) | Percentage of SSA (%) | Percentage of TPV (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2~4 nm | 4~10 nm | 10~100 nm | 2~4 nm | 4~10 nm | 10~100 nm | |||||
| A | HG | 0.34 | 3.8 | 4.42 | 26 | 38 | 36 | 5.3 | 9.7 | 85 |
| SJS | 0.24 | 1.9 | 4.45 | 21 | 40 | 39 | 4.5 | 17.5 | 78 | |
| FZ | 0.23 | 1.9 | 5.37 | 13.4 | 50.6 | 36 | 2.28 | 14.12 | 83.6 | |
| B | JZJ | 0.28 | 1.2 | 3.42 | 40 | 43 | 17 | 14.3 | 20.4 | 65.3 |
| SJD | 0.14 | 0.9 | 3.41 | 43.5 | 38.5 | 18 | 16.4 | 21.8 | 61.8 | |
| C | DHS | 0.35 | 1.2 | 3.42 | 42.4 | 41.6 | 16 | 16.1 | 23.2 | 60.7 |
| DS | 0.39 | 1.4 | 3.42 | 41.7 | 46.3 | 12 | 19.4 | 30 | 50.6 | |
| HF | 0.27 | 1.1 | 3.43 | 30.9 | 50.1 | 19 | 10.1 | 23.1 | 66.8 | |
| SB | 0.08 | 1.2 | 3.42 | 15.5 | 63.5 | 21 | 3.79 | 19.11 | 77.1 | |
| Sample | Rank | Pore Volume (cm3/g) | SSA (m2/g) | Average Pore Width (nm) | |||||
|---|---|---|---|---|---|---|---|---|---|
| DFT | D–R | D–A | DFT | D–R | DFT | D–R | D–A | ||
| HG | Middle | 0.019 | 0.045 | 0.043 | 65 | 123 | 0.645 | 1.23 | 1.32 |
| SJS | 0.021 | 0.046 | 0.053 | 57 | 137 | 0.627 | 1.28 | 1.53 | |
| FZ | 0.024 | 0.044 | 0.044 | 66 | 132 | 0.627 | 1.20 | 1.46 | |
| JZJ | 0.052 | 0.104 | 0.122 | 140 | 313 | 0.627 | 1.261 | 1.50 | |
| SJD | 0.057 | 0.146 | 0.073 | 164 | 438 | 0.458 | 1.28 | 1.38 | |
| DHS | High | 0.053 | 0.119 | 0.054 | 165 | 355 | 0.50 | 1.18 | 1.32 |
| DS | 0.068 | 0.138 | 0.089 | 197 | 414 | 0.60 | 1.19 | 1.38 | |
| HF | 0.056 | 0.167 | 0.075 | 182 | 502 | 0.458 | 1.25 | 1.36 | |
| SB | 0.060 | 0.137 | 0.062 | 186 | 411 | 0.501 | 1.189 | 1.32 | |
| Group | Rank | Coal Sample | Dv1 | Dv2 |
|---|---|---|---|---|
| A | Middle | HG | 2.26 | 2.44 |
| SJS | 2.18 | 2.48 | ||
| FZ | 2.38 | 2.43 | ||
| JZJ | 2.57 | 2.61 | ||
| B | High | DHS | 2.69 | 2.52 |
| HF | 2.20 | 2.63 | ||
| C | SJD | 2.51 | 2.62 | |
| DS | 2.35 | 2.51 | ||
| SB | 2.50 | 2.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Quan, F.; Zhang, S.; Zhao, Y.; Shi, H.; Yin, T.; Qin, Z. Adsorption Pore Volume Distribution Heterogeneity of Middle and High Rank Coal Reservoirs and Determination of Its Influencing Factors. Processes 2025, 13, 429. https://doi.org/10.3390/pr13020429
Wang K, Quan F, Zhang S, Zhao Y, Shi H, Yin T, Qin Z. Adsorption Pore Volume Distribution Heterogeneity of Middle and High Rank Coal Reservoirs and Determination of Its Influencing Factors. Processes. 2025; 13(2):429. https://doi.org/10.3390/pr13020429
Chicago/Turabian StyleWang, Kai, Fangkai Quan, Shizhao Zhang, Yubo Zhao, He Shi, Tingting Yin, and Zhenyuan Qin. 2025. "Adsorption Pore Volume Distribution Heterogeneity of Middle and High Rank Coal Reservoirs and Determination of Its Influencing Factors" Processes 13, no. 2: 429. https://doi.org/10.3390/pr13020429
APA StyleWang, K., Quan, F., Zhang, S., Zhao, Y., Shi, H., Yin, T., & Qin, Z. (2025). Adsorption Pore Volume Distribution Heterogeneity of Middle and High Rank Coal Reservoirs and Determination of Its Influencing Factors. Processes, 13(2), 429. https://doi.org/10.3390/pr13020429







