Risk Assessment Method for Power Distribution Systems Based on Spatiotemporal Characteristics of the Typhoon Disaster Chain
Abstract
:1. Introduction
- (1)
- Systematic analysis of the formation process of the typhoon disaster chain is conducted, identifying the underlying logic and key factors involved. A spatiotemporal correlation model for the typhoon disaster chain is proposed, which captures the interaction and evolution of different disaster events (such as heavy rainfall, flooding, etc.) triggered by a typhoon.
- (2)
- A method for calculating the failure probability of distribution system equipment under the influence of the typhoon disaster chain is introduced. Compared with existing papers in which independent disasters are considered, the influence of the typhoon disaster chain on the failure probability of different distribution system equipment is taken into account. Furthermore, the failure probability of energy storage devices is investigated.
- (3)
- A disaster risk assessment model for the distribution system is proposed, integrating the reliability, security, and economic index of the distribution system. Compared with existing papers that mainly focus on the reliability index, this work assesses the risk of distribution systems under the influence of typhoon disaster chains by employing the non-sequential Monte Carlo simulation approach.
2. The Spatiotemporal Correlation Model for the Typhoon Disaster Chain
2.1. The Formation Mechanisms of the Typhoon Disaster Chain
2.2. Typhoon, Heavy Rainfall, and Waterlogging Disaster Chain Modeling
2.2.1. Typhoon Disaster Model
- Calculate the distance r between O and P, angle α, and Coriolis parameter f using known θ and the location of O and P;
- Substitute r, α, f, c, B, ∆p, and Rmax into Equation (1) to obtain gradient wind speed Vg(α,r). Use Equation (2) to find corresponding wind direction ψg (α);
- 3.
- Determine friction velocity u* and angle βs from Equations (3) and (4), where z0 is surface roughness, decided by terrain conditions;
- 4.
- Obtain surface wind speed Vz(α,r) by substituting u* and z into Equation (5). Use Equation (6) to estimate angle ψz (α,r);
- 5.
- Adjust Vz(α,r) by multiplying it by 1.1 if 0.5Rmax ≤ r ≤ Rmax, and by 1 + 0.1 sin[πr/(2Rmax)] if Rmax < r ≤ 2Rmax.
2.2.2. Heavy Rainfall Disaster Model Under Typhoon Conditions
2.2.3. Waterlogging Disaster Model Under Typhoon–Heavy Rainfall Conditions
3. Modeling of the Distribution System Equipment Failure Probability Under Typhoon Disaster Chain
3.1. Modeling of Substation Failure Probability
3.2. Modeling of Line Failure Probability
3.2.1. Modeling of Line Failure Probability Under Typhoon Disaster
3.2.2. Modeling of Line Failure Probability Under Heavy Rainfall Disaster
3.3. Modeling of Failure Probability for Energy Storage Devices
4. Distribution System Disaster Risk Assessment Methodology
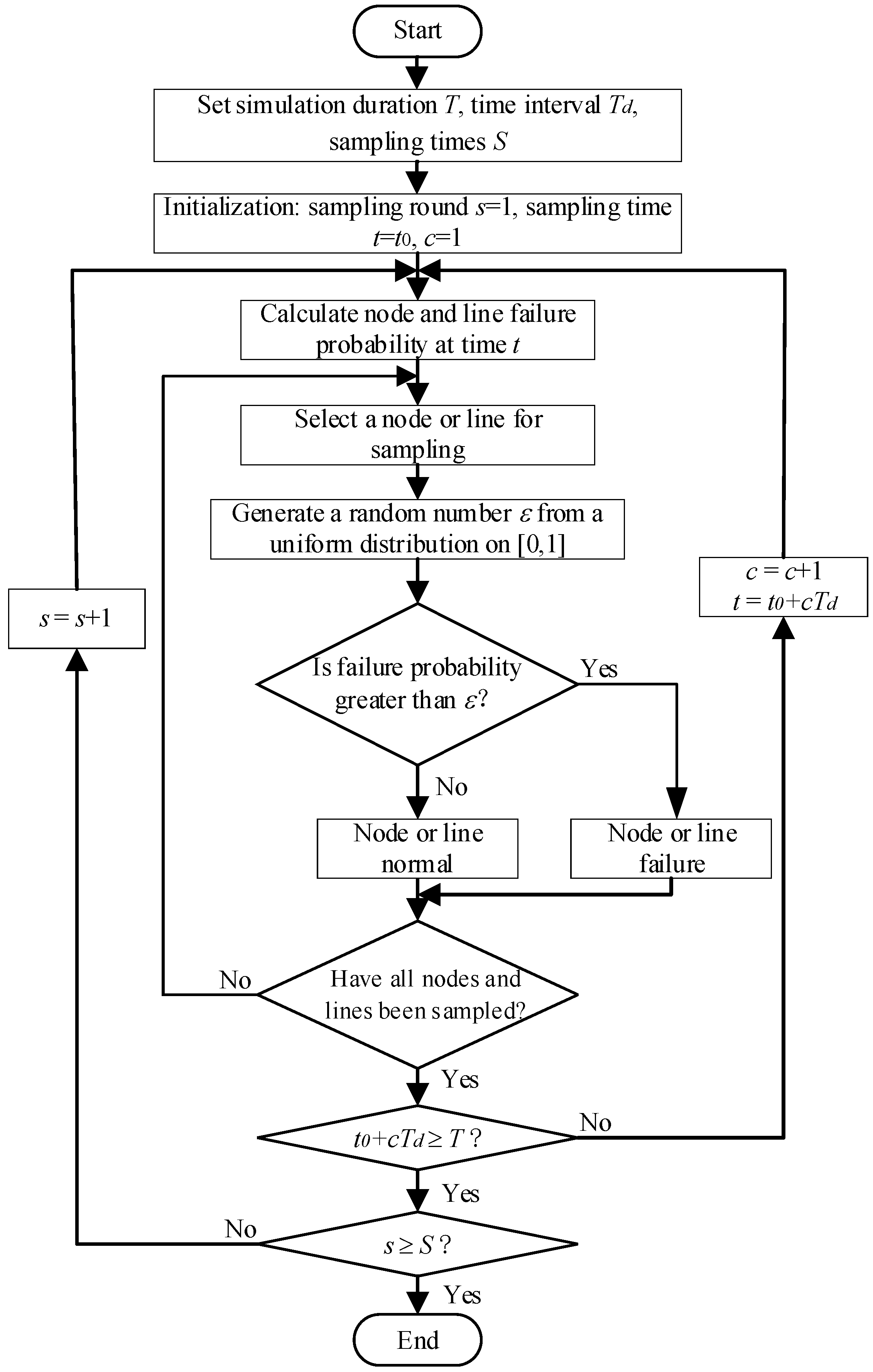
4.1. Simulation of Power Outage Scenarios in Distribution System Under Typhoon Disaster Chain
- Set parameters: simulation duration, time interval, and sampling times.
- Calculate the failure probability of nodes and lines.
- Judge whether the nodes and lines are faulty or not.
- Until all node and line state sampling is completed at all moments.
4.2. The Disaster Risk Assessment System of the Distribution System Under the Typhoon Disaster Chain
4.2.1. Reliability Risk Indicators
4.2.2. Security Risk Indicators
4.2.3. Economy Risk Indicators
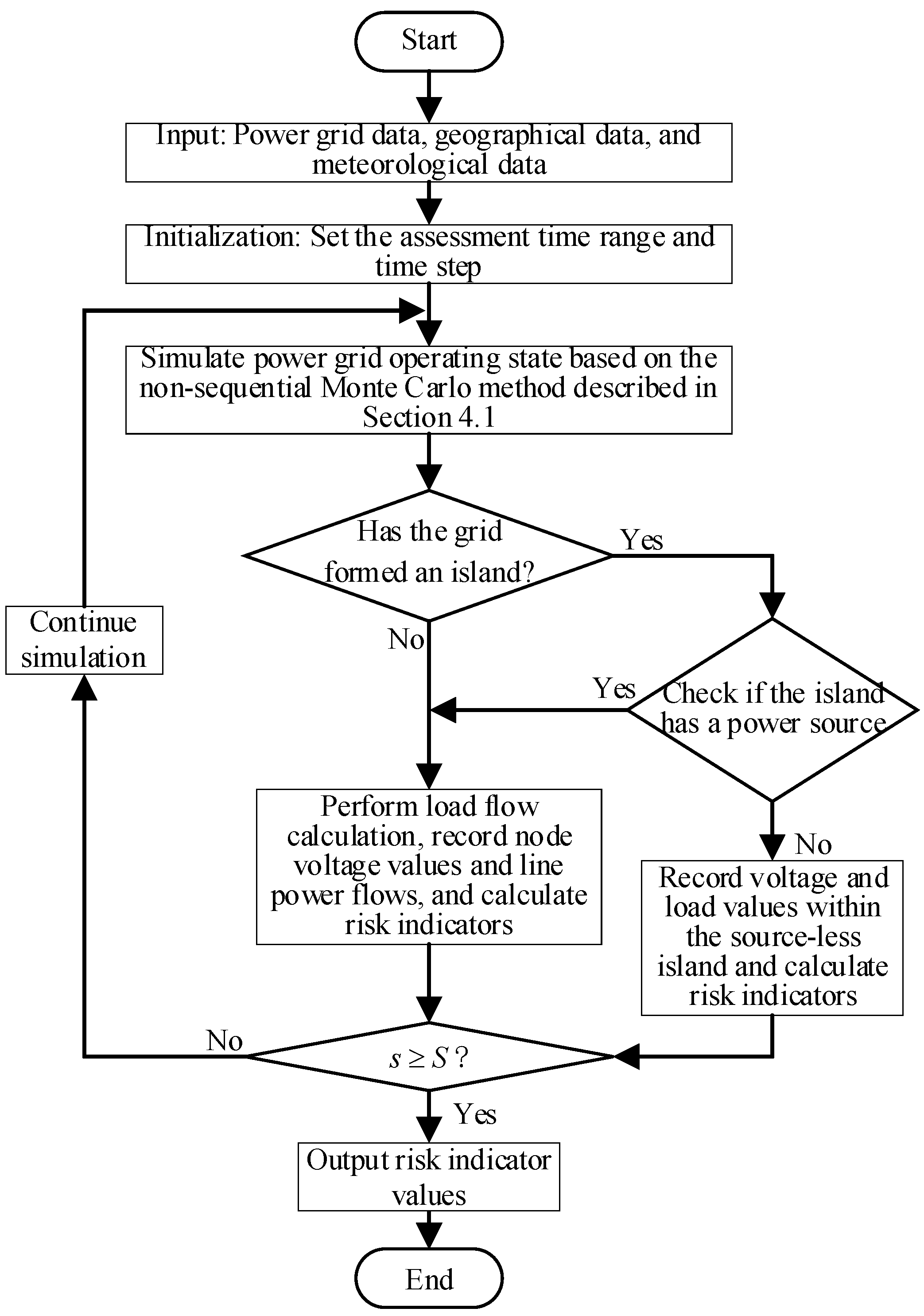
4.3. The Disaster Risk Assessment Process of the Distribution System Under the Typhoon Disaster Chain
- Obtain power grid data, including topology, node location, and geographic information; obtain geographic data of the simulation area; and obtain meteorological data such as typhoon tracks.
- Calculate the node and line failure probability according to the typhoon disaster chain model.
- Simulate the operation state of the distribution system according to the non-temporal Monte Carlo state sampling method.
- Judge whether there is an islanding in the distribution system. If there is an island, then determine whether the island is active or not, obtain the risk indicator value after the current calculation for active islands, and directly calculate the indicator value for passive islands; if there is no island, then directly carry out the current calculation, and then calculate the risk indicator value.
- Until the end of the simulation is completed.
5. Case Study
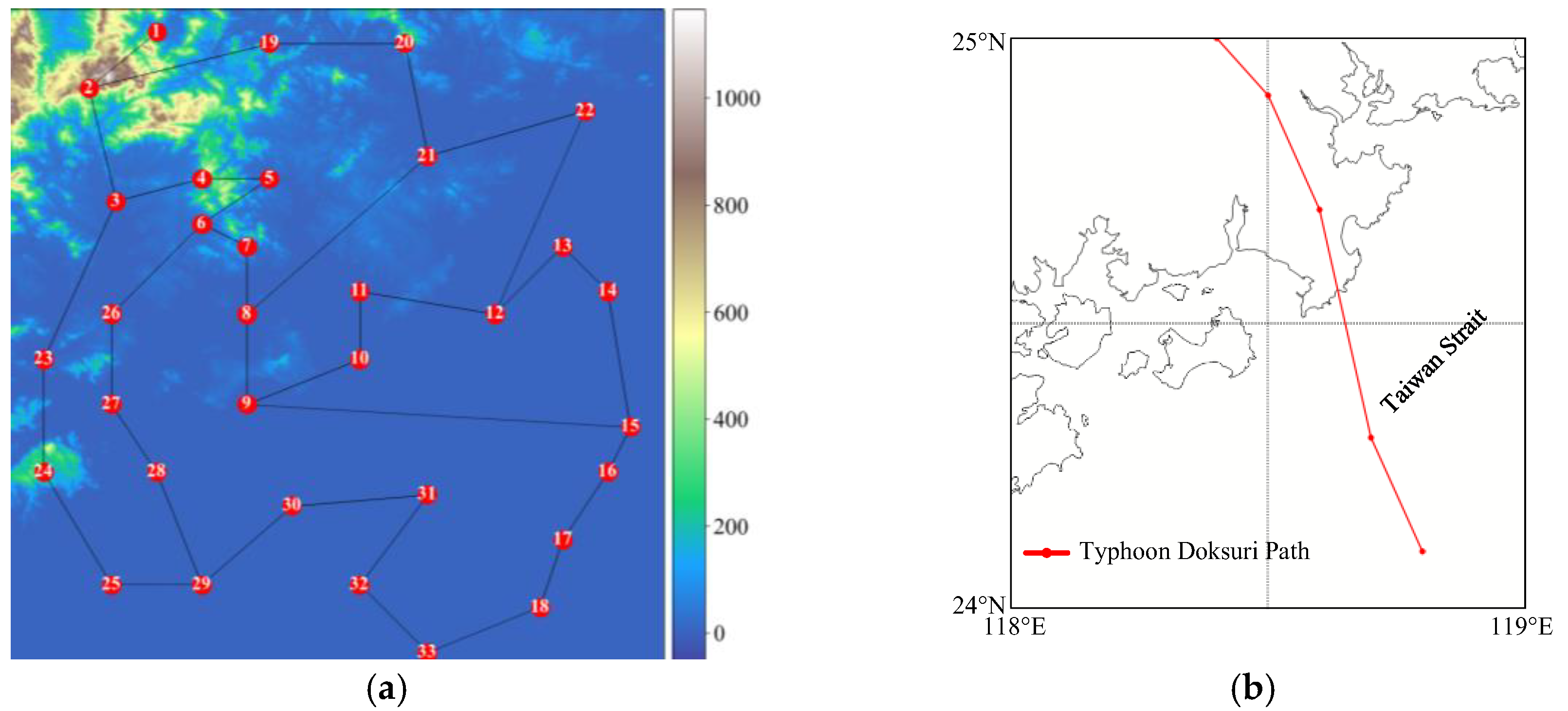
5.1. Simulation System Settings
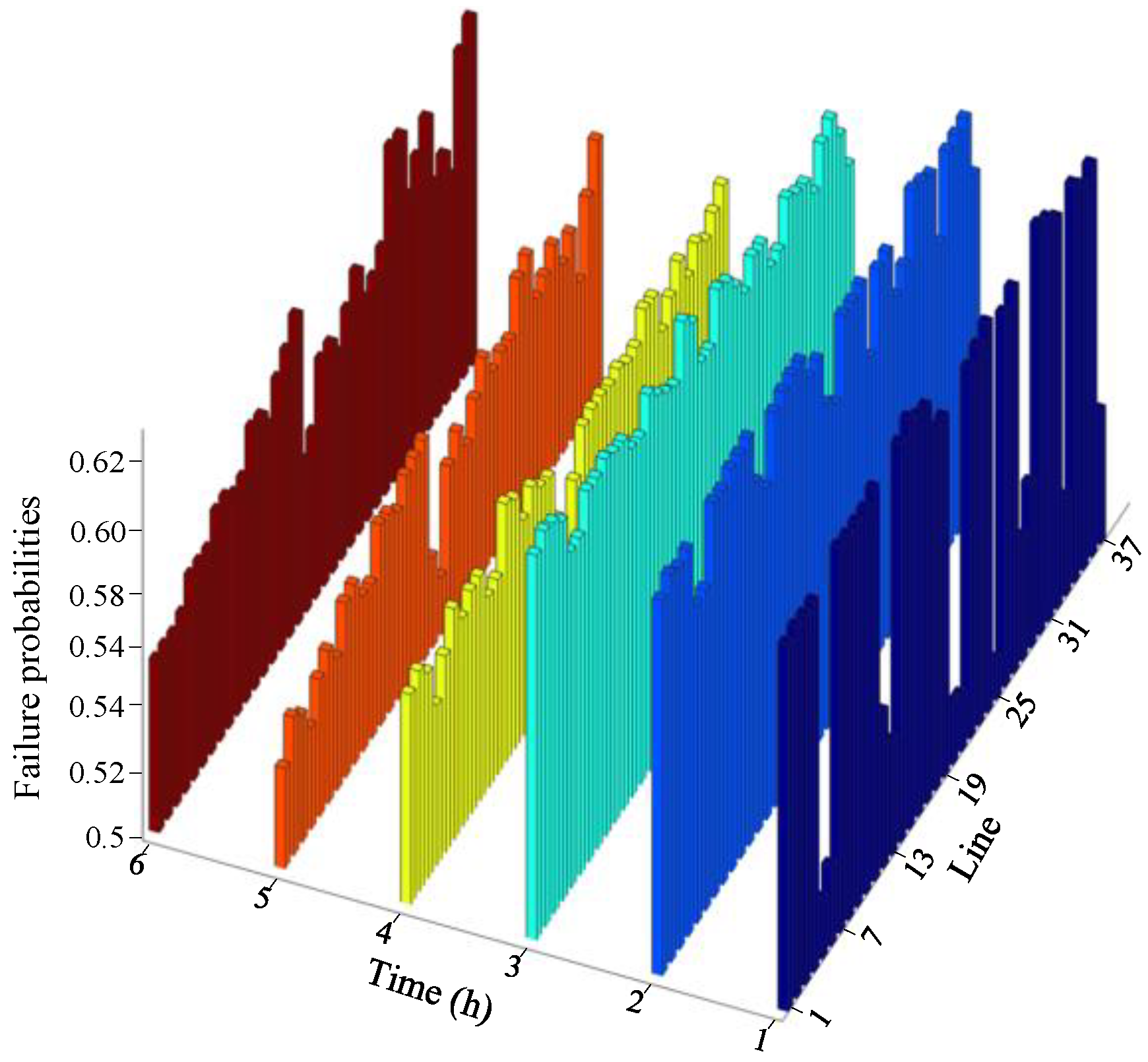
5.2. Typhoon Disaster Chain Simulation and Component Failure Probability
5.3. Systemic Risk Indicators
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xi Stresses Healthy Growth of Platform Economy, Efforts for Carbon Peak and Neutrality. Available online: http://en.qstheory.cn/2021-03/16/c_603674.htm (accessed on 31 October 2024).
- The Latest! “Doksuri” caused 1,304,700 Power Outages in Fujian! Power Has Been Restored to 323,600 Households! Available online: https://m.gmw.cn/2023-07/28/content_1303458416.htm?source=sohu (accessed on 31 October 2024).
- Sun, L.; Wang, H.; Huang, Z.; Wen, F.; Ding, M. Coordinated Islanding Partition and Scheduling Strategy for Service Restoration of Active Distribution Networks Considering Minimum Sustainable Duration. IEEE Trans. Smart Grid 2024, 15, 5539–5554. Available online: https://ieeexplore.ieee.org/document/10609444 (accessed on 19 December 2024). [CrossRef]
- Fan, R.; Zeng, W.; Ming, Z.; Zhang, W.; Huang, R.; Liu, J. Risk Reliability Assessment of Transmission Lines under Multiple Natural Disasters in Modern Power Systems. Energies 2023, 16, 6548. [Google Scholar] [CrossRef]
- Hou, H.; Yu, S.; Wang, H.; Huang, Y.; Wu, H.; Xu, Y.; Li, X.; Geng, H. Risk Assessment and Its Visualization of Power Tower under Typhoon Disaster Based on Machine Learning Algorithms. Energies 2019, 12, 205. [Google Scholar] [CrossRef]
- Liu, X.; Liu, J.; Zhao, Y.; Ding, T.; Liu, X.; Liu, J. A Bayesian Deep Learning-Based Probabilistic Risk Assessment and Early-Warning Model for Power Systems Considering Meteorological Conditions. IEEE Trans. Ind. Inform. 2024, 20, 1516–1527. [Google Scholar] [CrossRef]
- Xu, L.; Lin, N.; Xi, D.; Feng, K.; Poor, H.V. Hazard Resistance-Based Spatiotemporal Risk Analysis for Distribution Network Outages During Hurricanes. arXiv 2024, arXiv:2401.10418. [Google Scholar] [CrossRef]
- Wang, J.; Xiong, Z.; Zhang, T.; Ouyang, J. Short-Term Multiple Fault Risk Assessment for Power Systems Considering Unexpected Actions of Protection System Under Weather Disasters. Int. J. Electr. Power Energy Syst. 2024, 162, 110254. [Google Scholar] [CrossRef]
- Afzal, S.; Mokhlis, H.; Illias, H.A.; Bajwa, A.A.; Mekhilef, S.; Mubin, M.; Muhammad, M.A.; Shareef, H. Modelling Spatiotemporal Impact of Flash Floods on Power Distribution System and Dynamic Service Restoration with Renewable Generators Considering Interdependent Critical Loads. IET Gener. Transm. Distrib. 2024, 18, 368–387. [Google Scholar] [CrossRef]
- Ti, B.; Li, G.; Zhou, M.; Wang, J. Resilience Assessment and Improvement for Cyber-Physical Power Systems Under Typhoon Disasters. IEEE Trans. Smart Grid 2022, 13, 783–794. [Google Scholar] [CrossRef]
- Souto, L.; Yip, J.; Wu, W.-Y.; Austgen, B.; Kutanoglu, E.; Hasenbein, J.; Yang, Z.-L.; King, C.W.; Santoso, S. Power System Resilience to Floods: Modeling, Impact Assessment, and Mid-Term Mitigation Strategies. Int. J. Electr. Power Energy Syst. 2022, 135, 107545. [Google Scholar] [CrossRef]
- Lian, X.; Qian, T.; Li, Z.; Chen, X.; Tang, W. Resilience Assessment for Power System Based on Cascading Failure Graph Under Disturbances Caused by Extreme Weather Events. Int. J. Electr. Power Energy Syst. 2023, 145, 108616. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, Z.; Wei, R.; Huang, Y.; Liang, Y.; Li, X. Review of failure risk and outage prediction in power system under wind hazards. Electr. Power Syst. Res. 2022, 210, 108098. [Google Scholar] [CrossRef]
- Wu, F.; Huang, G. Refined Empirical Model of Typhoon Wind Field and Its Application in China. J. Struct. Eng. 2019, 145, 04019122. [Google Scholar] [CrossRef]
- Kim, D.; Park, D.-S.R.; Nam, C.C.; Bell, M.M. The Parametric Hurricane Rainfall Model with Moisture and Its Application to Climate Change Projections. NPJ Clim. Atmos. Sci. 2022, 5, 86. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, B.; Zhang, C.; Or, S.W.; Gao, X.; Da, Z. A Hybrid Data and Knowledge Driven Risk Prediction Method for Distributed Photovoltaic Systems Considering Spatio-Temporal Characteristics of Extreme Rainfalls. IEEE Trans. Ind. Applicat. 2024, 1–11. [Google Scholar] [CrossRef]
- He, Y. Study on the Enhancing the Response Capacity of Disaster of Distribution Network with Distributed Generation; Northeastern University: Boston, MA, USA, 2018. (In Chinese) [Google Scholar]
- Gautam, P.; Piya, P.; Karki, R. Resilience Assessment of Distribution Systems Integrated with Distributed Energy Resources. IEEE Trans. Sustain. Energy 2021, 12, 338–348. [Google Scholar] [CrossRef]
- Fu, X.; Li, H.-N.; Li, G. Fragility Analysis and Estimation of Collapse Status for Transmission Tower Subjected to Wind and Rain Loads. Struct. Saf. 2016, 58, 1–10. [Google Scholar] [CrossRef]
- Hu, B.; Xie, K.; Shao, C.; Pan, C.; Lin, C.; Zhao, Y. Commentary on risk of new power system under goals of carbon emission peak and carbon neutrality: Characteristics, indices and assessment methods. Autom. Electr. Power Syst. 2023, 47, 1–15. (In Chinese) [Google Scholar]
- U.S. Geological Survey. Earth Explorer. Available online: https://earthexplorer.usgs.gov (accessed on 31 October 2024).
- A Dataset of Typhoon Tracks in Offshore China (1945–2023). Available online: http://msdc.qdio.ac.cn (accessed on 31 October 2024).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. Complete ERA5 from 1940: Fifth generation of ECMWF atmospheric reanalysis of the global climate. Copernic. Clim. Chang. Serv. (C3S) Data Store (CDS) 2017, 10. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network Reconfiguration in Distribution Systems for Loss Reduction and Load Balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]





| Time | (Longitude, Latitude) | Maximum Wind Speed (m/s) | Central Pressure (hPa) | Approach Angle (°) | Translation Speed (km/h) |
|---|---|---|---|---|---|
| 08:00 | (118.8, 24.1) | 52 | 935 | 337.5 | 24 |
| 09:00 | (118.7, 24.3) | 52 | 935 | 337.5 | 24 |
| 10:00 | (118.6, 24.7) | 50 | 945 | 337.5 | 25 |
| 11:00 | (118.5, 24.9) | 42 | 960 | 337.5 | 30 |
| 12:00 | (118.4, 25) | 38 | 970 | 337.5 | 30 |
| 13:00 | (118.3, 25.4) | 38 | 970 | 337.5 | 30 |
| Node | Degree of Voltage Overrun | Node | Ratio of Load Shedding (%) |
|---|---|---|---|
| 6 | 0.701 | 6 | 73.5 |
| 26 | 0.590 | 26 | 61.4 |
| 12 | 0.588 | 12 | 61.2 |
| 27 | 0.554 | 27 | 57.7 |
| 29 | 0.544 | 29 | 56.7 |
| Line | Number of Line Failures (Times/Thousand Times) |
|---|---|
| l30–31 | 649 |
| l2–19 | 647 |
| l12–22 | 640 |
| l25–29 | 636 |
| l10–11 | 633 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Sun, N.; Chen, H.; Zhang, L.; Wan, J.; Su, J. Risk Assessment Method for Power Distribution Systems Based on Spatiotemporal Characteristics of the Typhoon Disaster Chain. Processes 2025, 13, 699. https://doi.org/10.3390/pr13030699
Chen B, Sun N, Chen H, Zhang L, Wan J, Su J. Risk Assessment Method for Power Distribution Systems Based on Spatiotemporal Characteristics of the Typhoon Disaster Chain. Processes. 2025; 13(3):699. https://doi.org/10.3390/pr13030699
Chicago/Turabian StyleChen, Bin, Nuoling Sun, Hao Chen, Linyao Zhang, Jiawei Wan, and Jie Su. 2025. "Risk Assessment Method for Power Distribution Systems Based on Spatiotemporal Characteristics of the Typhoon Disaster Chain" Processes 13, no. 3: 699. https://doi.org/10.3390/pr13030699
APA StyleChen, B., Sun, N., Chen, H., Zhang, L., Wan, J., & Su, J. (2025). Risk Assessment Method for Power Distribution Systems Based on Spatiotemporal Characteristics of the Typhoon Disaster Chain. Processes, 13(3), 699. https://doi.org/10.3390/pr13030699






