The Multi-Point Cooperative Control Strategy for Electrode Boilers Supporting Grid Frequency Regulation
Abstract
1. Introduction
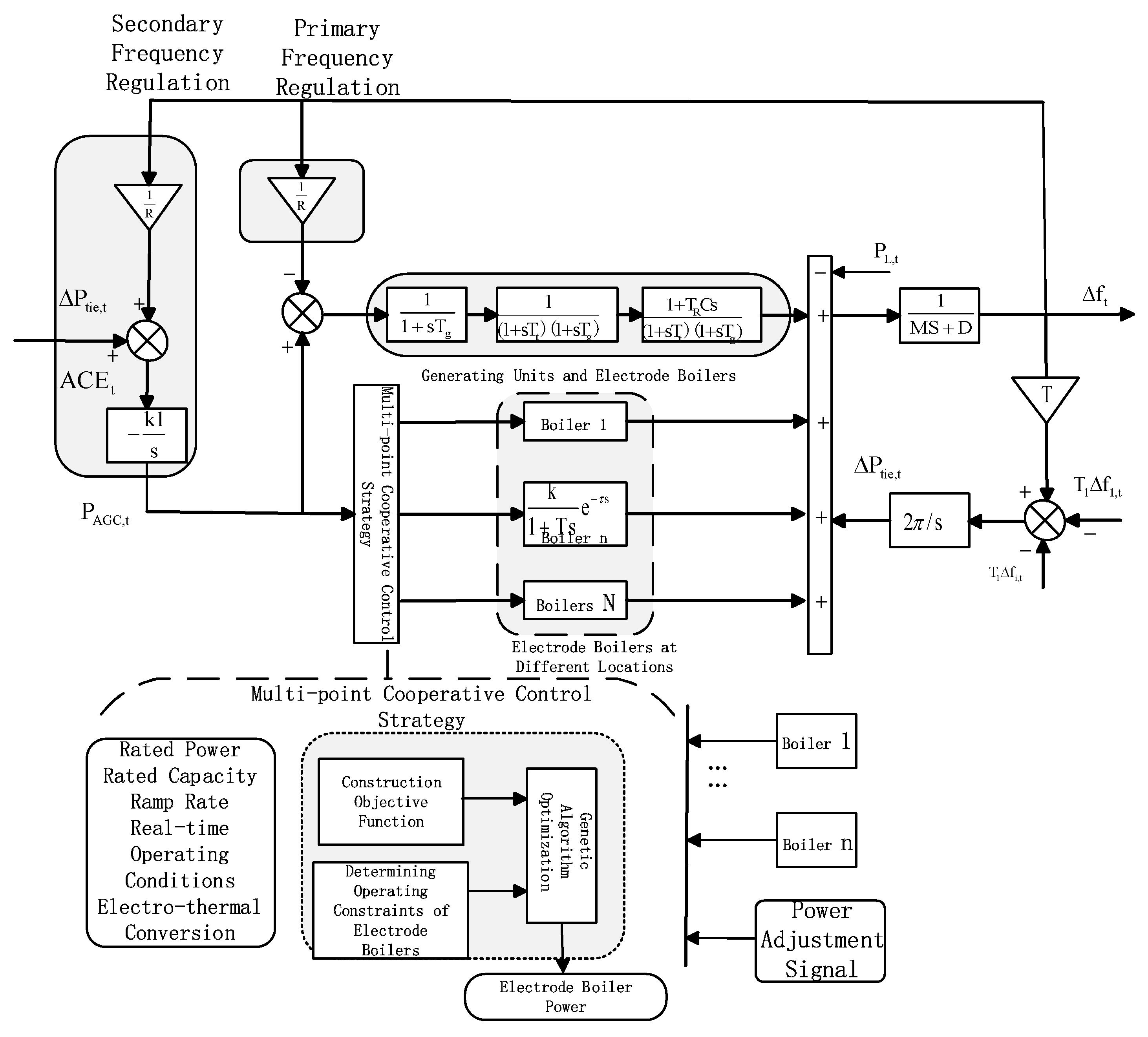
2. Multi-Point Collaborative Control Architecture for Electrode Boilers
2.1. Typical Control Architecture of Electrode Boilers
2.2. Dynamic Response Model of Electrode Boilers and Generation Units
3. Multi-Point Coordinated Control Model of Electrode Boilers
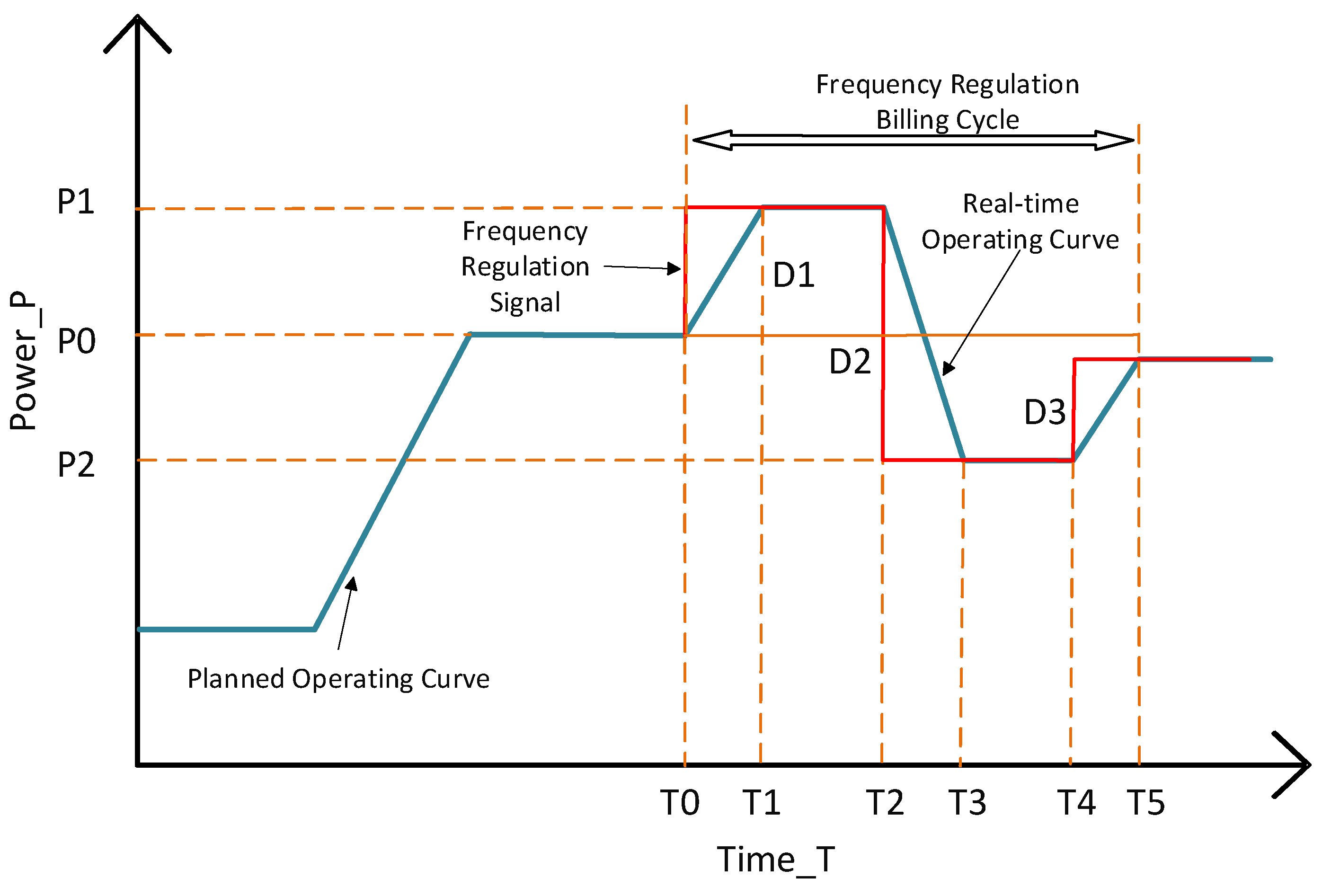
3.1. Benefit Model
3.2. Cost Model
3.3. Loss Model
3.4. Frequency Model
4. Multi-Point Coordinated Optimization Model of Electrode Boilers
4.1. Optimization Objective Function
4.2. System Operational Constraints
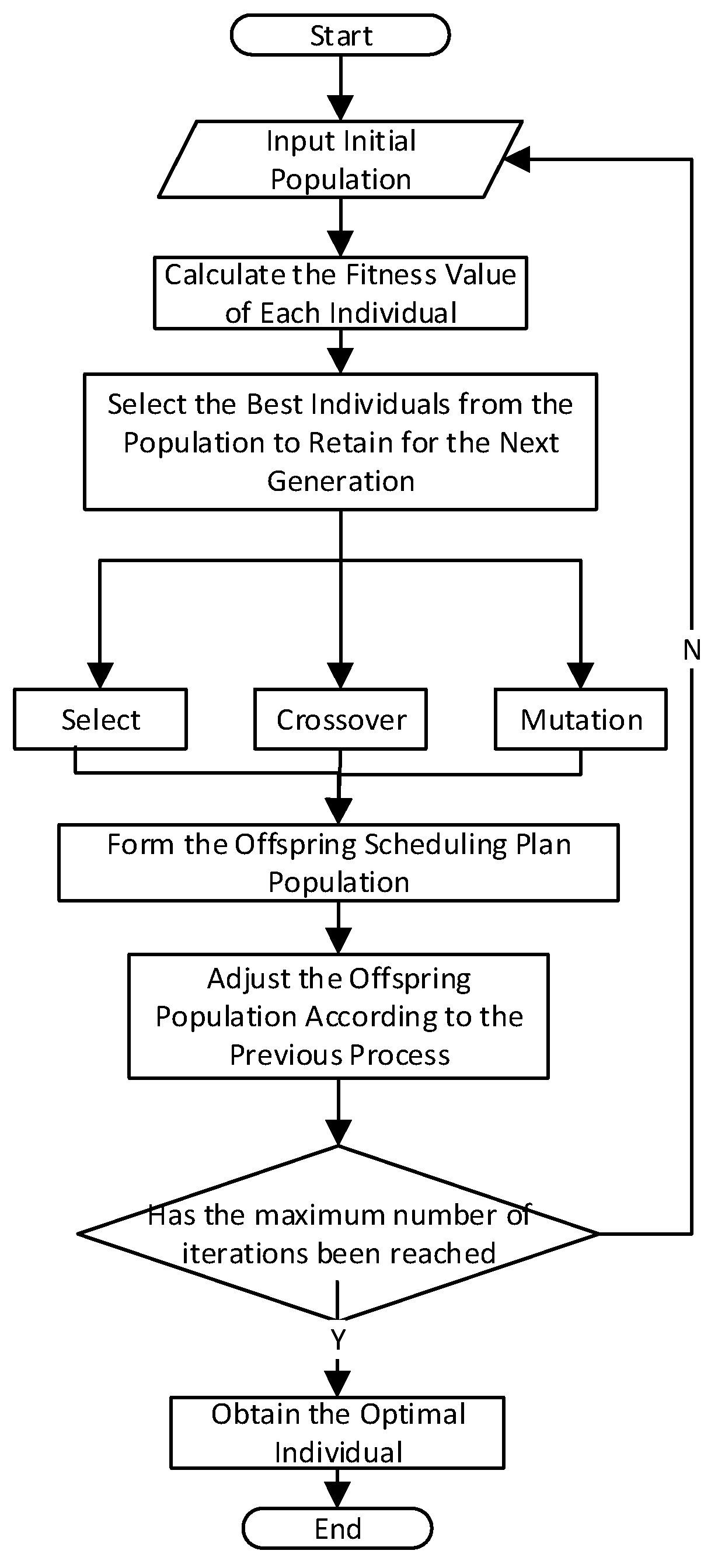
5. Optimization Algorithm Design
5.1. Basic Principle of the Algorithm
5.2. Algorithm Application Design
| Algorithm 1. Genetic Algorithm (GA) for Optimizing Power Allocation of Electrode Boilers |
| Input: P_AGC, P_init, P_max, Q_max, C_base, c, alpha, weights |
| Output: best_position: Optimal power allocation best_value: Optimal objective function value |
| Step 1: Initialize Genetic Algorithm Parameters Initialize population size (n_population), number of generations (n_generations), etc. |
| Step 2: Generate Initial Population Create n_population individuals, randomly initialize power values, and normalize according to P_max |
| Step 3: Define Fitness Evaluation Function 1. Calculate objective functions (f1: power difference, f2: operation and maintenance cost, f3: heat loss) 2. Normalize the objective functions 3. Combine the objective functions into a comprehensive fitness value F based on weights 4. Clip power values to ensure they are within the [P_init, P_max] range |
| Step 4: Selection Operation 1. Calculate selection probabilities based on fitness 2. Select individuals for the next generation based on fitness proportion |
| Step 5: Crossover Operation 1. Randomly perform crossover on parent individuals 2. Exchange genes to generate offspring individuals |
| Step 6: Mutation Operation 1. Randomly mutate power values of some individuals |
| Step 7: Update Population Replace the current population with the new offspring individuals |
| Step 8: Repeat Steps 3–7 until the maximum number of iterations is reached |
| Step 9: Return the optimal solution (best_position, best_value) |
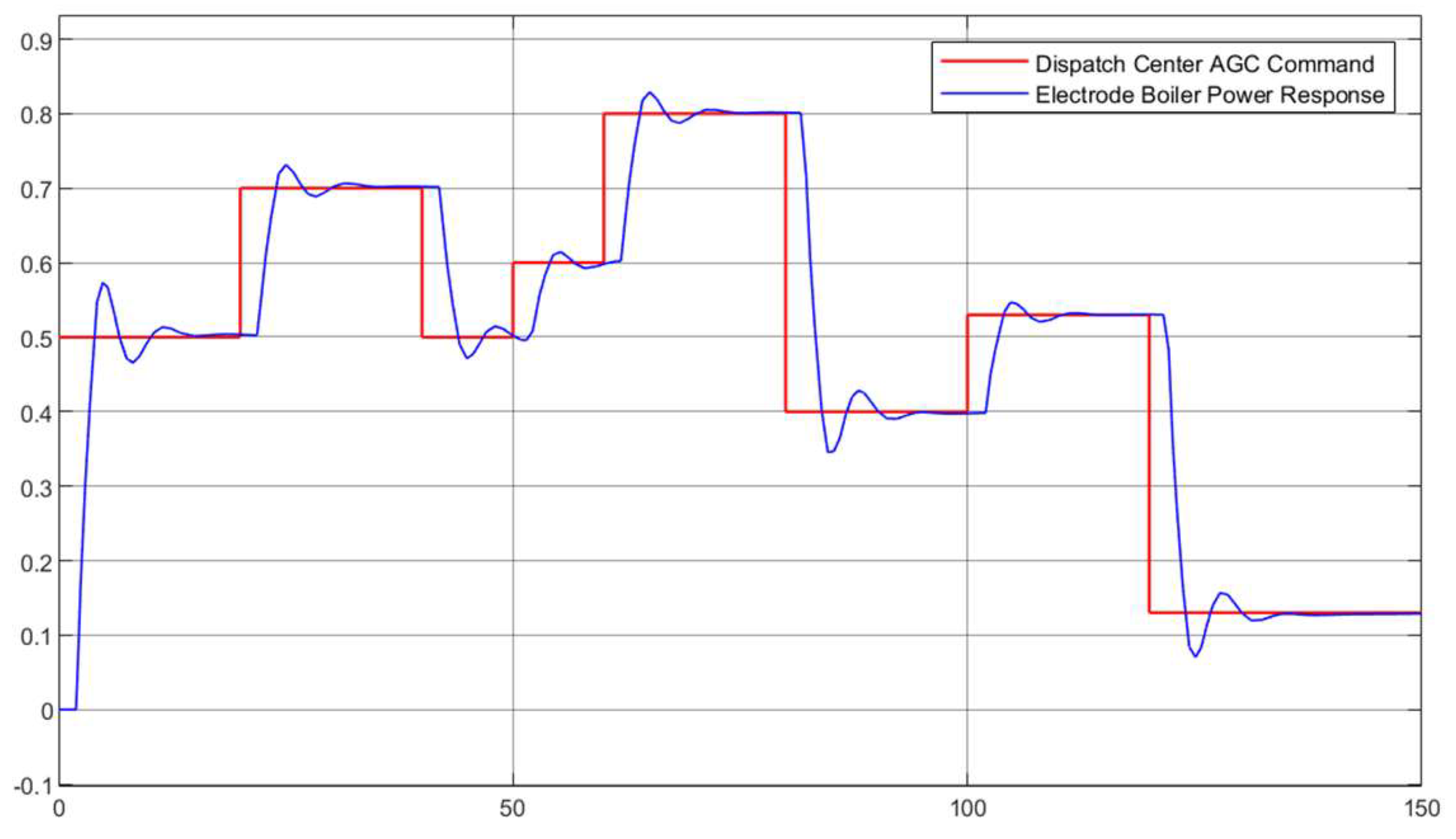
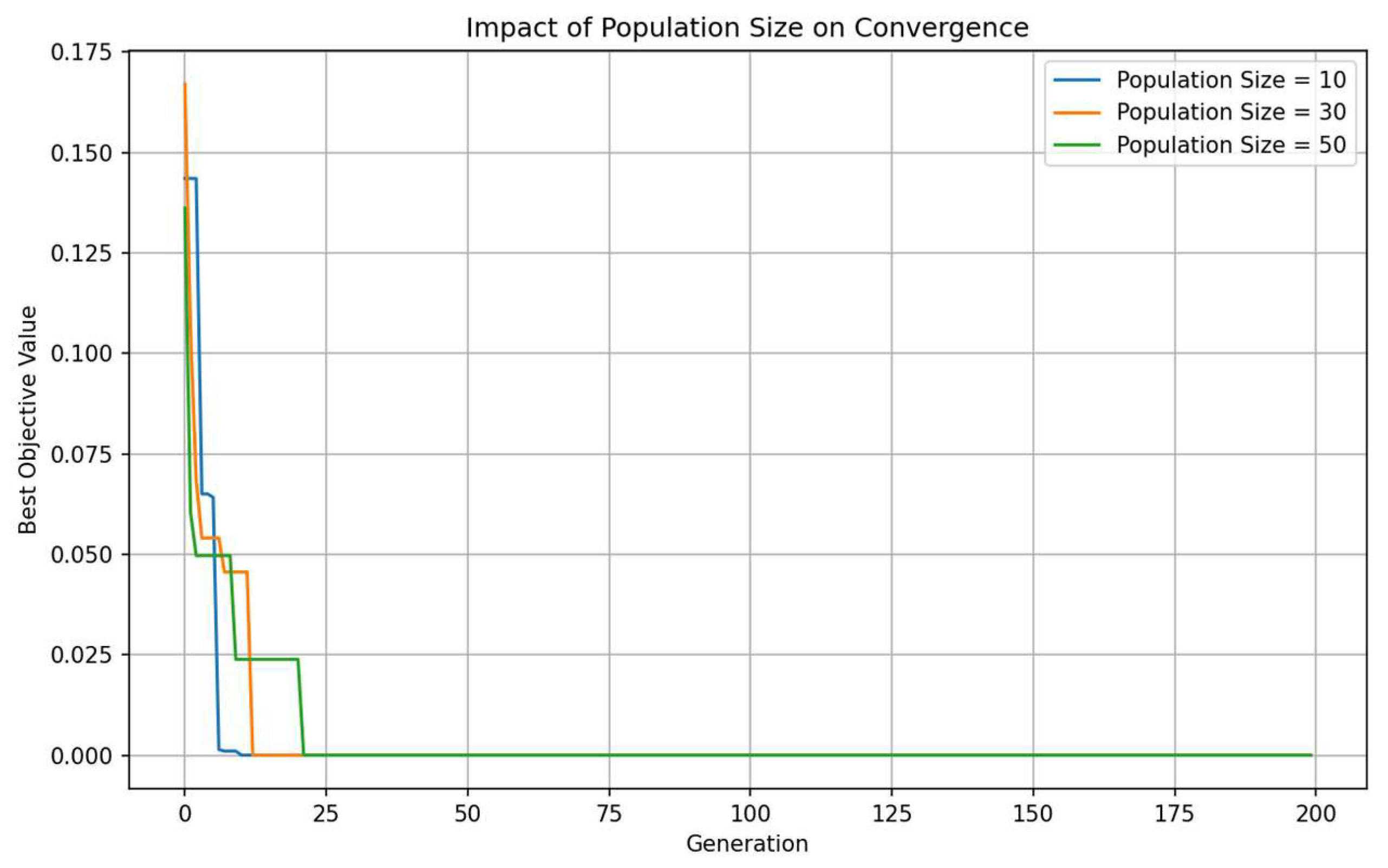
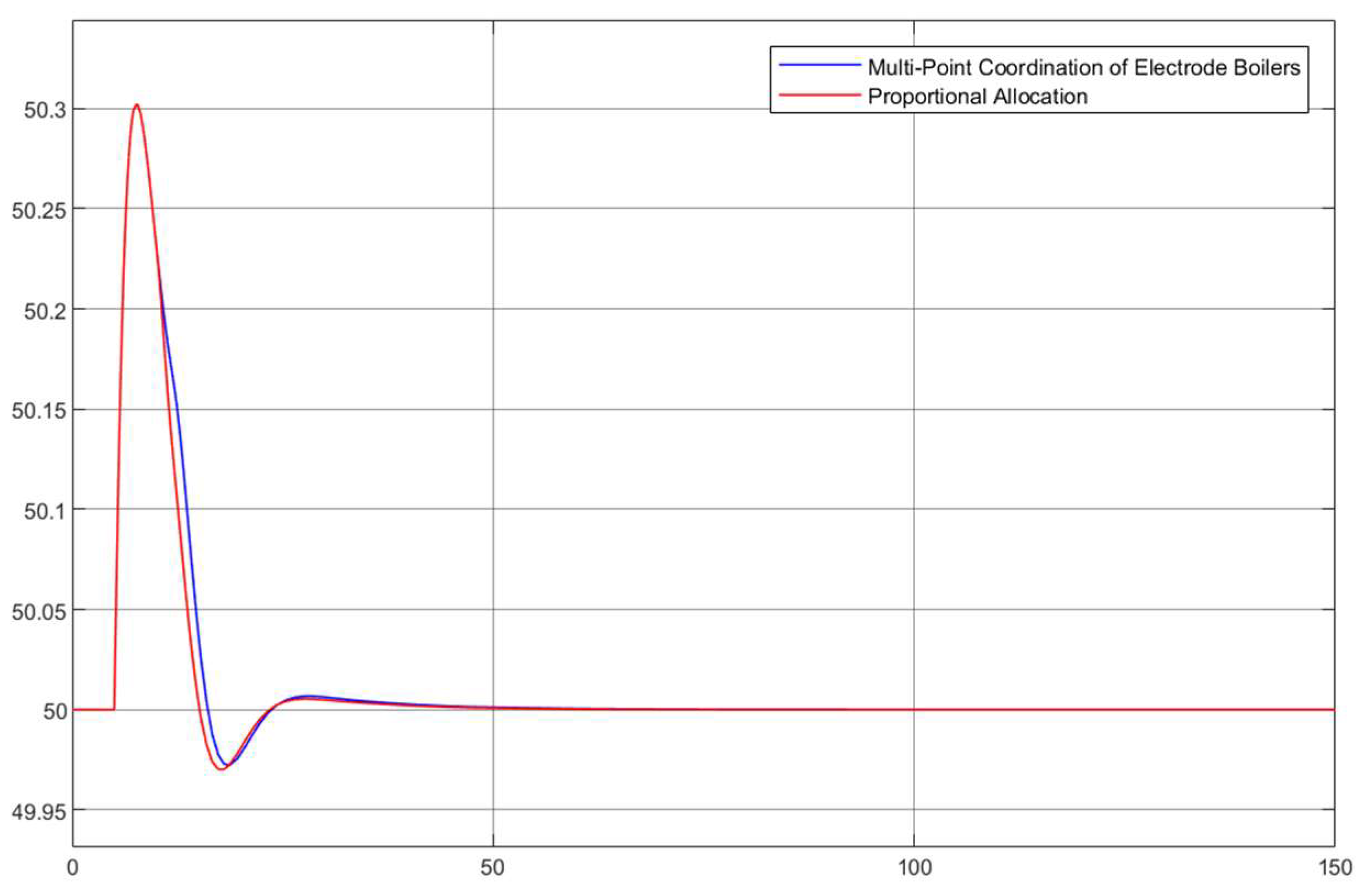
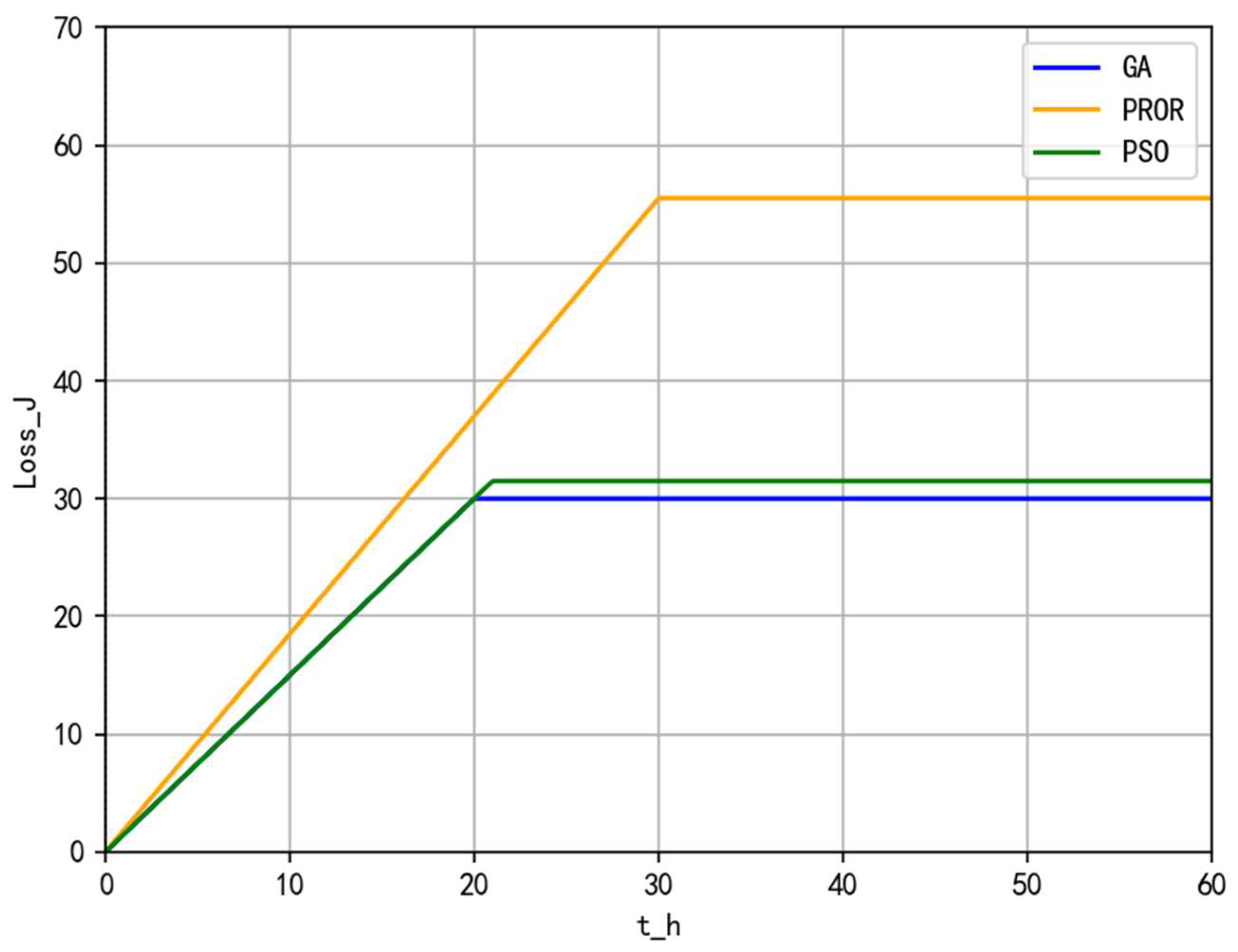
6. Case Study Analysis
6.1. Case System Description
6.2. Frequency Response Characteristics
6.3. Economic Benefit Comparison
6.4. Heat Loss Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| frequency regulation output of traditional units | MW | |
| adjustment power of electrode boiler n | MW | |
| system frequency deviation | HZ | |
| the secondary frequency regulation demand signal | MW | |
| the input adjustment power command for the i-th AGC unit | MW | |
| the actual output of the adjustment power for the i-th AGC unit | MW | |
| AGC control cycle | s | |
| the frequency regulation mileage | HZ | |
| the clearing price in the frequency regulation ancillary services market | ¥ | |
| the operation cost coefficients for the electric heating part | - | |
| the operation cost coefficients for the thermal storage device | - | |
| the output heat power of the electric heating part of the electrode boiler during the t-th period | MW | |
| the operating power of the thermal storage device of the i-th electrode boiler during the t-th period | MW | |
| the consumed curtailed wind power | MW·h | |
| the amount of low-cost electricity purchased from the grid | MW·h | |
| the price of low-cost electricity | ¥ | |
| the construction cost coefficient of the electrode boiler heating device | - | |
| the maximum heating power of the electrode boiler | MW | |
| the construction cost coefficient of the thermal storage device | - | |
| the maximum capacity of the thermal storage device | MW·h | |
| the heat transfer coefficient of the pipeline | W/m2·°C | |
| the surface area of the pipeline | m2 | |
| ,, | non-negative weights representing the relative importance of each objective | |
| the response power value of each electrode boiler | MW | |
| the power adjustment command value issued by the control center | MW | |
| the heating revenue from the electrode boiler | ¥ | |
| the subsidy for supporting grid frequency regulation | ¥ | |
| the operating cost of the electrode boiler | ¥ | |
| the thermal loss | MW·h | |
| the power value allocated to each electrode boiler | MW | |
| the minimum daily heating value guaranteed by the electrode boiler | MW | |
| the maximum power of the electrode boiler | MW | |
| the initial power value of the electrode boiler | MW | |
| the electrical-to-thermal conversion efficiency of the electrode boiler | - | |
| the initial capacity of the electrode boiler | MW·h | |
| the heat generated by the electrode boiler in response to power adjustment | MW·h | |
| the minimum thermal value required by the thermal storage tank to meet the heat demand | MW·h | |
| the maximum thermal value required by the thermal storage tank to meet the heat demand | MW·h | |
| the subsidy coefficient | - | |
| the cost of the electrode boiler participating in power adjustment | ¥ | |
| the basic operating cost of the electrode boiler | ¥ | |
| the operation and maintenance cost of the electrode boiler | ¥ | |
| the heat loss coefficient | - | |
| the objective function value | - | |
| the power value of the i-th electrode boiler | - |
References
- Li, C.; Li, J.; Li, J.; Zhang, X.; Hou, T. Optimization strategy of secondary frequency modulation based on dynamic loss model of the energy storage unit. J. Energy Storage 2022, 51, 104425. [Google Scholar] [CrossRef]
- Gicevskis, K.; Linkevics, O. The Role of Decentralized Electrode Boiler in Ancillary Services and District Heating: A Feasibility Assessment. Latv. J. Phys. Tech. Sci. 2023, 60, 32–42. [Google Scholar] [CrossRef]
- Liu, C.; Si, R.; Liu, C.; Li, M. Research on Control Strategy of Isolated Network Operation of Electric Boiler Auxiliary Thermal Power Unit. Jilin Electr. Power 2023, 51, 24–27. [Google Scholar]
- Zhao, H.; Zhang, X.; Xu, Y.; Bao, M. Optimal Allocation of Heat Storage in Integrated Energy System Considering Wind and Photovoltaic Un-certainty. Energy Energy Conserv. 2023, 8, 12–14+158. [Google Scholar]
- Zhang, L.; Zhang, J.; Yan, G.; Dong, X.; Cheng, F. Re-search on Wind Curtailment Consumption Strategy of Large-Scale Regenerative Electric Boiler Load. Electr. Power Constr. 2024, 45, 114–122. [Google Scholar]
- Wu, X. Low-Carbon Optimization Scheduling of Integrated Energy Systems Considering Thermal Storage Electric Boilers and Electric Vehicles. Master’s Thesis, Northeast Electric Power University, Jilin, China, 2024. [Google Scholar]
- Wang, Z.; Yang, L.; Tian, C.; Li, G. Energy Optimization for Combined System of Wind-electric Energy Storage-regenerative Electric Boiler Considering Wind Consumption. Proc. CSEE 2017, 37, 137–143. [Google Scholar] [CrossRef]
- Cui, Y.; Zhang, J.; Wang, Z.; Wang, M.; Zhao, Y. Strategy of Wind Curtailment Accommodation in Heating Season by Considering Joint Operation of Concentrated Solar Power Plant and Electric Boiler. High Volt. Eng. 2021, 47, 2250–2258. [Google Scholar] [CrossRef]
- Yan, G.; Yang, Y. Economic Analysis of Electric Heating for Wind Power Consumption Under the Background of Ancillary Service Market. J. Glob. Energy Interconnect. 2019, 2, 309–316. [Google Scholar] [CrossRef]
- Ji, X.; Chen, J. Optimization Analysis of AGC Function Strategy for a Hydropower Plant Based on Frequency Modulation Auxiliary Service Market. Hongshui River 2024, 43, 137–141+153. [Google Scholar]
- Zhang, S.; Liu, H.; Wang, F.; Huo, H.; Shi, T. A Balancing Control Strategy for “Power-X-Power” Energy Storage Cluster in System Load Frequency Control. Proc. CSEE 2022, 42, 886–900. [Google Scholar]
- Grigsby, L.L. Power System Stability and Control; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Yu, T.; Wang, Y.M.; Ye, W.J.; Zhou, B.; Chan, K.W. Stochastic optimal generation command dispatch based on improved hierarchical reinforcement learning approach. IET Gener. Transm. Distrib. 2011, 5, 789–797. [Google Scholar] [CrossRef]
- Datta, M.; Senjyu, T. Fuzzy control of distributed PV inverters/energy storage systems/electric vehicles for frequency regulation in a large power system. IEEE Trans. Smart Grid 2013, 4, 479–488. [Google Scholar] [CrossRef]
- Fan, J. Electric Boiler Temperature Control Based on the Fuzzy Self-tuning PID Algorithm. Master’s Thesis, Shenyang Ligong University, Shenyang, China, 2013. [Google Scholar]
- Xie, H.; Wang, C.; Liu, P.; Liu, H.; Xu, G. Application of Joint Frequency Regulation Technology of Energy Storage and Thermal Power in China South-ern Power Grid. Autom. Electr. Power Syst. 2021, 45, 172–179. [Google Scholar]
- Mi, L.; Bian, X. Development on genetic algorithm theory and its applications. Appl. Res. Comput. 2010, 27, 2425–2429+2434. [Google Scholar]
- Liu, J.; Li, J.; Bai, X. Reactive Power Optimization of Distribution Network Using Genetic Algorithm with Elitist Strategy. Electr. Eng. 2015, 4, 35–38. [Google Scholar]
- Man, K.F.; Tang, K.S.; Kwong, S. Genetic Algorithms: Concepts and Designs; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Yang, L.; Li, S.; Huang, W.; Zhang, D.; Ma, H. Optimal coordinated control of multi-source for AGC with participation of wind and solar energy. Power Syst. Prot. Control 2020, 48, 43–49. [Google Scholar]
- Yu, H. China’s Wind Power Development Study of the Cost and Wind Power Generators Selection. Master’s Thesis, North China Electric Power University, Beijing, China, 2009. [Google Scholar]
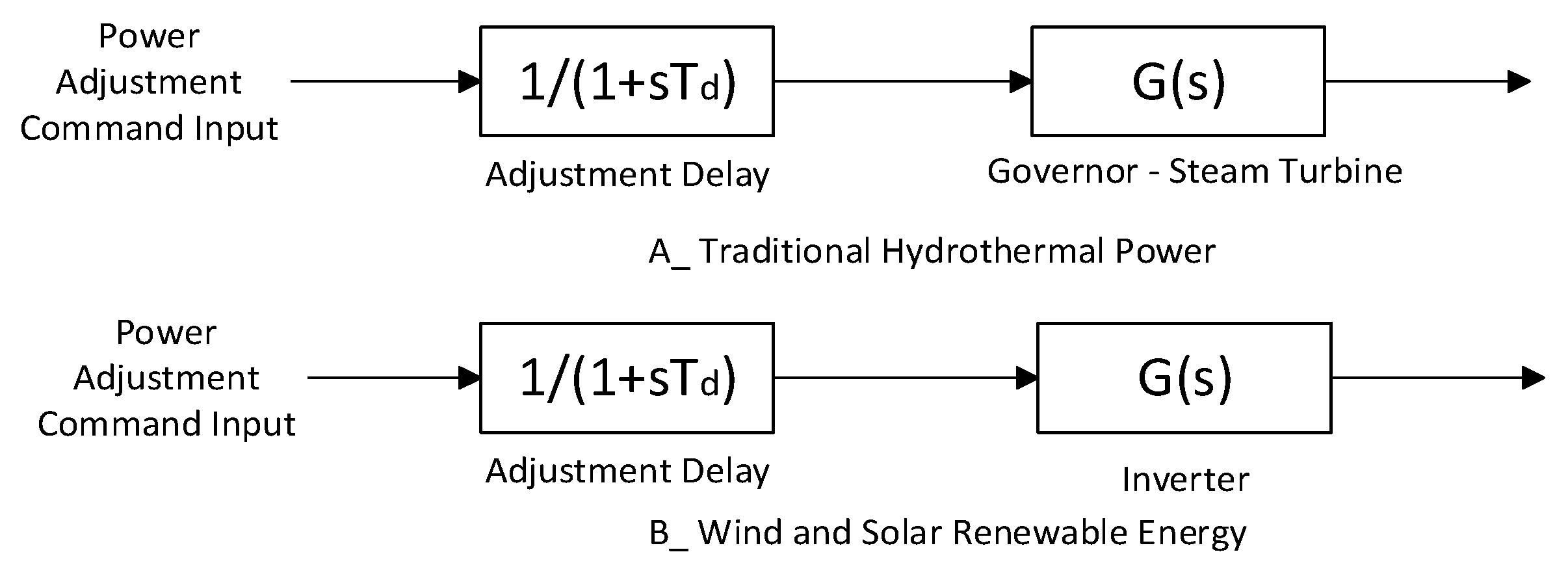


| Type | Types of Transfer Functions |
|---|---|
| Synchronous Units | |
| Wind and Solar Renewable Energy |
| Weight Combination | Power Deviation (kW) | Total Cost (¥) | Heat Loss (MJ) |
|---|---|---|---|
| Base Weight [0.4, 0.3, 0.3] | 5.2 | 6800 | 2.5 |
| w1↑ [0.48, 0.26, 0.26] | 3.1 (−40%) | 7120 (+4.7%) | 2.8 (+12%) |
| w1↓ [0.32, 0.34, 0.34] | 7.9 (+52%) | 6520 (−4.1%) | 2.1 (−16%) |
| w2↑ [0.34, 0.36, 0.30] | 6.5 (+25%) | 6380 (−6.2%) | 2.6 (+4%) |
| w2↓ [0.46, 0.24, 0.30] | 4.0 (−23%) | 7250 (+6.6%) | 2.9 (+16%) |
| w3↑ [0.34, 0.30, 0.36] | 6.8 (+31%) | 6950 (+2.2%) | 1.9 (−24%) |
| w3↓ [0.46, 0.30, 0.24] | 2.8 (−46%) | 7180 (+5.6%) | 3.2 (+28%) |
| Type | Transfer Function Parameters |
|---|---|
| Synchronous Units | = 2, = 0.05, = 5, = 0.2 |
| Wind Turbine Units | = 0.01 |
| Parameter ZHP-2850 | Electrode Boiler Model | Parameter RITEC-C50000-95 | Thermal Storage Tank Model |
|---|---|---|---|
| Rated Power/MW | 50 | Thermal Storage Power/MW | 60 |
| Maximum Heat Supply/MW | 50 | Heat Release Power/MW | 60 |
| Minimum Heat Supply/MW | 50 | Maximum Thermal Storage Capacity/MWH | 600 |
| Thermal Efficiency/% | 98 | Minimum Thermal Storage Capacity/MWH | 100 |
| Allocation Strategy | Equipment Type | AGC Adjustment Command/MW |
|---|---|---|
| Proportional Allocation | Electrode Boiler 1 | 10 |
| Electrode Boiler 2 | 5 | |
| Electrode Boiler 3 | 5 | |
| Electrode Boiler 4 | 10 | |
| Electrode Boiler 5 | 9.46 | |
| Generating Unit | 20 | |
| Multi-point Cooperative Optimization | Electrode Boiler 1 | 5.08 |
| Electrode Boiler 2 | 15.32 | |
| Electrode Boiler 3 | 15.4 | |
| Electrode Boiler 4 | 12.08 | |
| Electrode Boiler 5 | 1.81 | |
| Generating Unit | 10 |
| Optimization Algorithm | Power Deviation/MW | ||
|---|---|---|---|
| 60 | PROP | 0.54 | 0.09 |
| PSO | 0.35 | 0.075 | |
| GA | 0.3 | 0.07 |
| Type | Frequency Regulation Compensation Price/¥ | Electricity Price/¥ | Heat Price/¥ | Coal Price/¥ |
|---|---|---|---|---|
| Price | 10 | 0.4 | 44 | 700 |
| Type | Frequency Regulation Revenue/¥ | Operating Cost/¥ | Single Frequency Regulation Revenue/¥ |
|---|---|---|---|
| PROR | 600 | 360 | 240 |
| PSO | 600 | 335 | 265 |
| GA | 600 | 333 | 267 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, T.; Wang, C.; Chen, Z. The Multi-Point Cooperative Control Strategy for Electrode Boilers Supporting Grid Frequency Regulation. Processes 2025, 13, 785. https://doi.org/10.3390/pr13030785
Shi T, Wang C, Chen Z. The Multi-Point Cooperative Control Strategy for Electrode Boilers Supporting Grid Frequency Regulation. Processes. 2025; 13(3):785. https://doi.org/10.3390/pr13030785
Chicago/Turabian StyleShi, Tao, Chunlei Wang, and Zhiqiang Chen. 2025. "The Multi-Point Cooperative Control Strategy for Electrode Boilers Supporting Grid Frequency Regulation" Processes 13, no. 3: 785. https://doi.org/10.3390/pr13030785
APA StyleShi, T., Wang, C., & Chen, Z. (2025). The Multi-Point Cooperative Control Strategy for Electrode Boilers Supporting Grid Frequency Regulation. Processes, 13(3), 785. https://doi.org/10.3390/pr13030785







