Research on a Data-Driven Fast Calculation Method for Power Distribution in Small Nuclear Power Reactor Core
Abstract
:1. Introduction
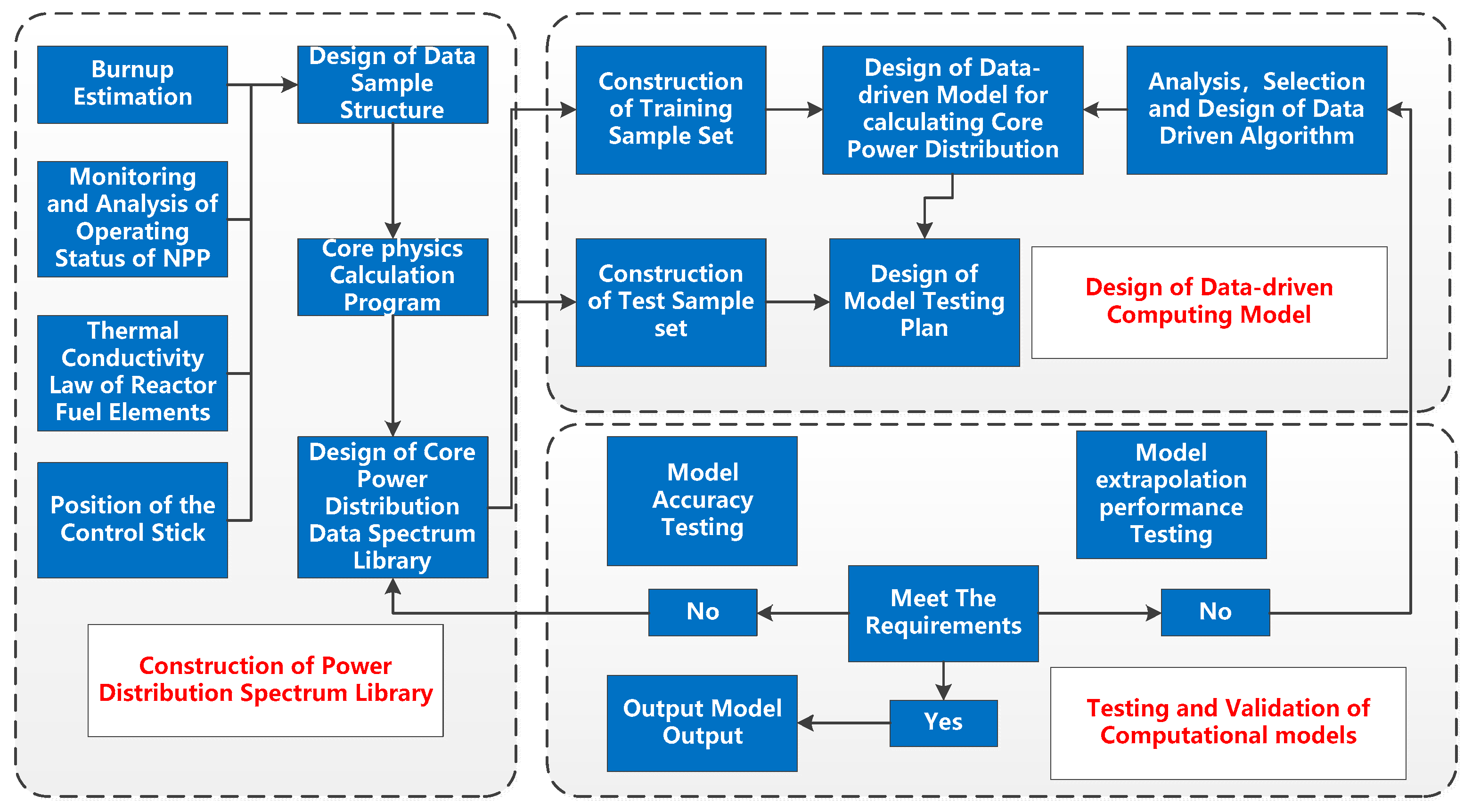
2. Core Power Distribution Calculation Agent Model
2.1. Construction of Power Distribution Spectrum Library
2.1.1. Selection and Modeling of Physical Computing Program
2.1.2. Design of Input and Output Parameters
- (1)
- The parameters are easy to obtain. The average temperature of the core can be calculated by the data of the reactor inlet temperature measuring point and the reactor outlet temperature measuring point. Since many control parameters choose the average temperature as a reference, this paper chooses the average temperature as an input parameter. The reactor burnup can be calculated quickly by integrating these two parameters with reference to the reactor power and operating time.
- (2)
- The parameters are simple and easy to analyze. Temperature is a widely known physical quantity, which can be easily accepted and quickly understood by reactor operators, and the analysis does not need to make very complex calculations or require research, so that people at all levels can quickly observe. Although the burnup involves integral calculation, as long as the reactor power and operation time are recorded, the required parameters can be quickly obtained through some calculation programs without further analysis and simplification.
- (3)
- The parameters are relatively independent. These two parameters are independent of some other parameters, especially the reactor burnup. This parameter is related to the core energy release and fuel quality, and will not be affected by other parameters. The reactor temperature has a great relationship with the core power, and has no direct relationship with the parameters such as pressure and spatial position.
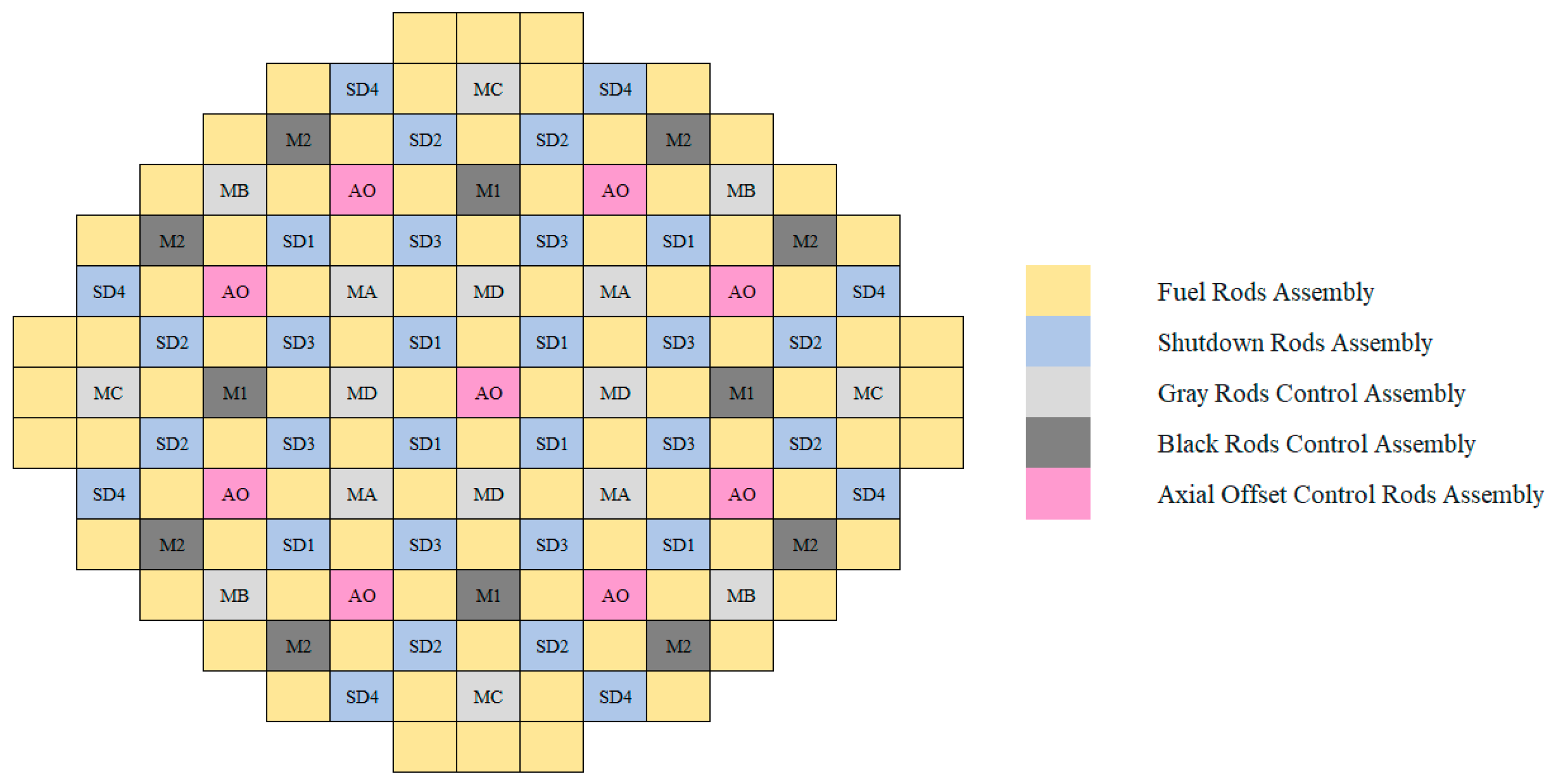
2.1.3. Core Operating Condition Design
- (1)
- Reactor core temperature range setting
- (2)
- Reactor burnup depth interval setting
2.2. Data-Driven Computing Model Design
3. Sample Set Construction and Training
- (1)
- Randomly extract a data point from the training set of the original data spectral library.
- (2)
- Add a random value in the normal distribution to all the elements of this data point. The mean value of the normal distribution is 0, and the standard deviation is 0.1, that is, N(0, 0.01), which constitutes a new data point.
- (3)
- Continue to repeat the above two steps until the number of data expands to 2000, thus completing data expansion.
- (1)
- Read the data of the test set to the corresponding path.
- (2)
- Extract independent variables and dependent variables, and load the data of independent variables into the model.
- (3)
- The model predicts the output of the independent variables in turn, and analyzes the error with the results of the test set.
- (4)
- Output prediction results, tabulate the prediction results, and compare them with the calculated true values.
- (5)
- Output the evaluation index of the model and judge the quality of the model.
4. Model Testing and Verification
4.1. Effect of Different Rounds on Prediction
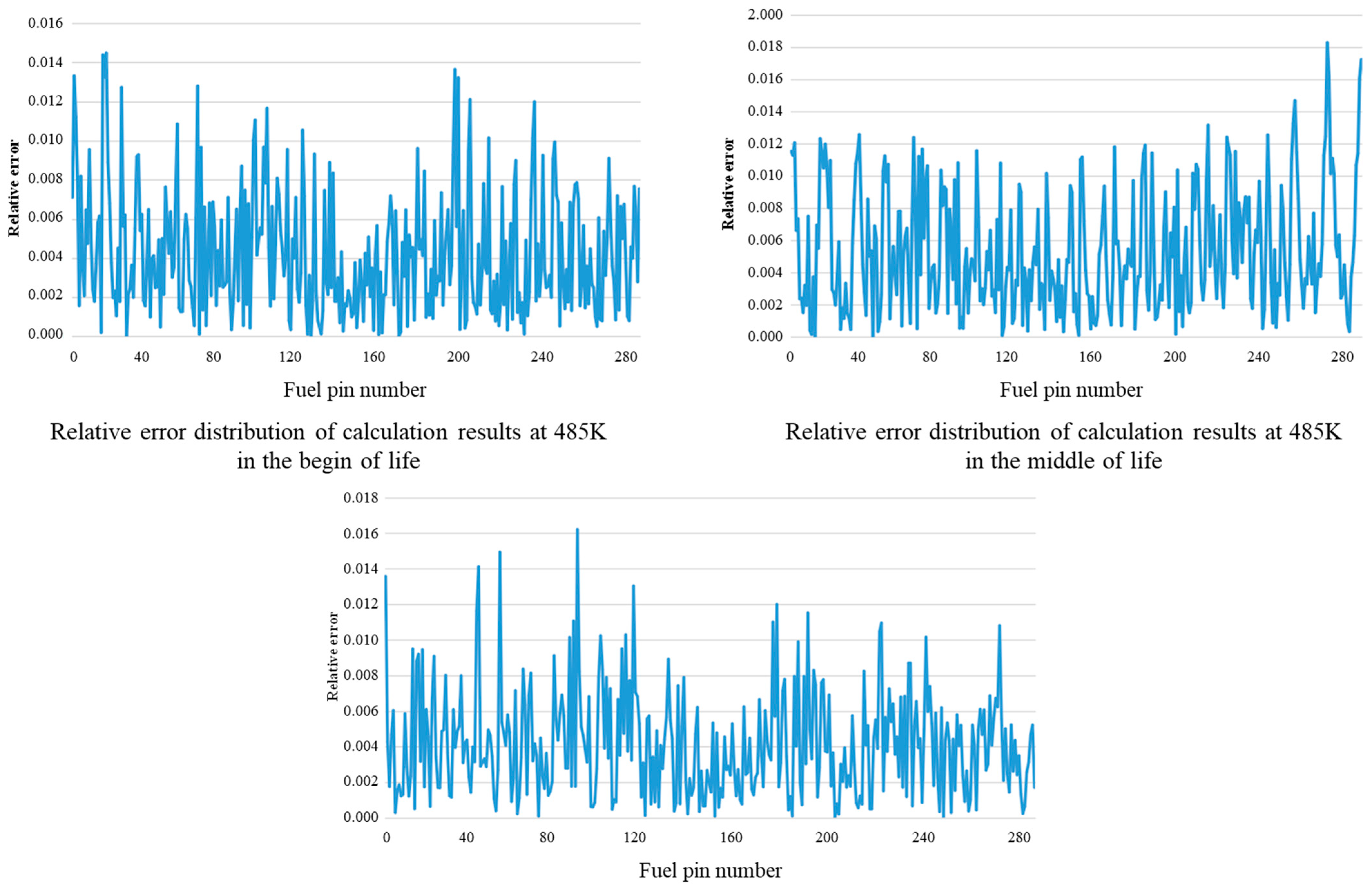
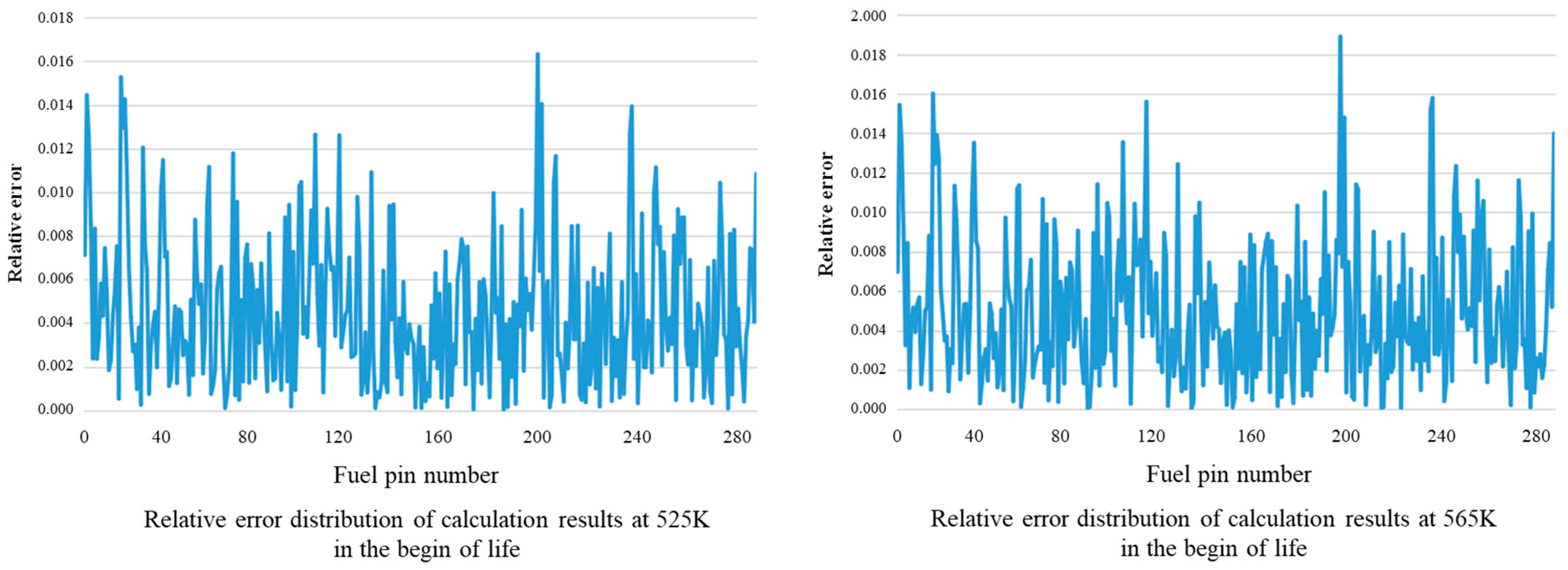
4.2. The Influence of Different Working Conditions on the Prediction
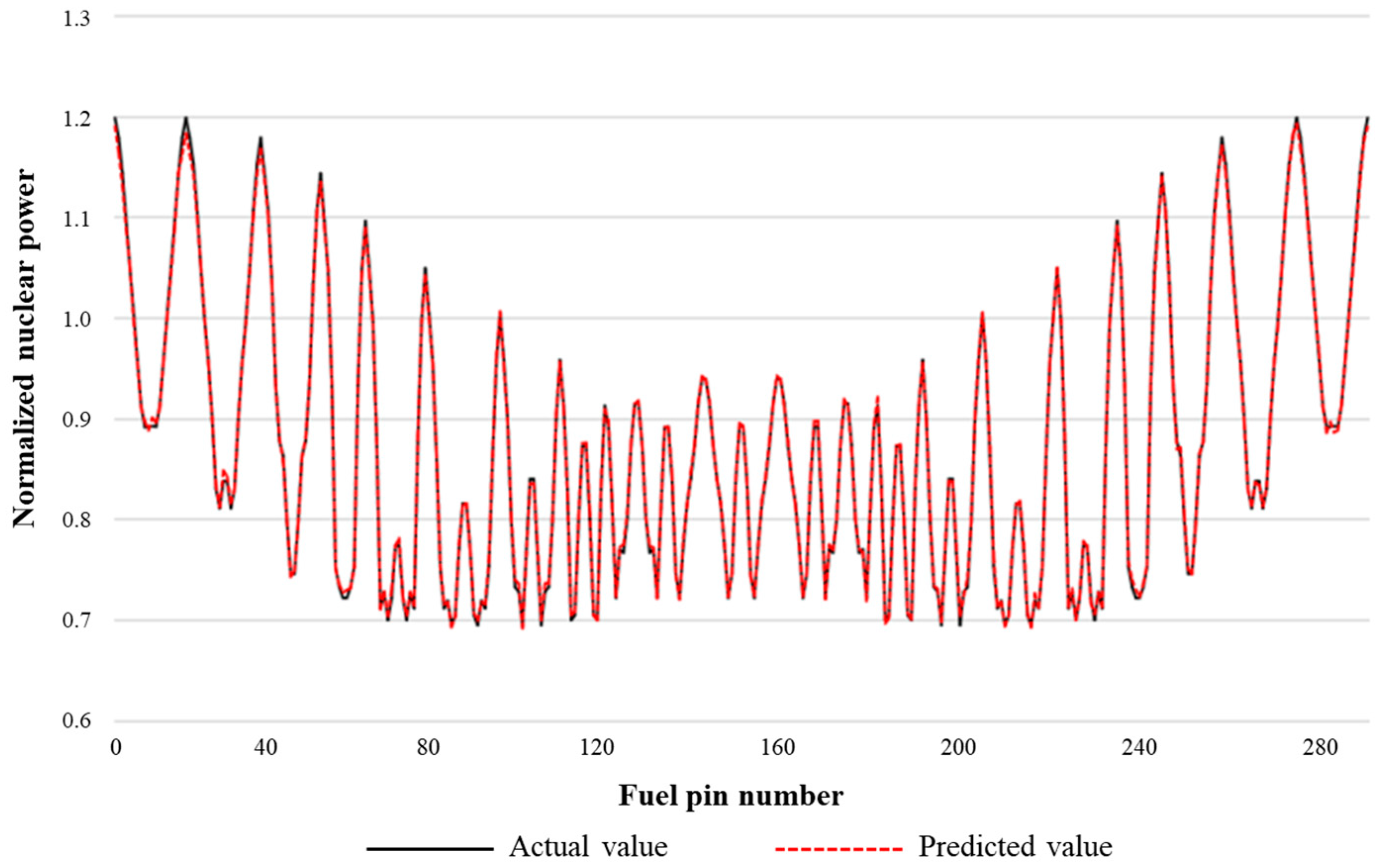
4.3. Prediction Results of Different Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, L.; Qi, L.; Lei, T.; Ping, A.; Fan, Y. Solving Multi-Dimensional Neutron Diffusion Equation Using Deep Machine Learning Technology Based on PINN Model. Nucl. Power Eng. 2022, 43, 1–8. [Google Scholar] [CrossRef]
- Wang, J.; Peng, X.; Chen, Z.; Zhou, B.; Zhou, Y.; Zhou, N. Surrogate modeling for neutron diffusion problems based on conservative physics-informed neural networks with boundary conditions enforcement. Ann. Nucl. Energy 2022, 176, 109234. [Google Scholar] [CrossRef]
- Yang, Y.; Gong, H.; Zhang, S.; Yang, Q.; Chen, Z.; He, Q.; Li, Q. A data-enabled physics-informed neural network with comprehensive numerical study on solving neutron diffusion eigenvalue problems. Ann. Nucl. Energy 2023, 183, 109656. [Google Scholar] [CrossRef]
- Prantikos, K.; Tsoukalas, L.H.; Heifetz, A. Physics-Informed Neural Network Solution of Point Kinetics Equations for a Nuclear Reactor Digital Twin. Energies 2022, 15, 7697. [Google Scholar] [CrossRef]
- Elhareef, M.H.; Wu, Z. Physics-Informed Neural Network Method and Application to Nuclear Reactor Calculations: A Pilot Study. Nucl. Sci. Eng. 2022, 197, 601–622. [Google Scholar] [CrossRef]
- Kharazmi, E.; Zhang, Z.; Karniadakis, G.E. hp-VPINNs: Variational physics-informed neural networks with domain decomposition. Comput. Methods Appl. Mech. Eng. 2021, 374, 113547. [Google Scholar] [CrossRef]
- Zeng, F.; Zhang, X.; Zhao, P. Study on Neutron Diffusion Calculation Method Based on hp-VPINN. Nucl. Power Eng. 2024, 45, 53–62. [Google Scholar] [CrossRef]
- Chen, H.; Hu, N.; Cheng, Z.; Zhang, L.; Zhang, Y. A deep convolutional neural network based fusion method of two-direction vibration signal data for health state identification of planetary gearboxes. Measurement 2019, 146, 268–278. [Google Scholar] [CrossRef]
- Chen, Z.; Gryllias, K.; Li, W. Mechanical fault diagnosis using Convolutional Neural Networks and Extreme Learning Machine. Mech. Syst. Signal Process. 2019, 133, 106272. [Google Scholar] [CrossRef]
- Dias, A.; Silva, F. Determination of the power density distribution in a PWR reactor based on neutron flux measurements at fixed reactor incore detectors. Ann. Nucl. Energy 2016, 90, 148–156. [Google Scholar] [CrossRef]
- Roop, J.P. A randomized neural network based Petrov–Galerkin method for approximating the solution of fractional order boundary value problems. Results Appl. Math. 2024, 23, 100493. [Google Scholar] [CrossRef]
- Talon, J.D.; Martinez, A.S.; Gonçalves, A.C. Continuous mapping of nuclear reactor core power using artificial neural network even in the presence of inactive detectors. Nucl. Eng. Technol. 2024, 56, 4983–4996. [Google Scholar] [CrossRef]
- Yadav, V.; Casel, M.; Ghani, A. RF-PINNs: Reactive flow physics-informed neural networks for field reconstruction of laminar and turbulent flames using sparse data. J. Comput. Phys. 2025, 524, 113698. [Google Scholar] [CrossRef]
- Fukaya, Y.; Okita, S.; Nakagawa, S.; Goto, M.; Ohashi, H. Computed tomography neutron detector system to observe power distribution in a core with long neutron flight path. Ann. Nucl. Energy 2022, 168, 108911. [Google Scholar] [CrossRef]
- Hong, Q.; Jun, M.; Bo, W.; Sichao, T.; Jiayi, Z.; Biao, L.; Tong, L.; Ruifeng, T. Application of Data-Driven technology in nuclear Engineering: Prediction, classification and design optimization. Ann. Nucl. Energy 2023, 194, 110089. [Google Scholar] [CrossRef]
- Li, W.; Ding, P.; Xia, W.; Chen, S.; Yu, F.; Duan, C.; Cui, D.; Chen, C. Artificial neural network reconstructs core power distribution. Nucl. Eng. Technol. 2022, 54, 617–626. [Google Scholar] [CrossRef]
- Riva, S.; Introini, C.; Cammi, A. Multi-physics model bias correction with data-driven reduced order techniques: Application to nuclear case studies. Appl. Math. Model. 2024, 135, 243–268. [Google Scholar] [CrossRef]
- Wang, P.; Liang, W.; Gong, H.; Chen, J. Decoupling control of core power and axial power distribution for large pressurized water reactors based on reinforcement learning. Energy 2024, 313, 133967. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, Y.; Wang, X.; Li, X. Using ex-core detectors and deep neural networks for monitoring power distribution in small space reactors. Nucl. Eng. Des. 2025, 431, 113721. [Google Scholar] [CrossRef]
- Xia, H.; Li, B.; Liu, J. Research on intelligent monitor for 3D power distribution of reactor core. Ann. Nucl. Energy 2014, 73, 446–454. [Google Scholar] [CrossRef]
- Birri, A.; Blue, T.E. Methodology for inferring reactor core power distribution from an optical fiber based gamma thermometer array. Prog. Nucl. Energy 2020, 130, 103552. [Google Scholar] [CrossRef]
- Daniell, J.; Kobayashi, K.; Alajo, A.; Alam, S.B. Digital twin-centered hybrid data-driven multi-stage deep learning framework for enhanced nuclear reactor power prediction. Energy AI 2025, 19, 100450. [Google Scholar] [CrossRef]
- Lin, C. Passive Safety Advanced Nuclear Power Plant AP1000; Atomic Energy Press: Beijing, China, 2008. [Google Scholar]

| Program | Type of Program | Advantage | Disadvantage |
|---|---|---|---|
| HELIOS | Deterministic calculation program | It can efficiently handle geometric problems and has been fully verified in engineering. | The energy group division is limited. |
| SERPENT | Monte Carlo simulation | It is capable of performing high-precision whole-core simulations. | It consumes a large number of computational resources. |
| MCNP | Monte Carlo simulation | It has the ability of multi-physics field coupling. | It has high requirements for complex modeling. |
| Burnup | Temperature (K) | ||||||
|---|---|---|---|---|---|---|---|
| 300 | 350 | 400 | … | 560 | 570 | 580 | |
| Begin of core life | Data set 1 | Data set 2 | Data set 3 | … | Data set 13 | Data set 14 | Data set 15 |
| Middle of core life | Data set 16 | Data set 17 | Data set 18 | … | Data set 28 | Data set 29 | Data set 30 |
| End of core life | Data set 31 | Data set 32 | Data set 33 | … | Data set 43 | Data set 44 | Data set 45 |
| Burnup | Temperature (K) | ||||
|---|---|---|---|---|---|
| 485 | 505 | 525 | 545 | 565 | |
| Begin of core life | Test Data Set 1 | Test Data Set 2 | Test Data Set 3 | Test Data Set 4 | Test Data Set 5 |
| Middle of core life | Test Data Set 6 | Test Data Set 7 | Test Data Set 8 | Test Data Set 9 | Test Data Set 10 |
| End of core life | Test Data Set 11 | Test Data Set 12 | Test Data Set 13 | Test Data Set 14 | Test Data Set 15 |
| Burnup | Normalized Power | ||||
|---|---|---|---|---|---|
| Begin of core life | 1.18631071 | 1.16744554 | 1.13338888 | … | 1.18631071 |
| Middle of core life | 1.06825895 | 1.05830290 | 1.04020645 | … | 1.06825906 |
| End of core life | 0.9931693 | 0.98777205 | 0.97811884 | … | 0.99316883 |
| Burnup | Value | Normalized Power | ||||
|---|---|---|---|---|---|---|
| Begin of core life | calculated value | 1.198592 | 1.178821 | 1.143291 | … | 1.198592 |
| predicted value | 1.190074 | 1.163124 | 1.130471 | … | 1.189555 | |
| Middle of core life | calculated value | 1.070453 | 1.060435 | 1.042371 | … | 1.070453 |
| predicted value | 1.084272 | 1.073732 | 1.056160 | … | 1.091116 | |
| End of core life | calculated value | 0.994609 | 0.989268 | 0.979757 | … | 0.994608 |
| predicted value | 0.978352 | 0.98424 | 0.981766 | … | 0.992567 | |
| Model | Total Deviation Value | Average Absolute Error | Mean Square Error | Computing Time (s) |
|---|---|---|---|---|
| Simple neural network | 987.4433 | 0.1959 | 0.2326 | <1 |
| Binary regression model | 53.6718 | 0.0106 | 0.0002 | <1 |
| Deep learning neural network | 21.3427 | 0.0042 | 0.00003 | <1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, S.; Zhang, Y.; Zhang, C. Research on a Data-Driven Fast Calculation Method for Power Distribution in Small Nuclear Power Reactor Core. Processes 2025, 13, 841. https://doi.org/10.3390/pr13030841
Wang X, Li S, Zhang Y, Zhang C. Research on a Data-Driven Fast Calculation Method for Power Distribution in Small Nuclear Power Reactor Core. Processes. 2025; 13(3):841. https://doi.org/10.3390/pr13030841
Chicago/Turabian StyleWang, Xiaolong, Song Li, Yongfa Zhang, and Cong Zhang. 2025. "Research on a Data-Driven Fast Calculation Method for Power Distribution in Small Nuclear Power Reactor Core" Processes 13, no. 3: 841. https://doi.org/10.3390/pr13030841
APA StyleWang, X., Li, S., Zhang, Y., & Zhang, C. (2025). Research on a Data-Driven Fast Calculation Method for Power Distribution in Small Nuclear Power Reactor Core. Processes, 13(3), 841. https://doi.org/10.3390/pr13030841





