Impact of Heterogeneity in Low-Permeability Reservoirs on Self-Diverting Acid Wormhole Formation and Acidizing Parameter Optimization

Abstract

Carbonate rocks typically exhibit strong heterogeneity, which can have a significant impact on the effectiveness of acidification processes, and different types of acids are needed in the field to achieve various acidizing goals. This article develops a self-diverting acidizing program based on the two-scale continuum model and open-source software FMOT, and investigates the influence of heterogeneity intensity on wormhole morphology and acidizing process parameters. The results indicate that different heterogeneity intensities significantly affected the morphology of the wormhole. At low intensity, the shape of the wormhole is close to a straight line, while at high intensity, it becomes tree-like. The reason for the significant impact is that the higher the heterogeneity intensity, the more obvious the dominant path within the rock, the more uneven the high viscosity zone formed, and the more obvious the turning of spent acid flow. The optimal injection rate of self-diverting acid increases with the increase in temperature. At lower injection rates, the self-diverting acid can produce more branching wormholes, and low temperatures enhance this effect, especially at high heterogeneity. Whether at a higher or lower acid injection rate, increasing the acid injection temperature appropriately is helpful to improve the acidizing efficiency. The acid injection rate and temperature should be adjusted to adapt to the pore heterogeneity of different intensities.

1. Introduction

Matrix acidizing is a technique in which acid is injected into a reservoir below the formation rupture pressure to dissolve substances that impede fluid flow and increase reservoir permeability [1]. The technology restores and enhances reservoir productivity by creating “acid wormholes” with high conductivity near the well [2]. However, due to the influence of formation heterogeneity, conventional acid fluids often flow along the path of least resistance, leading to uneven acid etching and affecting their potential for production enhancement [3]. To address this issue, self-diverting acids have been introduced. By adding specific chemicals (such as the viscoelastic surfactant (VES)), these acids can alter the flow direction, achieving a more uniform etching distribution and thereby overcom ing the limitations of conventional acidizing. Many studies have found that different parameters will affect the matrix acidizing effect [4,5,6], such as acid concentration, injection rate, formation characteristics and other factors that significantly affect the acid erosion mode. In the conventional acidizing process, the acid tends to advance along the most erosive path, resulting in limited treatment effectiveness [7]. While these studies provide an important reference for optimizing acid formulations, they also reveal the challenges that conventional acidizing methods face when dealing with heterogeneous layers. In contrast, self-diverting acids can not only better deal with reservoir heterogeneity but also reduce secondary damage to the reservoir [8,9]. For example, Chang et al. [10] found that VES acid has a better acidizing effect than traditional acids, especially when dealing with complex geological structures, and the change in VES viscosity can effectively guide the flow direction of acid and achieve a more uniform distribution of acid corrosion. In multi-zone well acidizing, Dilip et al. [11] also used self-diverting acid to prevent the acid from bypassing the low permeability zone into the high permeability zone. Cesin et al. [12] found that switching to an acid-formed viscoelastic system reduced leakage reduced the formation of wormholes near the wellbore and further extended the length of natural fractures in the reservoir.

In order to understand the complex physical and chemical phenomena in the acidizing process and optimize acidizing process design, numerical simulation has become an indispensable tool [13]. The two-scale continuum model (TSC) established by Panga et al. [14] has been widely used to describe the transport and reaction mechanism in the reactive dissolution process of porous media. Kalia et al. [15] explored the heterogeneity of porous media, while Didier et al. [16] investigated the competitive mechanism of wormhole growth. Liu et al. [17] analyzed the influence of acid injection conditions on the growth of acid etch wormholes, while Cunqi et al. [18] focused on the influence of the shape of porous media. Ferreira et al. employed real porosity and permeability distributions to characterize carbonate reservoirs and forecast the formation of acid wormhole pathways induced by acidizing processes [19]. P. Maheshwari et al. [20] determined the characteristics of the wormhole tip diameter and fractal dimension, and found that the tip diameter of the wormhole was the largest on the heterogeneous length scale and the transverse dispersion reaction length scale by comparing the experimental data. Bekibayev found that dominant wormholes grow faster than non-dominant wormholes, resulting in rapid acidic breakout, resulting in limited acidizing range [21]. These studies not only reveal the limitations of conventional acidizing but also lay the foundation for the numerical simulation development of self-diverting acids. For example, Liu et al. [22,23] investigated the effects of heterogeneity and biparallel acidizing, and modeled a temperature-sensitive acid, finding that the bottom hole temperature has a greater effect on the viscosity of the steering acid than the reaction rate and diffusion coefficient. In addition, Liu et al. investigated the impact of rock permeability on VES acid [24]. Bulgakova et al. [25] studied the effect of VES on acid rock reaction, and proposed a semi-empirical rheological model to describe the relationship between viscosity, rate and HCl. Zhang et al. [26] developed a VES to acid wormhole model and found that the main wormhole and viscosification have a competitive effect on leakage. Wormholes reduce the flow resistance, while viscosity and increased waste acid band width increase the flow resistance. Mou et al. [27] believed that the acid dissolution mode of VES was related to the injection rate, a certain acid injection rate formed a dominant wormhole, and the acid coordination effect of VES acid in heterogeneous layers was better than that of conventional acids. Compared to conventional acids, VES acids have fewer branches of wormholes. These studies show that self-diverting acids are widely used in the treatment of heterogeneous carbonate reservoirs, which can achieve better economic and technical results under complex geological conditions.

However, the influence of varying heterogeneous strengths on the formation pattern and breakthrough form of wormholes has not been clearly discussed in the numerical simulation of self-diverting acid, and the specific role of self-diverting acid process parameters has not been deeply discussed. Overall, it is essential to carry out detailed investigations into the aforementioned three aspects.

2. Mathematical Models

The self-diverting acid dissolves the rock to generate Ca²⁺, and it mixes the SDVA and spent acid together to form a high-viscosity zone. The high-viscosity forces the acid to change its flow direction. Based on the TSC model [14] and the temperature coupling model proposed by Kalia and Glasbergen [28], a two-scalar continuous self-diverting deciding model with ten parts can be derived [29,30].

(1)

Pressure equation:

The self-diverting acid is considered an incompressible fluid, which means the pressure equation can be expressed as follows [29,30]:

$$-\nabla ·(K\lambda \nabla P)=Q$$

(1)

Here, K is the permeability, $\lambda$ is the mobility, and P is the pressure field.

(2)

Velocity equation of the self-diverting acid:

The velocity equation of the self-diverting acid is formulated based on Darcy’s law [14]:

$$\mathit{U}=-\mathit{K}\lambda \nabla P$$

(2)

where $\mathit{U}$ represents the velocity field of the self-diverting acid.

(3)

Self-diverting acid concentration Equation ($H^{+}$):

Based on the acidizing (TSC) model, the scalar transport equation for the self-diverting acid can be expressed as [29,30]:

$${\displaystyle \frac{\partial \varphi C_f}{\partial t}}+\nabla ·\left(\mathit{U}{C}_f\right)=\nabla ·\left(\varphi {\mathit{D}}_e·\nabla C_f\right)-\underset{\mathrm{reaction}\mathrm{consumption}}{\underbrace{R\left(C_s\right)a_v}}$$

(3)

where $\varphi$ is the porosity, $C_f$ is the cup-mixing mass concentration of the self-diverting acid concentration ($H^{+}$), $R\left(C_s\right)$ is the effective dispersion tensor for the self-diverting acid concentration ($H^{+}$), and $a_v$ is the interfacial area of the rock.

(4)

Ca²⁺ concentration equation:

During the process of HCl dissolving rocks, of Ca²⁺ is generated, with 1 mol of Ca²⁺ produced for every 2 mol of HCl consumed. Hence, similar to H⁺, the scalar transport equation of Ca²⁺ within rock is [24,30]:

$${\displaystyle \frac{\partial \varphi C_{Ca}}{\partial t}}+\nabla ·\left(\mathit{U}{C}_{Ca}\right)=\nabla ·\left(\varphi {\mathit{D}}_{e,Ca}·\nabla C_{Ca}\right)+\underset{\mathrm{reaction}\mathrm{generate}}{\underbrace{0.5R\left(C_s\right)a_v}}$$

(4)

(5)

SDVA concentration equation:

SDVA does not participate in the reaction between acid and rock, and is transported within the pores. Similar to H⁺, the scalar transport equation of SDVA within rock is [24,30]:

$${\displaystyle \frac{\partial \varphi C_{SDVA}}{\partial t}}+\nabla ·\left(\mathit{U}{C}_{SDVA}\right)=\nabla ·\left(\varphi {\mathit{D}}_{e,SDVA}·\nabla C_{SDVA}\right)$$

(5)

(6)

Self-diverting acid temperature equation:

The fluid within the pores and the rock are assumed to undergo dynamic heat transfer processes. As a result, the acid and the rock each have distinct temperature equations. Below, we present the temperature equation for the acid [28,29,30]:

$${\displaystyle \frac{\partial \varphi {\rho }_l{C}_{p,l}{T}_l}{\partial t}}+\nabla ·\left({\mathit{U}}_i{\rho }_l{C}_{p,l}{T}_l\right)=\nabla ·(\varphi k_l\nabla T_l)+H_m{a}_v(T_r-T_l)$$

(6)

where ${\rho }_l$ is the density of acid, $C_{p,l}$ is the specific heat capacity of the self-diverting acid, $T_l$ is the acid temperature field, $k_l$ is the acid conductivity, $H_m$ is the convective heat transfer coefficient, and $T_r$ is the rock temperature field.

(7)

Rock temperature equation:

The heat exchange between rock and acid takes place via thermal conduction, eliminating the presence of a convective term. Additionally, as the acid dissolves the rock, heat is released, leading to the following equation for the rock [28,29,30]:

$${\displaystyle \frac{\partial (1-\varphi ){\rho }_r{C}_{p,r}{T}_r}{\partial t}}=\nabla ·((1-\varphi )k_r\nabla T_r)-H_m{a}_v(T_r-T_l)-\underset{\mathrm{chemical}\mathrm{reaction}\mathrm{heat}}{\underbrace{\Delta H_r\left(T_r\right)a_{v}R\left(C_s\right)}}$$

(7)

where ${\rho }_r$ is the density of rock, $C_{p,r}$ is the specific heat capacity of rock, $k_r$ is the rock conductivity, and $H_r\left(T_r\right)$ is the acid–rock molar reaction heat.

(8)

Chemical reaction process of self-diverting acid and rock:

The reaction equation is as follows:

$$2{\mathrm{H}}^{+}+{\mathrm{CaCO}}_3\left(\mathrm{s}\right)\stackrel{r_s}{\to }{\mathrm{Ca}}^{2+}+{\mathrm{H}}_2\mathrm{O}+{\mathrm{CO}}_2\left(\mathrm{g}\right)$$

(8)

where $r_s$ is the reaction rate at the interface between fluid and solid in rock pores. The interaction between HCl and CaCO₃ is modeled as an irreversible first-order reaction. Consequently, the formula used to compute the chemical reaction terms is expressed as follows:

$$\begin{array}{cc}\hfill & R\left(C_s\right)={\displaystyle \frac{k_c{k}_s}{k_c+k_s}}{C}_f\hfill \\ \hfill & k_s=0.015exp(-18616/RT)C_f^{1.1997}\hfill \\ \hfill & k_c={\displaystyle \frac{\left(S{h}_{\infty }+\frac{0.7}{m^{1/2}}{Re}_p^{1/2}S{c}^{1/3}\right)D_m}{2r_p}}\hfill \end{array}$$

(9)

where $k_c$ is the mass transfer coefficient, $k_s$ is the reaction rate constant, R is the gas constant, $S{h}_{\infty }$ is the, m is the asymptotic Sherwood number, $R{e}_p$ is the ratio of the pore length to pore diameter, $Sc$ is the pore Reynolds number, and $r_p$ is the average pore radius.

(9)

Rock quantity update:

During the process of dissolving rocks, the transformation of acid can change the pore structure. Based on the TSC model, the updating of rock physical quantities can be divided into the Darcy scale and the pore scale. The updated calculation formula for quantity at the Darcy scale is [14]:

$${\displaystyle \frac{\partial \varphi }{\partial t}}={\displaystyle \frac{R\left(C_s\right)a_v{\alpha }_c}{{\rho }_s}}$$

(10)

where $a_c$ is the dissolving power of the acid. The updated calculation formula for quantity at the poro scale is [14]:

$${\displaystyle \frac{K_{new}}{K_{init}}}={\displaystyle \frac{{\varphi }_{new}}{{\varphi }_{init}}}{\left[{\displaystyle \frac{{\varphi }_{new}(1-{\varphi }_{init})}{{\varphi }_{init}(1-{\varphi }_{new})}}\right]}^{2\beta }$$

(11a)

$${\displaystyle \frac{r_{p,new}}{r_{p,init}}}=\sqrt{{\displaystyle \frac{K_{new}{\varphi }_{init}}{K_{init}{\varphi }_{new}}}}$$

(11b)

$${\displaystyle \frac{a_{v,new}}{a_{v,init}}}={\displaystyle \frac{{\varphi }_{new}{r}_{p,init}}{{\varphi }_{init}{r}_{p,new}}}$$

(11c)

$$\begin{array}{cc}\hfill & D_L^e={\alpha }_{os}{D}_e+{\displaystyle \frac{2{\lambda }_L\left|\mathit{U}\right|r_p}{\varphi }}\hfill \\ \hfill & D_T^e={\alpha }_{os}{D}_e+{\displaystyle \frac{2{\lambda }_T\left|\mathit{U}\right|r_p}{\varphi }}\hfill \end{array}$$

(11d)

$K_{init}$ and ${\varphi }_{init}$ correspond to the initial permeability and porosity, respectively. These values remain unchanged throughout the calculation process, serving as fixed constants. Moreover, $D_L^e$ and $D_T^e$ indicate the effective diffusion coefficients in the x and y directions. ${\alpha }_{os}$, ${\lambda }_L$, and ${\lambda }_T$ represent structural constants related to the pore characteristics.

(10)

Viscosity of the self-diverting acid update:

As the chemical reaction between acid and rock progresses, the viscosity of the spent acid of self-diverting acid can change. Based on Liu’s experiment, the updated formula for the viscosity of the spent acid is [24]:

$$\begin{array}{cc}\hfill {\mu }_{eff}& ={\displaystyle \frac{{\mu }_0}{12}}{\left(9+{\displaystyle \frac{3}{n}}\right)}^n{\left(150K\varphi \right)}^{(1-n)/2}\hfill \\ \hfill \times & \left[\begin{array}{c}1+{\displaystyle \frac{{\mu }_{max}}{{\mu }_0}}exp\left(-0.5{\left({\displaystyle \frac{C_{\mathrm{SDVA}}-C_{SDVA,max}}{W_1}}\right)}^2\right)\hfill \\ \times exp\left(-{\left({\displaystyle \frac{C_{Ca}-C_{Ca,max}}{W_2}}\right)}^2\right)\times {\displaystyle \frac{\left(erf\right(bPH-c)+1)}{W_3}}\hfill \end{array}\right]\hfill \end{array}$$

(12)

where ${\mu }_0$ and ${\mu }_{max}$ are the initial and max viscosity of self-diverting acid, respectively. In this paper, the max viscosity is 350 mPa·s (0.35 Pa·s). $C_{Ca,max}$ and $C_{SDVA,max}$ are the max concentration of Ca²⁺ and SDVA, and the max values are 2.109 and 0.06, respectively. b, c, $W_1$, $W_2$ and $W_3$ are both empirical coefficients with the value are 1, 1, 0.0173, 1.1 and 2, respectively. The pH value can be calculated by the equilibrium equation of acid concentration:

$$pH=-lg\left(C_f\right)$$

(13)

3. Numerical Methods

The finite volume method is employed to solve Equations (1)–(12). Leveraging the PDE solver program software FMOT [29,30], we carry out the simulation process described in this paper. Below, we present the discrete forms and computational procedures of the equations used herein. It is worth noting that the program verification for this study can be referenced in Chang’s published work.

3.1. Discretition Method

In this paper, the discrete scheme we use is shown in the

Table 1. The discrete scheme used in this paper.

Operator	Symbol	Discrete Scheme	Accuracy
Temporal term	${\displaystyle \frac{\partial }{\partial t}}$	Backward Euler	$O\left(\Delta x^2\right)$
Convective term	$\nabla ·\left(\right)$	First-order upwind	$O\left(\Delta x^1\right)$
Laplacian term	$\nabla ·(\nabla )$	Center difference	$O\left(\Delta x^2\right)$

. Here, we provide the algebraic form of equations calculated by implicit methods. It is important to note that the surface value is indicated by the subscript f, which is determined through interpolation of the physical quantities located at the centers of two neighboring cells. Moreover, the surface flux computed using the first-order upwind scheme is represented by $F_f$.

Based on the discrete scheme of each operator, we provide the algebraic forms of all implicit equations after discretization. The form of algebraic equations is:

$$A_P{x}_P+A_N{x}_N+A^{up}{x}_{up}={\mathit{S}}_u$$

(14)

where $A_P$, $A_N$, $A^{up}$, and ${\mathit{S}}_u$ are the principal component coefficients, non-principal component coefficients, upwind format discretized coefficients of discretize matrix and source terms. Based on this form, the algebraic equation for each equation is:

(1)

Pressure equation:

$$\begin{array}{cc}\hfill & A_P{P}_P+A_N{P}_N={\mathit{S}}_u\hfill \\ \hfill & A_P=\sum K_f{\lambda }_f{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill & \hfill A_N=-\sum K_f{\lambda }_f{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\\ \hfill & {\mathit{S}}_u=V_{p}Q\hfill \end{array}$$

(15)

(2)

Self-diverting acid concentration equation ($H^{+}$):

$$\begin{array}{cc}\hfill & A_P{C}_{f,P}^{t+\Delta t}+A_N{C}_{f,P}^{t+\Delta t}+A^{up}{C}_{f,P}^{up,t+\Delta t}={\mathit{S}}_u\hfill \\ \hfill & A_P=V_p{\varphi }^t+\Delta t\sum {{\varphi }_f}^t{\mathit{D}}_{e,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \\ \hfill & A_N=-\Delta t\sum {{\varphi }_f}^t{\mathit{D}}_{e,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \\ \hfill & A^{up}=\Delta t\sum {\mathit{F}}_f^t\hfill \\ \hfill & {\mathit{S}}_u=V_p{\varphi }^t{C}_{f,P}^t+\Delta t{V}_{p}R\left(C_s\right)a_v\hfill \end{array}$$

(16)

(3)

Ca²⁺ concentration equation:

$$\begin{array}{cc}\hfill & A_P{C}_{Ca,P}^{t+\Delta t}+A_N{C}_{Ca,P}^{t+\Delta t}+A^{up}{C}_{Ca,P}^{up,t+\Delta t}={\mathit{S}}_u\hfill \\ \hfill & A_P=V_p{\varphi }^t+\Delta t\sum {{\varphi }_f}^t{\mathit{D}}_{e,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \\ \hfill & A_N=-\Delta t\sum {{\varphi }_f}^t{\mathit{D}}_{e,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \\ \hfill & A^{up}=\Delta t\sum {\mathit{F}}_f^t\hfill \\ \hfill & {\mathit{S}}_u=V_p{\varphi }^t{C}_{Ca,P}^t+0.5\Delta t{V}_{p}R\left(C_s\right)a_v\hfill \end{array}$$

(17)

(4)

SDVA concentration equation:

$$\begin{array}{cc}\hfill & A_P{C}_{SDVA,P}^{t+\Delta t}+A_N{C}_{SDVA,P}^{t+\Delta t}+A^{up}{C}_{SDVA,P}^{up,t+\Delta t}={\mathit{S}}_u\hfill \\ \hfill & A_P=V_p{\varphi }^t+\Delta t\sum {{\varphi }_f}^t{\mathit{D}}_{e,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \\ \hfill & A_N=-\Delta t\sum {{\varphi }_f}^t{\mathit{D}}_{e,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \\ \hfill & A^{up}=\Delta t\sum {\mathit{F}}_f^t\hfill \\ \hfill & {\mathit{S}}_u=V_p{\varphi }^t{C}_{SDVA,P}^t\hfill \end{array}$$

(18)

(5)

Self-diverting acid temperature equation:

$$\begin{array}{cc}\hfill & A_P{T}_{P,l}^{t+\Delta t}+A_N{T}_{N,l}^{t+\Delta t}+A^{up}{T}_P^{up,t+\Delta t}={\mathit{S}}_u\hfill \\ \hfill & A_P=V_p{\varphi }^t{\rho }_l^t{C}_{p,l}^t+\Delta t\sum {\varphi }_f^t{k}_{l,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}+\Delta t{V}_p{H}_m^t{a}_v^t\hfill \\ \hfill & A_N=-\Delta t\sum {\varphi }_f^t{k}_{l,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \\ \hfill & A_{up}=\Delta t\sum {\mathit{F}}_f^t\hfill \\ \hfill & {\mathit{S}}_u=V_p{\varphi }^t{\rho }_l^t{C}_{p,l}^t{T}_{P,l}^t+\Delta t{V}_p{H}_m^t{a}_v^t{T}_r^t\hfill \end{array}$$

(19)

(6)

Rock temperature equation:

$$\begin{array}{cc}\hfill & A_P{T}_{P,r}^{t+\Delta t}+A_N{T}_{N,r}^{t+\Delta t}={\mathit{S}}_u\hfill \\ \hfill & A_P=V_p{(1-\varphi )}^t{\rho }_s^t{C}_{p,s}^t+\Delta t\sum {(1-\varphi )}_f^t{k}_{s,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}+\Delta t{V}_p{H}_m^t{a}_v^t\hfill \\ \hfill & A_N=-\Delta t\sum {(1-\varphi )}_f^t{k}_{s,f}^t{\displaystyle \frac{|{\mathit{S}}_f|}{\left|\mathit{d}\right|}}\hfill \\ \hfill & {\mathit{S}}_u=V_p{(1-\varphi )}^t{\rho }_s^t{C}_{p,s}^t{T}_{P,r}^t+\Delta t{V}_p{H}_m^t{a}_v^t{T}_l^t-V_p\Delta H_r{\left(T\right)}^t{a}_v^t{\displaystyle \frac{k_c^t{k}_s^t}{k_c^t+k_s^t}}{C}_f^{t+\Delta t}\hfill \end{array}$$

(20)

3.2. Numerical Discretization Method and Test Parameters

The numerical simulation process is illustrated in Figure 1, and the general parameters employed for the simulations in this study are outlined in

Table 2. General parameters of simulation cases.

Parameter	L [m]	H [m]	$C_{f,in}$ [kmol/m3]	${\mathit{U}}_{\mathit{i}\mathit{n}}$ [cm/s]
Value	0.3	0.1	4.4178 (15 wt% HCL)	1–$1\times {10}^{-3}$
Parameter	$\varphi$ [%]	K [m2]	${\mu }_w$ [mPa·s]	$C_{p,l}$ [J/(kg·°C)]
Value	0.01–0.5	Calculated	1	4180
Parameter	$C_{p,r}$ [J/(kg·°C)]	$k_l$ [W/(m·°C)]	$a_c$ [kg/kmol]	$k_r$ [W/(m·°C)]
Value	999	0.6508	50	5.2
Parameter	$a_v$ [m2/m3]	$D_e$ [m2/s]	$a_c$ [kg/kmol]	$H_m$ [W/(m2·°C)]
Value	5000	$3.6\times {10}^{-9}$	50	600

.

3.3. Model Validation

Due to the randomness of porosity distribution, the accuracy of the developed program is generally verified in seepage problems by comparing the trend of pressure curve changes. This paper compares and verifies the calculation results of the developed program with the pressure curve obtained from Gomaa’s experiment [8] and the simulation results with Liu [24].

Figure 2 displays the three pressure curves, it can be seen that the pressure curve trend we calculated (Figure 2a) is highly consistent with the numerical simulation results of Liu [24] (Figure 2b) and the experimental results of Gomaa [8] (Figure 2c). Therefore, our program is accurate.

4. Results and Analysis

In this paper, we first examine the impact of varying heterogeneity levels on the wormhole morphology in self-diverting systems. Additionally, we analyze how different heterogeneity intensities affect the optimal injection rate and temperature.

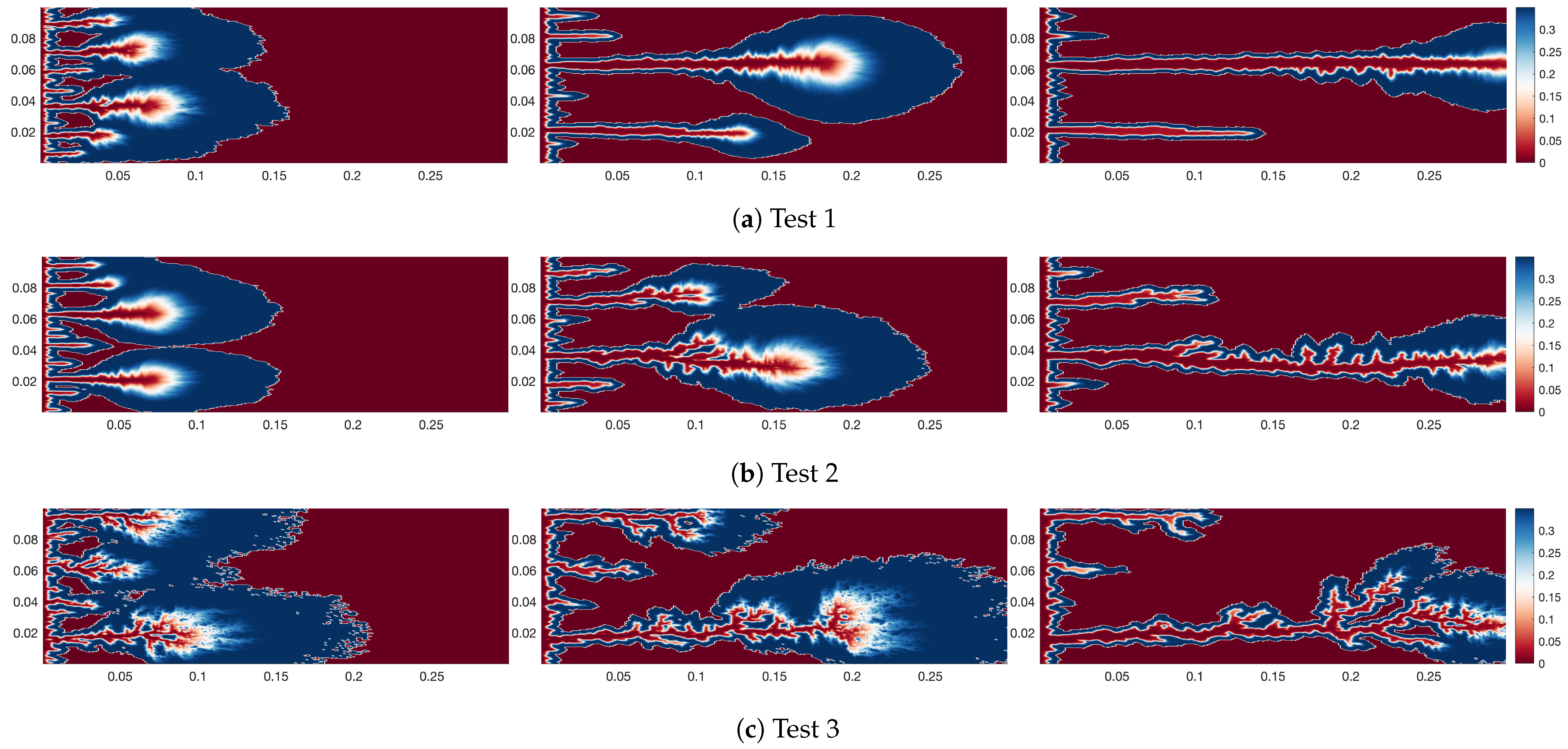
4.1. Effect of Different Heterogeneity Intensity on Wormhole Morphology of Self-Diverting

In this paper, we discuss three different heterogeneity porosity distributions that use random numbers to generate. Hence, we set up three cases to investigate this issue. The case parameter is shown in

Table 3. Parameters of Test 1 to Test 3.

Parameter	Symbol	Test 1	Test 2	Test 3
Porosity of matrix [%]	$\varphi$	[15, 25]	[10, 30]	[5, 40]
Inject acid temperature [°C]	$T_{inject}$	60
Inject velocity [cm/s]	${\mathit{U}}_{in}$	$5\times {10}^{-4}$

, and the porosity distribution is shown in Figure 3.

Furthermore, the Carman–Kozeny relation provides a formula that can be used to establish the relationship between porosity and permeability [31,32]:

$$K={\displaystyle \frac{1}{72\tau }}{\displaystyle \frac{{\varphi }^3{d}_p^2}{{(1-\varphi )}^2}},$$

(21)

where $\tau$ and $dp$ are the tortuosity and the hypothetical pressure drop, respectively. Based on Equation (21), the permeability distribution is shown in Figure 4.

Figure 5 shows the development process of wormholes under three different porosity distribution conditions. At low heterogeneity (Test 1), the development trajectory of wormholes approaches a straight line. And there are no obvious branches developed on the main stem of the wormhole, as shown in Figure 5a. As heterogeneity increases, the developmental trajectory of the main stem of the wormhole gradually bends and develops distinct branches, as shown in Figure 5b. In cases of strong heterogeneity, wormholes exhibit distinct branching, presenting a ‘tree like’ appearance, as shown in Figure 5a,b. Overall, the stronger the heterogeneity, the more pronounced the turning effect of self-diverting acid.

Figure 6 displays the viscosity distribution of self-diverting acid under different heterogeneous conditions. It can be observed that the high viscosity zone formed by spent acid wraps around the wormhole. In low porosity heterogeneity, spent acid advances slowly within the rock, while high viscosity zones develop uniformly, as shown in Figure 6a. As the heterogeneity of porosity increases, the advantageous path within the rock becomes more apparent. The advantageous path can accelerate the pushing speed of spent acid inside the rock, and form non-uniform high viscosity zones, as shown in Figure 6c.

It is precisely this non-uniform high viscosity zone that constantly forces the acid solution to change its flow direction, forming a more complex wormhole morphology.

Additionally, we analyze the development of wormholes along the x-axis direction, with the calculation formula presented in Equation (22). Figure 7 inllustrates the calculate result. At low heterogeneity (Test 1), the value of ${\varphi }_{en}$ is in the range of 0.5–1, as shown in Figure 7a. As heterogeneity increases, longer and more complex branches develop on the wormhole, and the value of ${\varphi }_{en}$ also increases. At high heterogeneity (Test 3), the value of ${\varphi }_{en}$ is in the range of 1–2, as shown in Figure 7c.

$${\varphi }_{en}=({\varphi }_b-{\varphi }_{init}/{\varphi }_{init})$$

(22)

where ${\varphi }_{en}$, ${\varphi }_b$ and ${\varphi }_{init}$ are the enhanced porosity, porosity when rock is broken throughand and initial porosity.

Figure 8 presents the $P{V}_{BT}$ values for tests 1 through 3. As the heterogeneity of porosity increases, the continuous turning of wormholes within the rock increases the flow distance of the self-diverting acid. Therefore, as heterogeneity increases, $P{V}_{BT}$ gradually increases.

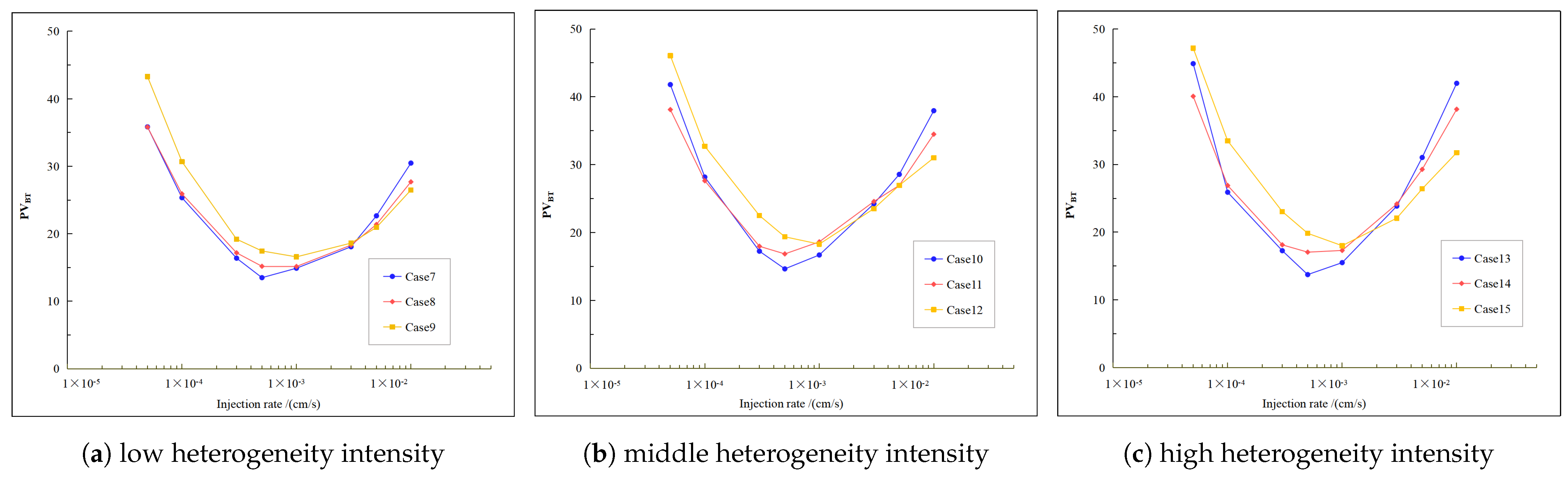
4.2. Influence of Varying Heterogeneity Intensity on the Wormhole Breakthrough Curve

We examine how different levels of heterogeneity intensity influence the breakthrough curve, with the case parameters provided in

Table 4. Parameters of Test 4 to Test 6.

Parameter	Symbol	Test 4	Test 5	Test 6
Porosity of matrix [%]	$\varphi$	[15, 25]	[10, 30]	[5, 40]
Inject acid temperature [°C]	$T_{inject}$	60
Inject velocity [cm/s]	${\mathit{U}}_{in}$	$5\times {10}^{-5}$–$5\times {10}^{-2}$

.

When analyzing the breakthrough curve, it was found that under heterogeneous conditions of different intensities, the optimal injection rate of the self-diverting acid remained stable at 0.05 m/s (aligned with the lowest point of the curve), at which point the $P{V}_{BT}$ values were very similar (refer to Figure 9). Significantly different from conventional acid treatment, the $P{V}_{BT}$ value of the breakthrough curve increases with increased pore heterogeneity, especially in strongly heterogeneous pore structures, where acid diversion can induce the generation of more branching wormhole (as shown in Figure 5), resulting in a wider area of acidizing. It is worth noting that there is little difference in the $P{V}_{BT}$ value of the self-diverting acid either at high or low injection rates. However, during the simulation experiment, it was observed that the maximum injection pressure in the core showed a gradual decline with the increase in injection rate, which indicates that the effect of self-diverting acid weakens with the increase in injection rate. Therefore, in order to improve the effectiveness of the self-steering acid under certain conditions, it is recommended to appropriately reduce the injection rate.

4.3. Influence of Varying Injection Temperatures on the Breakthrough Curve

Lastly, we examine the impact of varying injection temperatures, with the test parameters presented in

Table 5. Parameters of Test 7 to Test 15.

Parameter	Symbol	Test 7	Test 8	Test 9
Porosity of matrix [%]	$\varphi$	[15, 25]
Inject acid temperature [°C]	$T_{inject}$	20	60	100
Inject velocity [cm/s]	${\mathit{U}}_{in}$	$5\times {10}^{-5}$–$5\times {10}^{-2}$
Parameter	Symbol	Test 10	Test 11	Test 12
Porosity of matrix [%]	$\varphi$	[10, 30]
Inject acid temperature [°C]	$T_{inject}$	20	60	100
Inject velocity [cm/s]	${\mathit{U}}_{in}$	$5\times {10}^{-5}$–$5\times {10}^{-2}$
Parameter	Symbol	Test 13	Test 14	Test 15
Porosity of matrix [%]	$\varphi$	[5, 40]
Inject acid temperature [°C]	$T_{inject}$	20	60	100
Inject velocity [cm/s]	${\mathit{U}}_{in}$	$5\times {10}^{-5}$–$5\times {10}^{-2}$

.

Figure 10 presents the wormhole breakthrough curves of self-diverting acid in porous media with low, middle, and high heterogeneous intensity under varying injection temperatures. The optimal injection rate of self-steering acid increases with the increase in temperature, which is particularly significant when the pore heterogeneity is high. With the increase in temperature, the reaction rate of acid and rock per unit time is accelerated, resulting in the optimal injection rate increasing with the increase in temperature. However, under high temperature conditions, the $P{V}_{BT}$ curve is relatively high, indicating a higher breakthrough volume; it is worth noting that this trend reverses at high injection rates. This finding matches the results of Kalia’s research [28]. In particular, Figure 10a,c show the different behavior characteristics of the diverting acid compared to the conventional acid: especially at low injection rates and low temperatures, the $P{V}_{BT}$ value of the self-steering acid increases significantly. This is mainly because at lower injection rates, the effect of turning acid is more significant, more branching wormhole paths can be formed, and the acid’s advance distance along the x-axis is relatively short. The lower temperature plays a catalytic role in this process, especially in environments with higher pore heterogeneity. Specifically, at lower acid injection temperature, the $P{V}_{BT}$ values were 35.84, 41.80 and 44.88, respectively, under three different levels of pore heterogeneity, showing a trend of increasing $P{V}_{BT}$ values with increasing heterogeneity. Therefore, for the self-steering to acid treatment, whether at a higher or lower acid injection rate, an appropriate increase in the acid injection temperature can help improve the acidizing efficiency. Especially in highly heterogeneous reservoirs, it is particularly important to adjust the combination of acid injection temperature and rate to optimize the acidizing effect.

5. Conclusions

In this study, we first examined the influence of heterogeneity intensity on wormhole morphology by considering three distinct heterogeneous porosity distributions: low, middle, and high. Subsequently, the optimal acid injection rate was determined. Finally, the optimal injection temperature was identified. The key findings of this research are summarized below.

(1)

The heterogeneity intensity significantly affects the wormhole morphology. At low heterogeneity intensity, the wormhole morphology approaches a straight line. At moderate non-uniform strength, the shape of the wormhole can undergo some bending. At high heterogeneity intensity, the wormhole appears tree-like.

(2)

The impact of heterogeneity intensity on wormhole morphology primarily originates from the distribution of high-viscosity zones. At low intensities, no clear dominant pathways exist within the rock, causing the spent acid to advance relatively uniformly and create a consistent high-viscosity region. As heterogeneity intensity increases, the dominance of specific pathways becomes more pronounced, leading to more uneven progression of the spent acid. This non-uniform advancement generates irregular high-viscosity areas, which ultimately contribute to the complex morphology of wormholes.

(3)

The stronger the heterogeneity, the longer the flow distance of acid in the rock, and the higher the $P{V}_{BT}$. Although the efficiency of rock breakthrough has slowed down, the improvement effect of porosity inside the rock has become stronger.

(4)

With the increase in heterogeneity intensity, the optimal injection rate of self-steering acid remains unchanged. In particular, under strong heterogeneous pore conditions, the self-diverting acid can produce more branching wormholes, which leads to a wider area of acidizing, but the difference in $P{V}_{BT}$ values at larger and smaller acid injection rates is not significant. In order to enhance the effect of self-steering acid, it is recommended to appropriately reduce the acid injection rate.

(5)

The optimal injection rate of self-steering acid increases with increasing temperature. At a low injection rate, more wormholes can be produced, and lower temperature promotes this phenomenon, and the effect is more obvious with the increase in heterogeneity.