A New Method for Optimizing the Jet-Cleaning Performance of Self-Cleaning Screen Filters: The 3D CFD-ANN-GA Framework
Abstract
1. Introduction
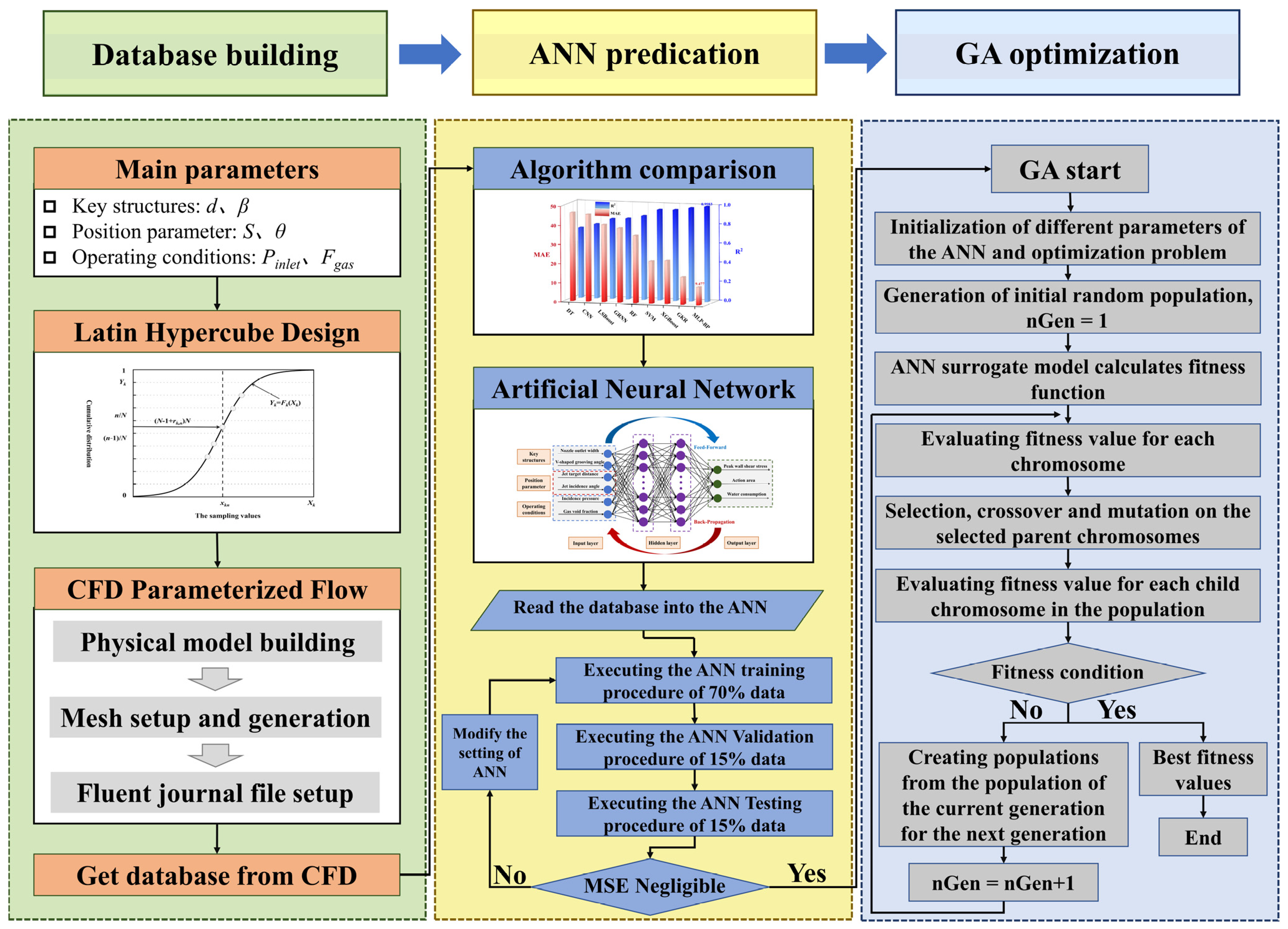
2. Materials and Methods
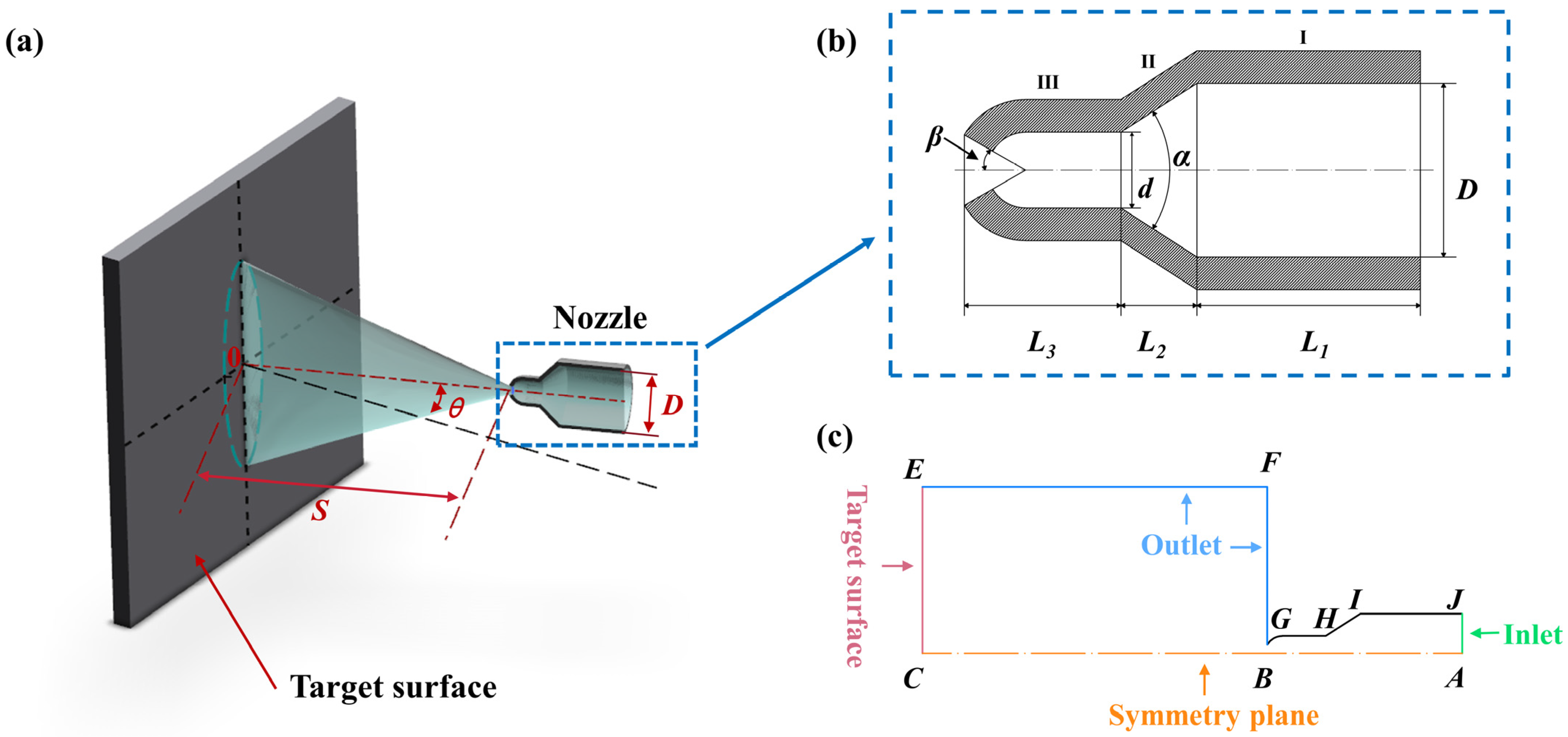
2.1. Jet-Cleaning 3D CFD Modeling
2.1.1. Model Description
- Both gas and liquid phases are incompressible media, immiscible with each other;
- The temperature remains constant throughout the flow process;
- All wall surfaces are smooth with no-slip conditions;
- Gravitational effects in the flow field are negligible.
2.1.2. Performance Index for Jet-Cleaning Models
2.1.3. Selection of Parameters for Jet Cleaning
2.1.4. Mathematical Representation
- Mass conservation equation
- 2.
- Momentum conservation equation
- 3.
- Energy conservation equation
- 4.
- Turbulence model equations
2.1.5. Boundary Conditions and Solver Settings
2.2. Predictive Algorithm Selection
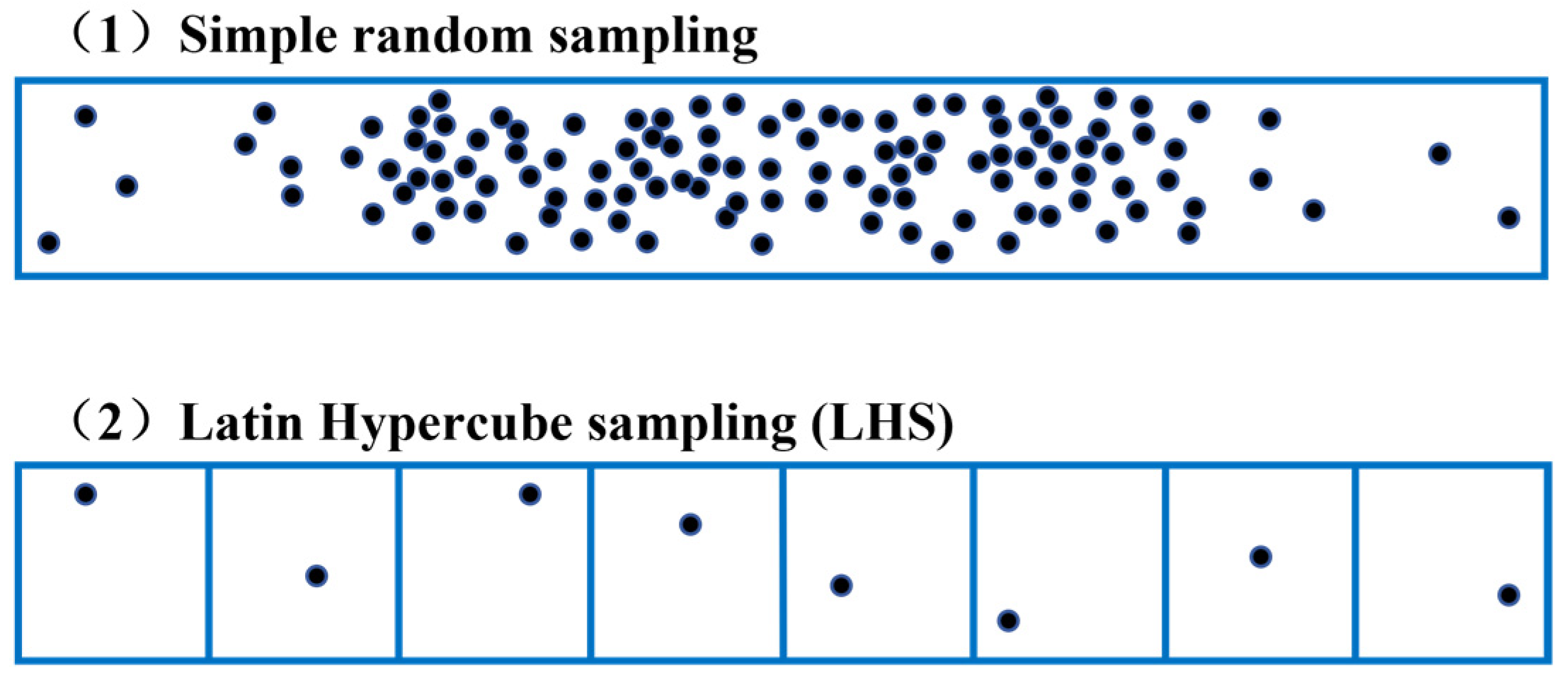
2.2.1. Latin Hypercube Sampling
- For each input variable, partition its cumulative probability range into N equiprobable intervals based on its probability distribution.
- Randomly draw one cumulative probability value from each interval, yielding N stratified samples per variable.
- Convert the sampled cumulative probabilities to actual variable values using the inverse cumulative distribution function.
- Perform random pairwise permutations of sampled values across variables to eliminate spurious correlations.
- The resultant N samples form a multidimensional input space with minimized spatial clustering.
2.2.2. Performance Prediction Using Intelligent Algorithms
2.3. Prediction Modeling Combining CFD and ANN
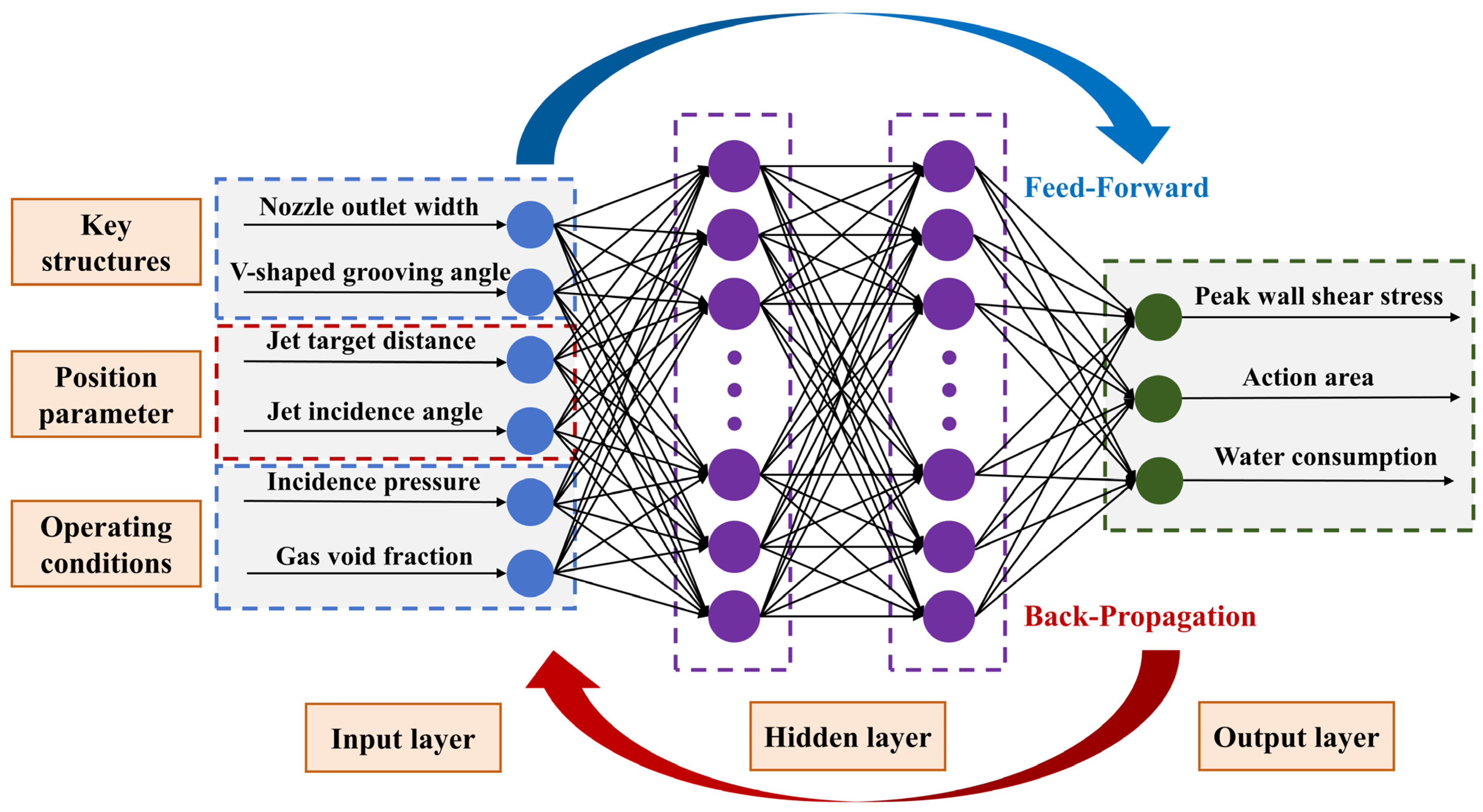
2.3.1. Artificial Neural Network (ANN)
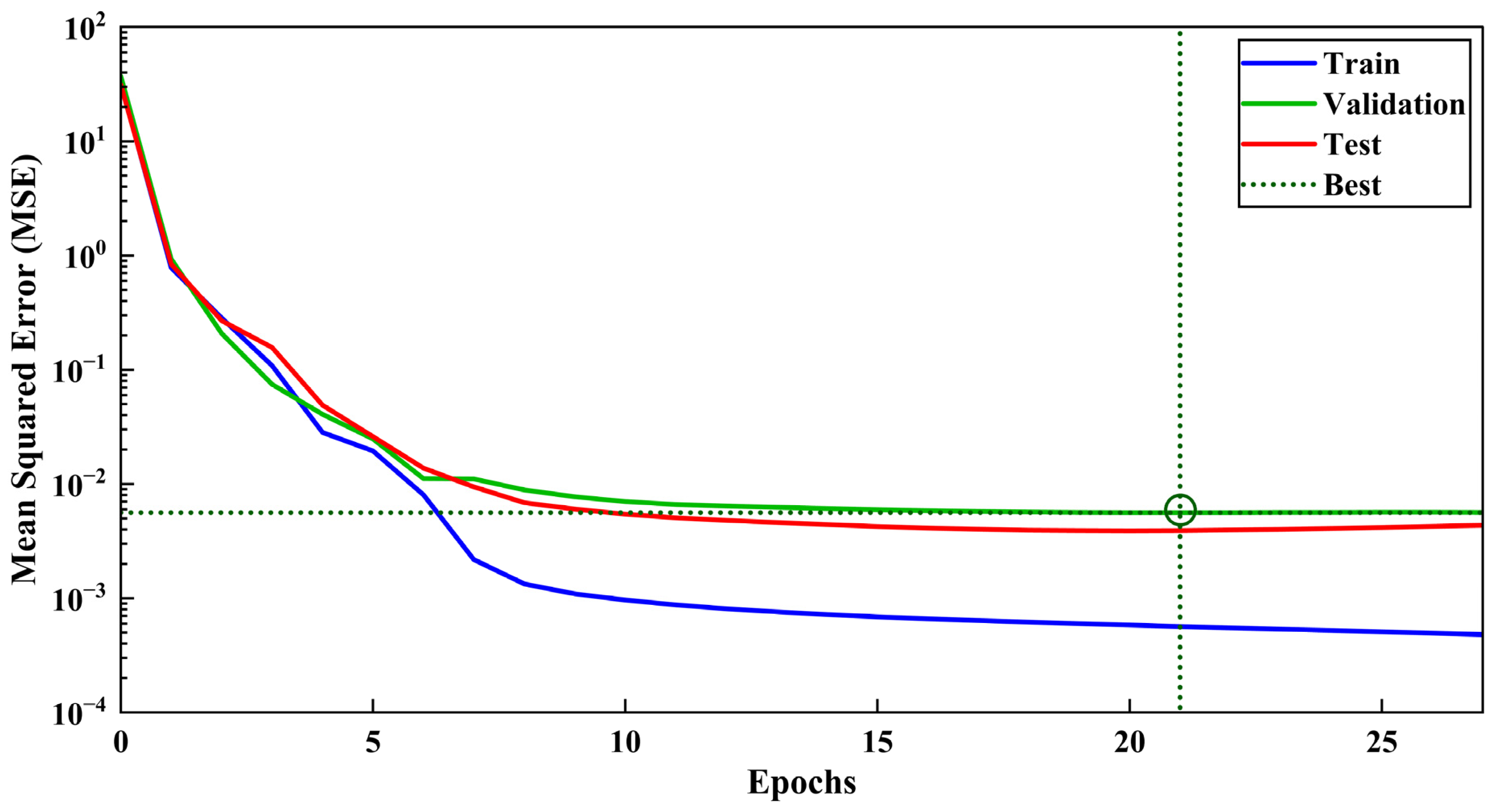
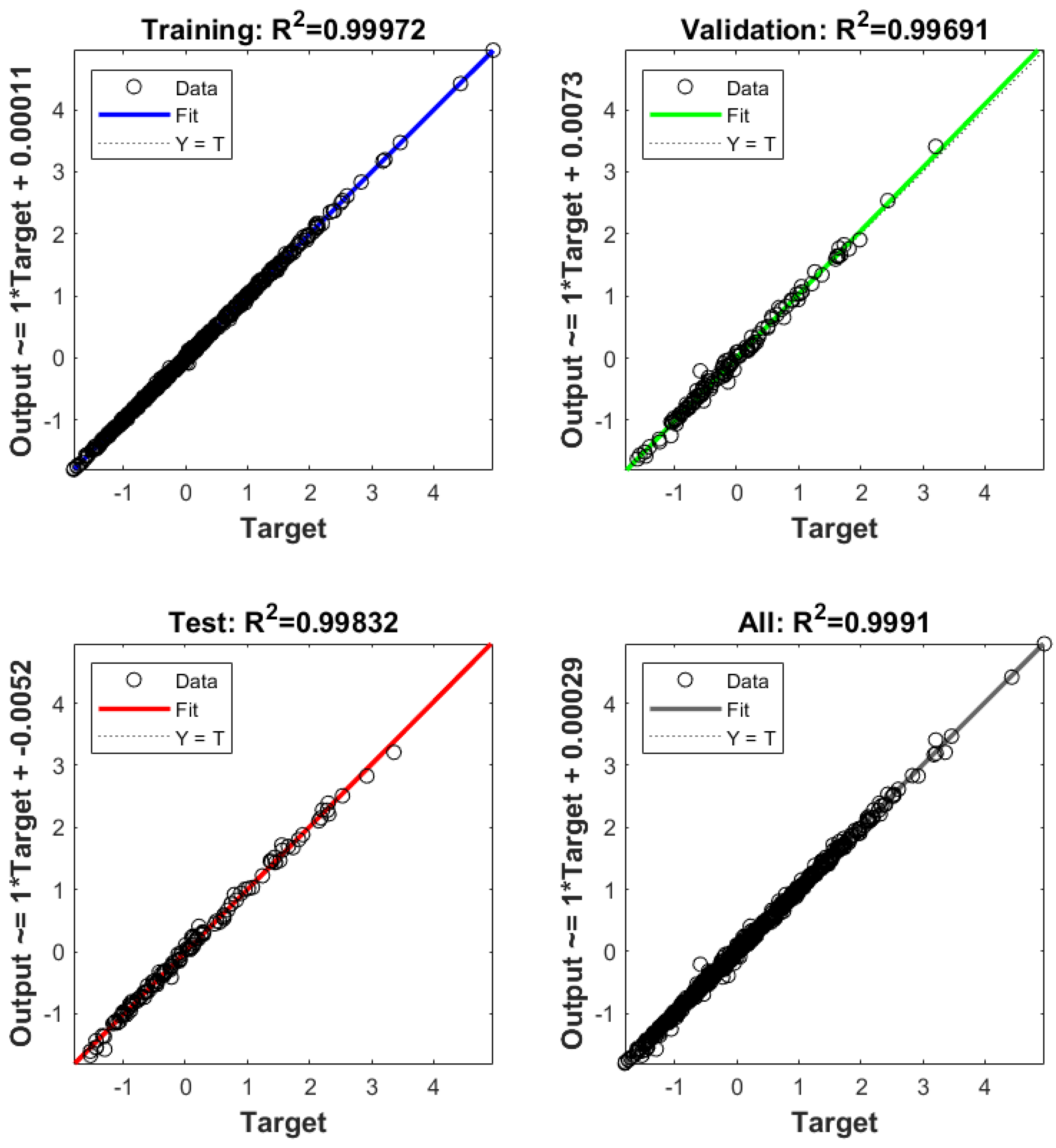
2.3.2. Performance Prediction of Jet-Cleaning Using ANN
2.4. Optimization Procedure Combining ANN and GA
2.4.1. Genetic Optimization Algorithm (GA)
2.4.2. Performance Optimization of Jet-Cleaning Using GA
3. Results and Discussions
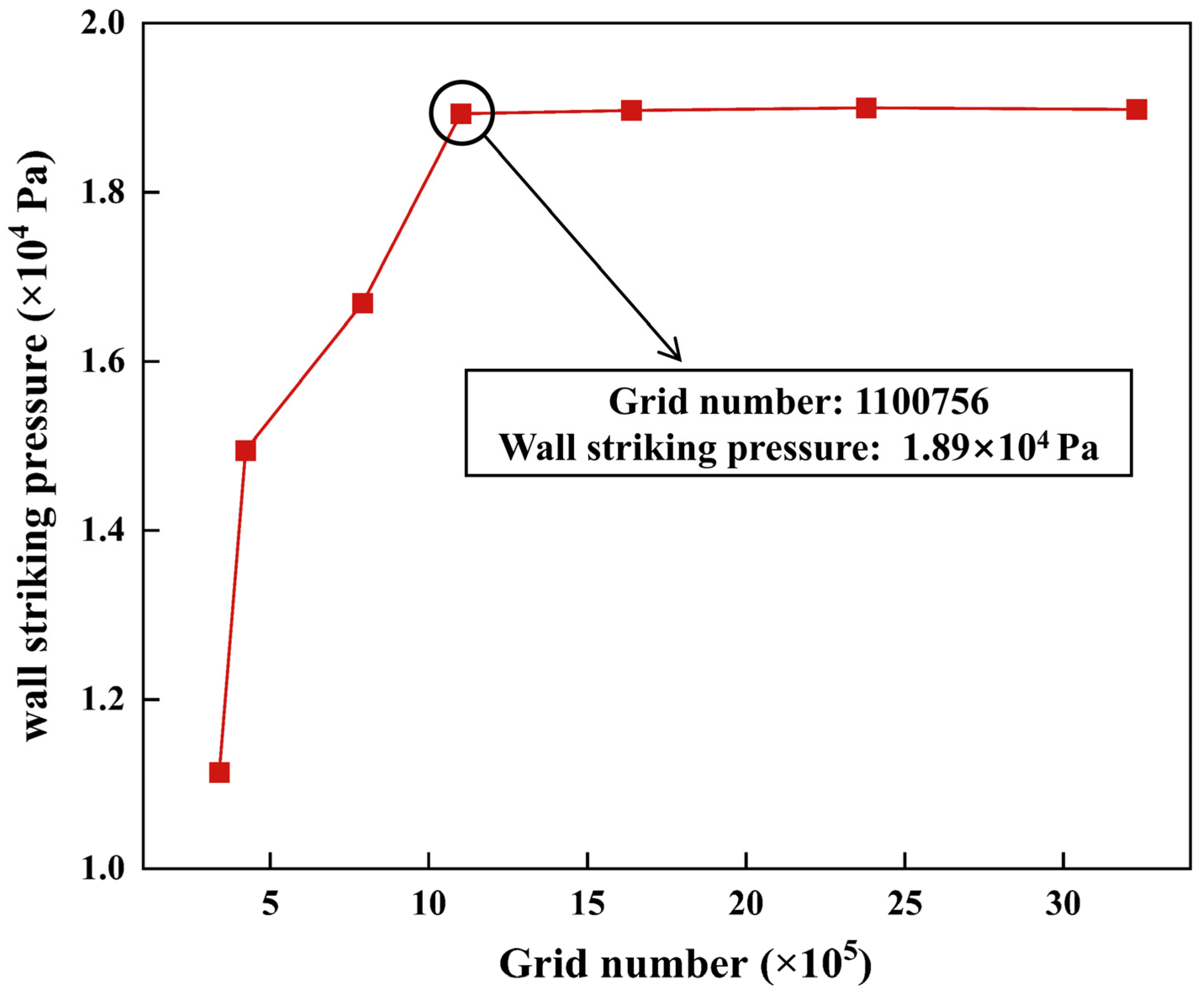
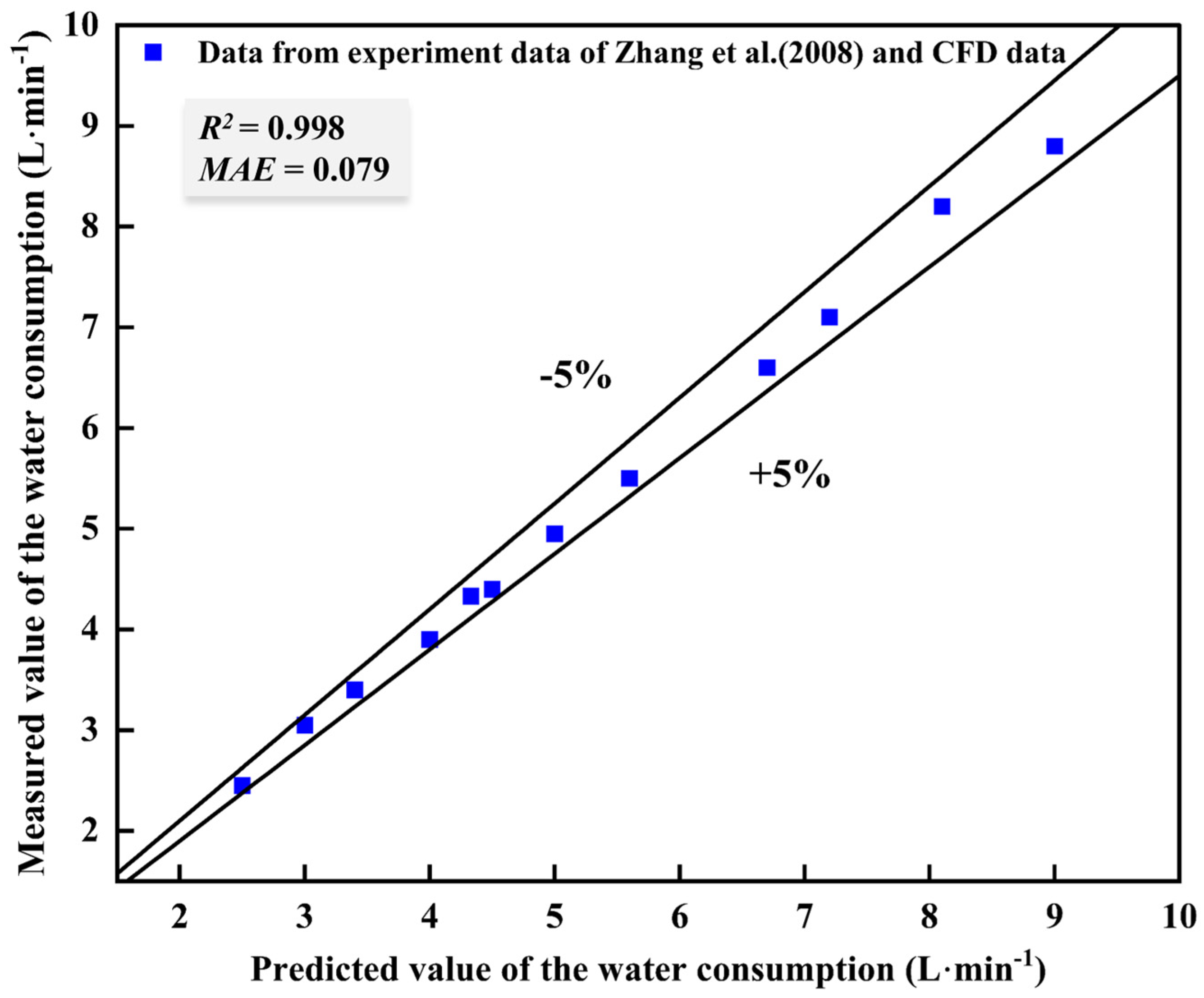
3.1. Grid Independency Test and Model Validation
3.2. Selection of Nozzle Key Structural Parameters
3.3. Jet-Cleaning Model Prediction
3.4. Optimization Procedure Based on ANN with Genetic Algorithm (GA)
4. Conclusions
- (1)
- Among the main influencing parameters of the nozzle, the incident cross-section diameter d and V-groove half-angle β have the greatest influence on the peak wall shear stress, action area, and cleaning water consumption, with a total contribution rate of about 97.00%, 98.43%, and 98.01, which should be treated as key influencing parameters in the optimization.
- (2)
- The CFD numerical simulation model is verified to have an error of 5% or less, which meets the accuracy requirements and can be used to obtain the basic data for prediction and optimization instead of physical tests.
- (3)
- Among the nine commonly used AI algorithms tested, the artificial neural network ANN has the best prediction performance (R2 = 0.9991, MAE = 9.477). The prediction model results were within 3% error from the CFD simulation results, which has high prediction accuracy and can replace the CFD numerical simulation model for predicting the jet-cleaning performance over the full parameter range.
- (4)
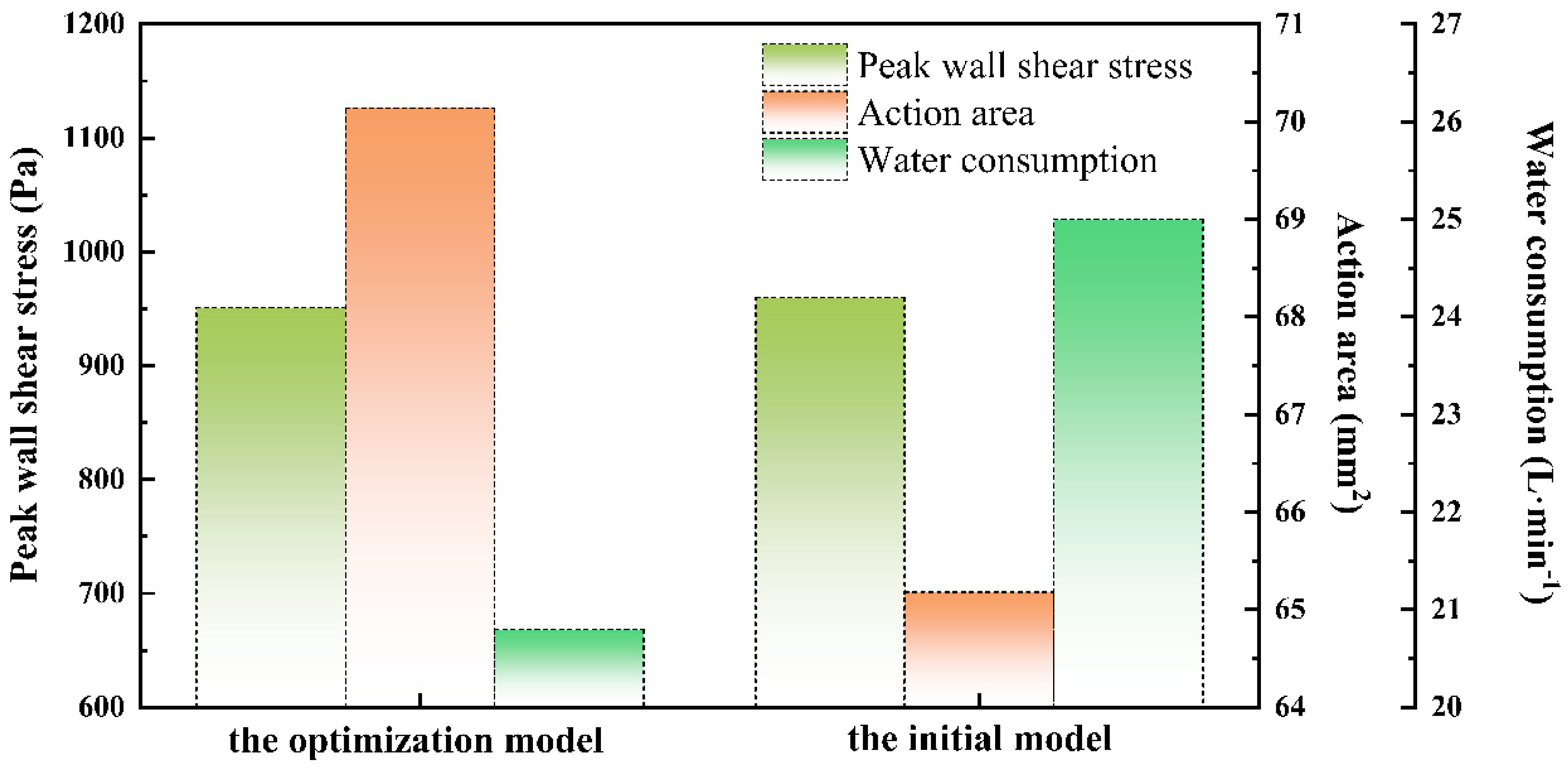
- The optimization resulted in a 1.34% reduction in the peak wall shear stress, a 16.82% reduction in cleaning water consumption, and a 7.6% increase in the action area for the optimal model compared to the base model. It is investigated that the genetic algorithm GA optimization framework based on the artificial neural network ANN prediction model can achieve the prediction of jet cleaning performance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, Z.; Liu, J.; Zhang, J.; Yin, F.; Guo, L.; Wen, Y.; Song, L.; Zhu, Y.; Liang, Y.; Wang, Z. Ultra-wide film mulching with moderate irrigation water salinity enhances cotton growth under drip irrigation in Xinjiang, China. Field Crops Res. 2024, 315, 109485. [Google Scholar] [CrossRef]
- Xing, S.; Du, K.; Liu, N.; Li, M.; Li, W.; Zhang, J.; Yin, F.; Zhang, J.; Wang, Z. Effect of dynamic pressure and emitter type on irrigation and fertigation uniformity of drip irrigation systems. Agric. Water Manag. 2025, 312, 109418. [Google Scholar] [CrossRef]
- Liu, Z.; Long, Y.; Li, J.; Liu, D. Analysis of three-dimensional cake thickness structure characteristics in a screen filter for drip irrigation based on the CFD–DEM coupling method. Biosyst. Eng. 2025, 250, 1–14. [Google Scholar] [CrossRef]
- Barrero-Moreno, M.C.; Diaz-Vargas, C.A.; Restrepo-Parra, E. Computational Simulation of Filters Used in the Removal of Heavy Metals Using Rice Husks. Agriculture 2021, 11, 146. [Google Scholar] [CrossRef]
- Liu, Z.; Muhammad, T.; Puig-Bargués, J.; Han, S.; Ma, Y.; Li, Y. Horizontal roughing filter for reducing emitter composite clogging in drip irrigation systems using high sediment water. Agric. Water Manag. 2021, 258, 107215. [Google Scholar] [CrossRef]
- Zong, Q.; Zheng, T.; Liu, H.; Li, C. Development of head loss equations for self-cleaning screen filters in drip irrigation systems using dimensional analysis. Biosyst. Eng. 2015, 133, 116–127. [Google Scholar] [CrossRef]
- Duran-Ros, M.; Pujol, J.; Pujol, T.; Cufí, S.; Arbat, G.; Ramírez de Cartagena, F.; Puig-Bargués, J. Solid Removal across the Bed Depth in Media Filters for Drip Irrigation Systems. Agriculture 2023, 13, 458. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H.; Qiu, X.; Wang, J.; Wang, S.; Wang, H.; Shen, T. Study on the Performance of Filters Under Biogas Slurry Drip Irrigation Systems. Agriculture 2024, 15, 30. [Google Scholar] [CrossRef]
- Liu, J.; Ouyang, Y.; Wang, Q. Design and research on the new type self-cleaning filters with scraper. Mach. Tool Hydraul. 2013, 41, 26–28. [Google Scholar]
- Du, S.; Han, Q.; Lan, J.; Guo, Z.; Li, H.; Huang, X. Experimental Study on Hydraulic Performance of the Hand-operated Cleaning Screen Filter. J. Irrig. Drain. 2021, 40, 66–72. [Google Scholar] [CrossRef]
- Taleghani, A.S.; Hesabi, A.; Esfahanian, V. Numerical Study of Flow Control to Increase Vertical Tail Effectiveness of an Aircraft by Tangential Blowing. Int. J. Aeronaut. Space Sci. 2024, 26, 785–799. [Google Scholar] [CrossRef]
- Abdolahipour, S. Review on flow separation control: Effects of excitation frequency and momentum coefficient. Front. Mech. Eng. 2024, 10, 1380675. [Google Scholar] [CrossRef]
- Abdolahipour, S. Effects of low and high frequency actuation on aerodynamic performance of a supercritical airfoil. Front. Mech. Eng. 2023, 9, 1290074. [Google Scholar] [CrossRef]
- Abdolahipour, S.; Mani, M.; Shams Taleghani, A. Parametric study of a frequency-modulated pulse jet by measurements of flow characteristics. Phys. Scr. 2021, 96, 125012. [Google Scholar] [CrossRef]
- Park, S.; Kainuma, S.; Yang, M.; Kim, A.; Ikeda, T.; Toyota, Y.; Arakawa, T. Advancements in abrasive water-jet treatment for efficient surface cleaning and comprehensive corrosion removal in steel structures. J. Build. Eng. 2024, 84, 108623. [Google Scholar] [CrossRef]
- Cano-Salinas, L.; Sourd, X.; Moussaoui, K.; Le Roux, S.; Salem, M.; Hor, A.; Zitoune, R. Effect of process parameters of Plain Water Jet on the cleaning quality, surface and material integrity of Inconel 718 milled by Abrasive Water Jet. Tribol. Int. 2023, 178, 108094. [Google Scholar] [CrossRef]
- Li, S.; Ye, H.; Wang, Z.; Liu, N. Study on cleaning elfeet and damage of jet cleaning on filter screen of micro-irrigation filter. J. Drain. Irrig. Mach. Eng. 2024, 24, 102–108. [Google Scholar]
- Qin, Z.; Liu, N.; Zhang, J.; Wang, Z.; Liang, W.; Li, M.; Zhang, J. Development and performance evaluation of novel jet self-cleaning for screen filters in drip irrigation systems: More efficient, water-saving, and cleaner. Agric. Water Manag. 2025, 312, 109424. [Google Scholar] [CrossRef]
- Sun, S.; Hai, Y.; Wu, J.; Hu, B.; Luo, X.; Ma, Z. Jet impact self-cleaning: Research on impurity filtration and collection method before irrigation system pump. J. Water Process Eng. 2025, 72, 107587. [Google Scholar] [CrossRef]
- Qian, Y.; Chean, H.; Dai, H.; Liu, T.; Kuang, t.; Bian, L. Experimental study of the nozzle settings on blow tube in a pulse-jet cartridge filter. Sep. Purif. Technol. 2018, 191, 224–249. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, D.; Chen, H.; Wang, M.; Liang, C.; WU, X.; Li, W. Effect of nozzle type on pulse-jet cleaning performance of ceramic filter tube. Adv. Powder Technol. 2023, 34, 104180. [Google Scholar] [CrossRef]
- Careddu, N.; Akkoyun, O. An investigation on the efficiency of water-jet technology for graffiti cleaning. J. Cult. Herit. 2016, 19, 426–434. [Google Scholar] [CrossRef]
- Wang, T.; Davidson, J.F.; Wilson, D.I. Flow patterns and cleaning behaviour of horizontal liquid jets impinging on angled walls. Food Bioprod. Process. 2015, 93, 333–342. [Google Scholar] [CrossRef]
- Kim, W.-J.; Karuppuchamy, V.; Heldman, D.R. Evaluation of maximum wall shear stress from air impingement to remove food deposits from stainless steel surfaces. J. Food Eng. 2022, 316, 110825. [Google Scholar] [CrossRef]
- Andersen, B.O.; Nielsen, N.F.; Walther, J.H. Numerical and experimental study of pulse-jet cleaning in fabric filters. Powder Technol. 2016, 291, 284–298. [Google Scholar] [CrossRef]
- Chen, L.; Sun, W.; Qian, F.; Fang, C.; Zheng, Z.; Zhuang, Q.; Han, Y.; Lu, J. An Experimental and Numerical Study on the Cleaning of Pleated Bag Filters Using Low-Pressure Pulsed-Jets. Fluid Dyn. Mater. Process. 2022, 18, 41–56. [Google Scholar] [CrossRef]
- Fernandes, R.R.; Tsai, J.H.; Wilson, D.I. Comparison of models for predicting cleaning of viscoplastic soil layers by impinging coherent turbulent water jets. Chem. Eng. Sci. 2022, 248, 117060. [Google Scholar] [CrossRef]
- Kawale, S.; Chandramohan, V.P. CFD simulation of estimating critical shear stress for cleaning flat soiled surface. Sādhanā 2017, 42, 2137–2145. [Google Scholar] [CrossRef]
- Huang, L.-Y.; Chen, Z.S. Effect of technological parameters on hydrodynamic performance of ultra-high-pressure water-jet nozzle. Appl. Ocean Res. 2022, 129, 103410. [Google Scholar] [CrossRef]
- Carvalho, A.R.d.; Pita, R.P.; Oliveira, T.M.d.; Silva, G.J.B.; Mendes, J.C. Exploratory literature review and scientometric analysis of artificial intelligence applied to geopolymeric materials. Eng. Appl. Artif. Intell. 2025, 145, 110210. [Google Scholar] [CrossRef]
- Dawkins, M.S. Smart farming and Artificial Intelligence (AI): How can we ensure that animal welfare is a priority? Appl. Anim. Behav. Sci. 2025, 283, 106519. [Google Scholar] [CrossRef]
- Saad Alotaibi, B.; Ibrahim Shema, A.; Umar Ibrahim, A.; Awad Abuhussain, M.; Abdulmalik, H.; Aminu Dodo, Y.; Atakara, C. Assimilation of 3D printing, Artificial Intelligence (AI) and Internet of Things (IoT) for the construction of eco-friendly intelligent homes: An explorative review. Heliyon 2024, 10, e36846. [Google Scholar] [CrossRef]
- Xu, A.; Han, L.; Fu, J.; Huangfu, S.; Zhao, R. The tiered competition genetic algorithm and its application in the wind-resistant optimization of a cable-stayed mast structure. Eng. Struct. 2025, 327, 119592. [Google Scholar] [CrossRef]
- Cui, Y.; Ye, L.; Yao, Z.; Gu, X.; Wang, X. Performance optimization of cement calciner based on CFD simulation and machine learning algorithm. Energy 2024, 302, 131926. [Google Scholar] [CrossRef]
- Zhu, B.; Zhu, X.; Zhao, W.; Cao, L. Design and simulation of gas-liquid two-phase jet cleaning device. Fluid Mach. 2021, 49, 36–42. [Google Scholar] [CrossRef]
- TU, Y.; Fan, C.; Qian, Y.; Wang, X. Structure optimization of central-body in dual cavitating jet andthe behavior of coal breaking under its impact. J. China Coal Soc. 2022, 47, 3250–3259. [Google Scholar]
- Guha, A.; Barron, R.M.; Balachandar, R. An experimental and numerical study of water jet cleaning process. J. Mater. Process. Technol. 2011, 211, 610–618. [Google Scholar] [CrossRef]
- Hsu, C.-Y.; Liang, C.-C.; Teng, T.-L.; Nguyen, A.-T. A numerical study on high-speed water jet impact. Ocean Eng. 2013, 72, 98–106. [Google Scholar] [CrossRef]
- Li, J.; Wang, P.; Wu, D.; Chen, D.-R. Numerical study of opposing pulsed-jet cleaning for pleated filter cartridges. Sep. Purif. Technol. 2020, 234, 116086. [Google Scholar] [CrossRef]
- Eryoldaş, Y.; Durmuşoğlu, A. An efficient parameter tuning method based on the Latin Hypercube Hammersley Sampling and fuzzy C-Means clustering methods. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 8307–8322. [Google Scholar] [CrossRef]
- Liu, D.; Wang, S.; Shi, J.; Liu, D. Sequential search-based Latin hypercube sampling scheme for digital twin uncertainty quantification with application in EHA. Chin. J. Aeronaut. 2024, 38, 103310. [Google Scholar] [CrossRef]
- Wang, J.-X.; Jin, C.-T.; Gao, S. Anti-collapse on the fragility and sensitivity analysis of composite frame with CFST columns based on the improved Latin hypercube sampling. Structures 2024, 63, 106402. [Google Scholar] [CrossRef]
- Han, X.; Zhao, X.; Qu, Z.; Wu, Y.; Li, G. LS-SVM-based nonlinear multi-physical steady-state field coupled problems computing method. Appl. Math. Model. 2025, 142, 115987. [Google Scholar] [CrossRef]
- Weerakoon, A.H.S.; Assadi, M. Artificial Neural Network (ANN) driven Techno-Economic Predictions for Micro Gas Turbines (MGT) based Energy Applications. Energy AI 2025, 20, 100483. [Google Scholar] [CrossRef]
- Jeon, H.S.; Yeon, S.H.; Park, J.K.; Kim, M.H.; Yoon, Y.; Kim, C.H.; Lee, K.H. ANN based solar thermal energy forecasting model and its heating energy saving effect through thermal storage. Appl. Therm. Eng. 2025, 267, 125740. [Google Scholar] [CrossRef]
- Wei, Y.; Lu, M.; Yu, Q.; Li, W.; Wang, C.; Tang, H.; Wu, W. The normalized difference yellow vegetation index (NDYVI): A new index for crop identification by using GaoFen-6 WFV data. Comput. Electron. Agric. 2024, 226, 109417. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, Z.; Hao, P.; Li, Y. Design of flat fan nozzles and its experimental study. Mach. Des. Res. 2008, 24, 89–92. [Google Scholar]
- Ren, Y.; Li, Q.; Guo, Y.; Pedrycz, W.; Xing, L.; Liu, A.; Song, Y. A distance similarity-based genetic optimization algorithm for satellite ground network planning considering feeding mode. Expert Syst. Appl. 2025, 268, 126303. [Google Scholar] [CrossRef]
- Xie, Y.; Ren, J.; Huang, H. Grid independence analysis of computational fluid dynamics based on Chisquare test. Sci. Technol. Eng. 2020, 20, 123–127. [Google Scholar]
- Liu, W.; Zhou, X.; Li, Q. Effect of fan-shaped nozzle structure optimization on jet impact force based on response surface analysis. Sci. Technol. Eng. 2025, 25, 1467–1474. [Google Scholar]
- Chen, Y.-J.; Chen, Z.-S. A prediction model of wall shear stress for ultra-high-pressure water-jet nozzle based on hybrid BP neural network. Eng. Appl. Comput. Fluid Mech. 2022, 16, 1902–1920. [Google Scholar] [CrossRef]
- Singh, V.K.; Kumar, D.; Tripathi, R.J. Multi objective optimization of novel phase change material-based desalination system using genetic algorithms. J. Energy Storage 2024, 103, 114388. [Google Scholar] [CrossRef]
- Liu, F.; Chen, Y.; Qin, W.; Li, J. Optimal design of liquid cooling structure with bionic leaf vein branch channel for power battery. Appl. Therm. Eng. 2023, 218, 119283. [Google Scholar] [CrossRef]





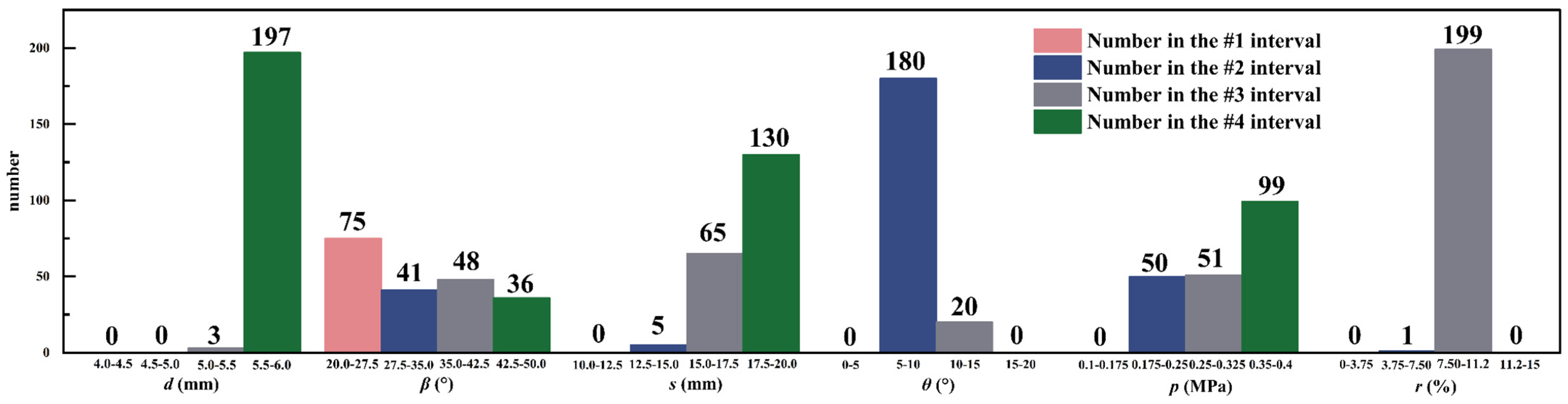
| Main Structural Parameters | Notation | Level 1 | Level 2 | Level 3 | |
|---|---|---|---|---|---|
| 1 | Inlet section diameter (mm) | D | 10 | 12 | 14 |
| 2 | Incident section diameter (mm) | d | 4 | 5 | 6 |
| 3 | Inlet length (mm) | L1 | 10 | 20 | 30 |
| 4 | Incident length (mm) | L3 | 2 | 4 | 6 |
| 5 | Shrinkage segment angle (°) | α | 80 | 100 | 120 |
| 6 | V-groove half angle (°) | β | 20 | 35 | 50 |
| D | d | L1 | L3 | α | β | |
|---|---|---|---|---|---|---|
| 1 | 10 | 4 | 10 | 2 | 80 | 20 |
| 2 | 10 | 4 | 20 | 4 | 120 | 50 |
| 3 | 10 | 5 | 10 | 6 | 120 | 35 |
| 4 | 10 | 5 | 30 | 2 | 100 | 50 |
| 5 | 10 | 6 | 20 | 6 | 100 | 20 |
| 6 | 10 | 6 | 30 | 4 | 80 | 35 |
| 7 | 12 | 4 | 10 | 6 | 100 | 50 |
| 8 | 12 | 4 | 30 | 2 | 120 | 35 |
| 9 | 12 | 5 | 20 | 4 | 100 | 35 |
| 10 | 12 | 5 | 30 | 6 | 80 | 20 |
| 11 | 12 | 6 | 10 | 4 | 120 | 20 |
| 12 | 12 | 6 | 20 | 2 | 80 | 50 |
| 13 | 14 | 4 | 20 | 6 | 80 | 35 |
| 14 | 14 | 4 | 30 | 4 | 100 | 20 |
| 15 | 14 | 5 | 10 | 4 | 80 | 50 |
| 16 | 14 | 5 | 20 | 2 | 120 | 20 |
| 17 | 14 | 6 | 10 | 2 | 100 | 35 |
| 18 | 14 | 6 | 30 | 6 | 120 | 50 |
| Geometric Parameters | Range of Values | |
|---|---|---|
| Key structures | d (mm) | 4–6 |
| β (°) | 20–50 | |
| Position parameters | s (mm) | 10–20 |
| θ (°) | 0–20 | |
| Operating conditions | p (Mpa) | 0.1–0.4 |
| r (%) | 0–15 | |
| Features | Description |
|---|---|
| Network topology | Feed-forward |
| Training algorithm | Back-propagation |
| Training set | 70% |
| Test set | 15% |
| Validation set | 15% |
| Number of neurons in the input layer | 6 |
| Number of neurons in hidden-layer layers | 32 |
| Number of neurons in the output-layer layer | 3 |
| Maximum number of iterations | 1000 |
| Parameters | Value |
|---|---|
| Number of variables | 6 |
| Population size | 200 |
| Maximum number of genetic iterations | 150 |
| The fitness function deviation | 1.0 × 10−4 |
| Crossover fraction | 0.85 |
| Mutation rate | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Z.; Chen, Z.; Chen, R.; Zhang, J.; Liu, N.; Li, M. A New Method for Optimizing the Jet-Cleaning Performance of Self-Cleaning Screen Filters: The 3D CFD-ANN-GA Framework. Processes 2025, 13, 1194. https://doi.org/10.3390/pr13041194
Qin Z, Chen Z, Chen R, Zhang J, Liu N, Li M. A New Method for Optimizing the Jet-Cleaning Performance of Self-Cleaning Screen Filters: The 3D CFD-ANN-GA Framework. Processes. 2025; 13(4):1194. https://doi.org/10.3390/pr13041194
Chicago/Turabian StyleQin, Zhouyang, Zhaotong Chen, Rui Chen, Jinzhu Zhang, Ningning Liu, and Miao Li. 2025. "A New Method for Optimizing the Jet-Cleaning Performance of Self-Cleaning Screen Filters: The 3D CFD-ANN-GA Framework" Processes 13, no. 4: 1194. https://doi.org/10.3390/pr13041194
APA StyleQin, Z., Chen, Z., Chen, R., Zhang, J., Liu, N., & Li, M. (2025). A New Method for Optimizing the Jet-Cleaning Performance of Self-Cleaning Screen Filters: The 3D CFD-ANN-GA Framework. Processes, 13(4), 1194. https://doi.org/10.3390/pr13041194





