Numerical Study on Compound Heat Transfer Enhancement by New Inserts of Lubricating Oil in Tubes
Abstract
1. Introduction
2. Geometric Structure and Simulation Models
2.1. Physical Models
2.2. Mathematical Equations
2.3. Data Reduction
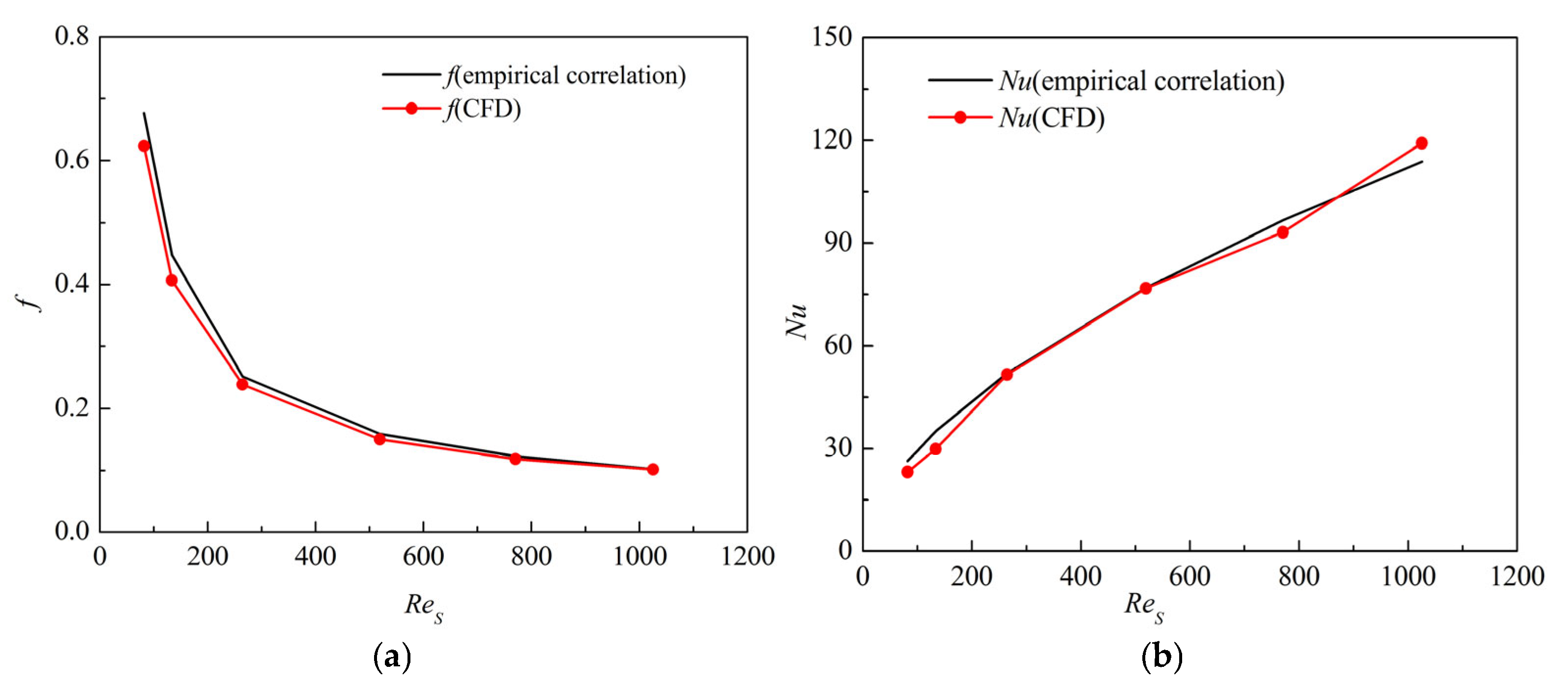
2.4. Numerical Validation
3. Analysis of Geometrical Models
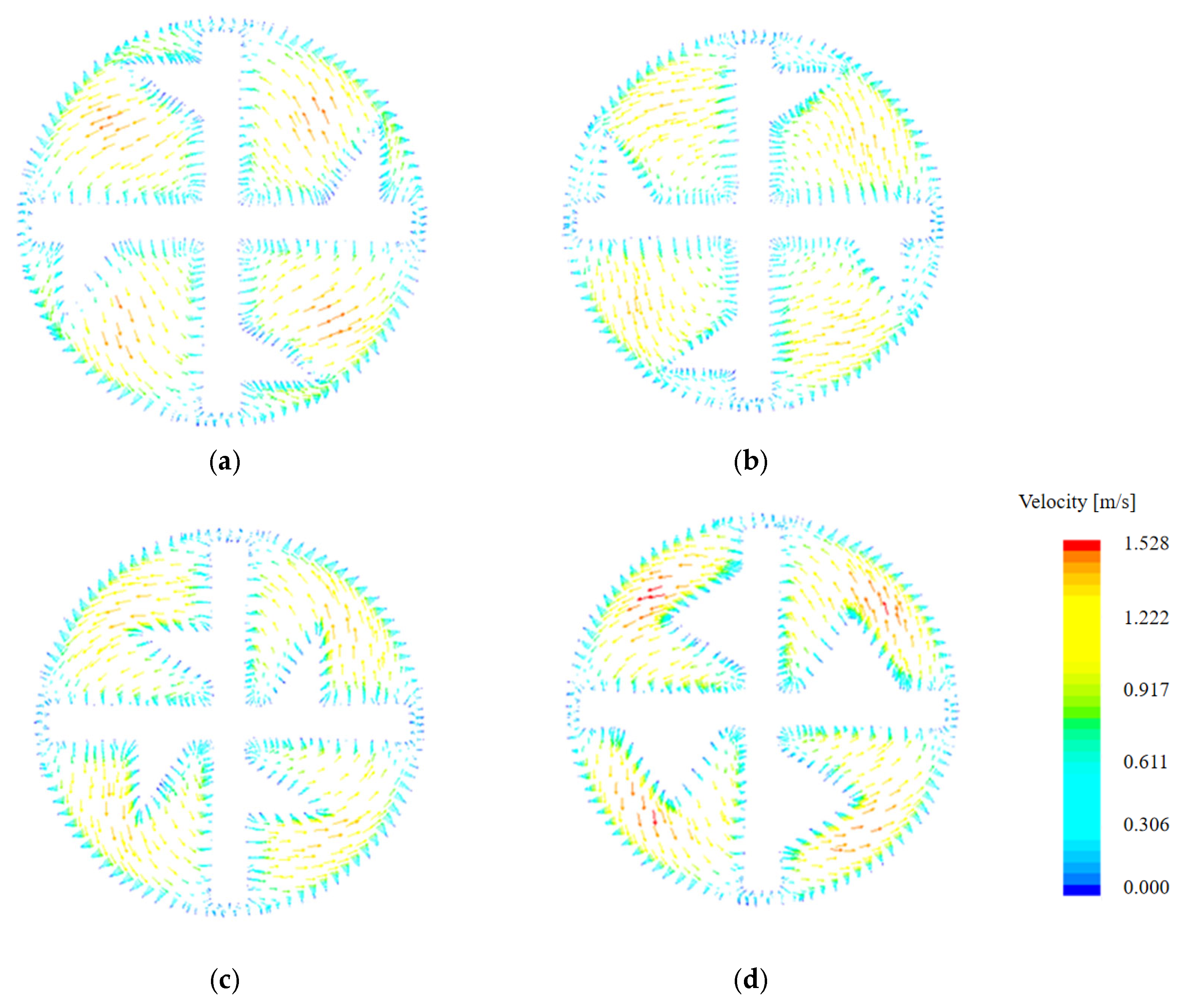
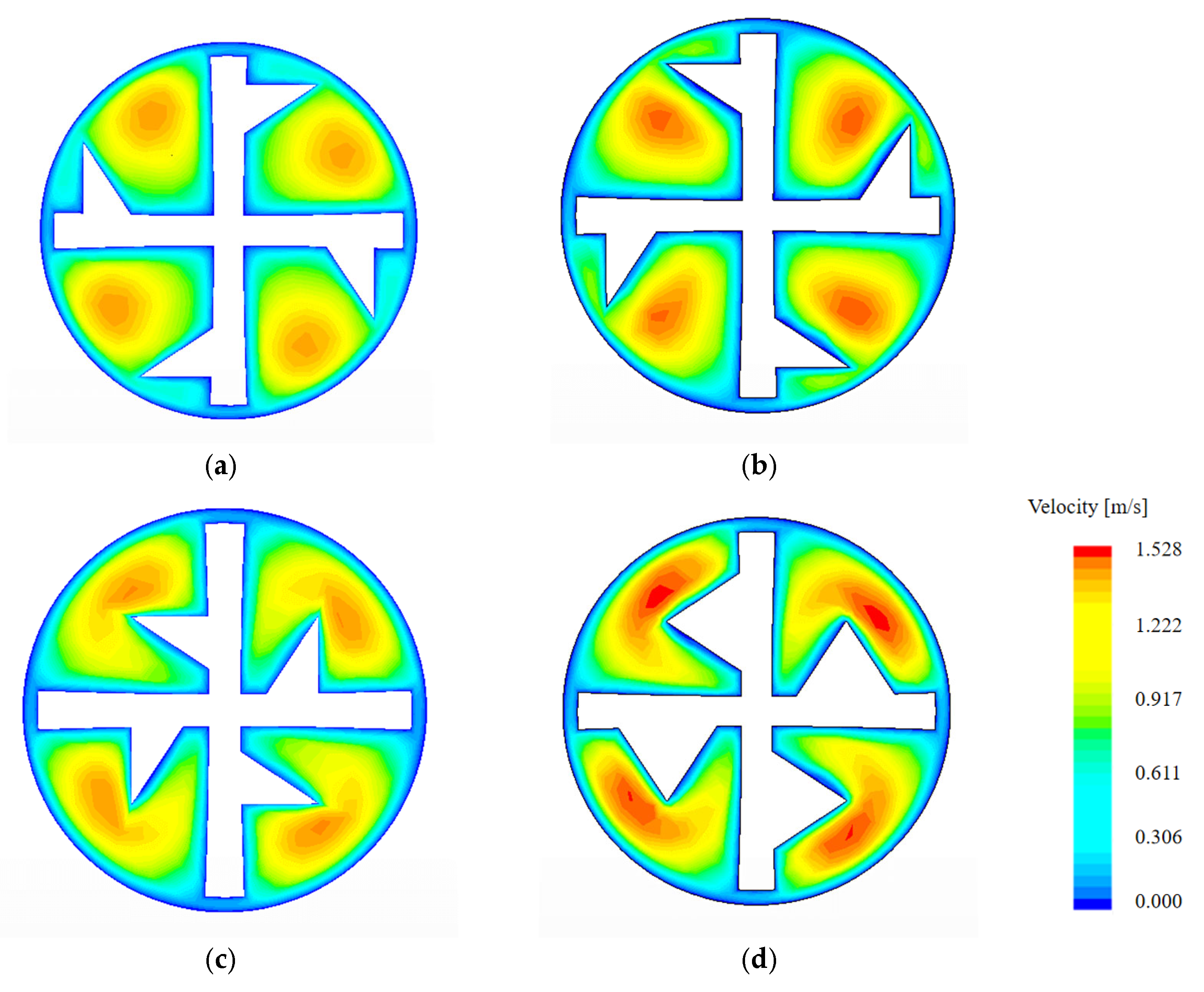
3.1. Velocity Field
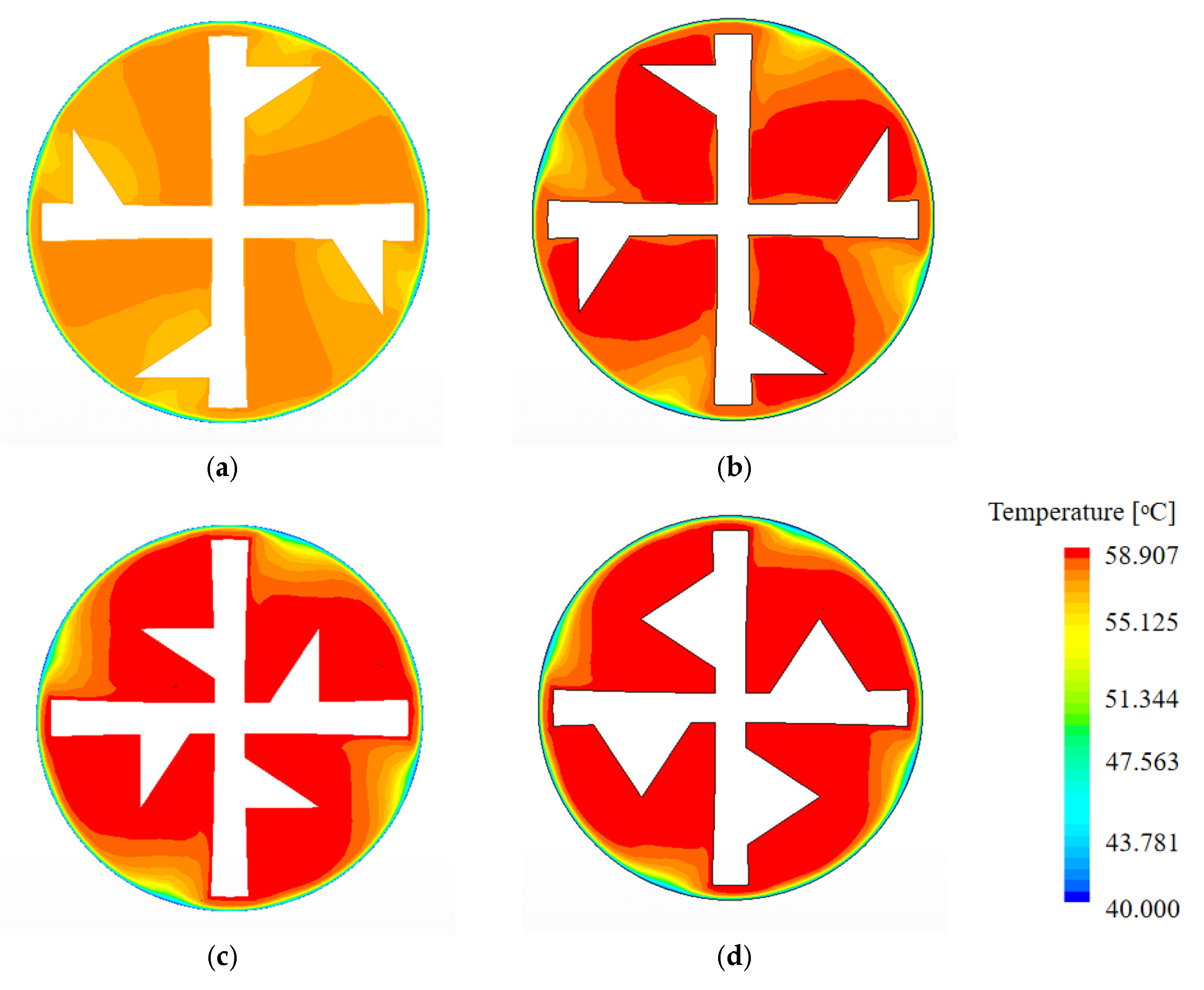
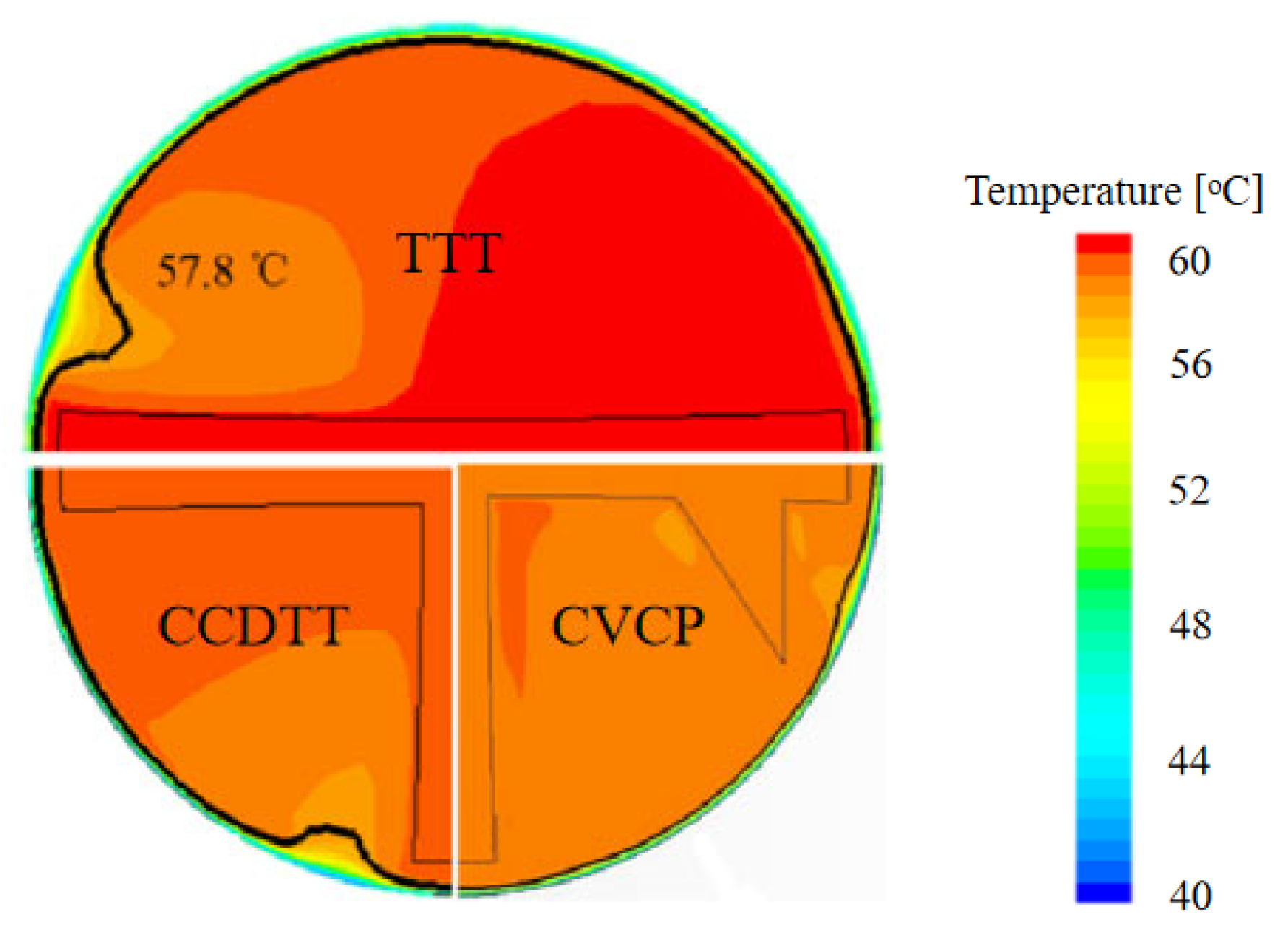
3.2. Temperature Field
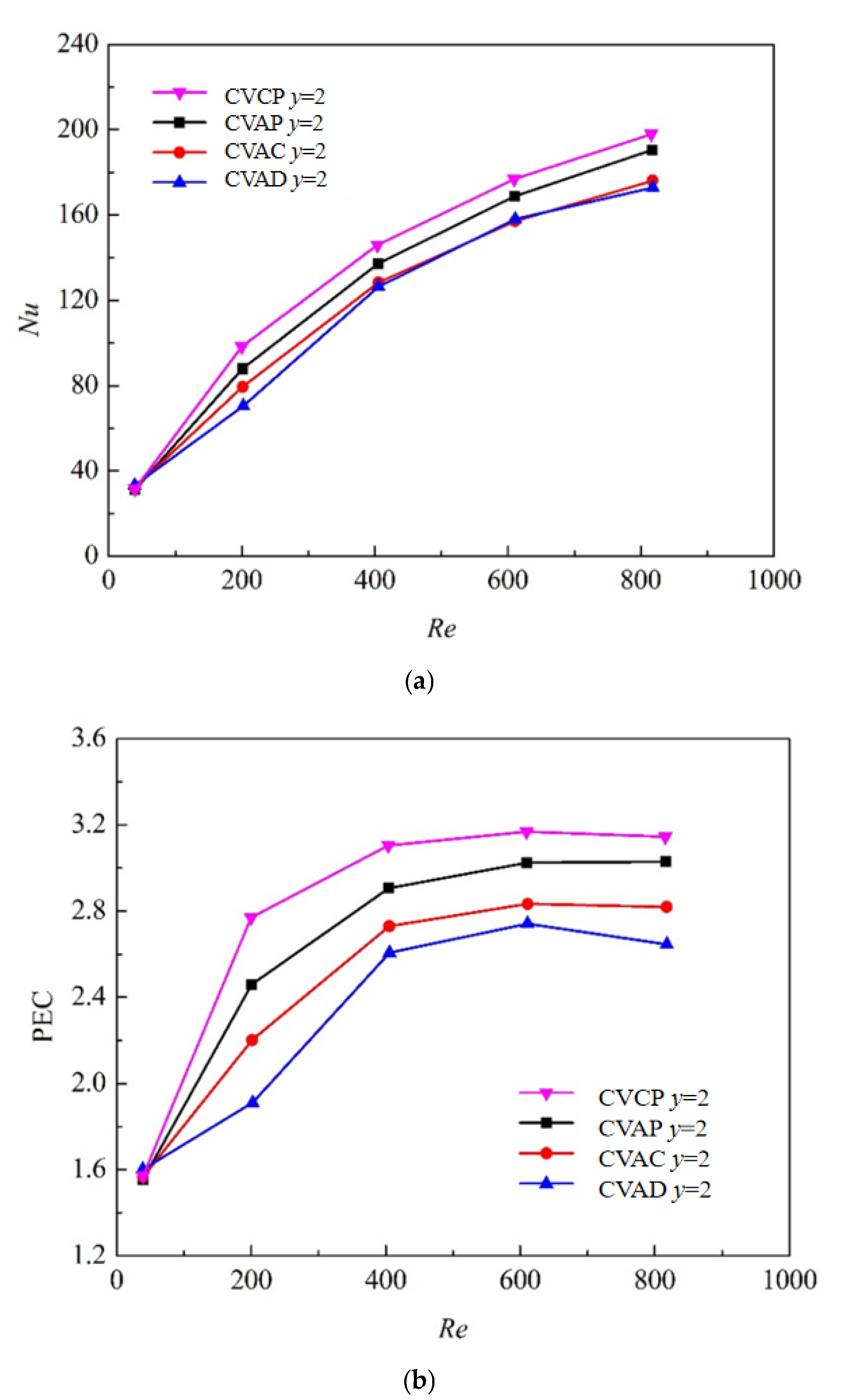
3.3. Convective Heat Transfer Characteristics
4. Analysis of Influencing Factors
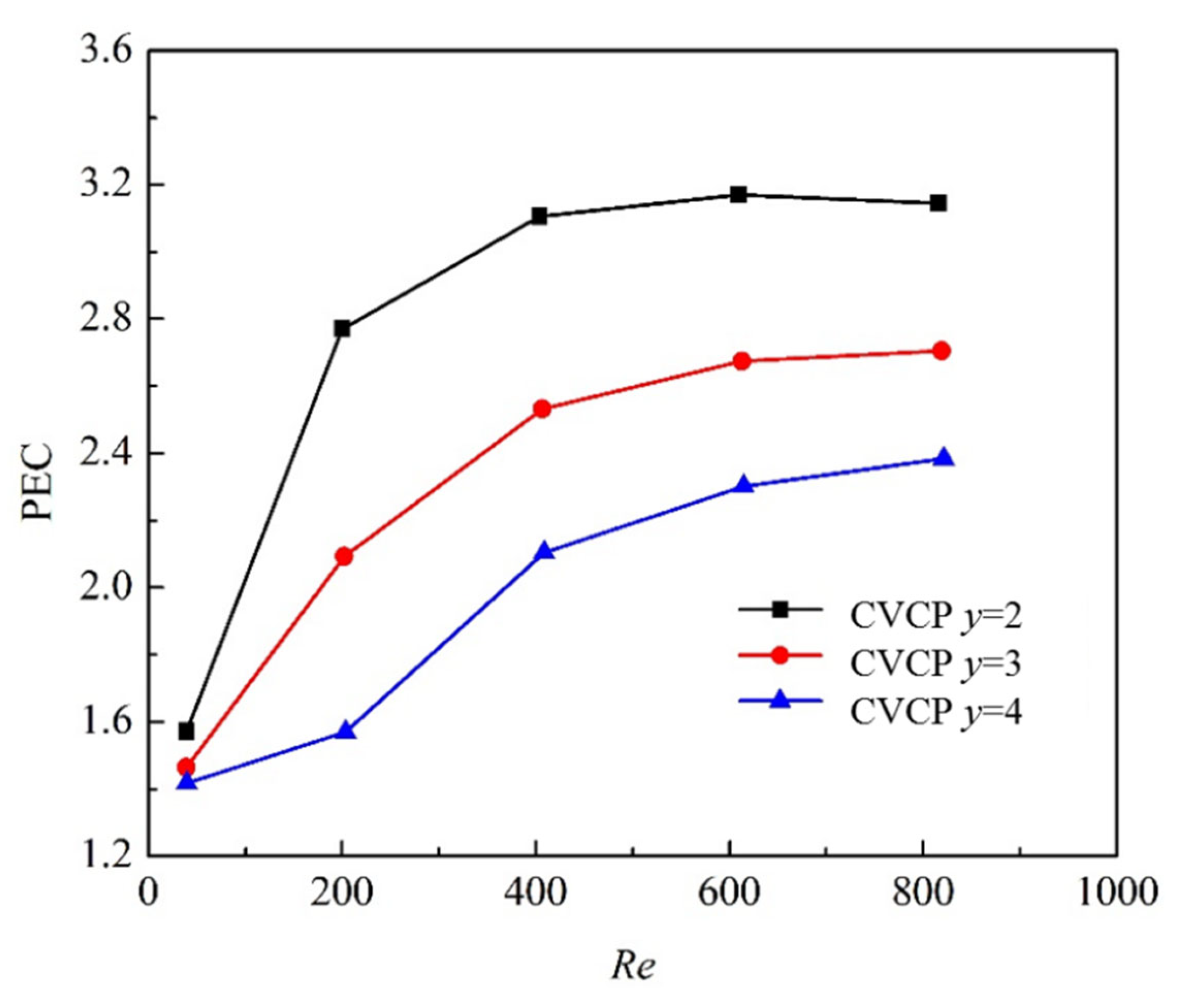
4.1. Effect of Twist Ratio
4.2. Effect of Angle
5. Compared with CCDTT and TTT
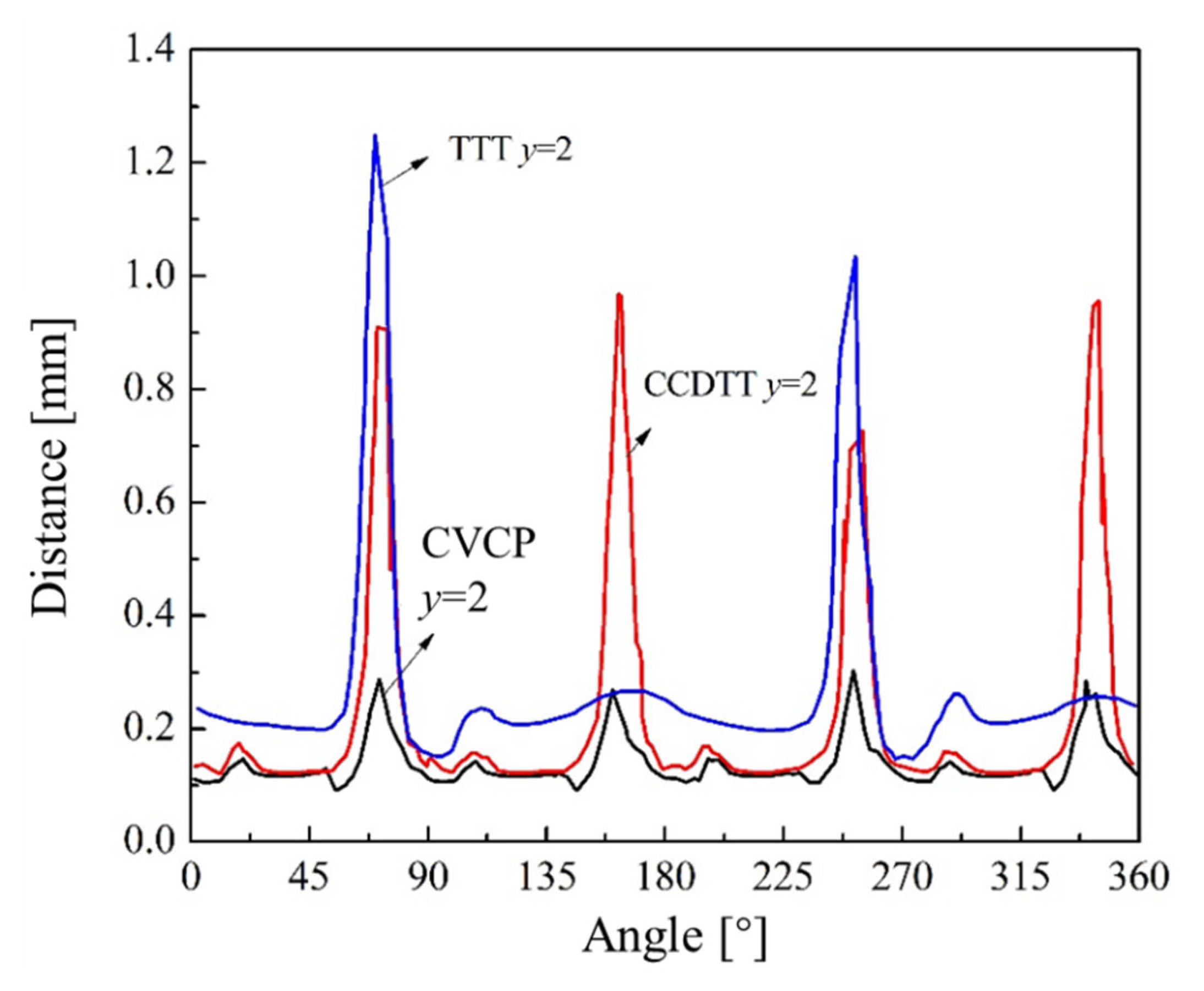
5.1. Local Flow Field
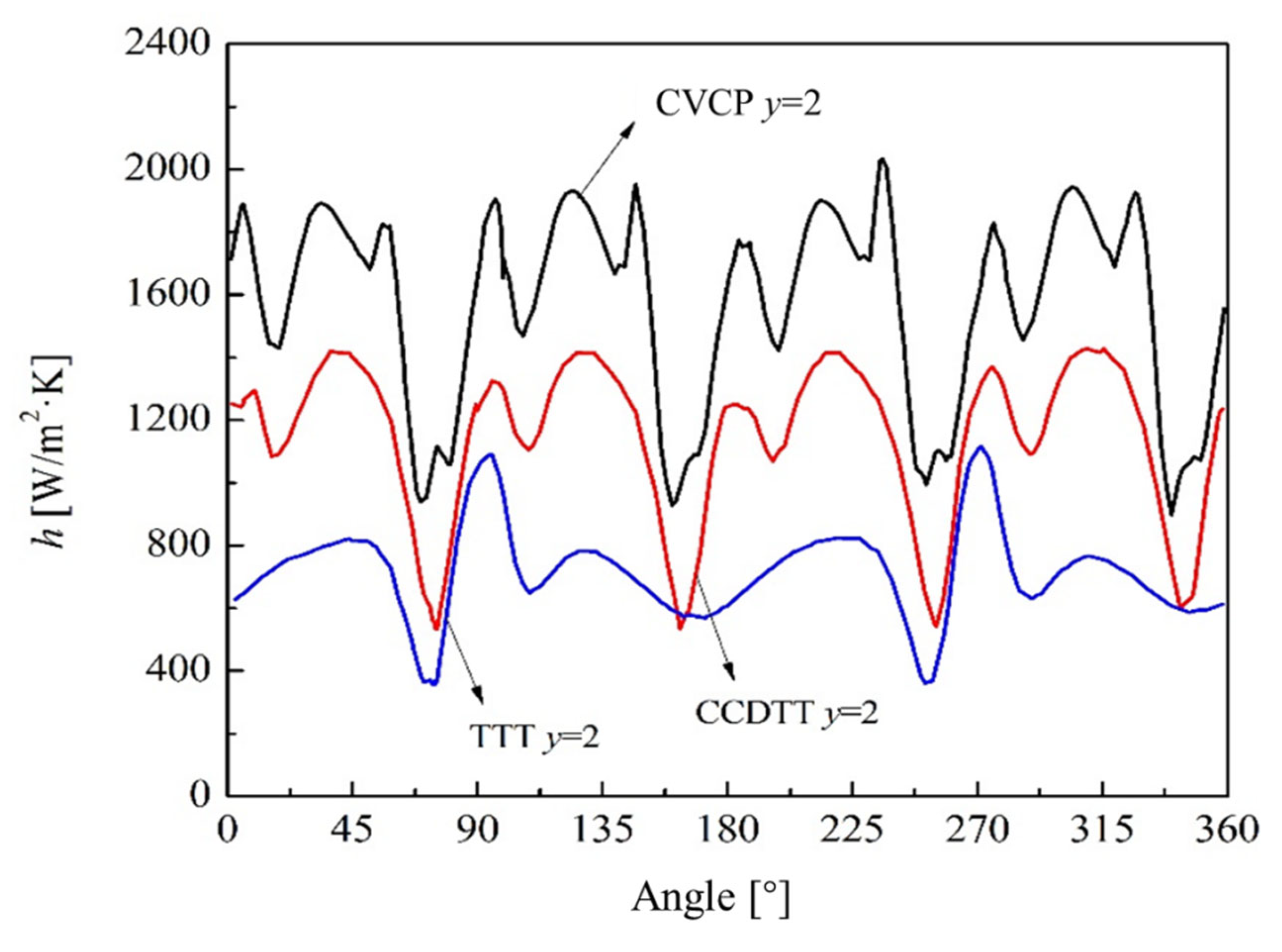
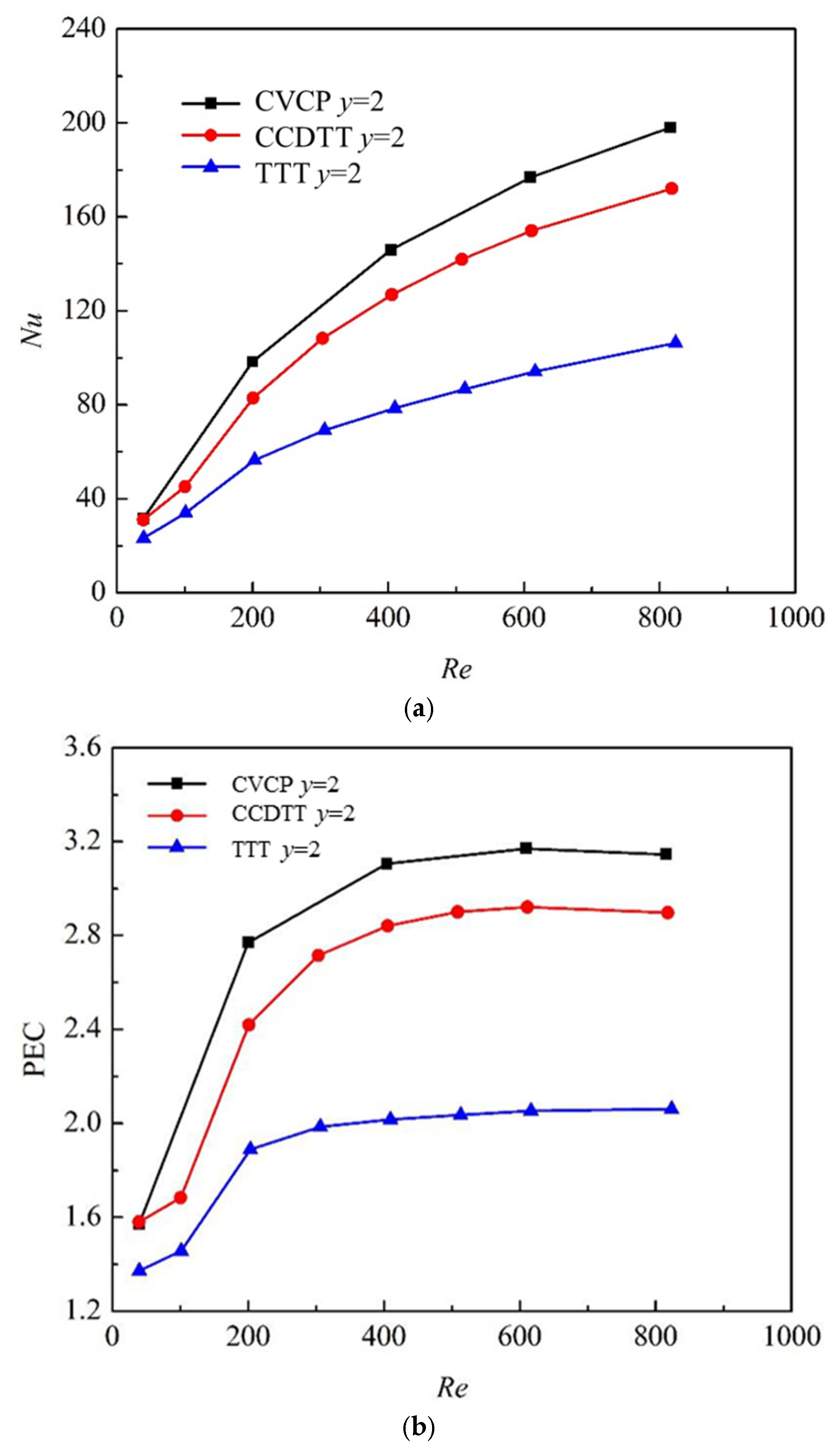
5.2. Heat Transfer
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Cp | specific heat capacity, kJ/(kg·K) | δ | thickness, m |
| D | diameter of the tube, mm | Λ | heat conductivity, W/(m·K) |
| f | friction factor | υ | kinetic viscosity, Pa·s |
| h | convective heat transfer coefficient, W/(m2·K) | μ | dynamic viscosity, m2/s |
| L | test section length, m | ρ | density, kg/m3 |
| Nu | Nusselt number | ||
| ΔP | pressure drop, Pa | Subscripts | |
| PEC | performance evaluation criterion | c | for the average |
| Pr | Prandtl number | f | for the fluid |
| Re | Reynolds number | in | for the inlet |
| Res | Reynolds number based on swirl velocity | s | for the solid |
| T | temperature, oC | o | for the oil |
| u | velocity, m/s | out | for the outlet |
| y | twist ratio | x, y, z | coordinates |
| w | for the wall | ||
| Greek letters | 0 | for the plain tube | |
| α | angle, ° | ||
References
- Bergles, A.E. Handbook of Heat Transfer Applications; McGraw-Hill: New York, NY, USA, 1985; Volume 13. [Google Scholar]
- Bergles, A.E. Heat transfer enhancement the encouragement and accommodation of high heat fluxes. ASME J. Heat Transf. 1997, 119, 8–19. [Google Scholar]
- Bergles, A.E. Exhft for fourth generation heat transfer technology. Exp. Therm. Fluid Sci. 2002, 26, 335–344. [Google Scholar]
- Hsieh, S.S.; Huang, I.W. Heat transfer and pressure drop of laminar flow in horizontal tubes with/without longitudinal inserts. J. Heat Transf. (ASME) 2000, 122, 465–475. [Google Scholar]
- Manglik, R.M.; Bergles, A.E. Heat transfer and pressure drop correlations for twisted tape inserts in isothermal tubes: Part I-laminar flows. Trans. ASME J. Heat Transf. 1993, 115, 881–889. [Google Scholar]
- Manglik, R.M.; Bergles, A.E. Heat transfer and pressure drop correlations for twisted-tape inserts in isothermal tubes, part II: Transition and turbulent flows. Trans. ASME J. Heat Transf. 1993, 115, 890–896. [Google Scholar]
- Kumar, C.N.; Murugesan, P. Review on twisted tapes heat transfer enhancement. Int. J. Sci. Eng. Res. 2012, 3, 1–9. [Google Scholar]
- Saha, S.K.; Dutta, A.; Dhal, S.K. Friction and heat transfer characteristic of laminar swirl through a circular tube fitted with regularly spaced twisted-tape elements. Int. J. Heat Mass. Transf. 2001, 44, 4211–4223. [Google Scholar]
- Pal, P.K.; Saha, S.K. Experimental investigation of laminar flow of viscous oil through a circular tube having integral spiral corrugation roughness and fitted with twisted tapes with oblique teeth. Exp. Therm. Fluid. Sci. 2014, 57, 301–309. [Google Scholar]
- Liu, X.; Li, C.; Cao, X.; Yan, C.; Ding, M. Numerical analysis on enhanced performance of new coaxial cross twisted tapes for laminar convective heat transfer. Int. J. Heat Mass Transf. 2018, 121, 1125–1136. [Google Scholar]
- Zhou, G.; Feng, Z. Experimental investigations of heat transfer enhancement by plane and curved winglet type vortex generators with punched holes. Int. J. Therm. Sci. 2014, 78, 26–35. [Google Scholar]
- Modi, A.J.; Rathod, M.K. Comparative study of heat transfer enhancement and pressure drop for fin-and-circular tube compact heat exchangers with sinusoidal wavy and elliptical curved rectangular winglet vortex generator. Int. J. Heat Mass. Tran. 2019, 141, 310–326. [Google Scholar]
- Song, K.; Tagawa, T.; Chen, Z.; Zhang, Q. Heat transfer characteristics of concave and convex curved vortex generators in the channel of plate heat exchanger under laminar flow. Int. J. Therm. Sci. 2019, 137, 215–228. [Google Scholar]
- Naphon, P. Heat transfer and pressure drop in the horizontal double pipes with and without twisted tape insert. Int. Commun. Heat Mass Transf. 2006, 33, 166–175. [Google Scholar]
- Luo, C.; Wu, S.; Song, K.; Hua, L.; Wang, L. Thermo-hydraulic performance optimization of wavy fin heat exchanger by combining delta winglet vortex generators. Appl. Therm. Eng. 2019, 163, 114343. [Google Scholar]
- Rout, P.K.; Saha, S.K. Laminar flow heat transfer and pressure drop in a circular tube having wire-coil and helical screw-tape inserts. J. Heat Transf. (ASME) 2013, 135, 021901. [Google Scholar]
- Al-Fahed, S.; Chamra, L.; Chakroun, W. Pressure drop and heat transfer comparison for both micro fin tube and twisted tape inserts in laminar flow. Exp. Therm. Fluid. Sci. 1999, 18, 323–333. [Google Scholar]
- Sivashanmugam, P.; Suresh, S. Experimental studies on heat transfer and friction factor characteristics of laminar flow through a circular tube fitted with helical screw tape inserts. Appl. Therm. Eng. 2006, 26, 1990–1997. [Google Scholar]
- Khoshvaght-Aliabadi, M.; Davoudi, S.; Dibaei, M. Performance of agitated-vessel U tube heat exchanger using spiky twisted tapes and water based metallic nanofluids. Chem. Eng. Res. Des. 2018, 133, 26–39. [Google Scholar]
- Khoshvaght-Aliabadi, M.; Ghodrati, P.; Khaligh, S.F.; Kang, Y.T. Improving supercritical CO2 cooling using conical tubes equipped with non-uniform twisted inserts. Int. Commun. Heat Mass Transf. 2024, 150, 107171. [Google Scholar]
- Alkhamis, N. Heat transfer enhancement for fluid flow inside a channel by using metal foam. Int. Commun. Heat Mass Transf. 2025, 162, 108574. [Google Scholar]
- Jeon, Y.H.; Hong, J.H.; Kang, H.C. An empirical correlation for enhanced heat transfer in spirally fluted tube crossflow convection. Results Eng. 2025, 25, 103596. [Google Scholar]
- Hong, Y.; Kang, Z.; Fan, J. Heat transfer enhancement of pulsating heat pipes with novel structures. Appl. Therm. Eng. 2025, 268, 125720. [Google Scholar]
- Murugesan, P.; Mayilsamy, K.; Suresh, S. Heat transfer and friction factor studies in a circular tube fitted with twisted tapes consisting of wire nails. Chin. J. Chem. Eng. 2010, 18, 1038–1042. [Google Scholar]
- Webb, R.L.; Kim, N.H. Principles of Enhanced Heat Transfer; Taylor & Francis Group: New York, NY, USA, 2005. [Google Scholar]

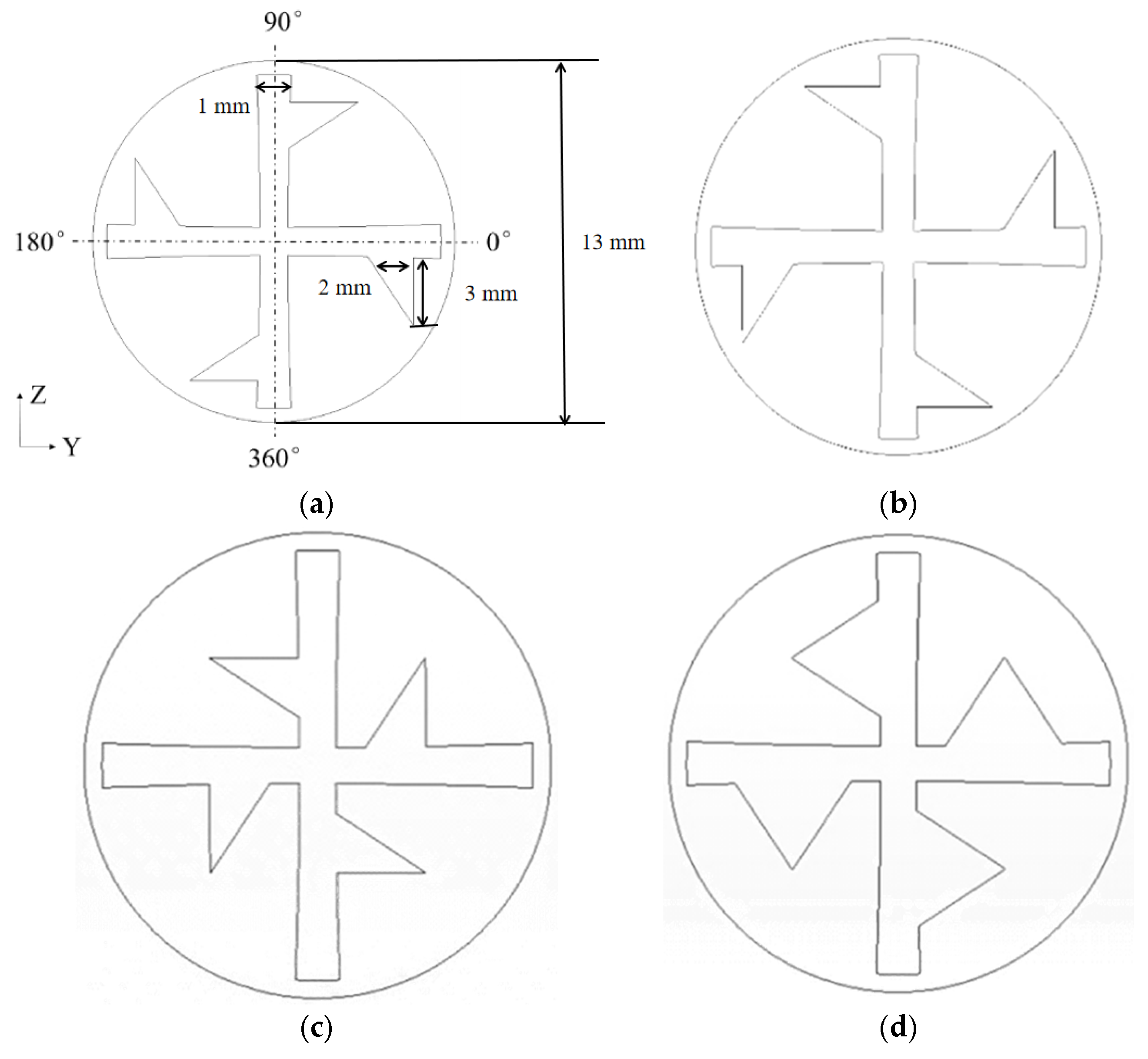
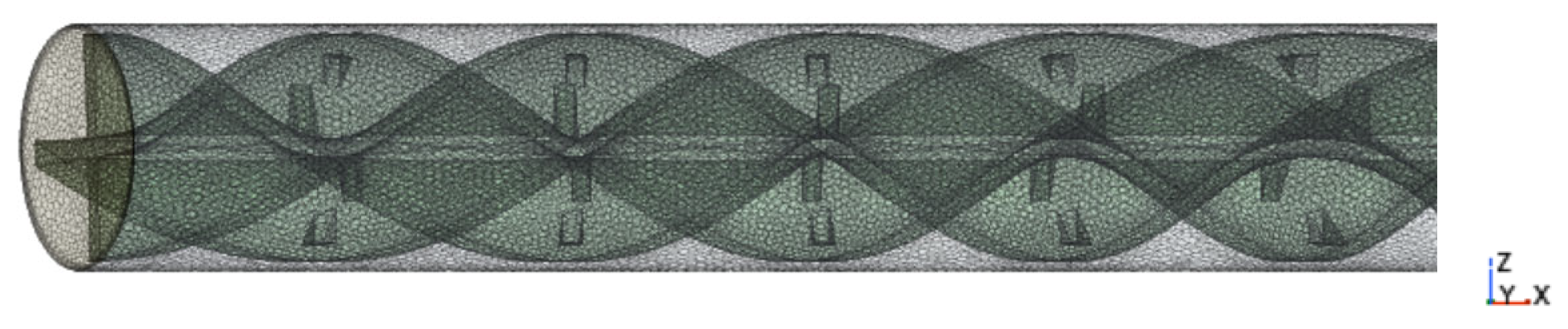



| Technology Category | Representative Study | Method | Key Findings | Application Scenarios | Ref. |
|---|---|---|---|---|---|
| Twisted Tapes | |||||
| Conventional Twisted Tapes (TTT) | Manglik & Bergles, Kumar | Experimental and Theoretical | Universal correlations for Nu and f in laminar/turbulent flows; validated secondary flow effects | Low-viscosity fluids (laminar/turbulent) | [5,6,7] |
| Periodically Spaced Tapes | Saha et al. | Experimental (laminar) | Periodic spacing enhances Nu by 1.8× and f by 2.1× (Re = 1000–5000) | High-viscosity laminar flows | [8] |
| Oblique-Teeth Twisted Tapes | Pal & Saha | Experimental (laminar) | Oblique teeth improve fluid mixing; Nu increases 3.2× vs. Smooth tube (Re = 500–2000) | High-viscosity oils | [9] |
| Coaxial Cross Double-Twisted Tapes (CCDTT) | Liu et al. | Numerical (laminar) | Dual-tape cross structure generates bidirectional vortices; Nu 35% higher than TTT; f increases only 18% | High-viscosity fluids (lubricants) | [10] |
| Vortex Generators | |||||
| Flat Winglet VG with Perforations | Zhou et al. | Experimental (Laminar/Turbulent) | Perforated winglets increase Nu by 25% but raise f by 40% | Air/low-viscosity fluids | [11] |
| Sinusoidal vs. Elliptical VG | Modi & Rathod | Numerical | Elliptical VG achieves 12% higher Nu and 8% lower pressure drop than sinusoidal VG | Compact heat exchangers | [12] |
| Concave/Convex Curved VG | Song et al. | Experimental (laminar) | Convex VG yields 18% higher Nu than concave VG with comparable pressure drop | Plate heat exchangers | [13] |
| Compound Techniques | |||||
| Twisted Tapes + Corrugated Tubes | Naphon | Experimental (Double-Pipe Laminar) | Nu enhanced 2.5×, but pressure drop increased 3.8× (Re = 800–3000) | High-viscosity oils | [14] |
| Twisted Tapes + VG | Luo et al. | Numerical | 45° VG attack angle achieves PEC = 1.28 (19% higher than single techniques) | Compact finned heat exchangers | [15] |
| Helical Screw Tapes + Wire Coils | Rout & saha | Experimental (laminar) | Combined inserts improve Nu by 40% vs. single inserts; f increases 2.3× | High-viscosity fluids (e.g., polymer melts) | [16] |
| Other Passive Techniques | |||||
| Microfin Tubes | Al-Fahed & Chakroun | Experimental (laminar) | Microfin tubes increase Nu by 30% vs. smooth tubes; f increases 1.5× (Re = 500–1500) | Low-viscosity laminar flows | [17] |
| Helical Screw Inserts | Sivashanmugam et al. | Experimental (laminar) | Periodic shear-induced mixing improves Nu by 2.6×; f increases 6.4× (Re = 20–100) | High-viscosity laminar flows (e.g., polymer solutions) | [18] |
| Spiky Twisted Tapes | Khoshvaght-Aliabadi | Experimental (turbulent) | Heat transfer coefficient is increased by 11–67% | Water-based metal-lic nanofluids | [19] |
| Conical Horizontal Tubes (CHTs) | Khoshvaght-Aliabadi | Numerical | The heat transfer coefficient is increased by 43.1% and the pressure drop is reduced by 36.7% | Supercritical CO2 | [20] |
| Model | Grid Number | ΔP [Pa] | To [°C] |
|---|---|---|---|
| #1 | 1,396,841 | 22,674.32 | 55.68 |
| #2 | 2,452,702 | 22,823.47 | 56.73 |
| #3 | 3,312,913 | 22,886.65 | 56.87 |
| #4 | 5,049,568 | 22,888.52 | 56.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhao, X.; Ran, L.; Li, M.; Zhang, Y.; Zhang, Y.; Li, S.; Xiao, H.; Ding, M. Numerical Study on Compound Heat Transfer Enhancement by New Inserts of Lubricating Oil in Tubes. Processes 2025, 13, 938. https://doi.org/10.3390/pr13040938
Liu X, Zhao X, Ran L, Li M, Zhang Y, Zhang Y, Li S, Xiao H, Ding M. Numerical Study on Compound Heat Transfer Enhancement by New Inserts of Lubricating Oil in Tubes. Processes. 2025; 13(4):938. https://doi.org/10.3390/pr13040938
Chicago/Turabian StyleLiu, Xiaoya, Xinwen Zhao, Lingke Ran, Muzhen Li, Yinxing Zhang, Yongfa Zhang, Song Li, Hongguang Xiao, and Ming Ding. 2025. "Numerical Study on Compound Heat Transfer Enhancement by New Inserts of Lubricating Oil in Tubes" Processes 13, no. 4: 938. https://doi.org/10.3390/pr13040938
APA StyleLiu, X., Zhao, X., Ran, L., Li, M., Zhang, Y., Zhang, Y., Li, S., Xiao, H., & Ding, M. (2025). Numerical Study on Compound Heat Transfer Enhancement by New Inserts of Lubricating Oil in Tubes. Processes, 13(4), 938. https://doi.org/10.3390/pr13040938





