SCA Fracturing Mechanisms of Rock Mass and Application in Overhanging Roof Structure Fragmentation of Mine Goaf
Abstract
1. Introduction
2. Theoretical Analysis of Coal Rock Stress Under Expansion Pressure
2.1. Theoretical Analyses of Rock Models with Single and Double Expansion Holes
2.2. Theoretical Analyses of the Cantilevered Rock Strata Model
2.3. Simulation Analysis of Free Surface Effects
3. Stress Distribution in the Cantilevered Roof
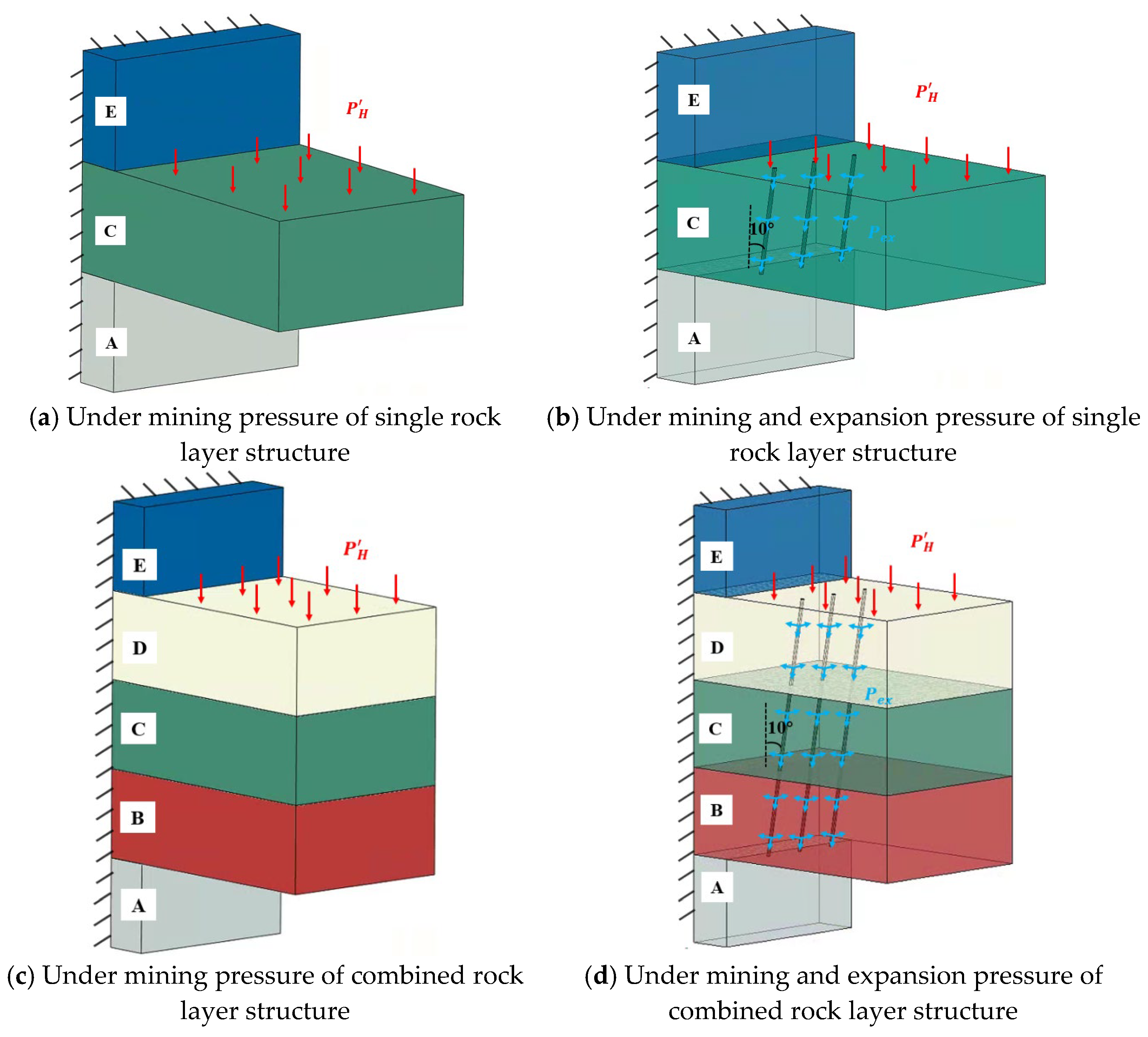
3.1. Simulation Scheme of the Cantilever Roof
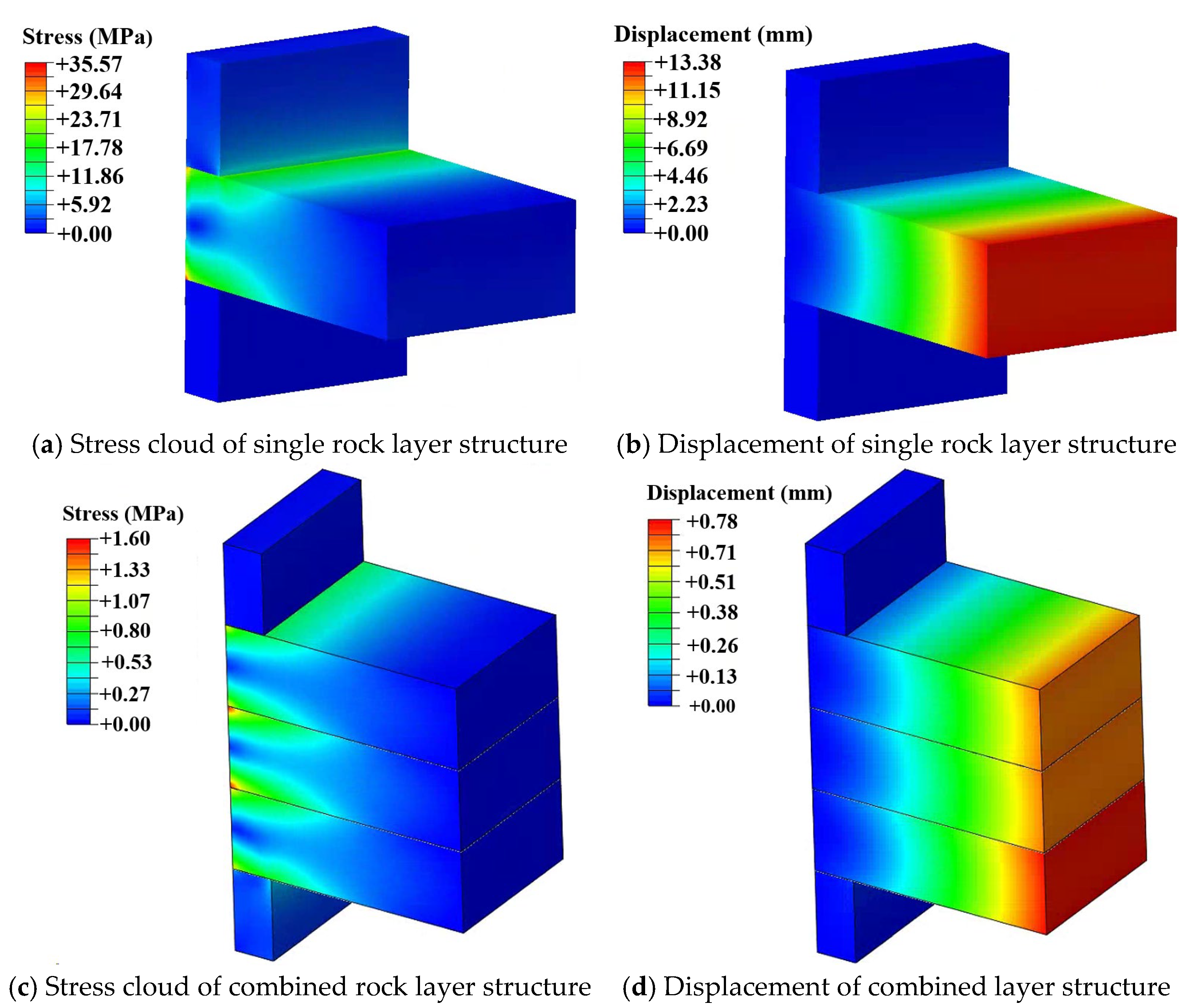
3.2. Simulation Analysis of the Cantilever Roof Under Mineral Pressure Only
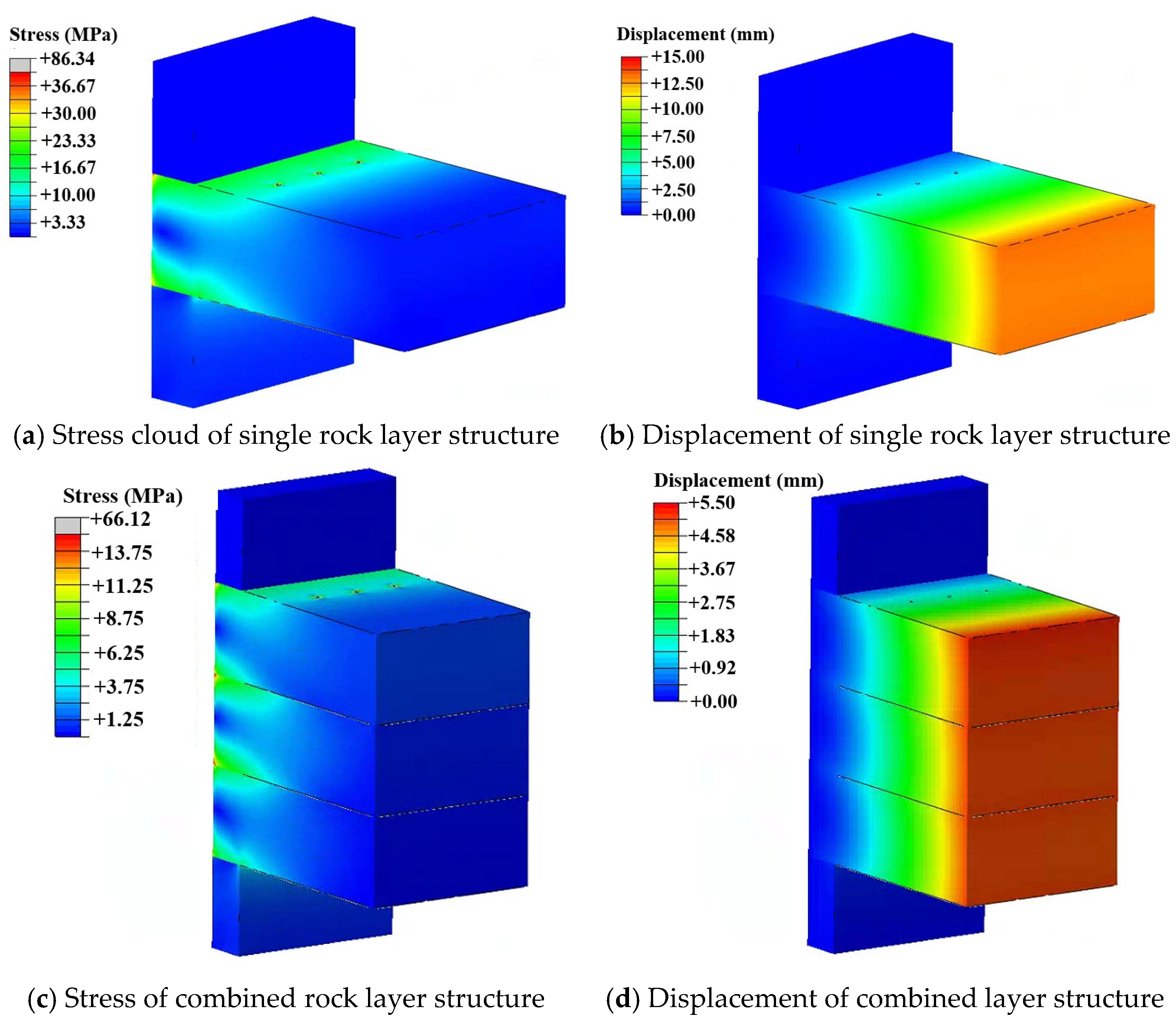
3.3. Simulation Analysis of the Cantilever Roof Under the Mining and Expansion Pressure
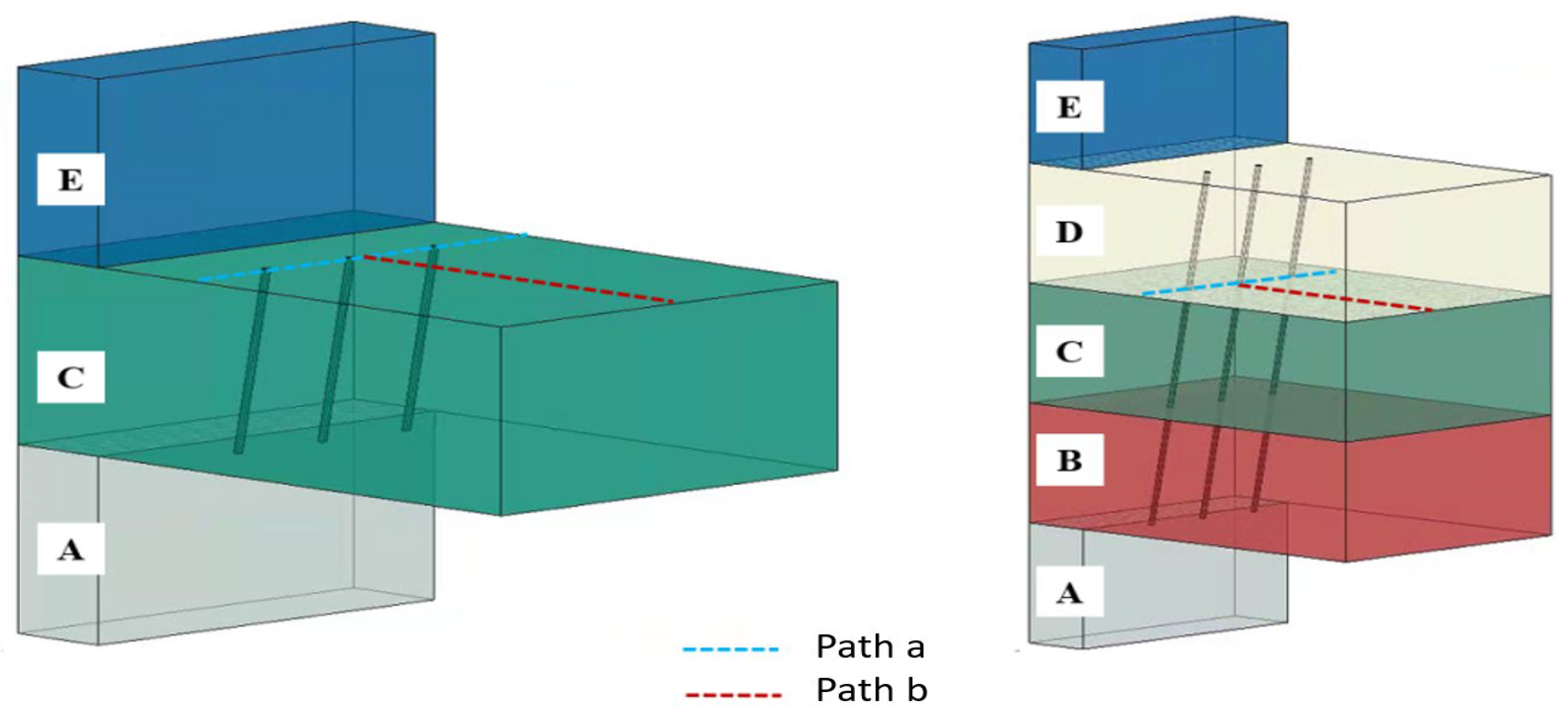
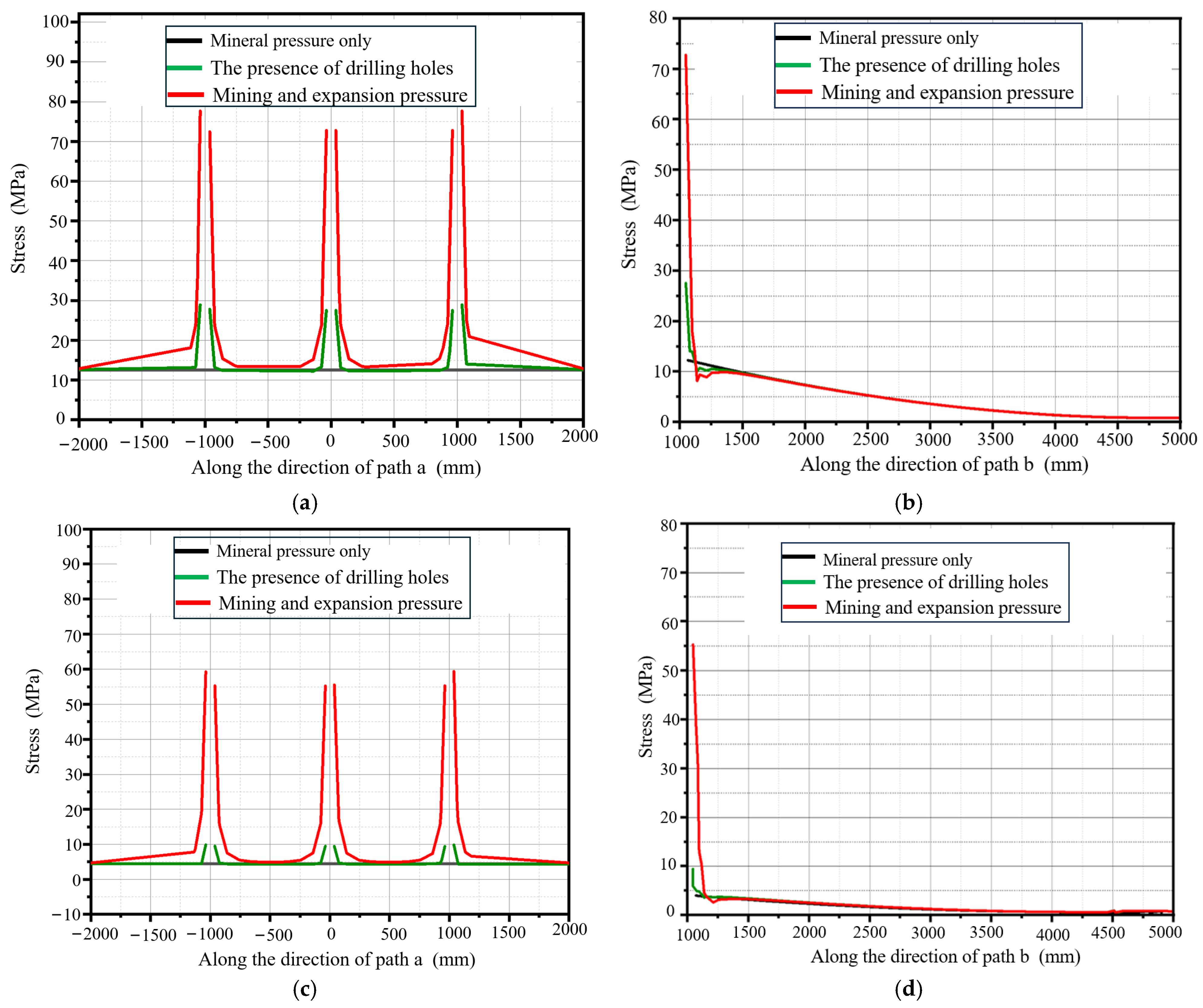
3.4. Comparison of Three Working Conditions
4. Engineering Application
5. Conclusions
- (1)
- The optimization study of expansion pressure parameters shows that the stress doubling effect of a single rock layer significantly changes the stress distribution around borehole due to expansion pressure (Pex = 30 MPa). The peak stress reaches 86.34 MPa, which is 242.73% of the mining pressure condition (35.57 MPa) and 156.98% of the compressive strength of the rock mass ( = 55 MPa). For multi-layer coordinated deformation, the peak stress reaches 66.12 MPa, which is 413.25% of the mining pressure condition (1.60 MPa). An on-site industrial application verified technical reliability; after adopting the drilling scheme with a 75 mm diameter and a 6 m spacing, the hanging roof area at the end of the mining face is reduced to below 20 m2.
- (2)
- At a free surface distance f = 100 mm, the annular stress of the proximal free surface (y = 0) reaches 39.14 MPa, yielding a stress concentration factor Kt = 1.3 (normalized to the internal expansive pressure Pex = 30 MPa). A progressive weakening of stress concentration is observed with increasing f. At f = 200 mm, annular stress reduces to 33.25 MPa, representing a 15.05% decrease compared to the f = 100 mm case. At f = 400 mm, stress further diminishes to 31.25 MPa, achieving a 20.16% reduction relative to the baseline scenario.
- (3)
- The cantilever beam model reveals the gradient evolution law of roof fracture. The results indicate that bending stress increases gradually with the growth of and reaches its maximum value at the restrained end of the cantilever beam—the compressive stress. The cantilever beam deflection achieves its maximum value at the free end.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Debjeet, M.; Roy, P.N.S.; Manoj, K. Roof fall threat analysis using fractal pattern recognition and neural network over mine microseismicity in a Central Indian longwall panel overlain by massive sandstone roof. Geosyst. Geoenviron. 2023, 2, 100138. [Google Scholar]
- Yang, J.; Zheng, K.; Wang, Z.; Pang, N. Technology of weakening and danger-breaking dynamic disasters by hard roof. J. China Coal Soc. 2020, 45, 3371–3379. [Google Scholar]
- Song, Y. Techniques for Controlling Hard and Hard-to-Rise Roof Slabs in Coal Seams; Coal Industry Publishing House: Beijing, China, 2002; pp. 67–69. [Google Scholar]
- Fang, X.; Hao, X.; Lan, Y. Determination of reasonable forced caving interval in shallow-buried seam with hard and thin bedrock. Chin. J. Rock Mech. Eng. 2010, 29, 388–393. [Google Scholar]
- Huang, B.; Liu, J.; Zhang, Q. The reasonable breaking location of overhanging hard roof for directional hydraulic fracturing to control strong strata behaviors of gob-side entry. Int. J. Rock Mech. Min. Sci. 2018, 103, 1–11. [Google Scholar] [CrossRef]
- Marek, J.; Andrzej, H.; Mateusz, Ć. Directional Hydraulic Fracturing (DHF) of the Roof, as an Element of Rock Burst Prevention in the Light of Underground Observations and Numerical Modelling. Energies 2021, 14, 562. [Google Scholar] [CrossRef]
- Xia, B.; Zhang, X.; Yu, B.; Jia, J. Weakening effects of hydraulic fracture in hard roof under the influence of stress arch. Int. J. Min. Sci. Technol. 2017, 28, 951–958. [Google Scholar] [CrossRef]
- Klishin, I.V.; Opruk, Y.G.; Teleguz, S.A.; Galkin, A.V. Spectral acoustic and seismological monitoring of enclosing rock condition in the face area during roof softening by means of directional hydraulic fracturing (DHF). IOP Conf. Ser. Earth Environ. Sci. 2018, 206, 012023. [Google Scholar] [CrossRef]
- Wang, C.; Zheng, K.; Wang, H.; Li, Y.; Wang, L. Comprehensive treatment technology of hydraulic fracturing in initial mining of the first mining face under hard roof. Coal Eng. 2023, 55, 63–69. [Google Scholar]
- Shakib, T.; Shahri, A. Analysis of hydraulic fracturing in fractured reservoir: Interaction between hydraulic fracture and natural fractures. Life Sci. J. 2012, 9, 1854–1862. [Google Scholar]
- Matsui, K.; Shimada, H.; Anzwar, H.Z. Acceleration of massive roof caving in a longwall gob using a hydraulic fracturing. In Proceedings of the 4th International Symposium on Mining Science and Technology, Beijing, China, 29–31 August 1999. [Google Scholar]
- Sawmliana, C.; Roy, P.P. A New Blastability Index for Hard Roof Management in Blasting Gallery Method. Geotech. Geol. Eng. 2012, 30, 1357–1367. [Google Scholar] [CrossRef]
- Mondal, A.; Pathrikar, A.; Karekal, S. Phase-Field Based Peridynamics Implementation to Model Blast-Induced Fracture in Brittle Solids. Rock Mech. Rock Eng. 2024, 57, 5685–5703. [Google Scholar] [CrossRef]
- Slavko, T.; Veljko, L. Rock fracturing mechanisms by blasting. Podzemn. Rad. 2018, 32, 15–31. [Google Scholar]
- Zhang, Z. Failure of hanging roofs in sublevel caving by shock collision and stress superposition. J. Rock Mech. Geotech. Eng. 2016, 8, 886–895. [Google Scholar] [CrossRef]
- Gautam, A.; Kumar, A.; Ram, S.; Skrzypkowski, K.; Zagórski, K.; Zagórska, A.; Madziarz, M.; Migda, K. Strata Control by Roof Blasting for Bord and Pillar Mining Method in Mechanized Depillaring Panels. Appl. Sci. 2025, 15, 1403. [Google Scholar] [CrossRef]
- Ren, X.; Guo, J.; Zhang, B.; Xi, Z.; Lu, C.; Li, H. Mine pressure manifestation law of dynamic pressure roadway with multilayer hard roof and roof cutting control technology of deep and shallow hole combination blasting. Min. Res. Dev. 2024, 44, 48–55. [Google Scholar]
- Enrico, C.D.; Andrea, L.; Andrea, T. A novel extension of the SYNTHSEP methodology for the optimal synthesis and design of supercritical CO2 cycles in waste heat recovery applications. Energy Convers. Manag. 2023, 276, 116535. [Google Scholar]
- Sampath, K.; Perera, M.; Ranjith, P.; Ranjith, P.G.; Matthai, S.K. CO2 interaction induced mechanical characteristics alterations in coal: A review. Int. J. Coal Geol. 2019, 204, 113–129. [Google Scholar] [CrossRef]
- Hol, S.; Spiers, J.C.; Peach, J.C. Microfracturing of coal due to interaction with CO2 under unconfined conditions. Fuel 2012, 97, 569–584. [Google Scholar] [CrossRef]
- Kiyama, T.; Nishimoto, S.; Fujioka, M.; Xue, Z.; Ishijima, Y.; Pan, Z.; Connell, L.D. Coal swelling strain and permeability change with injecting liquid/supercritical CO2 and N2 at stress-constrained conditions. Int. J. Coal Geol. 2011, 85, 56–64. [Google Scholar] [CrossRef]
- Lu, G. Study on CO2 gas-phase fracturing for coal seam roof weakening in fully mechanised top coal caving face. Coal Eng. 2017, 49, 58–59+62. [Google Scholar]
- Raskildinov, B.U. Increasing the effectiveness of blasting in underground mines. In Proceedings of the 17th International Mining Congress and Exhibition of Turkey, Ankara, Turkey, 19–22 June 2001. [Google Scholar]
- Zhang, W.; Cao, L.; Zhang, D.; Hu, Y.; Chang, J.; Zhang, Z. Deformation and Fracture Mechanisms of Thick Hard Roofs in Upward Mining Coalfaces: A Mechanical Model and Its Validation. Appl. Sci. 2024, 14, 10278. [Google Scholar] [CrossRef]
- He, Y.; Huang, Q. Simulation Study on Spatial Form of the Suspended Roof Structure of Working Face in Shallow Coal Seam. Sustainability 2023, 15, 921. [Google Scholar] [CrossRef]
- Liu, H.; Hao, C.; Han, Z.; Liu, Q.; Wang, H.; Liang, J.; Zhang, D. Study on the Mechanism of a Hanging Roof at a Difficult Caving End in a Fully-Mechanized Top Coal Caving Face. Sustainability 2023, 15, 812. [Google Scholar] [CrossRef]
- Zhu, X.; Zhai, C.; Yu, X.; Xu, J.; Sun, Y.; Cong, Y.; Zheng, Y.; Tang, W.; Chen, A. Fracture damage characteristics of hard roof with different bedding angles induced by modified soundless cracking agents. Eng. Fract. Mech. 2023, 289, 109387. [Google Scholar] [CrossRef]
- Eugene, S.; Wu, W. Experimental analysis of expansion and stress generation of the static cracking agent on supporting beam. Energy Build. 2023, 298, 113548. [Google Scholar] [CrossRef]
- Li, C.; He, S.; Hou, W.; Ma, D. Experimental study on expansion and cracking properties of static cracking agents in different assembly states. Int. J. Min. Sci. Technol. 2022, 32, 1259–1272. [Google Scholar] [CrossRef]
- Wu, S.; Zhai, C.; Xu, J.; Qin, L.; Sun, Y.; Dong, R. The performance of soundless cracking agents for weakening rock roof under different notch angles. Arab. J. Geosci. 2019, 12, 1–13. [Google Scholar] [CrossRef]
- Yuan, R.; Lian, Z.; Zhang, Q.; Li, M.; Li, H.; Li, Y.; Wu, W. Rock Fracturing Characteristics and Roadway Expansion Application of Static Crushing Agent under Multi-Row Drilling Condition. Appl. Sci. 2024, 14, 9032. [Google Scholar] [CrossRef]
- Jin, Z.; Liao, H.; Zhu, W. Splitting mechanism of rock and concrete under expansion pressure. Chin. J. Rock Mech. Eng. 1989, 1989, 19–26. [Google Scholar]
- Salençon, J.; Halphen, B. Calcul des structures Anélastiques. In Élasto-Plasticité; Presses de l’École des Ponts ParisTech: Puteaux, France, 1985. [Google Scholar]




| Layer Number | Modulus of Elasticity (Gpa) | Poisson’s Ratio | Size (m) |
|---|---|---|---|
| A | 10 | 0.2 | 1 × 4 × 2 |
| B | 15 | 0.2 | 6 × 4 × 2 |
| C | 20 | 0.2 | 6 × 4 × 2 |
| D | 15 | 0.2 | 6 × 4 × 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Yuan, R.; Zai, P.; Zhang, Q.; Feng, C. SCA Fracturing Mechanisms of Rock Mass and Application in Overhanging Roof Structure Fragmentation of Mine Goaf. Processes 2025, 13, 1275. https://doi.org/10.3390/pr13051275
Li H, Yuan R, Zai P, Zhang Q, Feng C. SCA Fracturing Mechanisms of Rock Mass and Application in Overhanging Roof Structure Fragmentation of Mine Goaf. Processes. 2025; 13(5):1275. https://doi.org/10.3390/pr13051275
Chicago/Turabian StyleLi, Hui, Ruifu Yuan, Penghui Zai, Qunlei Zhang, and Chun Feng. 2025. "SCA Fracturing Mechanisms of Rock Mass and Application in Overhanging Roof Structure Fragmentation of Mine Goaf" Processes 13, no. 5: 1275. https://doi.org/10.3390/pr13051275
APA StyleLi, H., Yuan, R., Zai, P., Zhang, Q., & Feng, C. (2025). SCA Fracturing Mechanisms of Rock Mass and Application in Overhanging Roof Structure Fragmentation of Mine Goaf. Processes, 13(5), 1275. https://doi.org/10.3390/pr13051275







