Research on the Effect of Damping Grooves on the Pressure and Cavitation Characteristics of Axial Piston Pumps
Abstract
1. Introduction
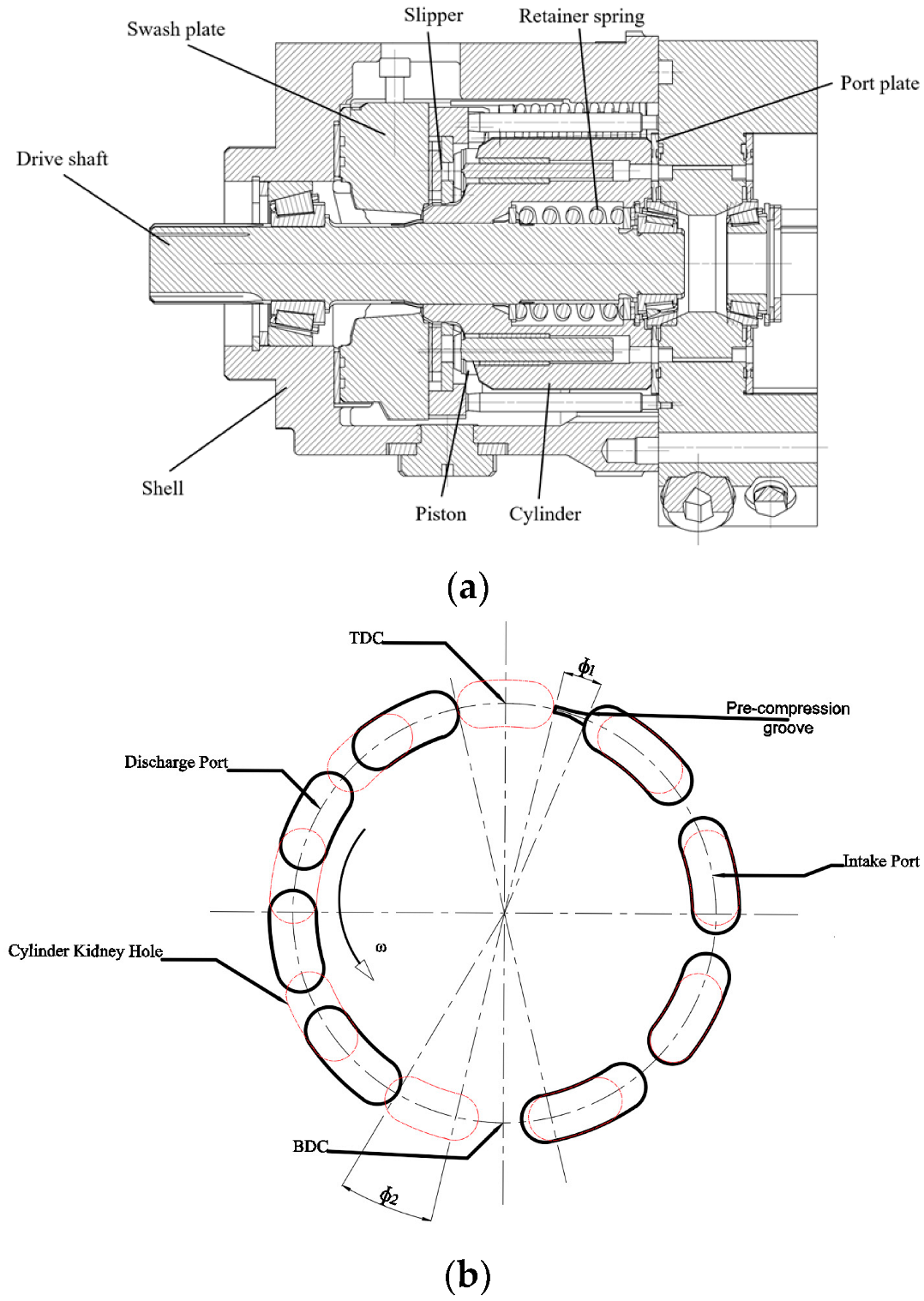
2. The Three-Dimensional Model of the Axial Piston Pump
3. CFD Modeling of the Axial Piston Pump
3.1. Turbulence Model
3.2. Cavitation Model
3.3. CFD Model Grid Generation
3.4. Mesh Independence Verification
3.5. Initialization and Boundary Conditions
4. Simulation Structure and Analysis
4.1. Transient Analysis of Damping Groove Flow Field Characteristics
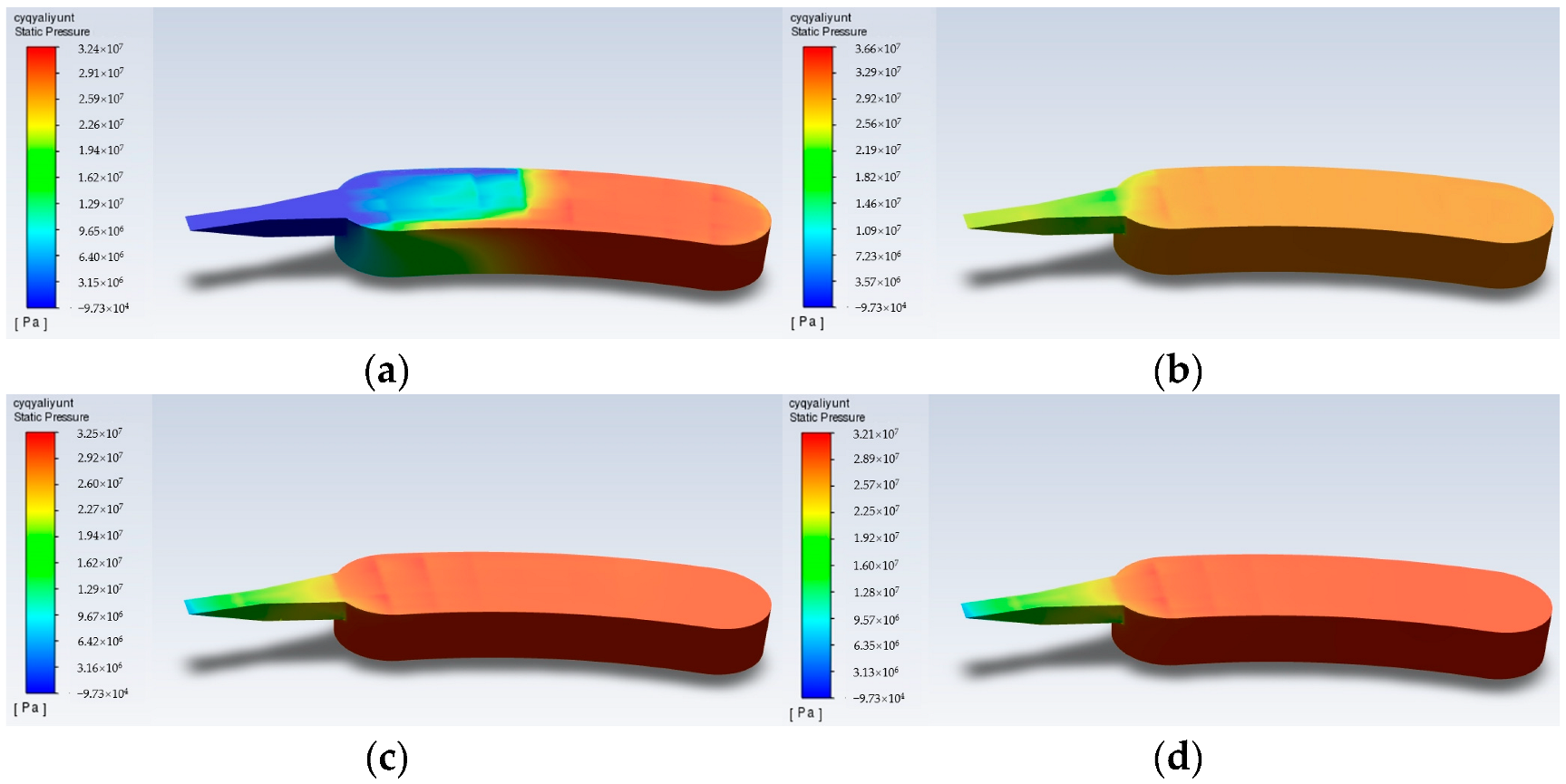
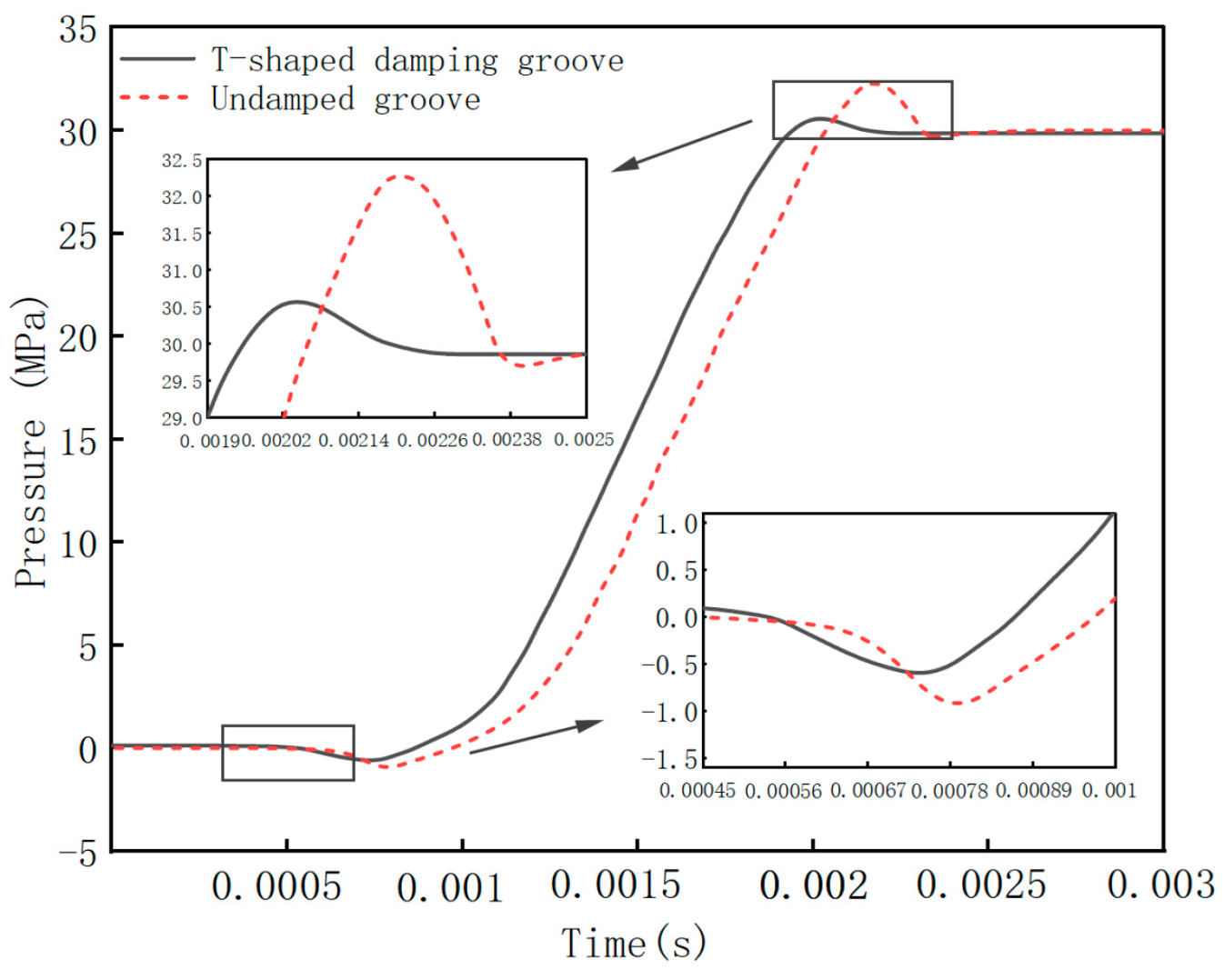
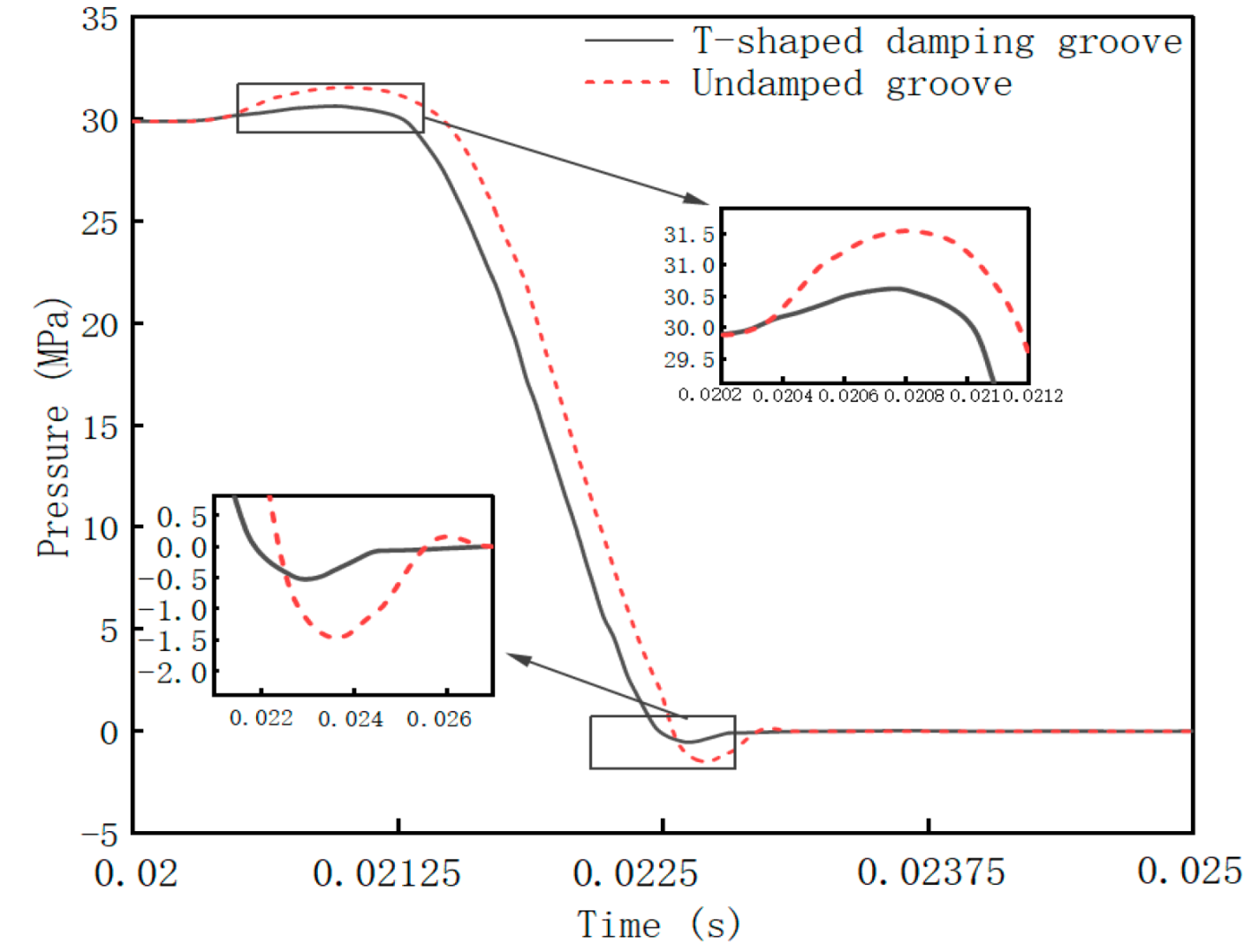
4.1.1. Pressure Characteristic Analysis
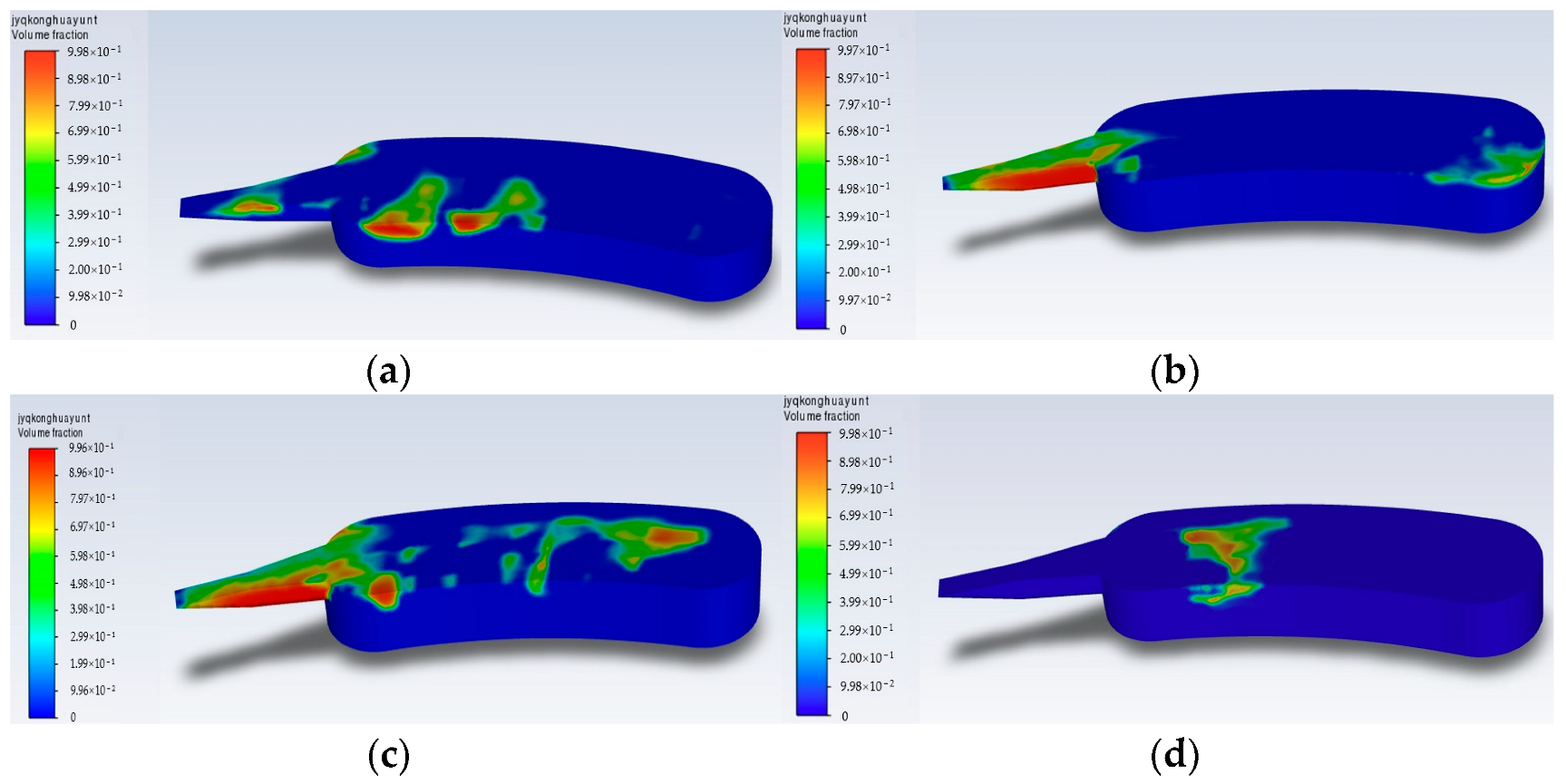
4.1.2. Cavitation Characteristic Analysis
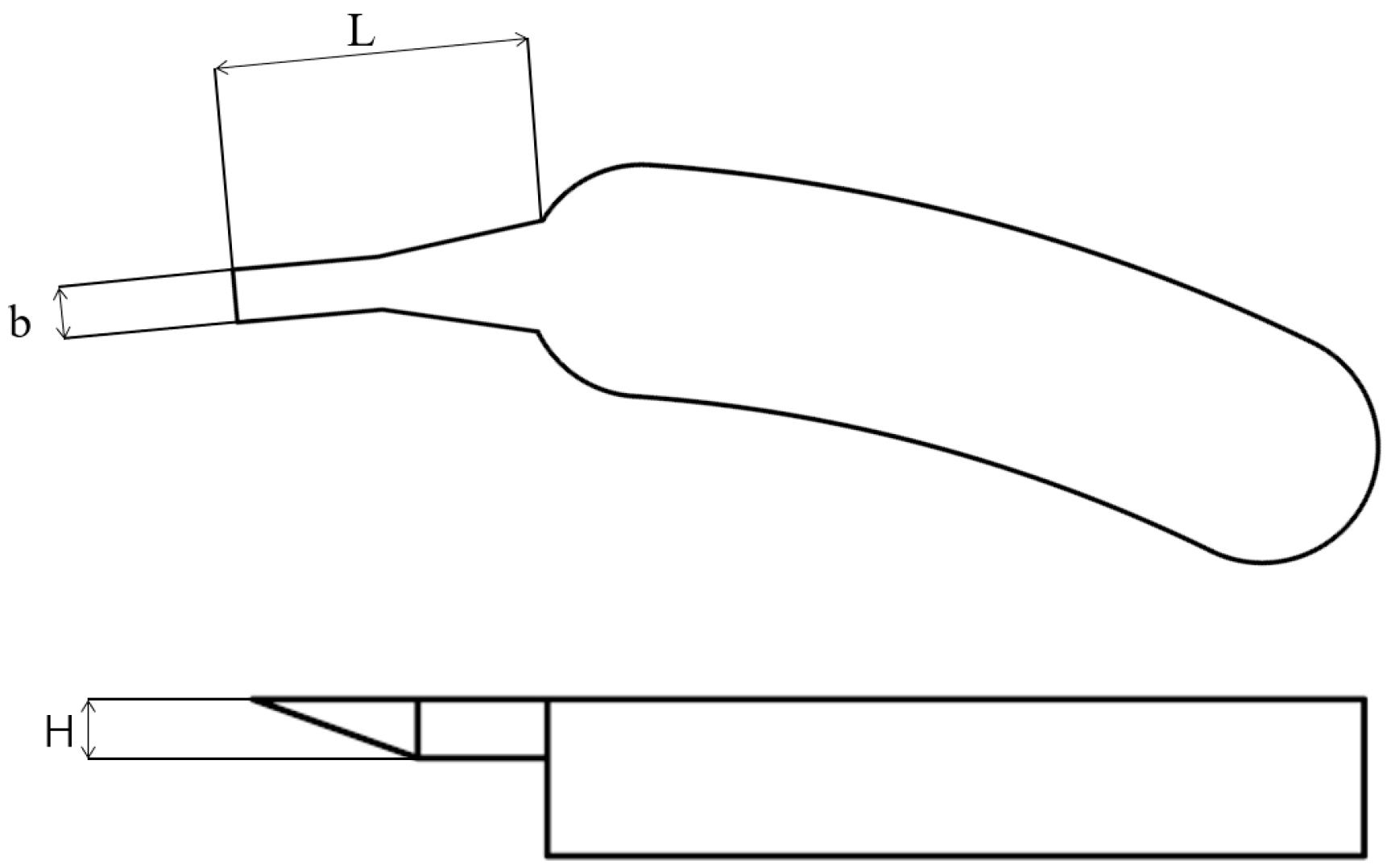
4.2. Study on the Structural Parameters of the T-Shaped Damping Groove
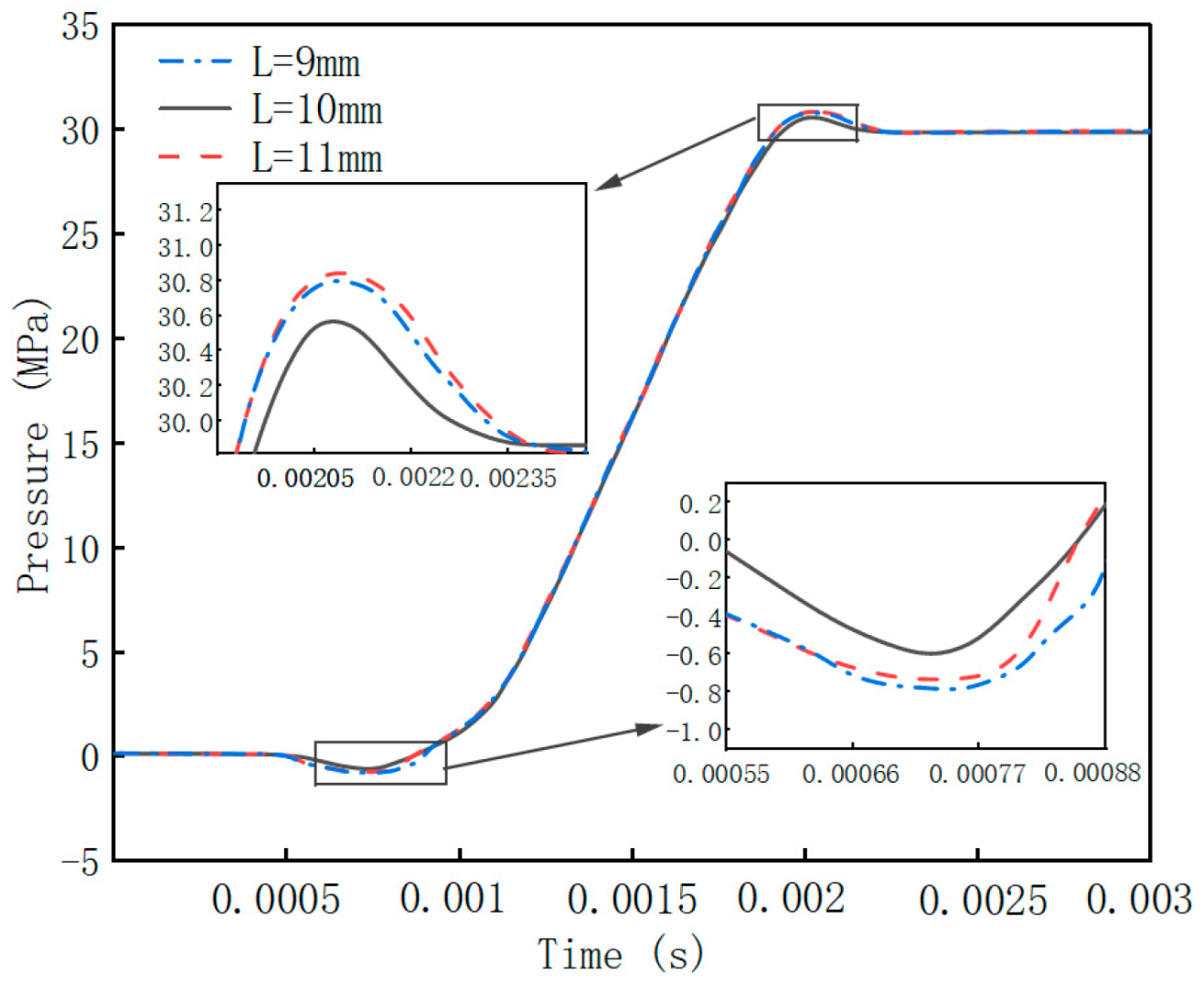
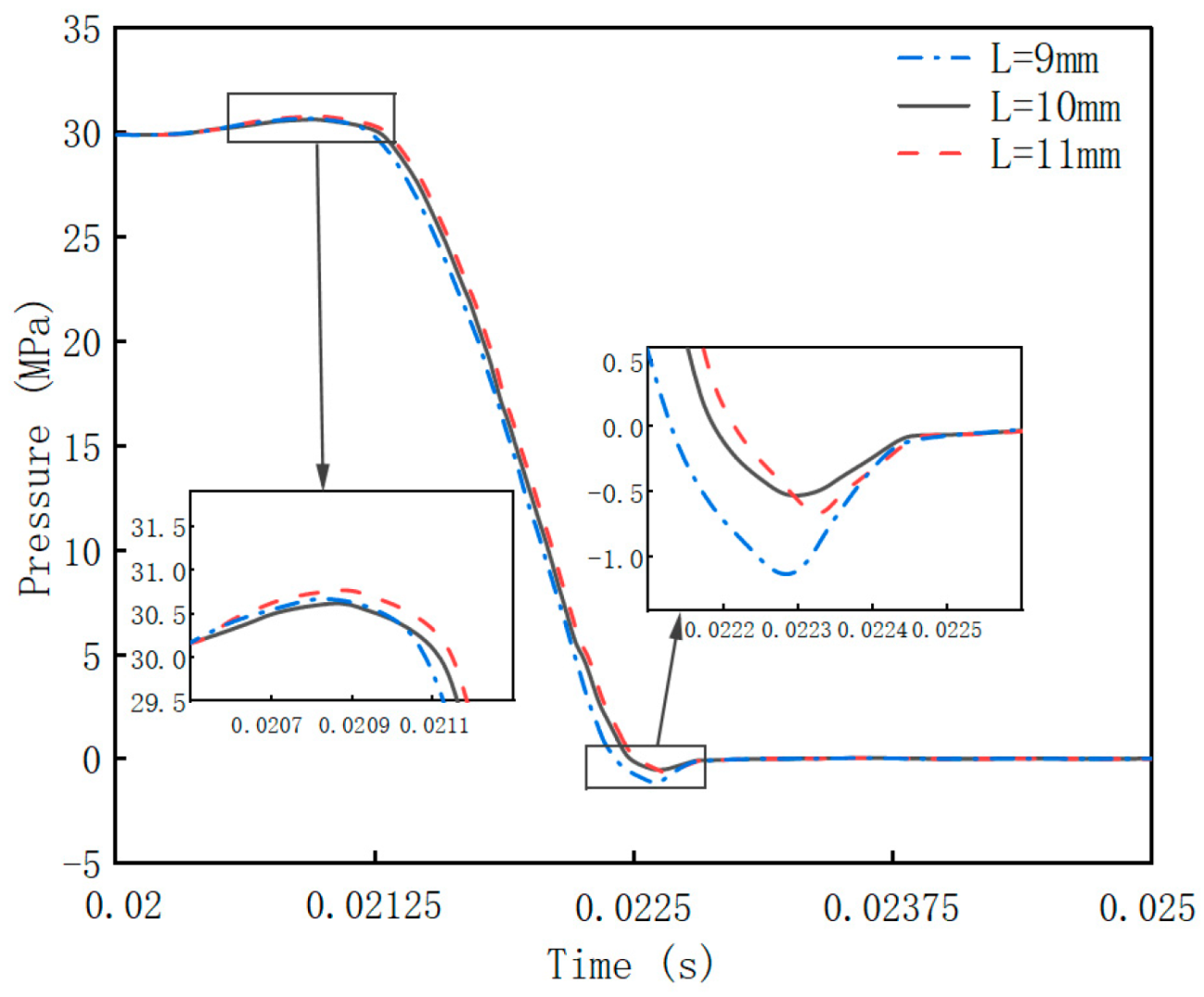
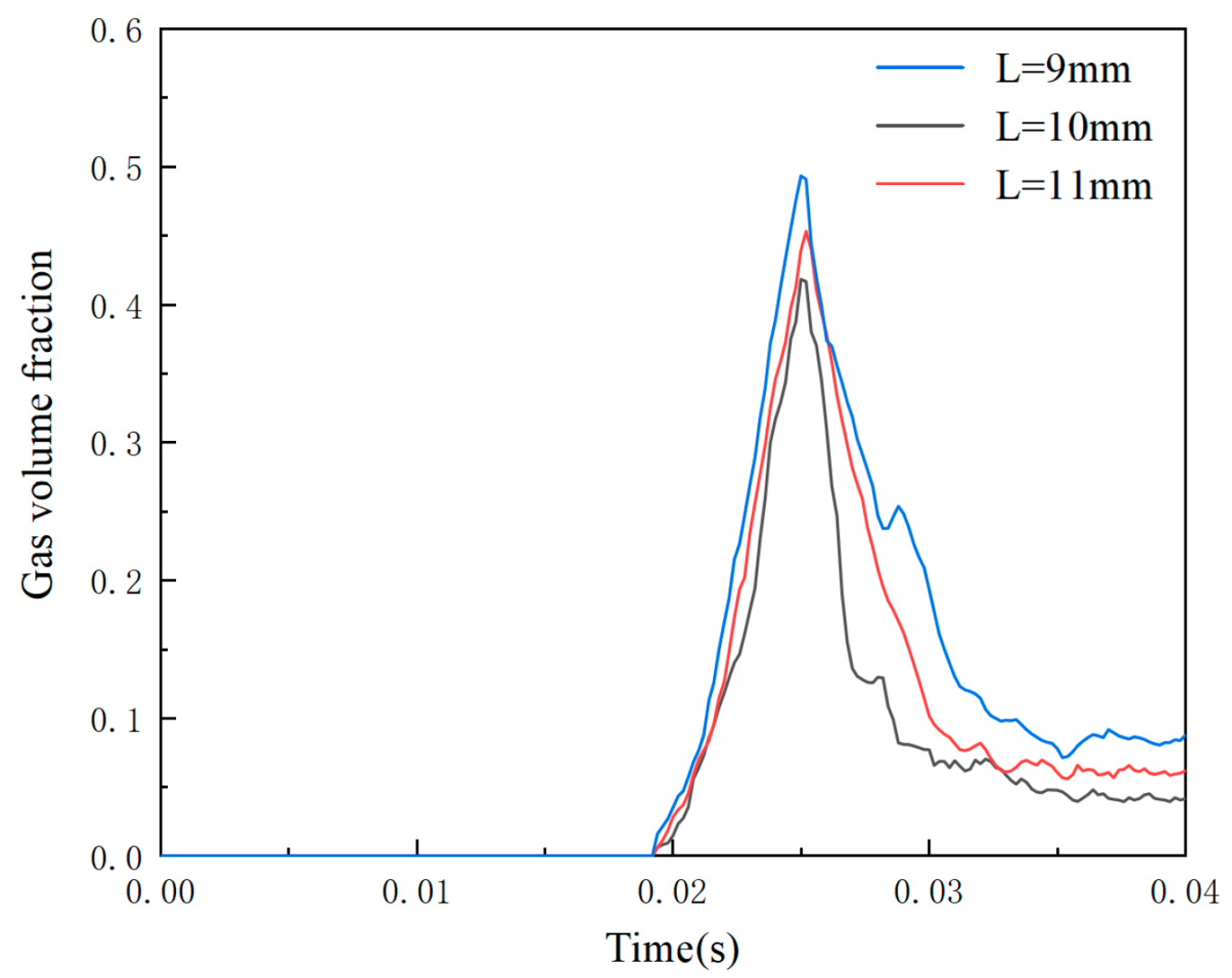
4.2.1. Effect of the T-Shaped Damping Groove Length (L) on Flow Field Performance
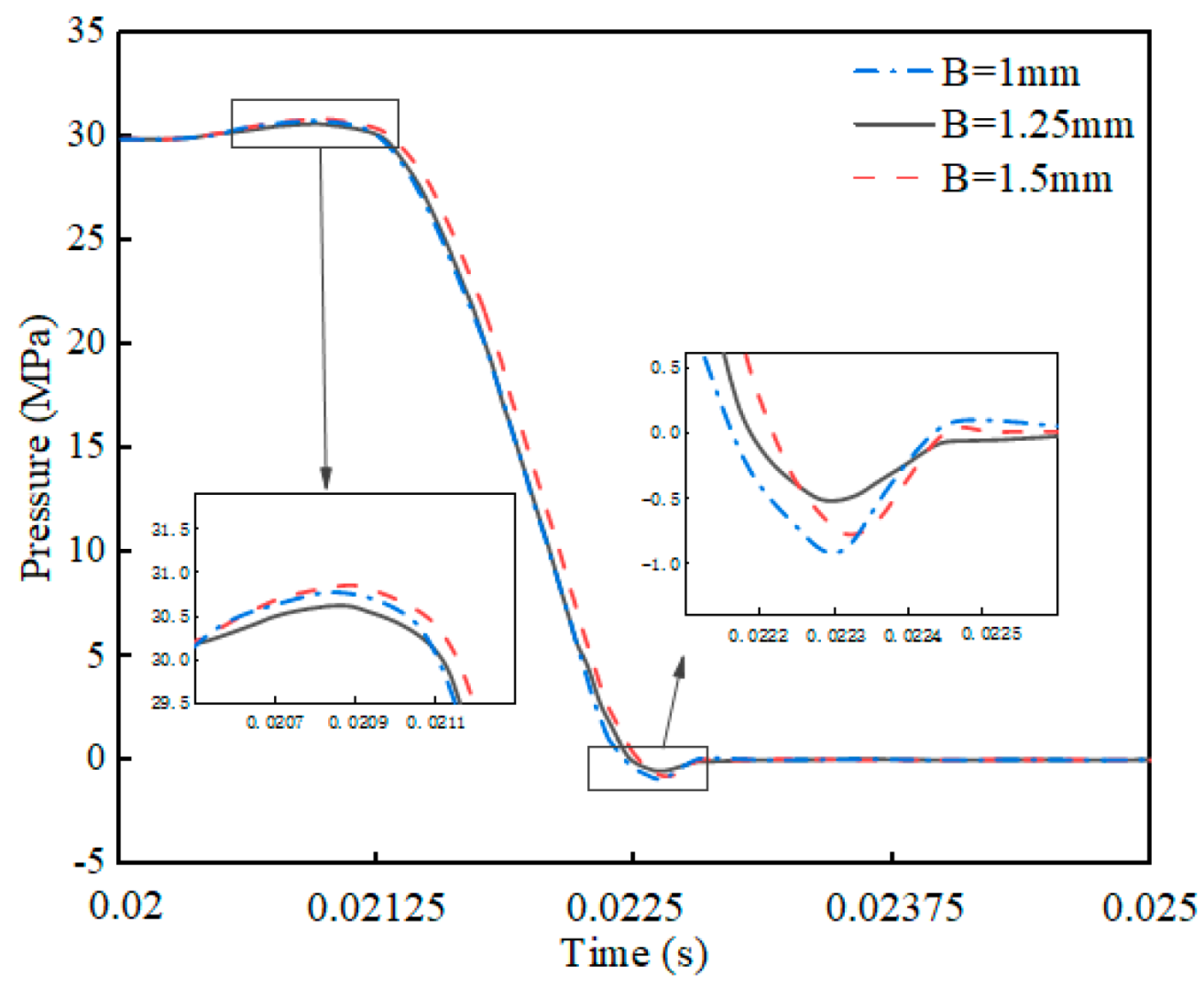
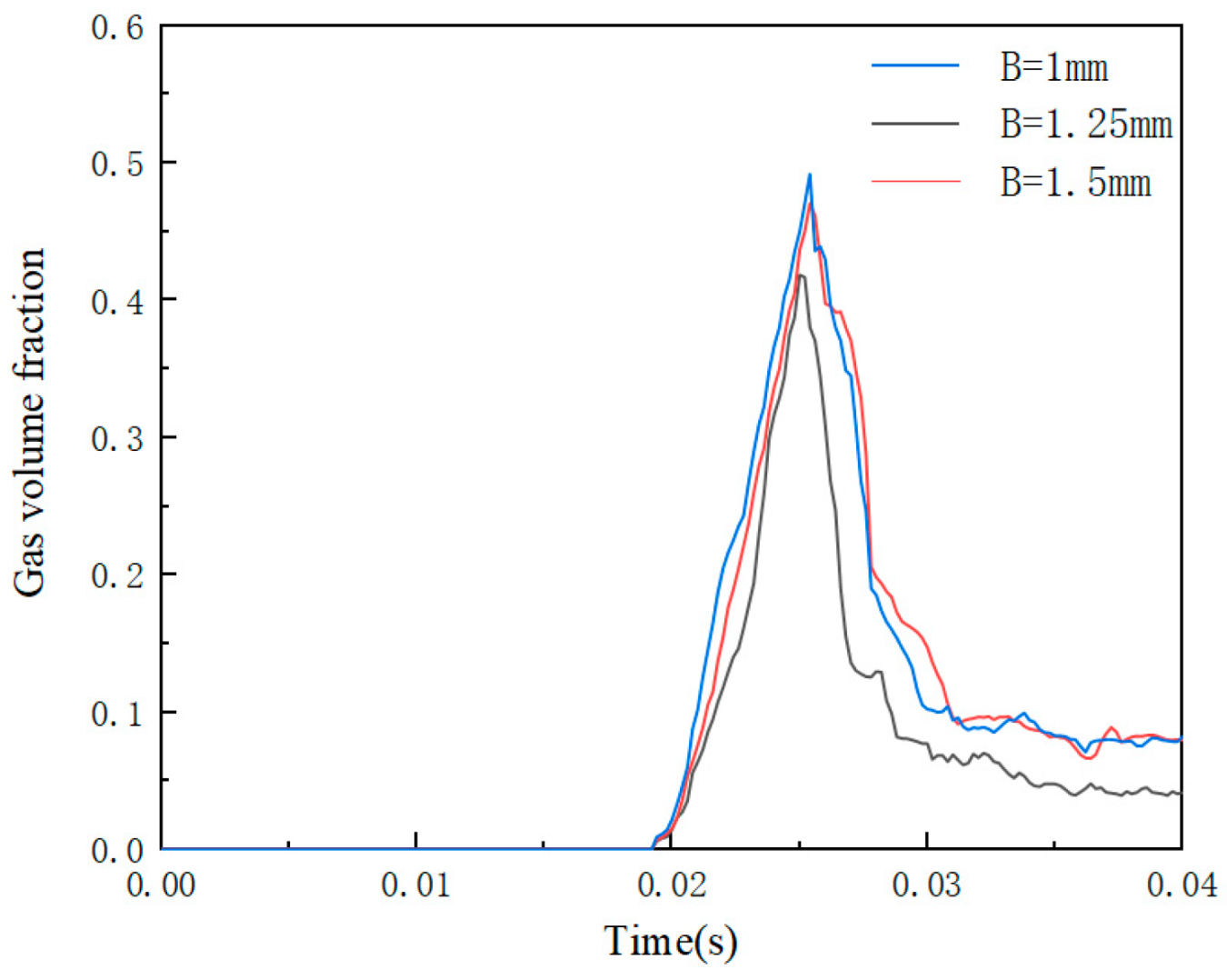
4.2.2. Effect of the T-Shaped Damping Groove Width (B) on Flow Field Characteristics
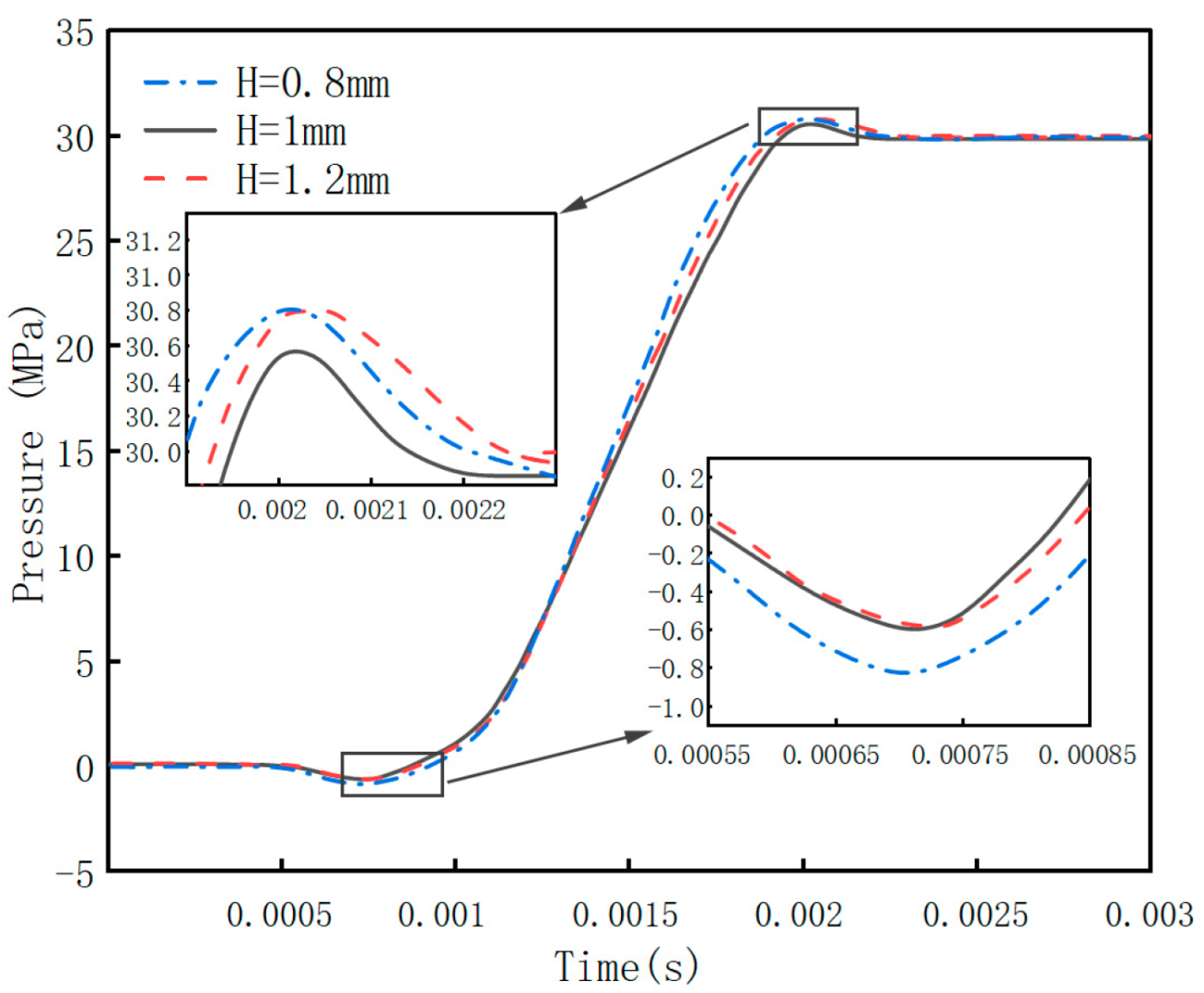
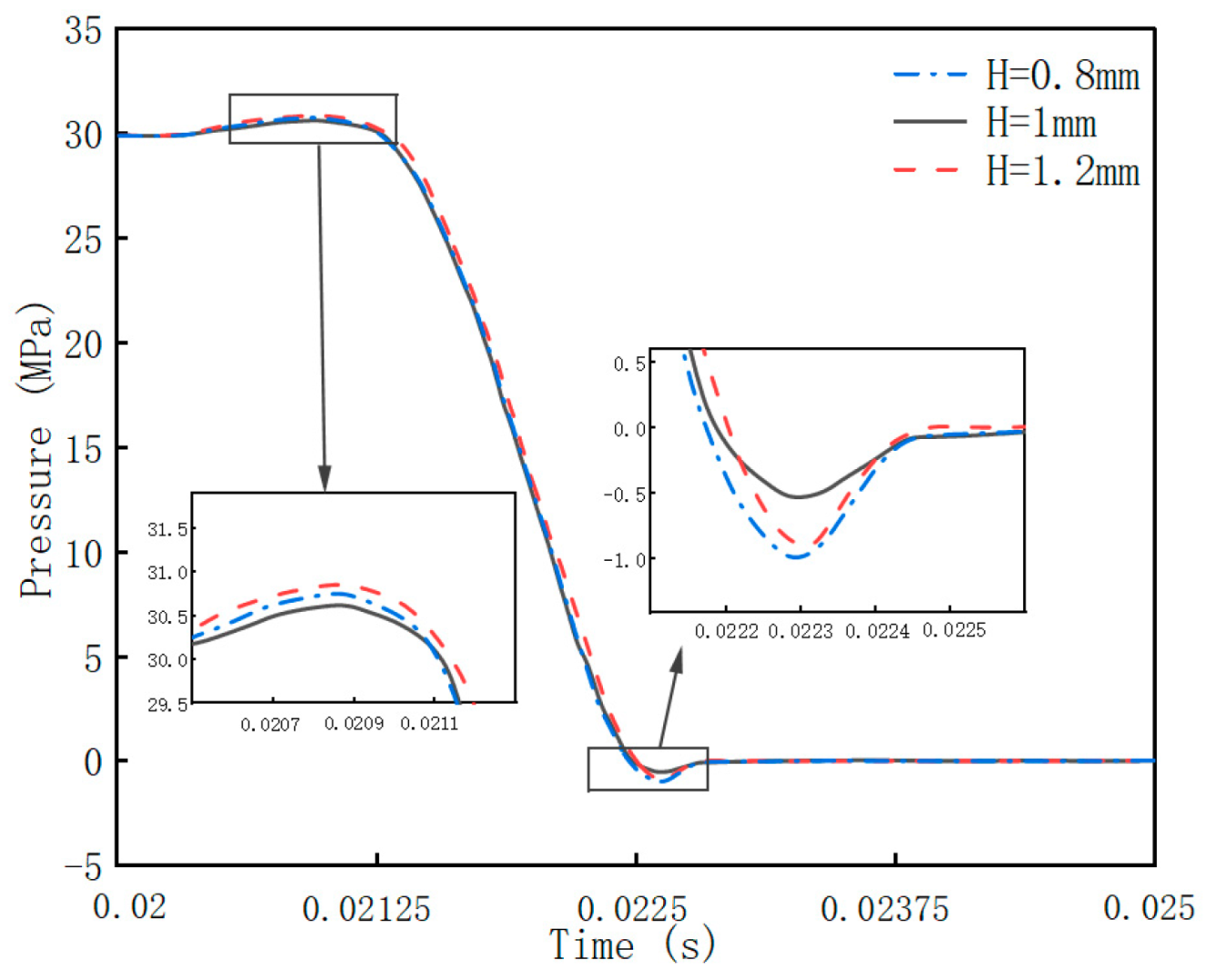
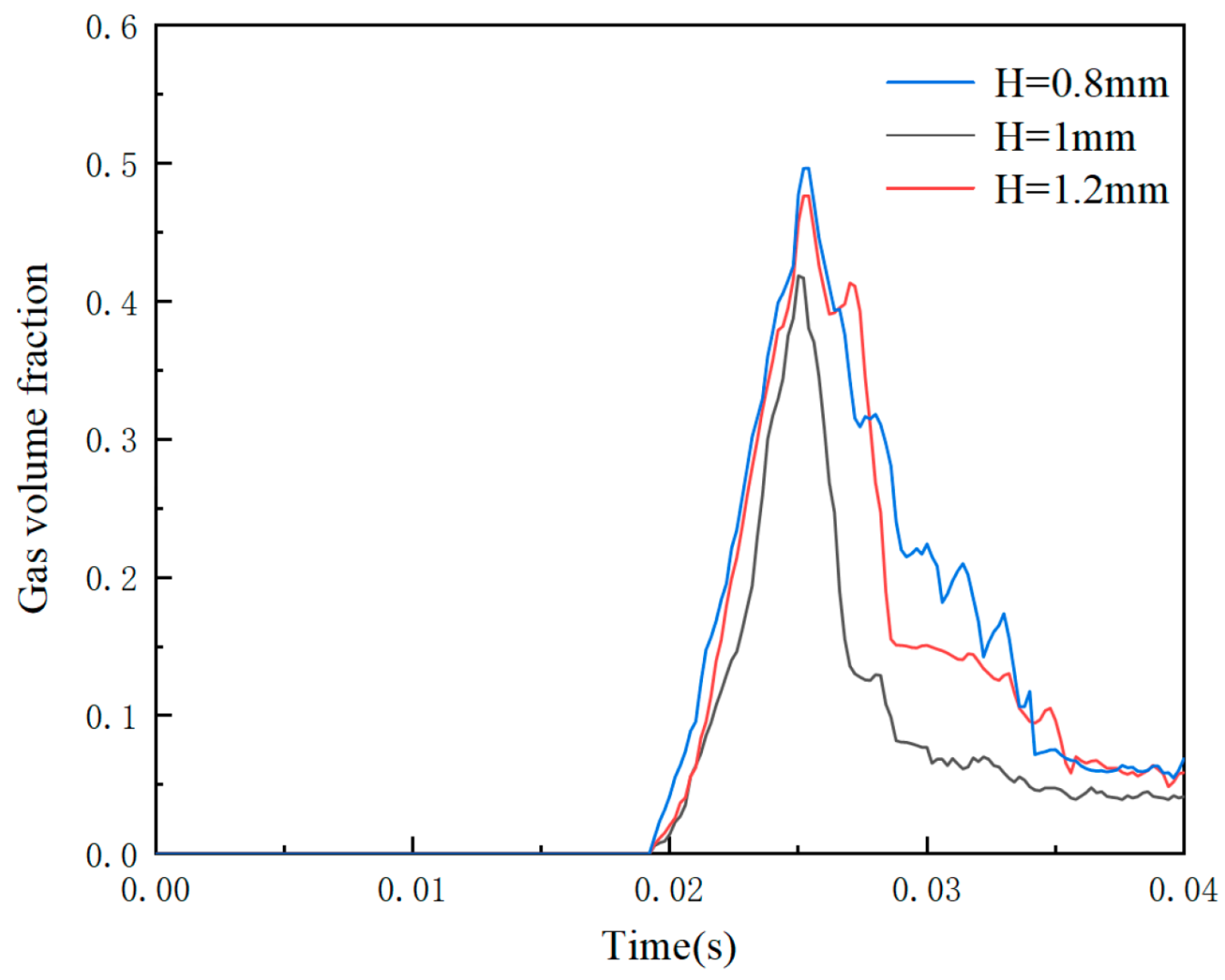
4.2.3. Effect of the T-Shaped Damping Groove Depth (H) on Flow Field Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bergada, J.M.; Kumar, S.; Davies, D.L.; Watton, J. A complete analysis of axial piston pump leakage and output flow ripples. Appl. Math. Model. 2012, 36, 1731–1751. [Google Scholar] [CrossRef]
- Li, R.; Liu, J.; Ding, X.; Liu, Q. Study on the influence of flow distribution structure of piston pump on the output of pulsation pump. Processes 2022, 10, 1077. [Google Scholar] [CrossRef]
- Berta, G.L.; Casoli, P.; Vacca, A.; Guidetti, M. Simulation model of an axial piston pump inclusive of cavitation. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 17–22 November 2002; Volume 36312, pp. 29–37. [Google Scholar]
- Manring, N.D. The control and containment forces on the swash plate of an axial piston pump utilizing a secondary swash-plate angle. In Proceedings of the 2002 American Control Conference (IEEE Cat. No. CH37301), Anchorage, AK, USA, 8–10 May 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 6, pp. 4837–4842. [Google Scholar]
- Liu, X.; Yu, L.; Liu, H.; Ke, J. Cavitation erosion mechanism of port plate of hydraulic axial planger pump. Chin. J. Mech. Eng. 2008, 44, 203–208. [Google Scholar] [CrossRef]
- Kumar, S.; Bergada, J.M. The effect of piston grooves performance in an axial piston pumps via CFD analysis. Int. J. Mech. Sci. 2013, 66, 168–179. [Google Scholar] [CrossRef]
- Shi, X.; Zhao, D. Structure Optimization of the valve plate of aviation piston pump. Mach. Tool Hydra Lics 2015, 43, 57–60. [Google Scholar]
- Wang, J.; Liu, Y. Design of distribution tray for improving volumetric efficiency of axial piston pump. Chin. Hydraul. Pneum. Seal. 2022, 42, 79–83. [Google Scholar]
- Shan, L.; Wang, J.; Ji, H.; Guo, H.; Zhao, T. Influence of relief groove of spherical valve plate on axial Ppston pump flow ripple. Chin. Hydraul. Pneum. 2015, 2, 31–36. [Google Scholar]
- Wang, C. Research on the Effect of Unloading Groove on the Output Pressure and Cavitation Characteristics of Axial Piston Pumps. Master’s Thesis, Central South University, Shanxi, China, 2023. [Google Scholar]
- Kunkis, M.; Weber, J. Experimental and numerical assessment of an axial piston pump’s speed limit. In Proceedings of the BATH/ASME 2016 Symposium on Fluid Power and Motion Control, Bath, UK, 7–9 September 2016; American Society of Mechanical Engineers: New York, NY, USA, 2016; p. 50060. [Google Scholar]
- Stosiak, M.; Yatskiv, I.; Prentkovskis, O.; Karpenko, M. Reduction of Pressure Pulsations over a Wide Frequency Range in Hydrostatic Systems. Machines 2025, 13, 25. [Google Scholar] [CrossRef]
- Karpenko, M. Aircraft hydraulic drive energy losses and operation delay associated with the pipeline and fitting connections. Aviation 2024, 28, 1–8. [Google Scholar] [CrossRef]
- Wang, D.; Chen, C.; Dong, H. Investigation of the Pressure Fluctuation of Piston Chambers with Variable Slot Geometry. Machines 2023, 11, 225. [Google Scholar] [CrossRef]
- Guan, C.; Jiao, Z.; He, S. Theoretical study of flow ripple for an aviation axial-piston pump with damping holes in the valve plate. Chin. J. Aeronaut. 2014, 27, 169–181. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, J.; Li, R.; Yuan, W.; Sun, Q.; Chen, S.; Li, D.; Sun, Y. Analysis and optimization of flow field characteristics of axial piston motor based on CFD. Flow Meas. Instrum. 2024, 99, 102669. [Google Scholar] [CrossRef]
- Tan, D.; Li, Y.; Wilkes, I.; Vagnoni, E.; Miorini, R.L.; Katz, J. Experimental Investigation of the Role of Large Scale Cavitating Vortical Structures in Performance Breakdown of an Axial Waterjet Pump. J. Fluids Eng. 2015, 137, 317–320. [Google Scholar] [CrossRef]
- Song, X.; Wang, L.; Park, Y.C. Analysis and optimization of butterfly valve disc. J. Process Mech. Eng. 2009, 223, 81–89. [Google Scholar] [CrossRef]
- Hong, H.; Zhao, C.; Zhang, B.; Bai, D.; Yang, H. Flow Ripple Reduction of Axial-Piston Pump by Structure Optimizing of Outlet Triangular Damping Groove. Processes 2020, 8, 1664. [Google Scholar] [CrossRef]
- Pei, Y.; Liu, Q.; Wang, C.; Wang, G. Energy efficiency prediction model and energy characteristics of subsea disc pump based on velocity slip and similarity theory. Energy 2021, 229, 120690. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Fan, K.; Ma, W.; Lei, H. Prediction method for low speed characteristics of compressor based on modified similarity theory with genetic algorithm. IEEE Access 2018, 6, 36834–36839. [Google Scholar] [CrossRef]








| Numbers | Minimum Size/mm | Total Number of Mesh Cells | Outlet Pressure/MPa |
|---|---|---|---|
| 1 | 0.008 | 1,259,532 | 24.9 |
| 2 | 0.007 | 1,455,034 | 27.6 |
| 3 | 0.006 | 1,766,814 | 29.8 |
| 4 | 0.005 | 2,045,778 | 29.9 |
| Category | Parameters Before Optimization | Parameters After Optimization |
|---|---|---|
| Number of Pistons | 9 | |
| Rotation speed | 1500 | r/min |
| Swash Plate Angl | 15 | deg |
| Inlet Pressure | 0.1 | MPa |
| Outlet Pressure | 30 | MPa |
| Initial Fluid Density | 870 | Kg/m3 |
| Initial Fluid Viscosity | 0.0457 | N·s/m2 |
| Saturated Vapor Pressure | 4000 | Pa |
| Vapor Density of Hydraulic Oil | 0.483 | Kg/m3 |
| Vapor Viscosity of Hydraulic Oil | 8.25 × 10−5 | N·s/m2 |
| Initial Fluid Temperature | 298 | K |
| Parameters | Value Range | Unit |
|---|---|---|
| L | 9–11 | mm |
| b | 1–1.5 | mm |
| H | 0.8–1.2 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Li, D.; Li, Z.; Wu, T.; Xu, J. Research on the Effect of Damping Grooves on the Pressure and Cavitation Characteristics of Axial Piston Pumps. Processes 2025, 13, 1274. https://doi.org/10.3390/pr13051274
Li R, Li D, Li Z, Wu T, Xu J. Research on the Effect of Damping Grooves on the Pressure and Cavitation Characteristics of Axial Piston Pumps. Processes. 2025; 13(5):1274. https://doi.org/10.3390/pr13051274
Chicago/Turabian StyleLi, Ruichuan, Dongrun Li, Zhengyu Li, Tong Wu, and Jikang Xu. 2025. "Research on the Effect of Damping Grooves on the Pressure and Cavitation Characteristics of Axial Piston Pumps" Processes 13, no. 5: 1274. https://doi.org/10.3390/pr13051274
APA StyleLi, R., Li, D., Li, Z., Wu, T., & Xu, J. (2025). Research on the Effect of Damping Grooves on the Pressure and Cavitation Characteristics of Axial Piston Pumps. Processes, 13(5), 1274. https://doi.org/10.3390/pr13051274





