Bayesian Optimization for Chemical Synthesis in the Era of Artificial Intelligence: Advances and Applications
Abstract
1. Introduction
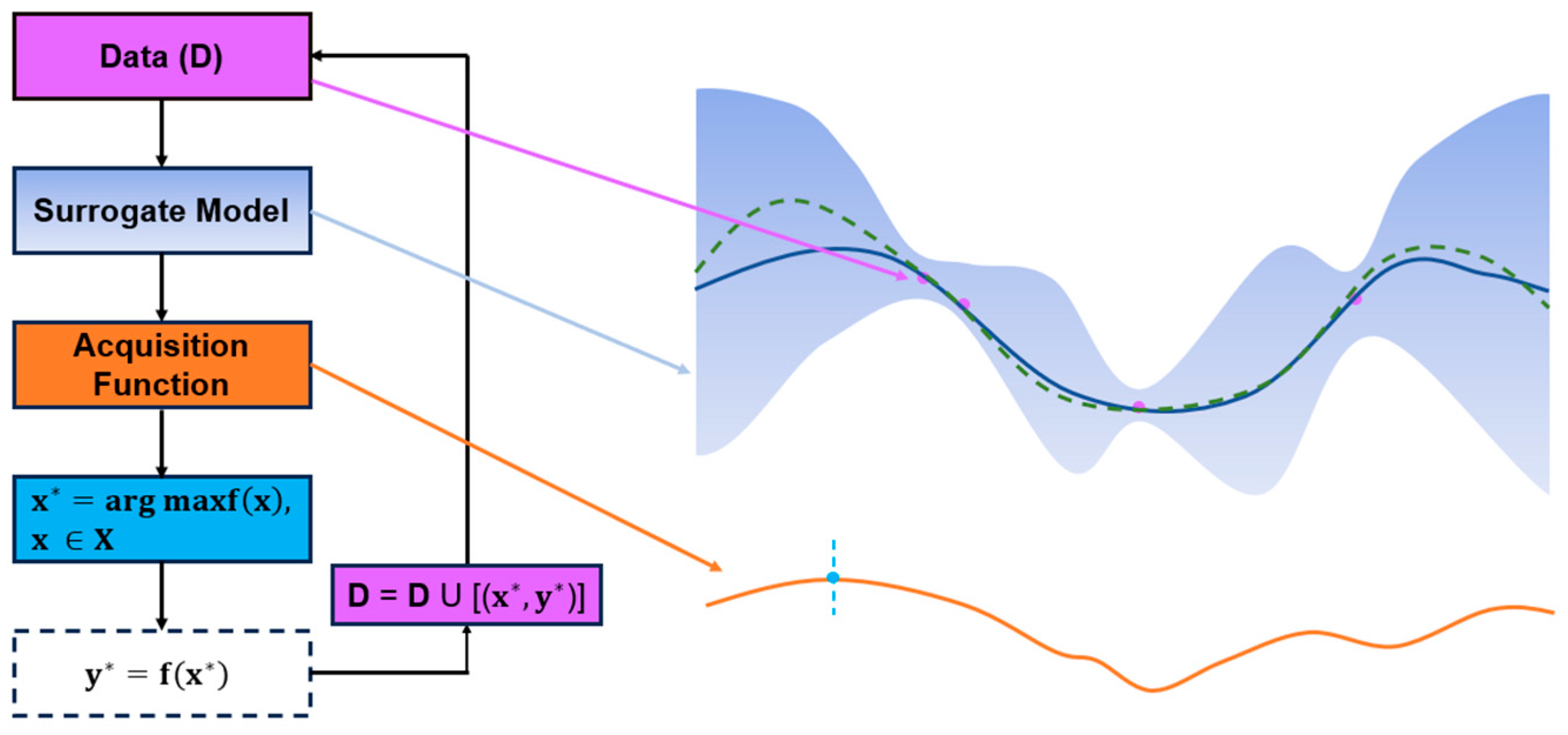
2. Bayesian Optimization for Chemical Synthesis
2.1. The Evolution of Optimization Methods
2.2. Applying Bayesian Optimization in Reaction Process Optimization
2.2.1. The Development of AFs in Bayesian Optimization
2.2.2. The Development of the Bayesian Optimizer
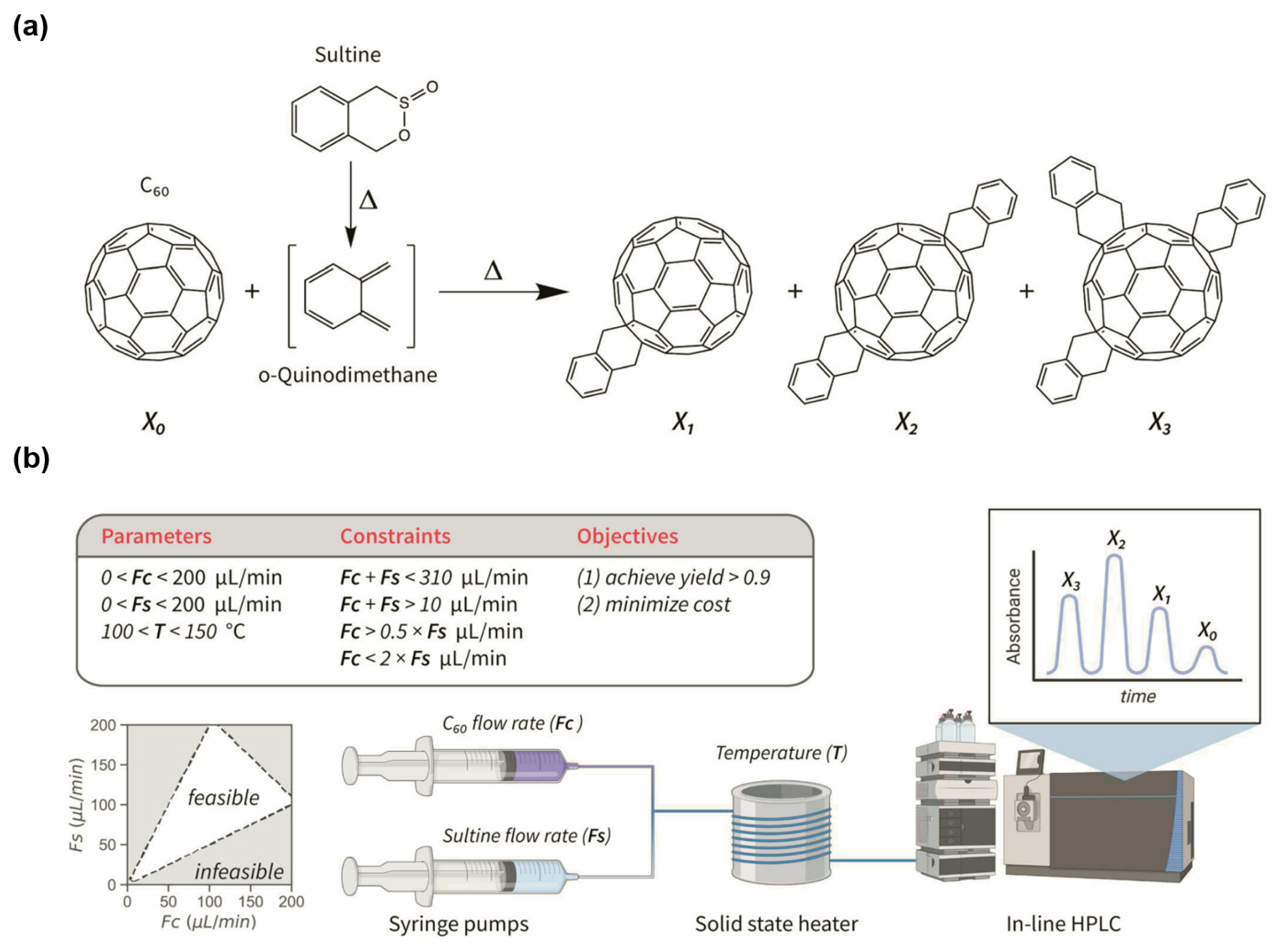
2.2.3. Integrating Reaction Constraints with Bayesian Optimization
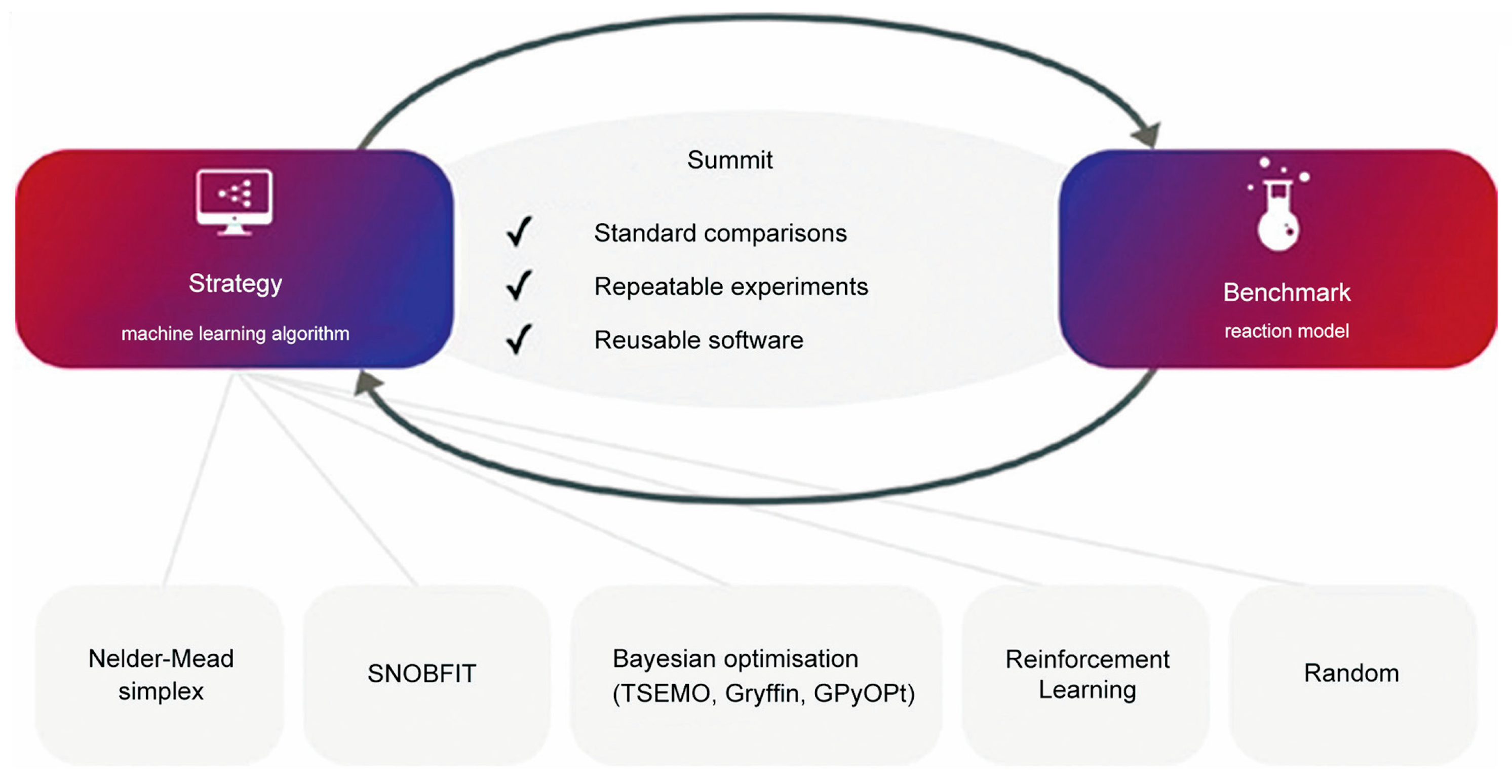
2.2.4. Comparative Studies with Other Traditional Optimization Methods
2.3. Bayesian Optimization with a Focus on Cost Awareness
2.4. Integrating Bayesian Optimization into Catalyst Screening
2.5. Bayesian Optimization Coupled with Transfer Learning
2.6. Bayesian Optimization in the Context of Molecular Design
2.7. Leveraging Bayesian Optimization in Synthetic Route Planning
2.8. Bayesian Optimization Integrated with Self-Optimization Platforms
2.9. Bayesian Optimization in Self-Driven Laboratories (SDLs): Intelligent Agents
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tsay, C.; Pattison, R.C.; Piana, M.R.; Baldea, M. A Survey of Optimal Process Design Capabilities and Practices in the Chemical and Petrochemical Industries. Comput. Chem. Eng. 2018, 112, 180–189. [Google Scholar] [CrossRef]
- Wang, X.; Han, D.; Lin, Y.; Du, W. Recent Progress and Challenges in Process Optimization: Review of Recent Work at ECUST. Can. J. Chem. Eng. 2018, 96, 2115–2123. [Google Scholar] [CrossRef]
- Meuwly, M. Machine Learning for Chemical Reactions. Chem. Rev. 2021, 121, 10218–10239. [Google Scholar] [CrossRef]
- Shim, E.; Tewari, A.; Cernak, T.; Zimmerman, P.M. Machine Learning Strategies for Reaction Development: Toward the Low-Data Limit. J. Chem. Inf. Model. 2023, 63, 3659–3668. [Google Scholar] [CrossRef]
- Baum, Z.J.; Yu, X.; Ayala, P.Y.; Zhao, Y.; Watkins, S.P.; Zhou, Q. Artificial Intelligence in Chemistry: Current Trends and Future Directions. J. Chem. Inf. Model. 2021, 61, 3197–3212. [Google Scholar] [CrossRef]
- Taylor, C.J.; Pomberger, A.; Felton, K.C.; Grainger, R.; Barecka, M.; Chamberlain, T.W.; Bourne, R.A.; Johnson, C.N.; Lapkin, A.A. A Brief Introduction to Chemical Reaction Optimization. Chem. Rev. 2023, 123, 3089–3126. [Google Scholar] [CrossRef]
- Wang, X.; Jin, Y.; Schmitt, S.; Olhofer, M. Recent Advances in Bayesian Optimization. ACM Comput. Surv. 2023, 55, 1–36. [Google Scholar] [CrossRef]
- Guo, J.; Ranković, B.; Schwaller, P. Bayesian Optimization for Chemical Reactions. Chimia 2023, 77, 31. [Google Scholar] [CrossRef]
- Wu, Y.; Walsh, A.; Ganose, A. Race to the Bottom: Bayesian Optimisation for Chemical Problems. Digit. Discov. 2024, 3, 1086–1100. [Google Scholar] [CrossRef]
- Seeger, M. Gaussian Processes for Machine Learning. Int. J. Neural Syst. 2004, 14, 69–106. [Google Scholar] [CrossRef]
- Feng, D.; Svetnik, V.; Liaw, A.; Pratola, M.; Sheridan, R.P. Building Quantitative Structure–Activity Relationship Models Using Bayesian Additive Regression Trees. J. Chem. Inf. Model. 2019, 59, 2642–2655. [Google Scholar] [CrossRef]
- Mei, H.; Wang, Z.; Huang, B. Molecular-Based Bayesian Regression Model of Petroleum Fractions. Ind. Eng. Chem. Res. 2017, 56, 14865–14872. [Google Scholar] [CrossRef]
- Li, Q.; Chen, H.; Koenig, B.C.; Deng, S. Bayesian Chemical Reaction Neural Network for Autonomous Kinetic Uncertainty Quantification. Phys. Chem. Chem. Phys. 2023, 25, 3707–3717. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Zhang, Z.; Li, Z.; Ke, J. Acquisition Function Selection: Bayesian Optimization in Neural Network Technique. In Proceedings of the 2020 the 4th International Conference on Big Data Research (ICBDR’20), Tokyo, Japan, 27 November 2020. [Google Scholar]
- Hu, J.; Jiang, Y.; Li, J.; Yuan, T. Alternative Acquisition Functions of Bayesian Optimization in Terms of Noisy Observation. In Proceedings of the 2021 2nd European Symposium on Software Engineering, Larissa, Greece, 19 November 2021. [Google Scholar]
- Bouneffouf, D. Finite-Time Analysis of the Multi-Armed Bandit Problem with Known Trend. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 1 July 2016. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. In Proceedings of the 26th International Conference on Neural Information Processing Systems, Lake Tahoe, Nevada, 3 December 2012. [Google Scholar]
- Othman, A.R.; Sheng, Y.J.; Kofli, N.T.; Kamaruddin, S.K. Improving Methanol Production by Methylosinus trichosporium through the One Factor at a Time (OFAT) Approach. Greenh. Gases Sci. Technol. 2022, 12, 661–668. [Google Scholar] [CrossRef]
- Lendrem, D.W.; Lendrem, B.C.; Woods, D.; Rowland-Jones, R.; Burke, M.; Chatfield, M.; Isaacs, J.D.; Owen, M.R. Lost in Space: Design of Experiments and Scientific Exploration in a Hogarth Universe. Drug Discov. Today 2015, 20, 1365–1371. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- McMullen, J.P.; Jensen, K.F. An Automated Microfluidic System for Online Optimization in Chemical Synthesis. Org. Process Res. Dev. 2010, 14, 1169–1176. [Google Scholar] [CrossRef]
- Williams, J.D.; Pöchlauer, P.; Okumura, Y.; Inami, Y.; Kappe, C.O. Photochemical Deracemization of a Medicinally-relevant Benzopyran Using an Oscillatory Flow Reactor. Chem. Eur. J. 2022, 28, e202200741. [Google Scholar] [CrossRef]
- Weissman, S.A.; Anderson, N.G. Design of Experiments (DoE) and Process Optimization. A Review of Recent Publications. Org. Process Res. Dev. 2014, 19, 11. [Google Scholar] [CrossRef]
- Huyer, W.; Neumaier, A. SNOBFIT—Stable Noisy Optimization by Branch and Fit. ACM Trans. Math. Softw. 2008, 35, 1–25. [Google Scholar] [CrossRef]
- Lee, R. Statistical Design of Experiments for Screening and Optimization. Chem. Ing. Tech. 2019, 91, 191–200. [Google Scholar] [CrossRef]
- Owen, M.R.; Luscombe, C.; Godbert, S.; Crookes, D.L.; Emiabata-Smith, D. Efficiency by Design: Optimisation in Process Research. Org. Process Res. Dev. 2001, 5, 308–323. [Google Scholar] [CrossRef]
- Schweidtmann, A.M.; Clayton, A.D.; Holmes, N.; Bradford, E.; Bourne, R.A.; Lapkin, A.A. Machine Learning Meets Continuous Flow Chemistry: Automated Optimization towards the Pareto Front of Multiple Objectives. Chem. Eng. J. 2018, 352, 277–282. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Cui, Y.; Geng, Z.; Zhu, Q.; Han, Y. Review: Multi-Objective Optimization Methods and Application in Energy Saving. Energy 2017, 125, 681–704. [Google Scholar] [CrossRef]
- Bradford, E.; Schweidtmann, A.M.; Lapkin, A. Efficient Multiobjective Optimization Employing Gaussian Processes, Spectral Sampling and a Genetic Algorithm. J. Glob. Optim. 2018, 71, 407–438. [Google Scholar] [CrossRef]
- Felton, K.C.; Rittig, J.G.; Lapkin, A.A. Summit: Benchmarking Machine Learning Methods for Reaction Optimisation. Chem. Methods 2021, 1, 116–122. [Google Scholar] [CrossRef]
- Jorayev, P.; Russo, D.; Tibbetts, J.D.; Schweidtmann, A.M.; Deutsch, P.; Bull, S.D.; Lapkin, A.A. Multi-Objective Bayesian Optimisation of a Two-Step Synthesis of p-Cymene from Crude Sulphate Turpentine. Chem. Eng. Sci. 2022, 247, 116938. [Google Scholar] [CrossRef]
- Jose, N.A. Pushing Nanomaterials up to the Kilogram Scale—An Accelerated Approach for Synthesizing Antimicrobial ZnO with High Shear Reactors, Machine Learning and High-Throughput Analysis. Chem. Eng. J. 2021, 426, 131345. [Google Scholar] [CrossRef]
- Karan, D.; Chen, G.; Jose, N.; Bai, J.; McDaid, P.; Lapkin, A.A. A Machine Learning-Enabled Process Optimization of Ultra-Fast Flow Chemistry with Multiple Reaction Metrics. React. Chem. Eng. 2024, 9, 619–629. [Google Scholar] [CrossRef]
- Hao, Z.; Caspari, A.; Schweidtmann, A.M.; Vaupel, Y.; Lapkin, A.A.; Mhamdi, A. Efficient Hybrid Multiobjective Optimization of Pressure Swing Adsorption. Chem. Eng. J. 2021, 423, 130248. [Google Scholar] [CrossRef]
- Daulton, S.; Balandat, M.; Bakshy, E. Parallel Bayesian Optimization of Multiple Noisy Objectives with Expected Hypervolume Improvement. In Proceedings of the 35th International Conference on Neural Information Processing Systems, Virtual, 6 December 2021. [Google Scholar]
- Qi, T.; Luo, G.; Xue, H.; Su, F.; Chen, J.; Su, W.; Wu, K.-J.; Su, A. Continuous Heterogeneous Synthesis of Hexafluoroacetone and Its Machine Learning-Assisted Optimization. J. Flow. Chem. 2023, 13, 337–346. [Google Scholar] [CrossRef]
- Luo, G.; Yang, X.; Su, W.; Qi, T.; Xu, Q.; Su, A. Optimizing Telescoped Heterogeneous Catalysis with Noise-Resilient Multi-Objective Bayesian Optimization. Chem. Eng. Sci. 2024, 298, 120434. [Google Scholar] [CrossRef]
- Zhang, J.; Sugisawa, N.; Felton, K.C.; Fuse, S.; Lapkin, A.A. Multi-Objective Bayesian Optimisation Using q -Noisy Expected Hypervolume Improvement (q-NEHVI) for the Schotten–Baumann Reaction. React. Chem. Eng. 2024, 9, 706–712. [Google Scholar] [CrossRef]
- Zhang, J.; Semochkina, D.; Sugisawa, N.; Woods, D.C.; Lapkin, A.A. Multi-Objective Reaction Optimization under Uncertainties Using Expected Quantile Improvement. Comput. Chem. Eng. 2025, 194, 108983. [Google Scholar] [CrossRef]
- Häse, F.; Roch, L.M.; Kreisbeck, C.; Aspuru-Guzik, A. Phoenics: A Bayesian Optimizer for Chemistry. ACS Cent. Sci. 2018, 4, 1134–1145. [Google Scholar] [CrossRef] [PubMed]
- Zhan, D.; Xing, H. Expected Improvement for Expensive Optimization: A Review. J. Glob. Optim. 2020, 78, 507–544. [Google Scholar] [CrossRef]
- Häse, F.; Aldeghi, M.; Hickman, R.J.; Roch, L.M.; Aspuru-Guzik, A. G ryffin: An Algorithm for Bayesian Optimization of Categorical Variables Informed by Expert Knowledge. Appl. Phys. Rev. 2021, 8, 31406. [Google Scholar] [CrossRef]
- Clayton, A.D.; Schweidtmann, A.M.; Clemens, G.; Manson, J.A.; Taylor, C.J.; Niño, C.G.; Chamberlain, T.W.; Kapur, N.; Blacker, A.J.; Lapkin, A.A.; et al. Automated Self-Optimisation of Multi-Step Reaction and Separation Processes Using Machine Learning. Chem. Eng. J. 2020, 384, 123340. [Google Scholar] [CrossRef]
- Manson, J.A.; Chamberlain, T.W.; Bourne, R.A. MVMOO: Mixed Variable Multi-Objective Optimisation. J. Glob. Optim. 2021, 80, 865–886. [Google Scholar] [CrossRef]
- Halstrup, M. Black-Box Optimization of Mixed Discrete-Continuous Optimization Problems. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Lille, France, 8 July 2021. [Google Scholar]
- Zhan, D.; Cheng, Y.; Liu, J. Expected Improvement Matrix-Based Infill Criteria for Expensive Multiobjective Optimization. IEEE Trans. Evol. Comput. 2017, 21, 956–975. [Google Scholar] [CrossRef]
- Hickman, R.J.; Aldeghi, M.; Häse, F.; Aspuru-Guzik, A. Bayesian Optimization with Known Experimental and Design Constraints for Chemistry Applications. Digit. Discov. 2022, 1, 732–744. [Google Scholar] [CrossRef]
- Hickman, R.; Aldeghi, M.; Aspuru-Guzik, A. Anubis: Bayesian Optimization with Unknown Feasibility Constraints for Scientific Experimentation. Digit. Discov. 2025, 4, 2104–2122. [Google Scholar] [CrossRef]
- Grimm, M.; Paul, S.; Chainais, P. Process-Constrained Batch Bayesian Approaches for Yield Optimization in Multi-Reactor Systems. Comput. Chem. Eng. 2024, 189, 108779. [Google Scholar] [CrossRef]
- Narayanan, H.; Dingfelder, F.; Condado Morales, I.; Patel, B.; Heding, K.E.; Bjelke, J.R.; Egebjerg, T.; Butté, A.; Sokolov, M.; Lorenzen, N.; et al. Design of Biopharmaceutical Formulations Accelerated by Machine Learning. Mol. Pharm. 2021, 18, 3843–3853. [Google Scholar] [CrossRef]
- Lehmann, C.; Eckey, K.; Viehoff, M.; Greve, C.; Röder, T. Autonomous Online Optimization in Flash Chemistry Using Online Mass Spectrometry. Org. Process Res. Dev. 2024, 28, 3108–3118. [Google Scholar] [CrossRef]
- Pickles, T.; Mustoe, C.; Brown, C.J.; Florence, A.J. Comparative Study on Adaptive Bayesian Optimization for Batch Cooling Crystallization for Slow and Fast Kinetic Regimes. Cryst. Growth Des. 2024, 24, 1245–1253. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Luo, G.; Chai, K.; Su, W.; Su, A. Continuous Flow Synthesis of N, O-Dimethyl-N′-Nitroisourea Monitored by Inline Fourier Transform Infrared Spectroscopy: Bayesian Optimization and Kinetic Modeling. Ind. Eng. Chem. Res. 2024, 63, 10162–10171. [Google Scholar] [CrossRef]
- Chai, K.; Xia, W.; Shen, R.; Luo, G.; Cheng, Y.; Su, W.; Su, A. Optimization of Heterogeneous Continuous Flow Hydrogenation Using FTIR Inline Analysis: A Comparative Study of Multi-Objective Bayesian Optimization and Kinetic Modeling. Chem. Eng. Sci. 2025, 302, 120901. [Google Scholar] [CrossRef]
- Schoepfer, A.A.; Weinreich, J.; Laplaza, R.; Waser, J.; Corminboeuf, C. Cost-Informed Bayesian Reaction Optimization. Digit. Discov. 2024, 3, 2289–2297. [Google Scholar] [CrossRef] [PubMed]
- Liang, R.; Hu, H.; Han, Y.; Chen, B.; Yuan, Z. CAPBO: A Cost-aware Parallelized Bayesian Optimization Method for Chemical Reaction Optimization. AIChE J. 2024, 70, e18316. [Google Scholar] [CrossRef]
- Liang, R.; Zheng, S.; Wang, K.; Yuan, Z. Cost-Aware Bayesian Optimization for Self-Driven Condition Screening of Flow Electrosynthesis. ACS Electrochem. 2025, 1, 360–368. [Google Scholar] [CrossRef]
- Ranković, B.; Griffiths, R.-R.; Moss, H.B.; Schwaller, P. Bayesian Optimisation for Additive Screening and Yield Improvements—Beyond One-Hot Encoding. Digit. Discov. 2024, 3, 654–666. [Google Scholar] [CrossRef]
- Okada, S.; Ohzeki, M.; Taguchi, S. Efficient Partition of Integer Optimization Problems with One-Hot Encoding. Sci. Rep. 2019, 9, 13036. [Google Scholar] [CrossRef]
- He, C.; Luo, G.; Su, W.; Duan, H.; Xie, Y.; Zhang, G.; Su, A. Ruthenium Complexes for Asymmetric Hydrogenation and Selective Dehalogenation Revealed via Bayesian Optimization. Ind. Eng. Chem. Res. 2025, 64, 11233–11242. [Google Scholar] [CrossRef]
- He, C.; Luo, G.; Duan, H.; Xie, Y.; Zhang, G.; Su, A.; Su, W. Optimizing Phosphine Ligands for Ruthenium Catalysts in Asymmetric Hydrogenation of β-Keto Esters: The Role of Water in Activity and Selectivity. Mol. Catal. 2025, 574, 114877. [Google Scholar] [CrossRef]
- Moriwaki, H.; Tian, Y.-S.; Kawashita, N.; Takagi, T. Mordred: A Molecular Descriptor Calculator. J. Cheminf. 2018, 10, 4. [Google Scholar] [CrossRef] [PubMed]
- Ahneman, D.T.; Estrada, J.G.; Lin, S.; Dreher, S.D.; Doyle, A.G. Predicting Reaction Performance in C–N Cross-Coupling Using Machine Learning. Science 2018, 360, 186–190. [Google Scholar] [CrossRef]
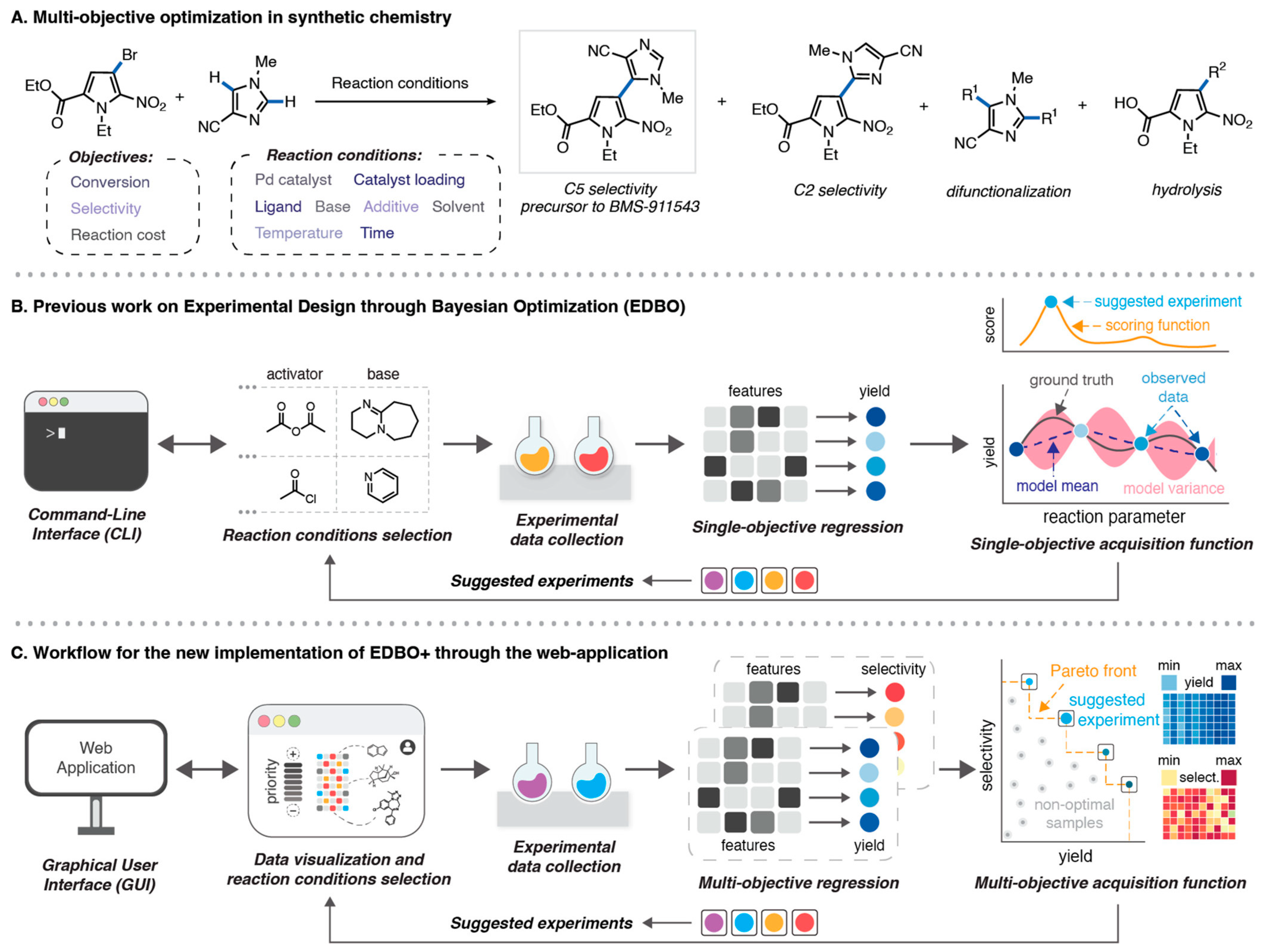
- Shields, B.J.; Stevens, J.; Li, J.; Parasram, M.; Damani, F.; Alvarado, J.I.M.; Janey, J.M.; Adams, R.P.; Doyle, A.G. Bayesian Reaction Optimization as a Tool for Chemical Synthesis. Nature 2021, 590, 89–96. [Google Scholar] [CrossRef]
- Gardner, J.R.; Pleiss, G.; Bindel, D.; Weinberger, K.Q.; Wilson, A.G. GPyTorch: Blackbox Matrix-Matrix Gaussian Process Inference with GPU Acceleration. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3 December 2018. [Google Scholar]
- Torres, J.A.G.; Lau, S.H.; Anchuri, P.; Stevens, J.M.; Tabora, J.E.; Li, J.; Borovika, A.; Adams, R.P.; Doyle, A.G. A Multi-Objective Active Learning Platform and Web App for Reaction Optimization. J. Am. Chem. Soc. 2022, 144, 19999–20007. [Google Scholar] [CrossRef] [PubMed]
- Daulton, S.; Balandat, M.; Bakshy, E. Differentiable Expected Hypervolume Improvement for Parallel Multi-Objective Bayesian Optimization. In Proceedings of the 34th International Conference on Neural Information Processing System, Vancouver, BC, Canada, 6 December 2020. [Google Scholar]
- Romer, N.P.; Min, D.S.; Wang, J.Y.; Walroth, R.C.; Mack, K.A.; Sirois, L.E.; Gosselin, F.; Zell, D.; Doyle, A.G.; Sigman, M.S. Data Science Guided Multiobjective Optimization of a Stereoconvergent Nickel-Catalyzed Reduction of Enol Tosylates to Access Trisubstituted Alkenes. ACS Catal. 2024, 14, 4699–4708. [Google Scholar] [CrossRef]
- Braconi, E.; Godineau, E. Bayesian Optimization as a Sustainable Strategy for Early-Stage Process Development? A Case Study of Cu-Catalyzed C–N Coupling of Sterically Hindered Pyrazines. ACS Sustain. Chem. Eng. 2023, 11, 10545–10554. [Google Scholar] [CrossRef]
- Morishita, T.; Kaneko, H. Enhancing the Search Performance of Bayesian Optimization by Creating Different Descriptor Datasets Using Density Functional Theory. ACS Omega 2023, 8, 33032–33038. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Che, Y.; Chen, L.; Liu, T.; Wang, K.; Liu, L.; Yang, H.; Pyzer-Knapp, E.O.; Cooper, A.I. Sequential Closed-Loop Bayesian Optimization as a Guide for Organic Molecular Metallophotocatalyst Formulation Discovery. Nat. Chem. 2024, 16, 1286–1294. [Google Scholar] [CrossRef] [PubMed]
- Niu, X.; Li, S.; Zhang, Z.; Duan, H.; Zhang, R.; Li, J.; Zhang, L. Accelerated Optimization of Compositions and Chemical Ordering for Bimetallic Alloy Catalysts Using Bayesian Learning. ACS Catal. 2025, 15, 4374–4383. [Google Scholar] [CrossRef]
- Kwon, Y.; Lee, D.; Kim, J.W.; Choi, Y.-S.; Kim, S. Exploring Optimal Reaction Conditions Guided by Graph Neural Networks and Bayesian Optimization. ACS Omega 2022, 7, 44939–44950. [Google Scholar] [CrossRef]
- Bonilla, E.V.; Chai, K.M.; Williams, C. Multi-Task Gaussian Process Prediction. In Proceedings of the 21st International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 3 December 2007. [Google Scholar]
- Theckel Joy, T.; Rana, S.; Gupta, S.; Venkatesh, S. A Flexible Transfer Learning Framework for Bayesian Optimization with Convergence Guarantee. Expert Syst. Appl. 2019, 115, 656–672. [Google Scholar] [CrossRef]
- Swersky, K.; Snoek, J.; Adams, R.P. Multi-Task Bayesian Optimization. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Lake Tahoe, Nevada, 5 December 2013. [Google Scholar]
- Taylor, C.J.; Felton, K.C.; Wigh, D.; Jeraal, M.I.; Grainger, R.; Chessari, G.; Johnson, C.N.; Lapkin, A.A. Accelerated Chemical Reaction Optimization Using Multi-Task Learning. ACS Cent. Sci. 2023, 9, 957–968. [Google Scholar] [CrossRef]
- Faurschou, N.V.; Taaning, R.H.; Pedersen, C.M. Substrate Specific Closed-Loop Optimization of Carbohydrate Protective Group Chemistry Using Bayesian Optimization and Transfer Learning. Chem. Sci. 2023, 14, 6319–6329. [Google Scholar] [CrossRef]
- Guo, J.; Chai, K.; Luo, G.; Su, W.; Su, A. Prior Knowledge-Based Multi-Round Multi-Objective Bayesian Optimization: Continuous Flow Synthesis and Scale-Up of O-Methylisourea. Chem. Eng. Process. Process Intensif. 2025, 215, 110376. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013. [Google Scholar] [CrossRef]
- Jin, W.; Barzilay, R.; Jaakkola, T. Artificial Intelligence in Drug Discovery; Royal Society of Chemistry: Cambridge, UK, 2020; pp. 228–249. [Google Scholar]
- Griffiths, R.-R.; Hernández-Lobato, J.M. Constrained Bayesian Optimization for Automatic Chemical Design Using Variational Autoencoders. Chem. Sci. 2020, 11, 577–586. [Google Scholar] [CrossRef]
- McDonald, M.A.; Koscher, B.A.; Canty, R.B.; Zhang, J.; Ning, A.; Jensen, K.F. Bayesian Optimization over Multiple Experimental Fidelities Accelerates Automated Discovery of Drug Molecules. ACS Cent. Sci. 2025, 11, 346–356. [Google Scholar] [CrossRef]
- Rogers, D.; Hahn, M. Extended-Connectivity Fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. [Google Scholar] [CrossRef]
- Griffiths, R.-R.; Klarner, L.; Moss, H.B.; Ravuri, A.; Truong, S.; Stanton, S.; Tom, G.; Rankovic, B.; Du, Y.; Jamasb, A.; et al. GAUCHE: A Library for Gaussian Processes in Chemistry. In Proceedings of the 37th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10 December 2023. [Google Scholar]
- Chen, Z.; Ayinde, O.R.; Fuchs, J.R.; Sun, H.; Ning, X. G2Retro as a Two-Step Graph Generative Models for Retrosynthesis Prediction. Commun. Chem. 2023, 6, 102. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Z.; Song, J.; Feng, Z.; Liu, T.; Jia, L.; Yao, S.; Hou, T.; Song, M. Recent Advances in Deep Learning for Retrosynthesis. WIREs Comput. Mol. Sci. 2024, 14, e1694. [Google Scholar] [CrossRef]
- Long, L.; Li, R.; Zhang, J. Artificial Intelligence in Retrosynthesis Prediction and Its Applications in Medicinal Chemistry. J. Med. Chem. 2025, 68, 2333–2355. [Google Scholar] [CrossRef]
- Coley, C.W.; Barzilay, R.; Jaakkola, T.S.; Green, W.H.; Jensen, K.F. Prediction of Organic Reaction Outcomes Using Machine Learning. ACS Cent. Sci. 2017, 3, 434–443. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Wu, S.; Ohno, M.; Yoshida, R. Bayesian Algorithm for Retrosynthesis. J. Chem. Inf. Model. 2020, 60, 4474–4486. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-Generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 25 July 2019. [Google Scholar]
- Westerlund, A.M.; Barge, B.; Mervin, L.; Genheden, S. Data-driven Approaches for Identifying Hyperparameters in Multi-step Retrosynthesis. Mol. Inf. 2023, 42, e202300128. [Google Scholar] [CrossRef]
- Köckinger, M.; Ciaglia, T.; Bersier, M.; Hanselmann, P.; Gutmann, B.; Kappe, C.O. Utilization of Fluoroform for Difluoromethylation in Continuous Flow: A Concise Synthesis of α-Difluoromethyl-Amino Acids. Green Chem. 2018, 20, 108–112. [Google Scholar] [CrossRef]
- Lebl, R.; Murray, T.; Adamo, A.; Cantillo, D.; Kappe, C.O. Continuous Flow Synthesis of Methyl Oximino Acetoacetate: Accessing Greener Purification Methods with Inline Liquid–Liquid Extraction and Membrane Separation Technology. ACS Sustain. Chem. Eng. 2019, 7, 20088–20096. [Google Scholar] [CrossRef]
- Hone, C.A.; Lopatka, P.; Munday, R.; O’Kearney-McMullan, A.; Kappe, C.O. Continuous-flow Synthesis of Aryl Aldehydes by Pd-catalyzed Formylation of Aryl Bromides Using Carbon Monoxide and Hydrogen. ChemSusChem 2019, 12, 326–337. [Google Scholar] [CrossRef] [PubMed]
- Ötvös, S.B.; Kappe, C.O. Continuous-flow Amide and Ester Reductions Using Neat Borane Dimethylsulfide Complex. ChemSusChem 2020, 13, 1800–1807. [Google Scholar] [CrossRef] [PubMed]
- Prieschl, M.; Ötvös, S.B.; Kappe, C.O. Sustainable Aldehyde Oxidations in Continuous Flow Using in Situ-Generated Performic Acid. ACS Sustain. Chem. Eng. 2021, 9, 5519–5525. [Google Scholar] [CrossRef]
- Sagmeister, P.; Williams, J.D.; Hone, C.A.; Kappe, C.O. Laboratory of the Future: A Modular Flow Platform with Multiple Integrated PAT Tools for Multistep Reactions. React. Chem. Eng. 2019, 4, 1571–1578. [Google Scholar] [CrossRef]
- Sagmeister, P.; Lebl, R.; Castillo, I.; Rehrl, J.; Kruisz, J.; Sipek, M.; Horn, M.; Sacher, S.; Cantillo, D.; Williams, J.D.; et al. Back Cover: Advanced Real-time Process Analytics for Multistep Synthesis in Continuous Flow (Angew. Chem. Int. Ed. 15/2021). Angew. Chem. Int. Ed. 2021, 60, 8556. [Google Scholar] [CrossRef]
- Sagmeister, P.; Ort, F.F.; Jusner, C.E.; Hebrault, D.; Tampone, T.; Buono, F.G.; Williams, J.D.; Kappe, C.O. Autonomous Multi-step and Multi-objective Optimization Facilitated by Real-time Process Analytics. Adv. Sci. 2022, 9, 2105547. [Google Scholar] [CrossRef]
- Wagner, F.; Sagmeister, P.; Jusner, C.E.; Tampone, T.G.; Manee, V.; Buono, F.G.; Williams, J.D.; Kappe, C.O. A Slug Flow Platform with Multiple Process Analytics Facilitates Flexible Reaction Optimization. Adv. Sci. 2024, 11, 2308034. [Google Scholar] [CrossRef]
- Wagner, F.L.; Sagmeister, P.; Tampone, T.G.; Manee, V.; Yerkozhanov, D.; Buono, F.G.; Williams, J.D.; Kappe, C.O. Self-Optimizing Flow Reactions for Sustainability: An Experimental Bayesian Optimization Study. ACS Sustain. Chem. Eng. 2024, 12, 10002–10010. [Google Scholar] [CrossRef]
- Kershaw, O.J.; Clayton, A.D.; Manson, J.A.; Barthelme, A.; Pavey, J.; Peach, P.; Mustakis, J.; Howard, R.M.; Chamberlain, T.W.; Warren, N.J.; et al. Machine Learning Directed Multi-Objective Optimization of Mixed Variable Chemical Systems. Chem. Eng. J. 2023, 451, 138443. [Google Scholar] [CrossRef]
- Knox, S.T.; Parkinson, S.J.; Wilding, C.Y.P.; Bourne, R.A.; Warren, N.J. Autonomous Polymer Synthesis Delivered by Multi-Objective Closed-Loop Optimisation. Polym. Chem. 2022, 13, 1576–1585. [Google Scholar] [CrossRef]
- Clayton, A.D.; Pyzer-Knapp, E.O.; Purdie, M.; Jones, M.F.; Barthelme, A.; Pavey, J.; Kapur, N.; Chamberlain, T.W.; Blacker, A.J.; Bourne, R.A. Bayesian Self-optimization for Telescoped Continuous Flow Synthesis. Angew. Chem. 2023, 135, e202214511. [Google Scholar] [CrossRef]
- Boyall, S.L.; Clarke, H.; Dixon, T.; Davidson, R.W.M.; Leslie, K.; Clemens, G.; Muller, F.L.; Clayton, A.D.; Bourne, R.A.; Chamberlain, T.W. Automated Optimization of a Multistep, Multiphase Continuous Flow Process for Pharmaceutical Synthesis. ACS Sustain. Chem. Eng. 2024, 12, 15125–15133. [Google Scholar] [CrossRef]
- Dixon, T.M.; Williams, J.; Besenhard, M.; Howard, R.M.; MacGregor, J.; Peach, P.; Clayton, A.D.; Warren, N.J.; Bourne, R.A. Operator-Free HPLC Automated Method Development Guided by Bayesian Optimization. Digit. Discov. 2024, 3, 1591–1601. [Google Scholar] [CrossRef]
- Shaw, T.; Clayton, A.D.; Houghton, J.A.; Kapur, N.; Bourne, R.A.; Hanson, B.C. Multi-Objective Bayesian Optimization of Continuous Purifications with Automated Phase Separation for on-Demand Manufacture of DEHiBA. Sep. Purif. Technol. 2025, 361, 131288. [Google Scholar] [CrossRef]
- Nandiwale, K.Y.; Hart, T.; Zahrt, A.F.; Nambiar, A.M.K.; Mahesh, P.T.; Mo, Y.; Nieves-Remacha, M.J.; Johnson, M.D.; García-Losada, P.; Mateos, C.; et al. Continuous Stirred-Tank Reactor Cascade Platform for Self-Optimization of Reactions Involving Solids. React. Chem. Eng. 2022, 7, 1315–1327. [Google Scholar] [CrossRef]
- Paria, B.; Kandasamy, K.; Póczos, B. A Flexible Framework for Multi-Objective Bayesian Optimization Using Random Scalarizations. In Proceedings of the 35th Uncertainty in Artificial Intelligence Conference, Tel Aviv, Israel, 22 July 2019. [Google Scholar]
- Kandasamy, K.; Vysyaraju, K.R.; Neiswanger, W.; Paria, B.; Collins, C.R.; Schneider, J.; Poczos, B.; Xing, E.P. Tuning Hyperparameters without Grad Students. J. Mach. Learn. Res. 2020, 21, 27. [Google Scholar]
- Dave, A.; Mitchell, J.; Burke, S.; Lin, H.; Whitacre, J.; Viswanathan, V. Autonomous Optimization of Non-Aqueous Li-Ion Battery Electrolytes via Robotic Experimentation and Machine Learning Coupling. Nat. Commun. 2022, 13, 5454. [Google Scholar] [CrossRef] [PubMed]
- Nambiar, A.M.K.; Breen, C.P.; Hart, T.; Kulesza, T.; Jamison, T.F.; Jensen, K.F. Bayesian Optimization of Computer-Proposed Multistep Synthetic Routes on an Automated Robotic Flow Platform. ACS Cent. Sci. 2022, 8, 825–836. [Google Scholar] [CrossRef]
- Langner, S.; Häse, F.; Perea, J.D.; Stubhan, T.; Hauch, J.; Roch, L.M.; Heumueller, T.; Aspuru-Guzik, A.; Brabec, C.J. Beyond Ternary OPV: High-throughput Experimentation and Self-driving Laboratories Optimize Multicomponent Systems. Adv. Mater. 2020, 32, 1907801. [Google Scholar] [CrossRef]
- Hickman, R.; Sim, M.; Pablo-García, S.; Woolhouse, I.; Hao, H.; Bao, Z.; Bannigan, P.; Allen, C.; Aldeghi, M.; Aspuru-Guzik, A. Atlas: A Brain for Self-Driving Laboratories. Digit. Discov. 2025, 4, 1006–1029. [Google Scholar] [CrossRef]
- Tom, G.; Schmid, S.P.; Baird, S.G.; Cao, Y.; Darvish, K.; Hao, H.; Lo, S.; Pablo-García, S.; Rajaonson, E.M.; Skreta, M.; et al. Self-Driving Laboratories for Chemistry and Materials Science. Chem. Rev. 2024, 124, 9633–9732. [Google Scholar] [CrossRef]
- Wu, T.; Kheiri, S.; Hickman, R.J.; Tao, H.; Wu, T.C.; Yang, Z.-B.; Ge, X.; Zhang, W.; Abolhasani, M.; Liu, K.; et al. Self-Driving Lab for the Photochemical Synthesis of Plasmonic Nanoparticles with Targeted Structural and Optical Properties. Nat. Commun. 2025, 16, 1473. [Google Scholar] [CrossRef]
- Bayley, O.; Savino, E.; Slattery, A.; Noël, T. Autonomous Chemistry: Navigating Self-Driving Labs in Chemical and Material Sciences. Matter 2024, 7, 2382–2398. [Google Scholar] [CrossRef]
- Slattery, A.; Wen, Z.; Tenblad, P.; Sanjosé-Orduna, J.; Pintossi, D.; Den Hartog, T.; Noël, T. Automated Self-Optimization, Intensification, and Scale-up of Photocatalysis in Flow. Science 2024, 383, eadj1817. [Google Scholar] [CrossRef]
- Ha, T.; Lee, D.; Kwon, Y.; Park, M.S.; Lee, S.; Jang, J.; Choi, B.; Jeon, H.; Kim, J.; Choi, H.; et al. AI-Driven Robotic Chemist for Autonomous Synthesis of Organic Molecules. Sci. Adv. 2024, 7, 2382–2398. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Nam, G.; Choi, J.; Jung, Y. A Perspective on Foundation Models in Chemistry. JACS Au 2025, 5, 1499–1518. [Google Scholar] [CrossRef] [PubMed]
- King-Smith, E. Transfer Learning for a Foundational Chemistry Model. Chem. Sci. 2024, 15, 5143–5151. [Google Scholar] [CrossRef] [PubMed]
- Soares, E.; Vital Brazil, E.; Shirasuna, V.; Zubarev, D.; Cerqueira, R.; Schmidt, K. An Open-Source Family of Large Encoder-Decoder Foundation Models for Chemistry. Commun. Chem. 2025, 8, 193. [Google Scholar] [CrossRef] [PubMed]


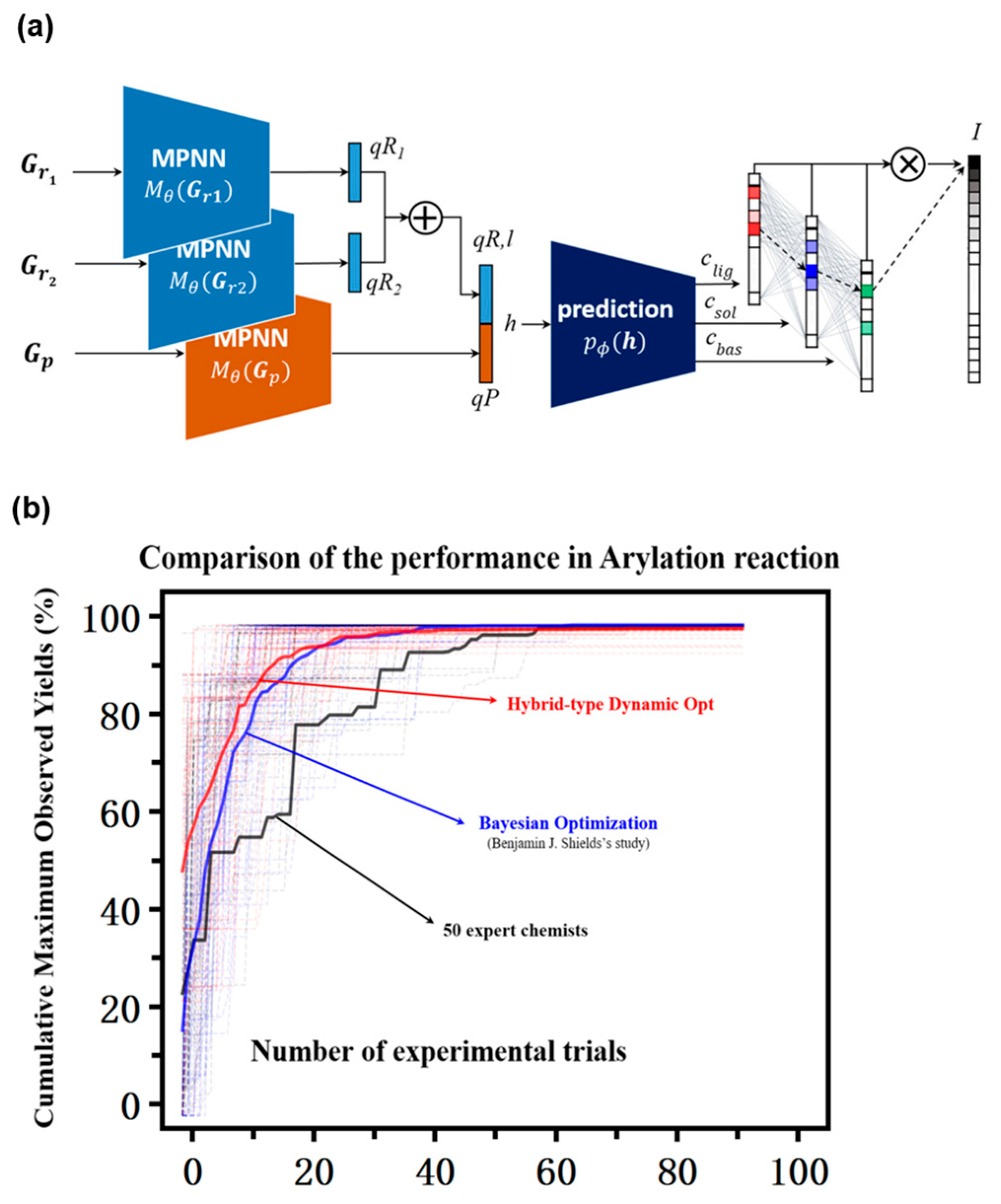
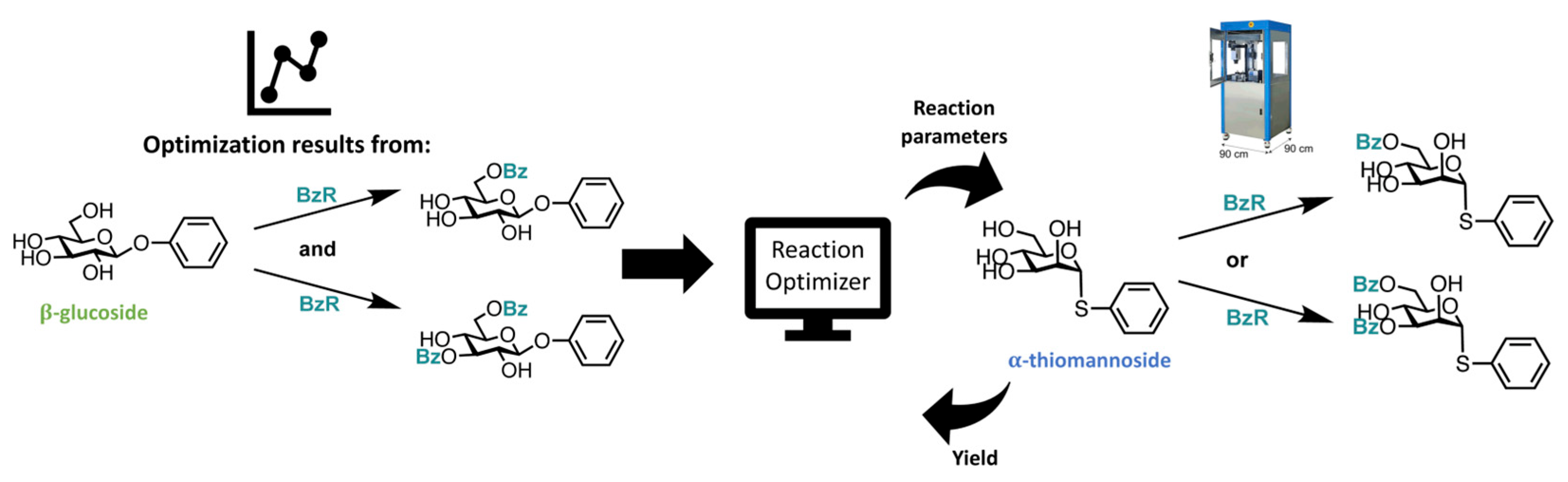



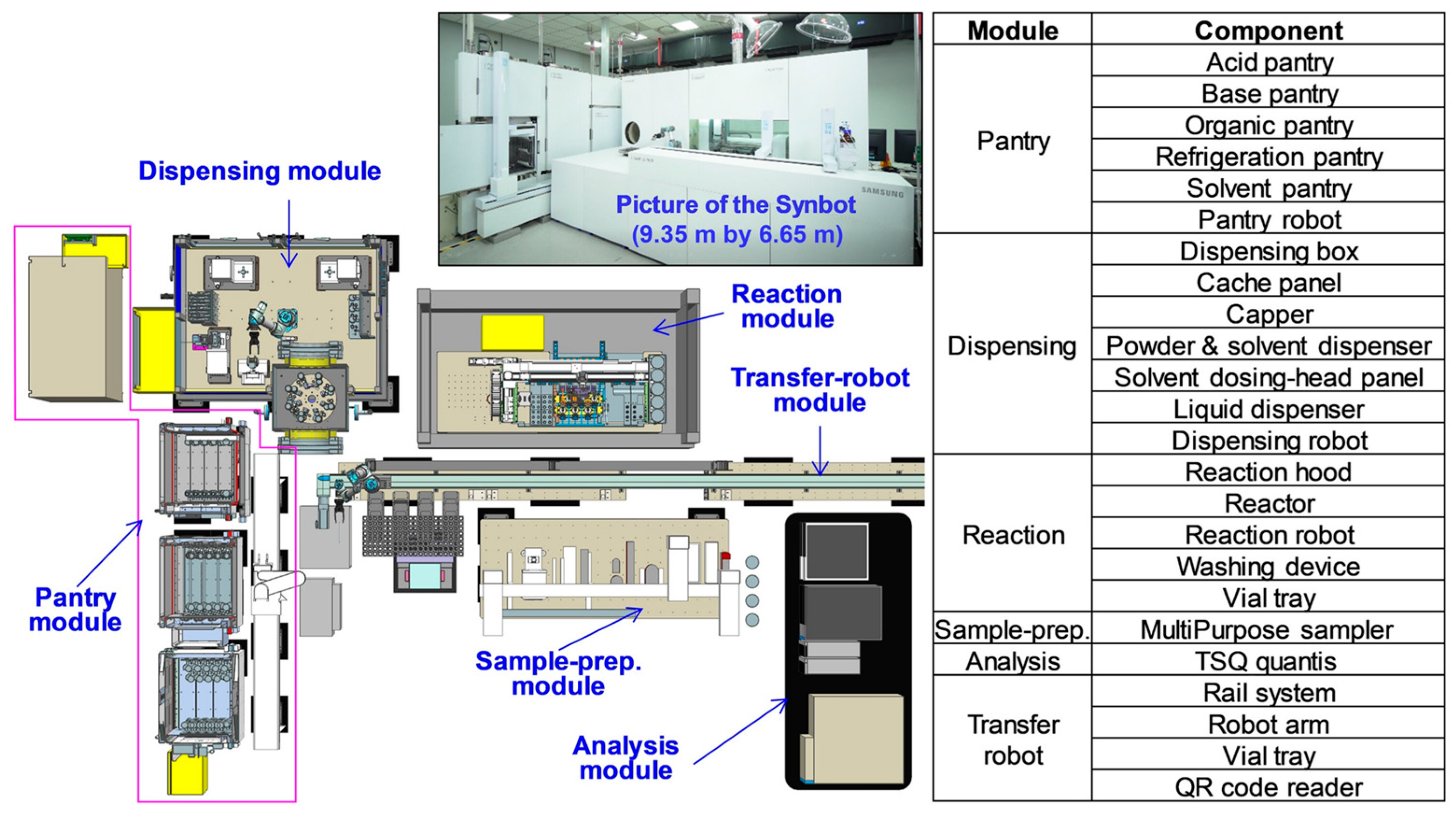
| Year | AF | Feature | References |
|---|---|---|---|
| 2018 | TSEMO | the first efficient multi-objective optimization algorithm based on Thompson sampling, suitable for most MOBO | [27] |
| 2021 | TSEMO + DyOS | after rapid optimization with TSEMO in the early stage, switch to DyOS for more refined convergence | [35] |
| 2023 | q-NEHVI | suitable for multi-objective optimization with multiple parameters | [37,38,39] |
| 2025 | MO-E-EQI | exhibits excellent noise resistance performance | [40] |
| References | Num Parameters | Num Objectives | Num Experiments | |||
|---|---|---|---|---|---|---|
| BO | DoE | SNOBFTT | Kinetic Model | |||
| [51] | 8 | 3 | 25 | 128 | / | / |
| [52] | 2 | 3 | 14–17 | / | >20 | / |
| [53] | 2 | 3 | 32 | 70 | / | / |
| [54] | 4 | 1 | 20 | / | / | >50 |
| [55] | 4 | 2 | 40 | / | / | >60 |
| Amine Nucleophile Subsets | The Cost of Standard BO | The Cost of CIBO | Cost Saved |
|---|---|---|---|
| aniline (An) subset | USD 2474 | USD 1124 | USD 1350 (54%) |
| phenethylamine (Ph) subset | USD 2170 | USD 142 | USD 2028 (93%) |
| morpholine (Mo) subset | USD 2105 | USD 2105 | USD 0 |
| benzamide (Be) subset | USD 2144 | USD 690 | USD 1454 (68%) |
| Year | Case | Optimization Parameters | Optimization Objectives | AFs or Optimizer |
|---|---|---|---|---|
| 2022 | Autonomous multi-step and multi-objective optimization facilitated by real-time process analytics [101] | temperature; concentration; residence time; equivalents | conversion; STY | TSEMO |
| 2024 | Self-optimization platform with Multiple Process Analysis [102] | loading of amine and catalyst; equivalents; concentration; temperature | STY; yield; cost | TSEMO |
| 2024 | Three AFs compared in the self-optimization system [103] | equivalents; concentration; temperature; residence time; coupling reagents | yield | EI; TSEMO; BOAEI |
| 2023 | Self-optimization of mixed variable chemical systems [104] | solvent; ligands; temperature; equivalents; concentration | STY; RME; optimal ligand; | MVMOO |
| 2022 | Closed-loop optimization of polymer synthesis [105] | temperature; residence time; types of RAFT agents; initiator concentration | monomer conversion; molar mass dispersity | TSEMO |
| 2023 | Autonomous synthesis optimization for 1-methyltetrahydroisoquinoline C5 functionalization precursor [106] | temperature; residence time; equivalents; flow rate ratio | yield | BOAEI |
| 2024 | Self-optimization of two-step synthesis of Paracetamol [107] | temperature R1; temperature R2; nitrophenol flow rate; flow rate ratio | yield | BOAEI |
| 2024 | Operator-free HPLC method development guided by Bayesian optimization [108] | initial organic modifier; concentration; gradient time | number of peaks; resolution; the elution time of the last peak | TSEMO/BOAEI * |
| 2025 | Self-optimizing purification of DEHiBA [109] | solvent ratio; acid concentration; alkali concentration | purity; recovery rate | BOAEI * |
| 2022 | Continuous stirred-tank reactor cascade platform for self-optimization of reactions involving solids [110] | photocatalysts; temperature; residence time; solvent composition | yield; diastereoselectivity | Dragonfly |
| 2022 | Autonomous optimization of non-aqueous Li-ion battery electrolytes [113] | ternary solvent combination; concentration | ionic conductivity | Dragonfly |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, R.; Luo, G.; Su, A. Bayesian Optimization for Chemical Synthesis in the Era of Artificial Intelligence: Advances and Applications. Processes 2025, 13, 2687. https://doi.org/10.3390/pr13092687
Shen R, Luo G, Su A. Bayesian Optimization for Chemical Synthesis in the Era of Artificial Intelligence: Advances and Applications. Processes. 2025; 13(9):2687. https://doi.org/10.3390/pr13092687
Chicago/Turabian StyleShen, Runqiu, Guihua Luo, and An Su. 2025. "Bayesian Optimization for Chemical Synthesis in the Era of Artificial Intelligence: Advances and Applications" Processes 13, no. 9: 2687. https://doi.org/10.3390/pr13092687
APA StyleShen, R., Luo, G., & Su, A. (2025). Bayesian Optimization for Chemical Synthesis in the Era of Artificial Intelligence: Advances and Applications. Processes, 13(9), 2687. https://doi.org/10.3390/pr13092687







