Bioenvironmental Zonal Controlling of Incubated Avian Embryo Using Localised Infrared Heating
Abstract
:1. Introduction
2. Materials and Methods
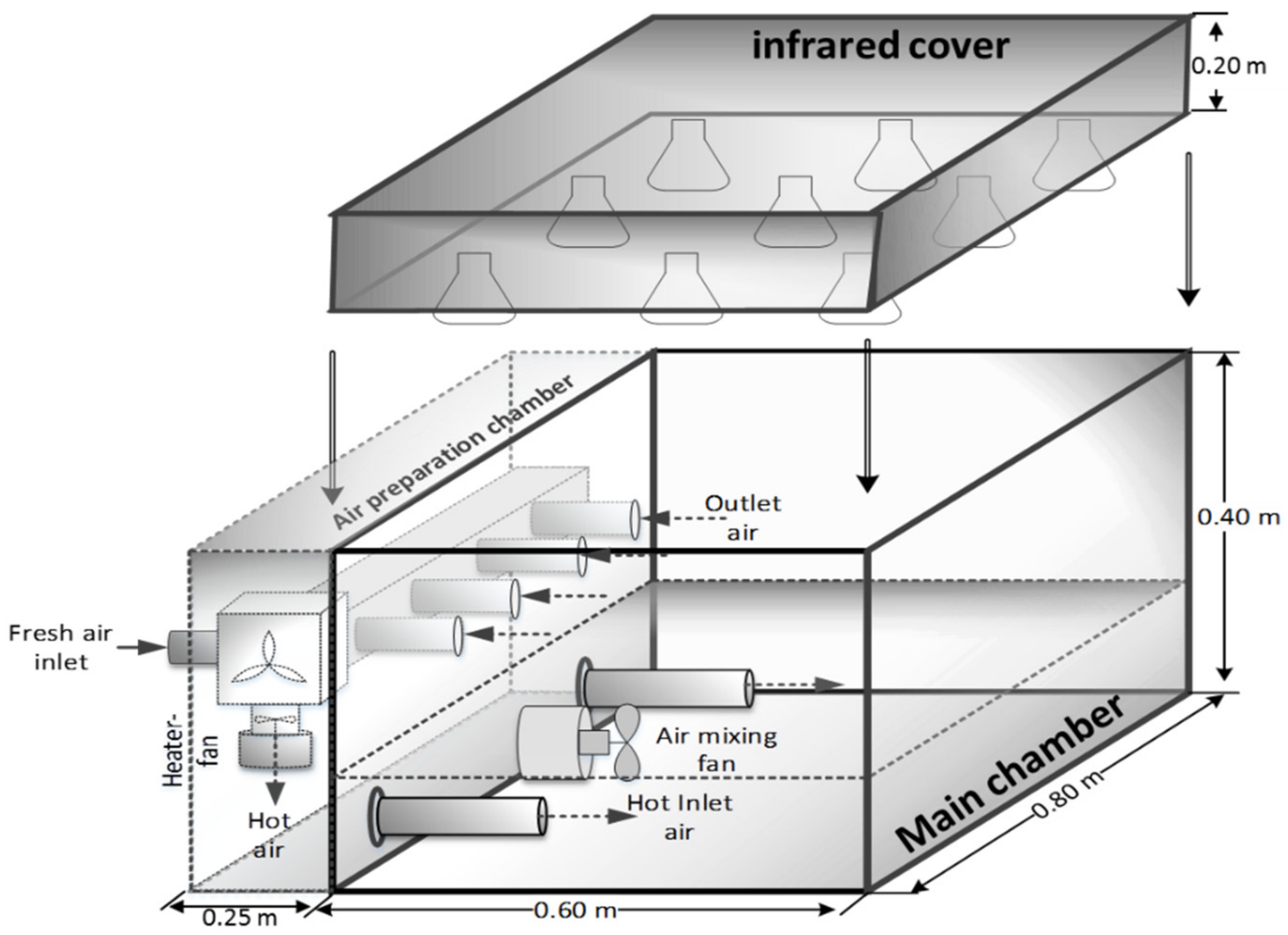
2.1. Experimental Setup
2.1.1. Experimental Incubator
2.1.2. Infrared Cover
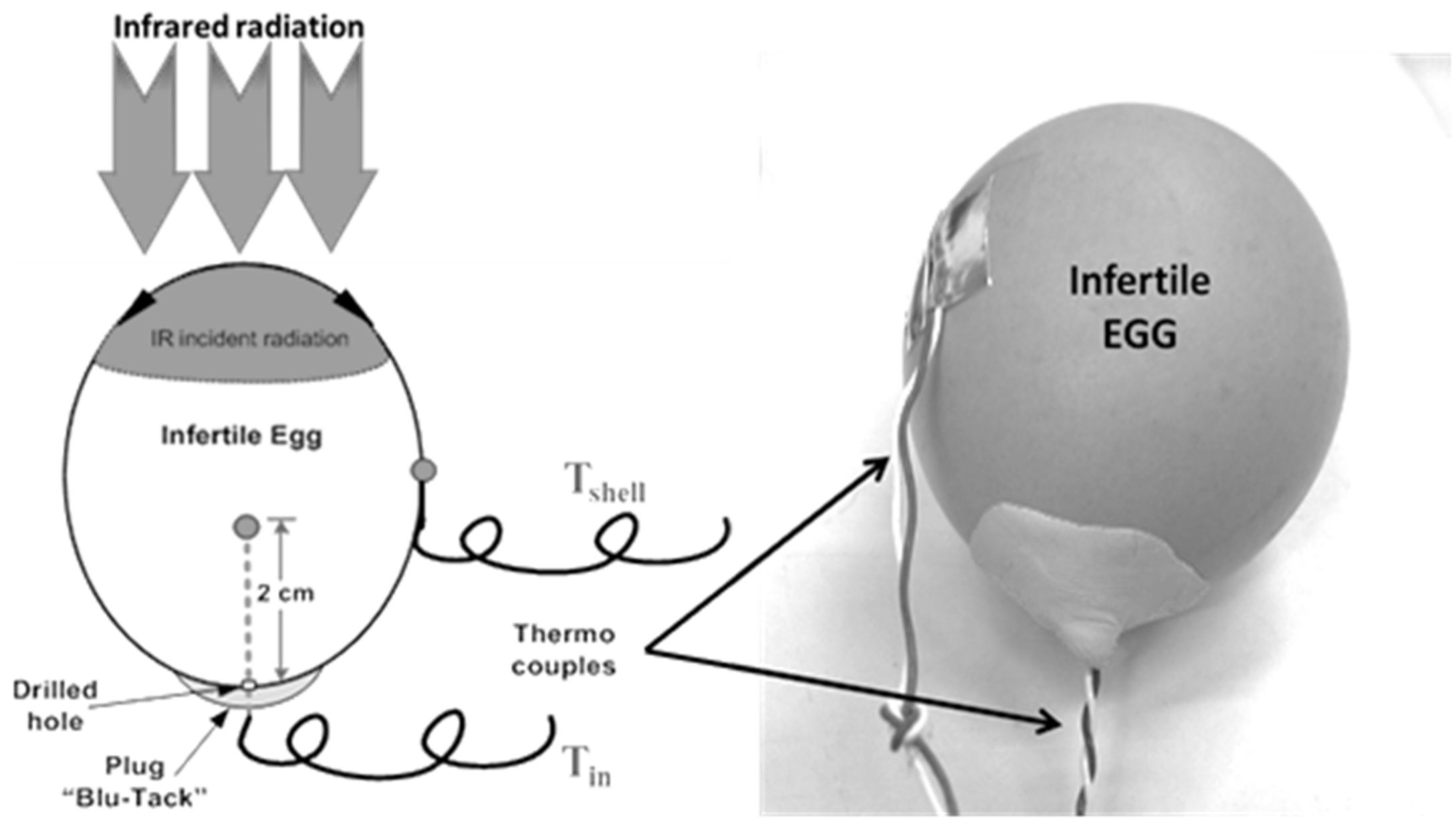
2.2. Measurements and Data Acquisition
2.3. Experiments
2.3.1. Pilot Experiments
2.3.2. Control and System Identification Experiments
2.3.3. Full Incubation Trials and Controller Implementation
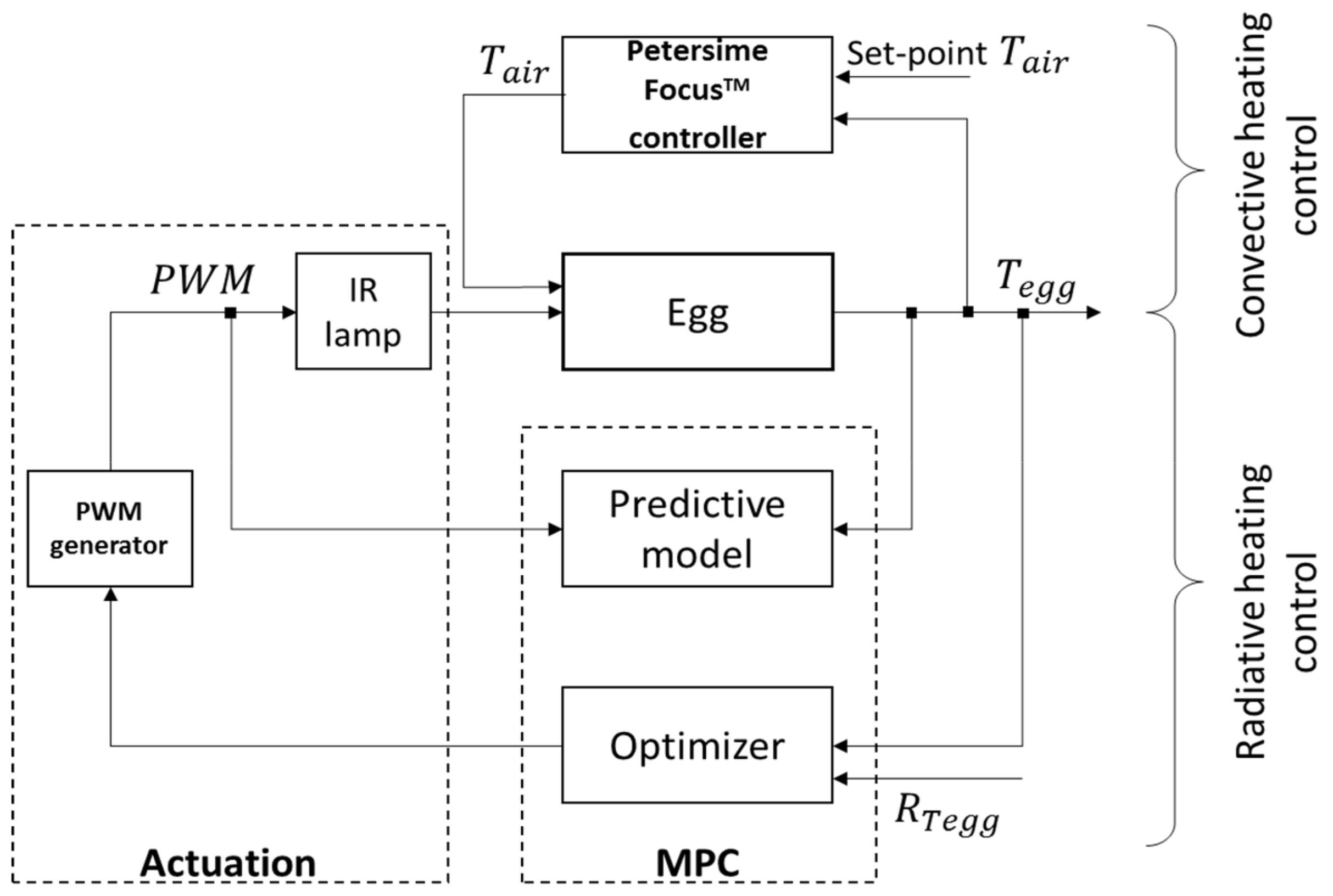
2.4. Model Predictive Controller (MPC) and System Identification
2.4.1. System Identification and Parameter Estimation
2.4.2. MPC and Cost Function Formulation
3. Results
3.1. Pilot Experiments
3.2. System Identification and Predictive Model Generation
3.3. Model Predictive Control Design
3.3.1. MPC Cost Function and Constraints
3.3.2. MPC Simulation
- Sampling time (or period) , which determines the rate at which the control algorithm was executed. The shorter the sampling period the better controller performance to deal with fast disturbances. On the other hand, diminishing can increase the computational burden. In any case, should not exceed the maximal expected time necessary for running one iteration of the MPC algorithm [29]. In the current study the sampling time was chosen to be one sample ( = 1 min), which corresponds to a value ten times smaller than the average observed rise time ( = 10.12 ± 0.22 min).
- Defining the prediction and control horizons, which should be at least same or larger than the settling time of the system. The control horizon in general should be less than the defined prediction horizon and based on many applications an optimal control horizon should be between 20–30% of the prediction horizon to ensure smooth control actions and yet low computational costs. In the current study, the prediction and control horizons were set to 20 samples ( > average settling time = 16.20 ± 1.13 min) and five samples (25% of the prediction horizon).
- To achieve a balanced performance between the competing control objectives (i.e., a close tracking of the set-point together with smooth control moves), the weighting factors α and λ were set to 0.9 and 0.8, respectively [30], to avoid any conflict between the control objectives.
3.3.3. MPC Implementation and Full Incubation Experiments
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- OECD/FAO. OECD-FAO Agricultural Outlook 2019–2028; OECD: Paris, France, 2017. [Google Scholar]
- Fasenko, G.M. Egg Storage and the Embryo. Poult. Sci. 2013, 86, 1020–1024. [Google Scholar] [CrossRef] [PubMed]
- Bergoug, H.; Burel, C.; Guinebretiere, M.; Tong, Q.; Roulston, N.; Romanini, C.E.; Exadaktylos, V.; McGonnell, I.M.; Demmers, T.G.; Verhelst, R.; et al. Effect of pre-incubation and incubation conditions on hatchability, hatch time and hatch window, and effect of post-hatch handling on chick quality at placement. World’s. Poult. Sci. J. 2013, 69, 313–334. [Google Scholar] [CrossRef]
- Uni, Z.; Noy, Y.; Sklan, D. Posthatch development of small intestinal function in the poult. Poult. Sci. 1999, 78, 215–222. [Google Scholar] [CrossRef] [PubMed]
- Noy, Y.; Sklan, D. Yolk and Exogenous Feed Utilization in the Posthatch Chick. Poult. Sci. 2001, 80, 1490–1495. [Google Scholar] [CrossRef] [PubMed]
- Romanini, C.E.; Exadaktylos, V.; Tong, Q.; McGonnel, I.; Demmers, T.G.; Bergoug, H.; Eterradossi, N.; Roulston, N.; Garain, P.; Bahr, C.; et al. Monitoring the hatch time of individual chicken embryos. Poult. Sci. 2013, 92, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Tong, Q.; McGonnell, I.M.; Roulston, N.; Bergoug, H.; Romanini, C.E.; Garain, P.; Eterradossi, N.; Exadaktylos, V.; Bahr, C.; Berckmans, D.; et al. Higher levels of CO2 during late incubation alter the hatch time of chicken embryos. Br. Poult. Sci. 2015, 56, 503–509. [Google Scholar] [CrossRef] [PubMed]
- Gucbilmez, M.; Ozlu, S.; Shiranjang, R.; Elibol, O.; Brake, J. Effects of preincubation heating of broiler hatching eggs during storage, flock age, and length of storage period on hatchability. Poult. Sci. 2013, 92, 3310–3313. [Google Scholar] [CrossRef]
- Hulet, R.; Gladys, G.; Hill, D.; Meijerhof, R.; El-Shiekh, T. Influence of egg shell embryonic incubation temperature and broiler breeder flock age on posthatch growth performance and carcass characteristics. Poult. Sci. 2007, 86, 408–412. [Google Scholar] [CrossRef]
- Lourens, A. Embryo Temperature during Incubation: Practice and Theory; Wageningen University: Wageningen, The Netherlands, 2008. [Google Scholar]
- Shelehov, I.Y.; Smirnov, E.I.; Inozemsev, V.P. Localized Electrical Heating System for Various Types of Buildings. IOP Conf. Ser. Mater. Sci. Eng. 2017, 262, 012083. [Google Scholar] [CrossRef]
- Youssef, A.; Exadaktylos, V.; Ozcan, S.E.; Berckmans, D. Proportional-Integral-Plus (PIP) Control System for Individual Thermal Zones in a Small Ventilated Space. ASHRAE Trans. 2011, 117, 48–56. [Google Scholar]
- Youssef, A.; Yen, H.; Özcan, S.E.; Berckmans, D. Data-based mechanistic modelling of indoor temperature distributions based on energy input. Energy Build. 2011, 43, 2965–2972. [Google Scholar] [CrossRef]
- Janssens, K.; van Brecht, A.; Desta, T.Z.; Boonen, C.; Berckmans, D. Modeling the internal dynamics of energy and mass transfer in an imperfectly mixed ventilated airspace. Indoor Air 2004, 14, 146–153. [Google Scholar] [CrossRef] [PubMed]
- Youssef, A.; Exadaktylos, V.; Berckmans, D. Modelling and quantification of the thermoregulatory responses of the developing avian embryo: Electrical analogies of a physiological system. J. Therm. Biol. 2014, 44, 14–19. [Google Scholar] [CrossRef] [PubMed]
- Tzschentke, B.; Rumpf, M. Embryonic development of endothermy. Respir. Physiol. Neurobiol. 2011, 178, 97–107. [Google Scholar] [CrossRef] [PubMed]
- Quanten, S.; de Valck, E.; Cluydts, R.; Aerts, J.-M.; Berckmans, D. Individualized and time-variant model for the functional link between thermoregulation and sleep onset. J. Sleep Res. 2006, 15, 183–198. [Google Scholar] [CrossRef] [PubMed]
- Youssef, A. Model-Based Control of Micro-Environment with Real-Time Feedback of Bioresponses; KU Leuven: Leuven, Belgium, 2014. [Google Scholar]
- Trentelman, H.L.; Stoorvogel, A.A.; Hautus, M. Control Theory for Linear Systems; Springer: London, UK, 2001. [Google Scholar]
- Leigh, J.R. Applied Control Theory; Rev Sub. P. Peregrinus Ltd. on behalf of the Institution of Electrical Engineers: London, UK, 1987. [Google Scholar]
- Camacho, E.F.; Bordons, C. Model Predictive Control; Springer: London, UK, 2007. [Google Scholar]
- Kaiser, E.; Kutz, J.N.; Brunton, S.L. Sparse identification of nonlinear dynamics for model predictive control in the low-data limit. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20180335. [Google Scholar] [CrossRef] [PubMed]
- Godina, R.; Rodrigues, E.M.G.; Pouresmaeil, E.; Catalão, J.P.S. Optimal residential model predictive control energy management performance with PV microgeneration. Comput. Oper. Res. 2018, 96, 143–156. [Google Scholar] [CrossRef]
- Young, P.C.; Chotai, A.; Tych, W. Identification, Estimation and Control of Continuous-Time Systems Described by Delta Operator Models; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Young, P.C.; Jakeman, A. Refined instrumental variable methods of recursive time-series analysis Part III. Extensions. Int. J. Control 1980, 31, 741–764. [Google Scholar] [CrossRef]
- Young, P.C. Recursive Estimation and Time-Series Analysis: An Introduction for the Student and Practitioner; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Camacho, E.F.; Bordons, C. Model Predictive Control. Int. J. Robust Nonlinear Control 1999, 13, 280. [Google Scholar]
- Cutler, C.R.; Ramaker, B.C. Dynamic Matrix Control? A Computer Control Algorithm. Autom. Control Conf. 1980, 17, 72. [Google Scholar] [CrossRef]
- Wysocki, A.; Ławryńczuk, M. On Choice of the Sampling Period and the Horizons in Generalized Predictive Control. In Recent Advances in Automation, Robotics and Measuring Techniques; Springer: Cham, Switzerland, 2014; pp. 329–339. [Google Scholar]
- Borrelli, F.; Bemporad, A.; Morari, M. Predictive Control for Linear and Hybrid Systems; Cambridge University Press: New York, NY, USA, 2017. [Google Scholar]
- Mueller, C.A.; Burggren, W.W.; Tazawa, H. The Physiology of the Avian Embryo Chapter 32. In Sturkie’s Avian Physiology; Academic Press: Cambridge, MA, USA, 2015; pp. 739–766. [Google Scholar]
- Whittow, G.C.; Tazawa, H. The early development of thermoregulation in birds. Physiol. Zool. 2002, 64, 1371–1390. [Google Scholar] [CrossRef]
- Janke, O.; Tzschentke, B.; Höchel, J.; Nichelmann, M. Metabolic responses of chicken and muscovy duck embryos to high incubation temperatures. Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2002, 131, 741–750. [Google Scholar] [CrossRef]
- Tzschentke, B. Monitoring the development of thermoregulation in poultry embryos and its influence by incubation temperature. Comput. Electron. Agric. 2008, 64, 61–71. [Google Scholar] [CrossRef]
- Fayeye, T.; Olapade, A. Hatch-Out Analysis and Repeatability Estimates of Common Hatchability Problems in Issa-Brown Breeder Stock. Agrosearch 2013, 13, 51. [Google Scholar] [CrossRef] [Green Version]
- Mauldin, J.M. Breakout Analyses Guide for Hatcheries|The Poultry Site. 2003. Available online: https://thepoultrysite.com/articles/breakout-analyses-guide-for-hatcheries-1 (accessed on 25 August 2019).









| 0.98 (± 0.01) | −13.00 (± 1.45) | ||||
| −1.997 (± 0.003) | 0.997 (± 0.003) | 0.0010 (± 0.0017) | −0.0010 (± 0.0017) | ||
| Constraints | |
|---|---|
| Manipulated variable (power to the IR, PWM, %) | |
| Change in the Manipulated variable (%) | |
| Controlled variable (average eggshell temperature, °C) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Youssef, A.; Norton, T.; Berckmans, D. Bioenvironmental Zonal Controlling of Incubated Avian Embryo Using Localised Infrared Heating. Processes 2019, 7, 651. https://doi.org/10.3390/pr7100651
Youssef A, Norton T, Berckmans D. Bioenvironmental Zonal Controlling of Incubated Avian Embryo Using Localised Infrared Heating. Processes. 2019; 7(10):651. https://doi.org/10.3390/pr7100651
Chicago/Turabian StyleYoussef, Ali, Tomas Norton, and Daniel Berckmans. 2019. "Bioenvironmental Zonal Controlling of Incubated Avian Embryo Using Localised Infrared Heating" Processes 7, no. 10: 651. https://doi.org/10.3390/pr7100651
APA StyleYoussef, A., Norton, T., & Berckmans, D. (2019). Bioenvironmental Zonal Controlling of Incubated Avian Embryo Using Localised Infrared Heating. Processes, 7(10), 651. https://doi.org/10.3390/pr7100651







