Bi-Level Model Predictive Control for Optimal Coordination of Multi-Area Automatic Generation Control Units under Wind Power Integration
Abstract
:1. Introduction
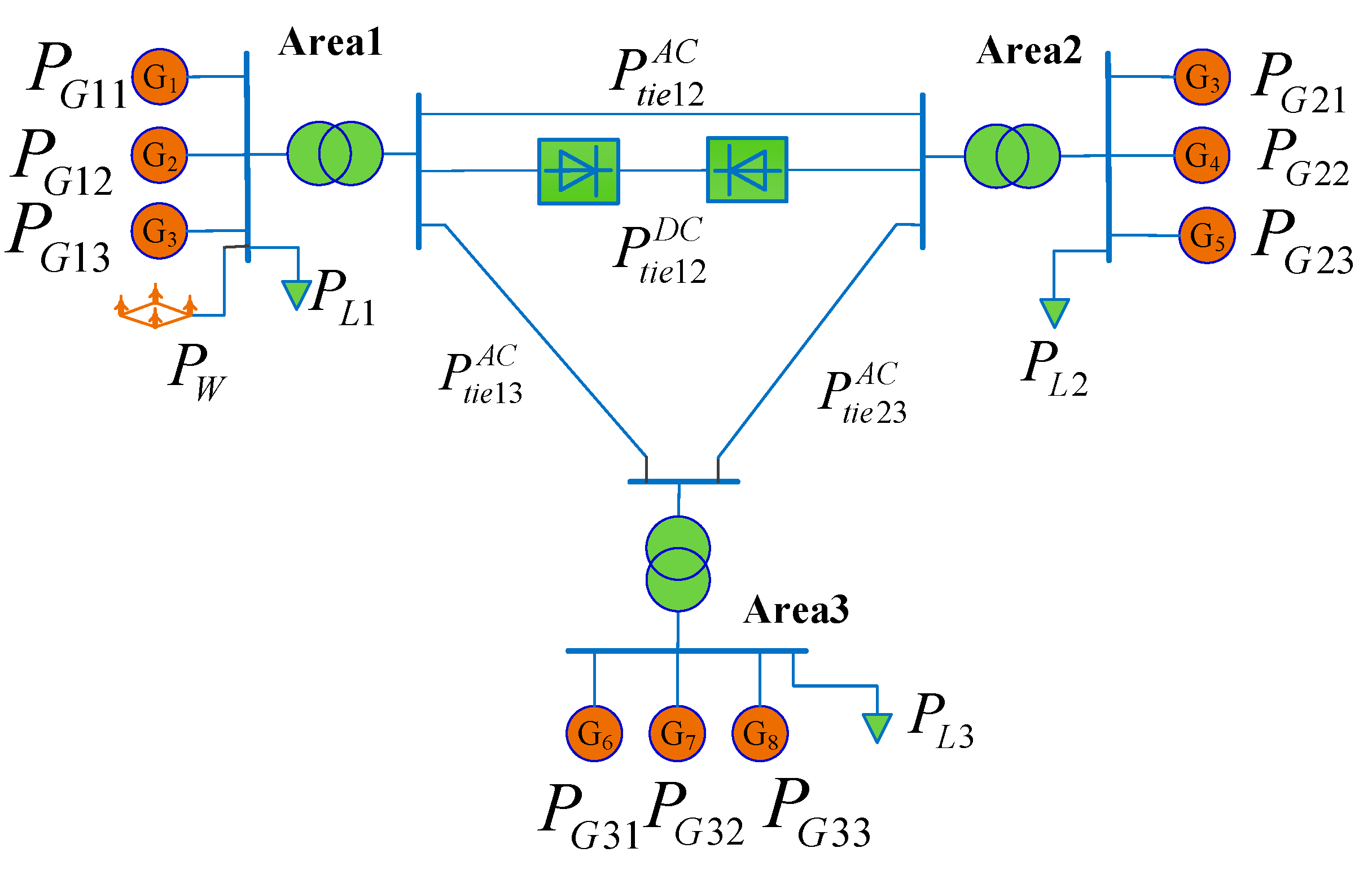
2. Automatic Generation Control Model of Multi-Area Power System with Wind Farm
3. Coordinated Control Strategy for Automatic Generation Control Units Based on Bi-Level Model Predictive Control
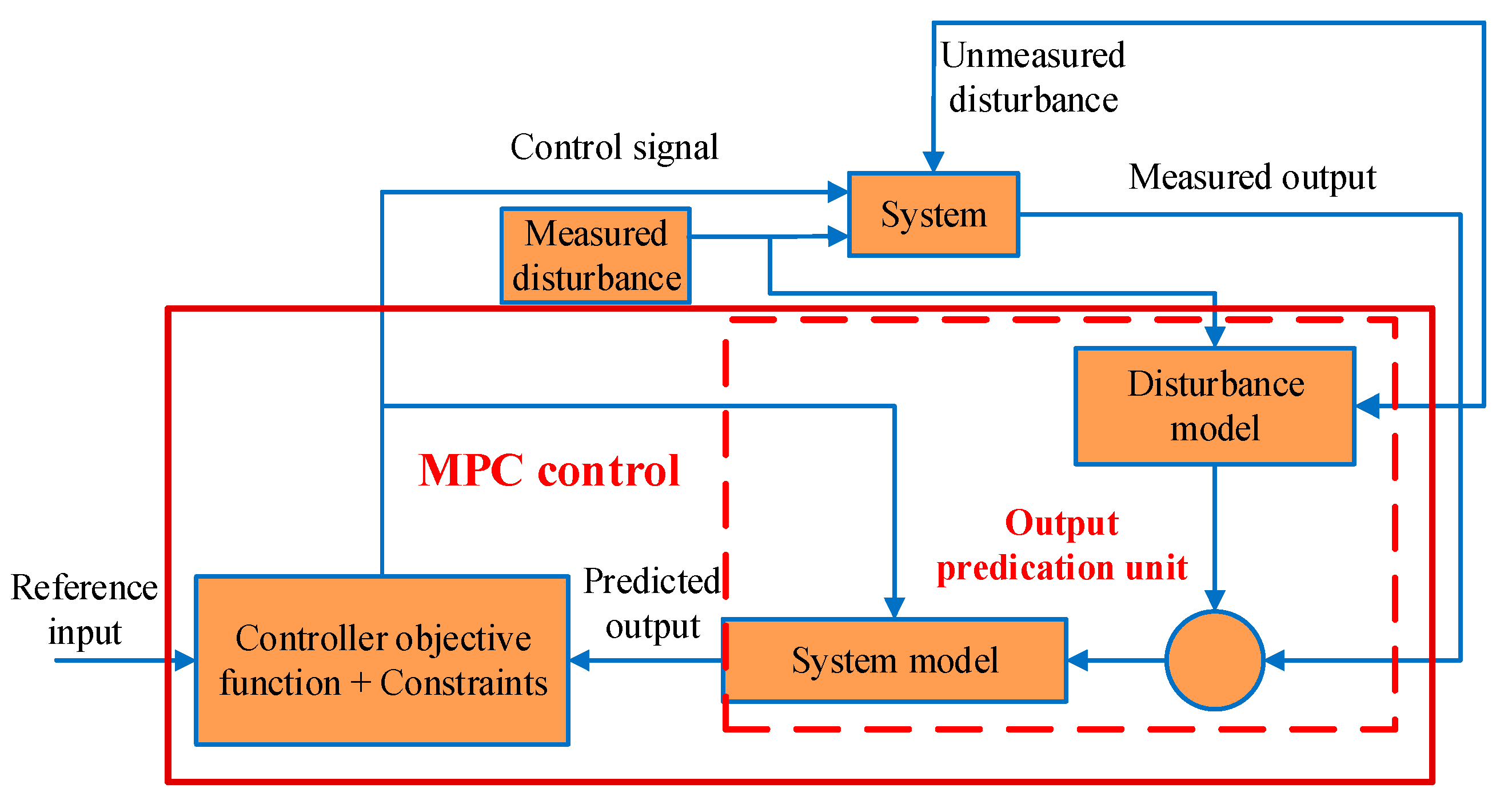
3.1. Bi-Level Model Predictive Control Framework
- A model of the system. This model is used to predict the future evolution of the system in an open loop, and the efficiency of the calculated control actions of an MPC highly depends on the accuracy of the model.
- A performance index over a finite horizon. This index will be minimized subject to constraints imposed by the system model, restrictions on control inputs and system state, and other considerations at each sampling time to obtain a trajectory of future control inputs.
- A receding horizon scheme. This scheme introduces the notion of feedback into the control law to compensate for disturbances and modeling errors.
3.2. Upper-Level Model Predictive Control Controller: Steady-State Power Allocation Layer
3.3. Lower-Level Model Predictive Control Controller: Dynamic Frequency Control Layer
4. Simulation Results and Discussion
4.1. Case 1: Different Load Step Disturbance
4.2. Case 2: Random Disturbance of Wind Farm
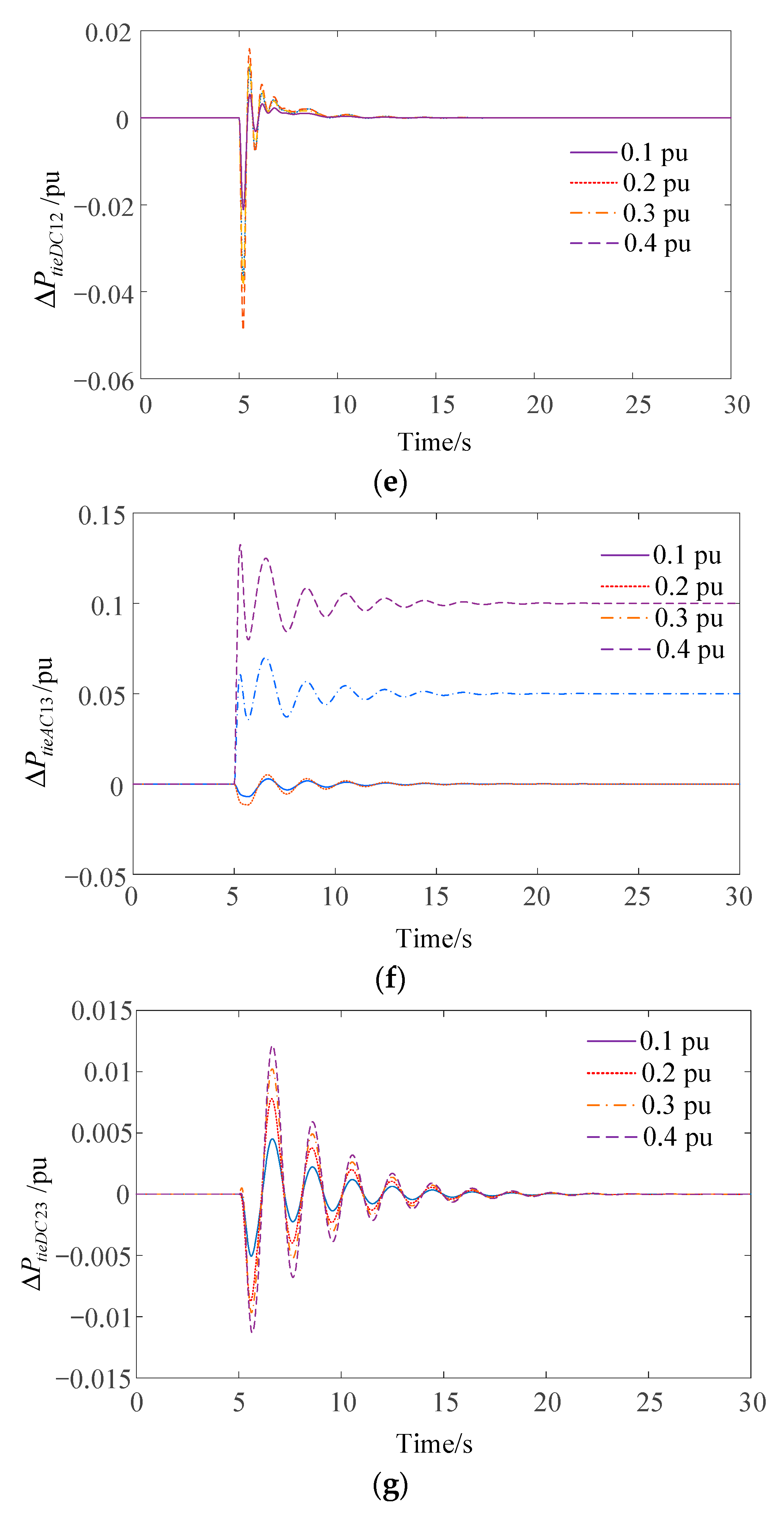
4.3. Case 3: Different Wind Power Penetration
5. Conclusions
- (1)
- Compared with the MPC method using TBC mode [36], the proposed BMPC method not only can keep the frequency deviation within a smaller range under disturbance but also can ensure the safety of AC tie-line power support.
- (2)
- The proposed BMPC method optimizes the output of AGC units in each area on a minute time scale, avoiding deviation of the AGC unit from the optimal operating point during scheduling periods, which can effectively reduce the frequency regulation cost of multi-area AGC units.
- (3)
- With increased wind power permeability, the frequency deviation of each regional system fluctuates greatly. When the penetration rate of wind power reaches 40%, the proposed control strategy can still maintain a frequency fluctuation range within ±0.2 Hz, and the wind power random fluctuation power shortage is allocated to maximize the frequency regulation capability of each area.
Author Contributions
Funding
Conflicts of Interest
References
- Fox, B. Introduction. In Wind Power Integration: Connection and System Operational Aspects; IET Power and Energy Series; Institution of Engineering and Technology: Stevenage, UK, 2007; Volume 50, pp. 77–85. [Google Scholar]
- Suh, J.; Yoon, D.H.; Cho, Y.S.; Jang, G. Flexible frequency operation strategy of power system with high renewable penetration. IEEE Trans. Sustain. Energy 2017, 8, 192–199. [Google Scholar] [CrossRef]
- Keyhani, A.; Chatterjee, A. Automatic generation control structure for smart power grids. IEEE Trans. Smart Grid 2012, 3, 1310–1316. [Google Scholar] [CrossRef]
- Zhang, L.; Luo, Y.; Ye, J.; Xiao, Y.-Y. Distributed coordination regulation marginal cost control strategy for automatic generation control of interconnected power system. IET Gener. Transm. Distrib. 2017, 11, 1337–1344. [Google Scholar] [CrossRef]
- Bevrani, H. Robust Power System Frequency Control, 2nd ed.; Springer: Gewerbestrasse, Switzerland, 2014. [Google Scholar]
- Chen, C.; Zhang, K.; Yuan, K.; Gao, Z.; Teng, X.; Ding, Q. Disturbance rejection-based LFC for multi-area parallel interconnected AC/DC system. IET Gener. Transm. Distrib. 2016, 10, 4105–4117. [Google Scholar] [CrossRef]
- Patel, R.B.; Li, C.; Yu, X.; McGrath, B. Optimal automatic generation control of an interconnected power system under network constraints. IEEE Trans. Ind. Electron. 2018, 65, 7220–7228. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Chandra Sekhar, G.T. A novel hybrid PSO-PS optimized fuzzy PI controller for AGC in multi area interconnected power systems. Int. J. Electr. Power Energy Syst. 2015, 64, 880–893. [Google Scholar] [CrossRef]
- Raju, M.; Saikia, L.C.; Sinha, N. Automatic generation control of a multi-area system using ant lion optimizer algorithm based PID plus second order derivative controller. Int. J. Electr. Power Energy Syst. 2016, 80, 52–63. [Google Scholar] [CrossRef]
- Arya, Y. AGC performance enrichment of multi-source hydrothermal gas power systems using new optimized FOFPID controller and redox flow batteries. Energy 2017, 127, 704–715. [Google Scholar] [CrossRef]
- Sharma, Y.; Saikia, L.C. Automatic generation control of a multi-area ST—Thermal power system using Grey Wolf Optimizer algorithm based classical controllers. Int. J. Electr. Power Energy Syst. 2015, 73, 853–862. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Model Predictive Control; Springer: London, UK, 2004; Volume 2. [Google Scholar]
- Mayne, D. Model predictive control: Recent developments and future promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB; Springer: London, UK, 2009. [Google Scholar]
- Ersdal, A.M.; Imsland, L.; Uhlen, K. Model predictive load-frequency control. IEEE Trans. Power Syst. 2015, 31, 777–785. [Google Scholar] [CrossRef]
- Mohamed, T.H.; Morel, J.; Bevrani, H.; Hiyama, T. Model predictive based load frequency control design concerning wind turbines. Int. J. Electr. Power Energy Syst. 2012, 43, 859–867. [Google Scholar] [CrossRef]
- Elsisi, M.; Soliman, M.; Aboelela, M.; Mansour, W. Bat inspired algorithm based optimal design of model predictive load frequency control. Int. J. Electr. Power Energy Syst. 2016, 83, 426–433. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Qiu, H. Networked coordination-based distributed model predictive control for large-scale system. IEEE Trans. Control Syst. Technol. 2013, 21, 991–998. [Google Scholar] [CrossRef]
- Venkat, A.N.; Hiskens, I.A.; Rawlings, J.B.; Wright, S.J. Distributed MPC strategies with application to power system automatic generation control. IEEE Trans. Control Syst. Technol. 2008, 16, 1192–1206. [Google Scholar] [CrossRef]
- Ma, M.; Chen, H.; Liu, X.; Allgöwer, F. Distributed model predictive load frequency control of multi-area interconnected power system. Int. J. Electr. Power Energy Syst. 2014, 62, 289–298. [Google Scholar] [CrossRef]
- Liu, X.; Kong, X.; Lee, K.Y. Distributed model predictive control for load frequency control with dynamic fuzzy valve position modelling for hydro–thermal power system. IET Control. Theory Appl. 2016, 10, 1653–1664. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhou, J.; Xu, Y.; Zhang, Y.; Qian, Z. A distributed model predictive control based load frequency control scheme for multi-area interconnected power system using discrete-time Laguerre functions. ISA Trans. 2017, 68, 127–140. [Google Scholar] [CrossRef]
- Ma, M.; Liu, X.; Zhang, C. LFC for multi-area interconnected power system concerning wind turbines based on DMPC. IET Gener. Transm. Distrib. 2017, 11, 2689–2696. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Lee, K.Y. Coordinated distributed MPC for load frequency control of power system with wind farms. IEEE Trans. Ind. Electron. 2017, 64, 5140–5150. [Google Scholar] [CrossRef]
- Christofides, P.D.; Scattolini, R.; de la Peña, D.M.; Liu, J. Distributed model predictive control: A tutorial review and future research directions. Comput. Chem. Eng. 2013, 51, 21–41. [Google Scholar] [CrossRef]
- Picasso, B.; De Vito, D.; Scattolini, R.; Colaneri, P. An MPC approach to the design of two-layer hierarchical control systems. Autom. 2010, 46, 823–831. [Google Scholar] [CrossRef]
- Zhang, T.; Gooi, H.B. Hierarchical MPC-based energy management and frequency regulation participation of a virtual power plant. In Proceedings of the IEEE Innovative Smart Grid Technologies Conference Europe, Istanbul, Turkey, 12–15 October 2014. [Google Scholar]
- Babahajiani, P.; Shafiee, Q.; Bevrani, H. Intelligent Demand Response Contribution in Frequency Control of Multi-Area Power Systems. IEEE Trans. Smart Grid 2018, 9, 1282–1291. [Google Scholar] [CrossRef]
- Sharma, G.; Nasiruddin, I.; Niazi, K.R.; Bansal, R.C. Robust automatic generation control regulators for a two-area power system interconnected via AC/DC tie-lines considering new structures of matrix Q. IET Gener. Transm. Distrib. 2016, 10, 3570–3579. [Google Scholar] [CrossRef]
- Niazi, K.R.; Bansal, R.C.; Sharma, G.; Nasiruddin, I. Optimal AGC of a multi-area power system with parallel AC/DC tie lines using output vector feedback control strategy. Int. J. Electr. Power Energy Syst. 2016, 81, 22–31. [Google Scholar]
- Scattolini, R. Architectures for distributed and hierarchical model predictive control–A review. J. Process Control 2009, 19, 723–731. [Google Scholar] [CrossRef]
- Mohamed, T.H.; Bevrani, H.; Hassan, A.A.; Hiyama, T. Decentralized model predictive based load frequency control in an interconnected power system. Energy Convers. Manag. 2011, 52, 1208–1214. [Google Scholar] [CrossRef]
- Mohamed, T.H.; Morel, J.; Bevrani, H.; Hassan, A.A.; Mohamed, Y.S.; Hiyama, T. Decentralized model predictive-based load-frequency control in an interconnected power system concerning wind turbines. IEEJ Trans. Electr. Electron. Eng. 2012, 7, 487–494. [Google Scholar] [CrossRef]
- Kennel, F.; Gorges, D.; Liu, S. Energy management for smart grids with electric vehicles based on hierarchical MPC. IEEE Trans. Ind. Inf. 2013, 9, 1528–1537. [Google Scholar] [CrossRef]
- Ma, M.; Zhang, C.; Liu, X.; Chen, H. distributed model predictive load frequency control of the multi-area power system after deregulation. IEEE Trans. Ind. Electron. 2017, 64, 5129–5139. [Google Scholar] [CrossRef]
- Liao, X.; Liu, K.; Wang, N.; Liang, Q.; Ma, Y.; Chen, Z.; Ding, K.; Zhou, Q. Cooperative DMPC-based load frequency control of AC/DC interconnected power system with solar thermal power plant. In Proceedings of the 2018 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Kota Kinabalu, Sabah, Malaysia, 7–10 October 2018; pp. 341–346. [Google Scholar]
- Zhang, Y.; Liu, K.; Qin, L.; An, X. Deterministic and probabilistic interval prediction for short-term wind power generation based on variational mode decomposition and machine learning methods. Energy Convers. Manag. 2016, 112, 208–219. [Google Scholar] [CrossRef]








| Symbol | Name of Parameter/Constant |
|---|---|
| Incremental frequency deviation of area i | |
| Total AC tie-line power change between area i and other areas | |
| Total DC tie-line power change between area i and other areas | |
| Wind farm disturbance signal of area i | |
| Load disturbance signal of area i | |
| Gain constant of power system of area i | |
| Time constant of power system of area i | |
| AC tie-line synchronizing coefficient between area i and area j | |
| Area control error of area i | |
| Input control signal from controller of area i | |
| Droop characteristic coefficient | |
| Steam turbine governor time constant | |
| Steam turbine time constant | |
| Power incremental change | |
| Governor-valve position incremental change | |
| AGC unit participation factor |
| AGC Unit | Hz/pu | ||||
|---|---|---|---|---|---|
| 0.08 | 0.40 | 3.30 | 120 | 20 | |
| 0.07 | 0.42 | 3.30 | |||
| 0.06 | 0.36 | 3.0 | |||
| 0.06 | 0.44 | 2.73 | 110 | 15 | |
| 0.06 | 0.42 | 2.67 | |||
| 0.08 | 0.40 | 2.50 | |||
| 0.07 | 0.40 | 2.82 | 100 | 24 | |
| 0.07 | 0.40 | 3.00 | |||
| 0.08 | 0.41 | 2.94 | |||
| pu/Hz | 0.086 | s | 0.2 | pu/Hz | 1.0 |
| AGC Unit | |||||
|---|---|---|---|---|---|
| 0 | 0.05 | 15.6 | 345 | 5.61 | |
| 0 | 0.08 | 19.4 | 381 | 7.82 | |
| 0 | 0.12 | 18.2 | 367 | 5.63 | |
| 0 | 0.05 | 24.1 | 429 | 5.25 | |
| 0 | 0.01 | 46.8 | 383 | 5.28 | |
| 0 | 0.05 | 38.2 | 603 | 5.85 | |
| 0 | 0.08 | 31.5 | 422 | 6.52 | |
| 0 | 0.06 | 24.8 | 284 | 7.26 | |
| 0 | 0.07 | 19.6 | 381 | 6.97 |
| Load Disturbance Amplitude | 0.1 pu | 0.2 pu | 0.3 pu | 0.4 pu | |
|---|---|---|---|---|---|
| AGC units of Area 1 | 0.05 pu | 0.05 pu | 0.05 pu | 0.05 pu | |
| 0.0 pu | 0.03 pu | 0.08 pu | 0.08 pu | ||
| 0.05 pu | 0.12 pu | 0.12 pu | 0.12 pu | ||
| AGC units of Area 2 | 0.0 pu | 0.0 pu | 0.0 pu | 0.04 pu | |
| 0.0 pu | 0.0 pu | 0.0 pu | 0.01 pu | ||
| 0.0 pu | 0.0 pu | 0.0 pu | 0.0 pu | ||
| AGC units of Area 3 | 0.0 pu | 0.0 pu | 0.0 pu | 0.0 pu | |
| 0.0pu | 0.0pu | 0.05 pu | 0.06 pu | ||
| 0.0pu | 0.0pu | 0.0 pu | 0.04 pu | ||
| Output | Maximum Deviation | Frequency Root Mean Square Error | ||
|---|---|---|---|---|
| MPC Using TBC Mode | BMPC | MPC Using TBC Mode | BMPC | |
| /Hz | 0.057 | 0.018 | 0.018 | 0.005 |
| /Hz | 0.079 | 0.010 | 0.025 | 0.003 |
| /Hz | 0.029 | 0.009 | 0.010 | 0.003 |
| /pu | 0.143 | 0.048 | 0.055 | 0.028 |
| /pu | 0.278 | 0.056 | 0.042 | 0.012 |
| /pu | 0.219 | 0.062 | 0.085 | 0.020 |
| /pu | 0.297 | 0.093 | 0.035 | 0.011 |
| /pu | 0.598 | 0.819 | 0.035 | 0.015 |
| /pu | 0.405 | 0.068 | 0.029 | 0.010 |
| /pu | 0.585 | 0.039 | 0.018 | 0.004 |
| Method | System Operating Cost Increment ($) |
|---|---|
| MPC using TBC mode | 19,279.50 |
| BMPC | 10,545.30 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, C.; Liu, H. Bi-Level Model Predictive Control for Optimal Coordination of Multi-Area Automatic Generation Control Units under Wind Power Integration. Processes 2019, 7, 669. https://doi.org/10.3390/pr7100669
Xia C, Liu H. Bi-Level Model Predictive Control for Optimal Coordination of Multi-Area Automatic Generation Control Units under Wind Power Integration. Processes. 2019; 7(10):669. https://doi.org/10.3390/pr7100669
Chicago/Turabian StyleXia, Chuan, and Huijia Liu. 2019. "Bi-Level Model Predictive Control for Optimal Coordination of Multi-Area Automatic Generation Control Units under Wind Power Integration" Processes 7, no. 10: 669. https://doi.org/10.3390/pr7100669
APA StyleXia, C., & Liu, H. (2019). Bi-Level Model Predictive Control for Optimal Coordination of Multi-Area Automatic Generation Control Units under Wind Power Integration. Processes, 7(10), 669. https://doi.org/10.3390/pr7100669




