Numerical Simulation of Darcy–Forchheimer 3D Unsteady Nanofluid Flow Comprising Carbon Nanotubes with Cattaneo–Christov Heat Flux and Velocity and Thermal Slip Conditions
Abstract
:1. Introduction
2. Modeling of Constitutive Equations
3. Similarity Transformation
4. Variables of Engineering Interest
5. Applied Numerical Scheme
6. Outcomes with Arguments
7. Conclusions
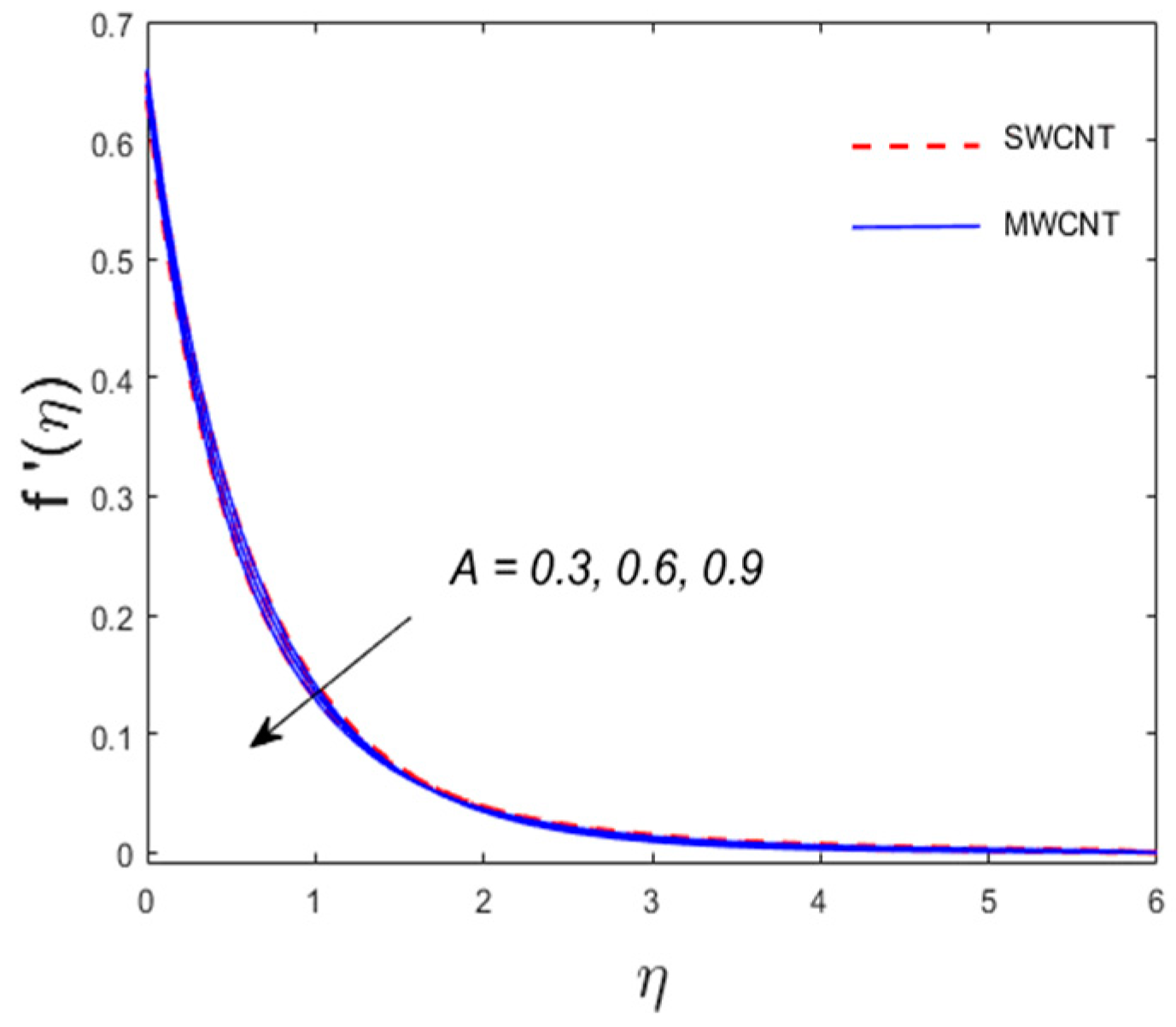
- The velocity component decreases while enhances for .
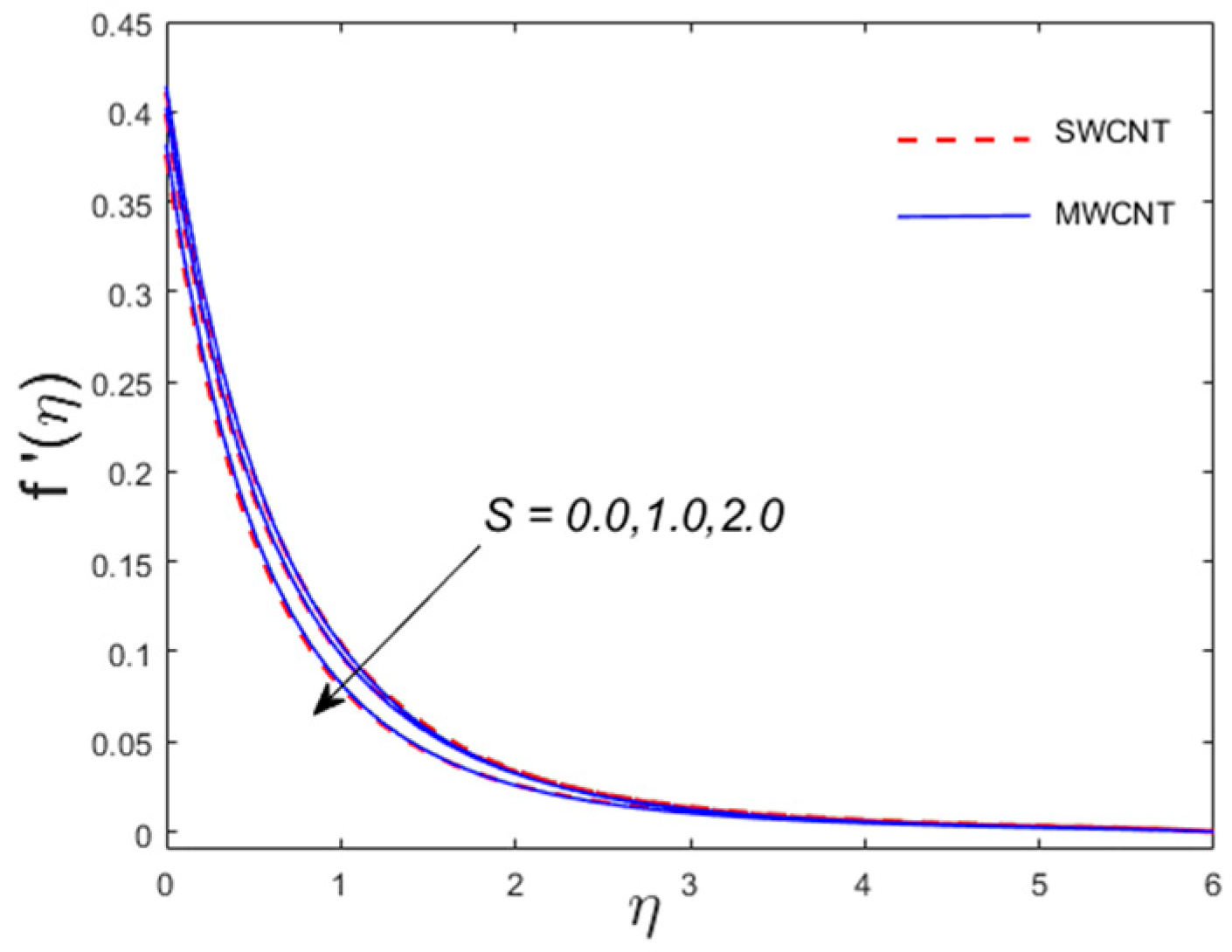
- The velocity profiles and have the same behavior for (unsteadiness parameter), while the opposite behavior is witnessed for the temperature profile.
- The thickness of thermal boundary layer decreases for the values of the Prandtl number, while the rate of heat transfer is boosted.
- The temperature shows a decreasing tendency for the thermal slip factor .
- The rate of shear stress increases for the inertia coefficient and porosity parameter and decreases versus the rotating factor for both SWCNT and MWCNT nanoparticles.
- The Nusselt number declines versus thermal slip parameter and relaxation time for both CNTs.
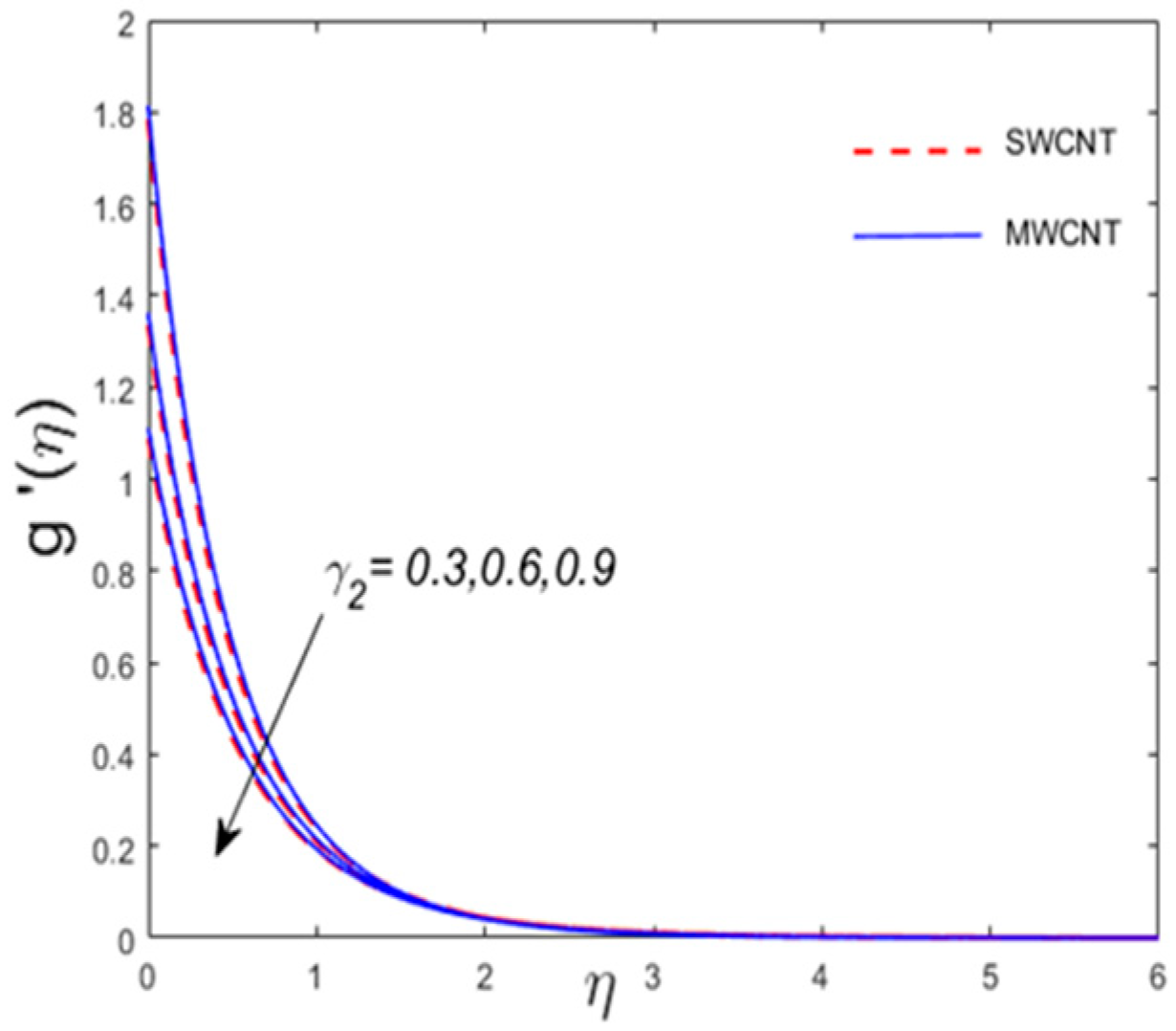
- The skin friction coefficients along x- and y-axes show opposite trend for the values of and
- The Nusselt number depicts similar behavior for escalating estimates of and
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbols | Description | Greek symbols | |
| along x-axis velocity component | Symbols | Description | |
| along y-axis velocity component | density of nanoparticle | ||
| permeability of porous medium | kinematic viscosity | ||
| the inertia coefficient of porous medium. | dynamic viscosity | ||
| porosity parameter, | shear stress along y-axis | ||
| Prandtl number | modified thermal diffusivity | ||
| unsteadiness parameter | velocity slip parameter | ||
| inertia coefficient | thermal slip parameter. | ||
| local Rayleigh number | constant angular velocity | ||
| ratio parameter | Nanofluid heat capacity | ||
| Specific heat | Dimensionless temperature function | ||
| surface drag force | local rotation parameter | ||
| Nusselt number | thermal relaxation time | ||
| Shear stress along x-axis | |||
References
- Fourier, J. Theorie Analytique de la Chaleur; Fourier, P.M., Ed.; Chez Firmin Didot, pére et fils; Cambridge University Press: Cambridge, UK, 1822. [Google Scholar]
- Cattaneo, C. Sulla Conduzione del Calore; Atti Sem. Mat. Fis. Univ. Modena 3; Springer: Berlin/Heidelberg, Germany, 1948; pp. 83–101. [Google Scholar]
- Christov, C. On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Oldroyd, J.G. On the formulation of rheological equations of state. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1950, 200, 523–541. [Google Scholar]
- Tibullo, V.; Zampoli, V. A uniqueness result for the Cattaneo–Christov heat conduction model applied to incompressible fluids. Mech. Res. Commun. 2011, 38, 77–79. [Google Scholar] [CrossRef]
- Ciarletta, M.; Straughan, B. Uniqueness and structural stability for the Cattaneo—Christov equations. Mech. Res. Commun. 2010, 37, 445–447. [Google Scholar] [CrossRef]
- Straughan, B. Thermal convection with the Cattaneo—Christov model. Int. J. Heat Mass Transf. 2010, 53, 95–98. [Google Scholar] [CrossRef]
- Alebraheem, J.; Ramzan, M. Flow of nanofluid with Cattaneo—Christov heat flux model. Appl. Nanosci. 2019, 1–11. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; Mohammad, M.; Howari, F.; Chung, J.D. A Thin Film Flow of Nanofluid Comprising Carbon Nanotubes Influenced by Cattaneo-Christov Heat Flux and Entropy Generation. Coatings 2019, 9, 296. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D. Influence of homogeneous-heterogeneous reactions on MHD 3D Maxwell fluid flow with Cattaneo-Christov heat flux and convective boundary condition. J. Mol. Liq. 2017, 230, 415–422. [Google Scholar] [CrossRef]
- Lu, D.; Li, Z.; Ramzan, M.; Shafee, A.; Chung, J.D. Unsteady squeezing carbon nanotubes based nano-liquid flow with Cattaneo–Christov heat flux and homogeneous–heterogeneous reactions. Appl. Nanosci. 2019, 9, 169–178. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Lockwood, F.E.; Grulke, E.A.; Zhang, Z.G.; Yu, W. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Ramasubramaniam, R.; Chen, J.; Liu, H. Homogeneous carbon nanotube/polymer composites for electrical applications. Appl. Phys. Lett. 2003, 83, 2928. [Google Scholar] [CrossRef]
- Kamali, R.; Binesh, A. Numerical investigation of heat transfer enhancement using carbon nanotube-based non-Newtonian nanofluids. Int. Commun. Heat Mass Transf. 2010, 37, 1153–1157. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, J.; Zhang, X.; Chen, Y. Heat transfer and pressure drop of nanofluids containing carbon nanotubes in laminar flows. Exp. Therm. Fluid Sci. 2013, 44, 716–721. [Google Scholar] [CrossRef]
- Haq, R.; Hammouch, Z.; Khan, A. Water-based squeezing flow in the presence of carbon nanotubes between two parallel disks. Therm. Sci. 2016, 20, 1973–1981. [Google Scholar] [CrossRef]
- Ramzan, M.; Mohammad, M.; Howari, F.; Chung, J.D. Entropy Analysis of Carbon Nanotubes Based Nanofluid Flow Past a Vertical Cone with Thermal Radiation. Entropy 2019, 21, 642. [Google Scholar] [CrossRef]
- Bilal, M.; Ramzan, M. Hall current effect on unsteady rotational flow of carbon nanotubes with dust particles and nonlinear thermal radiation in Darcy–Forchheimer porous media. J. Therm. Anal. Calorim. 2019, 1–11. [Google Scholar] [CrossRef]
- Muhammad, T.; Lu, D.-C.; Mahanthesh, B.; Eid, M.R.; Ramzan, M.; Dar, A. Significance of Darcy-Forchheimer Porous Medium in Nanofluid Through Carbon Nanotubes. Commun. Theor. Phys. 2018, 70, 361. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; Ahmad, S.; Chung, J.D.; Farooq, U. Upshot of binary chemical reaction and activation energy on carbon nanotubes with Cattaneo-Christov heat flux and buoyancy effects. Phys. Fluids 2017, 29, 123103. [Google Scholar] [CrossRef]
- Hayat, T.; Haider, F.; Muhammad, T.; Alsaedi, A. Numerical treatment for Darcy-Forchheimer flow of carbon nanotubes due to an exponentially stretching curved surface. J. Central South Univ. 2019, 26, 865–872. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Wakif, A.; Hussanan, A. Second Law Analysis of Dissipative Nanofluid Flow over a Curved Surface in the Presence of Lorentz Force: Utilization of the Chebyshev—Gauss—Lobatto Spectral Method. Nanomater 2019, 9, 195. [Google Scholar] [CrossRef]
- Kumanek, B.; Wasiak, T.; Stando, G.; Stando, P.; Łukowiec, D.; Janas, D. Simple Method to Improve Electrical Conductivity of Films Made from Single-Walled Carbon Nanotubes. Nanomater 2019, 9, 1113. [Google Scholar] [CrossRef] [PubMed]
- Boscarino, S.; Filice, S.; Sciuto, A.; Libertino, S.; Scuderi, M.; Galati, C.; Scalese, S. Investigation of ZnO-decorated CNTs for UV Light Detection Applications. Nanomater 2019, 9, 1099. [Google Scholar] [CrossRef] [PubMed]
- Kemelbay, A.; Tikhonov, A.; Aloni, S.; Kuykendall, T.R. Conformal High-K Dielectric Coating of Suspended Single-Walled Carbon Nanotubes by Atomic Layer Deposition. Nanomater 2019, 9, 1085. [Google Scholar] [CrossRef] [PubMed]
- Bajpai, A.; Carlotti, S. The Effect of Hybridized Carbon Nanotubes, Silica Nanoparticles, and Core-Shell Rubber on Tensile, Fracture Mechanics and Electrical Properties of Epoxy Nanocomposites. Nanomater 2019, 9, 1057. [Google Scholar] [CrossRef] [PubMed]
- Forchheimer, P. Wasserbewegung durch boden. Zeitschrift fur Acker und Pflanzenbau 1901, 45, 1782–1788. [Google Scholar]
- Muskat, M. The Flow of Homogeneous Fluids Through Porous Media. Soil Sci. 1938, 46, 169. [Google Scholar] [CrossRef]
- Seddeek, M. Influence of viscous dissipation and thermophoresis on Darcy–Forchheimer mixed convection in a fluid saturated porous media. J. Colloid Interface Sci. 2006, 293, 137–142. [Google Scholar] [CrossRef] [PubMed]
- Pal, D.; Mondal, H. Hydromagnetic convective diffusion of species in Darcy–Forchheimer porous medium with non-uniform heat source/sink and variable viscosity. Int. Commun. Heat Mass Transf. 2012, 39, 913–917. [Google Scholar] [CrossRef]
- Waqas, M.; Hayat, T.; Alsaedi, A. A theoretical analysis of SWCNT–MWCNT and H2O nanofluids considering Darcy–Forchheimer relation. Appl. Nanosci. 2019, 9, 1183–1191. [Google Scholar] [CrossRef]
- Sadiq, M.A.; Waqas, M.; Hayat, T.; Alsaedi, A. Modeling and analysis of Maxwell nanofluid considering mixed convection and Darcy–Forchheimer relation. Appl. Nanosci. 2019, 9, 1155–1162. [Google Scholar] [CrossRef]
- Rashid, S.; Hayat, T.; Qayyum, S.; Ayub, M.; Alsaedi, A. Three-dimensional rotating Darcy–Forchheimer flow with activation energy. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 935–948. [Google Scholar] [CrossRef]
- Farooq, M.; Ahmad, S.; Javed, M.; Anjum, A. Melting heat transfer in squeezed nanofluid flow through Darcy Forchheimer medium. J. Heat Transf. 2019, 141, 012402. [Google Scholar] [CrossRef]
- Nasir, S.; Shah, Z.; Islam, S.; Bonyah, E.; Gul, T. Darcy Forchheimer nanofluid thin film flow of SWCNTs and heat transfer analysis over an unsteady stretching sheet. AIP Adv. 2019, 9, 015223. [Google Scholar] [CrossRef] [Green Version]
- Montessori, A.; Prestininzi, P.; La Rocca, M.; Succi, S. Lattice Boltzmann approach for complex nonequilibrium flows. Phys. Rev. E 2015, 92, 043308. [Google Scholar] [CrossRef] [PubMed]
- Montessori, A.; Amadei, C.A.; Falcucci, G.; Sega, M.; Vecitis, C.D.; Succi, S. Extended friction elucidates the breakdown of fast water transport in graphene oxide membranes. EPL 2017, 116, 54002. [Google Scholar] [CrossRef]
- Montessori, A.; Prestininzi, P.; La Rocca, M.; Falcucci, G.; Succi, S.; Kaxiras, E. Effects of Knudsen diffusivity on the effective reactivity of nanoporous catalyst media. J. Comput. Sci. 2016, 17, 377–383. [Google Scholar] [CrossRef] [Green Version]








| Physical Properties | Base Fluid | Nanoparticles | |
|---|---|---|---|
| Engine oil | MWCNTs | SWCNTs | |
| Cp (J/kgK) | 1910 | 796 | 425 |
| (kg/m3) | 884 | 1600 | 2600 |
| K (W/mK) | 0.144 | 3000 | 6600 |
| SWCNTs | MWCNTs | SWCNTs | MWCNTs | ||||||
| 0.0 | 0.1 | 0.1 | 0.2 | 0.3 | 0.1 | 1.6916 | 1.6916 | 1.4286 | 1.4286 |
| 0.05 | 1.9014 | 1.8698 | 1.6087 | 1.5861 | |||||
| 0.1 | 2.1549 | 1.9754 | 1.8169 | 1.7696 | |||||
| 0.2 | 1.921 | 1.889 | 1.6211 | 1.5983 | |||||
| 0.4 | 1.9592 | 1.9263 | 1.6452 | 1.6220 | |||||
| 0.6 | 1.996 | 1.9624 | 1.6683 | 1.6448 | |||||
| 0.2 | 1.5926 | 1.5702 | 1.5926 | 1.5702 | |||||
| 0.3 | 1.3741 | 1.3573 | 1.5806 | 1.5583 | |||||
| 0.4 | 1.2105 | 1.1973 | 1.5712 | 1.5490 | |||||
| 0.2 | 1.9014 | 1.8698 | 1.6087 | 1.5861 | |||||
| 0.3 | 1.8842 | 1.8529 | 1.3859 | 1.3690 | |||||
| 0.4 | 1.8709 | 1.8397 | 1.2194 | 1.2062 | |||||
| 0.3 | 1.9014 | 1.8698 | 1.6087 | 1.5861 | |||||
| 0.5 | 1.9377 | 1.9071 | 1.6357 | 1.6140 | |||||
| 0.7 | 1.973 | 1.9433 | 1.6618 | 1.6409 | |||||
| 0.1 | 1.9014 | 1.8698 | 1.6087 | 1.5861 | |||||
| 0.3 | 1.7694 | 1.7409 | 1.4791 | 1.4594 | |||||
| 0.4 | 1.6945 | 1.6677 | 1.4087 | 1.3906 | |||||
| SWCNTs | MWCNTs | ||||||||
| 0.0 | 0.1 | 0.1 | 1 | 0.3 | 0.1 | 0.2 | 1 | 0.4515 | 0.4515 |
| 0.05 | 1.1944 | 1.1139 | |||||||
| 0.1 | 2.4895 | 2.2247 | |||||||
| 0.2 | 1.1924 | 1.1120 | |||||||
| 0.4 | 1.1886 | 1.1084 | |||||||
| 0.6 | 1.1852 | 1.1051 | |||||||
| 0.2 | 1.1425 | 1.0647 | |||||||
| 0.3 | 1.1143 | 1.0388 | |||||||
| 0.4 | 1.0987 | 1.0250 | |||||||
| 1 | 1.1944 | 1.1139 | |||||||
| 1.3 | 1.0180 | 0.9515 | |||||||
| 1.5 | 0.9267 | 0.8673 | |||||||
| 0.3 | 1.1944 | 1.1139 | |||||||
| 0.5 | 1.1853 | 1.1049 | |||||||
| 0.7 | 1.7720 | 1.0969 | |||||||
| 0.1 | 1.1944 | 1.1139 | |||||||
| 0.3 | 1.2330 | 1.1489 | |||||||
| 0.4 | 1.2630 | 1.1772 | |||||||
| 0.2 | 1.1944 | 1.1139 | |||||||
| 0.4 | 1.3589 | 1.2734 | |||||||
| 0.6 | 1.4573 | 1.3690 | |||||||
| 1 | 1.1944 | 1.1139 | |||||||
| 1.3 | 1.2644 | 1.1808 | |||||||
| 1.5 | 1.3016 | 1.2163 | |||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, J.u.; Khan, U.; Ahmad, S.; Ramzan, M.; Suleman, M.; Lu, D.; Inam, S. Numerical Simulation of Darcy–Forchheimer 3D Unsteady Nanofluid Flow Comprising Carbon Nanotubes with Cattaneo–Christov Heat Flux and Velocity and Thermal Slip Conditions. Processes 2019, 7, 687. https://doi.org/10.3390/pr7100687
Rahman Ju, Khan U, Ahmad S, Ramzan M, Suleman M, Lu D, Inam S. Numerical Simulation of Darcy–Forchheimer 3D Unsteady Nanofluid Flow Comprising Carbon Nanotubes with Cattaneo–Christov Heat Flux and Velocity and Thermal Slip Conditions. Processes. 2019; 7(10):687. https://doi.org/10.3390/pr7100687
Chicago/Turabian StyleRahman, Jamshaid ul, Umair Khan, Shafiq Ahmad, Muhammad Ramzan, Muhammad Suleman, Dianchen Lu, and Saba Inam. 2019. "Numerical Simulation of Darcy–Forchheimer 3D Unsteady Nanofluid Flow Comprising Carbon Nanotubes with Cattaneo–Christov Heat Flux and Velocity and Thermal Slip Conditions" Processes 7, no. 10: 687. https://doi.org/10.3390/pr7100687
APA StyleRahman, J. u., Khan, U., Ahmad, S., Ramzan, M., Suleman, M., Lu, D., & Inam, S. (2019). Numerical Simulation of Darcy–Forchheimer 3D Unsteady Nanofluid Flow Comprising Carbon Nanotubes with Cattaneo–Christov Heat Flux and Velocity and Thermal Slip Conditions. Processes, 7(10), 687. https://doi.org/10.3390/pr7100687






