Optimization of Microwave Coupled Hot Air Drying for Chinese Yam Using Response Surface Methodology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Apparatus
2.3. Experimental Procedure
2.4. Determination of RR
2.5. Determination of TSC
2.6. Experimental Design, Statistical Analysis, and Optimization
3. Results and Discussion
3.1. Single Factorial Experiment
3.1.1. Effects of Independent Variables on RR
3.1.2. Effects of Independent Variables on TSC
3.2. RSM Experiment
3.2.1. Analysis of RR
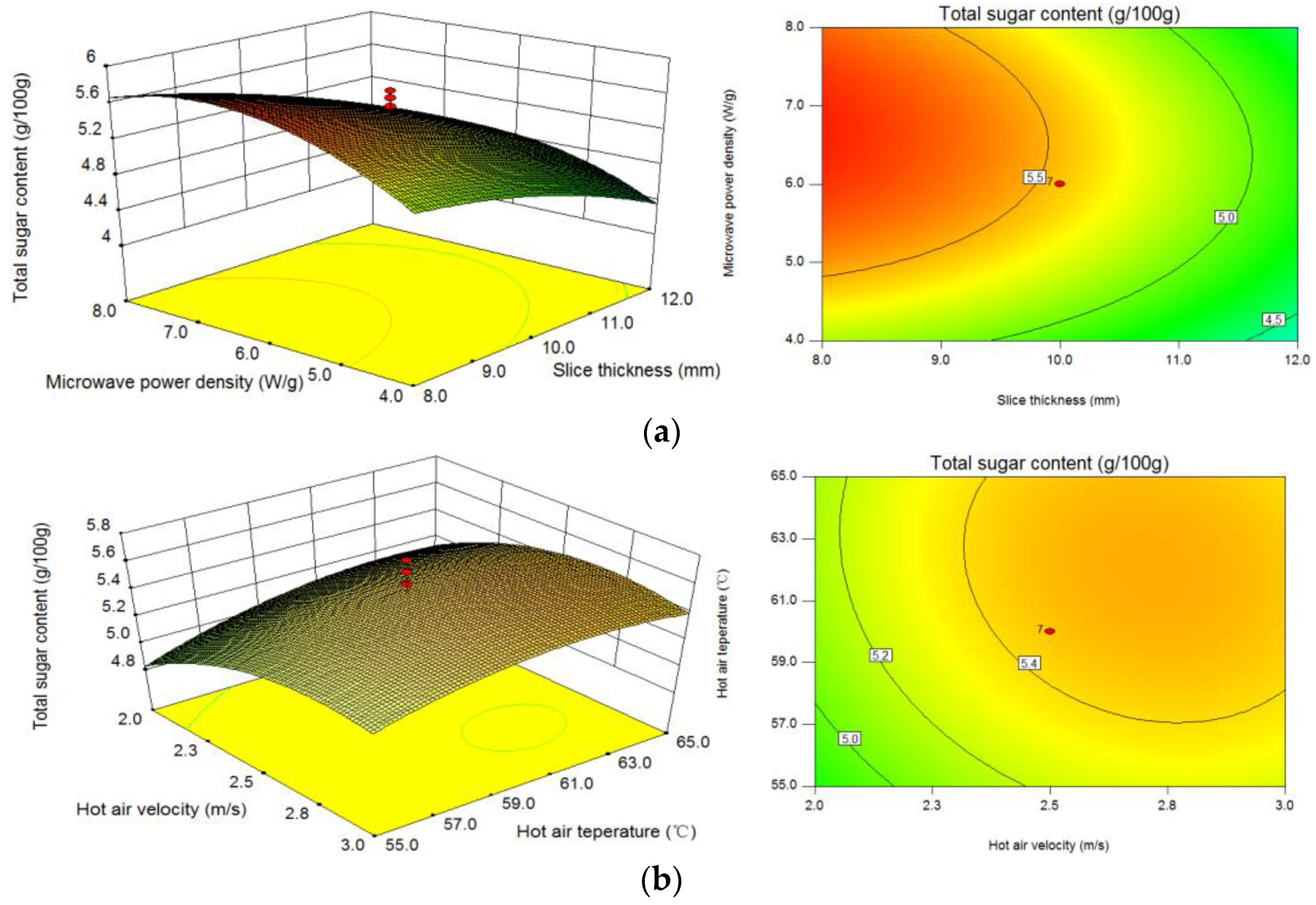
3.2.2. Analysis of TSC
4. Optimization and Model Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, W.; Wang, Y.; Li, X.; Yu, P. Purification and structural characterization of Chinese yam polysaccharide and its activities. Carbohydr. Polym. 2015, 117, 1021–1027. [Google Scholar] [CrossRef] [PubMed]
- Ju, H.-Y.; Zhang, Q.; Mujumdar, A.; Fang, X.-M.; Xiao, H.-W.; Gao, Z.-J. Hot-air Drying Kinetics of Yam Slices under Step Change in Relative Humidity. Int. J. Food Eng. 2016, 12, 783–792. [Google Scholar] [CrossRef]
- Chen, Y.-F.; Zhu, Q.; Wu, S. Preparation of oligosaccharides from Chinese yam and their antioxidant activity. Food Chem. 2015, 173, 1107–1110. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.-H.; Cheng, J.-Y.; Deng, M.-C.; Chou, C.-H.; Jan, T.-R. Prebiotic effect of diosgenin, an immunoactive steroidal sapogenin of the Chinese yam. Food Chem. 2012, 132, 428–432. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-P.; Lee, T.-Y.; Tsen, J.-H.; King, V.A.-E. Dehydration of yam slices using FIR-assisted freeze drying. J. Food Eng. 2007, 79, 1295–1301. [Google Scholar] [CrossRef]
- Xiao, H.; Yao, X.; Lin, H.; Yang, W.; Meng, J.; GAO, Z. Effect of SSB (superheated steam blanching) time and drying temperature on hot air impingement drying kinetics and quality attributes of yam slices. J. Food Process Eng. 2012, 35, 370–390. [Google Scholar] [CrossRef]
- Ju, H.; El-Mashad, H.M.; Fang, X.; Pan, Z.; Xiao, H.; Liu, Y.; Gao, Z. Drying characteristics and modeling of yam slices under different relative humidity conditions. Dry. Technol. 2016, 34, 296–306. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, W.; Li, X.; Jiang, Q.; Xia, Y.; Wang, H.; Huang, L.; Guo, L. Effect of different drying methods on the physicochemical and functional properties of Dioscorea opposita Thunb. starch. Starch-Stärke 2013, 65, 219–226. [Google Scholar] [CrossRef]
- Song, X.; Hu, H.; Zhang, B.; Xiaoyong, S.; Hao, H.; Baoling, Z. Drying characteristics of Chinese Yam (Dioscorea opposita Thunb.) by far-infrared radiation and heat pump. J. Saudi Soc. Agric. Sci. 2018, 17, 290–296. [Google Scholar] [CrossRef]
- Li, L.; Zhang, M.; Bhandari, B. Influence of drying methods on some physicochemical, functional and pasting properties of Chinese yam flour. LWT 2019, 111, 182–189. [Google Scholar] [CrossRef]
- Zhao, D.; An, K.; Ding, S.; Liu, L.; Xu, Z.; Wang, Z. Two-Stage Intermittent Microwave Coupled with Hot-Air Drying of Carrot Slices: Drying Kinetics and Physical Quality. Food Bioprocess Technol. 2014, 7, 2308–2318. [Google Scholar] [CrossRef]
- Tian, Y.; Liang, J.; Zeng, H.; Zheng, B. Microwave Drying Characteristics and Kinetics of Lotus (Nelumbo nucifera Gaertn.) Seeds. Int. J. Food Eng. 2013, 9, 91–98. [Google Scholar] [CrossRef]
- Thuto, W.; Banjong, K. Investigation of Heat and Moisture Transport in Bananas during Microwave Heating Process. Processes 2019, 7, 545. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, M.; Fang, Z.; Mujumdar, A.S.; Jiang, H.; Qian, H.; Ai, H. Drying kinetics and product quality of green soybean under different microwave drying methods. Dry. Technol. 2017, 35, 240–248. [Google Scholar] [CrossRef]
- Motavali, A.; Najafi, G.H.; Abbasi, S.; Minaei, S.; Ghaderi, A. Microwave–vacuum drying of sour cherry: Comparison of mathematical models and artificial neural networks. J. Food Sci. Technol. 2013, 50, 714–722. [Google Scholar] [CrossRef]
- Andrés, A.M.; Fito, P.; Heredia, A.; Rosa, E.M. Combined Drying Technologies for Development of High-Quality Shelf-Stable Mango Products. Dry. Technol. 2007, 25, 1857–1866. [Google Scholar] [CrossRef]
- An, K.; Zhao, D.; Wang, Z.; Wu, J.; Xu, Y.; Xiao, G. Comparison of different drying methods on Chinese ginger (Zingiber officinale Roscoe): Changes in volatiles, chemical profile, antioxidant properties, and microstructure. Food Chem. 2016, 197, 1292–1300. [Google Scholar] [CrossRef]
- Gowen, A.; Abu-Ghannam, N.; Frias, J.; Oliveira, J. Optimisation of dehydration and rehydration properties of cooked chickpeas (Cicer arietinum L.) undergoing microwave–hot air combination drying. Trends Food Sci. Technol. 2006, 17, 177–183. [Google Scholar] [CrossRef]
- Gowen, A.; Abu-Ghannam, N.; Frias, J.; Oliveira, J.; Gowen, A. Modeling dehydration and rehydration of cooked soybeans subjected to combined microwave–hot-air drying. Innov. Food Sci. Emerg. Technol. 2008, 9, 129–137. [Google Scholar] [CrossRef]
- Pu, G.; Song, G.; Song, C.; Wang, J. Analysis of thermal effect using Coupled Hot-air and Microwave heating at different position of potato. Innov. Food Sci. Emerg. Technol. 2017, 41, 244–250. [Google Scholar] [CrossRef]
- Varith, J.; Dijkanarukkul, P.; Achariyaviriya, A.; Achariyaviriya, S. Combined microwave-hot air drying of peeled longan. J. Food Eng. 2007, 81, 459–468. [Google Scholar] [CrossRef]
- Talens, C.; Castro-Giraldez, M.; Fito, P.J. Effect of Microwave Power Coupled with Hot Air Drying on Sorption Isotherms and Microstructure of Orange Peel. Food Bioprocess Technol. 2018, 11, 723–734. [Google Scholar] [CrossRef]
- Šumić, Z.; Vakula, A.; Tepić, A.; Čakarević, J.; Vitas, J.; Pavlić, B. Modeling and optimization of red currants vacuum drying process by response surface methodology (RSM). Food Chem. 2016, 203, 465–475. [Google Scholar] [CrossRef] [PubMed]
- Noshad, M.; Mohebbi, M.; Shahidi, F.; Mortazavi, S.A. Multi-objective optimization of osmotic–ultrasonic pretreatments and hot-air drying of quince using response surface methodology. Food Bioprocess Technol. 2012, 5, 2098–2110. [Google Scholar] [CrossRef]
- Erbay, Z.; Icier, F. Optimization of hot air drying of olive leaves using response surface methodology. J. Food Eng. 2009, 91, 533–541. [Google Scholar] [CrossRef]
- Kumar, D.; Prasad, S.; Murthy, G.S. Optimization of microwave-assisted hot air drying conditions of okra using response surface methodology. J. Food Sci. Technol. 2014, 51, 221–232. [Google Scholar] [CrossRef]
- Šumić, Z.; Tepić, A.; Vidović, S.; Jokić, S.; Malbasa, R. Optimization of frozen sour cherries vacuum drying process. Food Chem. 2013, 136, 55–63. [Google Scholar] [CrossRef]
- Yu, H.; Zuo, C.; Xie, Q. Parameter optimization for microwave coupled with hot air drying process of hawthorn slices using response-surface methodology. Int. J. Agric. Biol. Eng. 2015, 8, 121–134. [Google Scholar] [CrossRef]
- Alam, M.S.; Amarjit, S.; Sawhney, B.K. Response surface optimization of osmotic dehydration process for aonla slices. J. Food Sci. Technol. 2010, 47, 47–54. [Google Scholar] [CrossRef] [Green Version]
- Aksoy, A.; Karasu, S.; Akcicek, A.; Kayacan, S. Effects of Different Drying Methods on Drying Kinetics, Microstructure, Color, and the Rehydration Ratio of Minced Meat. Foods 2019, 8, 216. [Google Scholar] [CrossRef]
- Laurence, Y.M.; Sanagi, M.M.; Khan, M.S.; Majid, M.H.A.; Sarjadi, M.S. Effect of drying methods on the colour parameter, rehydration capacity and antioxidant activity of clinacanthus nutans leaves. Malays. J. Chem. 2019, 21, 62–69. [Google Scholar]
- GB/T 10782-2006. General Rule for Preserved Fruits (In Chinese). Available online: https://books.google.com.ph/books/about/GB_T_10782_2006_Translated_English_of_Ch.html?id=JX0kDwAAQBAJ&redir_esc=y (accessed on 10 May 2018).
- Zhang, J.; Ma, Q.; He, F.; Qu, F.; Li, W. Analysis of moisture and total sugar content of Huizao based on surface images. Int. J. Agric. Biol. Eng. 2017, 11, 238–243. [Google Scholar] [CrossRef]
- Cui, X.; Yang, J.; Shi, X.; Lei, W.; Huang, T.; Bai, C. Pelletization of Sunflower Seed Husks: Evaluating and Optimizing Energy Consumption and Physical Properties by Response Surface Methodology (RSM). Processes 2019, 7, 591. [Google Scholar] [CrossRef]
- Le, X.D.; Nguyen, M.C.; Vu, D.H.; Pham, M.Q.; Pham, Q.L.; Nguyen, Q.T.; Nguyen, T.A.; Pham, V.T.; Bach, L.G.; Nguyen, T.V.; et al. Optimization of Microwave-Assisted Extraction of Total Phenolic and Total Flavonoid from Fruits of Docynia indica (Wall.) Decne. Using Response Surface Methodology. Processes 2019, 7, 485. [Google Scholar] [CrossRef]
- Eren, I.; Kaymak-Ertekin, F. Optimization of osmotic dehydration of potato using response surface methodology. J. Food Eng. 2007, 79, 344–352. [Google Scholar] [CrossRef]
- Shi, Q.-L.; Xue, C.-H.; Zhao, Y.; Li, Z.-J.; Wang, X.-Y.; Luan, D.-L. Optimization of processing parameters of horse mackerel (Trachurus japonicus) dried in a heat pump dehumidifier using response surface methodology. J. Food Eng. 2008, 87, 74–81. [Google Scholar] [CrossRef]
- Han, Q.-H.; Yin, L.-J.; Li, S.-J.; Yang, B.-N.; Ma, J.-W. Optimization of Process Parameters for Microwave Vacuum Drying of Apple Slices Using Response Surface Method. Dry. Technol. 2010, 28, 523–532. [Google Scholar] [CrossRef]
- Giri, S.K.; Prasad, S. Optimization of Microwave-Vacuum Drying of Button Mushrooms Using Response-Surface Methodology. Dry. Technol. 2007, 25, 901–911. [Google Scholar] [CrossRef]
- Sharma, G.; Prasad, S. Drying of garlic (Allium sativum) cloves by microwave–hot air combination. J. Food Eng. 2001, 50, 99–105. [Google Scholar] [CrossRef]
- Seremet, L.; Botez, E.; Nistor, O.-V.; Andronoiu, D.G.; Mocanu, G.-D. Effect of different drying methods on moisture ratio and rehydration of pumpkin slices. Food Chem. 2016, 195, 104–109. [Google Scholar] [CrossRef]





| Variables | Levels | ||||||
|---|---|---|---|---|---|---|---|
| Slice Thickness/St (mm) | 4.0 | 6.0 | 8.0 | 10.0 | 12.0 | 14.0 | 16.0 |
| Hot air velocity/Hv (m/s) | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 |
| Hot air temperature/Ht (°C) | 45.0 | 50.0 | 55.0 | 60.0 | 65.0 | 70.0 | 75.0 |
| Microwave power density/Md (W/g) | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 |
| Independent Variables | Symbols | Levels | ||||
|---|---|---|---|---|---|---|
| −2 | −1 | 0 | +1 | +2 | ||
| Slice thickness/St (mm) | x1 | 6.0 | 8.0 | 10.0 | 12.0 | 14.0 |
| Hot-air velocity/Hv (m/s) | x2 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
| Hot-air temperature/Ht (°C) | x3 | 50.0 | 55.0 | 60.0 | 65.0 | 70.0 |
| Microwave power density/Md (W/g) | x4 | 2.0 | 4.0 | 6.0 | 8.0 | 10.0 |
| Run | Variable Levels | RR, y1 (g/g) | TSC, y2 (g/100g) | |||
|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | |||
| 1 | −1 | −1 | −1 | −1 | 1.57 | 4.25 |
| 2 | 1 | −1 | −1 | −1 | 1.24 | 3.75 |
| 3 | −1 | 1 | −1 | −1 | 1.21 | 5.01 |
| 4 | 1 | 1 | −1 | −1 | 1.02 | 4.12 |
| 5 | −1 | −1 | 1 | −1 | 1.82 | 4.87 |
| 6 | 1 | −1 | 1 | −1 | 1.56 | 4.03 |
| 7 | −1 | 1 | 1 | −1 | 1.65 | 5.19 |
| 8 | 1 | 1 | 1 | −1 | 1.31 | 4.52 |
| 9 | −1 | −1 | −1 | 1 | 1.33 | 5.17 |
| 10 | 1 | −1 | −1 | 1 | 1.02 | 4.13 |
| 11 | −1 | 1 | −1 | 1 | 1.22 | 5.43 |
| 12 | 1 | 1 | −1 | 1 | 1.02 | 4.39 |
| 13 | −1 | −1 | 1 | 1 | 1.34 | 5.48 |
| 14 | 1 | −1 | 1 | 1 | 1.18 | 4.52 |
| 15 | −1 | 1 | 1 | 1 | 1.25 | 5.55 |
| 16 | 1 | 1 | 1 | 1 | 1.16 | 4.61 |
| 17 | −2 | 0 | 0 | 0 | 1.52 | 5.89 |
| 18 | 2 | 0 | 0 | 0 | 1.01 | 3.75 |
| 19 | 0 | −2 | 0 | 0 | 1.55 | 4.25 |
| 20 | 0 | 2 | 0 | 0 | 1.33 | 5.02 |
| 21 | 0 | 0 | −2 | 0 | 1.26 | 4.86 |
| 22 | 0 | 0 | 2 | 0 | 1.43 | 4.95 |
| 23 | 0 | 0 | 0 | −2 | 1.18 | 3.65 |
| 24 | 0 | 0 | 0 | 2 | 1.16 | 4.13 |
| 25 | 0 | 0 | 0 | 0 | 1.96 | 5.69 |
| 26 | 0 | 0 | 0 | 0 | 2.01 | 5.52 |
| 27 | 0 | 0 | 0 | 0 | 1.83 | 5.29 |
| 28 | 0 | 0 | 0 | 0 | 1.84 | 5.61 |
| 29 | 0 | 0 | 0 | 0 | 1.79 | 5.45 |
| 30 | 0 | 0 | 0 | 0 | 1.92 | 5.39 |
| 31 | 0 | 0 | 0 | 0 | 1.85 | 5.22 |
| Source | df | RR | TSC | ||||
|---|---|---|---|---|---|---|---|
| Coefficient | Sum of Squares | p-Value | Coefficient | Sum of Squares | p-Value | ||
| Model | 14 | 1.89 | 2.79 | <0.0001 | 5.45 | 12.08 | <0.0001 |
| x1 | 1 | −0.12 | 0.35 | <0.0001 | −0.47 | 5.19 | <0.0001 |
| x2 | 1 | −0.069 | 0.11 | 0.0024 | 0.17 | 0.72 | 0.0002 |
| x3 | 1 | 0.082 | 0.16 | 0.0006 | 0.11 | 0.3 | 0.0075 |
| x4 | 1 | −0.079 | 0.15 | 0.0008 | 0.19 | 0.84 | 0.0001 |
| x1x2 | 1 | 0.015 | 0.0036 | 0.5331 | −0.013 | 0.0025 | 0.7848 |
| x1x3 | 1 | 0.011 | 0.002 | 0.6392 | 0.00375 | 0.000225 | 0.9346 |
| x1x4 | 1 | 0.023 | 0.0081 | 0.3535 | −0.068 | 0.073 | 0.1532 |
| x2x3 | 1 | 0.01 | 0.0016 | 0.6767 | −0.043 | 0.029 | 0.3592 |
| x2x4 | 1 | 0.049 | 0.038 | 0.0549 | −0.079 | 0.099 | 0.0994 |
| x3x4 | 1 | −0.06 | 0.058 | 0.0215 | −0.028 | 0.012 | 0.5499 |
| 1 | −0.15 | 0.69 | <0.0001 | −0.14 | 0.54 | 0.0009 | |
| 1 | −0.11 | 0.35 | <0.0001 | −0.18 | 0.96 | <0.0001 | |
| 1 | −0.13 | 0.52 | <0.0001 | −0.12 | 0.38 | 0.0033 | |
| 1 | −0.18 | 0.91 | <0.0001 | −0.37 | 3.91 | <0.0001 | |
| Residual | 16 | 0.14 | 0.52 | ||||
| Lack of fit | 10 | 0.1 | 0.2779 | 0.35 | 0.4169 | ||
| Pure error | 6 | 0.038 | 0.17 | ||||
| Total | 30 | 2.93 | 12.6 | ||||
| R2 | 0.9516 | 0.9588 | |||||
| CV/% | 6.55 | 3.73 | |||||
| Optimal Drying Conditions | Response Variable | Test Value | Predicted Value |
|---|---|---|---|
| Slice thickness/8.5 mm | RR/(g/g) | 1.83 | 1.90 |
| Hot air velocity/2.5 m/s | |||
| Hot air temperature/61.7 °C | TSC/(g/100 g) | 5.72 | 5.74 |
| Microwave power density/5.9 W/g |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Liu, D.; Yu, H.; Wang, D.; Li, J. Optimization of Microwave Coupled Hot Air Drying for Chinese Yam Using Response Surface Methodology. Processes 2019, 7, 745. https://doi.org/10.3390/pr7100745
Wang H, Liu D, Yu H, Wang D, Li J. Optimization of Microwave Coupled Hot Air Drying for Chinese Yam Using Response Surface Methodology. Processes. 2019; 7(10):745. https://doi.org/10.3390/pr7100745
Chicago/Turabian StyleWang, Hanyang, Dan Liu, Haiming Yu, Donghai Wang, and Jun Li. 2019. "Optimization of Microwave Coupled Hot Air Drying for Chinese Yam Using Response Surface Methodology" Processes 7, no. 10: 745. https://doi.org/10.3390/pr7100745





