Absolute Stability Condition Derivation for Position Closed-Loop System in Hydraulic Automatic Gauge Control
Abstract
:1. Introduction
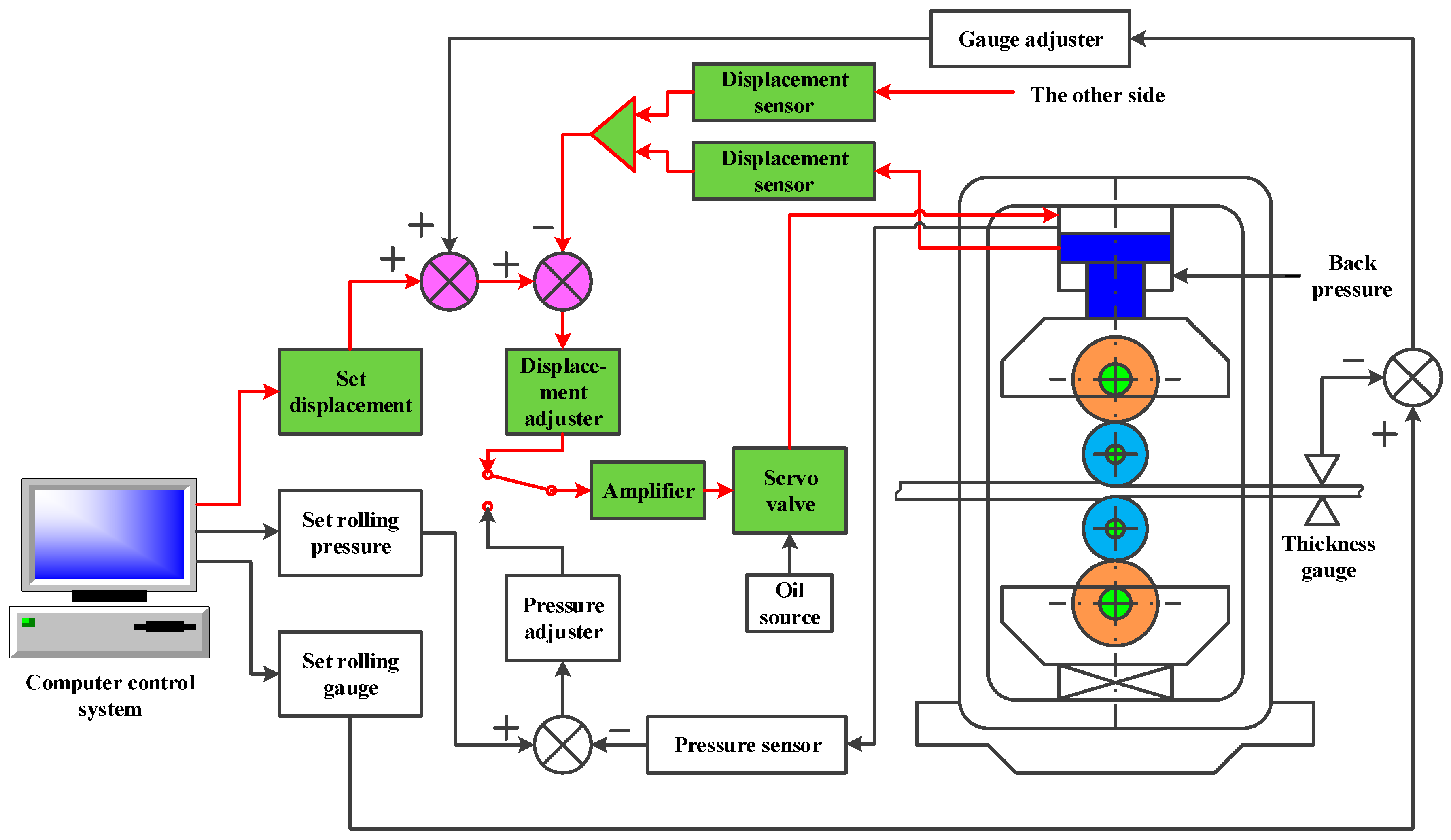
2. Mathematical Model of Position Closed-Loop System
2.1. Mathematical Model of Controller
2.2. Mathematical Model of Servo Amplifier
2.3. Mathematical Model of Hydraulic Power Mechanism
2.3.1. Flow Equation of Electro-Hydraulic Servo Valve
2.3.2. Basic Flow Equation of Hydraulic Cylinder
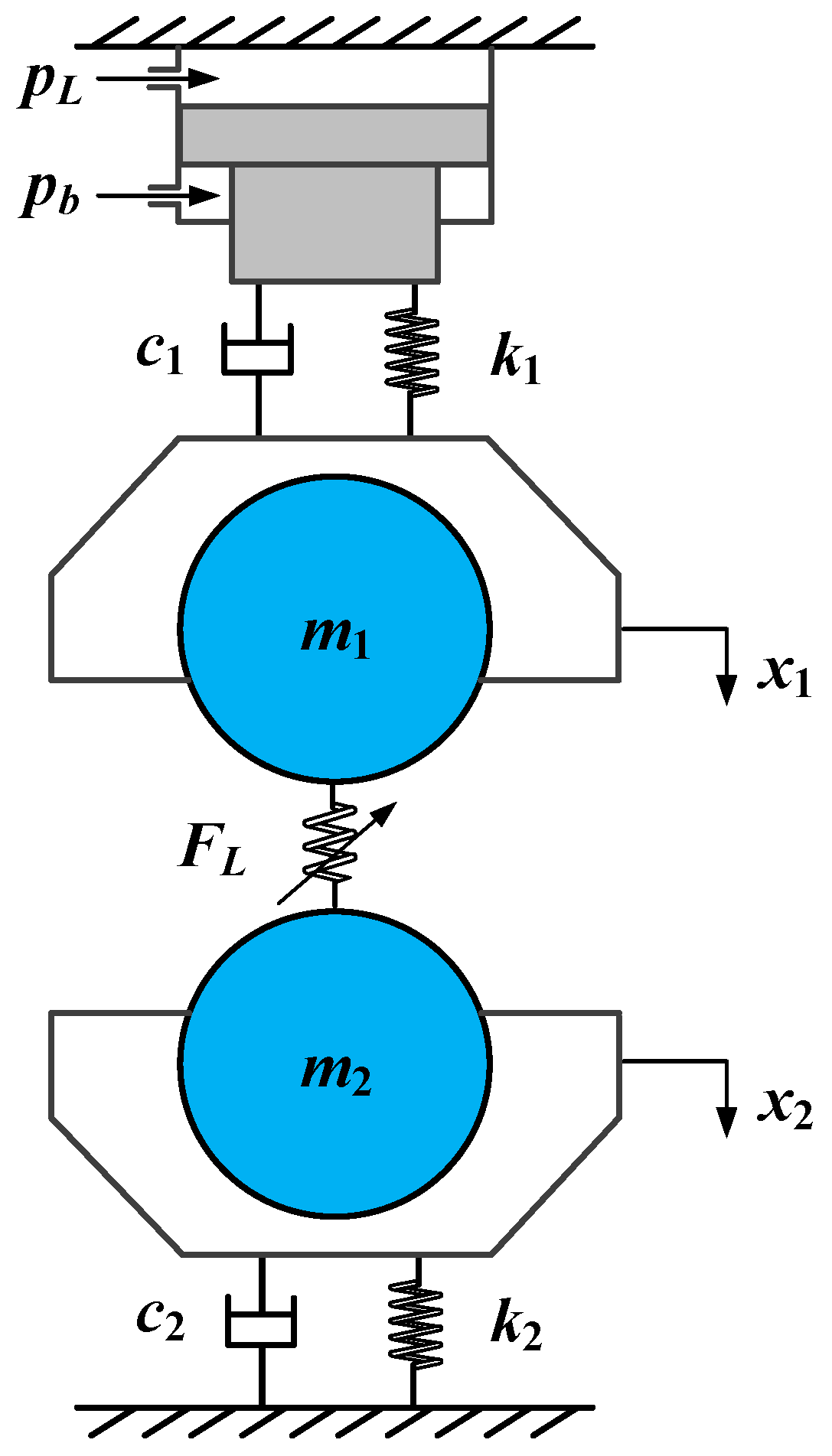
2.4. Mathematical Model of Load
2.5. Mathematical Model of Sensor
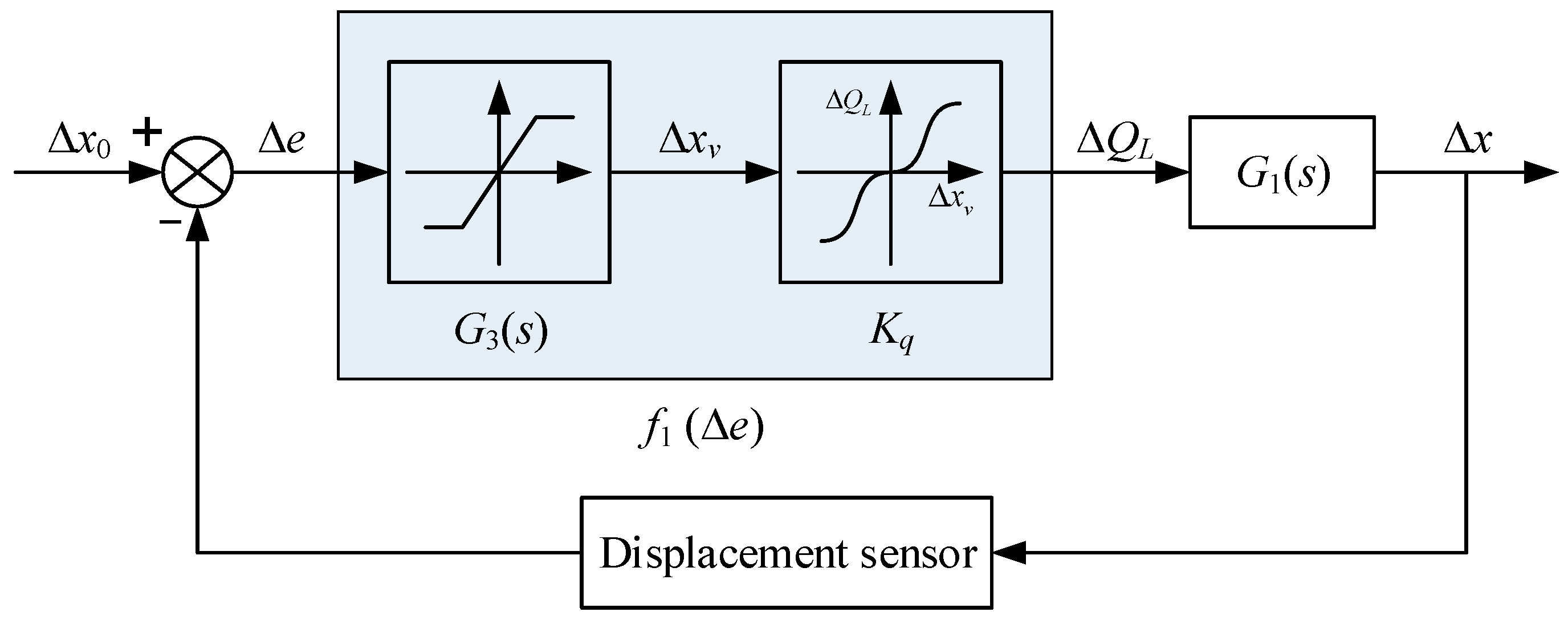
3. Incremental Transfer Model of Position Closed-Loop System
3.1. Incremental Transfer Model of Hydraulic Transmission Part
3.2. Incremental Transfer Model of the Feedback and Control Part
4. Absolute Stability Condition for Position Closed-Loop System
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| HAGC | hydraulic automatic gauge control |
| PID | Proportion-integration-differentiation |
| DOF | degree of freedom |
| Kp | proportionality coefficient |
| Ti | integral time constant |
| Td | differential time constant |
| s | Laplace operator |
| I | output current |
| U | input voltage |
| Ka | amplification coefficient |
| QL | load flow |
| xv | spool displacement |
| Cd | flow coefficient of valve port |
| W | area gradient of valve port |
| ρ | hydraulic oil density |
| ps | oil supply pressure |
| pt | return pressure |
| pL | working pressure of rodless chamber of hydraulic cylinder |
| Ic | input current of servo valve |
| Ksv | amplification coefficient of the spool displacement on the input current |
| ωsv | natural angular frequency of servo valve |
| ξsv | damping coefficient of servo valve |
| IN | rated current of servo valve |
| Ap | effective working area of piston |
| x1 | displacement of piston rod |
| Cip | internal leakage coefficient |
| Cep | external leakage coefficient |
| pb | working pressure of the rod chamber |
| V0 | initial volume of the control chamber |
| βe | bulk modulus of oil |
| m1 | equivalent mass of moving parts of the upper roll system (URS) |
| m2 | equivalent mass of the moving parts of the lower roll system (LRS) |
| c1 | linear damping coefficient of moving parts of URS |
| c2 | linear damping coefficient of moving parts of LRS |
| k1 | linear stiffness coefficient between upper frame beam and moving parts of URS |
| k2 | linear stiffness coefficient between lower frame beam and moving parts of LRS |
| x1 | displacement of URS |
| x2 | displacement of LRS |
| Ab | effective working area of rod chamber piston |
| FL | load force acting on roll system |
| Kx | amplification coefficient of the displacement sensor |
| Tx | time constant of the displacement sensor |
| QLA | the value of load flow at the working point A |
| xvA | the value of spool displacement at the working point A |
| pLA | the value of working pressure at the working point A |
| x1A | the value of piston rod displacement at the working point A |
| ΔQL | disturbance quantity of load flow at the working point A |
| Δxv | disturbance quantity of spool displacement at the working point A |
| ΔpL | disturbance quantity of working pressure at the working point A |
| Δx | disturbance quantity of piston rod displacement at the working point A |
| Kq | flow gain |
| Kc | flow–pressure coefficient |
| Kce | total flow–pressure coefficient |
References
- Tang, S.N.; Zhu, Y.; Li, W.; Cai, J.X. Status and prospect of research in preprocessing methods for measured signals in mechanical systems. J. Drain. Irrig. Mach. Eng. 2019, 37, 822–828. [Google Scholar]
- Tang, B.; Jiang, H.; Gong, X. Optimal design of variable assist characteristics of electronically controlled hydraulic power steering system based on simulated annealing particle swarm optimisation algorithm. Int. J. Veh. Des. 2017, 73, 189–207. [Google Scholar] [CrossRef]
- He, R.; Liu, X.; Liu, C. Brake performance analysis of ABS for eddy current and electrohydraulic hybrid brake system. Math. Probl. Eng. 2013, 2013, 979384. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Han, X.J.; Bi, Q.S. Dynamical behavior analysis and bifurcation mechanism of a new 3- D nonlinear periodic switching system. Nonlinear Dyn. 2013, 73, 1873–1881. [Google Scholar] [CrossRef]
- Roman, N.; Ceanga, E.; Bivol, I.; Caraman, S. Adaptive automatic gauge control of a cold strip rolling process. Adv. Electr. Comput. Eng. 2010, 10, 7–17. [Google Scholar] [CrossRef]
- Hu, Y.J.; Sun, J.; Wang, Q.L.; Yin, F.C.; Zhang, D.H. Characteristic analysis and optimal control of the thickness and tension system on tandem cold rolling. Int. J. Adv. Manuf. Technol. 2019, 101, 2297–2312. [Google Scholar] [CrossRef]
- Sun, J.L.; Peng, Y.; Liu, H.M. Dynamic characteristics of cold rolling mill and strip based on flatness and thickness control in rolling process. J. Cent. South Univ. 2014, 21, 567–576. [Google Scholar] [CrossRef]
- Prinz, K.; Steinboeck, A.; Muller, M.; Ettl, A.; Kugi, A. Automatic gauge control under laterally asymmetric rolling conditions combined with feedforward. IEEE Trans. Ind. Appl. 2017, 53, 2560–2568. [Google Scholar] [CrossRef]
- Prinz, K.; Steinboeck, A.; Kugi, A. Optimization-based feedforward control of the strip thickness profile in hot strip rolling. J. Process Control 2018, 64, 100–111. [Google Scholar] [CrossRef]
- Kovari, A. Influence of internal leakage in hydraulic capsules on dynamic behavior of hydraulic gap control system. Mater. Sci. Forum 2015, 812, 119–124. [Google Scholar] [CrossRef]
- Li, J.X.; Fang, Y.M.; Shi, S.L. Robust output-feedback control for hydraulic servo-position system of cold-strip rolling mill. Control Theory Appl. 2012, 29, 331–336. [Google Scholar]
- Sun, W.Q.; Shao, J.; Song, Y.; Guan, J.L. Research and development of automatic control system for high precision cold strip rolling mill. Adv. Mater. Res. 2014, 952, 283–286. [Google Scholar] [CrossRef]
- Yi, J.G. Modelling and analysis of step response test for hydraulic automatic gauge control. J. Mech. Eng. 2015, 61, 115–122. [Google Scholar] [CrossRef]
- Liu, H.S.; Zhang, J.; Mi, K.F.; Gao, J.X. Simulation on hydraulic-mechanical coupling vibration of cold strip rolling mill vertical system. Adv. Mater. Res. 2013, 694, 407–414. [Google Scholar] [CrossRef]
- Wang, J.; Sun, B.; Huang, Q.; Li, H. Research on the position-pressure master-slave control for rolling shear hydraulic servo system. Stroj. Vestn. 2015, 61, 265–272. [Google Scholar]
- Hua, C.C.; Yu, C.X. Controller design for cold rolling mill HAGC system with measurement delay perturbation. J. Mech. Eng. 2014, 50, 46–53. [Google Scholar] [CrossRef]
- Zhang, B.; Wei, W.; Qian, P.; Jiang, Z.; Li, J.; Han, J.; Mujtaba, M. Research on the control strategy of hydraulic shaking table based on the structural flexibility. IEEE Access 2019, 7, 43063–43075. [Google Scholar] [CrossRef]
- Wang, C.; Hu, B.; Zhu, Y.; Wang, X.; Luo, C.; Cheng, L. Numerical study on the gas-water two-phase flow in the self-priming process of self-priming centrifugal pump. Processes 2019, 7, 330. [Google Scholar] [CrossRef]
- Wang, C.; Shi, W.; Wang, X.; Jiang, X.; Yang, Y.; Li, W.; Zhou, L. Optimal design of multistage centrifugal pump based on the combined energy loss model and computational fluid dynamics. Appl. Energy 2017, 187, 10–26. [Google Scholar] [CrossRef]
- Qian, J.Y.; Gao, Z.X.; Liu, B.Z.; Jin, Z.J. Parametric study on fluid dynamics of pilot-control angle globe valve. ASME J. Fluids Eng. 2018, 140, 111103. [Google Scholar] [CrossRef]
- Qian, J.Y.; Chen, M.R.; Liu, X.L.; Jin, Z.J. A numerical investigation of the flow of nanofluids through a micro Tesla valve. J. Zhejiang Univ. Sci. A 2019, 20, 50–60. [Google Scholar] [CrossRef]
- Hou, C.W.; Qian, J.Y.; Chen, F.Q.; Jiang, W.K.; Jin, Z.J. Parametric analysis on throttling components of multi-stage high pressure reducing valve. Appl. Therm. Eng. 2018, 128, 1238–1248. [Google Scholar] [CrossRef]
- Wang, C.; He, X.; Zhang, D.; Hu, B.; Shi, W. Numerical and experimental study of the self-priming process of a multistage self-priming centrifugal pump. Int. J. Energy Res. 2019, 43, 4074–4092. [Google Scholar] [CrossRef]
- Wang, C.; He, X.; Shi, W.; Wang, X.; Wang, X.; Qiu, N. Numerical study on pressure fluctuation of a multistage centrifugal pump based on whole flow field. AIP Adv. 2019, 9, 035118. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Jiao, W.; Wang, C.; Cao, W. Influence of surface roughness on the pump performance based on Computational Fluid Dynamics. IEEE Access 2019, 7, 105331–105341. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.X.; Qiu, N.; Zhu, Y.; Shi, W.D. Numerical and experimental study on the pressure fluctuation, vibration, and noise of multistage pump with radial diffuser. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 481. [Google Scholar] [CrossRef]
- Hu, B.; Li, X.; Fu, Y.; Zhang, F.; Gu, C.; Ren, X.; Wang, C. Experimental investigation on the flow and flow-rotor heat transfer in a rotor-stator spinning disk reactor. Appl. Therm. Eng. 2019, 162, 114316. [Google Scholar] [CrossRef]
- Ye, S.G.; Zhang, J.H.; Xu, B.; Zhu, S.Q. Theoretical investigation of the contributions of the excitation forces to the vibration of an axial piston pump. Mech. Syst. Signal Process. 2019, 129, 201–217. [Google Scholar] [CrossRef]
- Zhang, J.H.; Xia, S.; Ye, S.; Xu, B.; Song, W.; Zhu, S.; Xiang, J. Experimental investigation on the noise reduction of an axial piston pump using free-layer damping material treatment. Appl. Acoust. 2018, 139, 1–7. [Google Scholar] [CrossRef]
- Bai, L.; Zhou, L.; Jiang, X.P.; Pang, Q.L.; Ye, D.X. Vibration in a multistage centrifugal pump under varied conditions. Shock Vib. 2019, 2019, 2057031. [Google Scholar] [CrossRef]
- Bai, L.; Zhou, L.; Han, C.; Zhu, Y.; Shi, W.D. Numerical study of pressure fluctuation and unsteady flow in a centrifugal pump. Processes 2019, 7, 354. [Google Scholar] [CrossRef]
- Wang, L.; Liu, H.L.; Wang, K.; Zhou, L.; Jiang, X.P.; Li, Y. Numerical simulation of the sound field of a five-stage centrifugal pump with different turbulence models. Water 2019, 11, 1777. [Google Scholar] [CrossRef]
- Ding, S.; Zheng, W.X. Controller design for nonlinear affine systems by control Lyapunov functions. Syst. Control Lett. 2013, 62, 930–936. [Google Scholar] [CrossRef]
- Liu, L.; Ding, S.H.; Ma, L.; Sun, H.B. A novel second-order sliding mode control based on the Lyapunov method. Trans. Inst. Meas. Control 2018, 41, 014233121878324. [Google Scholar] [CrossRef]
- Zhang, J. Integral barrier Lyapunov functions-based neural control for strict-feedback nonlinear systems with multi-constraint. Int. J. Control Autom. Syst. 2018, 16, 2002–2010. [Google Scholar] [CrossRef]
- Zhang, J.; Li, G.S.; Li, Y.H.; Dai, X.K. Barrier Lyapunov functions-based localized adaptive neural control for nonlinear systems with state and asymmetric control constraints. Trans. Inst. Meas. Control 2019, 41, 1656–1664. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, Q.; Zhou, L. Strongly absolute stability of Lur’e descriptor systems: Popov-type criteria. Int. J. Robust Nonlinear Control 2009, 19, 786–806. [Google Scholar] [CrossRef]
- Saeki, M.; Wada, N.; Satoh, S. Stability analysis of feedback systems with dead-zone nonlinearities by circle and Popov criteria. Automatica 2016, 66, 96–100. [Google Scholar] [CrossRef]
- Xia, L.; Jiang, H. An electronically controlled hydraulic power steering system for heavy vehicles. Adv. Mech. Eng. 2016, 8, 1687814016679566. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, Y.; Zhang, Z.D.; Bi, Q.S. Nonlinear behaviors as well as the bifurcation mechanism in switched dynamical systems. Nonlinear Dyn. 2015, 79, 465–471. [Google Scholar] [CrossRef]
- Bi, Q.S.; Li, S.L.; Kurths, J.; Zhang, Z.D. The mechanism of bursting oscillations with different codimensional bifurcations and nonlinear structures. Nonlinear Dyn. 2016, 85, 993–1005. [Google Scholar] [CrossRef]
- Xue, Z.H.; Cao, X.; Wang, T.Z. Vibration test and analysis on the centrifugal pump. J. Drain. Irrig. Mach. Eng. 2018, 36, 472–477. [Google Scholar]
- Zhu, Y.; Tang, S.N.; Quan, L.X.; Jiang, W.L.; Zhou, L. Extraction method for signal effective component based on extreme-point symmetric mode decomposition and Kullback-Leibler divergence. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 100. [Google Scholar] [CrossRef]
- Zhu, Y.; Qian, P.F.; Tang, S.N.; Jiang, W.L.; Li, W.; Zhao, J.H. Amplitude-frequency characteristics analysis for vertical vibration of hydraulic AGC system under nonlinear action. AIP Adv. 2019, 9, 035019. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Tang, S.; Wang, C.; Jiang, W.; Yuan, X.; Lei, Y. Bifurcation characteristic research on the load vertical vibration of a hydraulic automatic gauge control system. Processes 2019, 7, 718. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Chen, L.Q. Nonlinear Vibration; Higher Education Press: Beijing, China, 2001; pp. 57–123. [Google Scholar]
- Ding, W.J. Self-Excited Vibration; Tsinghua University Press: Beijing, China, 2009; Volume 84, pp. 238–242. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Tang, S.; Wang, C.; Jiang, W.; Zhao, J.; Li, G. Absolute Stability Condition Derivation for Position Closed-Loop System in Hydraulic Automatic Gauge Control. Processes 2019, 7, 766. https://doi.org/10.3390/pr7100766
Zhu Y, Tang S, Wang C, Jiang W, Zhao J, Li G. Absolute Stability Condition Derivation for Position Closed-Loop System in Hydraulic Automatic Gauge Control. Processes. 2019; 7(10):766. https://doi.org/10.3390/pr7100766
Chicago/Turabian StyleZhu, Yong, Shengnan Tang, Chuan Wang, Wanlu Jiang, Jianhua Zhao, and Guangpeng Li. 2019. "Absolute Stability Condition Derivation for Position Closed-Loop System in Hydraulic Automatic Gauge Control" Processes 7, no. 10: 766. https://doi.org/10.3390/pr7100766
APA StyleZhu, Y., Tang, S., Wang, C., Jiang, W., Zhao, J., & Li, G. (2019). Absolute Stability Condition Derivation for Position Closed-Loop System in Hydraulic Automatic Gauge Control. Processes, 7(10), 766. https://doi.org/10.3390/pr7100766






