Diffusion in Binary Aqueous Solutions of Alcohols by Molecular Simulation
Abstract
:1. Introduction
2. Molecular Simulation
3. Force Fields for Alcohols
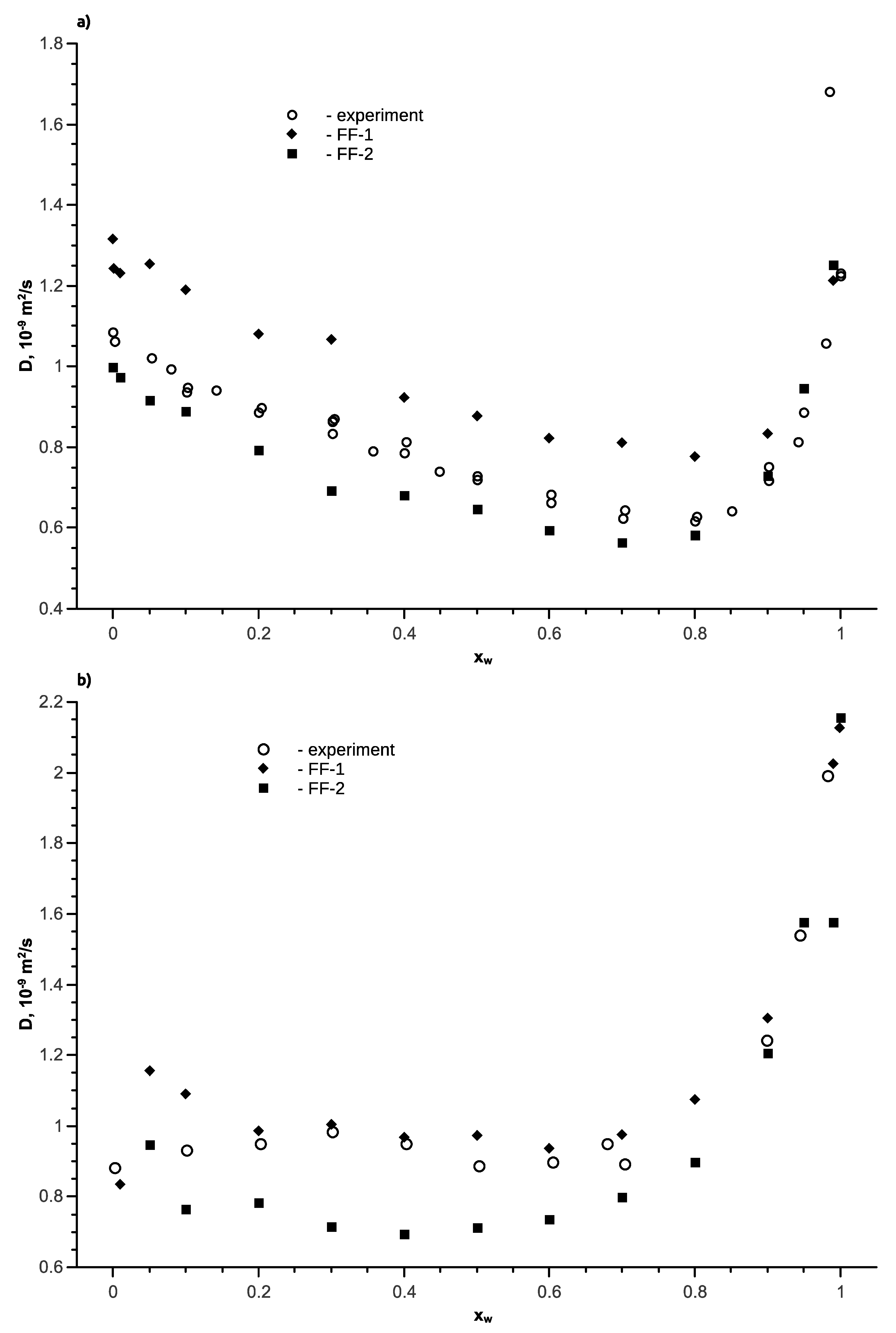
4. Diffusion Coefficients in Water-Alcohol Solutions
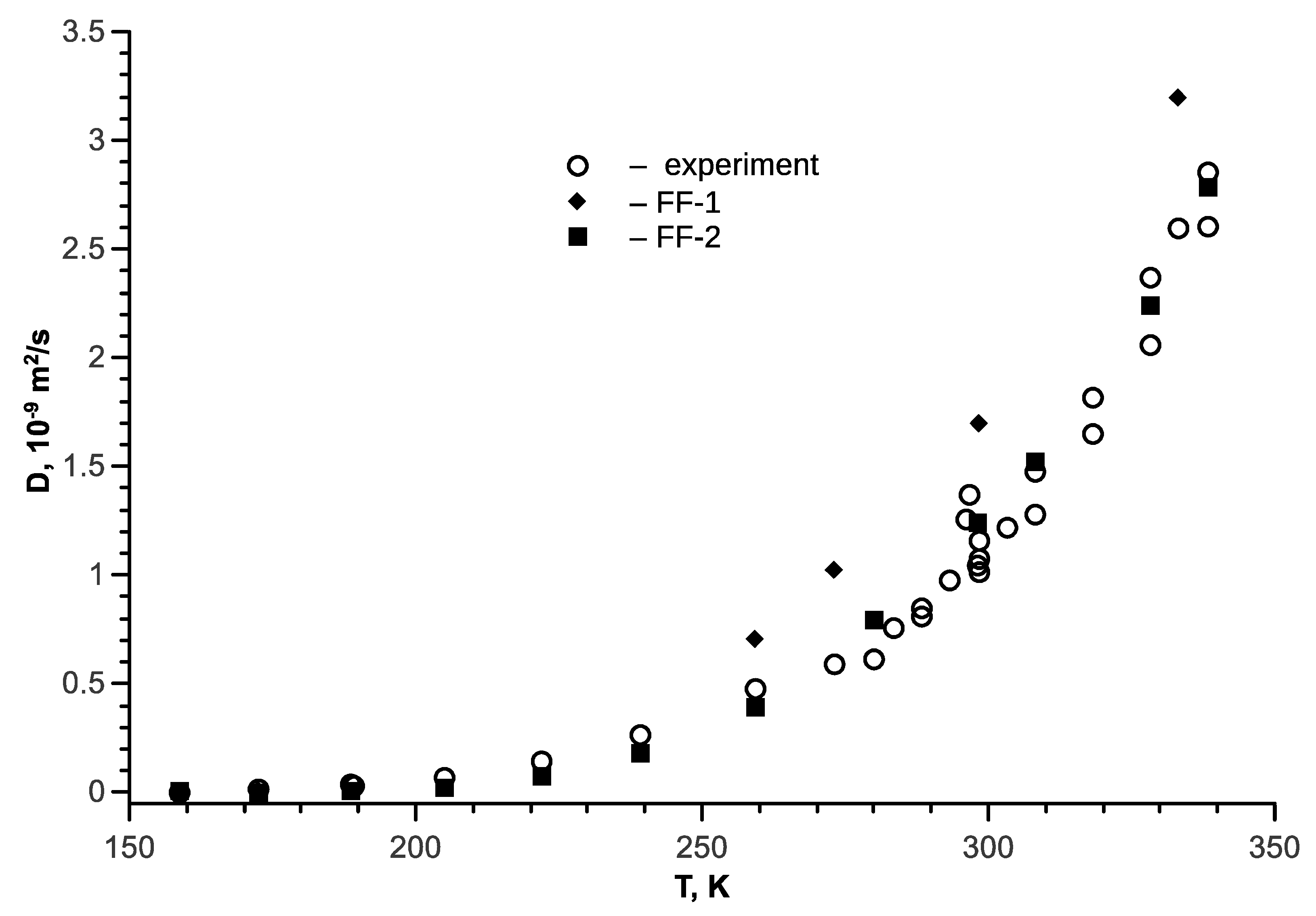
5. Ethanol-Water Mixture
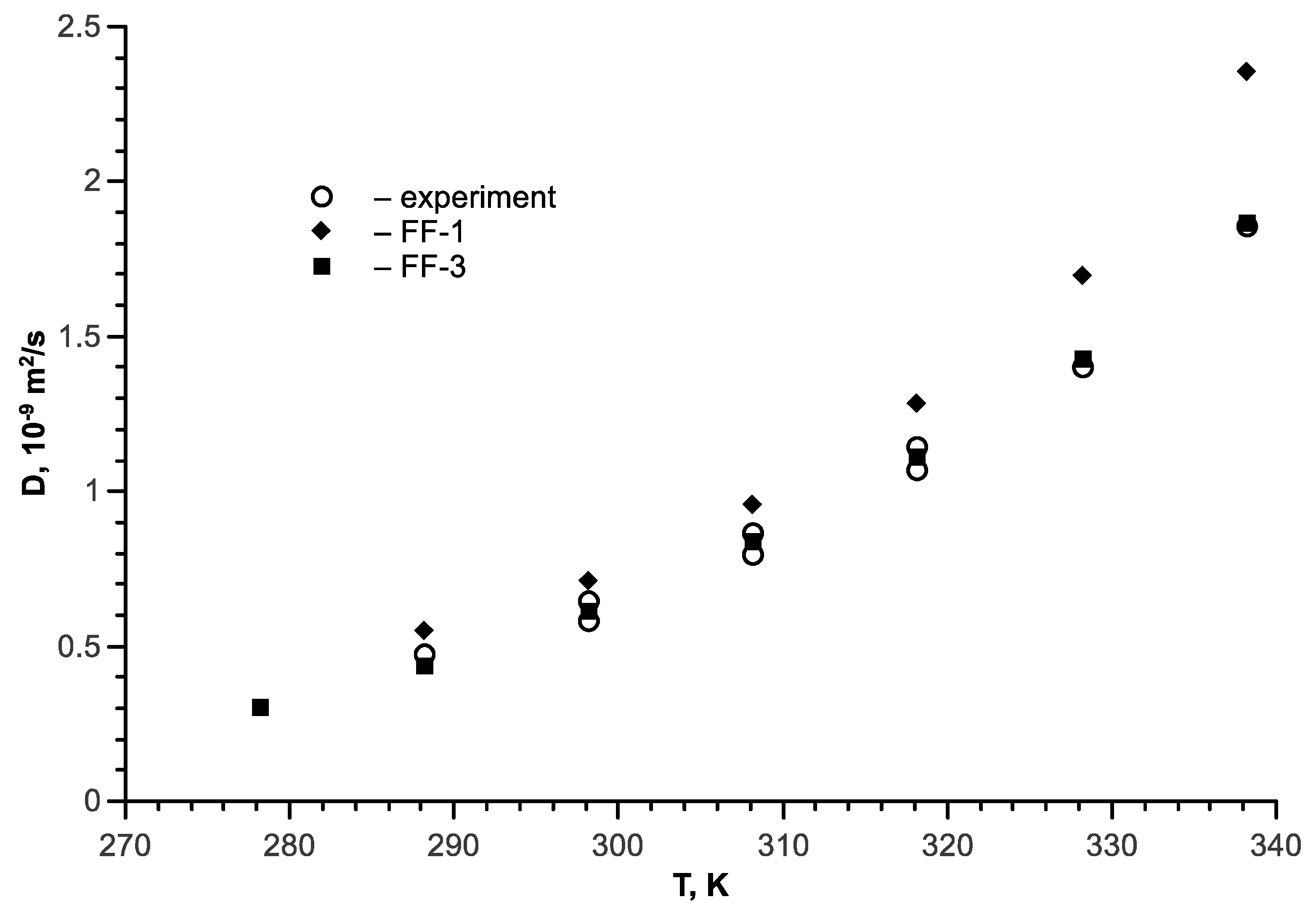
6. Isopropanol-Water Mixture
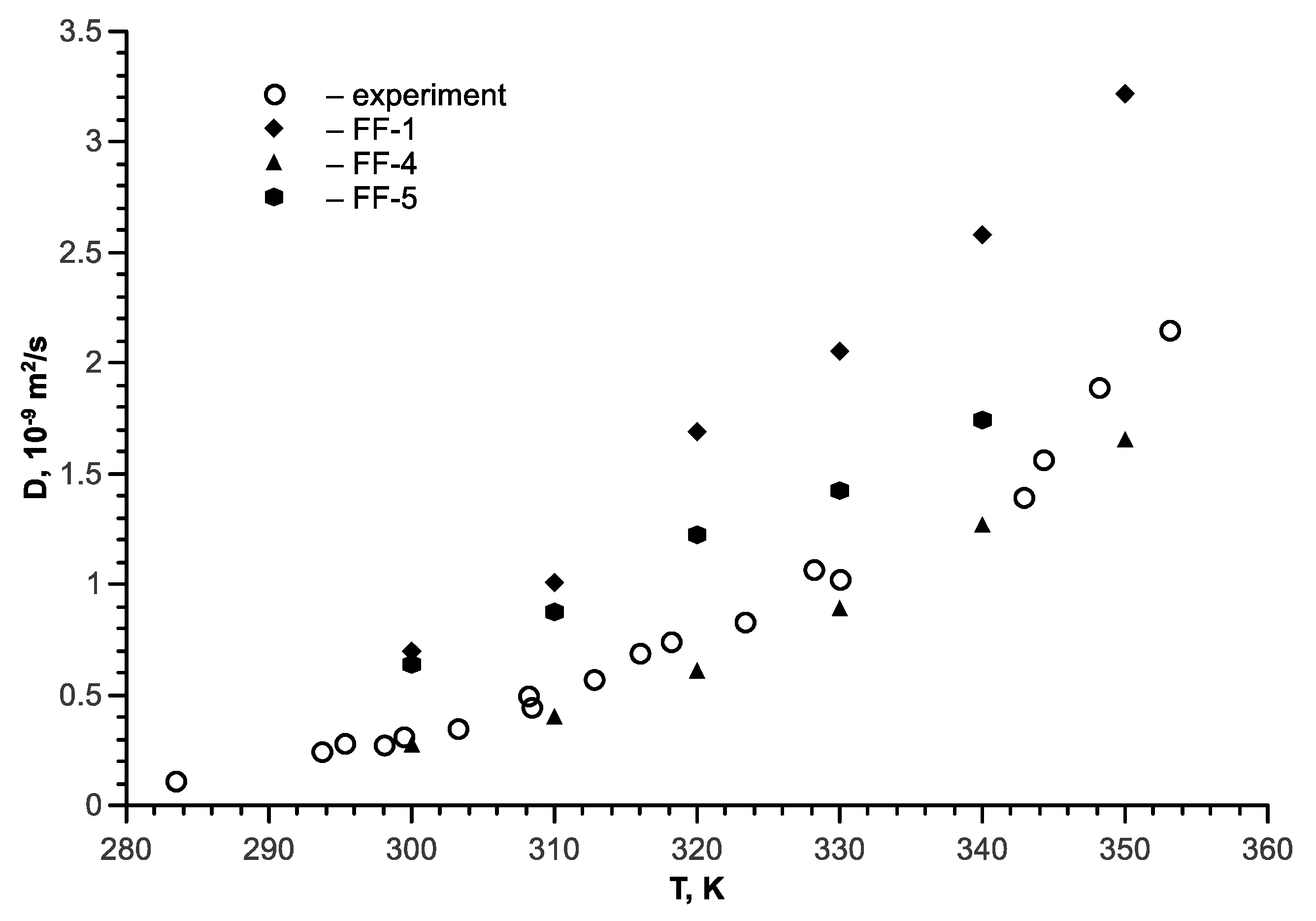
7. Tert-Butanol-Water Mixture
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Raeisi, Z.; Moheb, A.; Sadeghi, M.; Abdolmaleki, A.; Alibouri, M. Titanate nanotubes—Incorporated poly(vinyl alcohol) mixed matrix membranes for pervaporation separation of water-isopropanol mixtures. Chem. Eng. Res. Des. 2019, 145, 99–111. [Google Scholar] [CrossRef]
- Dudek, G.; Turczyn, R.; Gnus, M.; Konieczny, K. Pervaporative dehydration of ethanol/water mixture through hybrid alginate membranes with ferroferic oxide nanoparticles. Sep. Purif. Technol. 2018, 193, 398–407. [Google Scholar] [CrossRef]
- Chaudhari, S.; Kwon, Y.; Moon, M.; Shon, M.; Park, Y.; Nam, S. Melamine-modified silicotungstic acid incorporated into the polyvinyl alcohol/polyvinyl amine blend membrane for pervaporation dehydration of water/isopropanol mixtures. Vacuum 2018, 147, 115–125. [Google Scholar] [CrossRef]
- Miyabe, K.; Guiochon, G. Measurement of the parameters of the mass transfer kinetics in high performance liquid chromatography. J. Sep. Sci. 2003, 26, 155–173. [Google Scholar] [CrossRef]
- Kaplan, I.G. Intermolecular Interactions: Physical Picture, Computational Methods, Model Potentials; Wiley: Hoboken, NJ, USA, 2006; ISBN 978-0-470-86332-9. [Google Scholar]
- Waldrop, J.M.; Song, B.; Patkowski, K.; Wang, X. Accurate ab initio potential for the krypton dimer and transport properties of the low-density krypton gas. J. Chem. Phys. 2015, 142, 204307. [Google Scholar] [CrossRef]
- Bock, S.; Bich, E.; Vogel, E. A new intermolecular potential energy surface for carbon dioxide from ab initio calculations. Chem. Phys. 2000, 257, 147–156. [Google Scholar] [CrossRef]
- Li, A.H.T.; Wang, Y.S.; Chao, S.D. Molecular Dynamics Simulations with ab Initio Force Fields: A Review of Case Studies on CH4, CCl4, CHF3, and CHCl3 Dimers. Multiscale Sci. Eng. 2019, 1, 26–33. [Google Scholar] [CrossRef] [Green Version]
- Anashkin, I.P.; Klinov, A.V. Determining the parameters of the potential of intermolecular interaction by the Zeno line. Russ. J. Phys. Chem. A 2013, 87, 1781–1788. [Google Scholar] [CrossRef]
- Chen, B.; Potoff, J.J.; Siepmann, J.I. Monte Carlo Calculations for Alcohols and Their Mixtures with Alkanes. Transferable Potentials for Phase Equilibria. 5. United-Atom Description of Primary, Secondary, and Tertiary Alcohols. J. Phys. Chem. B 2001, 105, 3093–3104. [Google Scholar] [CrossRef]
- Schnabel, T.; Vrabec, J.; Hasse, H. Henry’s law constants of methane, nitrogen, oxygen and carbon dioxide in ethanol from 273 to 498 K: Prediction from molecular simulation. Fluid Phase Equilibria 2005, 233, 134–143. [Google Scholar] [CrossRef] [Green Version]
- Muñoz-Muñoz, Y.M.; Guevara-Carrion, G.; Vrabec, J. Molecular Insight into the Liquid Propan-2-ol + Water Mixture. J. Phys. Chem. B 2018, 122, 8718–8729. [Google Scholar] [CrossRef] [PubMed]
- Ferrando, N.; Lachet, V.; Teuler, J.M.; Boutin, A. Transferable Force Field for Alcohols and Polyalcohols. J. Phys. Chem. B 2009, 113, 5985–5995. [Google Scholar] [CrossRef] [PubMed]
- Luk’yanchikova, I.A.; Ivlev, D.V.; Kiselev, M.G.; Al’per, G.A. Concentration dependence of the viscosity of tert-butanol-water mixtures: Physical experiment and computer simulation. Russ. J. Gen. Chem. 2004, 74, 1156–1162. [Google Scholar] [CrossRef]
- Muñoz-Muñoz, Y.M.; Guevara-Carrion, G.; Llano-Restrepo, M.; Vrabec, J. Lennard-Jones force field parameters for cyclic alkanes from cyclopropane to cyclohexane. Fluid Phase Equilibria 2015, 404, 150–160. [Google Scholar] [CrossRef]
- Janzen, T. On Diffusion Coefficients of Multicomponent Liquid Mixtures Predicted by Equilibrium Molecular Dynamics Simulation. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2019. [Google Scholar]
- Mijaković, M.; Polok, K.D.; Kežić, B.; Sokolić, F.; Perera, A.; Zoranić, L. A comparison of force fields for ethanol–water mixtures. Mol. Simul. 2015, 41, 699–712. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Madura, J.D.; Swenson, C.J. Optimized intermolecular potential functions for liquid hydrocarbons. J. Am. Chem. Soc. 1984, 106, 6638–6646. [Google Scholar] [CrossRef]
- Jorgensen, W.L. Optimized intermolecular potential functions for liquid alcohols. J. Phys. Chem. 1986, 90, 1276–1284. [Google Scholar] [CrossRef]
- Jiao, Y. The Development of Accurate Force Fields for Protein Simulation. Ph.D. Thesis, Kansas State University, Manhattan, NY, USA, 2012. [Google Scholar]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, X. Molecular dynamics simulation of ethanol/water mixtures for structure and diffusion properties. Fluid Phase Equilibria 2005, 231, 1–10. [Google Scholar] [CrossRef]
- Gotlib, I.Y.; Piotrovskaya, E.M. Properties of Coexisting Phases for the Ethanol−Ethane Binary System by Computer Simulation. J. Phys. Chem. B 1999, 103, 7681–7686. [Google Scholar] [CrossRef]
- Van Leeuwen, M.E. Deviation from corresponding-states behaviour for polar fluids. Mol. Phys. 1994, 82, 383–392. [Google Scholar] [CrossRef]
- Ghoufi, A.; Artzner, F.; Malfreyt, P. Physical Properties and Hydrogen-Bonding Network of Water—Ethanol Mixtures from Molecular Dynamics Simulations. J. Phys. Chem. B 2016, 120, 793–802. [Google Scholar] [CrossRef] [PubMed]
- Abascal, J.L.F.; Vega, C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef]
- Cerar, J.; Jamnik, A.; Pethes, I.; Temleitner, L.; Pusztai, L.; Tomšič, M. Structural, rheological and dynamic aspects of hydrogen-bonding molecular liquids: Aqueous solutions of hydrotropic tert-butyl alcohol. J. Colloid Interface Sci. 2019. [Google Scholar] [CrossRef] [Green Version]
- Pothoczki, S.; Pusztai, L.; Bakó, I. Molecular Dynamics Simulation Studies of the Temperature-Dependent Structure and Dynamics of Isopropanol-Water Liquid Mixtures at Low Alcohol Content. J. Phys. Chem. B 2019, 123, 7599–7610. [Google Scholar] [CrossRef] [Green Version]
- Pothoczki, S.; Pusztai, L.; Bakó, I. Variations of the Hydrogen Bonding and Hydrogen-Bonded Network in Ethanol-Water Mixtures on Cooling. J. Phys. Chem. B 2018, 122, 6790–6800. [Google Scholar] [CrossRef] [Green Version]
- Pothoczki, S.; Pusztai, L.; Bakó, I. Temperature dependent dynamics in water-ethanol liquid mixtures. J. Mol. Liq. 2018, 271, 571–579. [Google Scholar] [CrossRef] [Green Version]
- Lenton, S.; Rhys, N.H.; Towey, J.J.; Soper, A.K.; Dougan, L. Temperature-Dependent Segregation in Alcohol-Water Binary Mixtures Is Driven by Water Clustering. J. Phys. Chem. B 2018, 122, 7884–7894. [Google Scholar] [CrossRef]
- Méndez-Bermúdez, J.G.; Dominguez, H.; Temleitner, L.; Pusztai, L. On the Structure Factors of Aqueous Mixtures of 1-Propanol and 2-Propanol: X-Ray Diffraction Experiments and Molecular Dynamics Simulations. Phys. Status Solidi B 2018, 255, 1800215. [Google Scholar] [CrossRef] [Green Version]
- Gereben, O.; Pusztai, L. Investigation of the Structure of Ethanol-Water Mixtures by Molecular Dynamics Simulation I: Analyses Concerning the Hydrogen-Bonded Pairs. J. Phys. Chem. B 2015, 119, 3070–3084. [Google Scholar] [CrossRef] [PubMed]
- Overduin, S.D.; Patey, G.N. Comparison of simulation and experimental results for a model aqueous tert-butanol solution. J. Chem. Phys. 2017, 147, 024503. [Google Scholar] [CrossRef] [PubMed]
- Overduin, S.D.; Perera, A.; Patey, G.N. Structural behavior of aqueous t-butanol solutions from large-scale molecular dynamics simulations. J. Chem. Phys. 2019, 150, 184504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Subramanian, D.; Klauda, J.B.; Collings, P.J.; Anisimov, M.A. Mesoscale Phenomena in Ternary Solutions of Tertiary Butyl Alcohol, Water, and Propylene Oxide. J. Phys. Chem. B 2014, 118, 5994–6006. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [Green Version]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Vega, C.; Abascal, J.L.F.; Conde, M.M.; Aragones, J.L. What ice can teach us about water interactions: A critical comparison of the performance of different water models. Faraday Discuss. 2009, 141, 251. [Google Scholar] [CrossRef] [Green Version]
- Suárez-Iglesias, O.; Medina, I.; Sanz, M.D.L.A.; Pizarro, C.; Bueno, J.L. Self-Diffusion in Molecular Fluids and Noble Gases: Available Data. J. Chem. Eng. Data 2015, 60, 2757–2817. [Google Scholar] [CrossRef]
- Dubbeldam, D.; Snurr, R.Q. Recent developments in the molecular modeling of diffusion in nanoporous materials. Mol. Simul. 2007, 33, 305–325. [Google Scholar] [CrossRef]
- Krishna, R.; van Baten, J.M. The Darken Relation for Multicomponent Diffusion in Liquid Mixtures of Linear Alkanes: An Investigation Using Molecular Dynamics (MD) Simulations. Ind. Eng. Chem. Res. 2005, 44, 6939–6947. [Google Scholar] [CrossRef]
- Liu, X.; Schnell, S.K.; Simon, J.M.; Bedeaux, D.; Kjelstrup, S.; Bardow, A.; Vlugt, T.J.H. Fick Diffusion Coefficients of Liquid Mixtures Directly Obtained From Equilibrium Molecular Dynamics. J. Phys. Chem. B 2011, 115, 12921–12929. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.; Krishna, R. Multicomponent Mass Transfer; Wiley series in chemical engineering; Wiley: New York, NY, USA, 1993; ISBN 978-0-471-57417-0. [Google Scholar]
- Guevara-Carrion, G.; Janzen, T.; Muñoz-Muñoz, Y.M.; Vrabec, J. Mutual diffusion of binary liquid mixtures containing methanol, ethanol, acetone, benzene, cyclohexane, toluene, and carbon tetrachloride. J. Chem. Phys. 2016, 144, 124501. [Google Scholar] [CrossRef] [PubMed]
- D’Agostino, C.; Mantle, M.D.; Gladden, L.F.; Moggridge, G.D. Prediction of binary diffusion coefficients in non-ideal mixtures from NMR data: Hexane-nitrobenzene near its consolute point. Chem. Eng. Sci. 2011, 66, 3898–3906. [Google Scholar] [CrossRef]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Reid, R.C.; Prausnitz, J.M.; Sherwood, T.K. The Properties of Gases and Liquids, 3rd ed.; McGraw-Hill chemical engineering series; McGraw-Hill: New York, NY, USA, 1977; ISBN 978-0-07-051790-5. [Google Scholar]
- Abrams, D.S.; Prausnitz, J.M. Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems. AIChE J. 1975, 21, 116–128. [Google Scholar] [CrossRef]
- Aspen HYSYS. Available online: https://www.aspentech.com/en/products/engineering/aspen-hysys (accessed on 10 November 2019).
- Harris, K.R.; Newitt, P.J.; Derlacki, Z.J. Alcohol tracer diffusion, density, NMR and FTIR studies of aqueous ethanol and 2,2,2-trifluoroethanol solutions at 25 °C. J. Chem. Soc. Faraday Trans. 1998, 94, 1963–1970. [Google Scholar] [CrossRef]
- Price, W.S.; Ide, H.; Arata, Y. Solution Dynamics in Aqueous Monohydric Alcohol Systems. J. Phys. Chem. A 2003, 107, 4784–4789. [Google Scholar] [CrossRef]
- Harris, K.R.; Goscinska, T.; Lam, H.N. Mutual diffusion coefficients for the systems water-enthanol and water-propan-1-ol at 25 °C. J. Chem. Soc. Faraday Trans. 1993, 89, 1969–1974. [Google Scholar] [CrossRef]
- Pratt, K.C.; Wakeham, W.A. The Mutual Diffusion Coefficient of Ethanol-Water Mixtures: Determination by a Rapid, New Method. Proc. R. Soc. Math. Phys. Eng. Sci. 1974, 336, 393–406. [Google Scholar] [CrossRef]
- Pratt, K.C.; Wakeham, W.A. The Mutual Diffusion Coefficient for Binary Mixtures of Water and the Isomers of Propanol. Proc. R. Soc. Math. Phys. Eng. Sci. 1975, 342, 401–419. [Google Scholar] [CrossRef]
- Leaist, D.G.; Deng, Z. Doubling of the apparent rates of diffusion of aqueous propanols near compositions of maximum refractive index. J. Phys. Chem. 1992, 96, 2016–2018. [Google Scholar] [CrossRef]
- Mialdun, A.; Yasnou, V.; Shevtsova, V.; Königer, A.; Köhler, W.; Alonso de Mezquia, D.; Bou-Ali, M.M. A comprehensive study of diffusion, thermodiffusion, and Soret coefficients of water-isopropanol mixtures. J. Chem. Phys. 2012, 136, 244512. [Google Scholar] [CrossRef]
- Harris, K.R.; Newitt, P.J. Diffusion and Structure in Water-Alcohol Mixtures: Water + tert-Butyl Alcohol (2-Methyl-2-Propanol). J. Phys. Chem. A 1999, 103, 6508–6513. [Google Scholar] [CrossRef]
- Kipkemboi, P.K.; Easteal, A.J. Self-Diffusion Coefficients of Each Component in Water+t-Butyl Alcohol and Water+t-Butylamine Binary Mixtures. Bull. Chem. Soc. Jpn. 1994, 67, 2956–2961. [Google Scholar] [CrossRef]




| Site Property | Parameter | FF-1 (TraPPE) [10] | FF-2 [11] | FF-3 [12] | FF-4 [13] | FF-5 [14] |
|---|---|---|---|---|---|---|
| (Ethanol, Isopropanol, Tert-Butanol) | (Ethanol) | (Isopropanol) | (Tert-Butanol) | (Tert-Butanol) | ||
| transferable | + | − | − | + | − | |
| Site parameters | ||||||
| CH3 | ε/kB, K | 98 | 120.15 | 103.59 | 120.150 | 64.38 |
| σ, Å | 3.75 | 3.6072 | 3.866 | 3.607 | 3.775 | |
| q, ē | 0 | 0 | 0 | 0 | 0.0089 | |
| CH2 | ε/kB, K | 46 | 86.291 | 86.29 | ||
| σ, Å | 3.95 | 3.4612 | 3.261 | |||
| q, ē | 0.265 | 0.2556 | 0.265 | |||
| CH | ε/kB, K | 10 | 20.2 | 50.98 | ||
| σ, Å | 4.33 | 3.238 | 3.363 | |||
| q, ē | 0.265 | 0.31 | 0.265 | |||
| C | ε/kB, K | 0.5 | 15.04 | 73.08 | ||
| σ, Å | 5.8 | 2.44 | 2.93 | |||
| q, ē | 0.265 | 0.265 | 0.293 | |||
| O | ε/kB, K | 93 | 85.053 | 85.9 | 125.010 | 28.52 |
| σ, Å | 3.02 | 3.1496 | 3.154 | 3.081 | 3.25 | |
| q, ē | −0.7 | −0.69711 | −0.747 | −0.700 | −0.7517 | |
| H | Q | 0.435 | 0.44151 | 0.437 | 0.435 | 0.432 |
| bond length | ||||||
| CH3-CH2 | l, Å | 1.54 | 1.9842 | |||
| CH3-CH | l, Å | 1.54 | 1.55 | |||
| CH3-C | l, Å | 1.54 | 1.751 | 1.53 | ||
| CHn-O | l, Å | 1.43 | 1.71581 | 1.465 | 1.44 | 1.42 |
| O – H | l, Å | 0.945 | 0.95053 | 0.969 | 0.945 | 0.95 |
| Constrains | Fixed bonds | Fixed atom coordinates | Fixed atom coordinates | Fixed atom coordinates | Fixed bonds | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klinov, A.; Anashkin, I. Diffusion in Binary Aqueous Solutions of Alcohols by Molecular Simulation. Processes 2019, 7, 947. https://doi.org/10.3390/pr7120947
Klinov A, Anashkin I. Diffusion in Binary Aqueous Solutions of Alcohols by Molecular Simulation. Processes. 2019; 7(12):947. https://doi.org/10.3390/pr7120947
Chicago/Turabian StyleKlinov, Alexander, and Ivan Anashkin. 2019. "Diffusion in Binary Aqueous Solutions of Alcohols by Molecular Simulation" Processes 7, no. 12: 947. https://doi.org/10.3390/pr7120947
APA StyleKlinov, A., & Anashkin, I. (2019). Diffusion in Binary Aqueous Solutions of Alcohols by Molecular Simulation. Processes, 7(12), 947. https://doi.org/10.3390/pr7120947





