The Effects of Water Friction Loss Calculation on the Thermal Field of the Canned Motor
Abstract
:1. Introduction
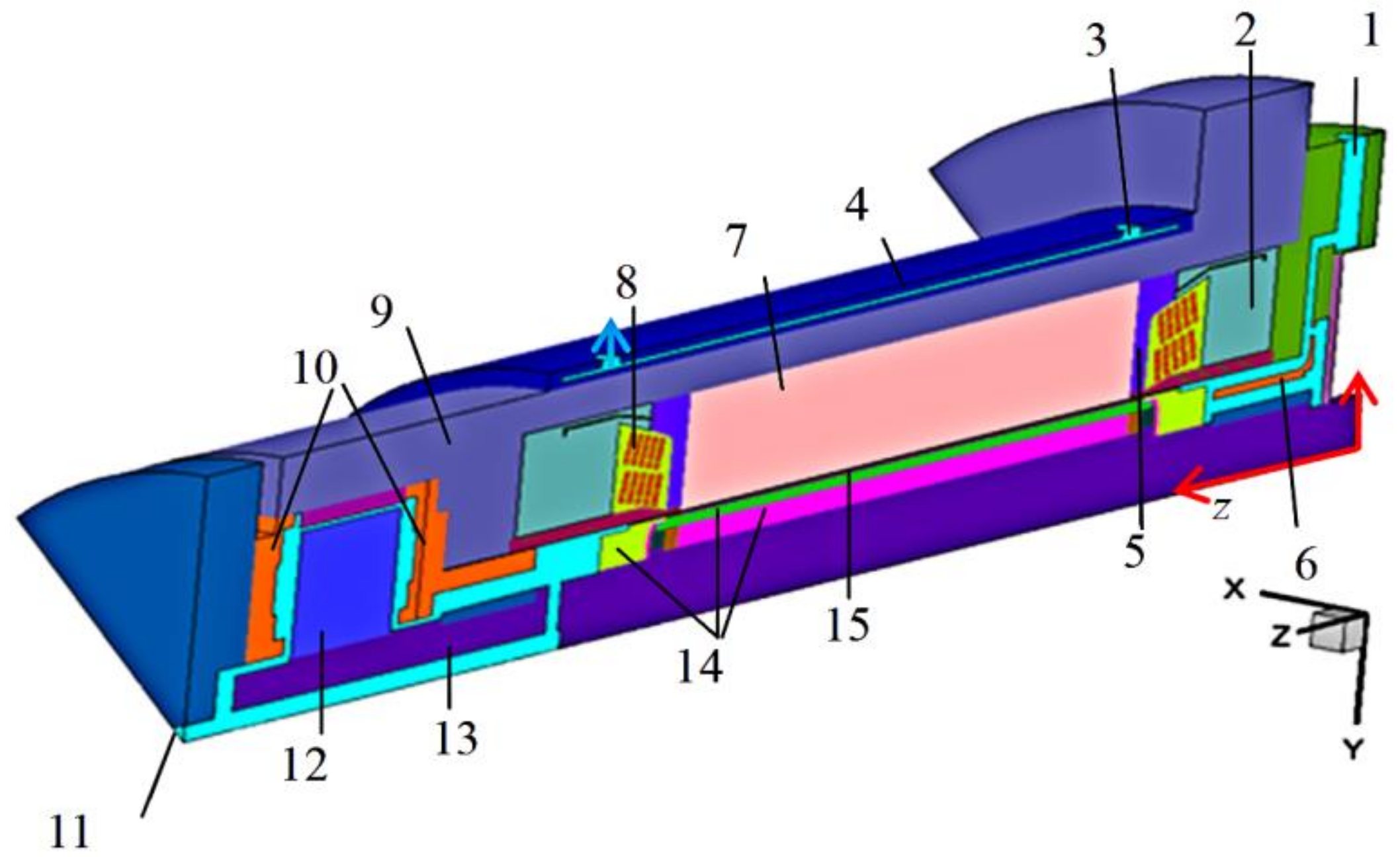
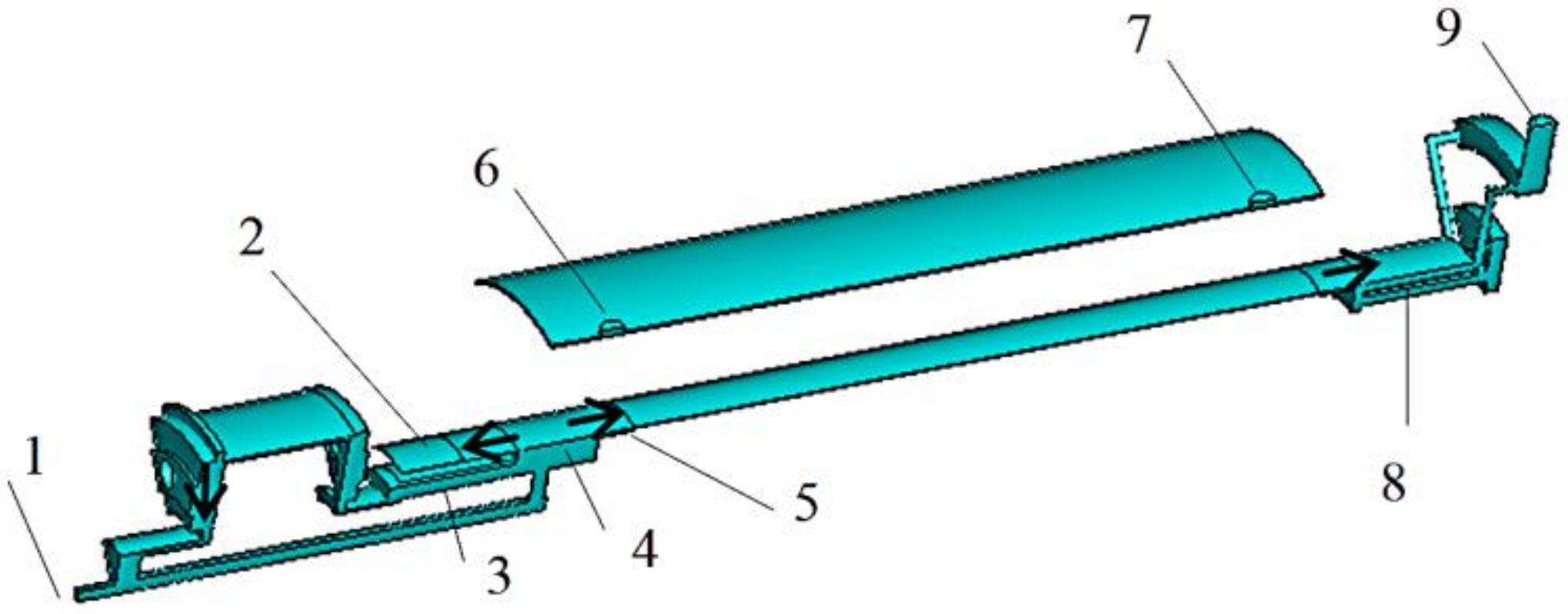
2. Physical Model
3. Solution Conditions
3.1. Basic Assumptions
- The water in the motor was an incompressible fluid because the Mach number (Ma = 0.24) was far less than 0.7. The mass flow rate (5.127 kg/s) of primary water was very large in the clearance of the motor. The Reynolds’s number (Re = 5363) showed that the flow was in the turbulence state.
- Only the steady state of fluid flow was considered. There was no contact thermal resistance between the adjacent bodies. The flow of the fluid in the internal passage was in the smooth region because the internal surface roughness of the wall in the motor was very small and the friction loss can be uniformly implemented for the corresponding positions of the water as volumetric heat sources inside the fluid.
- The electrical and harmonic losses and their distribution were calculated by another research institute using 3D software from the electromagnetic field. The corresponding loss in each body was uniformly distributed. Because the parameters of the thermo-physical properties of materials change with temperature variations, e.g., thermal conductivity, density, and specific heat at constant pressure, to be on the safe side, they were set as constant in the calculation process, so the minimum value of these parameters was chosen in the interval of the temperature through a large number of calculations. Among them, the thermal conductivity of the iron core lamination of rotor and stator was anisotropic, and the axial, radial, and tangential values of thermal conductivity were chosen experimentally. Except iron core lamination, other materials were isotropic, and their thermal conductivity values were selected conventionally.
3.2. Mathematical Model
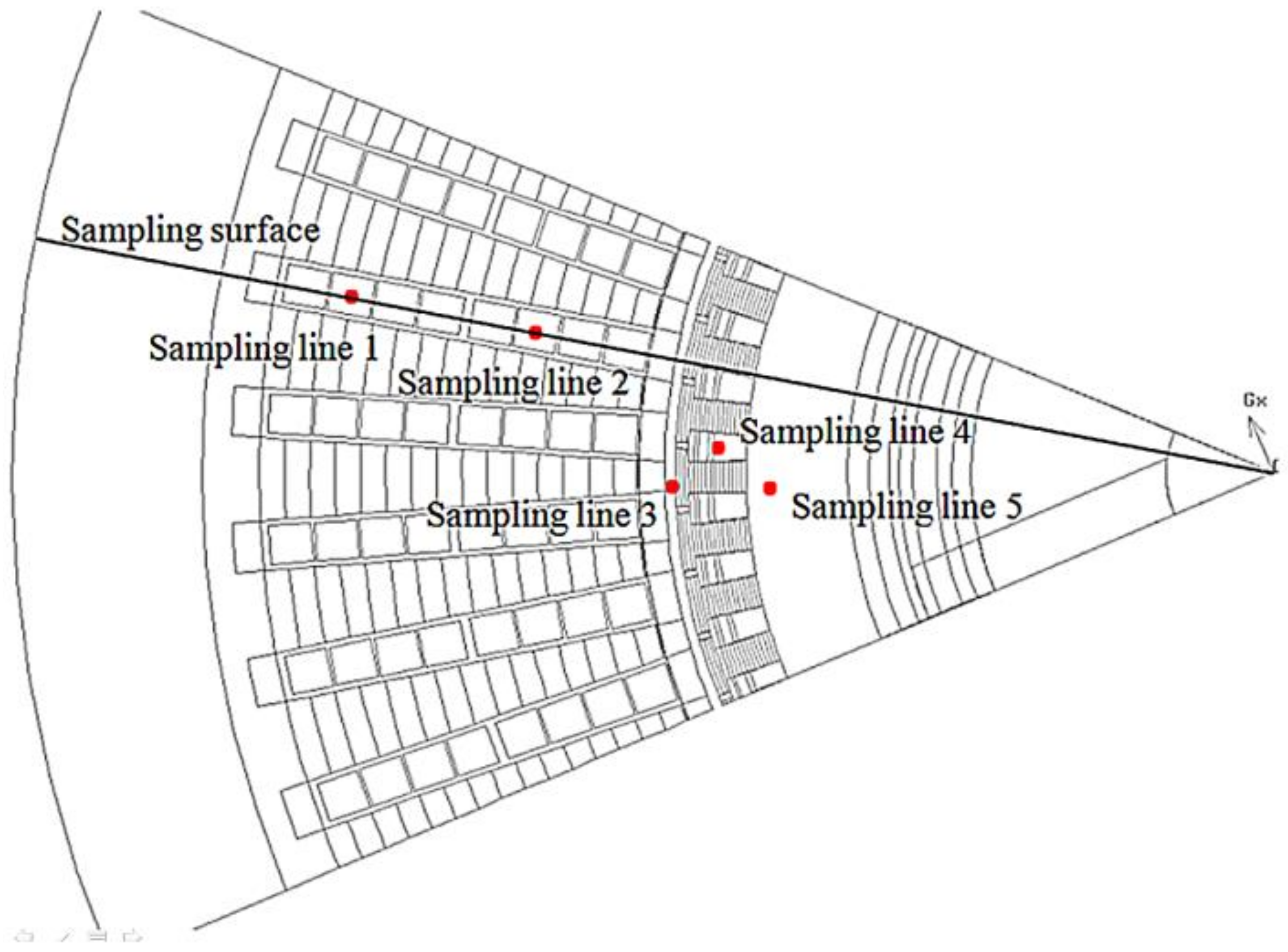
3.3. Mesh Generation
3.4. Loss and Boundary Conditions
3.4.1. Water Friction Loss
3.4.2. Electrical Loss
3.4.3. Boundary Conditions
4. Results and Discussion
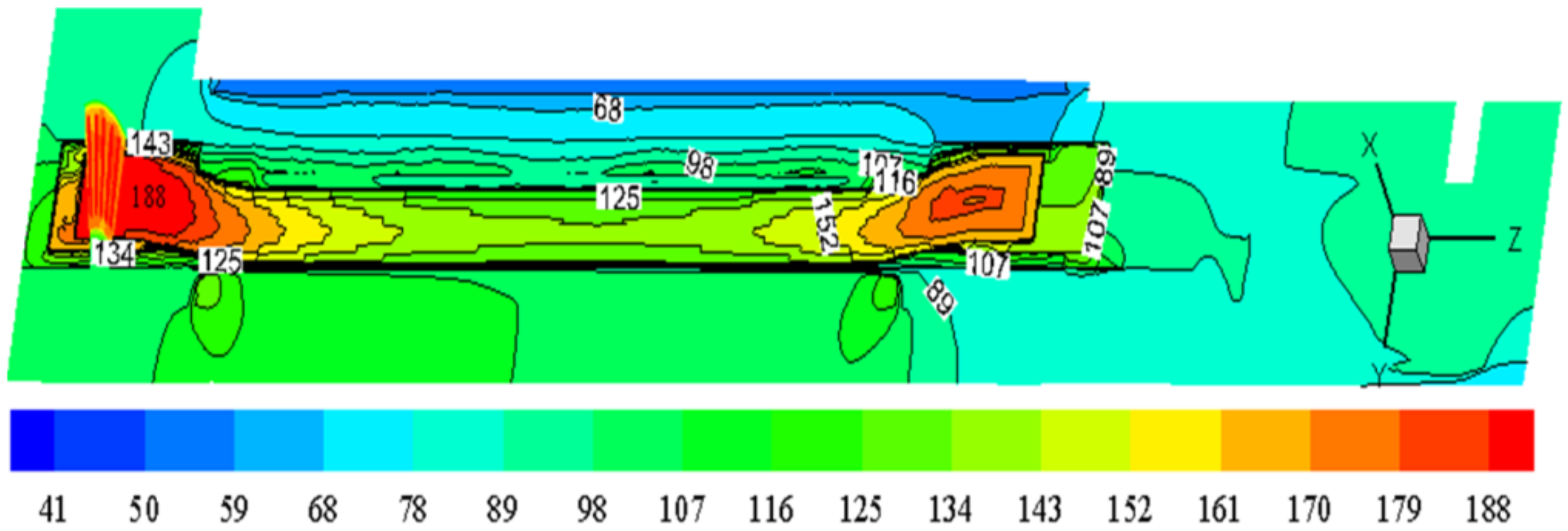
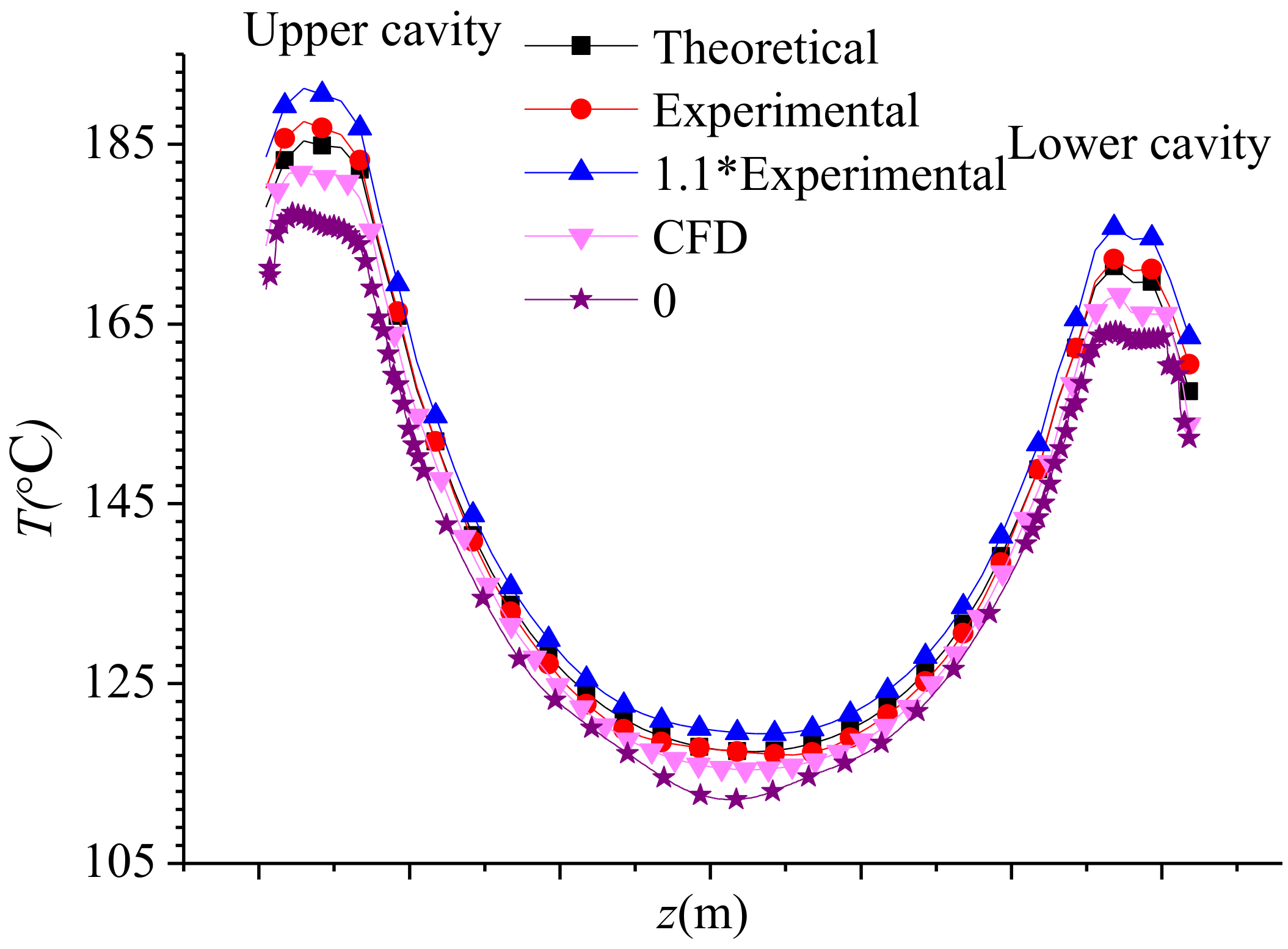
4.1. Temperature Analysis of the Stator Winding
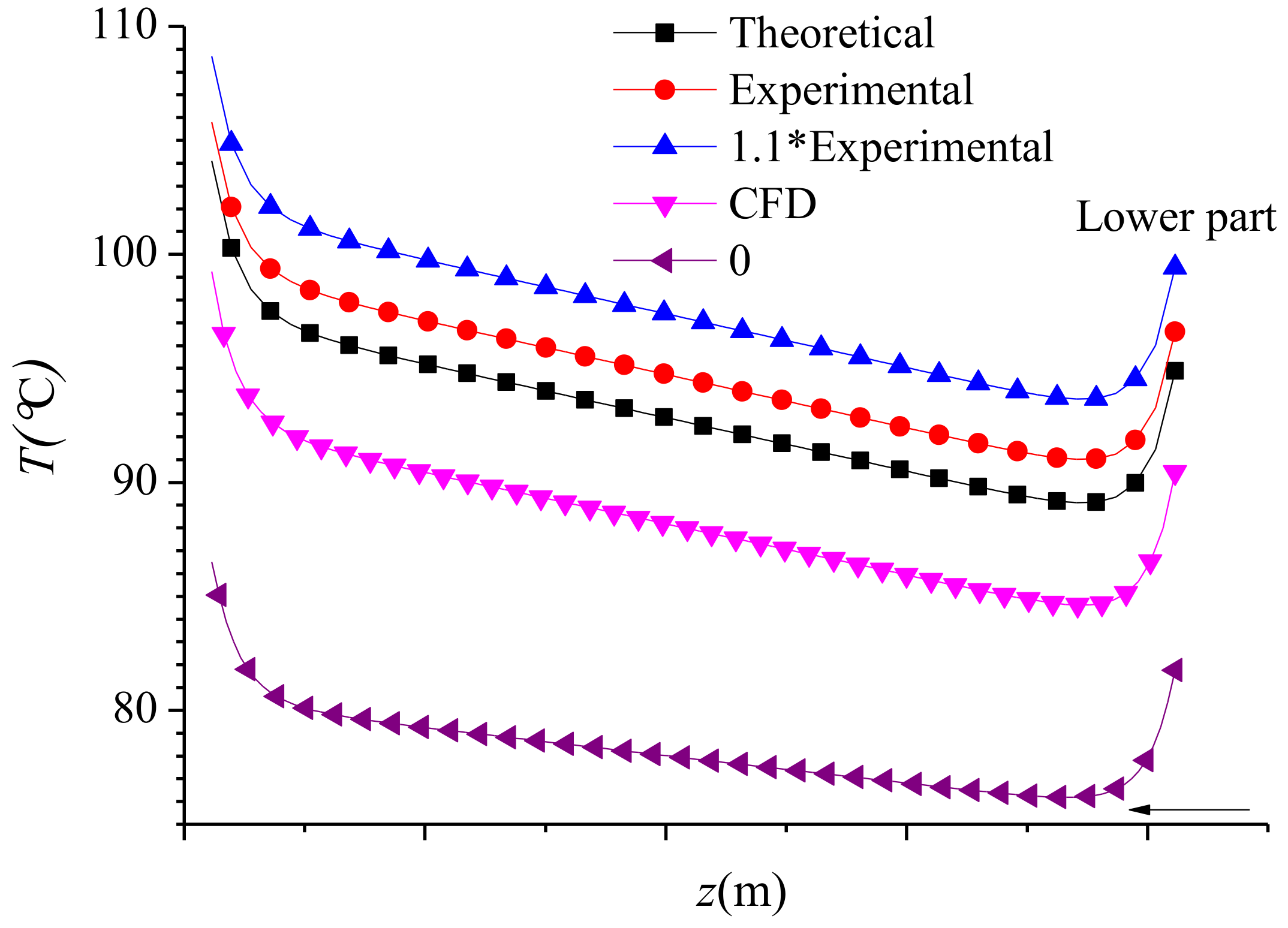
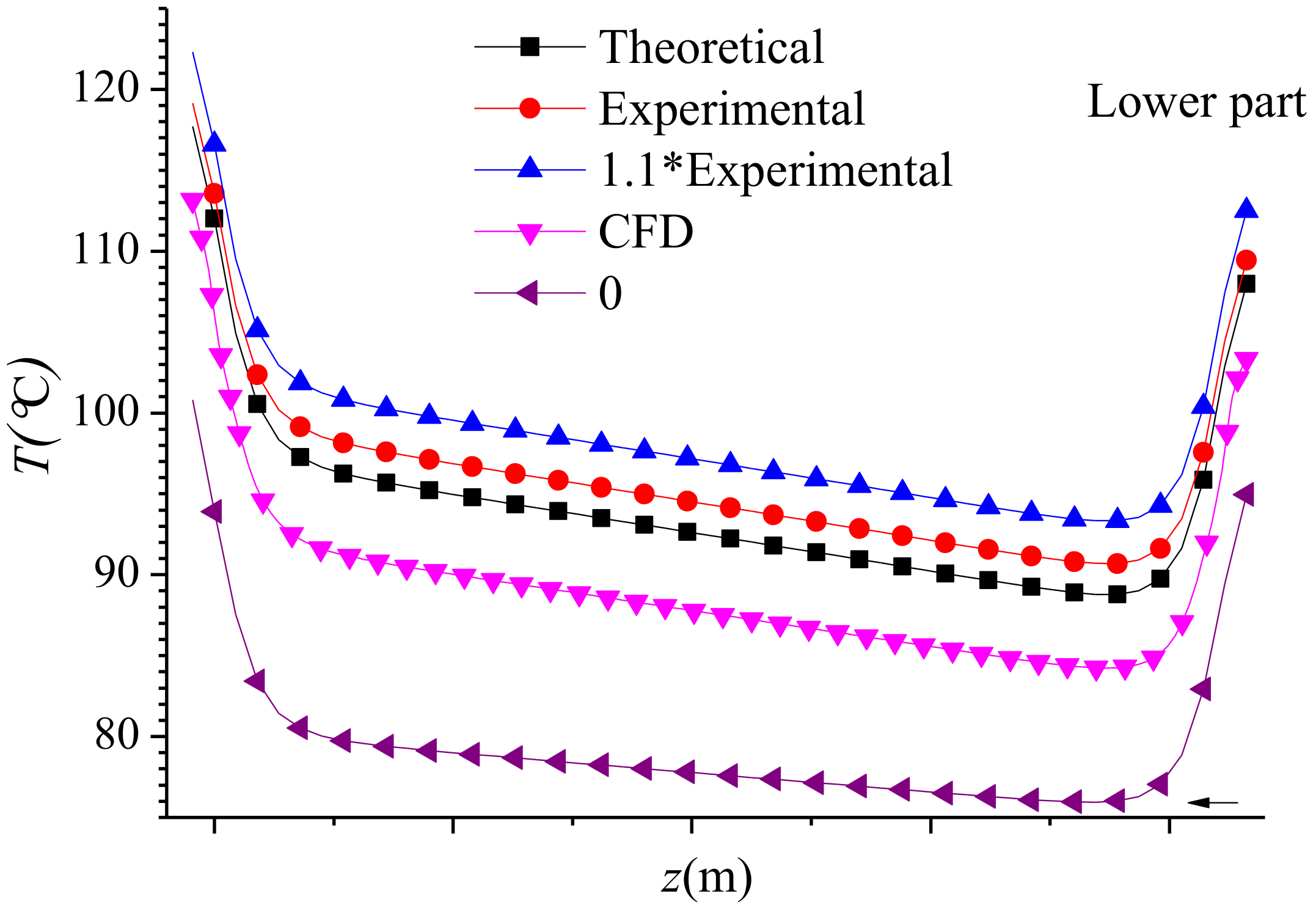
4.2. Temperature Analysis of the Primary Water Passage
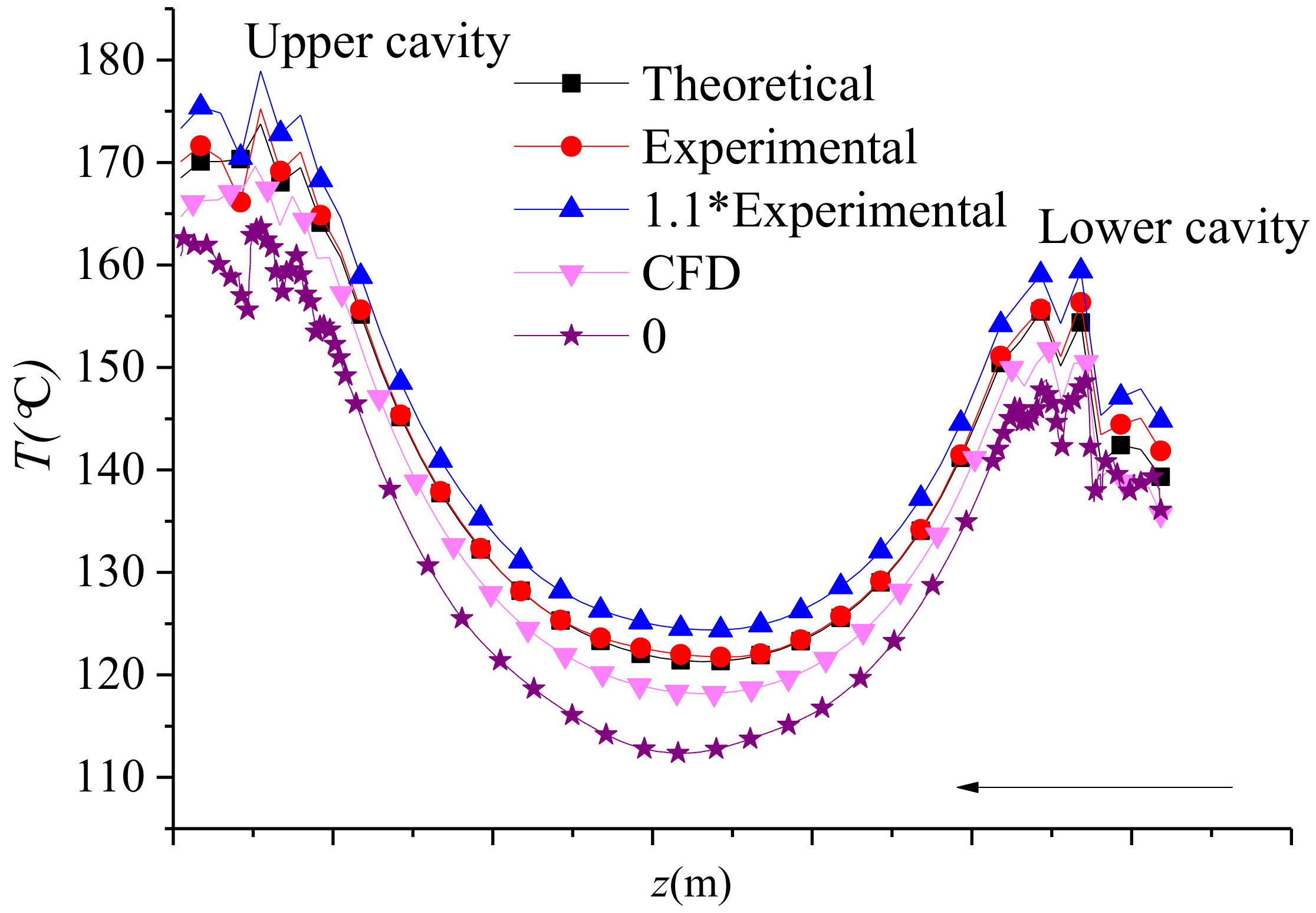
4.3. Temperature Analysis of the Rotor Copper Bar
4.4. Temperature Analysis of the Rotor Iron Core
4.5. Accuracy Analysis of Temperature Calculation Results
5. Conclusions
- The peak temperature of the motor winding was lower by −4.2% as compared to the water friction loss calculated by CFD with the proposed water friction loss per unit volume method. This method of, i.e., using given experimental water friction loss per unit volume as the source term did not change the characteristics of the temperature distribution of the components of the motor and intercooling water.
- The temperature along the axial direction increased with the increase of friction loss at the same position of the rotor copper bar, rotor iron core, and for water in the clearance of double cans, and the tendency of the temperature distribution increased linearly along the axial direction where the shield was located.
- The temperature distribution of the winding presented a concave curve, and the lowest temperature point in the upper and lower winding was near the axial center of the winding.
- For the water-cooled shielded motor, the water friction loss cannot be ignored. The calculation method of the water friction loss had a great influence on the conclusion about whether the water of the upper guide bearing was over temperature.
Author Contributions
Funding
Conflicts of Interest
References
- Boglietti, A.; Cavagnino, A. Evolution and modern approaches for thermal analysis of electrical machines. IEEE Trans. Ind. Electron. 2009, 56, 871–882. [Google Scholar] [CrossRef]
- Yetgin, A.G. Effects of induction motor end ring faults on motor performance. Experimental results. Eng. Fail. Anal. 2009, 96, 374–383. [Google Scholar] [CrossRef]
- Liang, Y.; Bian, X.; Yu, H.; Li, C. Finite-element evaluation and eddy-current loss decrease in stator end metallic parts of a large double-canned induction motor. IEEE Trans. Ind. Electron. 2015, 62, 6779–6785. [Google Scholar] [CrossRef]
- Huang, Z.; Fang, J.; Liu, X.; Han, B. Loss calculation and thermal analysis of rotors supported by active magnetic bearings for high-speed permanent-magnet electrical machines. IEEE Trans. Ind. Electron. 2016, 63, 2027–2035. [Google Scholar] [CrossRef]
- Chiu, H.C.; Jang, J.H.; Yan, W.M.; Shiao, R.B. Thermal performance analysis of a 30 kW switched reluctance motor. Int. J. Heat Mass Tran. 2017, 114, 145–154. [Google Scholar] [CrossRef]
- Kim, C.; Lee, K.S. Thermal nexus model for the thermal characteristic analysis of an open-type air-cooled induction motor. Appl. Therm. Eng. 2017, 112, 1108–1116. [Google Scholar] [CrossRef]
- Kim, C.; Lee, K.S. Numerical investigation of the air-gap flow heating phenomena in large-capacity induction motors. Int. J. Heat Mass Tran. 2017, 110, 746–752. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, L.; Zhang, D. Simulation and analysis of thermal fields of rotor multislots for nonsalient-pole motor. IEEE Trans. Ind. Electron. 2015, 62, 7678–7686. [Google Scholar] [CrossRef]
- Lancial, N.; Torriano, F.; Beaubert, F.; Harmand, S.; Rolland, G. Study of a Taylor-Couette-Poiseuille flow in an annular channel with a slotted rotor. In Proceedings of the International Conference on Electrical Machines (ICEM), Hangzhou, China, 2–5 September 2014; pp. 1422–1429. [Google Scholar]
- Traxler-Samek, G.; Zickermann, R.; Schwery, A. Cooling airflow, losses, and temperatures in large air-cooled synchronous machines. IEEE Trans. Ind. Electron. 2010, 57, 172–180. [Google Scholar] [CrossRef]
- Tu, J.; Yeoh, G.H.; Liu, C. Computational Fluid Dynamics: A Practical Approach, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Luomi, J.; Zwyssig, C.; Looser, A.; Kolar, J.W. Efficiency optimization of a 100-W 500,000-r/min permanent-magnet machine including air-friction losses. IEEE Trans. Ind. Appl. 2009, 45, 1368–1377. [Google Scholar] [CrossRef]
- Gengji, W.; Ping, W. Rotor loss analysis of PMSM in flywheel energy storage system as uninterruptable power supply. IEEE Trans. Appl. Superconduct. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Aglen, O.; Andersson, A. Thermal analysis of a high-speed generator. In Proceedings of the 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, Salt Lake City, UT, USA, 12–16 October 2003; Volume 1, pp. 547–554. [Google Scholar]
- Le, Y.; Sun, J.; Han, B. Modeling and design of 3-DOF magnetic bearing for high-speed motor including eddy-current effects and leakage effects. IEEE Trans. Ind. Electron. 2016, 63, 3656–3665. [Google Scholar] [CrossRef]
- Zhang, F.; Du, G.; Wang, T.; Wang, F.; Cao, W.; Kirtley, J.L. Electromagnetic design and loss calculations of a 1.12-MW high-speed permanent-magnet motor for compressor applications. IEEE Trans. Energy Convers. 2016, 31, 132–140. [Google Scholar] [CrossRef]
- Lomax, H.; Pulliam, T.H.; Zingg, D.W. Fundamentals of Computational Fluid Dynamics, 1st ed.; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Heins, G.; Ionel, D.M.; Patterson, D.; Stretz, S.; Thiele, M. Combined experimental and numerical method for loss separation in permanent-magnet brushless machines. IEEE Trans. Ind. Appl. 2016, 52, 1405–1412. [Google Scholar] [CrossRef]
- Saari, J. Thermal Analysis of High-Speed Induction Machines. Ph.D. Dissertation, Department of Electrical and Communications Engineering, Helsinki University of Technology, Espoo, Finland, 1998. [Google Scholar]


| Clearance Position | Assumed Value | Analysis Value | Test Value | Assumed Value |
|---|---|---|---|---|
| Shield sleeve | 0 | 384 | 407 | 407 × 1.1% |
| Upper radial bearing | 0 | 17 | 17 | 17 × 1.1% |
| Lower radial bearing | 0 | 17 | 17 | 17 × 1.1% |
| Upper fly wheel | 0 | 793 | 722 | 722 × 1.1% |
| Lower fly wheel | 0 | 580 | 690 | 690 × 1.1% |
| Auxiliary wheel | 0 | 7 | 7 | 7 × 1.1% |
| Total | 0 | 1798 | 1860 | 2046 |
| CFD | Assumed | Analysis | Test | Assumed Value | |
|---|---|---|---|---|---|
| Models-viscous-(SST) k-ω | on | on | on | on | on |
| Models-energy | on | on | on | on | on |
| Options-viscous heating | on | off | off | off | off |
| Boundary condition-moving wall | set | - | - | - | - |
| Shear condition | no slip | - | - | - | - |
| Wall roughness (mm) | 1.0 | - | - | - | - |
| Source item in water clearance region (kW/m3) | - | - | on | on | on |
| Components | Loss (kW) |
|---|---|
| Rotor copper bar | 72.0 |
| Rotor shield (casing) | 262.57 |
| Stator winding | 44.54 |
| Stator shield (casing) | 920.58 |
| Conical ring | 28.53 |
| Rotor copper bar | 72.0 |
| Rotor shield (casing) | 262.57 |
| Stator winding | 44.54 |
| Stator shield (casing) | 920.58 |
| Conical ring | 28.53 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Mustafa, A.; Abdullah Rehan, M.; Razzaq, S.; Ali, S.; Shahid, M.; Waleed Adnan, A. The Effects of Water Friction Loss Calculation on the Thermal Field of the Canned Motor. Processes 2019, 7, 256. https://doi.org/10.3390/pr7050256
Lu Y, Mustafa A, Abdullah Rehan M, Razzaq S, Ali S, Shahid M, Waleed Adnan A. The Effects of Water Friction Loss Calculation on the Thermal Field of the Canned Motor. Processes. 2019; 7(5):256. https://doi.org/10.3390/pr7050256
Chicago/Turabian StyleLu, Yiping, Azeem Mustafa, Mirza Abdullah Rehan, Samia Razzaq, Shoukat Ali, Mughees Shahid, and Ahmad Waleed Adnan. 2019. "The Effects of Water Friction Loss Calculation on the Thermal Field of the Canned Motor" Processes 7, no. 5: 256. https://doi.org/10.3390/pr7050256
APA StyleLu, Y., Mustafa, A., Abdullah Rehan, M., Razzaq, S., Ali, S., Shahid, M., & Waleed Adnan, A. (2019). The Effects of Water Friction Loss Calculation on the Thermal Field of the Canned Motor. Processes, 7(5), 256. https://doi.org/10.3390/pr7050256





