Optimal Design of a Carbon Dioxide Separation Process with Market Uncertainty and Waste Reduction

Abstract

The aim of this work is to optimize the conceptual design of an amine-based carbon dioxide (CO₂) separation process for Enhanced Oil Recovery (EOR). A systematic approach is applied to predict the economic profitability of the system while reducing the environmental impacts. Firstly, we model the process with UniSim and determine the governing degrees of freedom (DoF) through a sensitivity analysis. Then, we proceed with the formulation of the economic problem, where the employment of econometric models allows us to predict the highest dynamic economic potential (DEP). In the second part, we apply the Waste Reduction (WAR) algorithm to quantify the environmental risks of the studied process. This method is based on the minimization of the potential environmental indicator (PEI) by using the generalization of the Waste Reduction algorithm. Results show that the CO₂ separation plant is promising in terms of economic revenues. However, the PEI value indicates that the higher the profitability, the larger the environmental risk. The optimal value of the DEP corresponds to 0.0274 kmol/h and 60 °C, with a plant capacity according to the mole flow rate of the produced acid gas. In addition, the highest environmental risk is observed at the upper bounds of the DoF.

1. Introduction

Several stages exist to recover the original pressure of mature oil and gas wells. Among those already applied, the Enhanced Oil Recovery (EOR) with carbon dioxide (CO₂) proved to be a mid-term solution to increase the oil production to its original levels while capturing thousands of tonnes of CO₂ [1,2].

Haszeldine [3] states that the first injections of carbon dioxide into the microscopic pores of sedimentary rocks date from the early 1970s. Successful cases of CO₂-EOR have been reported in the United States, United Kingdom, Norway, and Canada by Wright et al. [4] and Mumford et al. [5]. The injection of CO₂ was also evaluated in the reservoirs of Argentina, a region where EOR pilot experiences were barely intended. Although the results provided good revenues, the CO₂-EOR in the region remains unmaterialized after more than twenty years since first being discussed [6].

The main problem related to this procedure is the large and continuous amount of CO₂ necessary to start the EOR injection [7]. In this regard, Herzog [8] reports that the common sources for large amounts of CO₂ correspond to the acid gas coming from natural gas processing.

Kwak et al. [9] compare different technologies for CO₂ separation from natural gas. Based on simulation and economic studies, they conclude that chemical absorption with methyldiethanolamine (MDEA) is the least expensive and most feasible option to separate carbon dioxide. Moreover, Leung et al. [10] note the amine processes’ high efficiency, large amounts of acid gas as a side product, and the possibility to regenerate the solvent. Other comparable processes include separation with polymeric membranes, cryogenic separation, physical solvents, and hybrid technologies.

Another task when evaluating CO₂-EOR possibilities is the large dependence of oil and gas companies upon economic conditions and countries’ institutional frameworks [11]. For instance, Ponzo et al. [12] state that changing market structures influence the long-term evolution of gas quotations and, consequently, the development of gas fields. Moreover, interdependency among variations of time with technical, operative, and economic conditions has been assigned to perform economic evaluation by Manolas et al. [13]. Classically, the interaction between the operating aspects and economic revenues during the definition of a process is first estimated according to the conventional conceptual design [14]. Conceptual process design (CD) consists of the selection of proper operation units, their sequences, and the recycling structure needed to obtain a specified product [15]. However, Sepiacci et al. [16] explain that this conventional method is no longer representative when considering market uncertainty, demand and offer fluctuations, and the price instability of commodities and utilities. Then, Manca and Grana [17] introduced the benefits of dynamic conceptual design (DCD). Based on CD and the economic potentials (EP) presented by [14], DCD takes into account the dynamic features of price/cost fluctuations within a given time horizon.

Indeed, the process design of chemical industries are considered complete when performing the environmental risk analysis of new process systems. Currently, there is a great deal of interest in the development of methods that can be used to minimize the generation of pollution, and there are numerous efforts underway in this area [18]. Specifically, this interest has increased with the world’s awareness of CO₂ emissions and made process engineering adopt practices to mitigate the effects of climate change [19].

For the above reasons, we apply the concept of DCD to obtain and condition CO₂ for EOR purposes. As can be anticipated, we focus our study to establish the conceptual design of the process in the context of market instability and future uncertainties. CO₂ for EOR is obtained from a natural gas sweetening design that uses MDEA as solvent; the specifications for the produced CO₂ include a 95 mol% concentration of the acid gas, compressed at 6500 kPa [20].

An optimization problem is formulated with the aim of minimizing the Dynamic Economic Potential (DEP) of the design. In this sense, Mores et al. [21] state that two degrees of freedom (DoF) govern the optimization problem of the CO₂ MDEA absorption—the recycled amine flow rate and its temperature. However, we extend the analysis to prove that the variable most affecting the energy demands of the plant is the water makeup of the amine solution, and thus more proper DoF.

Then, we analyze the historical prices of products and raw materials by using statistical tools. We present natural gas prices as references to estimate the evolution of the rest of the involved components by using numerical correlations. Linear Regression Models (such as AutoRegressive model with an eXternal input, ARX) are applied to interpret the behavior of past quotations. We switch the contribution of these economic models into econometrics to make them capable of predicting quotations and generating future market scenarios.

On the other hand, we perform an assessment to find the pair of DoF that reduce the environmental potential index. The method is adapted from the Waste-Reduction algorithm applied to chemical processes presented by Young et al. [22]. The Waste Reduction (WAR) algorithm has been developed to describe the flow and the generation of potential environmental impact through a chemical process.

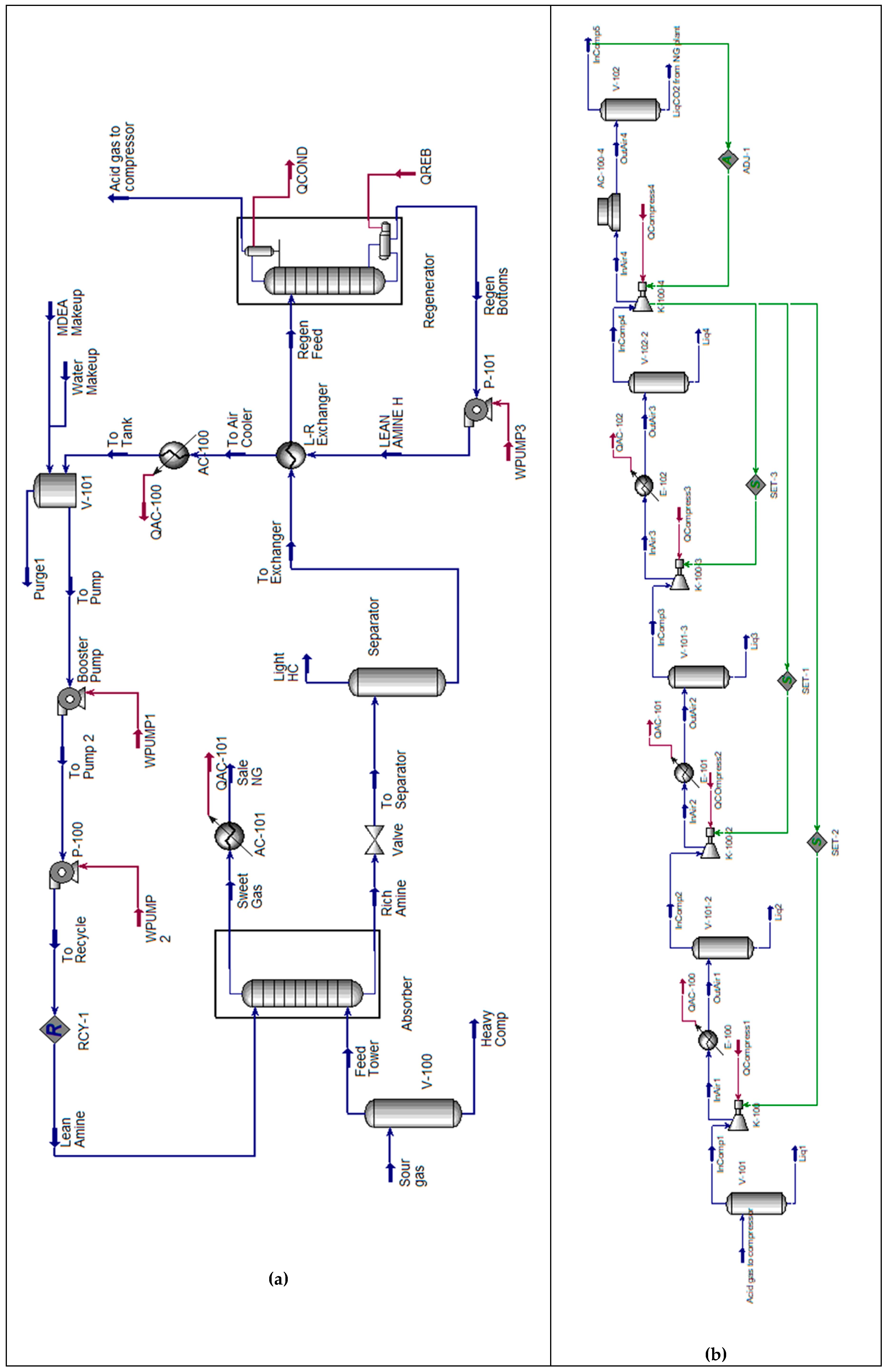
2. Process Description

The purpose of a natural gas sweetening process is to remove the acid gases from a sour natural gas stream. Due to the high selectivity of the solvent, the by-product of this process is a high-purity CO₂ material stream that, after conditioning, can be used as an EOR fluid.

The regular process of natural gas sweetening to obtain CO₂ is divided into two parts [23]. In the first stage, which consists of an absorber column, the natural acid is put in countercurrent contact with a descending MDEA aqueous solution—a so-called lean amine [24]. Fouad and Berrouk [25] and Kazemi et al. [26] indicate that low temperatures and high pressures favor the exothermic reaction that occurs in the unit. After contact, the aqueous solution of amine is pressurized, heated, and sent to the regeneration stage [27]. This second stage consists of a distillation column where the acid gas is removed from the amine solution due to an external heat contribution. Different studies have been performed in order to optimize the energy requirements of the regeneration column [28,29,30]. The liquid from the regenerator column is cooled and pumped back to the absorption stage [31,32]. Water and MDEA are placed in the stream from the bottom of the column to the absorption tower to compensate for leaks within the operation. Meanwhile, the high-purity CO₂ from the top of the regenerator is sent to a series of four centrifugal compressors to considerably increase the pressure. Original well pressures are required to dispose of the CO₂ as an injection fluid; in this case the value remains over 6500 kPa. The 4-stage compression design includes intercooling units and intermediate separation stages [33].

3. Methods

3.1. Simulation Base Case

A process of CO₂ absorption and compression is modeled by using UniSim [34]. Natural gas at a value of 2500 mm³/d is assumed as the plant’s capacity. The conditions of the plant are those reported in the work of Gutierrez et al. [19]: sour natural gas at 35 °C and 6178 kPa with 93 and 4 mol% of CH₄ and CO₂, respectively. Also, the conditions of the lean amine are reproduced. We consider 21,000 kmol/h of an aqueous MDEA solution (38 wt%), at 42 °C and 9610 kPa. A 24-tray absorption column operates at the pressure of the inlet gas. Rich MDEA from the bottom of the absorber is flashed at 441 kPa, heated up to 90 °C, and then sent to regeneration. The regeneration column consists of 24 trays and operates at 90 °C and 443 kPa. To provide the column with an external heat, we assume a reboiler unit using natural gas as fuel. Recycled MDEA is pumped and cooled, first exchanging heat with the rich amine, and then with a cooler so that it reproduces the temperature of absorption.

A 4-stage compression system is employed to increase the pressure of the produced CO₂ up to 6865 kPa [33]. Figure 1 shows the simulation of (a) the CO₂ separation plant and (b) the compression sector to produce the high-purity CO₂ stream.

Muhammad and GadelHak [35] explain that the main variables affecting CO₂ absorption are solvent flow rate and the absorber temperature, this last through the cooling of the lean amine stream.

As we anticipated, two streams conform the solvent inlet flow stream, one corresponding to a pure MDEA stream and the other connected to the makeup water. Generally speaking, two independent variables are related to the same degree of freedom, so in this study we determine whether there is a strong dependency between the main energy requirements and the independent variables. Similar to Torres-Ortega et al. [36], we perform a sensitivity analysis to evaluate suitable ranges of variation for the decision variables along the optimization.

3.2. Predictive Concept Design

This section provides the dynamic approach to the economic assessment for the CO₂ conditioning plant. Econometrics models (EM) are employed to simulate and evaluate future trajectories of prices and costs.

3.2.1. Development of Econometric Models

The first step while performing EM is the selection of a reference component (RC). Manca [37] employs RC historical quotations to estimate the economic dynamics of all commodities and utilities in the process he analyzed. Moreover, Manca [38] suggests that an RC must be representative of the sector where the plant operates, with the availability of frequent data and updated price evolution.

A good RC for the industry of Oil and Gas is crude oil (CO) [39]. CO, and also the evolution of natural gas (NG), quotations are traced daily for EIA [40]. However, the prices of natural gas produced in the basins of Argentina are also indicated monthly by the Ministry of Energy [41]. In this study, we perform the EM for both CO and NG as potential candidates for reference components.

A structural auto regression model is applied to separately autocorrelate both West Texas Intermediate (WTI) crude oil and US natural gas prices [42]. For both potential candidates, we analyze monthly quotations from July, 2007 to July, 2017 (the last available date). To correlate the historical values of the quotations, we use a similar methodology as the one used by Zhou et al. [43] regarding the coefficients of the Pearson equation (Equation (1)). Pearson coefficients (PCs) measure the strength and direction of the linear relationship between two random variables [44]. In this case, both variables represent the monthly quotations of the RC, but differ in one period:

$$r_k=\frac{{{\displaystyle \sum }}_{t=k+1}\left(Y_t-\overline{Y}\right)\left(Y_{t-k}-\overline{Y}\right)}{{{\displaystyle \sum }}_{t=1}^n{\left(Y_t-\overline{Y}\right)}^2}$$

(1)

where $r_k$ denotes the PC for a particular period. ${{\displaystyle \sum }}_{t=k+1}\left(Y_t-\overline{Y}\right)\left(Y_{t-k}-\overline{Y}\right)$ is the covariance of the quotations ($Y_t$) with respect to one-period of the previous quotations ($Y_{t-k}$), and ${{\displaystyle \sum }}_{t=1}^n{\left(Y_t-\overline{Y}\right)}^2$ is the squared of the standard deviation. $r_k$ varies from –1 to 1 and, in general, the higher the correlation coefficient, the stronger the relationship is [45]. Dancey and Reidy [46] state that if $r_k$ ranges from 0.7 to 0.9, the strength of correlation is high, and quite enough to determine the size of the correlation. This characteristic can be visualized when plotting the coefficient versus the time lag between the quotations.

3.2.2. Formulation of the Economic Optimization

Once the EM are identified, it is viable to run the grid-search optimization according to the regular process conceptual design (PCD). In the optimization problem, we determine the set of DoF that maximizes the cumulated value of the Dynamic Economic Potential of order four (DEP4), Equations (2)–(4).

$${\left(Cumulated\right)}_i={\displaystyle \sum }_{j=1}^{N}DEP{4}_{j,i}; i=1,\dots ,I$$

(2)

$$DEP{4}_i\left(\frac{USD}{y}\right)={\displaystyle \sum }_{j=1}^{N}Revenue{s}_{j,i}·nHpY-\frac{CAPEX}{N/12}$$

(3)

$$Revenue{s}_{j,i}\left(\frac{USD}{y}\right)={\displaystyle \sum }_{p=1}^{NP}{C}_{p,j,i}·F_P-{\displaystyle \sum }_{r=1}^{NR}{C}_{r,j,i}·F_r-OPE{X}_{j,i}$$

(4)

where $DEP4$ is the fourth-level economic potential calculated for the $i-th$ economic scenario. $j,i$ are the subscripts for a specific month and scenario, respectively; $nHpY$ is the number of working hours per year. N stands for the number of months to perform the economic assessment. $NP$, $NR$, $F_P$, and $F_r$ represent the number of products and reactants, their flow rates, and $C$ their costs. The $CAPEX$ term is estimated according to the empirical equations reported by Douglas [14]. Six main units are considered for the calculation: absorber and distillation columns, MDEA heat exchanger, and two air coolers.

The $OPEX$ term considers a price trajectory for each raw material, by-product, and utility, for the $i-th$ scenario. The main contributors of the $OPEX$ are two air coolers, a condenser, reboiler fuel, and the total power required for the acid gas compressors (Gutierrez et al. [19]). The material and energy balances required to calculate the $OPEX$ are taken from the steady-state simulation of the process.

The goal of the optimization is to determine the combination of DoF that maximizes the value of ${\left(Cumulated\right)}_i$, with respect to a set of generated scenarios, where the assessment becomes probabilistic. To obtain a high-purity CO₂ material stream, Gutierrez et al. [19] use a limit value of 2 mol% in the gas coming from the top of the absorber, so we consider the molar fraction of CO₂ as a restriction for the stated problem.

3.3. Waste Reduction Algorithm

We employ the Waste Reduction (WAR) algorithm to describe the flow and the generation potential environmental impact through the process under study [22]. The general methodology of the WAR algorithm defines Potential Environmental Impact (PEI) indexes to characterize the generation of the potential impact in a process, divided into eight categories.

The first four categories evaluate, globally, the environmental friendliness of a process: human toxicity potential by ingestion (HTPI), human toxicity potential by exposure (both dermal and inhalation) (HTPE), terrestrial toxicity potential (TTP), and aquatic toxicity potential (ATP).

On the other hand, the other four are related to the toxicological aspects of the involved chemicals within the process: global warming potential (GWP), ozone depletion potential (ODP), photochemical oxidation potential (PCOP), and acidification potential (AP).

The potential environmental impacts are calculated from stream mass flow rates, stream composition, and a relative potential environmental impact score for each chemical present in the separation process [18].

According to the notation of Young and Cabezas [47], the output PEI to the chemical process can be rewritten as Equation (5):

$$i_{out}^{\left(cp\right)}={\displaystyle \sum }_{w=1}^N{\dot{M}}_w^{\left(out\right)}{\displaystyle \sum }_i{x}_{i,w}{\psi }_i$$

(5)

$${\psi }_k={\displaystyle \sum }_l{\alpha }_l{\psi }_{i,l}^s$$

(6)

where ${\dot{M}}_w^{\left(out\right)}$ is the output mass flow rate of stream $w$, $x_{i,w}$ is the mass fraction of the chemical $i$ in the stream is $w$, and ${\psi }_i$ is the overall PEI for the chemical $k$. ${\psi }_i$ can be calculated from Equation (6). In Equation (6), ${\psi }_{i,l}^s$ is the normalized specific PEI of chemical $k$ for the impact category $l$, and ${\alpha }_l$ is the relative weighing factor of impact category $l$ [39,47]. A unitary value is assigned to $\alpha$, to illustrate the case where the eight categories have the same importance in our evaluation [48]. Normalized impact scores are obtained from the WAR algorithm add-in included in the latest release of the CAPE-OPEN to CAPE-OPEN (COCO) Simulation Environment, available from http://www.cocosimulator.org/ [49].

4. Results

4.1. Simulation Output

Figure 2 reports the evolution of the main energy requirements, according to the variation of the independent variables. For this case, we present the reboiler requirement versus (a) the flow rate of the make-up of MDEA, (b) the make-up of water, and (c) the temperature of the recycled amine.

Figure 3 reports the evolution of the condenser energy requirement, according to the variation of the chosen independent variables. Again, we present the condenser requirement versus (a) the flow rate of the make-up of MDEA, (b) the make-up of water, and (c) the temperature of the recycled amine.

Figure 4 shows the evolution of the total compressor power (kW), respect to the variation of the same independent variables. We present the compressor power demand versus (a) the flow rate of the make-up of MDEA, (b) the make-up of water, and (c) the temperature of the recycled amine.

Figure 5 shows the evolution of the cooling system requirements (kW), with respect to the variation of the available variables. We present the energy demand of the coolers (AC-100 and AC-101) versus (a) the flow rate of the make-up of MDEA, (b) the make-up of water, and (c) the temperature of the recycled amine.

Figure 2, Figure 3, Figure 4 and Figure 5 expose a remarkable dependency between the main energy consumptions and the temperature of the recycled MDEA. Moreover, it was illustrated that the energy requirements strongly depend on the flow rate of the water make up. On the other hand, the variation of the MDEA flow rate proves to not alter the energy requirement of the reboiler, condenser, compressors, and the air-coolers. With this analysis, it is demonstrated that the proper DoF, representing the reduction of the recycle MDEA flow rate, corresponds to the water makeup of the process. Previous articles state that the decision variable is the recycled aqueous amine flowrate, but it is demonstrated here that the variable of most impact is the water make-up to conform to that flowrate. Thus, for the objective functions in this work, the decision variables are the water mole flow and the temperature of the recycled amine.

4.2. Economic Scenarios

Figure 6 shows the autocorrelograms (PC versus lag time) of (a) CO and (b) NG.

By analyzing the autocorrelograms shown in Figure 6, one can deduce that the CO quotation at the month $k+1$ depends mostly on the two previous quotations.

4.2.1. Correlation

In this subsection, we evaluate the relationship among all involved commodities with respect to the potential RC. In Figure 7, we expose the correlation between (a) CO₂, (b) MDEA, and (c) Electric Energy (EE) with respect to crude oil quotations. It can be seen that correlation values change in the range of [−1, 1]. If the two sets are perfectly correlated (e.g., are the same set), the correlation index is 1. On the contrary, if they are anti-correlated (e.g., the two sets have opposite trends), it is −1.

Figure 8 exposes the correlation between the same components and natural gas quotations. CO₂ quotations were estimated in accordance with the work presented by Cook [50]. It can be seen that values of correlation between the set of quotations present higher values compared to the ones obtained by correlating the crude oil. Then, NG is selected as a reference component and econometric model, as presented in Section 4.2.2.

4.2.2. Econometric Models

From Figure 7 and Figure 8, we observe better correlation indexes when comparing to the NG quotations. Then, the EM of NG as RC becomes the one expressed through Equation (5).

Where $P_{NG,k+1}$ is the monthly quotation of NG. $\sigma$ and $\overline{P}$ are the standard deviation of the prices and the average of relative errors, respectively. $rand$ is a stochastic function normally distributed, and $A$, $B$, and $C$ are adaptive parameters calculated with linear regression, minimizing the square error between real quotations and those predicted by the model [51].

Manca [38] reports EM for toluene, benzene, propylene, and cumene prices based on a dedicated (auto)correlogram analysis. According to our correlation indexes, we elaborate the EM for the CO₂ conditioning process.

Table 1. ADL EM for NG, CO₂, and MDEA prices, without the stochastic factor.

Component	Model
CO2	$P_{C{O}_2,k+1}=A+B·P_{NG,k+1}+C·P_{C{O}_2,k}+D·P_{C{O}_2,k-1}$
MDEA	$P_{MDEA,k+1}=A+B·P_{NG,k+1}+C·P_{MDEA,k}+D·P_{MDEA,k-1}$

presents Autoregressive Distributed Lag (ADL) models for estimating each quotation evolution, without the stochastic factor.

$$P_{NG,k+1}=\left(A+B·P_{NG,k}+C·P_{NG,k-1}\right)·\left(1+rand·{\sigma }_{NG}+{\overline{P}}_{NG}\right).$$

(7)

To simply the forecast EE quotations, we adopt previous monthly prices of the Ministry of Energy [41]. Similar to Manca [52], the EM for EE is based on (auto)correlograms and the economic dependency of the EE to NG. From these observations, it is feasible to apply the model represented by Equation (8):

$$P_{EE,k+1}=A+B·P_{NG,k}+C·P_{EE,k}$$

(8)

where the price of EE ($P_{EE,k+1}$) is estimated employing previous quotations of NG and EE.

Table 2. Adaptive parameters of ADL EM of NG, CO₂, and MDEA.

Component	$\mathit{A}$	$\mathit{B}$	$\mathit{C}$	$\mathit{D}$	$\mathit{\sigma }$	$\overline{\mathit{P}}$
NG	0.0362	−0.0285	1.2205	-	0.1918	0.0705
CO2	0.0033	0.0078	1.4167	−0.4870	0.0606	0.0074
MDEA	0.1124	0.9731	0	−0.0171	0.0126	0.0002

reports the adaptive coefficients, including the models of NG, CO₂, MDEA, and EE.

We use the EM of CO₂, MDEA and EE to generate a set of random economic scenarios. Figure 9 shows eight predicted trajectories from the EM of NG, MDEA, CO₂, and EE, during a time horizon of 120 months, in different random colors. It shows a probabilistic approach, based on a distribution of multiple viable economic scenarios.

Particularly for the case of the Electric Energy (Figure 9d), we present a brief predictive model where A = 2.98, B = 1.316, and C = 0.81 (Sepiacci et al. [16]), in Equation (8). The predictive nature of this model is given by its dependency with the forecasted prices of NG. Other reported models associate the EE prices with the crude oil quotations, but those forecasts are also of random variability [53]. The Electric Energy has a great impact as a process utility because of the type of its cooling equipment and compression system. Although the prices of the utility vary periodically with the time domain, we assume this simplified behavior for the scope of this article.

Each colorful line corresponds to random trajectories generated from the econometric models of Equations (6)–(8). The prices of each item can follow one of the colorful trajectories within the time horizon.

4.3. Optimal Economic and Environmental Friendly Design

Results concerning the optimal design of the CO₂ separation plant are shown in this section.

4.3.1. DEP4 Cumulated

Figure 10 shows, on the y-axis, the value of the cumulated DEP4 (USD), and on the x-axis it shows the time series of market quotations. Each bar represents the value of the DEP4 calculated by considering the market quotations of the corresponding month based on the specific plant configuration that maximizes the DEP4 value.

The generated models are used to produce a set of economic scenarios that are distributed according to the modeled fluctuations of quotations and the stochastic contribution of the reference component. The cornerstone of this methodology is symbolized by the number of scenarios that are called for quantifying a set of different scenarios subject to the price/cost trajectories obtained by the econometric models through their stochastic contribution (Random). Therefore, it refers to a probabilistic concept of PCD that is grounded in the distribution of possible economic scenarios for this specific process. A necessary condition for economic sustainability is that the DEPs are positive.

It can be seen that DEP4 varies, even to negative values, during the time domain. Each bar of the graph represents the higher value of EP4, corresponding to the best combination of the DoF, at one particular month. In general, the economic potential fluctuation strongly depends on the price volatility of raw materials and final products. Where positive, the obtained DEP4 is of an eight-power magnitude, which demonstrates the economic potential of the plant in accordance with the predictive models.

4.3.2. Economic Optimal

Figure 11 illustrates the trend of the cumulated DEP4 as a function of the DoF, the water flow make-up, and the temperature of the recycled amine. The presented surface represents the maximization of Equation (4), where a total capital expenditure of 1.44 × 10⁷ USD is estimated from the calculation. As previously stated, the DEP4 is not represented by a single value but by a distribution of values, one for each scenario. In order to have a simple representation of the economic objective function, we present the average value of the cumulated DEP4. The results of Equation (4) show that the average of the cumulated DEP4 reaches eight order values.

The configuration yielding the maximum value of the cumulated DEP4 corresponds to a temperature equal to 60 °C for the MDEA to recycle and value the water amine flow rate equal to 0.0274 kmol/h.

Based on this experience, high temperatures of MDEA imply that the conversion of the absorption reaction is increased and, consequently, the produced CO₂ is increased. Interestingly, an increment of the water flow rate proves that the MDEA concentration of 38 wt% can be modified to obtain a better performance in terms of the economical aspect of this process. At the same value of temperature, 60 °C, and 0.1074 kmol/h, the cumulated DEP4 is equal to 1.06 × 10⁸ USD. The order of magnitude of this DEP4 is even higher than the one obtained by Sepiacci et al. [16], who obtained a six-order DEP4 while applying this methodology in a petrochemical process.

4.3.3. Minimal Environmental Risks

Figure 12 shows the behavior of the PEI. In this case, the highest environmental risk is observed at the upper bounds of the DoF.

A probabilistic approach to future scenarios is concerned to find the combination of decisive DoF that maximizes the indicator of economic sustainability. Similarly, the potential environmental risk is also evaluated. Results show that this CO₂ separation design is promising, although the PEI indicates that the higher the profitability, the larger the environmental risk is. The environmental risk appears at high values of water make-up flow and recycle amine temperatures. This situation may be explained by the toxicological aspects of the involved chemicals within the process—an increase in the power of the cooling stage and modification of the reboiler combustion parameters.

5. Conclusions and Future Developments

This paper evaluates the process to obtain and condition CO₂ to be used as an EOR fluid, in the Argentine Basin of Neuquén. We focus the study on the evaluation of economic aspects in a context of market variability and price uncertainties. PCD methodology is adopted to achieve the aim of the article. With this technique, a probabilistic approach to future scenarios is used to find the combination of decisive DoF that maximizes the indicator of economic sustainability. According to the results, the implementation of the plant at this stage of the study is feasible and suggests promising values for revenues and economic profitability.

The results of this preliminary study are promising. The economic potential of the four order is proven to be high, with a magnitude of eight order in USD/y. Further, the statistical indexes prove that the plant is profitable within 12 years of the process time’s life. Finally, the conditions of the plant maximizing the EP are identified—a recycle amine flow of 0.0274 kmol/h at 60 °C proved to be an optimal combination of the decision variables. In respect to the ‘green’ risks, it is demonstrated that the higher the upper bounds of the DoF, the higher the environmental risk is.

The evaluation of DoF and their impact on the energy requirements of the plant have led to a notable conclusion—the decision variable affecting the consumer is the water makeup of the plant. Thus, a new perspective for authors working with a similar process is presented in this paper.

Future work can extend the limits of this methodology and include a higher number of DoFs, such as the ones related to the regeneration of the column, which is rarely discussed in the bibliography. In addition, the economic potential evaluation can be extended with heat integration coming from the pinch technology.

The last important aspect to be noted is that the CO₂ was historically considered to be a by-product, and in the past, it was a common practice to flare it. However, the recuperation and condition of this gas, and the installation of a proper plant operating at proper conditions, might be the starting point for implementing the technology of EOR in the region, taking into account volatile market scenarios.