A Novel MPC with Actuator Dynamic Compensation for the Marine Steam Turbine Rotational Control with a Novel Energy Dynamic Model
Abstract
1. Introduction
2. Materials and Methods
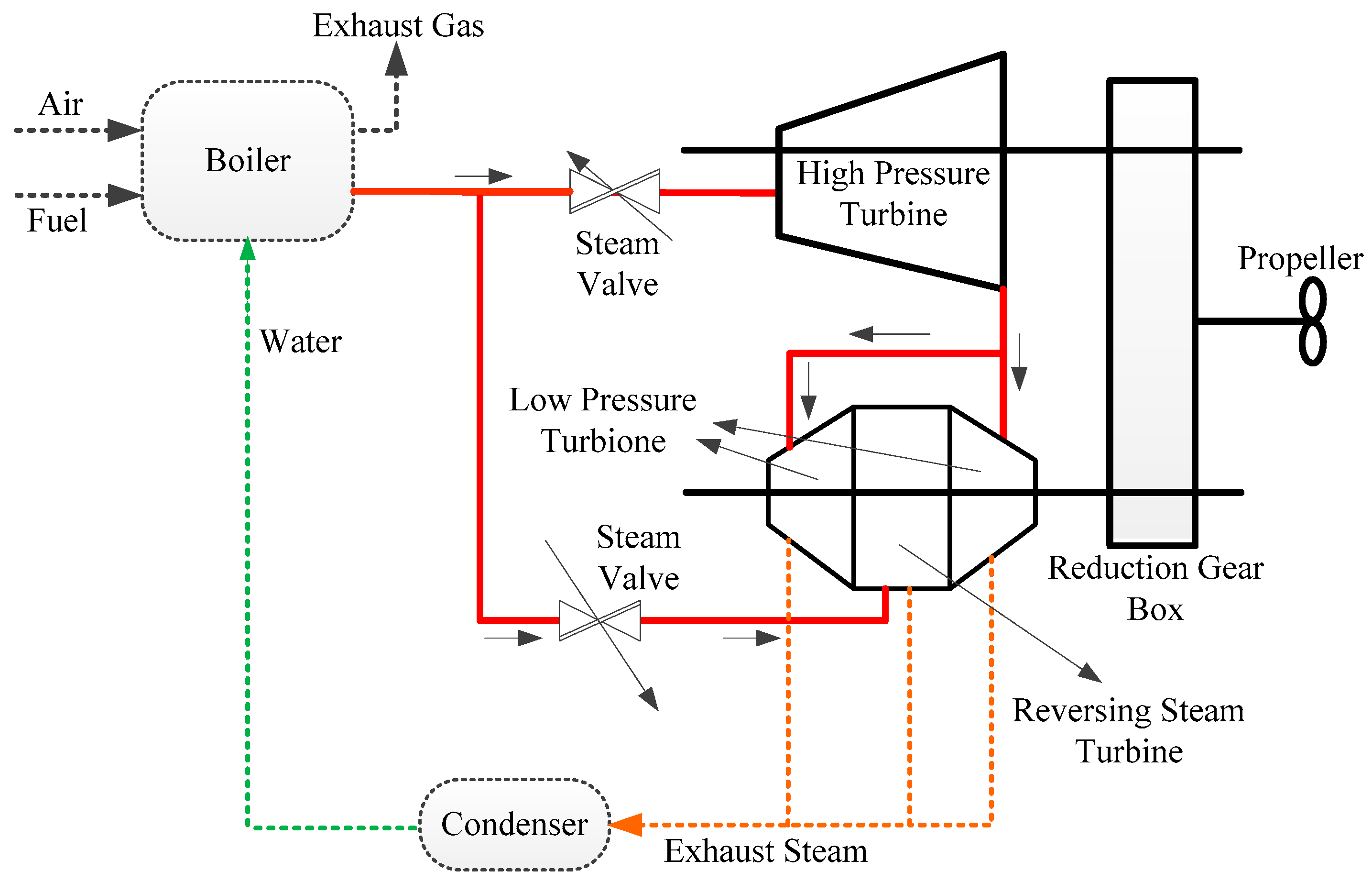
2.1. Marine Steam Turbine Rotational Control Modeling
PT(s) = KTu(t)
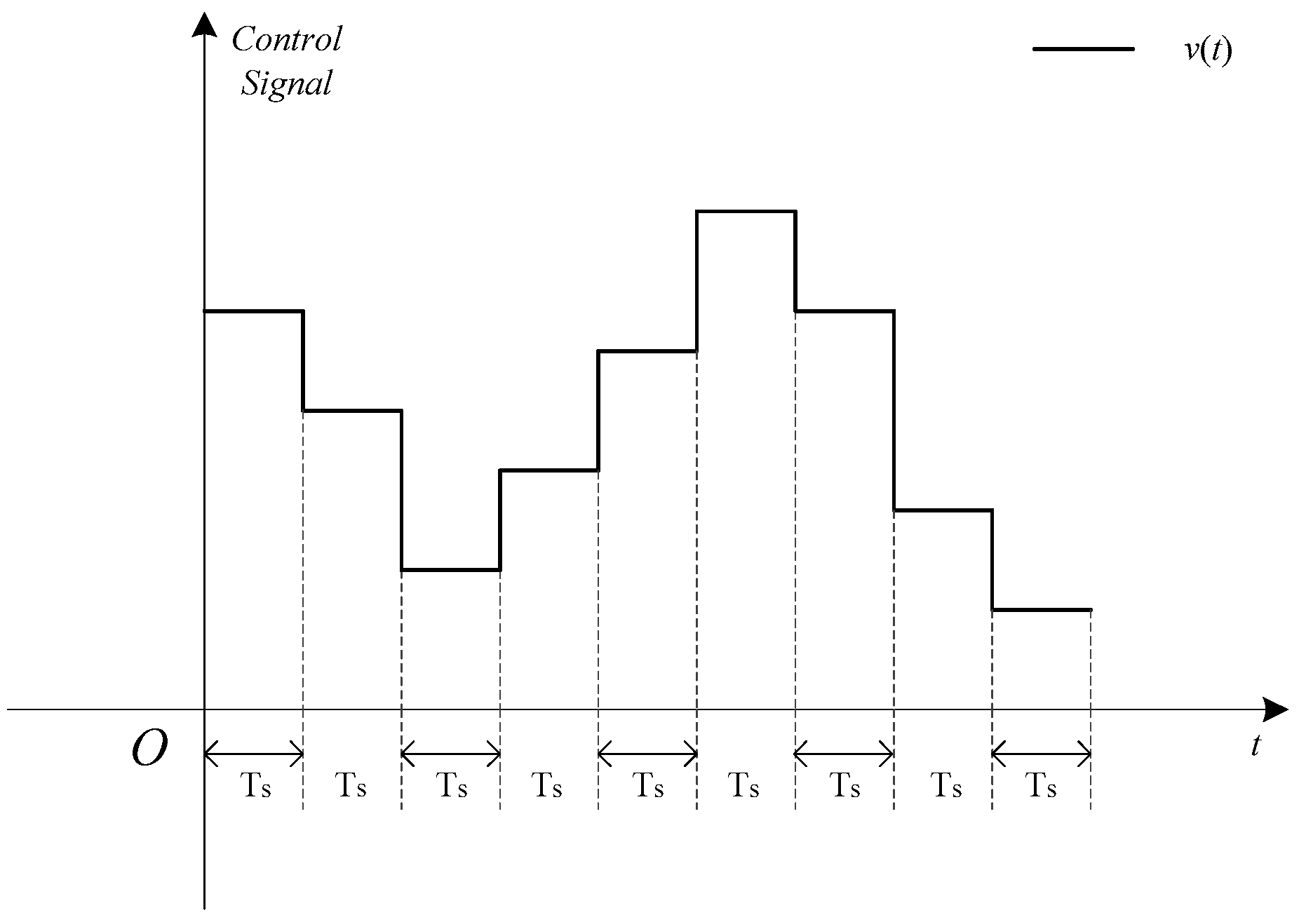
2.2. Formulation of the Control Problem
2.3. CMPC Algorithm
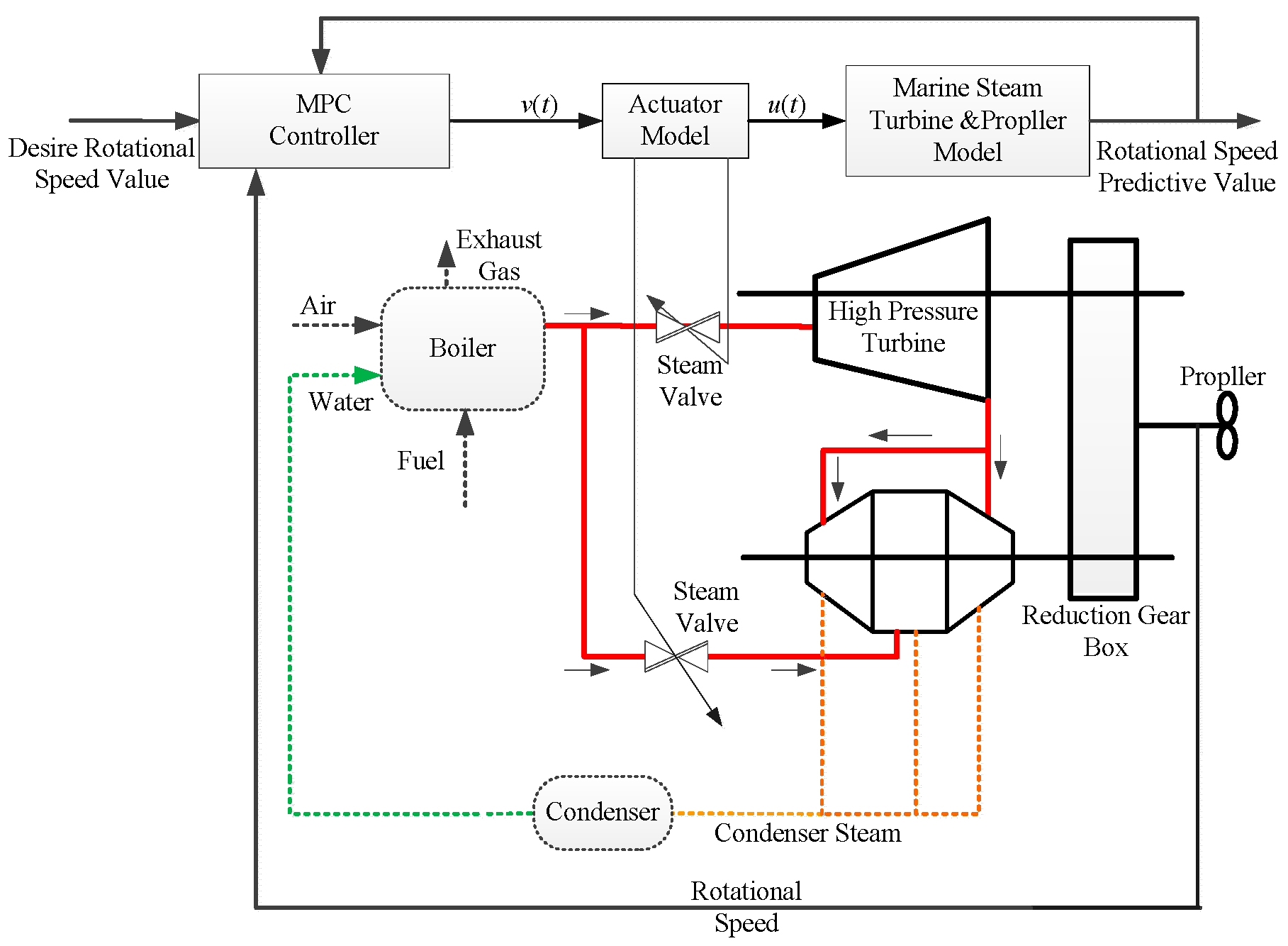
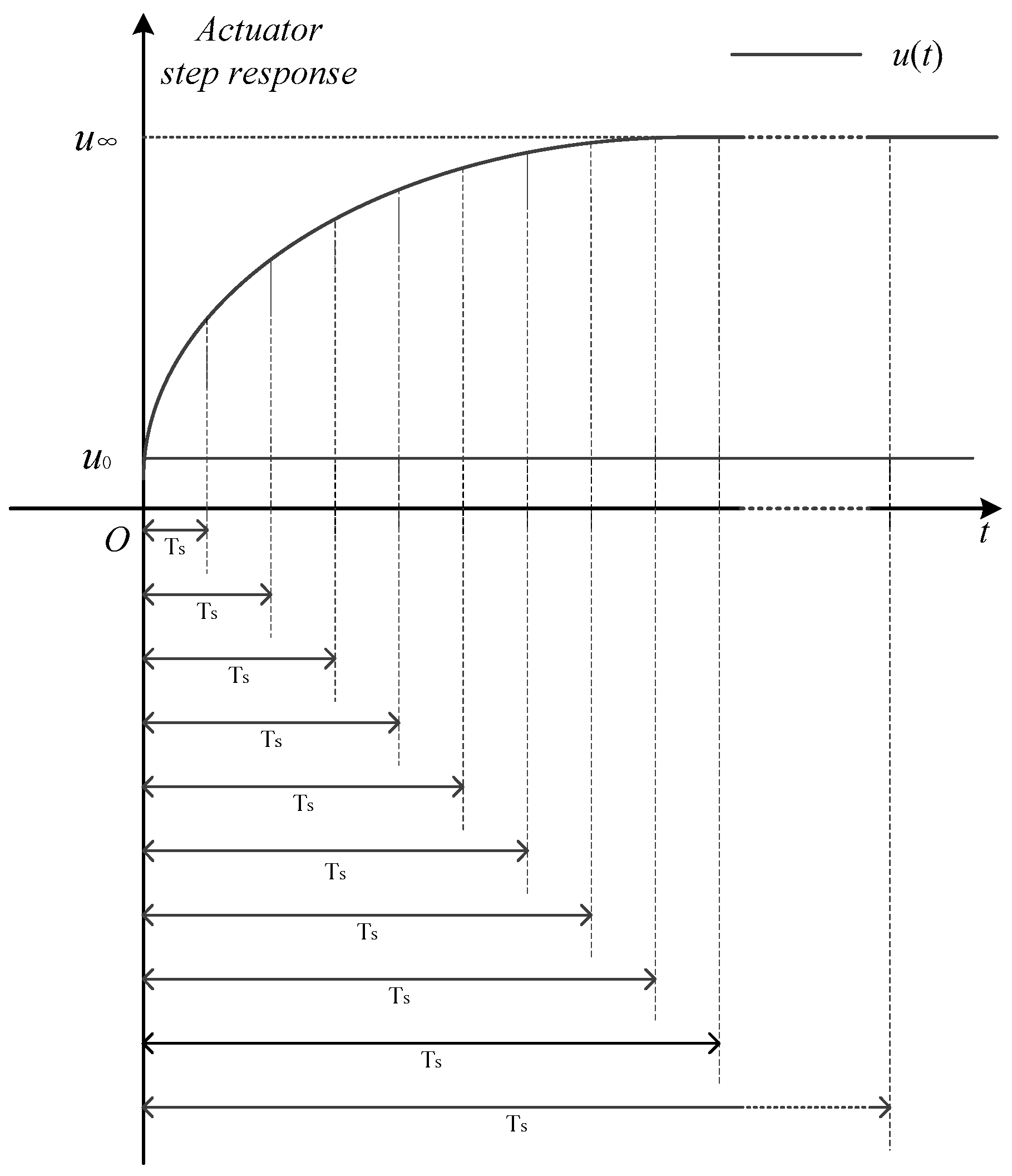
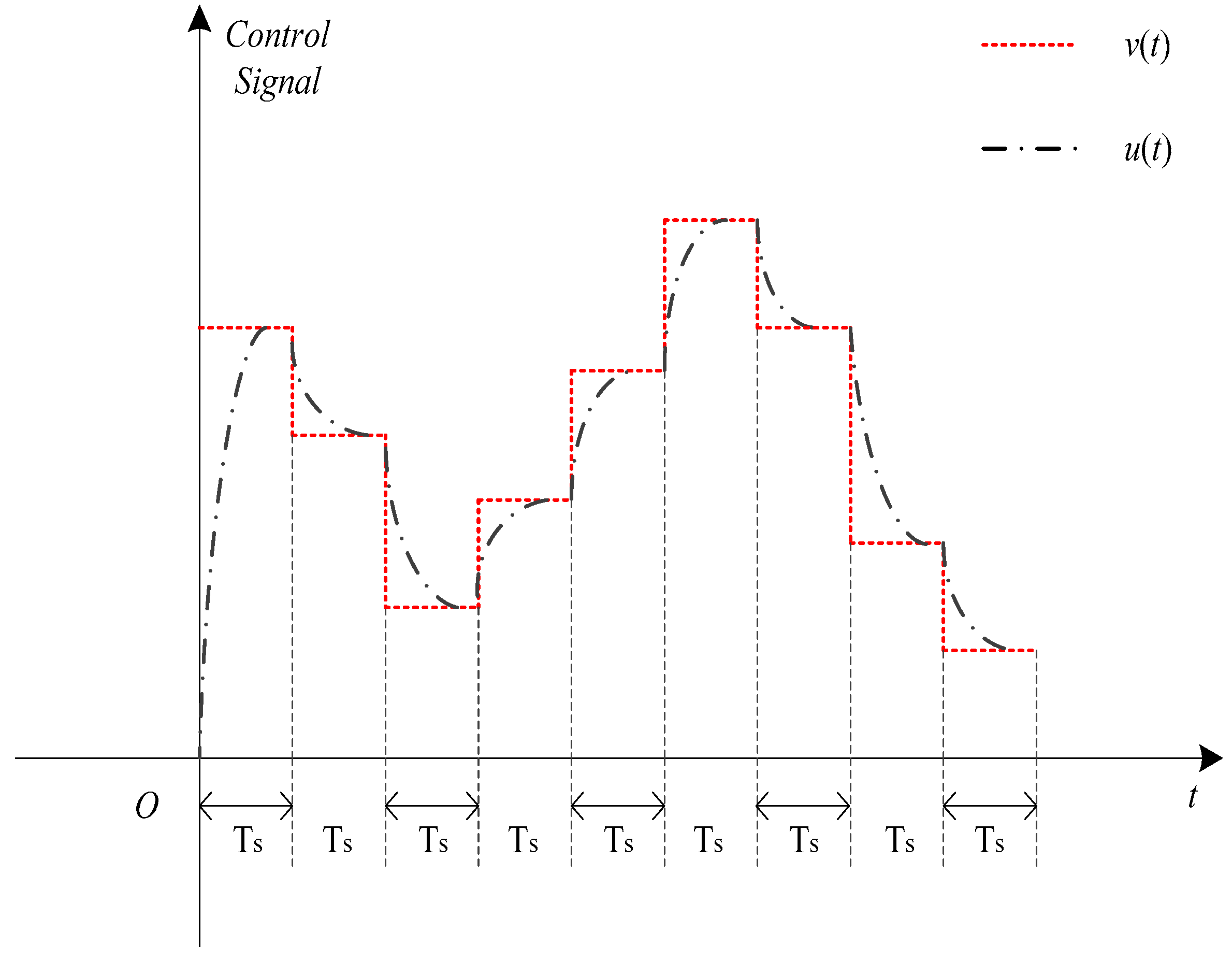
2.4. Actuator Compensation Predictive Control Algorithm
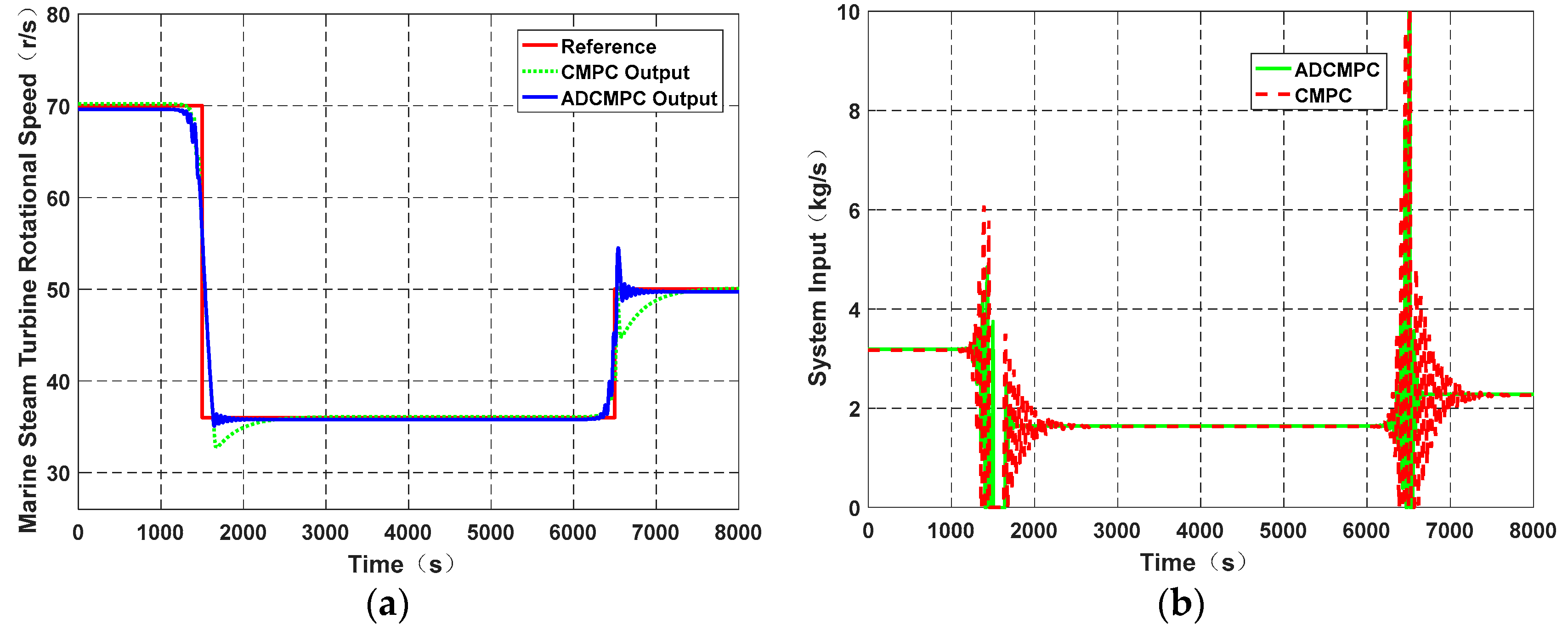
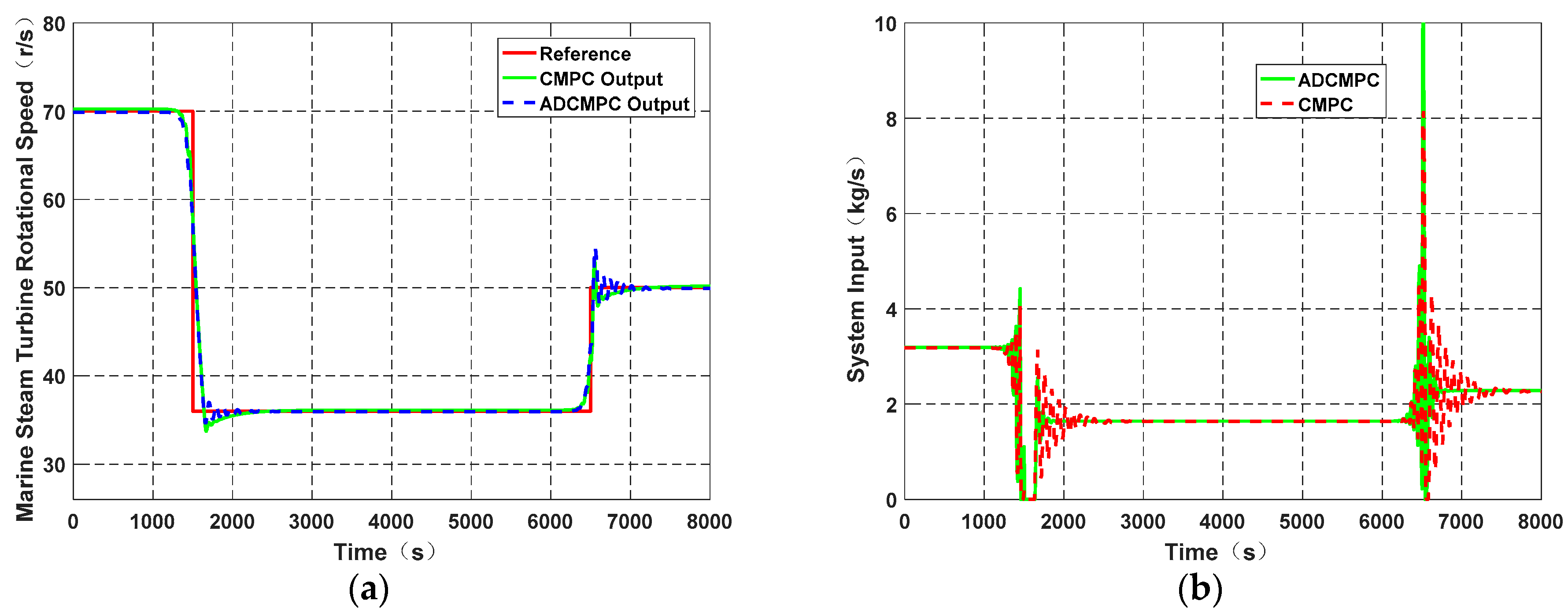
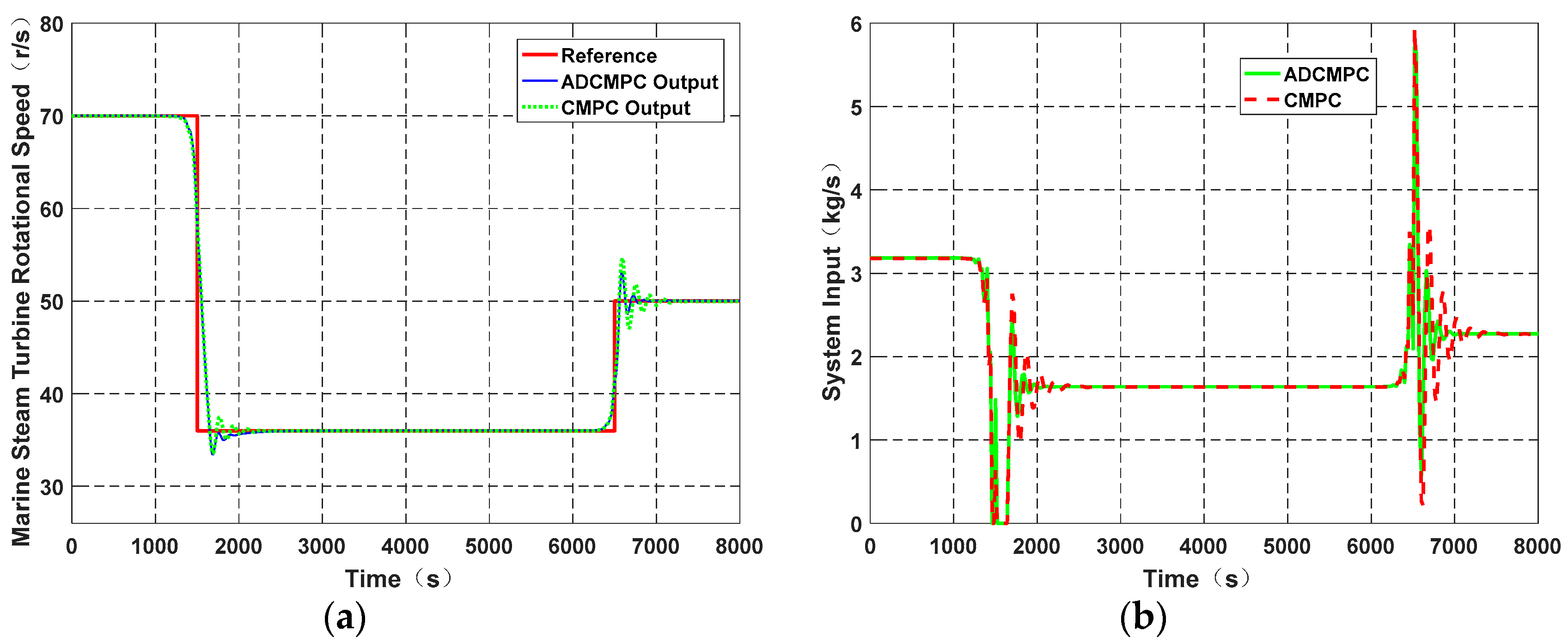
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Ts | Sampling period |
| V | The ship navigation speed |
| Fpropi | Thrust of the ith propeller |
| td | The dimensionless thrust deduction coefficient |
| Fdrag | The backward drafting force of a ship when it is sailing |
| m | The quality of the ship |
| ma | The dimensionless additional mass coefficient of the ship |
| Ek(t) | The rotational kinetic energy of MSTRSCS |
| PT(t) | The steam expansion work power in the marine steam turbine |
| PP(t) | The load power of the propeller |
| J∑ | The whole rotary inertia of MSTRSCS |
| KT | The total work done by the expansion of the unit mass steam in the marine steam turbine |
| nt(t) | The rotational speed of MSTRSCS |
| u(t) | The mass flow of the steam intake to the turbine |
| TP | The load torque of propeller |
| KQ | The dimensionless torque coefficient |
| ρ | The sea water density |
| D | The diameter of the propeller |
| κ | The drag coefficient of propeller |
| nmax | The maximum rotational speed |
| Δκ | Symbol of KQ(nmax − nt(t)) |
| y(t) | Symbol of n2t(t) |
| Y(s) | Laplace transform of y(t) |
| U(s) | Laplace transform of u(t) |
| v(t) | The control signal generated by the controller |
| T0 | The time constant of the actuator |
| K | Symbol of KT/κ |
| Nu | The control horizon |
| Ny | The prediction horizon |
| Q | Ny-dimensional positive definite diagonal matrix |
| R | Nu-dimensional positive definite diagonal matrix |
| J | Cost function of MPC |
References
- Xia, G.; Tang, Z.; Wang, Y.; Ren, L. Decoupling Coordinated Control System Based on PID Neural Network for Marine Steam Power Plant. In Proceedings of the 2009 WRI World Congress on Computer Science and Information Engineering, Los Angeles, CA, USA, 31 March–2 April 2009; pp. 116–120. [Google Scholar]
- Salamati, S.A.; Taghirad, H.D.; Chaibakhsh, A. Robust control of a steam turbine power based on a precise nonlinear model. In Proceedings of the 5th Conference on Thermal Power Plants, Tehran, Iran, 10–11 June 2014. [Google Scholar]
- Zhang, Y.; Zhu, Q. Predictive function control based on the LS-SVM for marine steam turbine system. In Proceedings of the Sixth International Conference on Natural Computation, ICNC 2010, Yantai, China, 10–12 August 2010. [Google Scholar]
- Kochummen, S.A.; Jaffar, N.E.; Nasar, A. Model Reference Adaptive Controller designs of steam turbine speed based on MIT Rule. In Proceedings of the 2015 International Conference on Control Communication & Computing India (ICCC), Trivandrum, India, 19–21 November 2015; pp. 7–11. [Google Scholar]
- Wu, K.; Zhang, T.; Lv, J.; Xiang, W. Model Predictive Control for Nonlinear Boiler-Turbine System Based on Fuzzy Gain Scheduling. In Proceedings of the IEEE International Conference on Automation and Logistics, Qingdao, China, 1–3 September 2008; pp. 1115–1120. [Google Scholar]
- Sun, J.H.; Wang, W.; Yu, H.Y. Turbine speed control system based on a fuzzy-PID. J. Mar. Sci. Appl. 2008, 7, 268–272. [Google Scholar] [CrossRef]
- Zhu, Q.; Yu, Z.; Zhang, J. Design of Fuzzy Neural Network Controller for Marine Steam Turbine System. In Proceedings of the Fourth International Conference on Natural Computation, Jinan, China, 18–20 October 2008. [Google Scholar]
- Liu, H.; Li, S.; Chai, T. Intelligent decoupling control of power plant main steam pressure and power output. Int. J. Electr. Power Energy Syst. 2003, 25, 809–819. [Google Scholar] [CrossRef]
- Liu, X.; Guan, P.; Chan, C.W. Nonlinear multivariable power plant coordinate control by constrained predictive scheme. IEEE Trans. Control Syst. Technol. 2010, 18, 1116–1125. [Google Scholar] [CrossRef]
- Li, S.; Lui, H.; Cai, W.-J.; Soh, Y.-C.; Xie, L.-H. A new coordinated control strategy for boiler-turbine system of coal-fired power plant. IEEE Trans. Control Syst. Technol. 2005, 13, 943–954. [Google Scholar]
- Åström, K.J.; Bell, R.D. Drum-boiler dynamics. Automatica 2000, 36, 363–378. [Google Scholar] [CrossRef]
- Åström, K.J.; Eklund, K. A simple non-linear drum boiler model. Int. J. Control 1975, 22, 739–740. [Google Scholar] [CrossRef]
- Bell, R.D.; Åström, K.J. Dynamics models for boiler-turbine alternator units: Data logs and parameter estimation for a 160 MW unit. Dept. Autom. Control Lund Inst. Technol. Lund Sweden Tech. Rep. 1987, TFRT-3192, 1–137. [Google Scholar]
- Tristan, P. Ship Motion Control: Course Keeping and Roll Stabilisation Using Rudder and Fins; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Zhang, L.J.; Jia, H.M.; Qi, X. NNFFC-adaptive output feedback trajectory tracking control for a surface ship at high speed. Ocean Eng. 2011, 38, 1430–1438. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Model Predictive Control; Springer: London, UK, 2004. [Google Scholar]
- Rechaler, J.; Richalet, J.; Rault, A.; Papon, J. Model Predictive Heuristic Control: Applications to Industrial processes. Automatica 1978, 14, 413–428. [Google Scholar]
- Rouhani, R.; Mehra, R.K. Model Algorithmic Control (MAC): Basic Theoretical properties. Automattica 1982, 18, 401–414. [Google Scholar] [CrossRef]
- Cutler, C.R.; Ramaker, B.L. Dnamic matrix control-a computer control algorithm. In Proceedings of the American Control Conference, San Francisco, CA, USA, 1 January 1980. [Google Scholar]
- Garcia, C.E.; Morari, M. Internal model control—A unifying review and some new results. IEC Process Des. Dev. 1982, 21, 308–323. [Google Scholar] [CrossRef]
- Kuntze, H.B.; Jacubasch, A.; Richalet, J.; Arber, C. On the Predictive Functional Control of an Elastic Industrial Robot. In Proceedings of the 25th IEEE Conference on Decision and Control, Athens, Greece, 10 December 1986; pp. 1877–1881. [Google Scholar]
- Clarke, D.W.; Monhtadl, C.; Tuffs, P.S. Generalize Predictive Control—Part Ⅰ. The Basic Algorithm. Automatica 1987, 23, 137–148. [Google Scholar] [CrossRef]
- Clarke, D.W.; Monhtadl, C.; Tuffs, P.S. Generalize Predictive Control—Part Ⅱ. Extensions and Interpretations. Automatica 1987, 23, 149–162. [Google Scholar] [CrossRef]
- Kwon, W.H.; Pearson, A.E. On feedback stabilization of time-varying discrete linear systems. IEEE Trans. Autom. Control 1978, 23, 479–481. [Google Scholar] [CrossRef]
- Scokaert, P.O.M.; Clarke, D.W. Stabilising properties of con-strained predictive control. IEE Proc. Control Theory Appl. 1994, 141, 295–304. [Google Scholar] [CrossRef]
- Clarke, D.W.; Scattolini, R. Constrained receding-horizon predictive control. IEE Proc. Control Theory Appl. 1991, 138, 347–354. [Google Scholar] [CrossRef]
- Keerthi, S.S.; Gilbert, E.G. Optimal infinite-horizon feedback laws for a general class of constrained discrete-time systems: Stability and moving-horizon approximations. J. Optim. Theory Appl. 1988, 57, 265–293. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Michalska, H. Receding horizon control of nonlinear systems. IEEE Trans. Autom. Control 1990, 35, 814–824. [Google Scholar] [CrossRef]
- Michalska, H.; Mayne, D.Q. Robust receding horizon control of constrained nonlinear systems. IEEE Trans. Autom. Control 1993, 38, 1623–1633. [Google Scholar] [CrossRef]
- Limon, D.; Alamo, T.; Salas, F.; Camacho, E.F. On the stability of constrained MPC without terminal constraint. IEEE Trans. Autom. Control 2006, 51, 832–836. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Hauser, J. On the stability of receding horizon control with a terminal cost. IEEE Trans. Autom. Control 2005, 50, 674–678. [Google Scholar] [CrossRef]
- Chmielewski, D.; Manousiouthakis, V. On constrained infinite-time linear quadratic optimal control. Syst. Control Lett. 1996, 29, 121–129. [Google Scholar] [CrossRef]
- De Nicolao, G.; Magni, L.; Scattolini, R. Stabilizing nonlinear receding horizon control via a nonquadratic penalty. In Proceedings of the IMACS Multiconference CESA, Lille, France, 1 January 1996; pp. 185–187. [Google Scholar]
- Gilbert, E.G.; Tan, K.T. Linear systems with state and control constraints: The theory and application of maximal output admissible sets. IEEE Trans. Autom. Control 1991, 36, 1008–1020. [Google Scholar] [CrossRef]
- Parisini, T.; Zoppoli, R. A receding horizon regulator for nonlinear systems and a neural approximation. Automatica 1995, 31, 1443–1451. [Google Scholar] [CrossRef]
- Sznaier, M.; Damborg, M.J. Suboptimal control of linear systems with state and control inequality constraints. In Proceeding of the 26th IEEE Conference on Decision and Control, Los Angeles, CA, USA, 9–11 December 1987; Volume 76, pp. 1–762. [Google Scholar]
- Scokaert, P.O.M.; Rawlings, J.B. Constrained linear quadratic regulation. IEEE Trans. Autom. Control 1998, 43, 1163–1169. [Google Scholar] [CrossRef]
- De Oliveira Kothare, L.K.; Morari, M. Contractive model predictive control for constrained nonlinear systems. IEEE Trans. Autom. Control 2000, 45, 1053–1071. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, F.O.M. Constrained model predictive control: Stability and optimality. Automaica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- De Nicolao, G.; Magni, L.; Scottolini, R. Stabilizing receding-horizon control of nonlinear time-varying systems. IEEE Trans. Autom. Control 1998, 43, 1030–1036. [Google Scholar] [CrossRef]
- Magni, L.; De Nicolao, G.; Magnani, L.; Scattolini, R. A stabilizing model-based predictive control algorithm for nonlinear systems. Automatica 2001, 37, 1351–1362. [Google Scholar] [CrossRef]
- Lee, J.W.; Kwon, W.H.; Choe, J. On stability of constrained receding horizon control with finite terminal weighting matrix. Automatic 1998, 34, 1607–1612. [Google Scholar] [CrossRef]
- Lee, J.W. Exponential stability of constrained receding horizon control with terminal ellipsoid constraints. IEEE Trans. Autom. Control 2000, 45, 83–88. [Google Scholar]
- Zhang, R.D.; Li, P.; Xue, A.K.; Jiang, A.P.; Wang, S.Q. A simplified linear iterative predictive functional control approach for chamber pressure of industrial coke furnace. J. Process Control 2010, 20, 464–471. [Google Scholar] [CrossRef]
- Gawthrop, P.J. Linear predictive pole-placement control: Practical issues. In Proceedings of the 39th IEEE Conference on Decision and Control (Cat. No.00CH37187), Sydney, Australia, 12–15 December 2000; Volume 1, pp. 160–165. [Google Scholar]
- Gawthrop, P.J.; Ronco, E. Predictive pole-placement control with linear models. Automatica 2002, 38, 421–432. [Google Scholar] [CrossRef][Green Version]
- Chen, W.H.; Gawthrop, P.J. Constrained predictive pole-placement control with linear models. Automatica 2006, 42, 613–618. [Google Scholar] [CrossRef]
- Nicotra, M.M.; Garone, E. The Explicit Reference Governor: A General Framework for the Closed-Form Control of Constrained Nonlinear Systems. IEEE Control Syst. Mag. 2018, 38, 89–107. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Garone, E. An Explicit Reference Governor for the Intersection of Concave Constraints. IEEE Trans. Autom. Control. 2019, 1. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Cotorruelo, A.; Limon, D.; Garone, E. Constrained Control of Linear Systems Subject to Combinations of Intersections and Unions of Concave Constraints. IEEE Control Syst. Lett. 2019, 3, 571–576. [Google Scholar] [CrossRef]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB®; Springer-Verlag London Limited: London, UK, 2009. [Google Scholar]
- Rajan, R.; Muhammed Salih, P.; Anilkumar, N. Speed Controller design for Steam Turbine. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. J. 2013, 2, 4400–4409. [Google Scholar]
- Carlton, J.S. Marine Propellers and Propulsion; Butterworth–Heinemann: Oxford, UK, 1994. [Google Scholar]
- Tupper, E.C.; Rawson, K.J. Basic Ship Theory, Combined Volume; Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar]
- Kashima, T.; Takata, J. An optimal control of marine propulsion system considering ship dynamics. In Proceedings of the International Conference on Control Applications, Glasgow, UK, 18–20 September 2002. [Google Scholar]
- Jiang, P.; Gao, L.; Dai, Y. A new non-linear model of steam turbine unit for dynamic analysis of power system. In Proceedings of the International Conference on Power System Technology, Hangzhou, China, 24–28 October 2010. [Google Scholar]
- Chaibakhsh, A.; Ghaffari, A. Steam turbine model. Simul. Model. Pract. Theory 2008, 16, 1145–1162. [Google Scholar] [CrossRef]
- Zhao, S.; Maxim, A.; Liu, S.; De Keyser, R.; Ionescu, C. Effect of Control Horizon in Model Predictive Control for Steam/Water Loop in Large-Scale Ships. Processes 2018, 6, 265. [Google Scholar] [CrossRef]

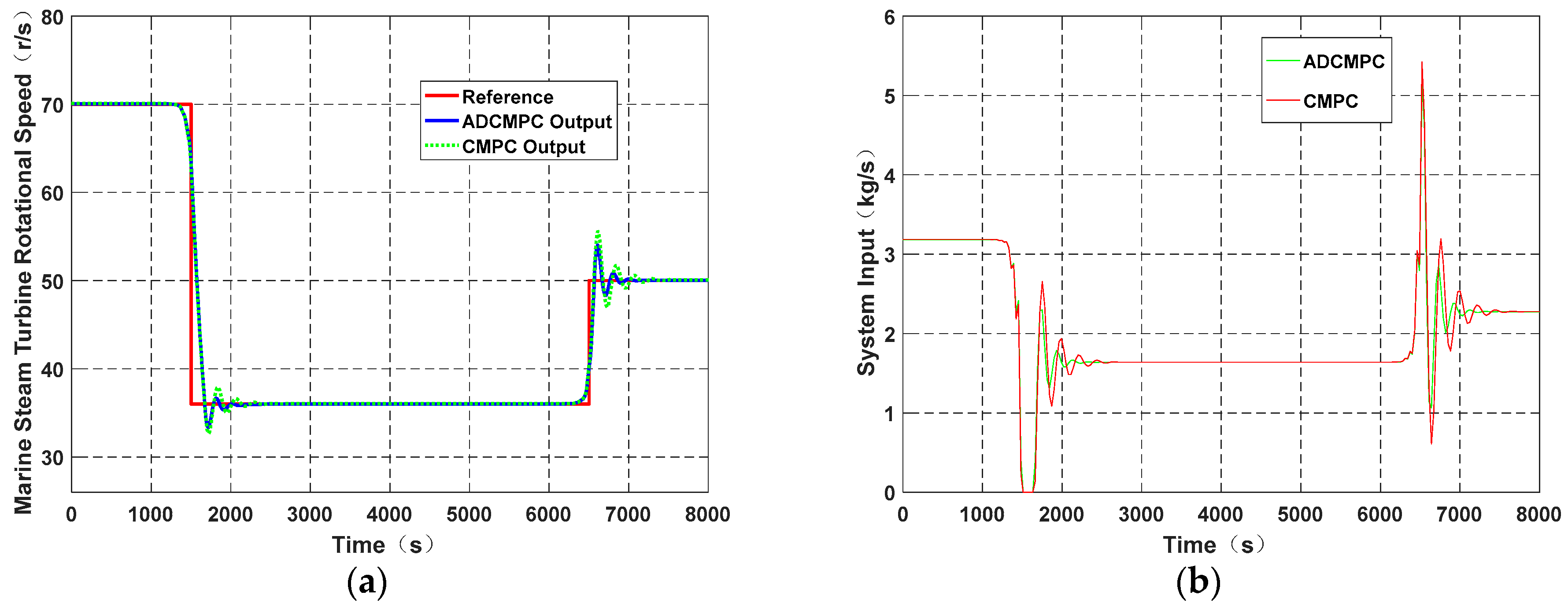
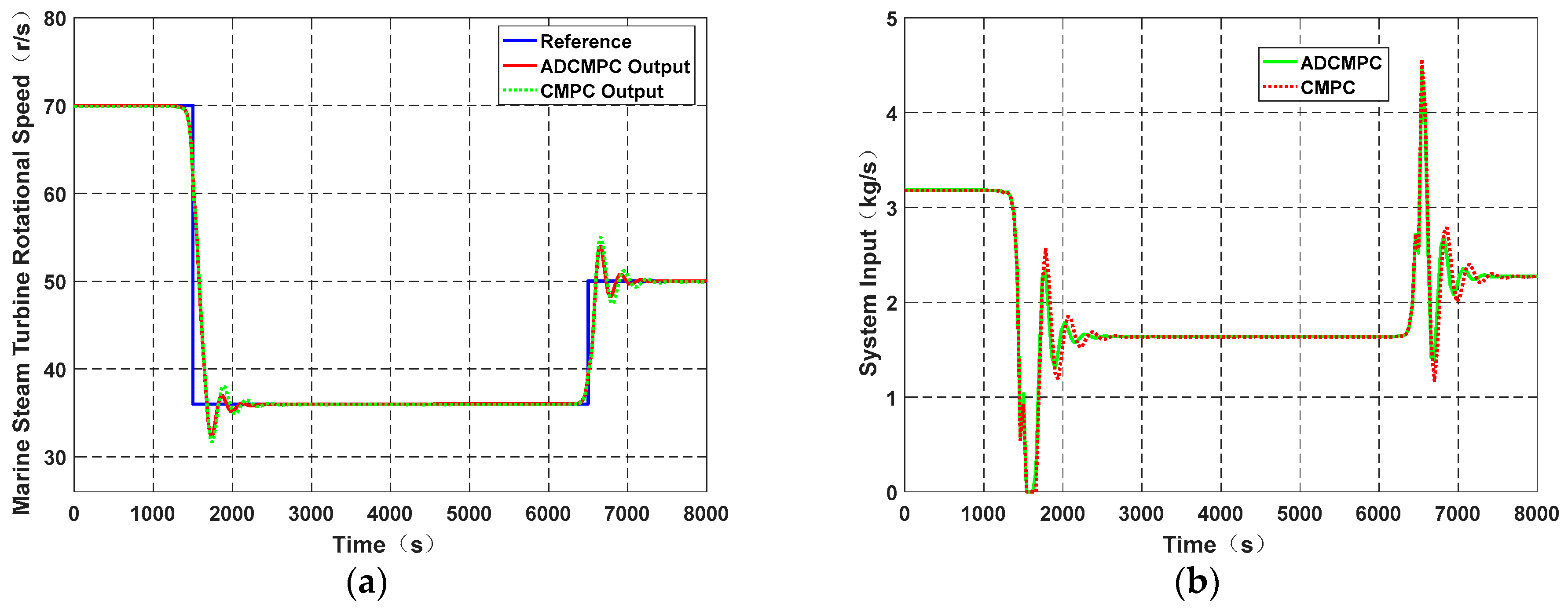
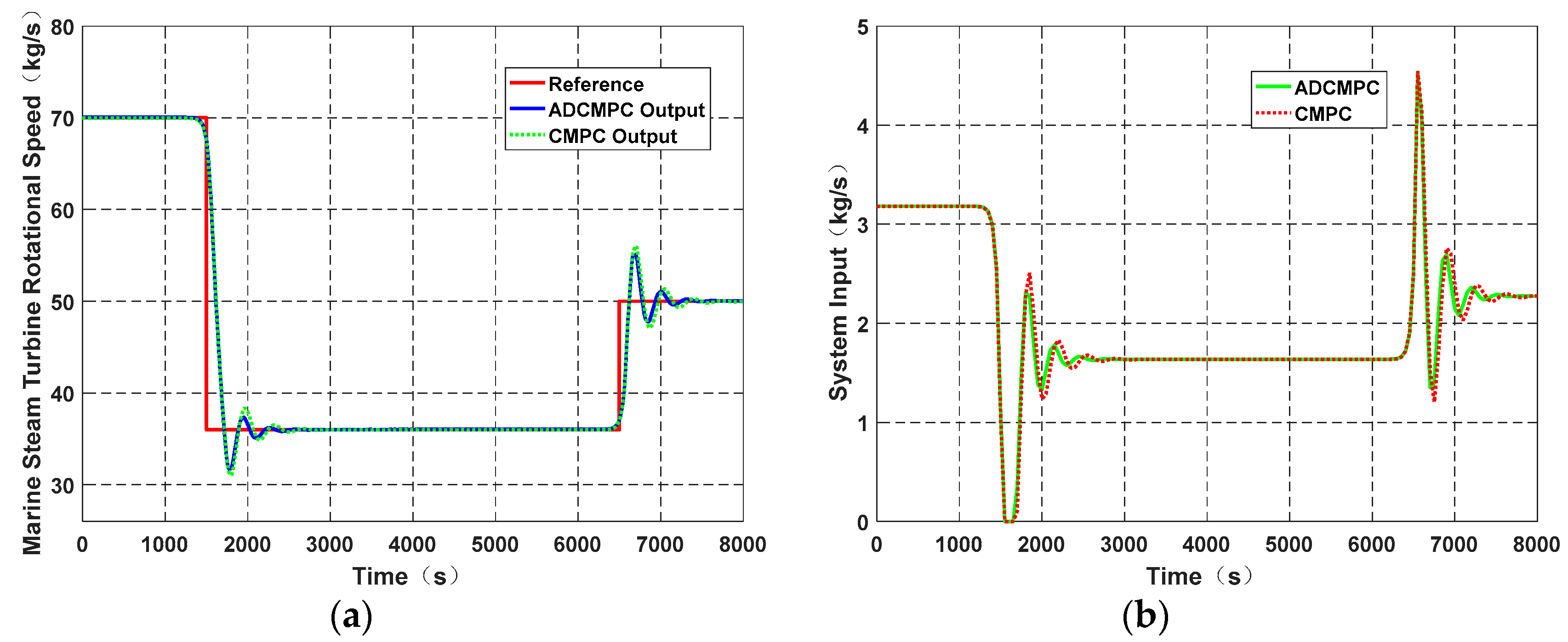
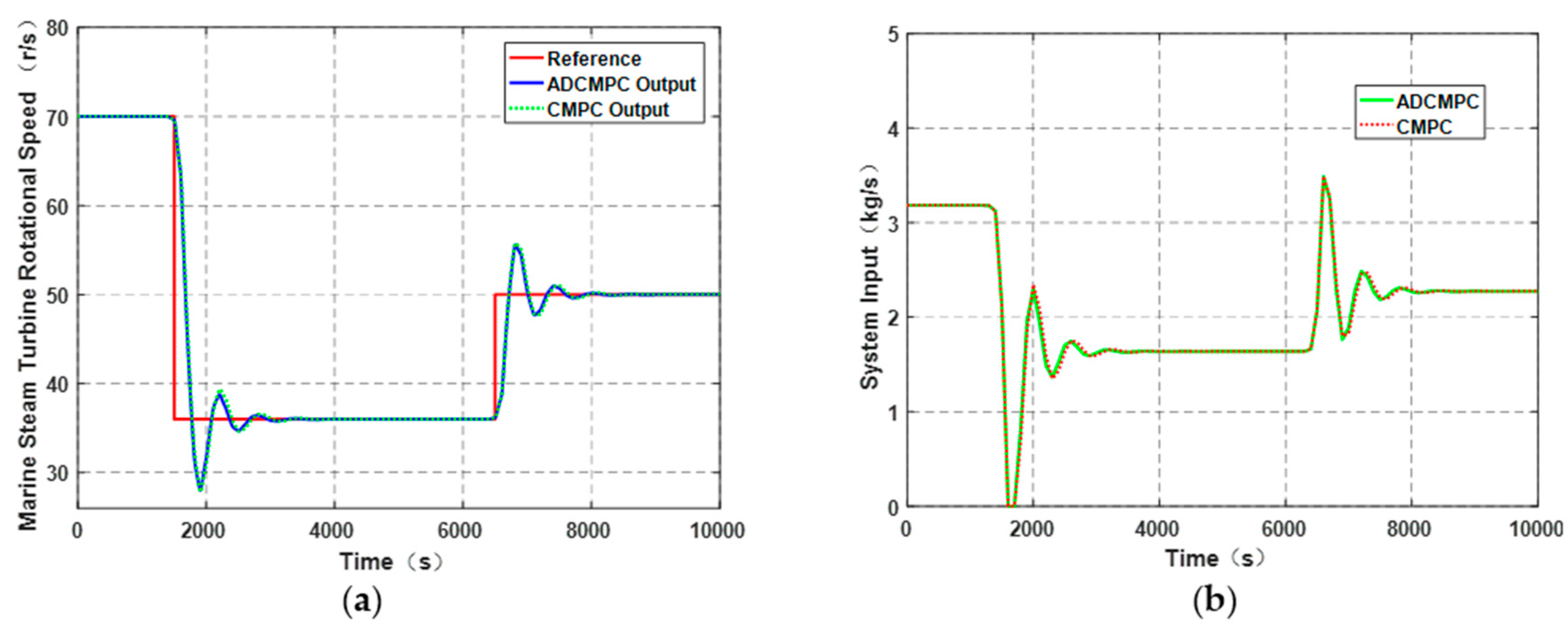
| Symbol | Value | SI-Unit |
|---|---|---|
| K | 22 | |
| T | 300 | s |
| T0 | 10 | s |
| τ | 120 | s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhao, B.; Wu, L. A Novel MPC with Actuator Dynamic Compensation for the Marine Steam Turbine Rotational Control with a Novel Energy Dynamic Model. Processes 2019, 7, 423. https://doi.org/10.3390/pr7070423
Liu S, Zhao B, Wu L. A Novel MPC with Actuator Dynamic Compensation for the Marine Steam Turbine Rotational Control with a Novel Energy Dynamic Model. Processes. 2019; 7(7):423. https://doi.org/10.3390/pr7070423
Chicago/Turabian StyleLiu, Sheng, Baoling Zhao, and Ling Wu. 2019. "A Novel MPC with Actuator Dynamic Compensation for the Marine Steam Turbine Rotational Control with a Novel Energy Dynamic Model" Processes 7, no. 7: 423. https://doi.org/10.3390/pr7070423
APA StyleLiu, S., Zhao, B., & Wu, L. (2019). A Novel MPC with Actuator Dynamic Compensation for the Marine Steam Turbine Rotational Control with a Novel Energy Dynamic Model. Processes, 7(7), 423. https://doi.org/10.3390/pr7070423





