Air-Core–Liquid-Ring (ACLR) Atomization Part II: Influence of Process Parameters on the Stability of Internal Liquid Film Thickness and Resulting Spray Droplet Sizes
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Solution
2.2. Air-Core–Liquid-Ring Atomizer
2.3. Spray Test Rig
2.4. Droplet Size Measurement
2.5. Visualisation of Internal Liquid Film Thickness
2.6. Simulation of Internal Flow Conditions
3. Results
3.1. Time Dependent Variation of x50,3
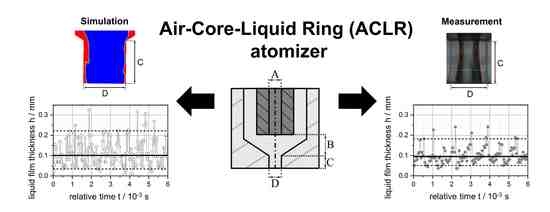
3.2. Optical Analysis of the Time Dependent Internal Liquid Film Thickness
3.3. Simulation of the Time Dependent Internal Liquid Film Thickness
3.4. Influence of Viscosity on Measured and Simulated Liquid Film Thickness
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lefebvre, A.H. Atomization and Sprays; Hemisphere Publishing Corp: Philadelphia, PA, USA, 1989; ISBN 0-89116-603-3. [Google Scholar]
- Ashgriz, N. Handbook of Atomization and Sprays; Springer: Berlin, Germany, 2011; ISBN 978-1-4419-7263-7. [Google Scholar]
- Lefebvre, A.H. Twin-fluid atomization: Factors influencing mean drop size. At. Sprays 1992, 2, 101–119. [Google Scholar] [CrossRef]
- Lefebvre, A.H. Energy Considerations in Twin-Fluid Atomization. J. Eng. Gas Turbines Power 1992, 114, 89–96. [Google Scholar] [CrossRef]
- Masters, K. Spray Drying in Practice; SprayDryConsult International ApS: Charlottenlund, Danmark, 2002; ISBN 87-986606-08-3. [Google Scholar]
- Mlkvik, M.; Stähle, P.; Schuchmann, H.P.; Gaukel, V.; Jedelsky, J.; Jicha, M. Twin-fluid atomization of viscous liquids: The effect of atomizer construction on breakup process, spray stability and droplet size. Int. J. Multiph. Flow 2015, 77, 19–31. [Google Scholar] [CrossRef]
- Buckner, H.J.; Sojka, P.E. Effervescent Atomization of High-Viscosity Fluids: Part I. Newtonian Liquids. At. Sprays 1991, 1, 239–252. [Google Scholar] [CrossRef]
- Jedelsky, J.; Jicha, M.; Slama, J.; Otahal, J. Development of an Effervescent Atomizer for Industrial Burners. Energy Fuels 2009, 23, 6121–6130. [Google Scholar] [CrossRef]
- Chin, J.S. Effervescent atomization and internal mixing air assist atomization. Int. J. Turbo Jet Engines 1995, 12, 119–127. [Google Scholar] [CrossRef]
- Stähle, P.; Gaukel, V.; Schuchmann, H.P. Influence of feed viscosity on the two-phase flow inside the exit orifice of an effervescent atomizer and on resulting spray characteristics. Food Res. Int. 2015, 77, 55–62. [Google Scholar] [CrossRef]
- Shepard, T.G. Bubble Size Effect on Effervescent Atomization. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2011. [Google Scholar]
- Lefebvre, A.H. Airblast Atomization. Prog. Energy Combust. Sci. 1980, 6, 233–261. [Google Scholar] [CrossRef]
- Rizk, N.K.; Lefebvre, A.H. The Influence of Liquid-Film Thickness on Airblast Atomization. J. Eng. Power 1980, 102, 706–710. [Google Scholar] [CrossRef]
- Déjean, B.; Berthoumieu, P.; Gajan, P. Experimental study on the influence of liquid and air boundary conditions on a planar air-blasted liquid sheet, Part I: Liquid and air thicknesses. Int. J. Multiph. Flow 2016, 79, 202–213. [Google Scholar] [CrossRef]
- Déjean, B.; Berthoumieu, P.; Gajan, P. Experimental study on the influence of liquid and air boundary conditions on a planar air-blasted liquid sheet, Part II: Prefilming zone length. Int. J. Multiph. Flow 2016, 79, 214–224. [Google Scholar] [CrossRef]
- Sattelmayer, T.; Wittig, S. Internal Flow Effects in Prefilming Airblast Atomizers: Mechanisms of Atomization and Droplet Spectra. J. Eng. Gas Turbines Power 1986, 108, 465. [Google Scholar] [CrossRef]
- Volz, M.; Nittel, L.; Habisreuther, P.; Zarzalis, N. Numerical Study of Liquid Film Characteristics at Varying Operating Conditions in Prefilmer Airblast Atomizer. Chem. Ing. Tech. 2016, 88, 192–199. [Google Scholar] [CrossRef]
- Stähle, P.; Gaukel, V.; Schuchmann, H.P. Comparison of an Effervescent Nozzle and a Proposed Air-Core-Liquid-Ring (ACLR) Nozzle for Atomization of Viscous Food Liquids at Low Air Consumption. J. Food Process Eng. 2017, 40, 12268. [Google Scholar] [CrossRef]
- Stähle, P.; Schuchmann, H.P.; Gaukel, V. Performance and Efficiency of Pressure-Swirl and Twin-Fluid Nozzles Spraying Food Liquids with Varying Viscosity. J. Food Process Eng. 2017, 40, 12317. [Google Scholar] [CrossRef]
- Kleinhans, A.; Georgieva, K.; Wagner, M.; Gaukel, V.; Schuchmann, H.P. On the characterization of spray unsteadiness and its influence on oil drop breakup during effervescent atomization. Chem. Eng. Process. Process Intensif. 2016, 104, 212–218. [Google Scholar] [CrossRef]
- Kleinhans, A.; Hornfischer, B.; Gaukel, V.; Schuchmann, H.P. Influence of viscosity ratio and initial oil drop size on the oil drop breakup during effervescent atomization. Chem. Eng. Process. Process Intensif. 2016, 109, 149–157. [Google Scholar] [CrossRef]
- Wittner, M.O.; Karbstein, H.P.; Gaukel, V. Spray performance and steadiness of an effervescent atomizer and an air-core-liquid-ring atomizer for application in spray drying processes of highly concentrated feeds. Chem. Eng. Process. Process Intensif. 2018, 128, 96–102. [Google Scholar] [CrossRef]
- Wittner, M.O.; Karbstein, H.P.; Gaukel, V. Pneumatic atomization: Beam steering correction in laser diffraction measurements of spray droplet size distributions. Appl. Sci. 2018, 8, 1738. [Google Scholar] [CrossRef]
- Wittner, M.; Karbstein, H.; Gaukel, V. Air-Core-Liquid-Ring (ACLR) Atomization: Influences of Gas Pressure and Atomizer Scale Up on Atomization Efficiency. Processes 2019, 7, 139. [Google Scholar] [CrossRef]
- Wittner, M.O.; Karbstein, H.P.; Gaukel, V. Spray drying of high viscous food concentrates: Investigations on the applicability of an Air-Core-Liquid-Ring (ACLR) nozzle for liquid atomization. In Proceedings of the 21st International Drying Symposium, IDS 21st International Drying Symposium, Valencia, Spain, 11–14 September 2018; Cárcel, J.A., Clemente, G., Mulet, A., Eds.; Editorial Universitat Politècnica de València: Valencia, Spain, 2018; pp. 1221–1228, ISBN 978-84-9048-688-7. [Google Scholar]
- Wittner, M.O.; Karbstein, H.P.; Gaukel, V. Energy efficient spray drying by increased feed dry matter content: Investigations on the applicability of Air-Core-Liquid-Ring atomization on pilot scale. Dry. Technol. 2019, 1–9. [Google Scholar] [CrossRef]
- Prewitt, J. Object Enhancement and Extraction. In Picture Processing and Psychopictorics; Lipkin, B.S., Ed.; Elsevier Science: Oxford, UK, 1970; pp. 75–150. ISBN 9780323146852. [Google Scholar]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Wilcox, D.C.; Rubesin, M.W. Progress in Turbulence Modeling for Complex Flow Fields Including Effects of Compressibility No. 19800012043, Moffett Field, CA, USA. 1980. Available online: https://ntrs.nasa.gov/search.jsp?R=19800012043 (accessed on 5 September 2019).
- Menter, F.R. Improved Two-Equation K-Omega Turbulence Models for Aerodynamic Flows No. 19930013620, Moffett Fields, CA, USA. 1992. Available online: https://ntrs.nasa.gov/search.jsp?R=19930013620 (accessed on 9 October 2018).
- Menter, F.R.; Smirnov, P.E.; Liu, T.; Avancha, R. A One-Equation Local Correlation-Based Transition Model. Flow Turbul. Combust. 2015, 95, 583–619. [Google Scholar] [CrossRef]
- Hewitt, G. Annular Two-Phase Flow; Elsevier Science: Burlington, NJ, USA, 1970; ISBN 9781483285238. [Google Scholar]
- Ghajar, A.J.; Bhagwat, S.M. Gas-Liquid Flow in Ducts. In Multiphase Flow Handbook; Michaelides, E.E., Crowe, C.T., Schwarzkopf, J.D., Eds.; CRC Press: Boca Raton, FL, USA, 2016; pp. 287–356. ISBN 9781315371924. [Google Scholar]











| cMD (% d.b.) | µ (Pa·s) | ur(µ) (%) | σ (N·m−1) | ur(σ) (%) | ρ (kg·m−3) | ur(ρ) (%) | RI (-) | ur(RI) (%) |
|---|---|---|---|---|---|---|---|---|
| 40 | 0.12 | 9.79 | 0.073 | 0.02 | 1175 | 0.02 | 1.40 | 0.07 |
| 47 | 0.39 | 3.79 | 0.074 | 0.05 | 1218 | 0.06 | 1.42 | 0.04 |
| ALR | Pressure Loss (MPa) | Wall Shear Stress (MPa) |
|---|---|---|
| 0.05 | 0.382 | 0.0396 |
| 0.13 | 0.322 | 0.0655 |
| Process Parameters | Liquid Film Thickness | Char. Droplet Size x50.3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Simulation | Optical Measurement | ||||||||||||
| µ | ALR | x5,0 | x50,0 | x95,0 | x5,0 | x50,0 | x95,0 | x5,0 | ur | x50,0 | ur | x95,0 | ur |
| (Pa·s) | (-) | (µm) | (µm) | (µm) | (µm) | (µm) | (µm) | (µm) | (%) | (µm) | (%) | (µm) | (%) |
| 0.12 | 0.15 | 35 | 108 | 222 | 51 | 95 | 182 | 83 | 1.7 | 100 | 1.6 | 128 | 1.6 |
| 0.39 | 0.05 | 118 | 186 | 524 | 96 | 184 | 409 | 115 | 5.2 | 169 | 6.2 | 351 | 6.0 |
| 0.39 | 0.13 | 78 | 149 | 342 | 59 | 112 | 215 | 84 | 7.6 | 107 | 7.0 | 160 | 6.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wittner, M.O.; Ballesteros, M.A.; Link, F.J.; Karbstein, H.P.; Gaukel, V. Air-Core–Liquid-Ring (ACLR) Atomization Part II: Influence of Process Parameters on the Stability of Internal Liquid Film Thickness and Resulting Spray Droplet Sizes. Processes 2019, 7, 616. https://doi.org/10.3390/pr7090616
Wittner MO, Ballesteros MA, Link FJ, Karbstein HP, Gaukel V. Air-Core–Liquid-Ring (ACLR) Atomization Part II: Influence of Process Parameters on the Stability of Internal Liquid Film Thickness and Resulting Spray Droplet Sizes. Processes. 2019; 7(9):616. https://doi.org/10.3390/pr7090616
Chicago/Turabian StyleWittner, Marc O., Miguel A. Ballesteros, Frederik J. Link, Heike P. Karbstein, and Volker Gaukel. 2019. "Air-Core–Liquid-Ring (ACLR) Atomization Part II: Influence of Process Parameters on the Stability of Internal Liquid Film Thickness and Resulting Spray Droplet Sizes" Processes 7, no. 9: 616. https://doi.org/10.3390/pr7090616
APA StyleWittner, M. O., Ballesteros, M. A., Link, F. J., Karbstein, H. P., & Gaukel, V. (2019). Air-Core–Liquid-Ring (ACLR) Atomization Part II: Influence of Process Parameters on the Stability of Internal Liquid Film Thickness and Resulting Spray Droplet Sizes. Processes, 7(9), 616. https://doi.org/10.3390/pr7090616