Analysis of Dynamic Characteristics and Control Strategies of a Solvent Dehydration Distillation Column in a Purified Terephthalic Acid Plant
Abstract
:1. Introduction
2. Steady-State Simulation
2.1. Steady-State Process for the Dehydration of HAc
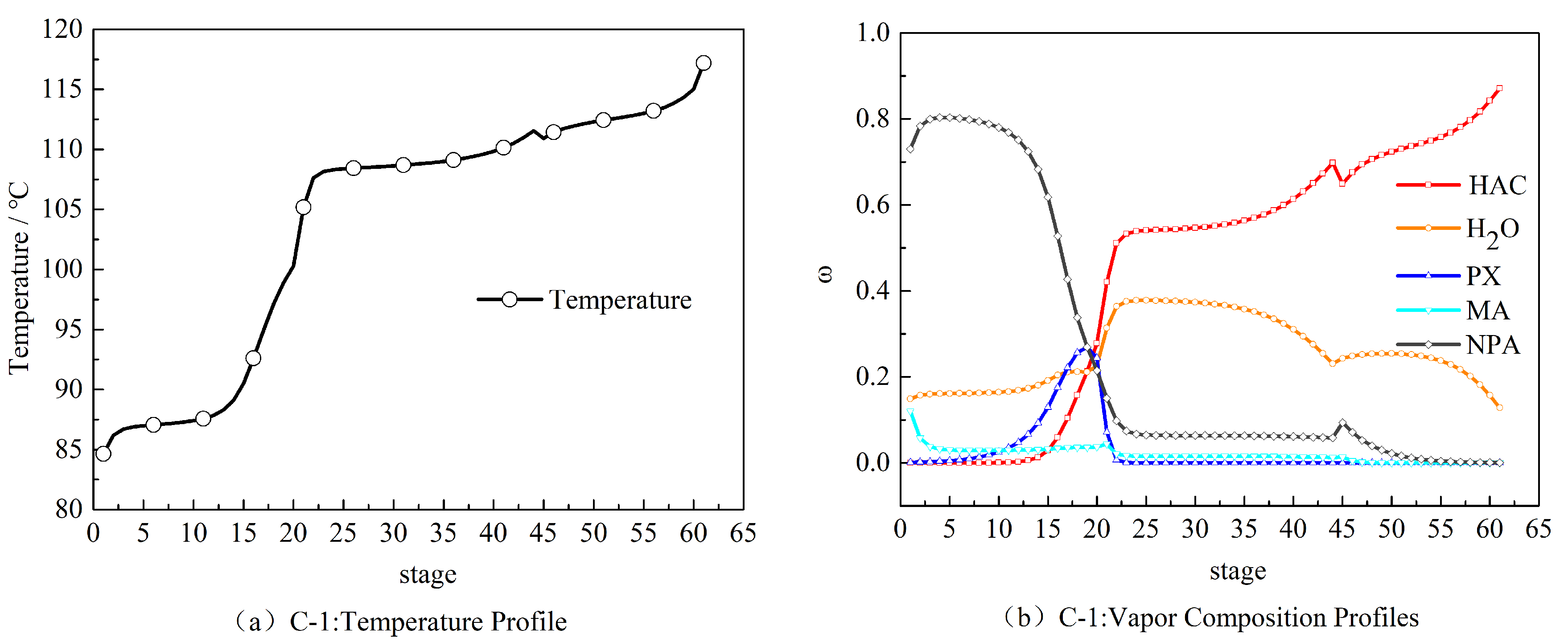
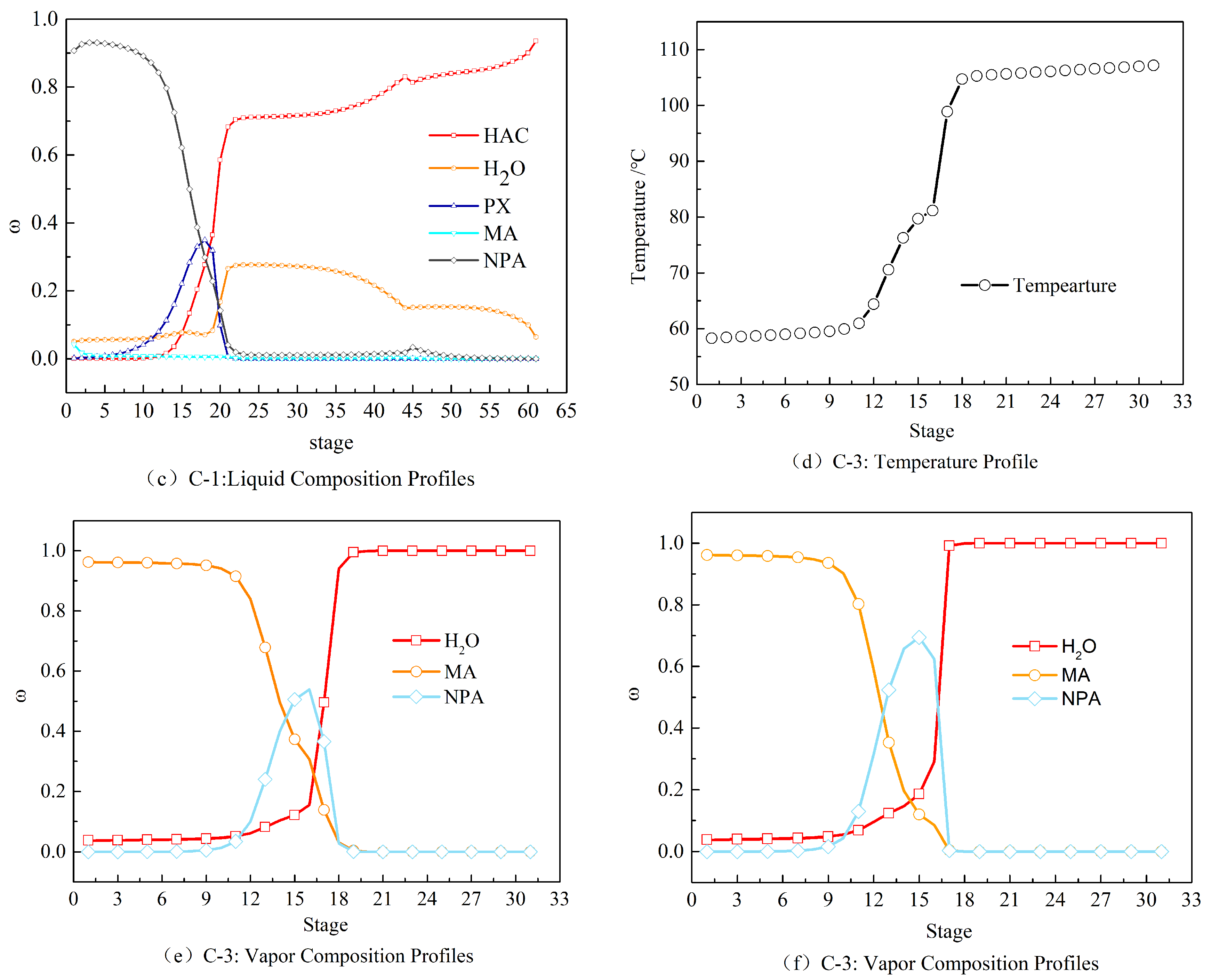
2.2. Steady-State Results of the HAc Dehydration Column
3. Dynamic Simulation and Control
3.1. Balanced Dynamic Mathematical Model
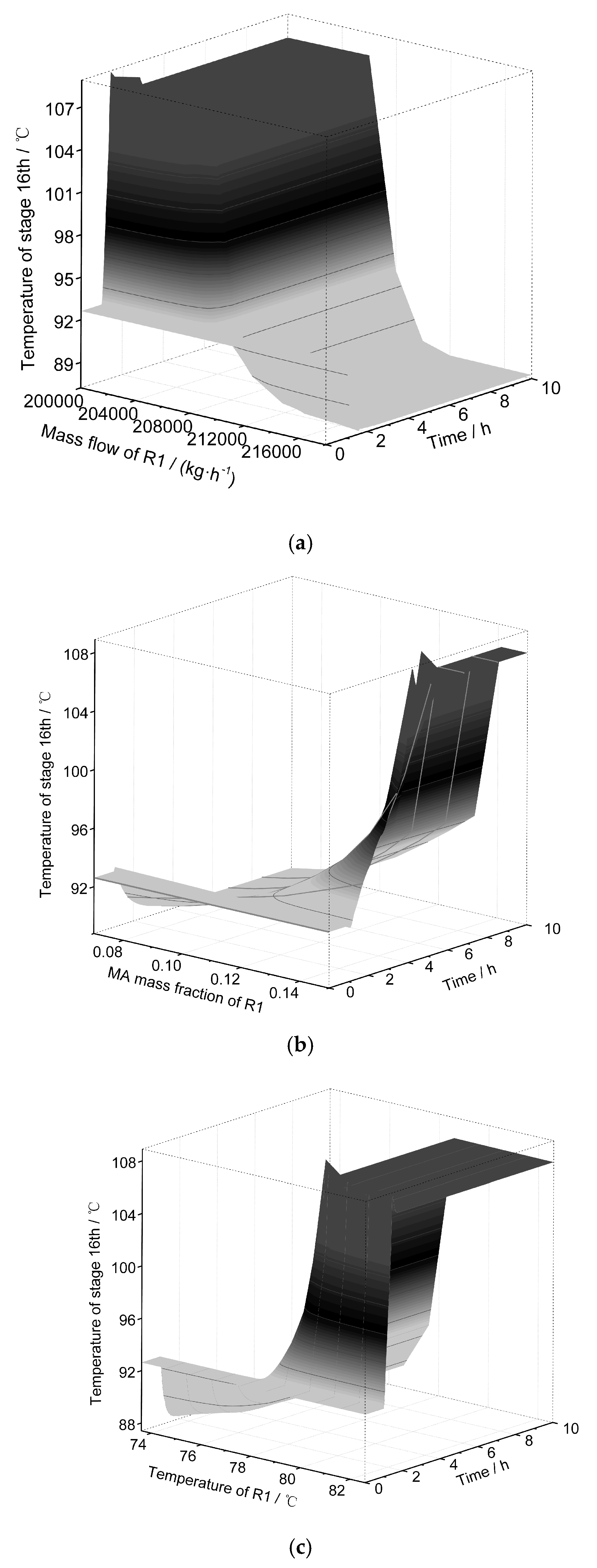
3.2. Determination of the Sensitive Plate
3.3. Dynamic Sensitivity Analysis
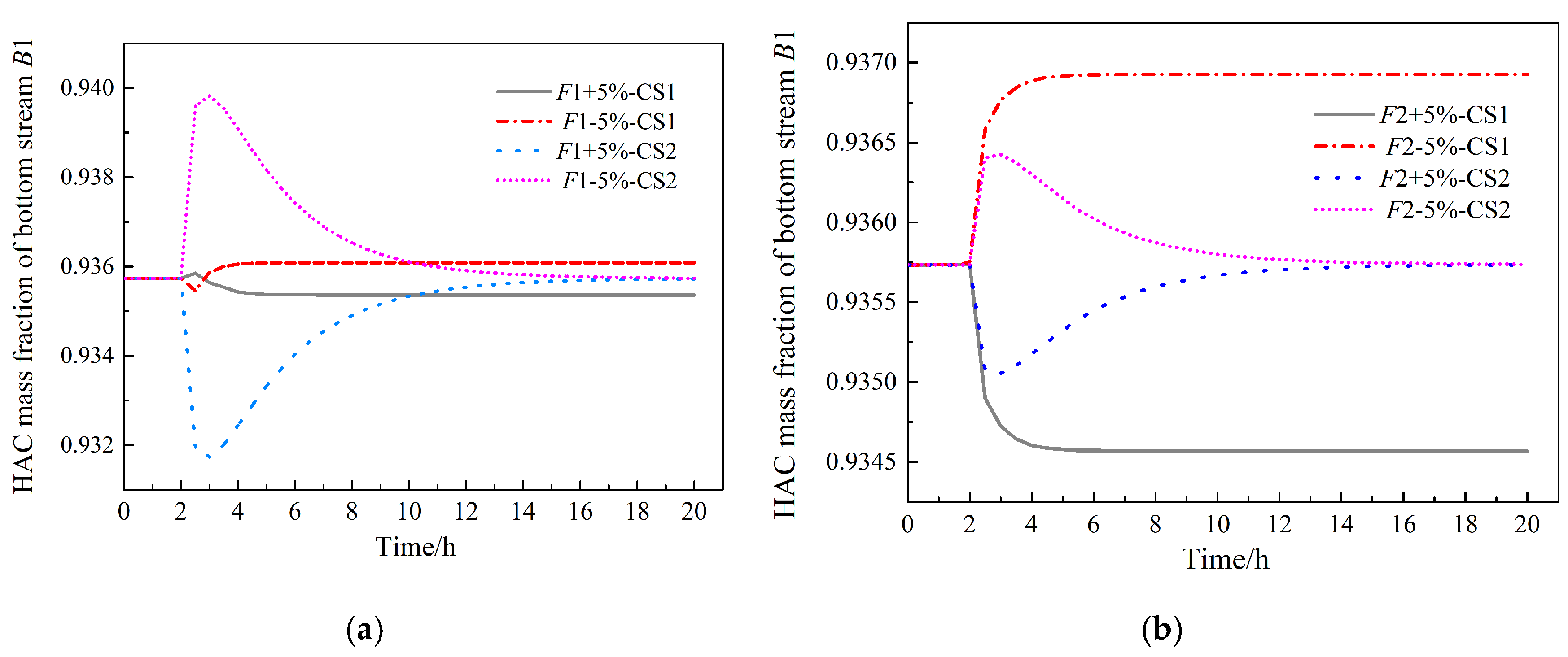
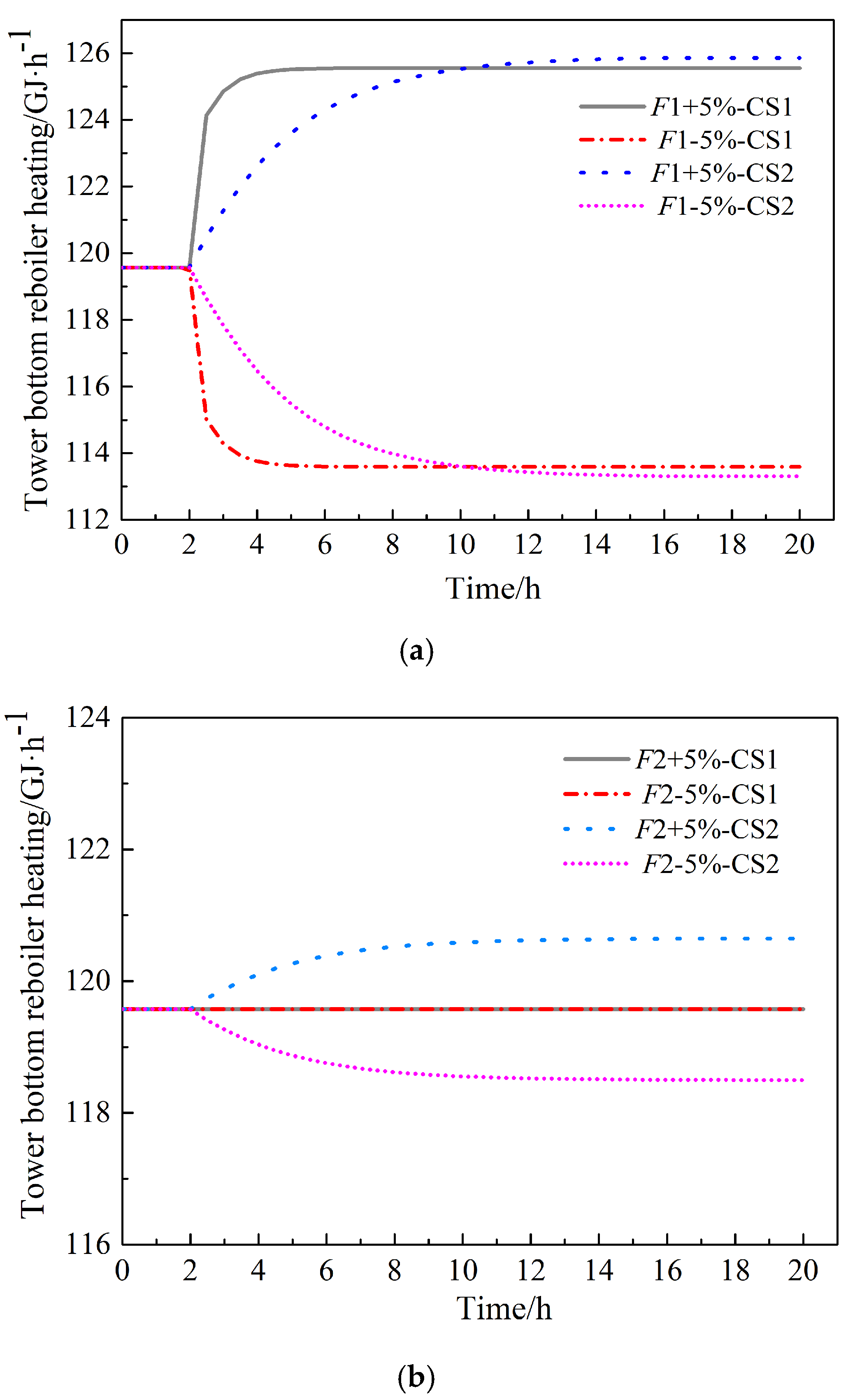
3.4. Analysis of Control Strategies
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| F | Feed mass flow: kg/h |
| h | Moore han |
| Lj | Liquid phase mass flow at stage j, kg/h |
| Mj | Mass flow at level j, kg/h |
| Liquid phase production, kg/h | |
| Gas phase production, kg/h | |
| Qj | Heat transfer with the outside world, kJ/h |
| Vj | Gas phase mass flow at stage j, kg/h |
| Xi,j | Liquid phase mass fraction of component i at level j |
| Yi,j | Gas phase mass fraction of component i at level j |
| Zi,j | Molar fraction of component i feed at stage j |
| Upper corner | |
| α, β | Representing two liquid phases |
| Lower corner | |
| i | Component |
| j | Tray level |
References
- Xing, J.L.; Zhao, J.; Jiang, P.F. Multivariable predictive control of PX oxidation reaction process. CIESC J. 2012, 63, 2726–2732. [Google Scholar]
- Huang, D.W.; Li, S.J. Multi-stable study on heterogeneous azeotropic distillation of acetic acid dehydration. Comput. Appl. Chem. 2010, 27, 1395–1398. [Google Scholar]
- Widagdo, S.; Seider, W.D. Journal review. Azeotropic distillation. AIChE J. 1996, 42, 96–130. [Google Scholar] [CrossRef]
- Hu, S.; Zhang, B.J.; She, Z.H. Application and research progress of azeotropic distillation in chemical production. Chem. Ind. Eng. Prog. 2010, 29, 2207–2219. [Google Scholar]
- Kurooka, T.; Yamashita, Y.; Nishitani, H.; Hashimoto, Y.; Yoshida, M.; Numata, M. Dynamic simulation and nonlinear control system design of a heterogeneous azeotropic distillation column. Comput. Chem. Eng. 2000, 24, 887–892. [Google Scholar] [CrossRef]
- Luyben, W.L. Control of the Heterogeneous Azeotropic n-Butanol/Water Distillation System. Energy Fuel 2008, 22, 4249–4258. [Google Scholar] [CrossRef]
- Wasylkiewicz, S.K.; Kobylka, L.C.; Castillo, F.J.L. Optimal design of complex azeotropic distillation columns. Chem. Eng. J. 2000, 79, 219–227. [Google Scholar] [CrossRef]
- Xing, J.L.; Huang, X.H.; Yuan, W.K. Process Simulation of Industrial Acetic Acid Dehydration System via Heterogeneous Azeotropic Distillation. CIESC J. 2012, 63, 2681–2687. [Google Scholar]
- Chien, I.L.; Chen, W.H.; Chang, T.S. Operation and decoupling control of a heterogeneous azeotropic distillatin column. Comput. Chem. Eng. 2000, 24, 893–899. [Google Scholar] [CrossRef]
- Wang, L.; Xi, L. Thermodynamic analysis and azeotropic distillation simulation for acetic acid-water-butyl acetate system. J. Chem. Ind. Eng. 2005, 56, 1260–1266. [Google Scholar]
- Pham, H.N.; Doherty, M.F. Design and Synthesis of Azeotropic Distillation: II. Residue Curve Maps. Chem. Eng. Sci. 1990, 45, 1837–1843. [Google Scholar] [CrossRef]
- Foucher, E.R.; Doherty, M.F.; Malone, M.F. Automatic screening of entrainers for homogeneous azeotropic distillation. Ind. Eng. Chem. Res. 1991, 30, 760–772. [Google Scholar] [CrossRef]
- Tripodi, A.; Compagnoni, M.; Ramis, G.; Rossetti, I. Pressure-swing or extraction-distillation for the recovery of pure acetonitrile from ethanol ammoxidation process: A comparison of efficiency and cost. Chem. Eng. Res. Des. 2017, 127, 92–102. [Google Scholar] [CrossRef]
- Tripodi, A.; Manzini, D.; Compagnoni, M.; Ramis, G.; Rossetti, I. Alternative integrated distillation strategies for the purification of acetonitrile from ethanol ammoxidation. J. Ind. Eng. Chem. 2018, 59, 35–49. [Google Scholar] [CrossRef]
- Chengfei, L. Dynamic Simulation and Analysis of Industrial Purified Terephthalic Acid Solvent Dehydration Process. Chin. J. Chem. Eng. 2011, 19, 89–96. [Google Scholar]
- Laroche, L.; Bekiaris, N.; Andersen, H.W.; Morari, M. The curious behavior of homogeneous azeotropic distillation—Implications for entrainer selection. AIChE J. 1992, 38, 1309–1328. [Google Scholar] [CrossRef]
- Skouras, S.; Kiva, V.; Skogestad, S. Feasible separations and entrainer selection rules for heteroazeotropic batch distillation. Chem. Eng. Sci. 2005, 60, 2895–2909. [Google Scholar] [CrossRef]
- Rashid, M.M.; Mhaskar, P.; Swartz, C.L.E. Handling multi-rate and missing data in variable duration economic model predictive control of batch processes. AIChE J. 2017, 63, 2705–2718. [Google Scholar] [CrossRef]
- Rashid, M.M.; Patel, N.; Mhaskar, P.; Swartz, C.L. Handling sensor faults in economic model predictive control of batch processes. AIChE J. 2019, 65, 617–628. [Google Scholar] [CrossRef]
- Zeng, G.B.; Li, S.J.; Qian, F. Dynamic simulation and control of acetic acid dehydration system. Comput. Appl. Chem. 2008, 25, 533–536. [Google Scholar]
- Han, K.; Zhao, J.; Zhu, Y.C. An MPC controller for online identification of disturbance model and its application in solvent dehydration column device. CIESC J. 2008, 59, 1657–1664. [Google Scholar]
- Wei, Q.Q.; Ma, F.Y.; Zhong, M. Study on the control of acetic acid dehydration extractive distillation. Comput. Appl. Chem. 2013, 30, 542–546. [Google Scholar]
- Wang, S.-J.; Huang, K. Design and control of acetic acid dehydration system via heterogeneous azeotropic distillation using p-xylene as an entrainer. Chem. Eng. Process. Process. Intensif. 2012, 60, 65–76. [Google Scholar] [CrossRef]
- Huang, X.; Li, Z.; Tian, Y. Process optimization of an industrial acetic acid dehydration progress via heterogeneous azeotropic distillation. Chin. J. Chem. Eng. 2018, 26, 1631–1643. [Google Scholar] [CrossRef]
- Huang, X.; Zhong, W.; Peng, C.; Qian, F. Isobaric Vapor-Liquid Equilibrium of Binary Systems: P-Xylene + (Acetic Acid, Methyl Acetate and n-Propyl Acetate) and Methyl Acetate + n-Propyl Acetate in an Acetic Acid Dehydration Process. Chin. J. Chem. Eng. 2013, 21, 171–176. [Google Scholar] [CrossRef]
- Huang, X.; Zhong, W.; Du, W.; Qian, F. Thermodynamic Analysis and Process Simulation of an Industrial Acetic Acid Dehydration System via Heterogeneous Azeotropic Distillation. Ind. Eng. Chem. Res. 2013, 52, 2944–2957. [Google Scholar] [CrossRef]
- Simonetty, J.; Yee, D.; Tassios, D. Prediction and correlation of liquid-liquid equilibriums. Ind. Eng. Chem. Process. Des. Dev. 1982, 21, 174–180. [Google Scholar] [CrossRef]
- Block, U.; Hegner, B. Development and application of a simulation model for three-phase distillation. AIChE J. 1976, 22, 582–589. [Google Scholar] [CrossRef]
- Zhou, S.H.; Tang, L.S. A Double Iterative Method for Solving the MESH Equations of Distillation Column. CIESC J. 1992, 43, 705–711. [Google Scholar]
- Goldstein, R.P.; Stanfield, R.B. Flexible Method for the Solution of Distillation Design Problems Using the Newton-Raphson Technique. Ind. Eng. Chem. Process. Des. Dev. 1970, 9, 78–84. [Google Scholar] [CrossRef]
- Naphtali, L.M.; Sandholm, D.P. Multicomponent separation calculations by linearization. AIChE J. 1971, 17, 148–153. [Google Scholar] [CrossRef]
- Shang, C.J. Study on Modeling and Optimization of Solvent Dehydration Column. Master’s Thesis, Zhejiang University, Zhejiang, China, 2003. [Google Scholar]
- Qiu, G.Y.; Ding, F.; Li, Q.S. Research and application of guided sieve column in acetic acid distillation. Chem. Ind. Eng. Prog. 2005, 24, 118–120. [Google Scholar]
- Liu, L.X.; Chen, M.Q.; Liu, Y.L. Study on the control of azeotropic dividing bulkhead columns and extractive dividing bulkhead columns. Chem. Ind. Eng. Prog. 2017, 36, 756–765. [Google Scholar]
- Li, Q.; Guan, W.; Wang, L.; Wan, H.; Guan, G. Dynamic Simulation and Control of a Complete Industrial Acetic Acid Solvent Dehydration System in Purified Terephthalic Acid Production. Ind. Eng. Chem. Res. 2015, 54, 11330–11343. [Google Scholar] [CrossRef]
- Luyben, W.; Lu, P. Application of Aspen Simulation Software in Distillation Design and Control; Shanghai East China University of Science and Technology Press: Shanghai, China, 2015; pp. 98–111. [Google Scholar]
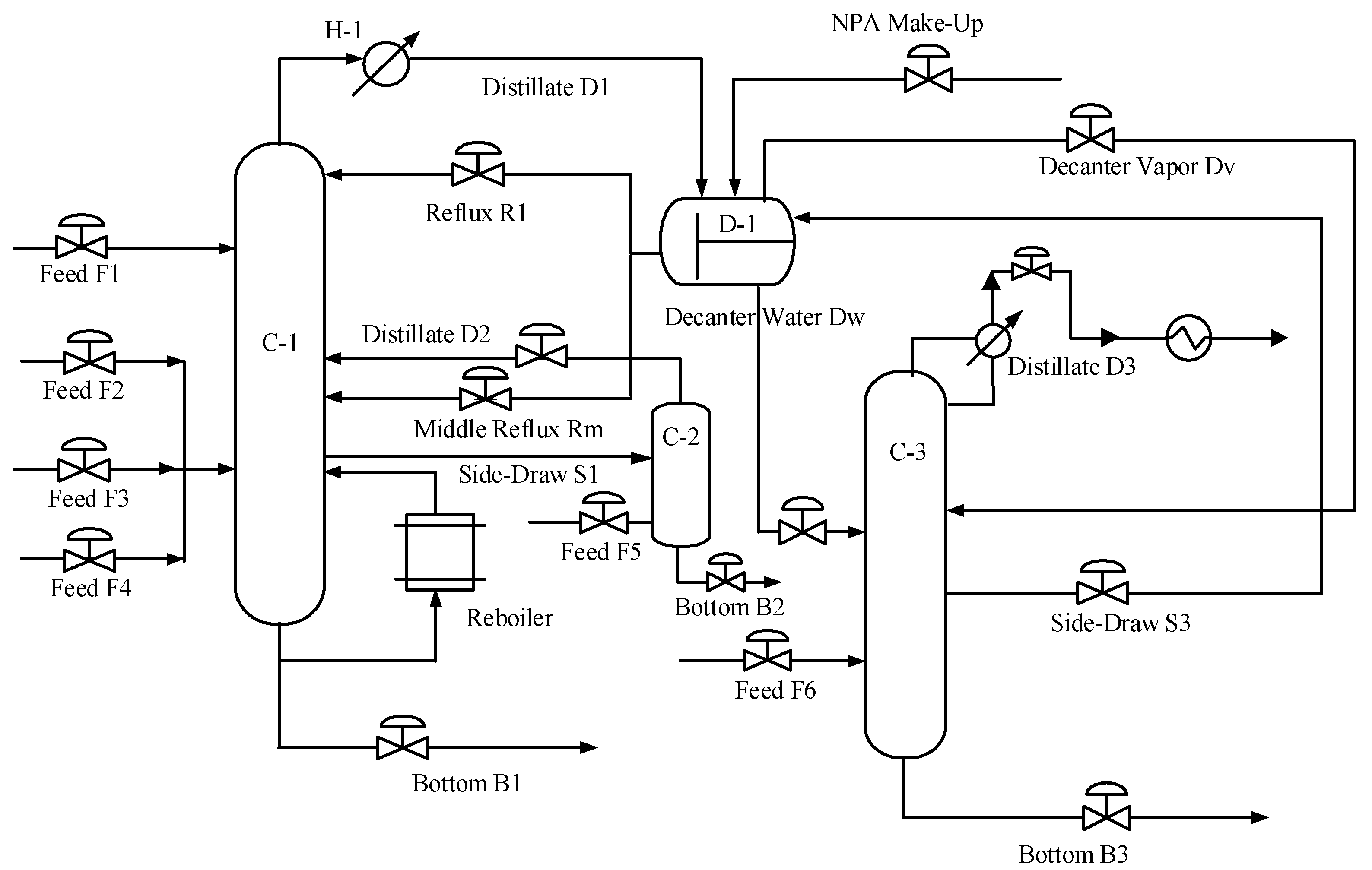


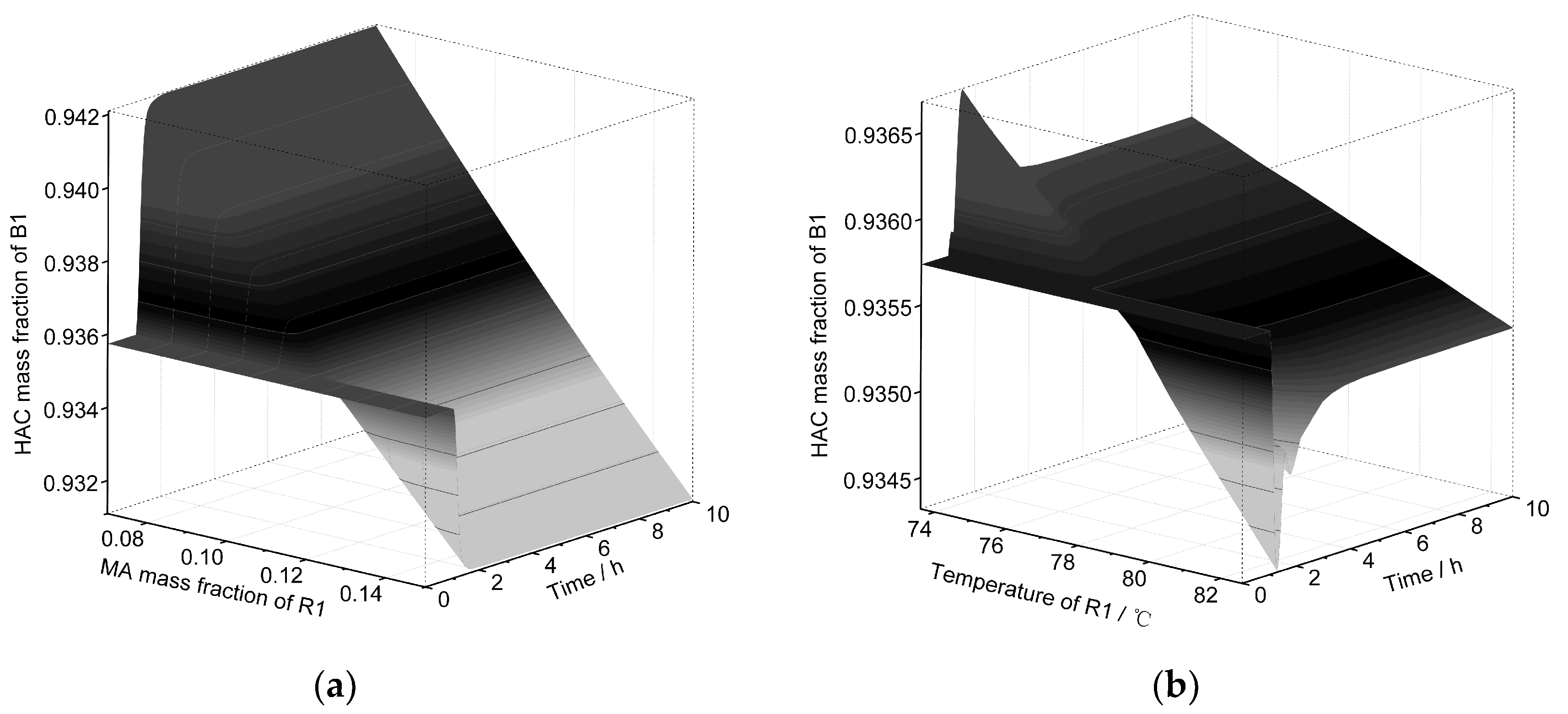
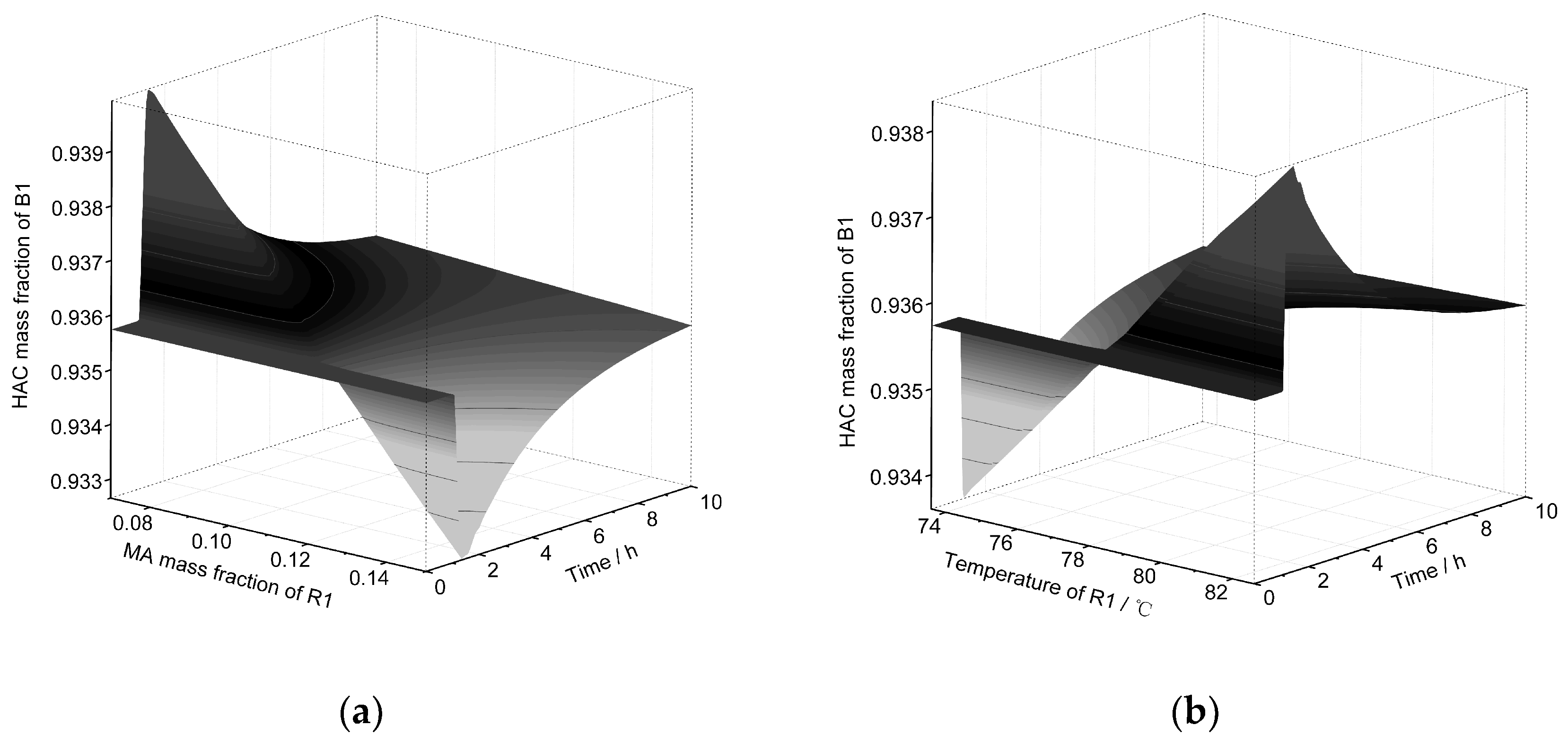
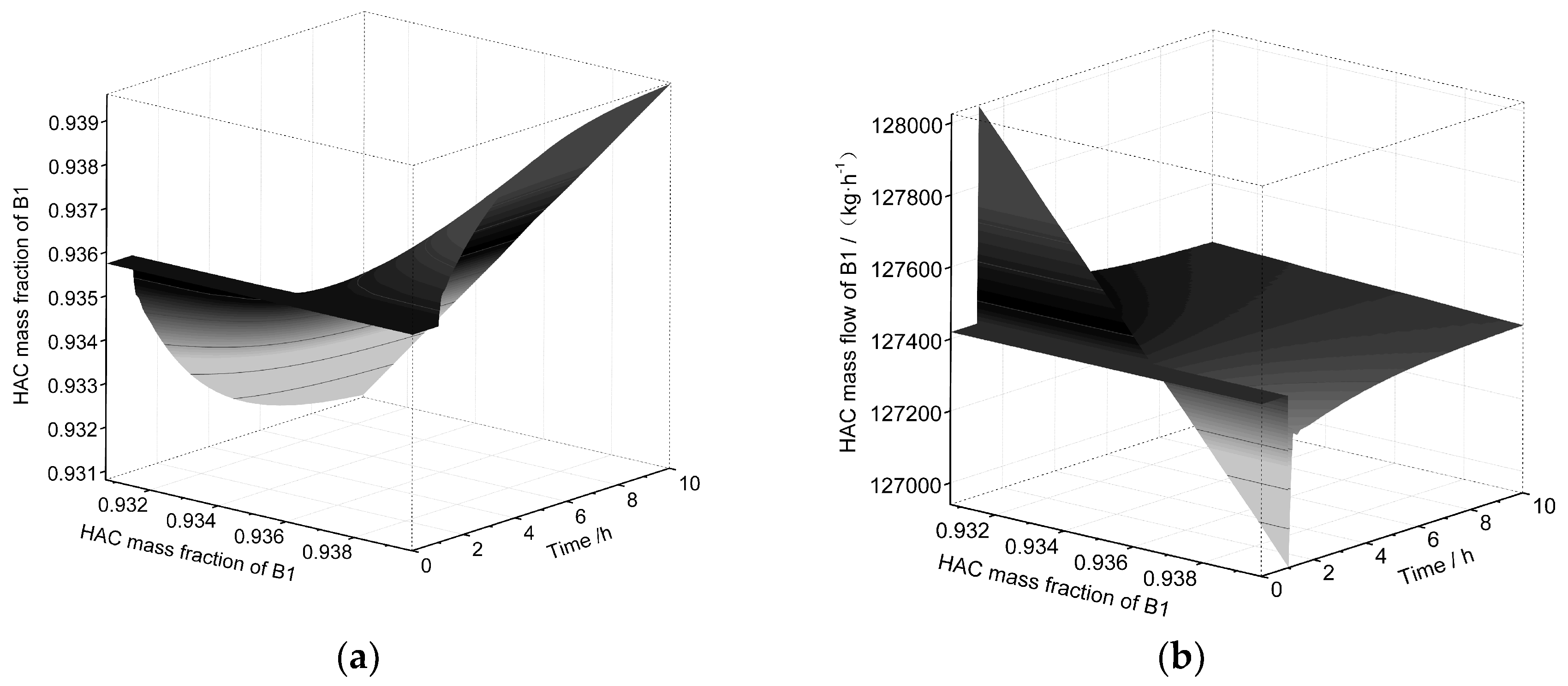

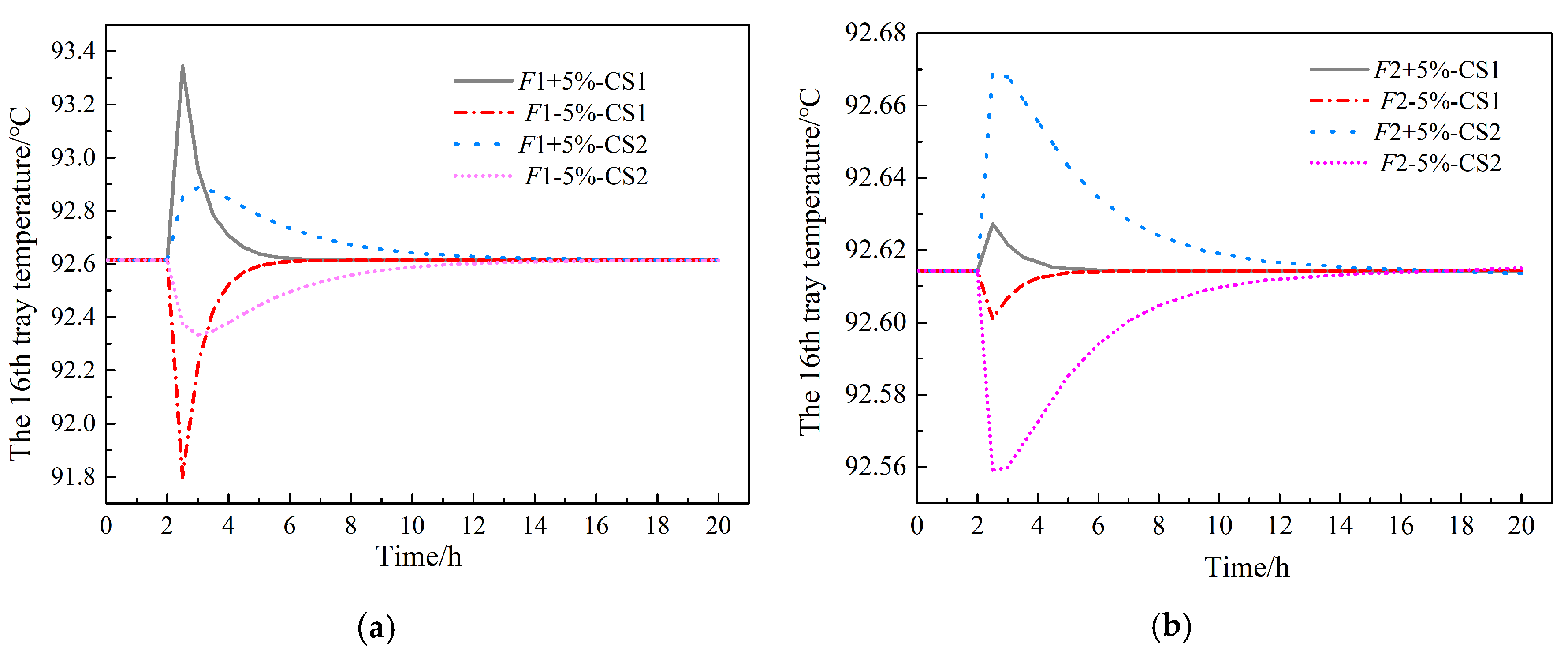

| Equipment | Outlet Stream | Temperature | Pressure | Flow | HAc | Water | NPA | PX | MA |
|---|---|---|---|---|---|---|---|---|---|
| °C | MPa | Kg·h−1 | wt% | wt% | wt% | wt% | wt% | ||
| C-1 | S1 | 105.2 | 0.123 | 8200 | 68.3 | 26.6 | 4 | 0.5 | 0.6 |
| D1 | 84.6 | 0.12 | 251,181 | 0 | 14.9 | 73 | 0.1 | 12 | |
| B1 | 117.2 | 0.13 | 136,142 | 93.6 | 6.4 | 0 | 0 | 0 | |
| C-3 | S3 | 81.2 | 0.12 | 20,500 | - | 29.1 | 62.4 | - | 8.5 |
| D3 | 58.3 | 0.11 | 3000 | - | 3.8 | 0 | - | 96.2 | |
| B3 | 107.2 | 0.13 | 33,900 | - | 1 | 0 | - | 0 |
| Equilibrium Equation | |
|---|---|
| M | |
| E | , |
| S | |
| H |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Wang, J.; Li, Z. Analysis of Dynamic Characteristics and Control Strategies of a Solvent Dehydration Distillation Column in a Purified Terephthalic Acid Plant. Processes 2020, 8, 125. https://doi.org/10.3390/pr8010125
Huang X, Wang J, Li Z. Analysis of Dynamic Characteristics and Control Strategies of a Solvent Dehydration Distillation Column in a Purified Terephthalic Acid Plant. Processes. 2020; 8(1):125. https://doi.org/10.3390/pr8010125
Chicago/Turabian StyleHuang, Xiuhui, Jun Wang, and Zeqiu Li. 2020. "Analysis of Dynamic Characteristics and Control Strategies of a Solvent Dehydration Distillation Column in a Purified Terephthalic Acid Plant" Processes 8, no. 1: 125. https://doi.org/10.3390/pr8010125
APA StyleHuang, X., Wang, J., & Li, Z. (2020). Analysis of Dynamic Characteristics and Control Strategies of a Solvent Dehydration Distillation Column in a Purified Terephthalic Acid Plant. Processes, 8(1), 125. https://doi.org/10.3390/pr8010125





