Nonlinear Structural Control Analysis of an Offshore Wind Turbine Tower System
Abstract
:1. Introduction
2. System Modeling
2.1. The Averaging Method
2.2. Periodic Solutions
2.3. Equilibrium Solutions and Stability Analyses
3. Analytical and Numerical Results
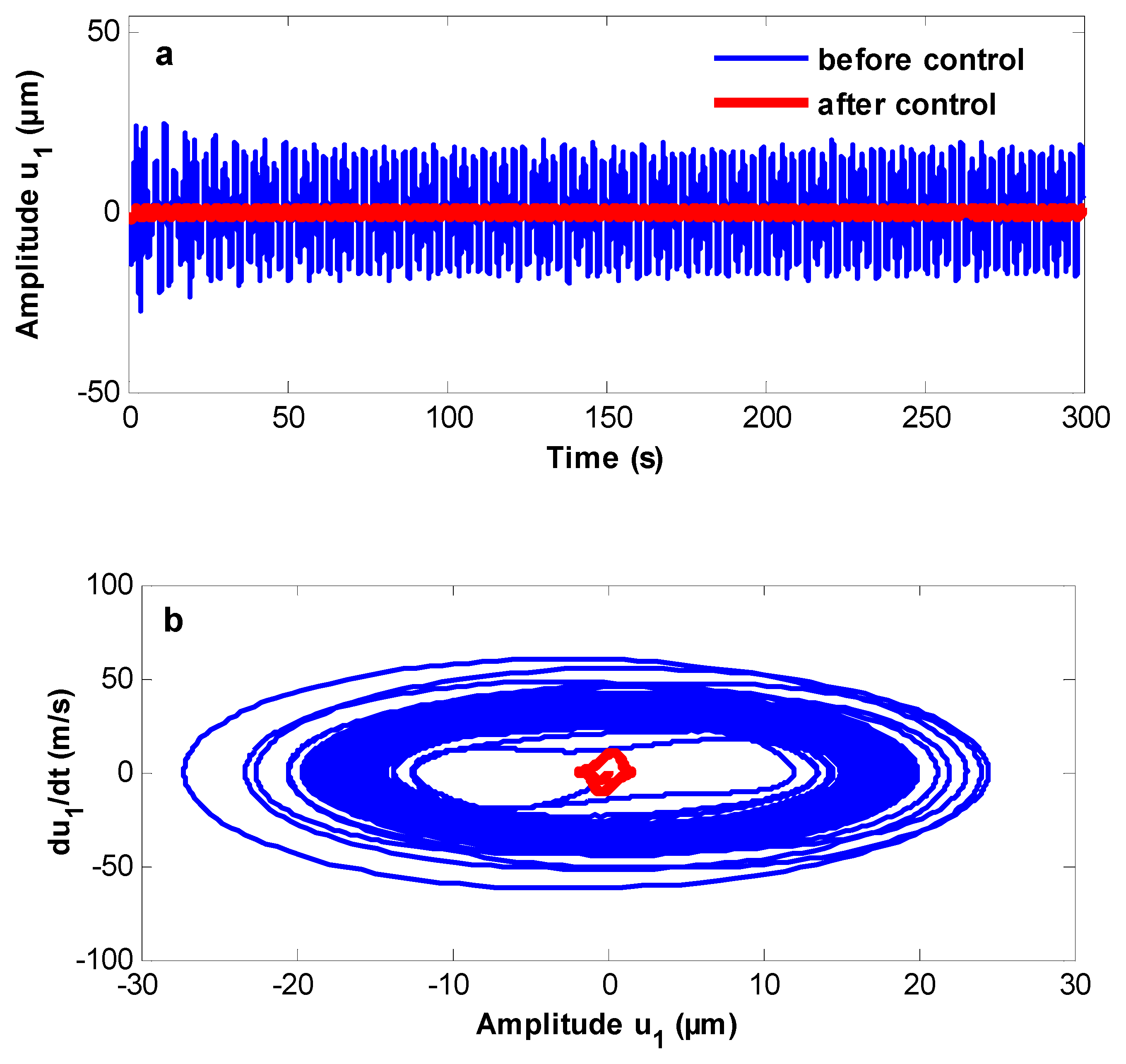
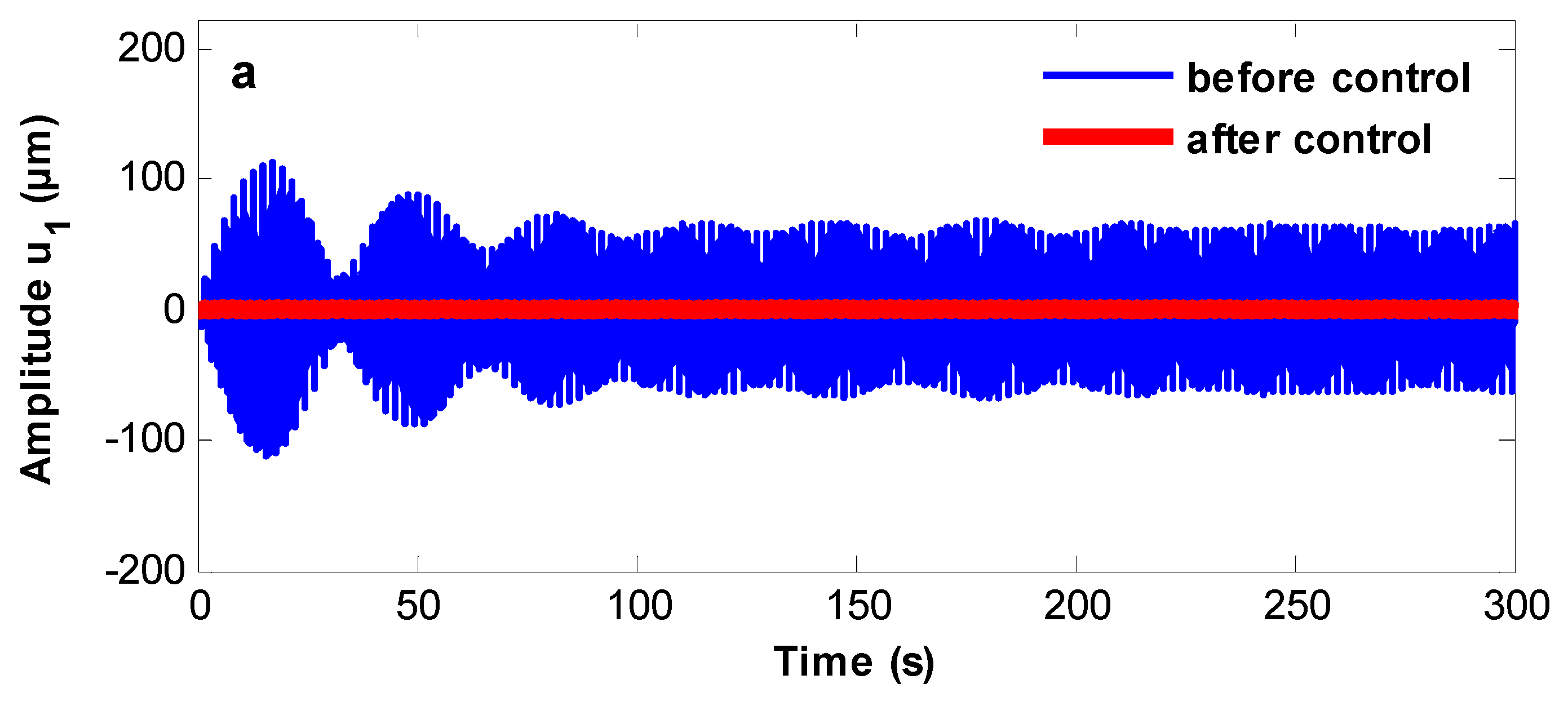
3.1. System Behavior and Energy Transfer in the Wind Turbine Tower System
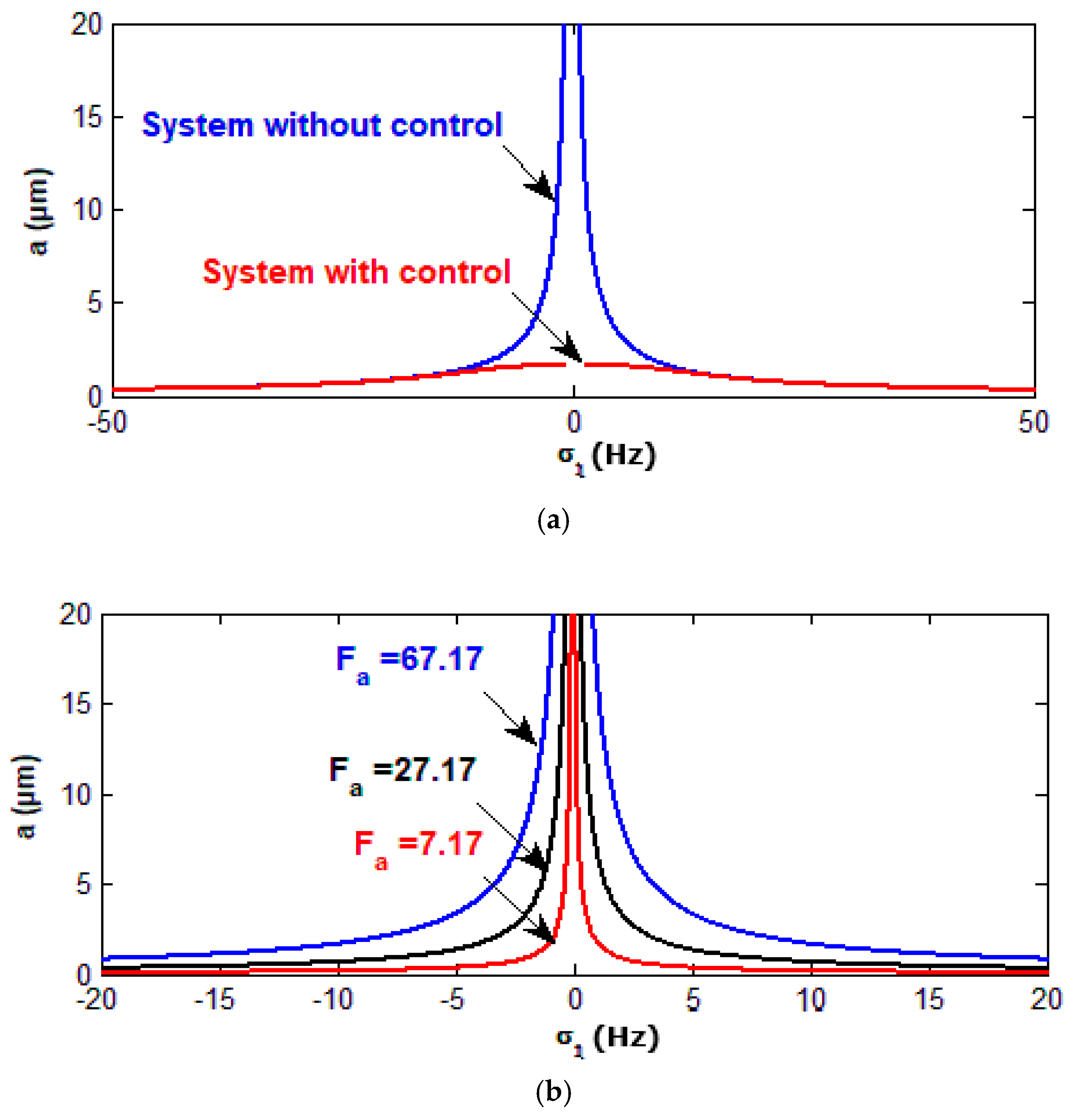
3.2. Frequency Response Curves of the Controlled System
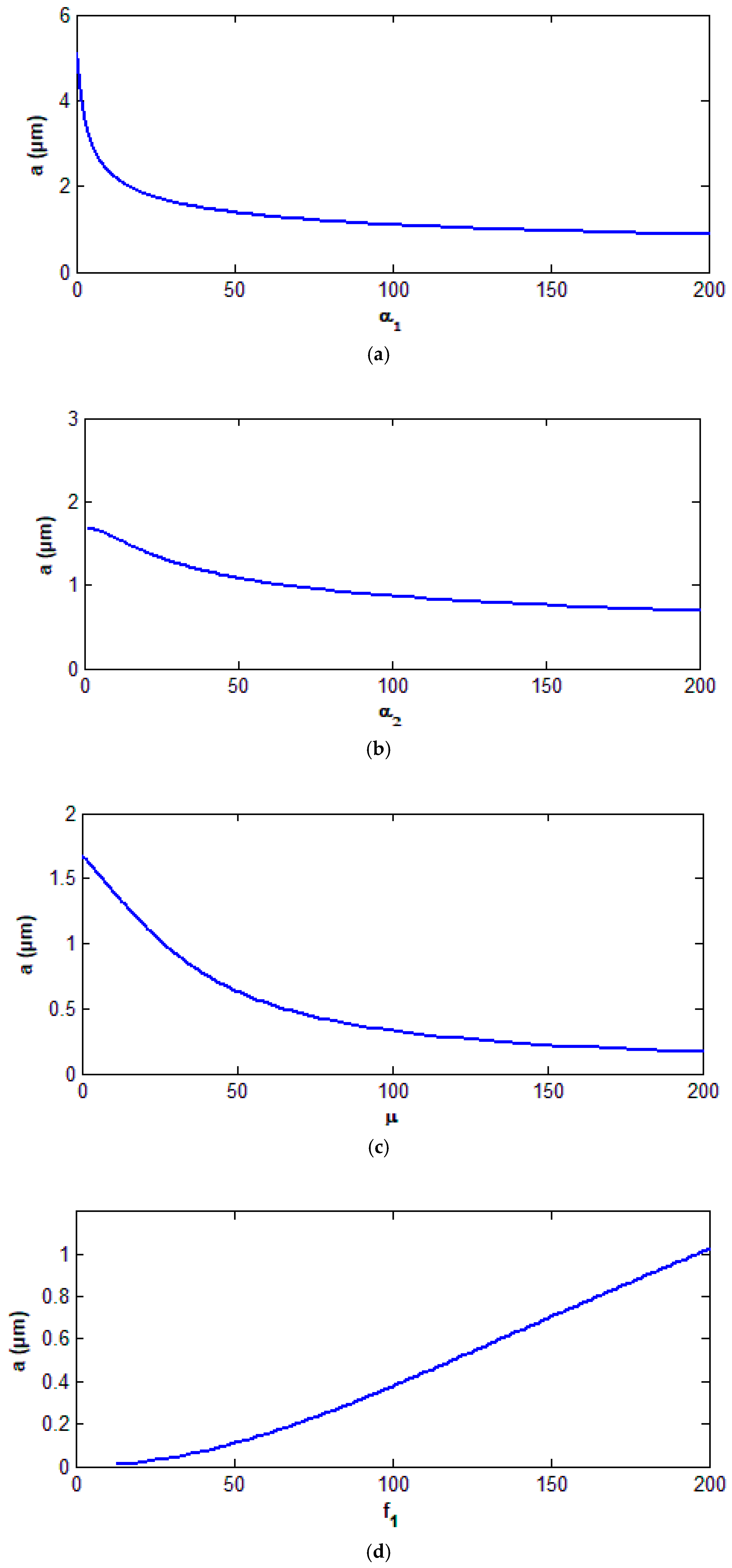
3.3. Effect of Some Different Parameters on the Controlled System
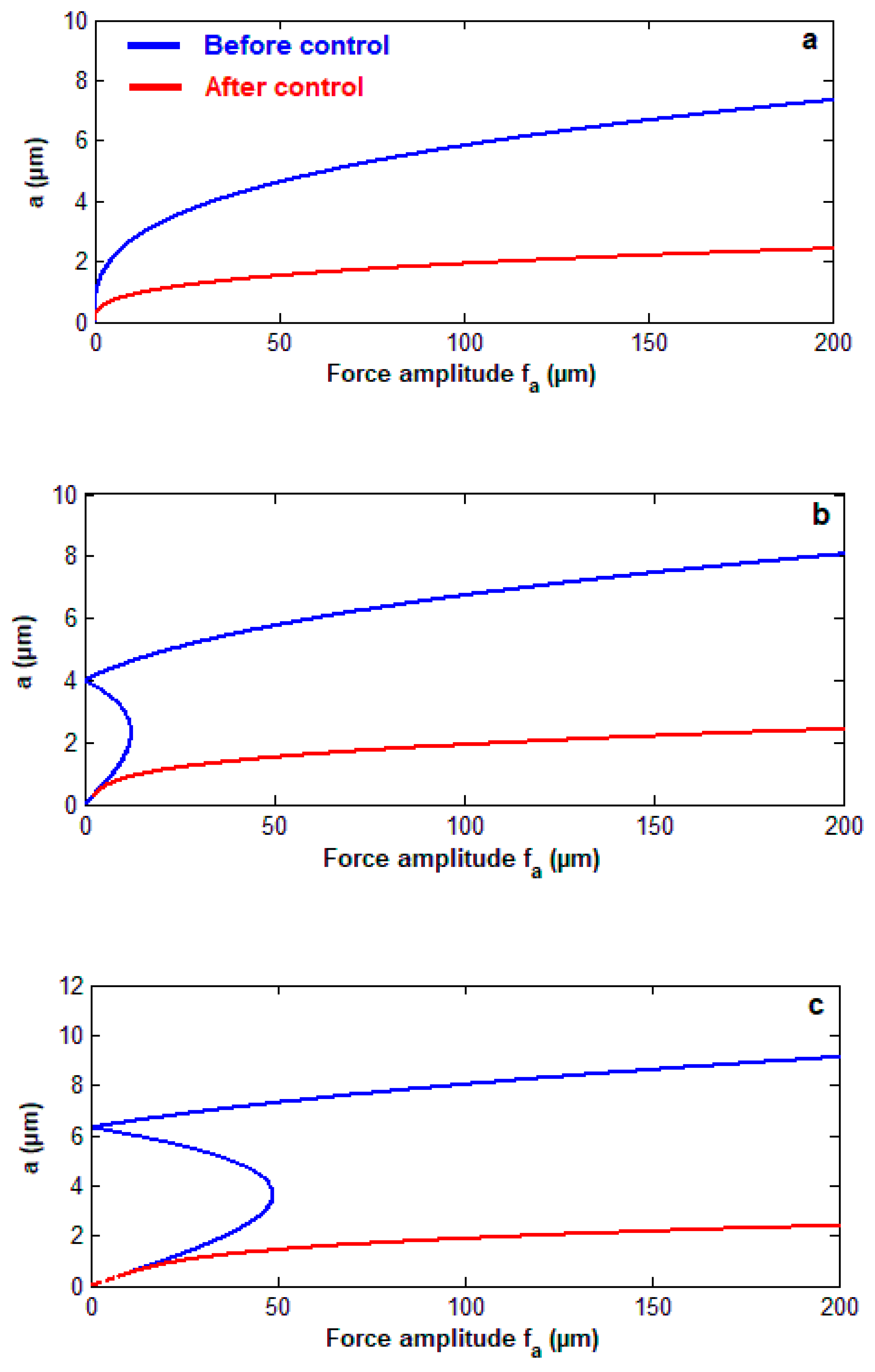
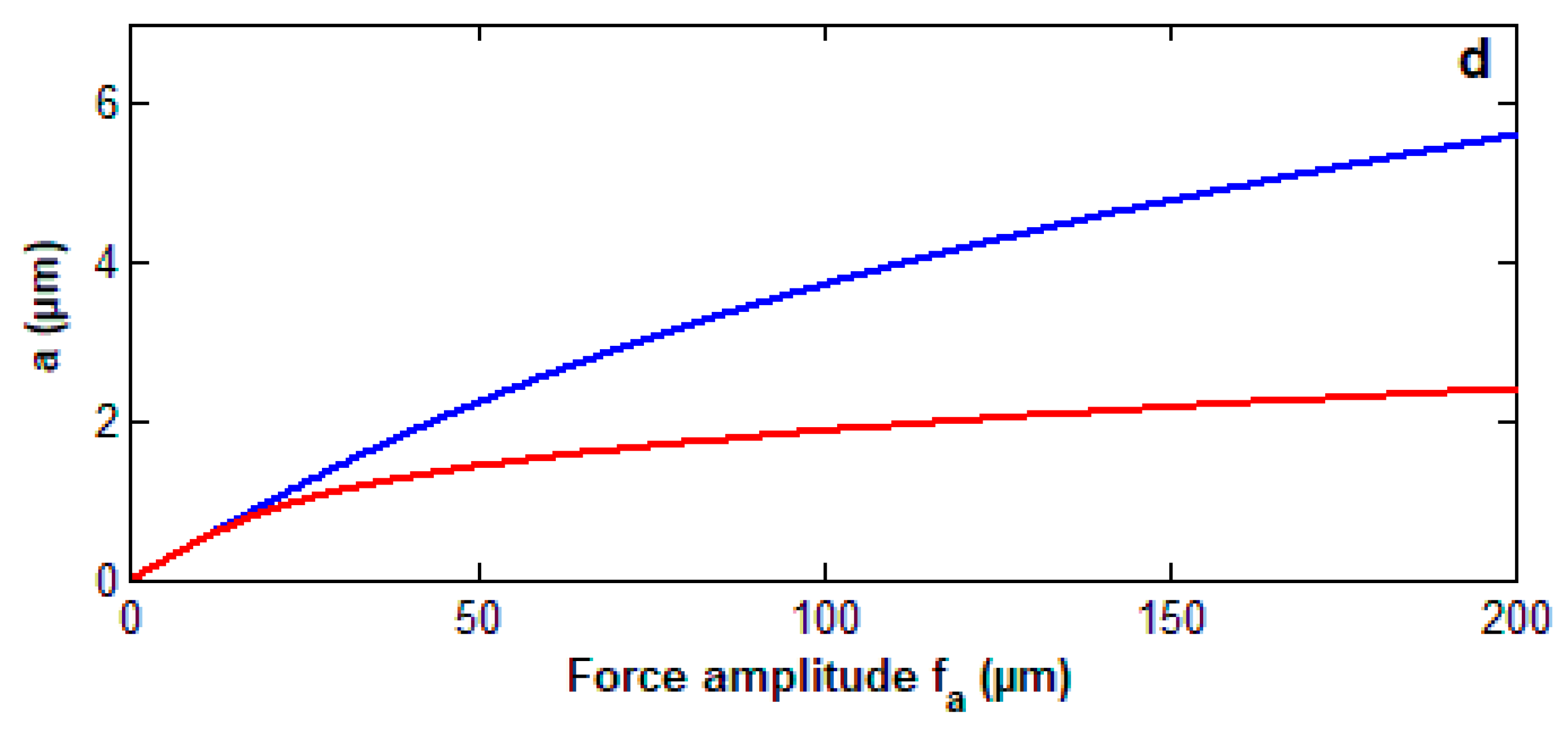
3.4. The Curves of Force Response for the Controlled System
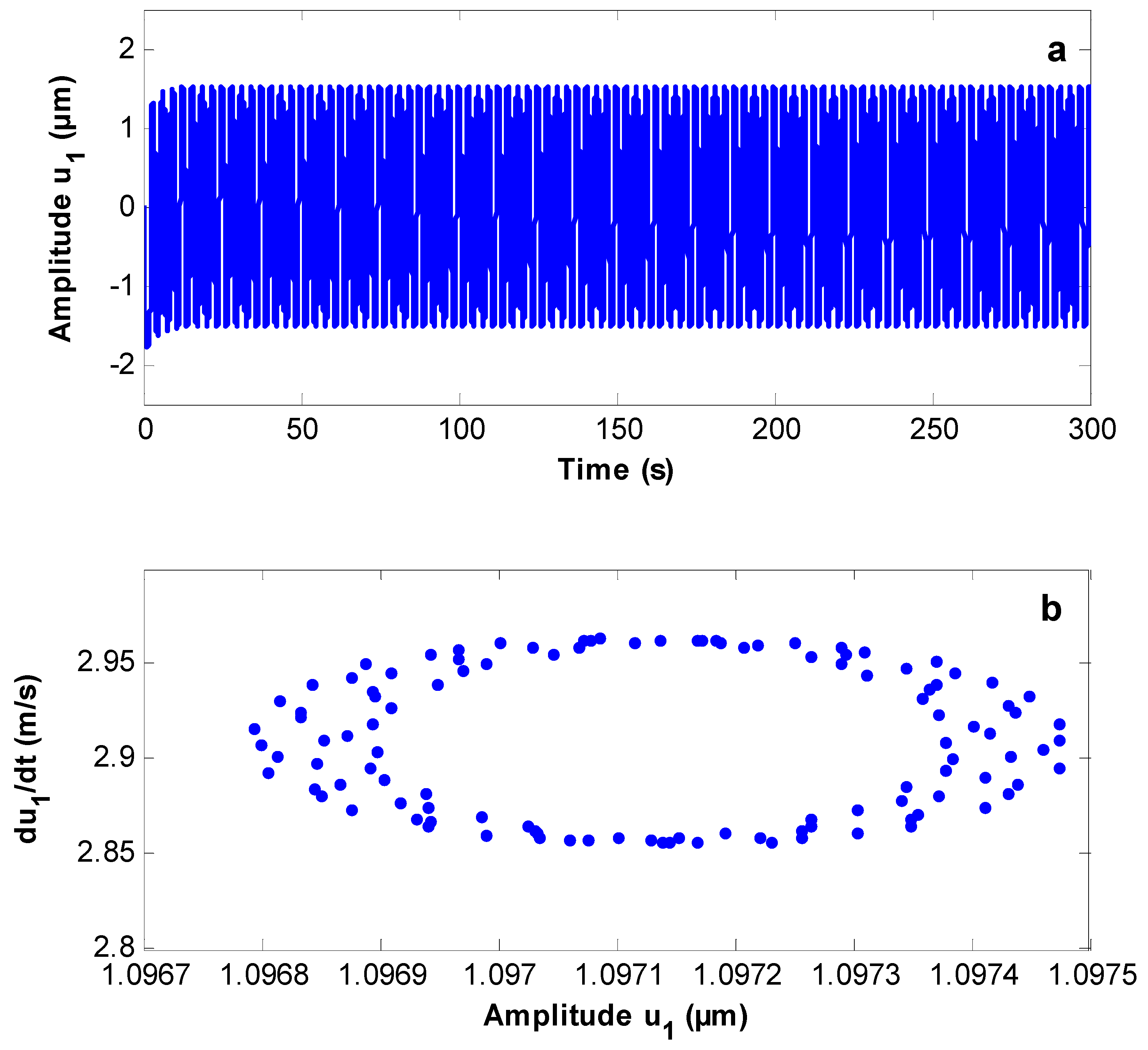
3.5. The Poincaré Maps
3.6. Comparison with Published Work
4. Conclusions
- The amplitudes were suppressed from about 18 and 60 to about 1.5 and 1.25 at resonance cases as well as respectively.
- The controlled system has an effectiveness and for the wind turbine system.
- The energy was transferred from the system before control to the system after adding the NPD controller at different values of natural, external excitation, and parametric excitation frequencies and .
- The behavior of the controlled system is a monotonic increasing function of the wind amplitude force and the parametric excitation force and is a monotonic decreasing function of the damping coefficient and control parameters and .
- The controlled system has a jump phenomenon with multiple solutions for positive and negative values of the nonlinear control parameter .
- The system amplitude before control has a nonlinear relation and a slightly increasing amplitude for large values of but it has a linear relation with small slope amplitudes after adding a controller.
- The system before control becomes stable, and periodic motion appears on Poincaré maps. The system also has a steady-state solution after control.
- The controlled system shows quasi-periodic motion and an unstable solution at
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| acceleration, velocity, and displacement of the wind turbine system. | |
| damping parameter of the controlled system. | |
| and | parametric, wind, and wave forces. |
| , and | natural and excitation frequencies of the wind turbine system. |
| and | coefficients of the nonlinear PD controller |
| small perturbation parameter (0 < << 1) |
References
- Silva, M.A.; Arora, J.S.; Brasil, R.M. Formulations for the optimal design of RC wind turbine towers. In Proceedings of the International Conference on Engineering Optimization (Eng Opt 2008), Rio de Janeiro, Brazil, 1–5 June 2008. [Google Scholar]
- Shi, W.; Han, J.; Kim, C.; Lee, D.; Shin, H.; Park, H. Feasibility study of offshore wind turbine substructures for southwest offshore wind farm project in Korea. Renew. Energy 2015, 74, 406–413. [Google Scholar] [CrossRef]
- Van der Woude, C.; Narasimhan, S. A study on vibration isolation for wind turbine structures. Eng. Struct. 2014, 60, 223–234. [Google Scholar] [CrossRef]
- Shi, F.; Patton, R. An active fault tolerant control approach to an offshore wind turbine model. Renew. Energy 2015, 75, 788–798. [Google Scholar] [CrossRef]
- Nguyen Dinh, V.; Basu, B. Passive control of floating offshore wind turbine nacelle and spar vibrations by multiple tuned mass dampers. Struct. Control Health Monit. 2015, 22, 152–176. [Google Scholar] [CrossRef]
- Hu, Y.; He, E. Active structural control of a floating wind turbine with a stroke-limited hybrid mass damper. J. Sound Vib. 2017, 410, 447–472. [Google Scholar] [CrossRef]
- Eisa, S.A.; Stone, W.; Wedeward, K. Mathematical analysis of wind turbines dynamics under control limits: Boundedness, existence, uniqueness, and multi time scale simulations. Int. J. Dyn. Control 2018, 6, 929–949. [Google Scholar] [CrossRef]
- Fitzgerald, B.; Sarkar, S.; Staino, A. Improved reliability of wind turbine towers with active tuned mass dampers (ATMDs). J. Sound Vib. 2018, 419, 103–122. [Google Scholar] [CrossRef]
- Dagli, B.Y.; Tuskan, Y.; Gokkus, U. Evaluation of Offshore Wind Turbine Tower Dynamics with Numerical Analysis. Adv. Civ. Eng. 2018, 2018, 3054851. [Google Scholar] [CrossRef] [Green Version]
- Kamel, M.M.; Hamed, Y.S. Non-Linear Analysis of an Inclined Cable under Harmonic Excitation. Acta Mech. 2010, 214, 315–325. [Google Scholar] [CrossRef]
- El-Ganaini, W.A.A.; Kamel, M.M.; Hamed, Y.S. Vibration reduction in ultrasonic machine to external and tuned excitation forces. Appl. Math. Model. 2009, 33, 2853–2863. [Google Scholar] [CrossRef]
- Kamel, M.M.; El-Ganaini, W.A.A.; Hamed, Y.S. Vibration suppression in ultrasonic machining described by non-linear differential equations. J. Mech. Sci. Technol. 2009, 23, 2038–2050. [Google Scholar] [CrossRef]
- Kamel, M.M.; El-Ganaini, W.A.A.; Hamed, Y.S. Vibration suppression in multi-tool ultrasonic machining to multi-external and parametric excitations. Acta Mech. Sinica 2009, 25, 403–415. [Google Scholar] [CrossRef]
- Hamed, Y.S.; EL-Sayed, A.T.; El-Zahar, E.R. On controlling the vibrations and energy transfer in MEMS gyroscopes system with simultaneous resonance. Nonlinear Dyn. 2016, 83, 1687–1704. [Google Scholar] [CrossRef]
- Hamed, Y.S.; Alharthi, M.R.; AlKhathami, H.K. Nonlinear vibration behavior and resonance of a Cartesian manipulator system carrying an intermediate end effector. Nonlinear Dyn. 2018, 91, 1429–1442. [Google Scholar] [CrossRef]
- Saeed, N.A.; Kamel, M. Nonlinear PD-controller to suppress the nonlinear oscillations of horizontally supported Jeffcott-rotor system. Int. J. Non Linear Mech. 2016, 87, 109–124. [Google Scholar] [CrossRef]
- Saeed, N.A.; El-Ganaini, W.A. Time-delayed control to suppress the nonlinear vibrations of a horizontally suspended Jeffcott-rotor system. Appl. Math. Model. 2017, 44, 523–539. [Google Scholar] [CrossRef]
- Cartmell, M.P. Introduction to Linear, Parametric and Nonlinear Vibrations; Chapman & Hall: London, UK, 1990. [Google Scholar]
- Nayfeh, A.H.; Balachandran, B. Applied Nonlinear Dynamics: Analytical, Computational and Experimental Methods; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Nayfeh, A.H. Problems in Perturbation; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley: New York, NY, USA, 1995. [Google Scholar]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamed, Y.S.; Aly, A.A.; Saleh, B.; Alogla, A.F.; Aljuaid, A.M.; Alharthi, M.M. Nonlinear Structural Control Analysis of an Offshore Wind Turbine Tower System. Processes 2020, 8, 22. https://doi.org/10.3390/pr8010022
Hamed YS, Aly AA, Saleh B, Alogla AF, Aljuaid AM, Alharthi MM. Nonlinear Structural Control Analysis of an Offshore Wind Turbine Tower System. Processes. 2020; 8(1):22. https://doi.org/10.3390/pr8010022
Chicago/Turabian StyleHamed, Y. S., Ayman A. Aly, B. Saleh, Ageel F. Alogla, Awad M. Aljuaid, and Mosleh M. Alharthi. 2020. "Nonlinear Structural Control Analysis of an Offshore Wind Turbine Tower System" Processes 8, no. 1: 22. https://doi.org/10.3390/pr8010022
APA StyleHamed, Y. S., Aly, A. A., Saleh, B., Alogla, A. F., Aljuaid, A. M., & Alharthi, M. M. (2020). Nonlinear Structural Control Analysis of an Offshore Wind Turbine Tower System. Processes, 8(1), 22. https://doi.org/10.3390/pr8010022





