Energy and Exergy Assessment of S-CO2 Brayton Cycle Coupled with a Solar Tower System
Abstract
:1. Introduction
2. Materials and Method
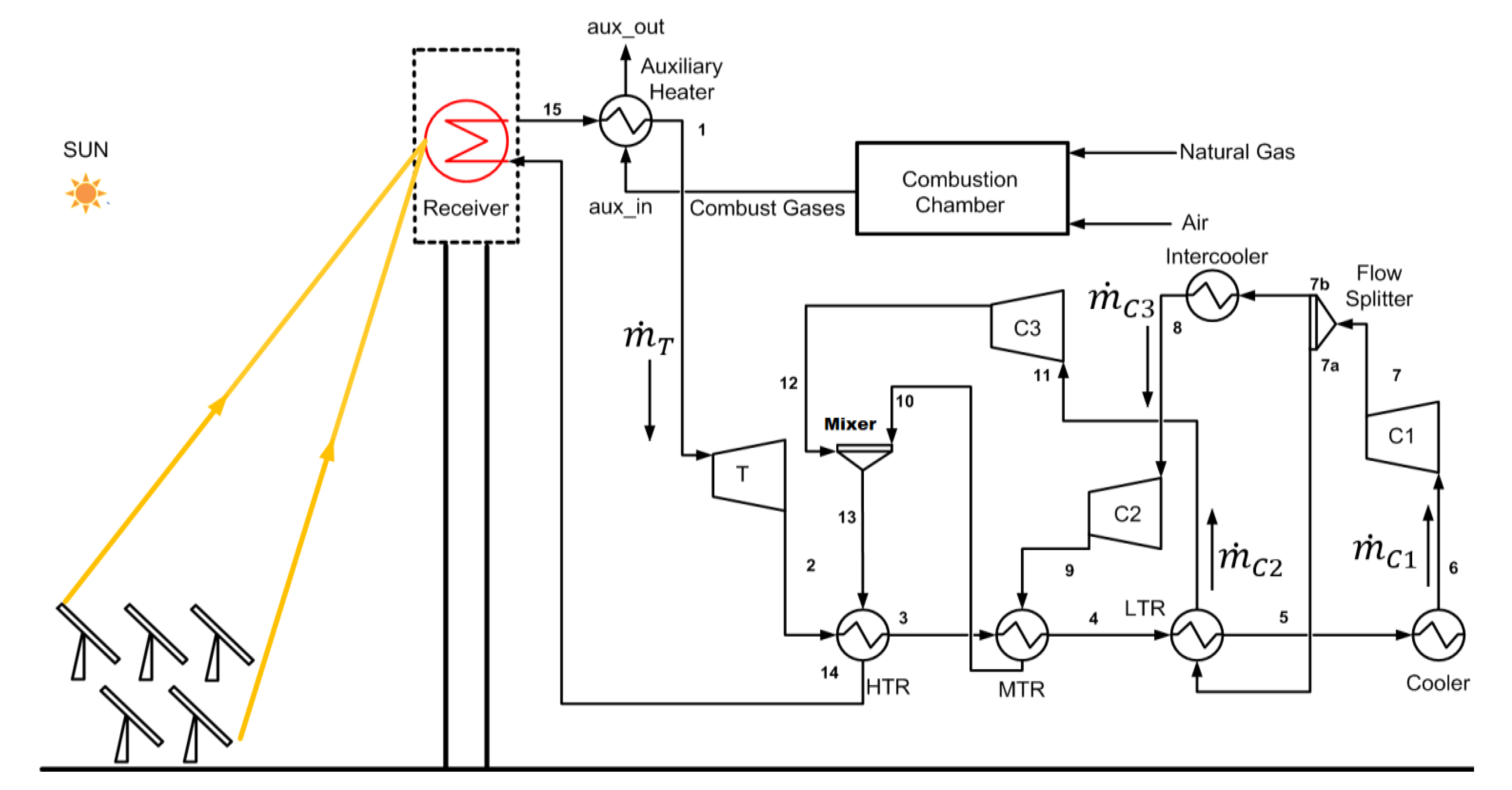
2.1. System Configuration and Key Concepts
2.2. Solar Radiation Model
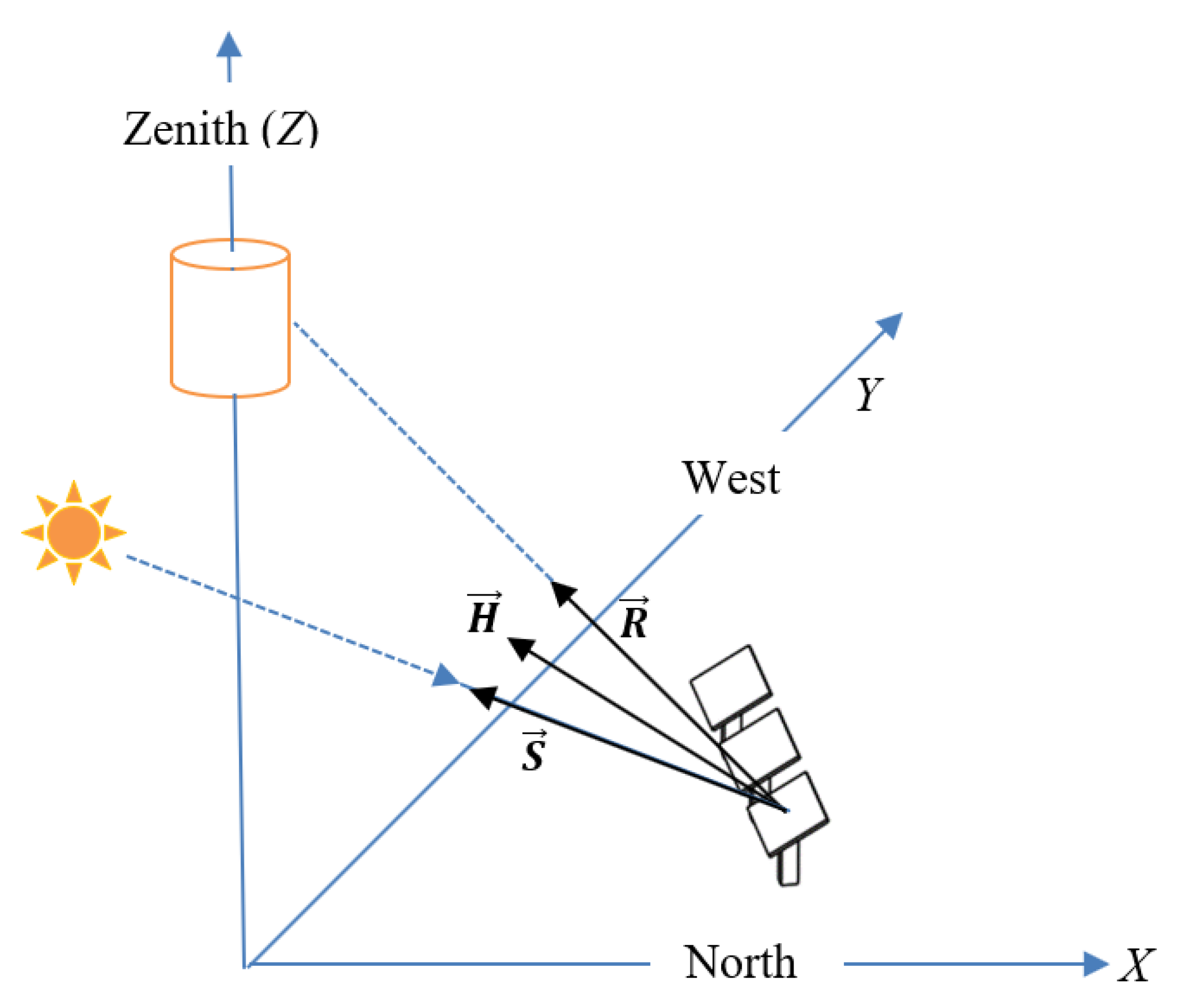
2.3. Heliostat Positioning Model
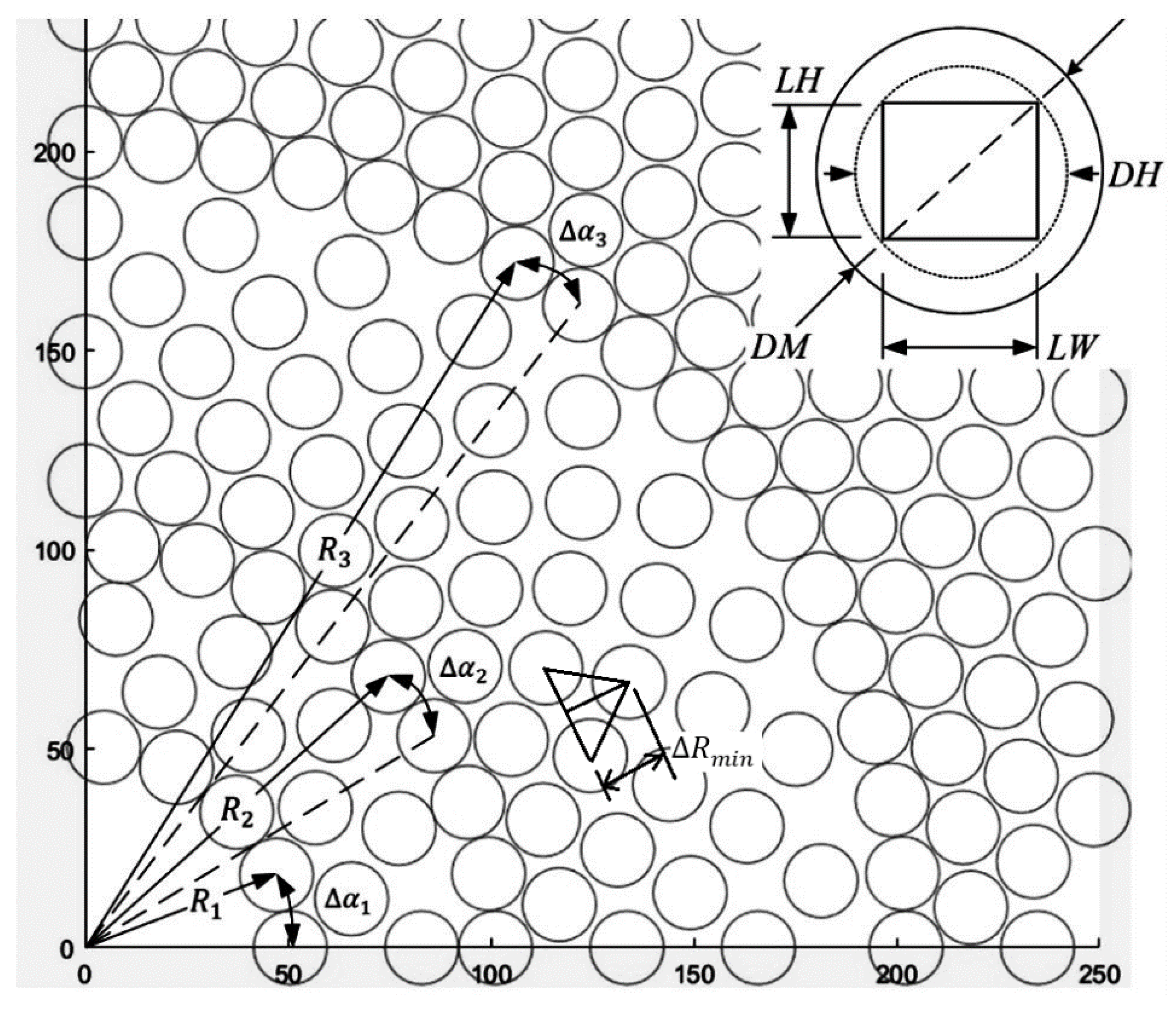
2.4. Heliostat Field Generation
2.4.1. Optical Efficiency of the Heliostat Field
2.4.2. Central Receiver and Heat Losses
2.5. Energy and Exergy Performance Assessments
2.5.1. Energy Model
2.5.2. Exergy Model
2.6. Operating Parameters and Simulation Environment
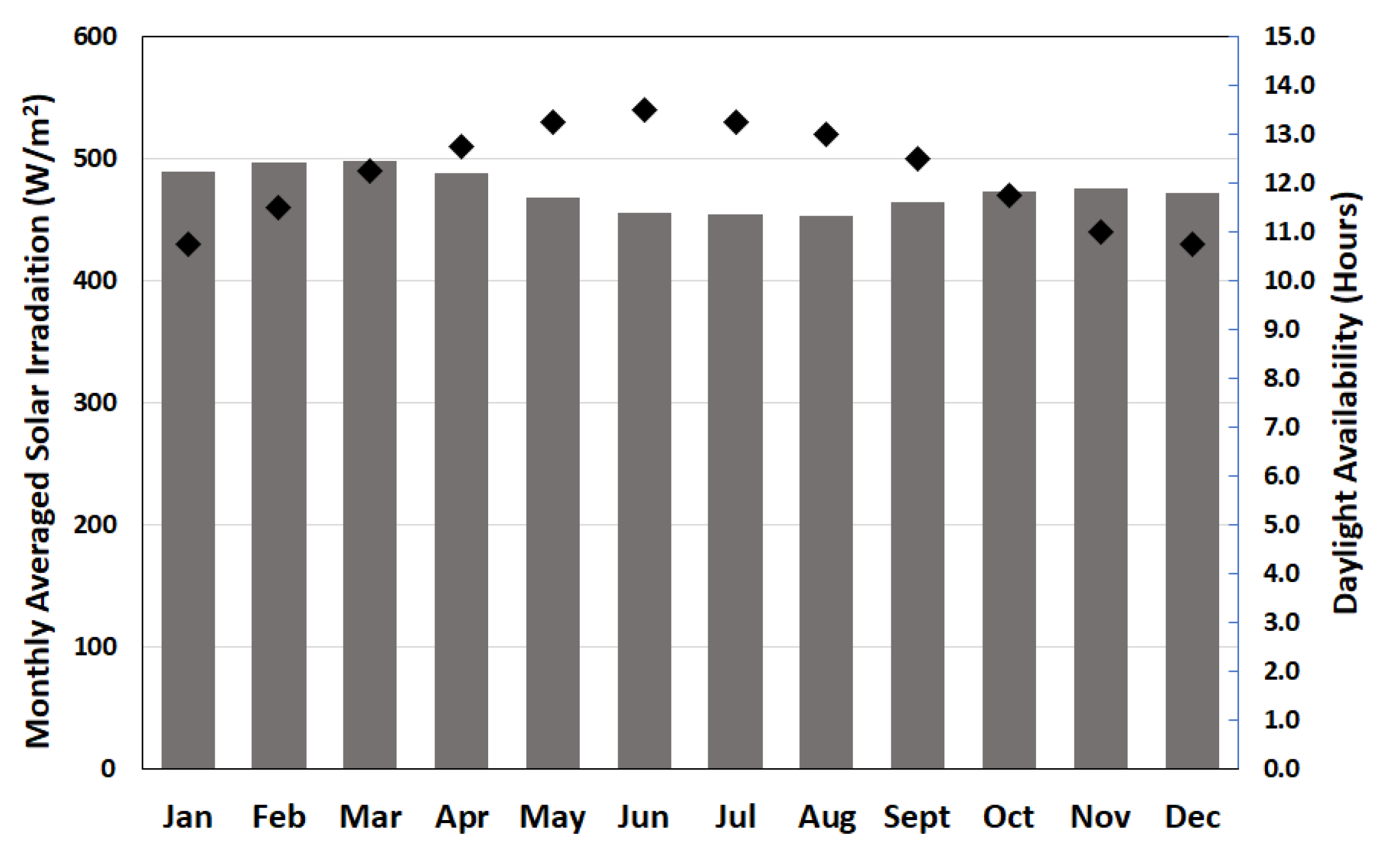
2.6.1. Solar Radiation, Heliostat Field and Receiver
2.6.2. S-CO2 Brayton Cycle
- The cycle operates under steady-state conditions with no pressure drop in the pipelines and heat exchangers.
- The turbine and compressor isentropic efficiencies are 93% and 89%, respectively.
- The heat exchanger effectiveness is 95% with a minimum pinch point temperature of 5 °C.
- Cooler and intercooler are dry cooled with air as coolant. Energy needed to operate air coolers is neglected.
- The cycle maximum pressure is 25 MPa.
- Compressor inlet temperature and pressure are maintained at 40 °C and 7.5 MPa corresponding to state 8.
- The turbine inlet temperature is 600 °C.
- Auxiliary heater effectiveness is 90%.
- The combustion chamber uses methane as a fuel with 300% excess air. This maintains the temperature of combustion gases at approximately at 673 °C.
- Cycle receives a constant power input of 80 MW.
- Energy consumed by solar tower auxiliaries is neglected.
3. Results and Discussions
4. Conclusions
- The average annual optical efficiency of the heliostat field was nearly 59 percent with a capability of providing 475 watts of power per unit heliostat’s area to the central receiver.
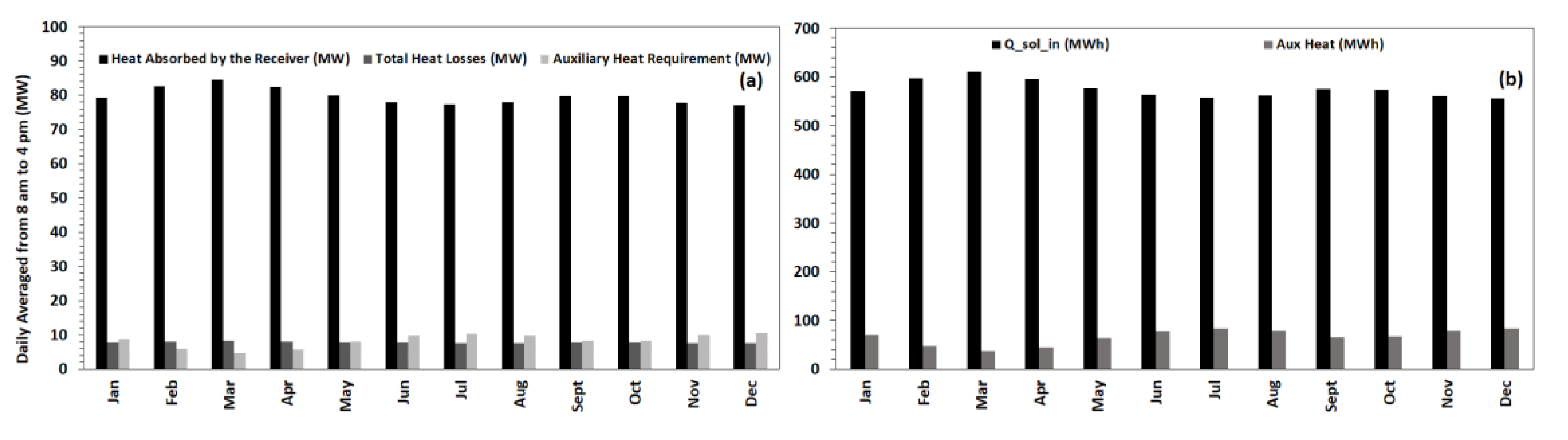
- The average annual solar heat absorbed by the receiver is approximately 79.7 MW, out of which nearly 10 percent is lost due to natural convection and radiation.
- The power cycle was operated with a turbine inlet temperature of 600 °C and provided a constant net power input of 80 MW.
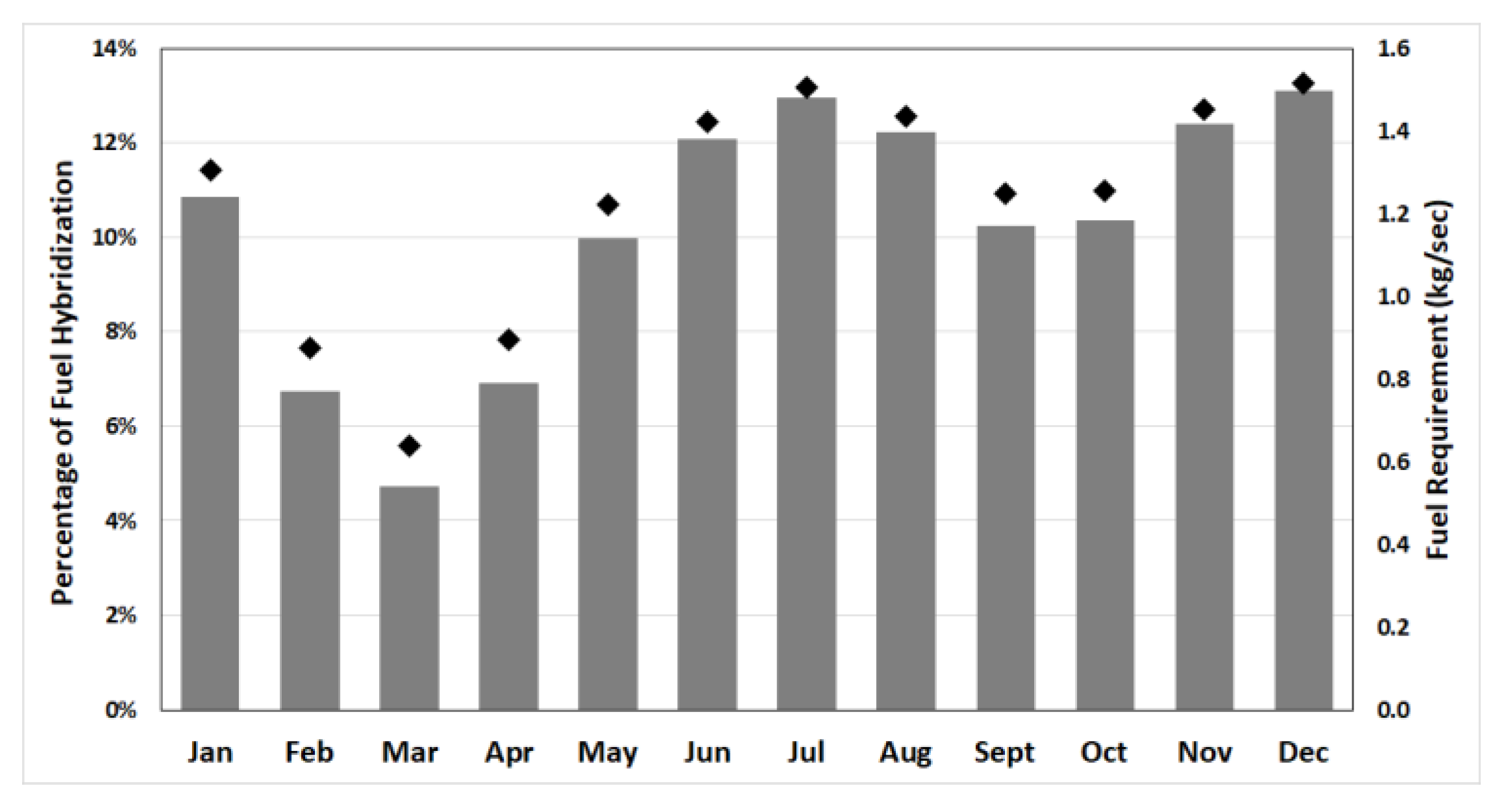
- The auxiliary heater, operating on combustion gases with methane as fuel in the combustion chamber, provided extra heat required for the steady operation of the cycle. The average annual fuel requirement is 1.2 kg/s.
- On a monthly basis, for the month of March, the plant was found to be least dependent on auxiliary heat and operated 95% on the solar energy, whereas, a maximum of 13% auxiliary heat support was required in December.
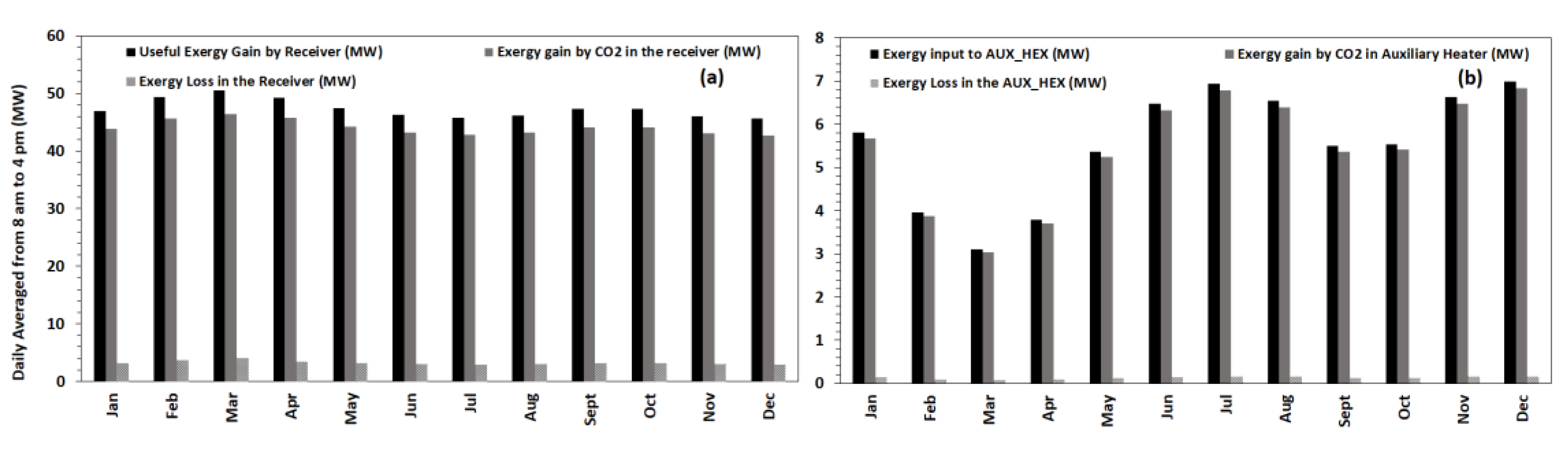
- Exergy analysis revealed a maximum loss occurs in the heliostat field, which is nearly 42.5% of incident solar exergy.
- Approximately 5% of exergy absorbed by the central receiver was lost due to natural convection and radiation. Furthermore, the central receiver experienced 7.5% loss in the remaining exergy while transferring heat to the working fluid (carbon dioxide).
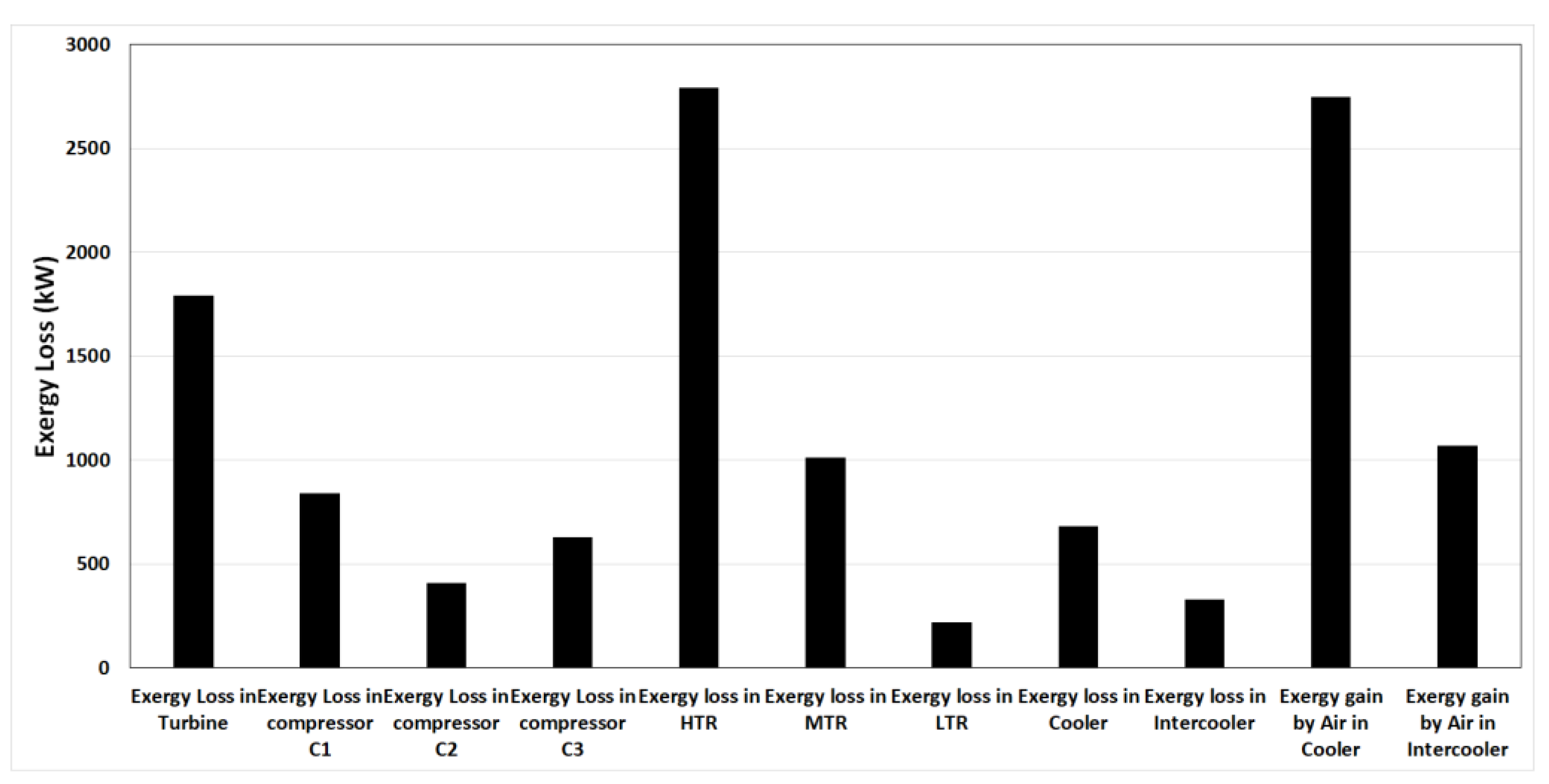
- Nearly 7.5% of the net exergy received by CO2 from the solar central receiver and the auxiliary heater is lost in turbomachines (turbine and compressors). On the other hand, heat recuperators (LTR, HTR and MTR) and coolers (cooler and intercooler) incurred approximately 8.1% and 10% of net exergy gain by CO2, respectively.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Apparent solar irradiation beyond the atmosphereW/m2 | Convective heat loss, MW | |
| B | Atmospheric extinction coefficient | Solar power input to the cycle, MW | |
| Heliostat surface area, m2 | Auxiliary power input to the cycle, MW | ||
| Square root of the area of the heliostat, m | Radius of the first ring of the first zone of the heliostat field, m | ||
| Extra security distance, m | , , | Spatial (x, y, z) components of the unit vector of reflected ray of the sun from heliostat pointing receiver | |
| DR | Diameter of the receiver, m | , , | Spatial (x, y, z) components of the unit vector directing sun ray |
| Characteristic diameter, m | Slant distance between the receiver and the heliostat, m | ||
| Heliostat diagonal, m | Entropy, kJ/kg | ||
| Direct normal irradiation, W/ m2 | Receiver surface temperature, K | ||
| EOT | Equation of time | Reference temperature, K | |
| Intercept factor of the heliostat | THT | Tower optical height, m | |
| Atmospheric attenuation factor | image dimension in the sagittal plane, m | ||
| Shading and blocking factor | Turbine power output, MW | ||
| Focal distance | Compressor 1 power consumption, MW | ||
| Degree of hybridization | Compressor 2 power consumption, MW | ||
| Radiation shape factor | x-coordinate on the receiver plane | ||
| Direct solar radiation, W/ m2 | , | x-coordinates of the receiver and the heliostat | |
| Hour angle, degree | , | y-coordinates of the receiver and the heliostat | |
| Mass enthalpy, kJ/kg | y-coordinate on the receiver plane | ||
| Convective heat transfer coefficient | Z | Altitude of the location, m | |
| image dimension in the tangential plane, m | , | z-coordinates of the receiver and the heliostat | |
| , , | Spatial (x, y, z) components of the surface normal unit vector of the heliostat | Solar altitude angle, degree | |
| HTR | High temperature recuperator | Absorptivity of the receiver | |
| Latitude of the location, m | Sun’s declination angle, degree | ||
| LST | Local solar time, hours | Solar incidence angle, degree | |
| Standard meridian of local time zone | Heliostat surface azimuth angle, degree | ||
| Longitude of the location | Heliostat tilt angle, degree | ||
| Heliostat width, m | Minimum radial spacing between heliostat rows, m | ||
| Heliostat height, m | Azimuthal spacing between heliostats in the ith zone of heliostat field, degree | ||
| LR | Length of the receiver, m | Thermal efficiency of the plant | |
| LTR | Low temperature recuperator | Exergy, kW or MW | |
| MTR | Medium temperature recuperator | Optical efficiency | |
| Mass flow rate in the turbine, kg/s | Reflectivity of the heliostat mirror | ||
| Mass flow rate in the compressor 1, kg/s | Emissivity of the receiver | ||
| Mass flow rate in the compressor 2, kg/s | Heat exchanger effectiveness | ||
| Mass flow rate in the compressor 3, kg/s | Stefan Boltzmann constant | ||
| N | Day number of the year | Standard deviation of the normal distribution | |
| Number of rows in the ith zone of heliostat field | Error factor for the sun shape | ||
| Number of heliostats in each row of the zone | Error factor for the quality of the beam | ||
| Solar power absorbed by receiver, MW | Error factor for the stigmatic effect | ||
| Radiative heat loss, MW | Error factor for the tracking |
References
- Pfahl, A. Survey of Heliostat Concepts for Cost Reduction. J. Sol. Energy Eng. 2013, 136, 014501. [Google Scholar] [CrossRef]
- Steinmann, W.-D. Thermal energy storage systems for concentrating solar power (CSP) technology. In Advances in Thermal Energy Storage Systems; Elsevier: Amsterdam, The Netherlands, 2015; pp. 511–531. [Google Scholar]
- Xu, B.; Li, P.; Chan, C.; Tumilowicz, E. General volume sizing strategy for thermal storage system using phase change material for concentrated solar thermal power plant. Appl. Energy 2015, 140, 256–268. [Google Scholar] [CrossRef] [Green Version]
- Islam, K.; Hosenuzzaman, M.; Rahman, M.; Hasanuzzaman, M.; Rahim, N.A. Thermal performance improvement of solar thermal power generation. In Proceedings of the 2013 IEEE Conference on Clean Energy and Technology (CEAT), Lankgkawi, Malaysia, 18–20 November 2013; pp. 158–162. [Google Scholar]
- Zhai, R.; Zhao, M.; Li, C.; Peng, P.; Yang, Y. Improved Optimization Study of Integration Strategies in Solar Aided Coal-Fired Power Generation System. Int. J. Photoenergy 2015, 2015, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Praveen, P.R. Performance Analysis and Optimization of Central Receiver Solar Thermal Power Plants for Utility Scale Power Generation. Sustainability 2019, 12, 127. [Google Scholar]
- Atif, M.; Al-Sulaiman, F.A. Energy and exergy analyses of solar tower power plant driven supercritical carbon dioxide recompression cycles for six different locations. Renew. Sustain. Energy Rev. 2017, 68, 153–167. [Google Scholar] [CrossRef]
- Han, Y.; Xu, C.; Xu, G.; Zhang, Y.; Yang, Y. An Improved Flexible Solar Thermal Energy Integration Process for Enhancing the Coal-Based Energy Efficiency and NOx Removal Effectiveness in Coal-Fired Power Plants under Different Load Conditions. Energies 2017, 10, 1485. [Google Scholar] [CrossRef] [Green Version]
- Noone, C.J.; Torrilhon, M.; Mitsos, A. Heliostat field optimization: A new computationally efficient model and biomimetic layout. Sol. Energy 2012, 86, 792–803. [Google Scholar] [CrossRef]
- Besarati, S.M.; Goswami, D. A computationally efficient method for the design of the heliostat field for solar power tower plant. Renew. Energy 2014, 69, 226–232. [Google Scholar] [CrossRef]
- Collado, F.J.; Guallar, J. Campo: Generation of regular heliostat fields. Renew. Energy 2012, 46, 49–59. [Google Scholar] [CrossRef]
- Collado, F.J.; Guallar, J. Fast and reliable flux map on cylindrical receivers. Sol. Energy 2018, 169, 556–564. [Google Scholar] [CrossRef]
- Cruz, N.; Redondo, J.L.; Berenguel, M.; Álvarez, J.; Ortigosa, P.; Álvarez, J.D. Review of software for optical analyzing and optimizing heliostat fields. Renew. Sustain. Energy Rev. 2017, 72, 1001–1018. [Google Scholar] [CrossRef]
- Feher, E. The supercritical thermodynamic power cycle. Energy Convers. 1968, 8, 85–90. [Google Scholar] [CrossRef]
- Angelino, G. Carbon Dioxide Condensation Cycles for Power Production. J. Eng. Power 1968, 90, 287–295. [Google Scholar] [CrossRef]
- Dostál, V.; Driscoll, M.J.; Hejzlar, P. A Supercritical Carbon Dioxide Cycle for Next Generation Nuclear Reactors. Tech. Rep. MIT-ANP-TR-100; Massachusetts Institute of Technology: Cambridge, MA, USA, 2004; pp. 1–137. [Google Scholar]
- Angelino, G. Real Gas Effects in Carbon Dioxide Cycles. In Proceedings of the ASME 1969 Gas Turbine Conference and Products Show, Cleveland, OH, USA, 9–13 March 1969. [Google Scholar]
- Turchi, C.S.; Ma, Z.; Dyreby, J. Supercritical Carbon Dioxide Power Cycle Configurations for Use in Concentrating Solar Power Systems. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; pp. 967–973. [Google Scholar]
- Ahn, Y.; Bae, S.J.; Kim, M.; Cho, S.K.; Baik, S.; Lee, J.I.; Cha, J.E. Review of supercritical CO2 power cycle technology and current status of research and development. Nucl. Eng. Technol. 2015, 47, 647–661. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Lundqvist, P.; Johansson, A.; Platell, P. A comparative study of the carbon dioxide transcritical power cycle compared with an organic rankine cycle with R123 as working fluid in waste heat recovery. Appl. Therm. Eng. 2006, 26, 2142–2147. [Google Scholar] [CrossRef]
- Vesely, L.; Dostal, V.; Hajek, P. Design of Experimental Loop with Supercritical Carbon Dioxide. In Proceedings of the 22nd International Conference on Nuclear Engineering, Prague, Czech Republic, 7–11 July 2014. [Google Scholar]
- Turchi, C.S. Supercritical CO2 for Application in Concentrating Solar Power Systems. In Proceedings of the supercritical CO2 Power Cycle Symposium, Troy, NY, USA, 29–30 April 2009. [Google Scholar]
- Wang, X.; Dai, Y. Exergoeconomic analysis of utilizing the transcritical CO2 cycle and the ORC for a recompression supercritical CO2 cycle waste heat recovery: A comparative study. Appl. Energy 2016, 170, 193–207. [Google Scholar] [CrossRef]
- Santini, L.; Accornero, C.; Cioncolini, A. On the adoption of carbon dioxide thermodynamic cycles for nuclear power conversion: A case study applied to Mochovce 3 Nuclear Power Plant. Appl. Energy 2016, 181, 446–463. [Google Scholar] [CrossRef]
- Shi, D.; Xie, Y. Aerodynamic Optimization Design of a 150 kW High Performance Supercritical Carbon Dioxide Centrifugal Compressor without a High Speed Requirement. Appl. Sci. 2020, 10, 2093. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Li, J.; Zhang, D.; Xie, Y. Numerical Investigation on Aerodynamic Performance of SCO2 and Air Radial-Inflow Turbines with Different Solidity Structures. Appl. Sci. 2020, 10, 2087. [Google Scholar] [CrossRef] [Green Version]
- Kulhánek, M.; Dostál, V. Thermodynamic Analysis and Comparison of Supercritical Carbon Dioxide Cycles. In Proceedings of the Supercritical CO2 Power Cycle Symposium, Boulder, CO, USA, 24–25 May 2011. [Google Scholar]
- Moisseytsev, A.; Sienicki, J.J. Investigation of alternative layouts for the supercritical carbon dioxide Brayton cycle for a sodium-cooled fast reactor. Nucl. Eng. Des. 2009, 239, 1362–1371. [Google Scholar] [CrossRef]
- Siddiqui, M.E.; Almitani, K.H. Proposal and Thermodynamic Assessment of S-CO2 Brayton Cycle Layout for Improved Heat Recovery. Entropy 2020, 22, 305. [Google Scholar] [CrossRef] [Green Version]
- Neises, T.; Turchi, C. A Comparison of Supercritical Carbon Dioxide Power Cycle Configurations with an Emphasis on CSP Applications. Energy Procedia 2014, 49, 1187–1196. [Google Scholar] [CrossRef] [Green Version]
- Al-Sulaiman, F.A.; Atif, M. Performance comparison of different supercritical carbon dioxide Brayton cycles integrated with a solar power tower. Energy 2015, 82, 61–71. [Google Scholar] [CrossRef]
- Gao, W.; Yao, M.; Chen, Y.; Li, H.; Zhang, Y.; Zhang, L. Performance of S-CO2 Brayton Cycle and Organic Rankine Cycle (ORC) Combined System Considering the Diurnal Distribution of Solar Radiation. J. Therm. Sci. 2019, 28, 463–471. [Google Scholar] [CrossRef]
- Singh, R.; Miller, S.A.; Rowlands, A.S.; Jacobs, P.A. Dynamic characteristics of a direct-heated supercritical carbon-dioxide Brayton cycle in a solar thermal power plant. Energy 2013, 50, 194–204. [Google Scholar] [CrossRef]
- Chacartegui, R.; De Escalona, J.M.; Sánchez, T.; Monje, B.; Sanchez, D. Alternative cycles based on carbon dioxide for central receiver solar power plants. Appl. Therm. Eng. 2011, 31, 872–879. [Google Scholar] [CrossRef]
- Siddiqui, M.E.; Taimoor, A.; Almitani, K.H. Energy and Exergy Analysis of the S-CO2 Brayton Cycle Coupled with Bottoming Cycles. Processes 2018, 6, 153. [Google Scholar] [CrossRef] [Green Version]
- Crespi, F.; Gavagnin, G.; Sánchez, D.; Martínez, G.S. Supercritical carbon dioxide cycles for power generation: A review. Appl. Energy 2017, 195, 152–183. [Google Scholar] [CrossRef]
- Reyes-Belmonte, M.; Sebastián, A.; Romero, M.; González-Aguilar, J. Optimization of a recompression supercritical carbon dioxide cycle for an innovative central receiver solar power plant. Energy 2016, 112, 17–27. [Google Scholar] [CrossRef]
- Concentrating Solar Power Projects Concentrating Solar Power Projects. Available online: https://solarpaces.nrel.gov/ (accessed on 21 May 2020).
- ASHRAE. Handbook of Fundamentals; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 1985. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Talebizadeh, P.; Mehrabian, M.A.; Rahimzadeh, H. Optimization of Heliostat Layout in Central Receiver Solar Power Plants. J. Energy Eng. 2014, 140, 04014005. [Google Scholar] [CrossRef]
- Atif, M.; Al-Sulaiman, F.A. Development of a mathematical model for optimizing a heliostat field layout using differential evolution method. Int. J. Energy Res. 2015, 39, 1241–1255. [Google Scholar] [CrossRef]
- Collado, F.J.; Giménez, F.J.C. Quick evaluation of the annual heliostat field efficiency. Sol. Energy 2008, 82, 379–384. [Google Scholar] [CrossRef]
- Schmitz, M.; Schwarzbözl, P.; Buck, R.; Pitz-Paal, R. Assessment of the potential improvement due to multiple apertures in central receiver systems with secondary concentrators. Sol. Energy 2006, 80, 111–120. [Google Scholar] [CrossRef] [Green Version]
- Leary, P.L.; Hankins, J.D. User’s Guide for MIRVAL: A Computer Code for Comparing Designs of Heliostat-Receiver Optics for Central Receiver Solar Power Plants; Sandia National Lab: Livermore, CA, USA, 1979. [Google Scholar]
- Schwarzbözl, P.; Schmitz, M.; Pitz-Paal, R. Visual HFLCAL—A Software Tool for Layout and Optimisation Of Heliostat Fields. In Proceedings of the SolarPACES, Berlin, Germany, 15–18 September 2009. [Google Scholar]
- Collado, F.J.; Guallar, J. A review of optimized design layouts for solar power tower plants with campo code. Renew. Sustain. Energy Rev. 2013, 20, 142–154. [Google Scholar] [CrossRef] [Green Version]
- Sheu, E.J.; Mitsos, A. Optimization of a hybrid solar-fossil fuel plant: Solar steam reforming of methane in a combined cycle. Energy 2013, 51, 193–202. [Google Scholar] [CrossRef]
- Segal, A.; Epstein, M. Comparative performances of ‘tower-top’ and ‘tower-reflector’ central solar receivers. Sol. Energy 1999, 65, 207–226. [Google Scholar] [CrossRef]
- Siddiqui, M.E.; Almitani, K.H. Energy Analysis of the S-CO2 Brayton Cycle with Improved Heat Regeneration. Processes 2018, 7, 3. [Google Scholar] [CrossRef] [Green Version]
- Padilla, R.V.; Too, Y.C.S.; Benito, R.; Stein, W. Exergetic analysis of supercritical CO2 Brayton cycles integrated with solar central receivers. Appl. Energy 2015, 148, 348–365. [Google Scholar] [CrossRef]
- Besarati, S.M.; Goswami, D.Y. Analysis of Advanced Supercritical Carbon Dioxide Power Cycles With a Bottoming Cycle for Concentrating Solar Power Applications. J. Sol. Energy Eng. 2013, 136, 010904. [Google Scholar] [CrossRef]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering Thermodynamics, 7th ed.; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Petela, R. Exergy of Heat Radiation. J. Heat Transf. 1964, 86, 187–192. [Google Scholar] [CrossRef]
- Atif, M.; Al-Sulaiman, F. Optimization of heliostat field layout in solar central receiver systems on annual basis using differential evolution algorithm. Energy Convers. Manag. 2015, 95, 1–9. [Google Scholar] [CrossRef]
- Collado, F.J.; Guallar, J. Quick design of regular heliostat fields for commercial solar tower power plants. Energy 2019, 178, 115–125. [Google Scholar] [CrossRef]
- Turchi, C.S.; Ma, Z.; Neises, T.W.; Wagner, M.J. Thermodynamic Study of Advanced Supercritical Carbon Dioxide Power Cycles for Concentrating Solar Power Systems. J. Sol. Energy Eng. 2013, 135, 041007. [Google Scholar] [CrossRef]
- Sarkar, J. Second law analysis of supercritical CO2 recompression Brayton cycle. Energy 2009, 34, 1172–1178. [Google Scholar] [CrossRef]


| Month | A (W/m2) | B |
|---|---|---|
| January | 1230 | 0.142 |
| February | 1215 | 0.144 |
| March | 1186 | 0.156 |
| April | 1136 | 0.18 |
| May | 1104 | 0.196 |
| June | 1088 | 0.205 |
| July | 1085 | 0.207 |
| August | 1107 | 0.201 |
| September | 1151 | 0.177 |
| October | 1192 | 0.16 |
| November | 1221 | 0.149 |
| December | 1233 | 0.142 |
| Description of Parameter | Value | Reference |
|---|---|---|
| Tower optical height, THT | 130 m | [55] |
| Heliostat width, LW | 12.3 m | [55] |
| Heliostat height, LH | 9.75 m | [55] |
| Extra security distance, | 3 m | [55] |
| Receiver diameter, DR | 9.44 m | [55] |
| Receiver length, LR | 9.44 m | [55] |
| Mirror Reflectivity × cleanliness, | 0.88 × 0.95 | [56] |
| Standard deviation of sun shape error, | 2.51mrad | [56] |
| Standard deviation of tracking error, | 0.63 mrad | [56] |
| Standard deviation of beam quality error, | 1.88 mrad | [55] |
| Shading and blocking factor, | 0.95 | [10,43] |
| Number of heliostats in the first ring of zone 1 | 17 | assumed |
| Total number of heliostats considered | 1207 (22 rows) |
| Month | Intercept Factor (%) | Optical Efficiency (%) |
|---|---|---|
| January | 98.26 | 57.45 |
| February | 98.81 | 58.13 |
| March | 99.30 | 58.80 |
| April | 99.44 | 59.52 |
| May | 99.51 | 60.42 |
| June | 99.54 | 61.75 |
| July | 99.52 | 60.99 |
| August | 99.47 | 59.67 |
| September | 99.33 | 59.27 |
| October | 98.77 | 58.27 |
| November | 98.28 | 58.03 |
| December | 98.08 | 57.39 |
| Yearly average | 99.02 | 59.14 |
| Component | Energy (MW) |
|---|---|
| Yearly averaged solar energy incident on the field | 132.6 |
| Yearly averaged energy absorbed by the receiver | 79.67 |
| Yearly averaged net energy loss in the field and the receiver | 60.8 |
| Yearly averaged auxiliary heat requirement | 8.2 |
| Turbine power output | 59.60 |
| Energy consumed by Compressor 1 | 9.13 |
| Energy consumed by Compressor 2 | 4.79 |
| Energy consumed by Compressor 3 | 8.53 |
| Energy losses in Cooler and Intercooler | 28.1 and 14.76 respectively |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddiqui, M.E.; Almitani, K.H. Energy and Exergy Assessment of S-CO2 Brayton Cycle Coupled with a Solar Tower System. Processes 2020, 8, 1264. https://doi.org/10.3390/pr8101264
Siddiqui ME, Almitani KH. Energy and Exergy Assessment of S-CO2 Brayton Cycle Coupled with a Solar Tower System. Processes. 2020; 8(10):1264. https://doi.org/10.3390/pr8101264
Chicago/Turabian StyleSiddiqui, Muhammad Ehtisham, and Khalid H. Almitani. 2020. "Energy and Exergy Assessment of S-CO2 Brayton Cycle Coupled with a Solar Tower System" Processes 8, no. 10: 1264. https://doi.org/10.3390/pr8101264
APA StyleSiddiqui, M. E., & Almitani, K. H. (2020). Energy and Exergy Assessment of S-CO2 Brayton Cycle Coupled with a Solar Tower System. Processes, 8(10), 1264. https://doi.org/10.3390/pr8101264





