Dynamic Threshold Neural P Systems with Multiple Channels and Inhibitory Rules
Abstract
:1. Introduction
1.1. Related Work
1.2. Motivation
- (1)
- The conduction of nerve impulses between neurons is unidirectional, that is, nerve impulses can only be transmitted from the axon of one neuron to the cell body or dendrites of another neuron, but not in the opposite direction.
- (2)
- Synapses are divided into excitatory synapses and inhibitory synapses. According to the signal from the presynaptic cells, if the excitability of the postsynaptic cell is increased or excited, then the connection is excitatory synapse. If the excitability of the postsynaptic cell is decreased or the excitability is not easily generated, then it is inhibitory synapse.
- (1)
- DTNP-MCIR systems introduce firing rules with channel labels.
- (2)
- Inspired by SNP-IR systems, we introduce inhibitory rules to DTNP systems, but the form and firing conditions of inhibitory rules have been re-defined.
- (3)
- The firing rules of neuron (corresponds to register r) is in DTNP systems, is a default firing condition usually not displayed, because can be reflected in the rules. However, can also be a regular expression in DTNP-MCIR systems, for example , where , represents an odd number of spikes. The rule is only enabled when neuron contains an odd number of spikes and satisfies the default firing condition.
2. DTNP-MCIR Systems
2.1. Definition
- (1)
- is a singleton alphabet (the object a is called the spike);
- (2)
- is the channel labels;
- (3)
- are m neurons of the form where:
- (a)
- is the number of spikes contained in the feeding input unit of neuron ;
- (b)
- is the number of spikes as a (dynamic) threshold in neuron ;
- (c)
- is a finite set of channel labels used by neuron ;
- (d)
- is a finite set of rules of two types in ;
- (i)
- the form of firing rules is , where is a firing condition, , and ; when , the rule is known as a spiking rule, and when , , the rule is known as a forgetting rule, can be written as ;
- (ii)
- the form of inhibitory rules is , where the subscript represents an inhibitory arc between neuron and , , , , , and ;
- (4)
- with (synapse connections)
- (5)
- in indicate input neurons;
- (6)
- out indicate output neurons.
2.2. Illustrative Example
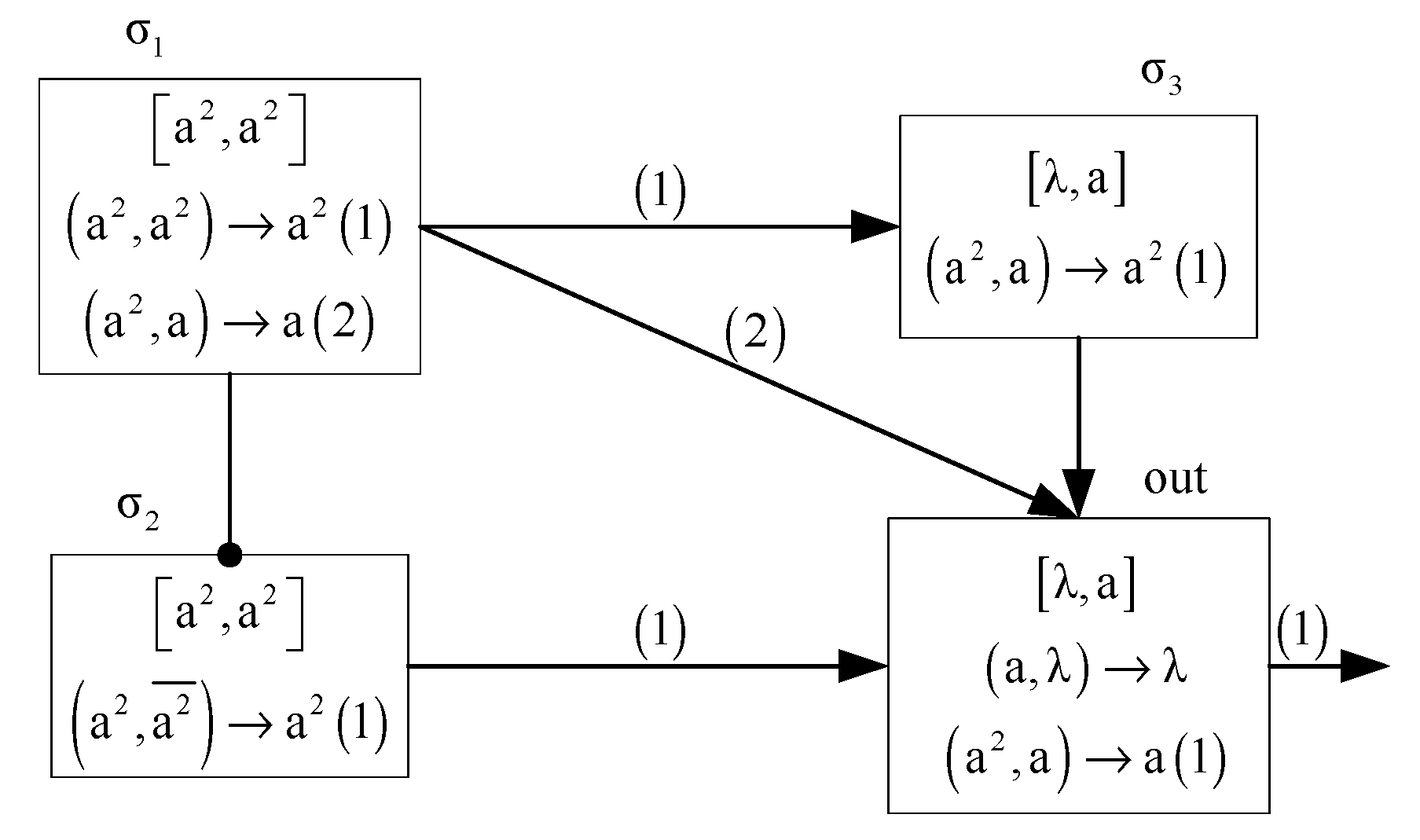
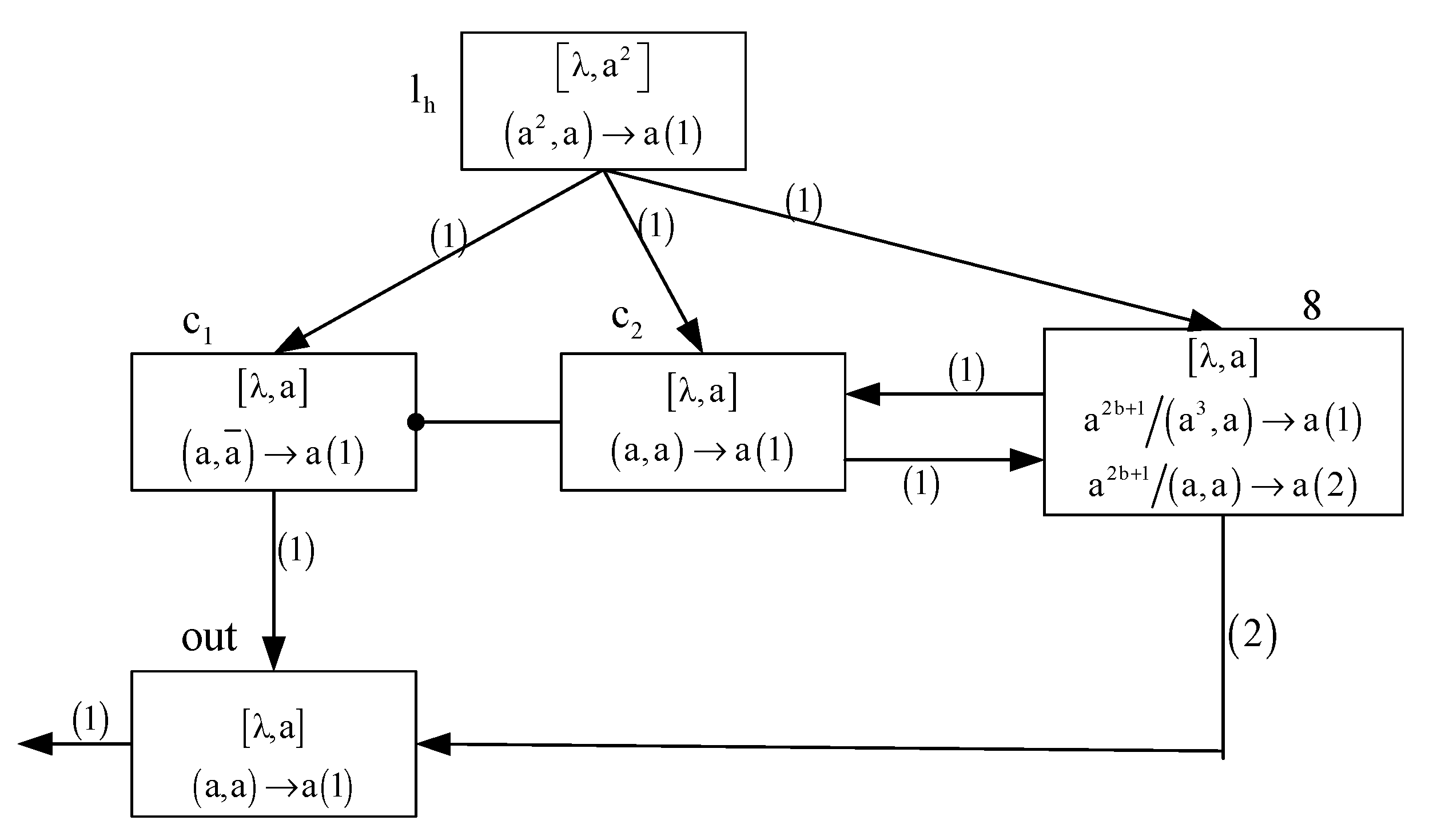
- (1)
- Case 1: if rule is applied in neuron at time 1, then neuron will consume two spikes in the feeding input unit and sends two spikes to the neuron through channel (1). Neuron is the inhibitory neuron of neuron , since and , rule reaches the firing condition in neuron , so neuron consumes two spikes in the feeding input unit and sends two spikes to the neuron out via channel (1) at time 1. Therefore, . At time 2, since , both rule and rule in neuron out can be applied. However, according to the maximum spike consumption strategy, rule will be applied and sends one spike to the environment through channel (1). Further, since , rule is enable in neuron and consumes two spikes in the feeding input unit and sends two spike to neuron out. Thus . At time 3, since , rule fires again and sends one spike to the environment. The system halts. Therefore, the spike train generated by this system is “011”.
- (2)
- Case 2: if rule is applied in neuron at time 1, then neuron consumes two spikes in the feeding input unit and sends one spikes to the neuron out through channel (2). Because the state of system is the same as that in case 1 at time 1, neuron consumes two spikes in the feeding input unit and sends two spikes to the neuron out through channel (1).So . At time 2, since , also according to the maximum spike consumption strategy, neuron out fires by the rule and sends one spike to the environment through channel (1). The configuration of System at this time is . At time 3, since , rule is applied and removes one spike in feeding input unit and the system halts. Therefore, the spike train generated is “010”.
3. Turing Universality of DTNP-MCIR Systems as Number-Generating/Accepting Device
- (1)
- (add 1 to register r and then move non-deterministically to one of the instructions with labels , ).
- (2)
- (if register r is non-zero, then subtract 1 from it, and go to the instruction with label ; otherwise go to the instruction with label ).
- (3)
- (halting instruction).
3.1. DTNP-MCIR Systems as Number Generating Devices
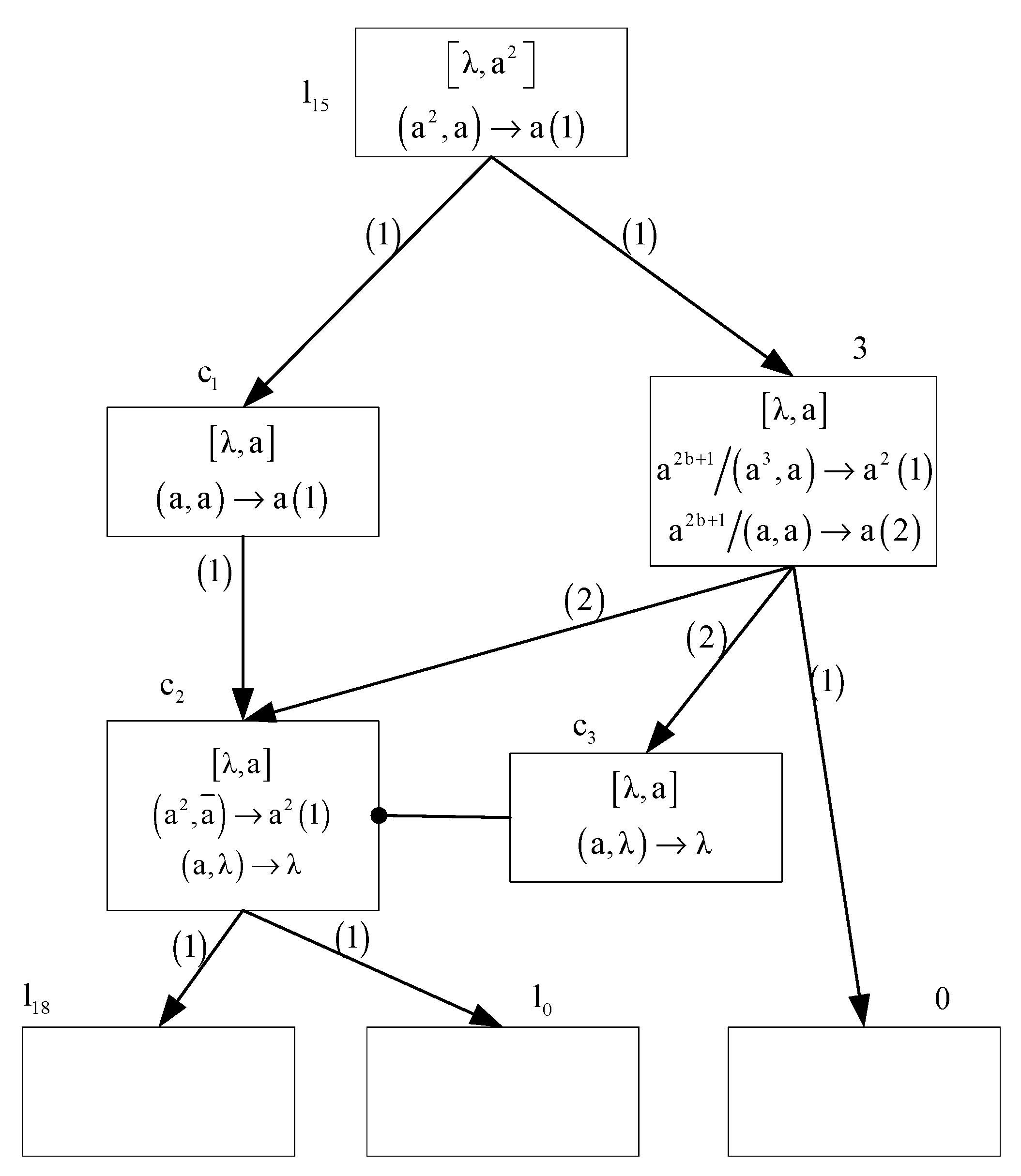
- (1)
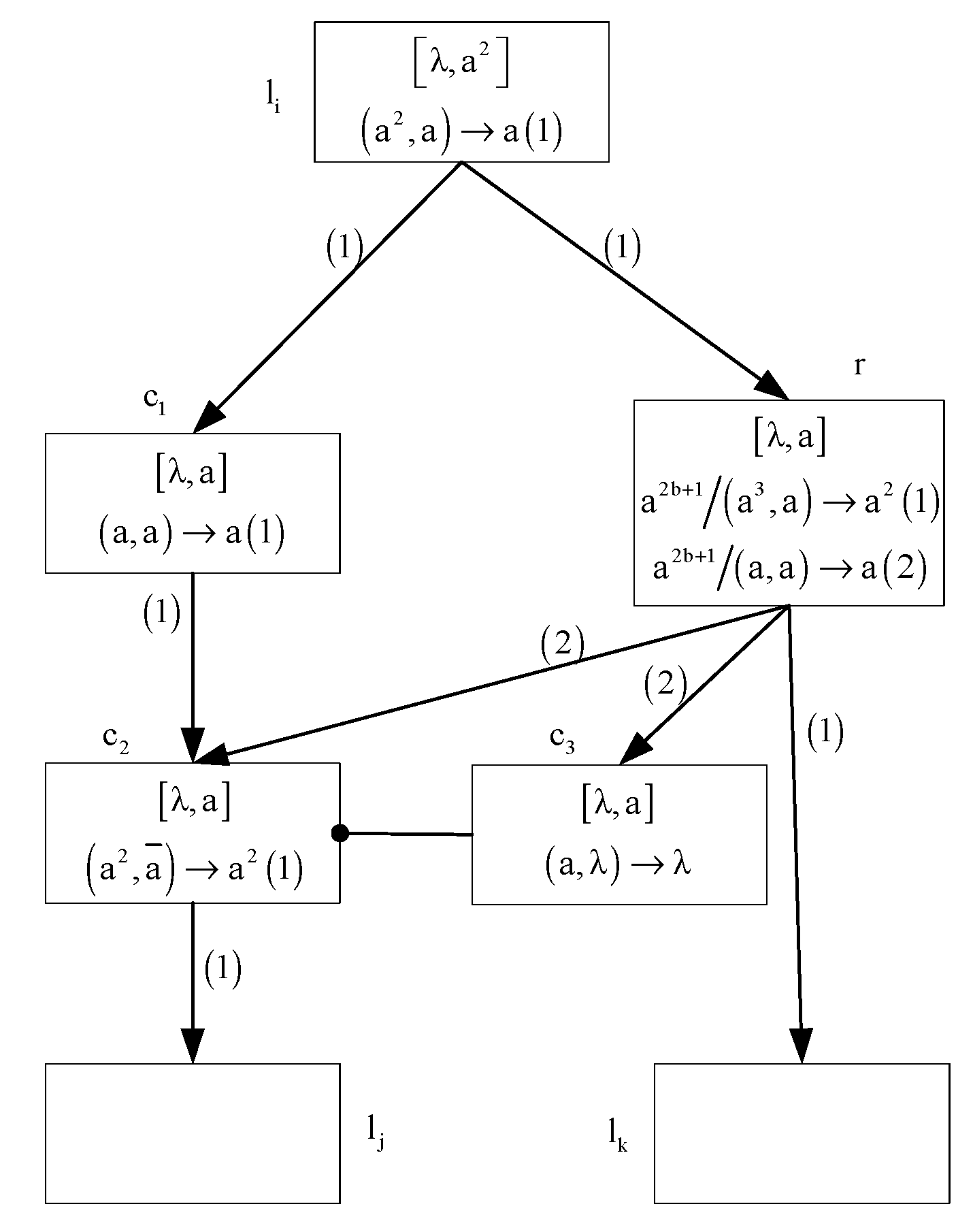
- ADD module (shown in Figure 3)—simulating an ADD instruction
- (i)
- At time t + 1, if rule is applied, neuron sends two spikes to neuron via channel (1). Then neuron receives two spikes, system starts to simulate instruction . Therefore . At time t + 3, since the rule of neuron is enabled and removes the only spike in the feeding input unit.
- (ii)
- At time t + 1, if rule is applied, neuron sends one spike to neurons and via channel (2). Thus, . Note that neuron is the inhibitory neuron of neuron , since , inhibitory rule is enabled, neuro n sends two spikes to neuron . This means that the system starts to simulate instruction . The configuration of at this time is .
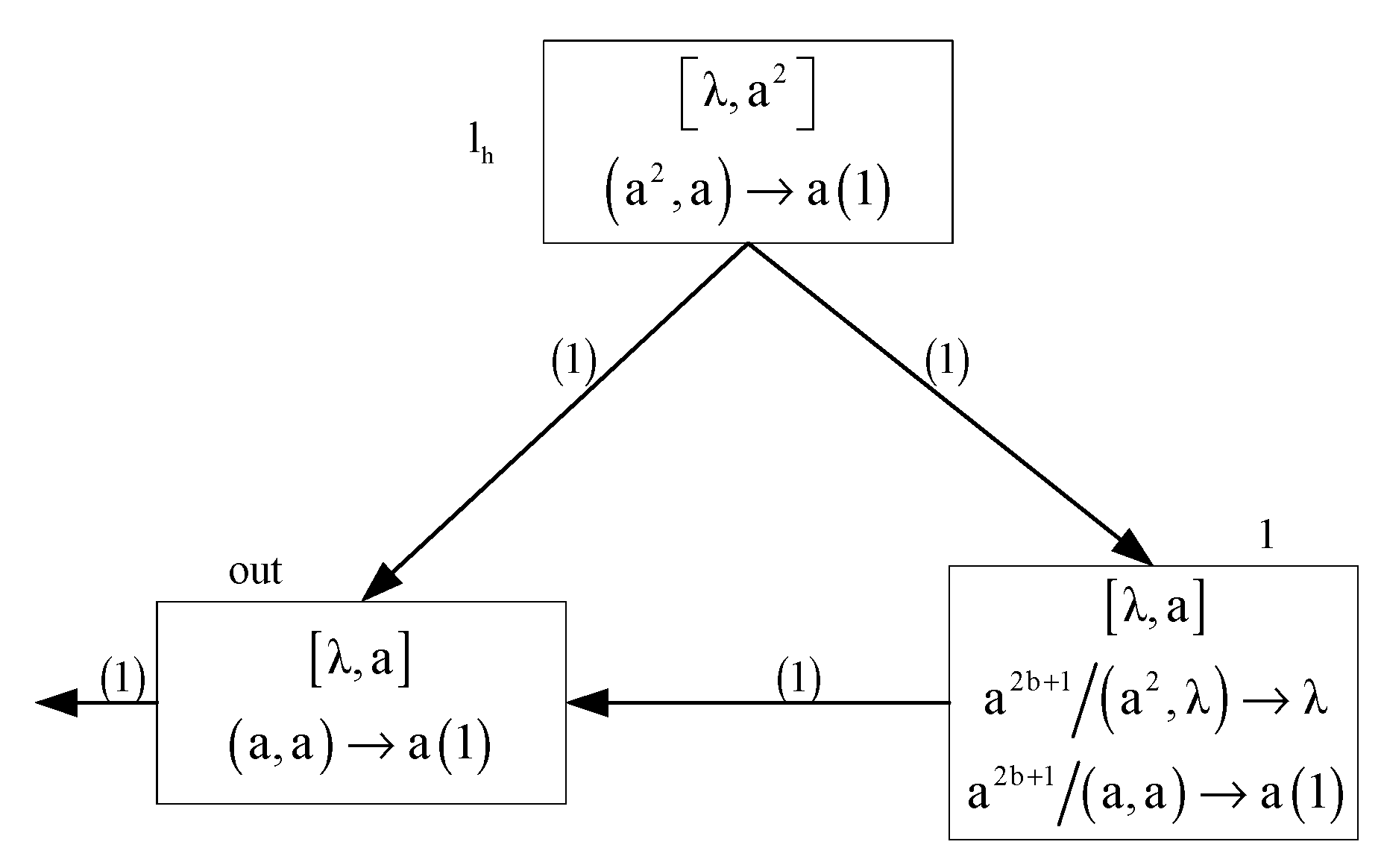
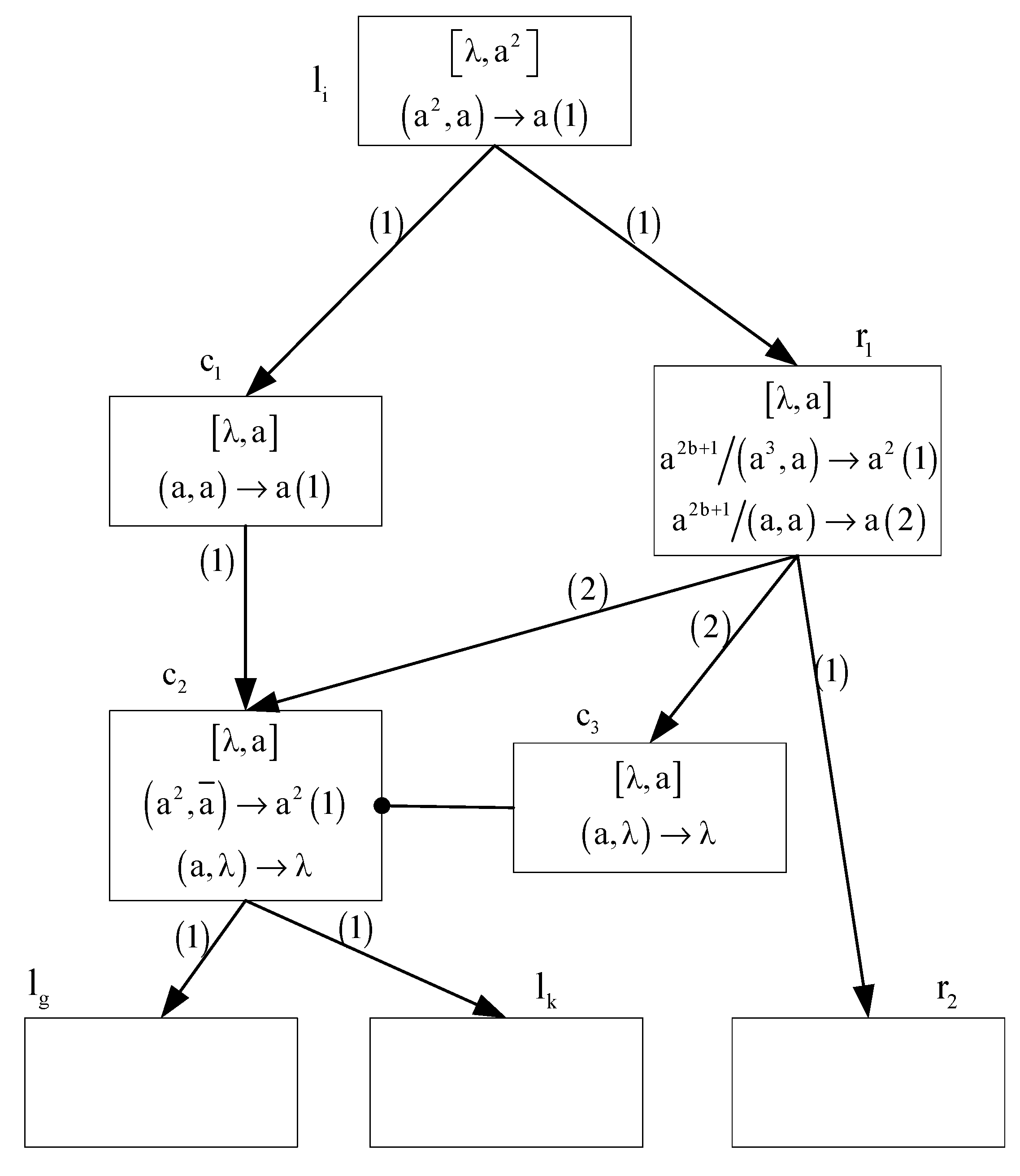
- (2)
- SUB module (shown in Figure 4)—simulating a SUB instruction .
- (i)
- If feeding input unit of neuron contains spikes at time t, then at time t + 1, neuron contains spikes. At time t + 2, rule will be enabled and neuron will send two spikes to neurons via channel (1). This indicates that system starts to simulate the instruction of register machine M. In addition, rule satisfies firing condition, neuron sends a spike to neuron . Thus . At time t+3, the forgetting rule of neuron is enabled and removes the only spike in the feeding input unit. Therefore, .
- (ii)
- If feeding input unit of neuron does not contain spikes at time t, then at time t + 1, neuron contains only one spike. At time t + 2, rule will be applied and neuron will transmit one spike to neurons and via channel (2). At the same time neuron also transmits a spike to neuron . So . Note that neuron is the inhibitory neuron of neuron . At time t + 3, the forgetting rule of neuron is enabled and removes the only spike in the feeding input unit. Moreover, since , rule is applied, neuron sends two spikes to neuron . This means that the system starts to simulate instruction . Thus, .
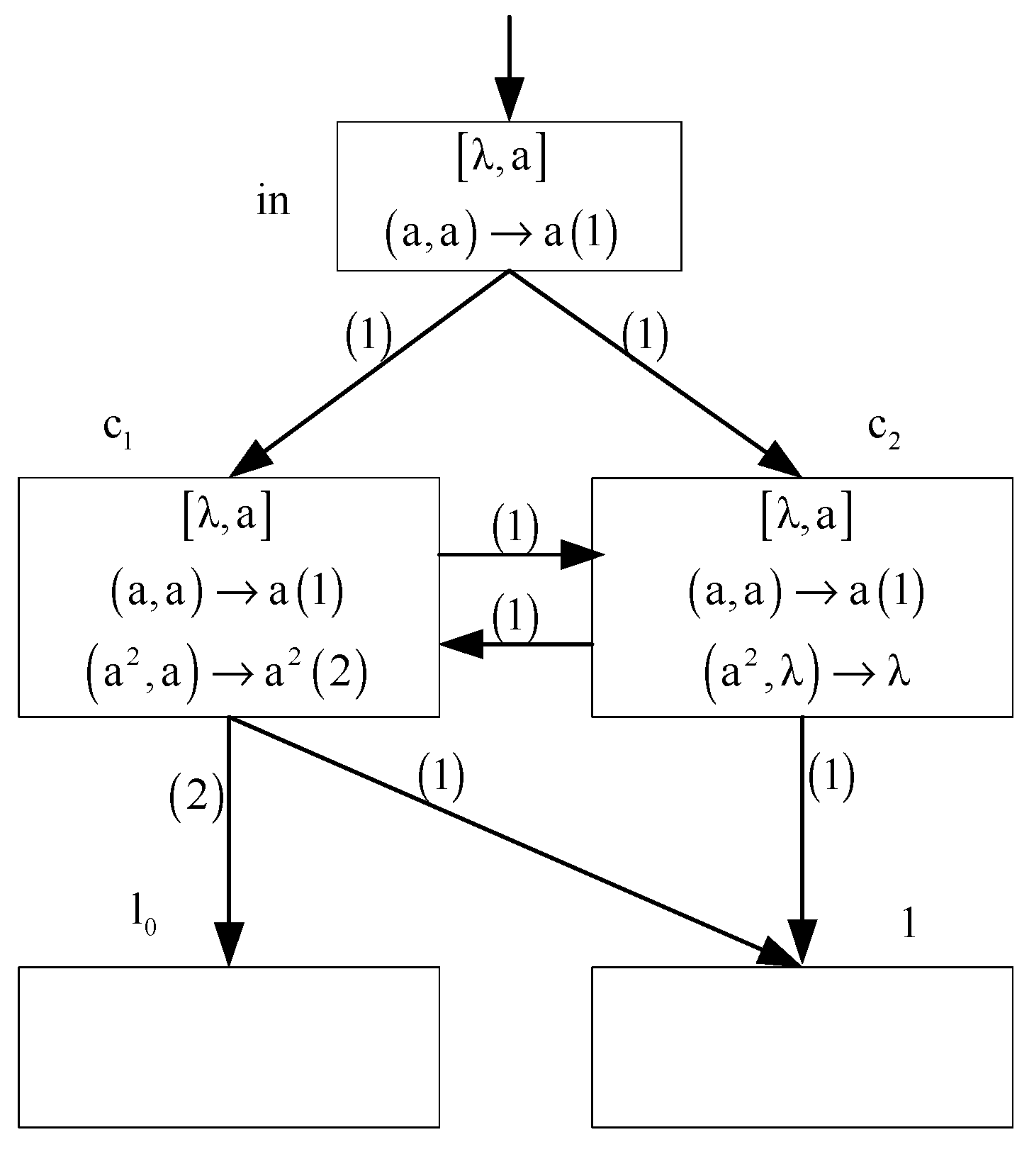
- (3)
- Module FIN (shown in Figure 5)—outputting the result of computation
3.2. Turing Universality of Systems Working in the Accepting Mode
4. DTNP-MCIR Systems as Function Computing Devices
5. Conclusions and Further Work
Author Contributions
Funding
Conflicts of Interest
References
- Păun, G. Computing with membranes. J. Comput. Syst. Sci. 2000, 61, 108–143. [Google Scholar] [CrossRef] [Green Version]
- Song, T.; Gong, F.; Liu, X. Spiking neural P systems with white hole neurons. IEEE Trans. NanoBiosci. 2016, 15, 666–673. [Google Scholar] [CrossRef]
- Freund, R.; Păun, G.; Pérez-Jiménez, M.J. Tissue-like P systems with channel-states. Theor. Comput. Sci. 2005, 330, 101–116. [Google Scholar] [CrossRef] [Green Version]
- Song, T.; Pan, L.; Wu, T. Spiking neural P Systems with leaning functions. IEEE Trans. NanoBiosci. 2019, 18, 176–190. [Google Scholar] [CrossRef] [PubMed]
- Cabarle, F.G.C.; Adorna, H.N.; Jiang, M.; Zeng, X. Spiking neural P systems with scheduled synapses. IEEE Trans. NanoBiosci. 2017, 16, 792–801. [Google Scholar] [CrossRef] [PubMed]
- Song, T.; Pan, L. Spiking neural P systems with rules on synapses working in maximum spiking strategy. IEEE Trans. NanoBiosci. 2015, 14, 465–477. [Google Scholar] [CrossRef]
- Ionescu, M.; Păun, G.; Yokomori, T. Spiking neural P systems. Fund. Inform. 2006, 71, 279–308. [Google Scholar]
- Song, T.; Pan, L. Spiking neural P systems with request rules. Neurocomputing 2016, 193, 193–200. [Google Scholar] [CrossRef]
- Zeng, X.; Zhang, X. Spiking Neural P Systems with Thresholds. Neural Comput. 2014, 26, 1340–1361. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X. Spiking Neural P Systems with Neuron Division and Dissolution. PLoS ONE 2016, 11, e0162882. [Google Scholar] [CrossRef]
- Wang, J.; Shi, P.; Peng, H.; Perez-Jimenez, M.J.; Wang, T. Weighted Fuzzy Spiking Neural P Systems. IEEE Trans. Fuzzy Syst. 2012, 21, 209–220. [Google Scholar] [CrossRef]
- Jiang, K.; Song, T.; Pan, L. Universality of sequential spiking neural P systems based on minimum spike number. Theor. Comput. Sci. 2013, 499, 88–97. [Google Scholar] [CrossRef]
- Zhang, X.; Luo, B. Sequential spiking neural P systems with exhaustive use of rules. Biosystems 2012, 108, 52–62. [Google Scholar] [CrossRef] [PubMed]
- Cavaliere, M.; Ibarra, O.H.; Păun, G.; Egecioglu, O.; Ionescu, M.; Woodworth, S. Asynchronous spiking neural P systems. Theor. Comput. Sci. 2009, 410, 2352–2364. [Google Scholar] [CrossRef] [Green Version]
- Song, T.; Pan, L.; Păun, G. Asynchronous spiking neural P systems with local synchronization. Inf. Sci. 2013, 219, 197–207. [Google Scholar] [CrossRef] [Green Version]
- Song, T.; Zou, Q.; Liu, X.; Zeng, X. Asynchronous spiking neural P systems with rules on synapses. Neurocomputing 2015, 151, 1439–1445. [Google Scholar] [CrossRef]
- Păun, G. Spiking neural P systems with astrocyte-like control. J. Univers. Comput. Sci. 2007, 13, 1707–1721. [Google Scholar]
- Wu, T.; Păun, A.; Zhang, Z.; Pan, L. Spiking Neural P Systems with Polarizations. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 3349–3360. [Google Scholar]
- Păun, A.; Păun, G. Small universal spiking neural P systems. BioSystems 2007, 90, 48–60. [Google Scholar] [CrossRef] [Green Version]
- Cabarle, F.; Adorna, H.; Perez-Jimenez, M.; Song, T. Spiking neuron P systems with structural plasticity. Neural Comput. Appl. 2015, 26, 1905–1917. [Google Scholar] [CrossRef]
- Peng, H.; Chen, R.; Wang, J.; Song, X.; Wang, T.; Yang, F.; Sun, Z. Competitive spiking neural P systems with rules on synapses. IEEE Trans. NanoBiosci. 2017, 16, 888–895. [Google Scholar] [CrossRef] [PubMed]
- Xiong, G.; Shi, D.; Zhu, L.; Duan, X. A new approach to fault diagnosis of power systems using fuzzy reasoning spiking neural P systems. Math. Probl. Eng. 2013, 2013, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Zhang, G.X.; Zhao, J.B.; He, Z.Y.; Wang, J.; Pérez-Jiménez, M.J. Fault diagnosis of electric power systems based on fuzzy reasoning spiking neural P systems. IEEE Trans. Power Syst. 2015, 30, 1182–1194. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J.; Ming, J.; Shi, P.; Pérez-Jiménez, M.J.; Yu, W.; Tao, C. Fault diagnosis of power systems using intuitionistic fuzzy spiking neural P systems. IEEE Trans. Smart Grid. 2018, 9, 4777–4784. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J.; Shi, P.; Pérez-Jiménez, M.J.; Riscos-Núñez, A. An extended membrane system with active membrane to solve automatic fuzzy clustering problems. Int. J. Neural Syst. 2016, 26, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Rong, H.; Neri, F.; Pérez-Jiménez, M. An optimization spiking neural P system for approximately solving combinatorial optimization problems. Int. J. Neural Syst. 2014, 24, 1440006. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Yang, J.; Wang, J.; Wang, T.; Sun, Z.; Song, X.; Lou, X.; Huang, X. Spiking neural P systems with multiple channels. Neural Netw. 2017, 95, 66–71. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Li, B.; Wang, J. Spiking neural P systems with inhibitory rules. Knowl.-Based Syst. 2020, 188, 105064. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J. Dynamic threshold neural P systems. Knowl.-Based Syst. 2019, 163, 875–884. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J. Coupled Neural P Systems. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1672–1682. [Google Scholar] [CrossRef]
- Korec, I. Small universal register machines. Theor. Comput. Sci. 1996, 168, 267–301. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zeng, X.; Pan, L. Smaller universal spiking neural P systems. Fundam. Inf. 2007, 87, 117–136. [Google Scholar]
- Siegelmann, H.T.; Sontag, E.D. On the computational power of neural nets. J. Comput. Syst. 1995, 50, 132–150. [Google Scholar] [CrossRef] [Green Version]
- Song, X.; Peng, H. Small universal asynchronous spiking neural P systems with multiple channels. Neurocomputing 2020, 378, 1–8. [Google Scholar] [CrossRef]





| Computing Models | Computing Functions |
|---|---|
| DTNP-MCIR systems | 73 |
| DTNP systems [29] | 109 |
| SNP systems [32] | 67 |
| SNP-IR systems [28] | 100 |
| Recurrent neural networks [33] | 886 |
| SNP-MC systems [34] | 38 |
| DTNP systems [29] | Dynamic threshold neural P systems |
| SNP-IR systems [28] | Spiking neural P systems with inhibitory rules |
| SNP-MC systems [27] | Spiking neural P systems with multiple channels |
| SNP systems [32] | Smaller universal spiking neural P systems |
| SNP-MC systems [34] | Small universal asynchronous spiking neural P systems with multiple channels. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, X.; Liu, X. Dynamic Threshold Neural P Systems with Multiple Channels and Inhibitory Rules. Processes 2020, 8, 1281. https://doi.org/10.3390/pr8101281
Yin X, Liu X. Dynamic Threshold Neural P Systems with Multiple Channels and Inhibitory Rules. Processes. 2020; 8(10):1281. https://doi.org/10.3390/pr8101281
Chicago/Turabian StyleYin, Xiu, and Xiyu Liu. 2020. "Dynamic Threshold Neural P Systems with Multiple Channels and Inhibitory Rules" Processes 8, no. 10: 1281. https://doi.org/10.3390/pr8101281
APA StyleYin, X., & Liu, X. (2020). Dynamic Threshold Neural P Systems with Multiple Channels and Inhibitory Rules. Processes, 8(10), 1281. https://doi.org/10.3390/pr8101281





