CFD Modeling of Spatial Inhomogeneities in a Vegetable Oil Carbonation Reactor
Abstract
1. Introduction
2. Reactor Model Development
2.1. Geometry Selection, Momentum Balance Calculation for the 2D and the 3D Model
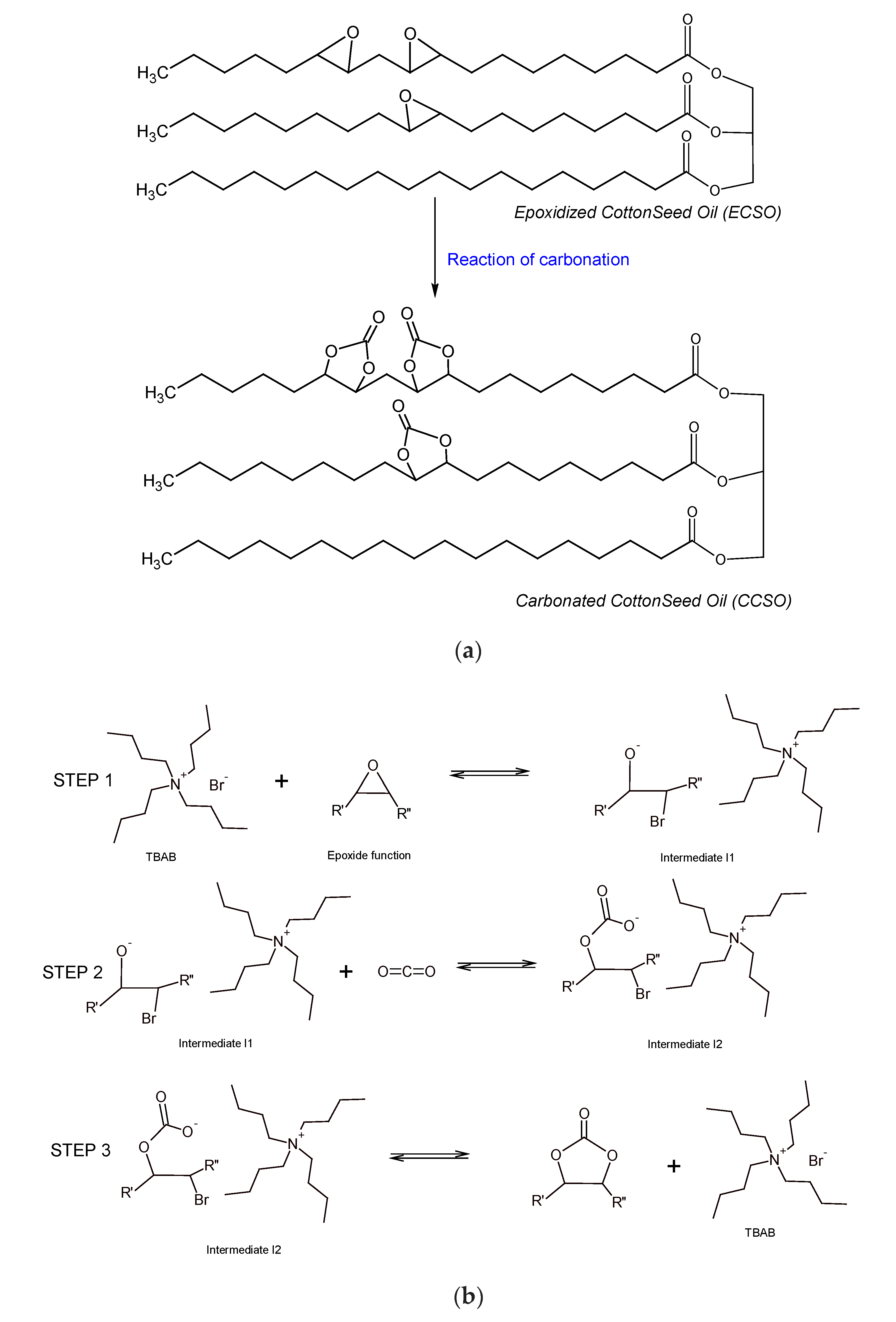
2.2. Carbonation Reaction Modeling
2.3. CFD Model of the Reactor
2.4. Experimental Work Considered
3. Results
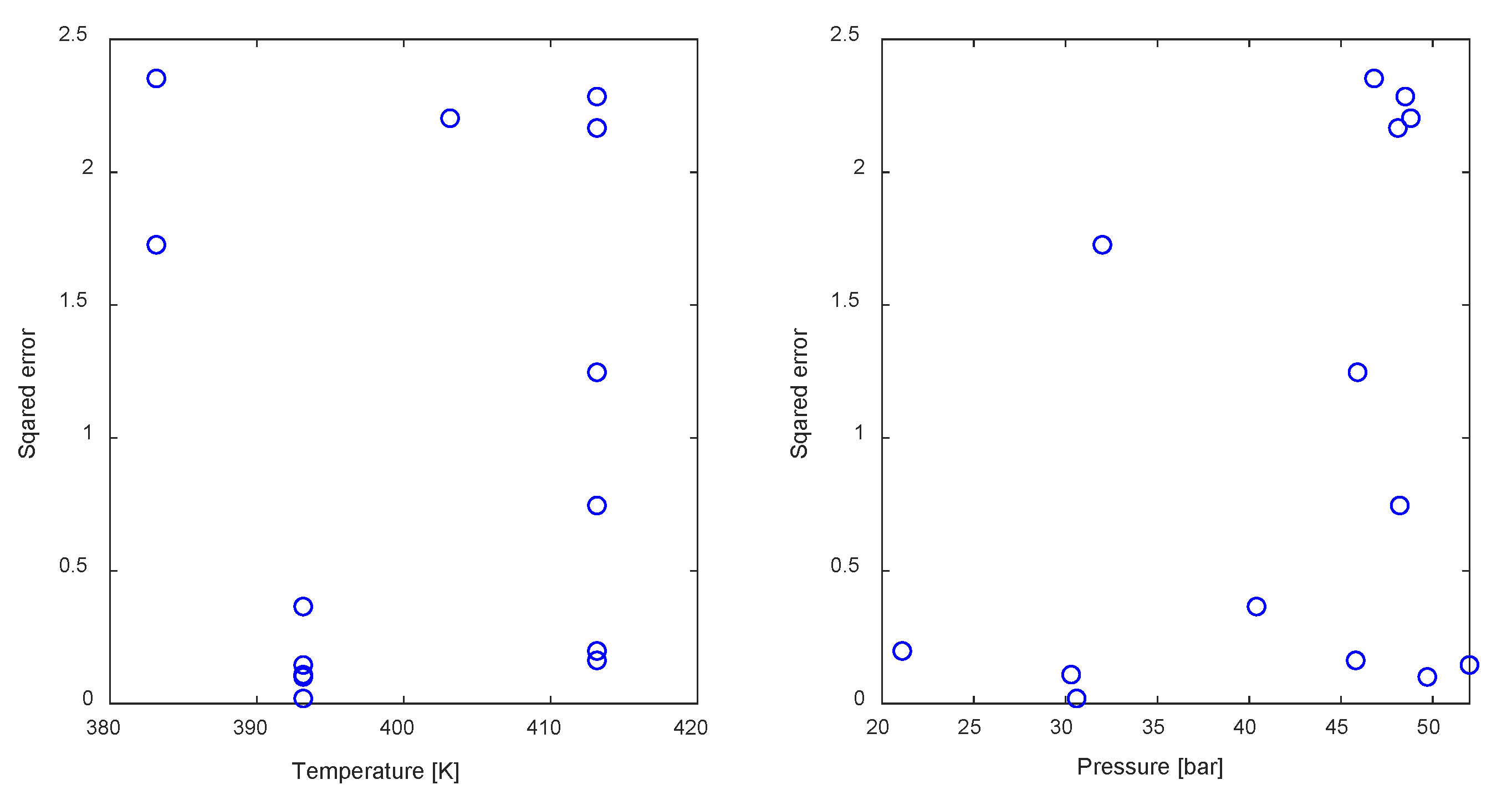
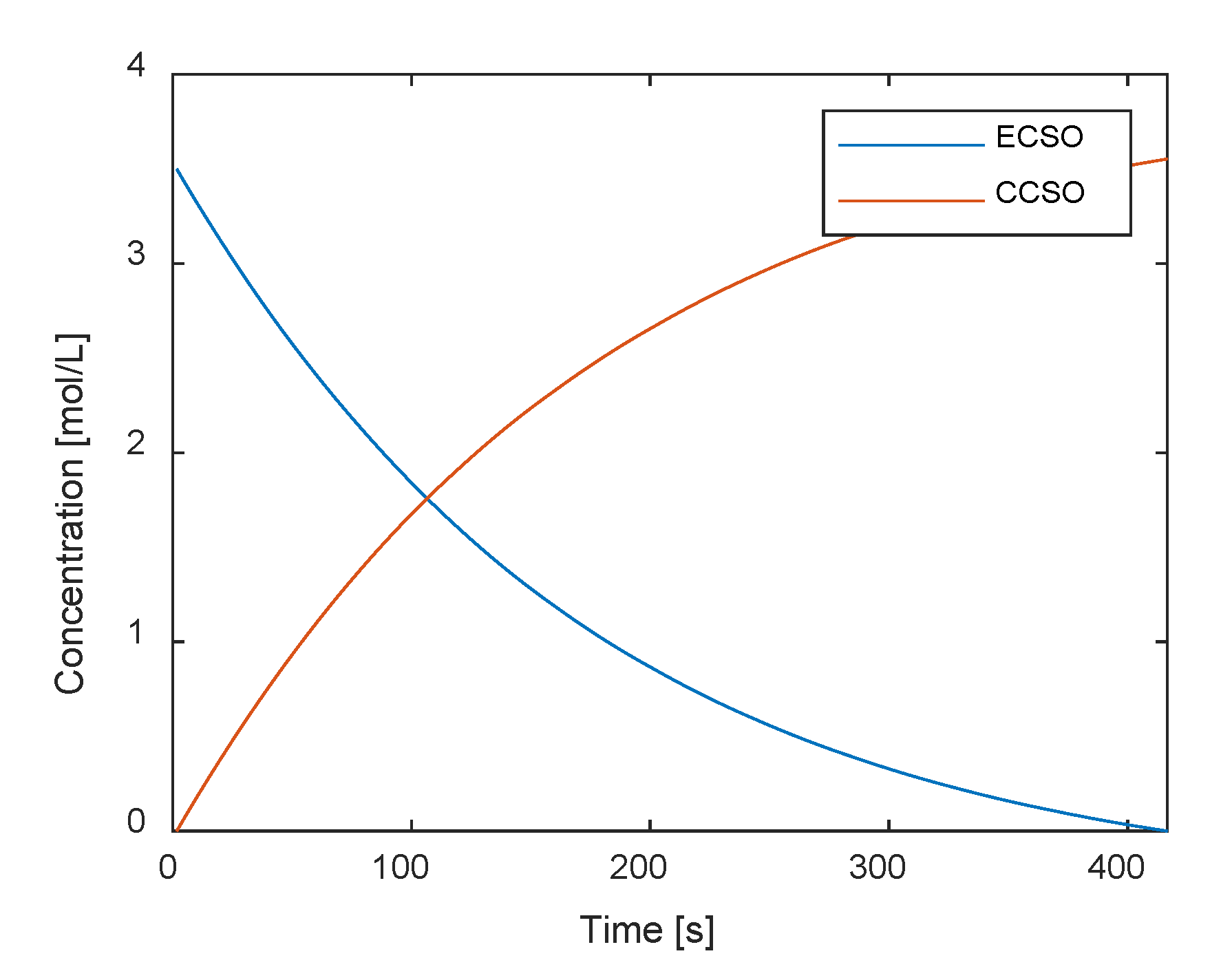
3.1. Model Parameter Identification
3.2. Sensitivity Analysis of the Revolution Speed (Experiment 1)
3.3. Optimization
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| w | weight percent |
| x | molar percent |
| α | k1∙k2 ∙k3 (s−2) |
| β | k2∙k3 (L∙ mol−1.s−2) |
| γ | k-2/k1 (mol∙L−1) |
| μ | liquid viscosity (Pa∙s) |
| ρ | mass density (kg/m3) |
| He | Henry’s coefficient (mol∙L−1∙bar−1) |
| c | Concentration (mol∙m−3) |
| CCSO | carbonated cottonseed oil |
| ECSO | epoxidized cottonseed oil |
| TBAB | tetra-n-butylammonium bromide |
| A, B | height dependent mass transfer constants |
| D | flux parameter |
| kcarbonation | carbonation rate of reaction (s−1) |
| Rcarbonation | carbonation source term (mol∙m−3∙s) |
| NCO2 | CO2 solution term (mol∙m−3∙s) |
| Treac | Reaction temperature (K) |
References
- Alagi, P.; Choi, Y.J.; Hong, S.C. Preparation of vegetable oil-based polyols with controlled hydroxyl functionalities for thermoplastic polyurethane. Eur. Polym. J. 2016, 78, 46–60. [Google Scholar] [CrossRef]
- Zhang, C.; Garrison, T.F.; Madbouly, S.A.; Kessler, M.R. Recent advances in vegetable oil-based polymers and their composites. Prog. Polym. Sci. 2017, 71, 91–143. [Google Scholar] [CrossRef]
- Issariyakul, T.; Dalai, A.K. Biodiesel from vegetable oils. Renew. Sustain. Energy Rev. 2014, 31, 446–471. [Google Scholar] [CrossRef]
- Torres-García, M.; García-Martín, J.F.; Jiménez-Espadafor Aguilar, F.J.; Barbin, D.F.; Álvarez-Mateos, P. Vegetable oils as renewable fuels for power plants based on low and medium speed diesel engines. J. Energy Inst. 2020, 93, 953–961. [Google Scholar] [CrossRef]
- Cai, X.; Zheng, J.L.; Wärnå, J.; Salmi, T.; Taouk, B.; Leveneur, S. Influence of gas-liquid mass transfer on kinetic modeling: Carbonation of epoxidized vegetable oils. Chem. Eng. J. 2017, 313, 1168–1183. [Google Scholar] [CrossRef]
- Guzmán, A.F.; Echeverri, D.A.; Rios, L.A. Carbonation of epoxidized castor oil: A new bio-based building block for the chemical industry. J. Chem. Technol. Biotechnol. 2016, 92, 1104–1110. [Google Scholar] [CrossRef]
- Wutz, J.; Waterkotte, B.; Heitmann, K.; Wucherpfennig, T. Computational fluid dynamics (CFD) as a tool for industrial UF/DF tank optimization. Biochem. Eng. J. 2020, 160, 107617. [Google Scholar] [CrossRef]
- Le Digabel, S. Algorithm 909: NOMAD: Nonlinear optimization with the MADS algorithm. ACM Trans. Math. Softw. 2011, 37, 1–15. [Google Scholar] [CrossRef]
- Audet, C.; Dennis, J.E., Jr. Mesh adaptive direct search algorithms for constrained optimization. SIAM J. Optim. 2006, 17, 188–217. [Google Scholar] [CrossRef]









| Number of Experiment | Initial ECSO Concentration (mol/L) | Initial Catalyst Concentration (mol/L) | Pressure (bar) | Temperature (°C) |
|---|---|---|---|---|
| 1 | 3.6 | 0.13 | 30.6 | 120 |
| 2 | 3.27 | 0.13 | 32 | 110 |
| 3 | 3.38 | 0.3 | 21.1 | 140 |
| 4 | 3.36 | 0.13 | 48.2 | 140 |
| 5 | 3.26 | 0.06 | 48.8 | 130 |
| 6 | 3.41 | 0.13 | 45.8 | 140 |
| 7 | 3.53 | 0.13 | 30.3 | 120 |
| 8 | 3.34 | 0.13 | 45.9 | 140 |
| 9 | 3.8 | 0.13 | 40.4 | 120 |
| 10 | 3.44 | 0.13 | 49.7 | 120 |
| 11 | 3.22 | 0.2 | 48.1 | 140 |
| 12 | 3.4 | 0.13 | 46.8 | 110 |
| 13 | 3.06 | 0.3 | 48.5 | 140 |
| 14 | 3.29 | 0.13 | 52 | 120 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Egedy, A.; Kummer, A.; Leveneur, S.; Varga, T.; Chován, T. CFD Modeling of Spatial Inhomogeneities in a Vegetable Oil Carbonation Reactor. Processes 2020, 8, 1356. https://doi.org/10.3390/pr8111356
Egedy A, Kummer A, Leveneur S, Varga T, Chován T. CFD Modeling of Spatial Inhomogeneities in a Vegetable Oil Carbonation Reactor. Processes. 2020; 8(11):1356. https://doi.org/10.3390/pr8111356
Chicago/Turabian StyleEgedy, Attila, Alex Kummer, Sébastien Leveneur, Tamás Varga, and Tibor Chován. 2020. "CFD Modeling of Spatial Inhomogeneities in a Vegetable Oil Carbonation Reactor" Processes 8, no. 11: 1356. https://doi.org/10.3390/pr8111356
APA StyleEgedy, A., Kummer, A., Leveneur, S., Varga, T., & Chován, T. (2020). CFD Modeling of Spatial Inhomogeneities in a Vegetable Oil Carbonation Reactor. Processes, 8(11), 1356. https://doi.org/10.3390/pr8111356








