Numerical Study of Single Taylor Bubble Movement Through a Microchannel Using Different CFD Packages
Abstract
:1. Introduction
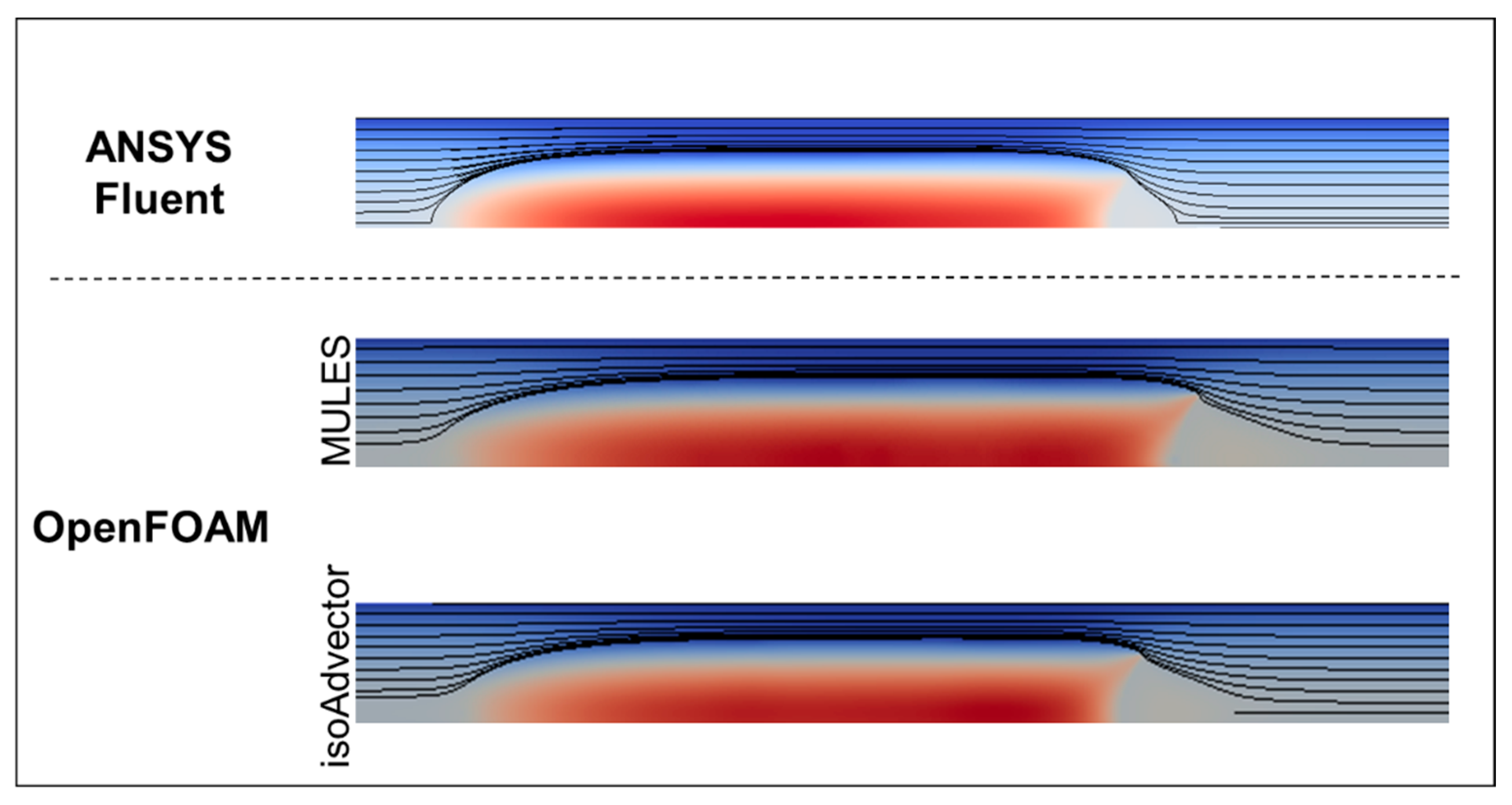
- In scenarios associated with high CaB, the bubble moves faster than the liquid phase that is absent of recirculation zones (assuming a reference frame moving with the bubble—MRF). It was also predicted the presence of a liquid film between the bubble and the wall—Case A.
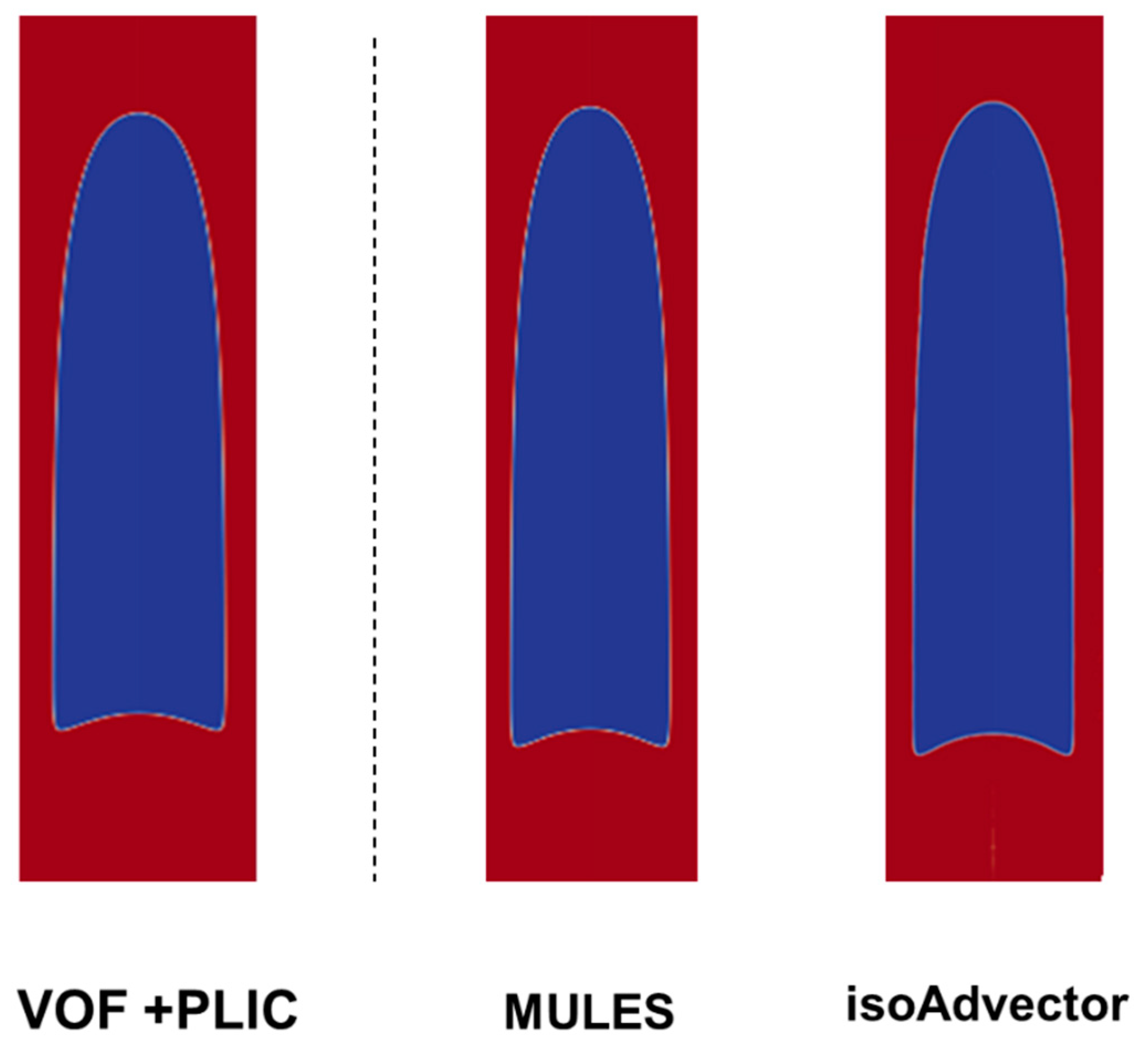
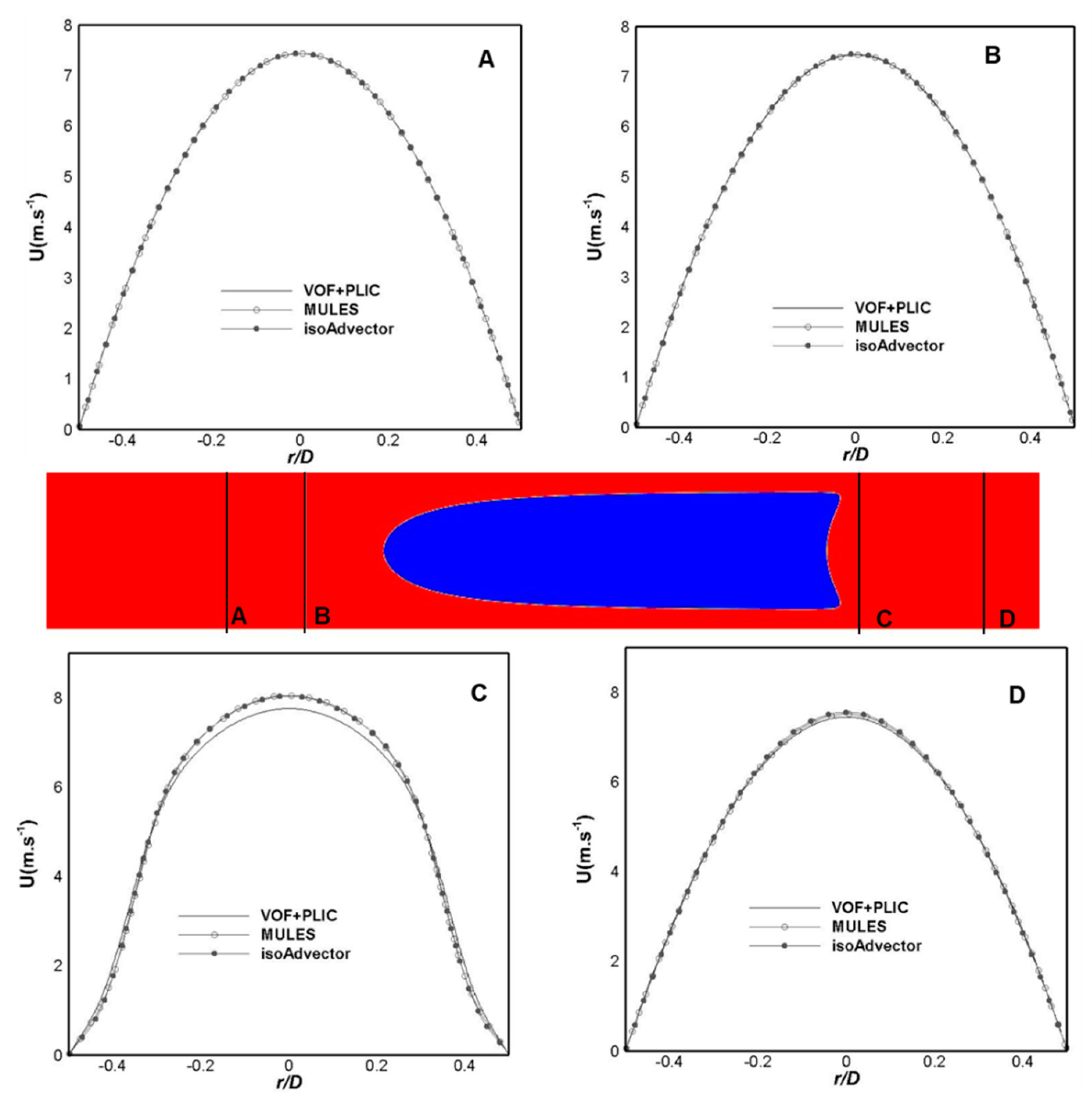
- For intermediate values of CaB, the bubble still moves faster than most of the liquid however, a closed recirculation wake appears below the bubble tail. The liquid film between the bubble and the wall is also present—Case B.
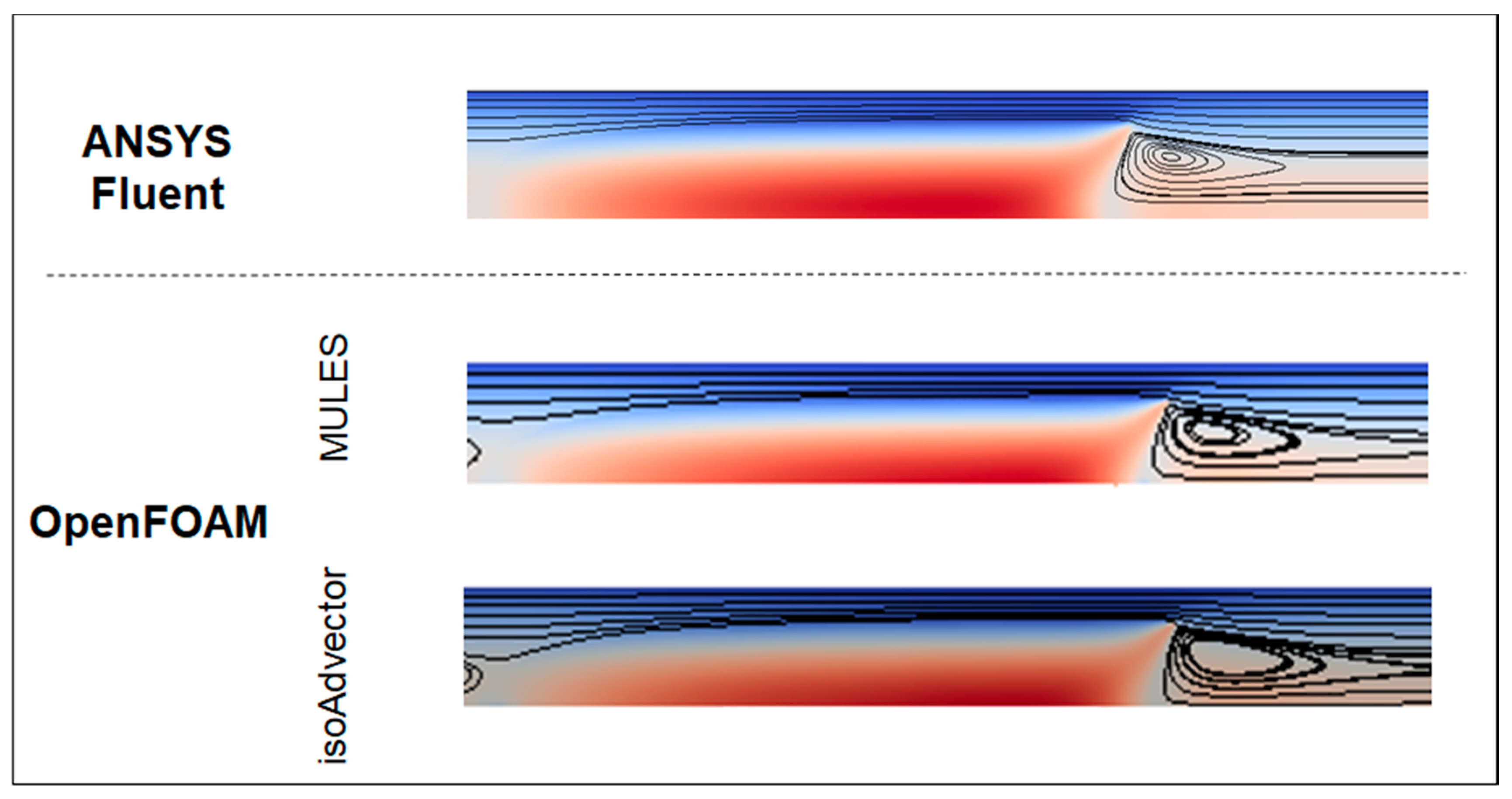
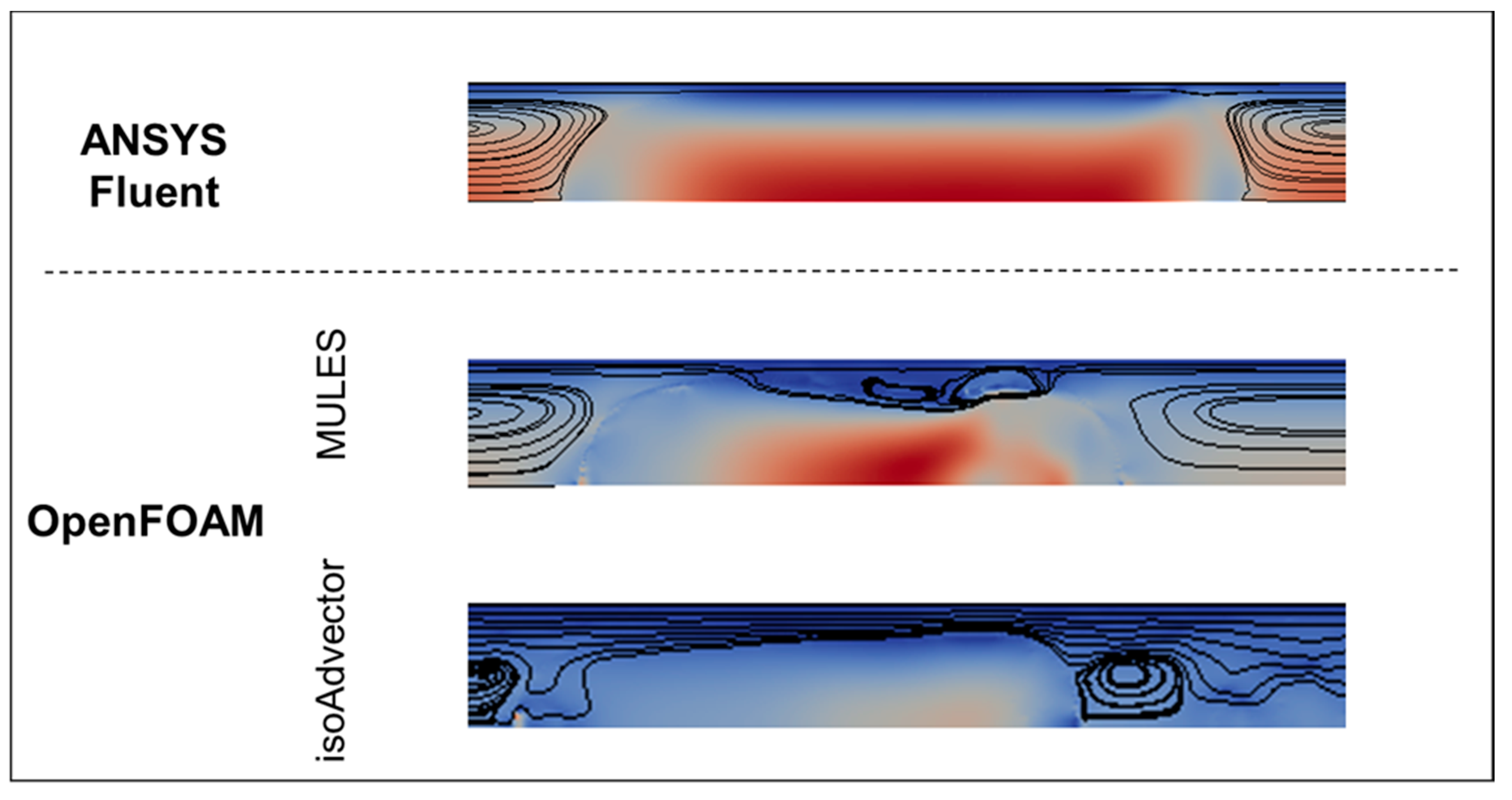
- Finally, for low values of CaB, the bubble and liquid phase flow with similar velocity. This scenario involves the presence of semi-infinite recirculation regions (in MRF) ahead and behind the bubble. Additionally, decreasing the CaB leads to recirculation regions that occupy a higher cross-sectional area—Case C.
2. Materials and Methods
2.1. Governing Equations
2.2. ANSYS Fluent® simulations
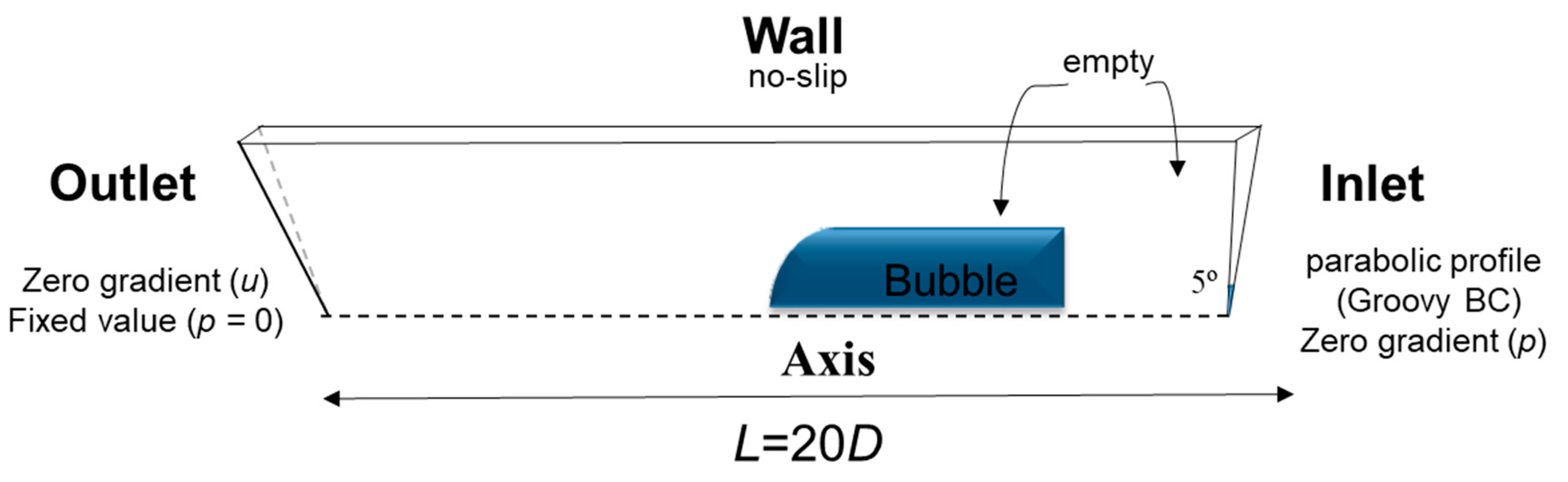
2.3. OpenFOAM® simulations
3. Results
3.1. Case A
3.2. Case B
3.3. Case C
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ganapathy, H.; Al-hajri, E.; Ohadi, M. Mass transfer characteristics of gas—Liquid absorption during Taylor flow in mini/microchannel reactors. Chem. Eng. Sci. 2013, 101, 69–80. [Google Scholar] [CrossRef]
- Ganapathy, H.; Shooshtari, A.; Dessiatoun, S.; Ohadi, M.; Alshehhi, M. Hydrodynamics and mass transfer performance of a microreactor for enhanced gas separation processes. Chem. Eng. J. 2015, 266, 258–270. [Google Scholar] [CrossRef]
- Silva, M.; Miranda, J.M.; Campos, J.; Araújo, J. Mass transfer from a Taylor bubble to the surrounding flowing liquid at the micro-scale: A numerical approach. Microfluid. Nanofluid. 2019, 23, 58. [Google Scholar] [CrossRef]
- Silva, M.; Campos, J.; Araújo, J. Mass transfer from a soluble wall into gas-liquid slug flow in a capillary tube. Int. J. Heat Mass Transf. 2019, 132, 745–761. [Google Scholar] [CrossRef]
- Butler, C.; Cid, E.; Billet-Duquenne, A. Modelling of mass transfer in Taylor flow: Investigation with the PLIF-I technique. Chem. Eng. Res. Des. 2016, 115, 292–302. [Google Scholar] [CrossRef] [Green Version]
- Abiev, R.; Butler, C.; Cid, E.; Lalanne, B.; Billet, A.-M. Mass transfer characteristics and concentration field evolution for gas-liquid Taylor flow in milli channels. Chem. Eng. Sci. 2019, 207, 1331–1340. [Google Scholar] [CrossRef] [Green Version]
- Jia, H.; Zhang, P. Investigation of the Taylor bubble under the effect of dissolution in microchannel. Chem. Eng. J. 2016, 285, 252–263. [Google Scholar] [CrossRef]
- Haase, S.; Murzin, D.Y.; Salmi, T.; Stefan, H.; Yu, M.D.; Tapio, S. Review on hydrodynamics and mass transfer in minichannel wall reactors with gas–liquid Taylor flow. Chem. Eng. Res. Des. 2016, 113, 304–329. [Google Scholar] [CrossRef]
- Asadolahi, A.N.; Gupta, R.; Fletcher, D.F.; Haynes, B.S. CFD approaches for the simulation of hydrodynamics and heat transfer in Taylor flow. Chem. Eng. Sci. 2011, 66, 5575–5584. [Google Scholar] [CrossRef]
- Tsoligkas, A.; Simmons, M.; Wood, J. Influence of orientation upon the hydrodynamics of gas–liquid flow for square channels in monolith supports. Chem. Eng. Sci. 2007, 62, 4365–4378. [Google Scholar] [CrossRef]
- Kreutzer, M.T.; Kapteijn, F.; Moulijn, J.A.; Kleijn, C.R.; Heiszwolf, J.J. Inertial and interfacial effects on pressure drop of Taylor flow in capillaries. AIChE J. 2005, 51, 2428–2440. [Google Scholar] [CrossRef]
- Howard, J.A.; Walsh, P.A. Review and extensions to film thickness and relative bubble drift velocity prediction methods in laminar Taylor or slug flows. Int. J. Multiph. Flow 2013, 55, 32–42. [Google Scholar] [CrossRef]
- Bento, D.; Sousa, L.; Yaginuma, T.; Garcia, V.; Lima, R.A.; Miranda, J.M. Microbubble moving in blood flow in microchannels: Effect on the cell-free layer and cell local concentration. Biomed. Microdevices 2017, 19, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Zaloha, P.; Křišťál, J.; Jiricny, V.; Völkel, N.; Xuereb, C.; Aubin, J. Characteristics of liquid slugs in gas–liquid Taylor flow in microchannels. Chem. Eng. Sci. 2012, 68, 640–649. [Google Scholar] [CrossRef] [Green Version]
- Gupta, R.; Fletcher, D.F.; Haynes, B.S. On the CFD modelling of Taylor flow in microchannels. Chem. Eng. Sci. 2009, 64, 2941–2950. [Google Scholar] [CrossRef]
- Abiev, R.S.; Lavretsov, I. Hydrodynamics of gas–liquid Taylor flow and liquid–solid mass transfer in mini channels: Theory and experiment. Chem. Eng. J. 2011, 176, 57–64. [Google Scholar] [CrossRef]
- Abiev, R.S. Simulation of the slug flow of a gas-liquid system in capillaries. Theor. Found. Chem. Eng. 2008, 42, 105–117. [Google Scholar] [CrossRef]
- Rocha, L.A.M.; Miranda, J.M.; Campos, J.B.L.M. Wide Range Simulation Study of Taylor Bubbles in Circular Milli and Microchannels. Micromachines 2017, 8, 154. [Google Scholar] [CrossRef] [Green Version]
- Wörner, M. Numerical modeling of multiphase flows in microfluidics and micro process engineering: A review of methods and applications. Microfluid. Nanofluid. 2012, 12, 841–886. [Google Scholar] [CrossRef]
- Gupta, R.; Fletcher, D.; Haynes, B.S. Taylor Flow in Microchannels: A Review of Experimental and Computational Work. J. Comput. Multiph. Flows 2010, 2, 1–31. [Google Scholar] [CrossRef]
- Yang, G.; Du, B.; Fan, L. Bubble formation and dynamics in gas–liquid–solid fluidization—A review. Chem. Eng. Sci. 2007, 62, 2–27. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Youngs, D.L. Time-dependent multi-material flow with large fluid distortion. In Numerical Methods for Fluid Dynamics; Morton, K.W., Baines, M.J., Eds.; Academic Press: Cambridge, MA, USA, 1982; pp. 273–285. [Google Scholar]
- Deshpande, S.S.; Anumolu, L.; Trujillo, M.F. Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Discov. 2012, 5, 014016. [Google Scholar] [CrossRef]
- Roenby, J.; Bredmose, H.; Jasak, H. A computational method for sharp interface advection. R. Soc. Open Sci. 2016, 3, 160405. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Shikazono, N. Measurement of the liquid film thickness in micro tube slug flow. Int. J. Heat Fluid Flow 2009, 30, 842–853. [Google Scholar] [CrossRef]
- Lafaurie, B.; Nardone, C.; Scardovelli, R.; Zaleski, S.; Zanetti, G. Modelling Merging and Fragmentation in Multiphase Flows with SURFER. J. Comput. Phys. 1994, 113, 134–147. [Google Scholar] [CrossRef]
- Zahedi, S.; Kronbichler, M.; Kreiss, G. Spurious currents in finite element based level set methods for two-phase flow. Int. J. Numer. Methods Fluids 2011, 69, 1433–1456. [Google Scholar] [CrossRef]
- Pan, Z.; Weibel, J.A.; Garimella, S.V. Spurious Current Suppression in VOF-CSF Simulation of Slug Flow through Small Channels. Numer. Heat Transf. Part A Appl. 2014, 67, 1–12. [Google Scholar] [CrossRef]
- Harvie, D.J.E.; Davidson, M.; Rudman, M. An analysis of parasitic current generation in Volume of Fluid simulations. Appl. Math. Model. 2006, 30, 1056–1066. [Google Scholar] [CrossRef]
- Gupta, R.; Fletcher, D.; Haynes, B.S. CFD modelling of flow and heat transfer in the Taylor flow regime. Chem. Eng. Sci. 2010, 65, 2094–2107. [Google Scholar] [CrossRef]
- Mehdizadeh, A.; Sherif, S.; Lear, W. Numerical simulation of thermofluid characteristics of two-phase slug flow in microchannels. Int. J. Heat Mass Transf. 2011, 54, 3457–3465. [Google Scholar] [CrossRef]
- Horgue, P.; Augier, F.; Quintard, M.; Prat, M. A suitable parametrization to simulate slug flows with the Volume-Of-Fluid method. Comptes Rendus Mécanique 2012, 340, 411–419. [Google Scholar] [CrossRef] [Green Version]
- Renardy, Y.; Renardy, M. PROST: A Parabolic Reconstruction of Surface Tension for the Volume-of-Fluid Method. J. Comput. Phys. 2002, 183, 400–421. [Google Scholar] [CrossRef] [Green Version]
- Jamet, D.; Torres, D.; Brackbill, J. On the Theory and Computation of Surface Tension: The Elimination of Parasitic Currents through Energy Conservation in the Second-Gradient Method. J. Comput. Phys. 2002, 182, 262–276. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Fletcher, D.F.; Haynes, B.S. Implementation of a height function method to alleviate spurious currents in CFD modelling of annular flow in microchannels. Appl. Math. Model. 2015, 39, 4665–4686. [Google Scholar] [CrossRef]
- Hysing, S. A new implicit surface tension implementation for interfacial flows. Int. J. Numer. Methods Fluids 2005, 51, 659–672. [Google Scholar] [CrossRef]
- Popinet, S.; Zaleski, S. A front-tracking algorithm for accurate representation of surface tension. Int. J. Numer. Methods Fluids 1999, 30, 775–793. [Google Scholar] [CrossRef]
- Meier, M.; Yadigaroglu, G.; Smith, B.L. A novel technique for including surface tension in PLIC-VOF methods. Eur. J. Mech. B/Fluids 2002, 21, 61–73. [Google Scholar] [CrossRef]
- Galusinski, C.; Vigneaux, P. On stability condition for bifluid flows with surface tension: Application to microfluidics. J. Comput. Phys. 2008, 227, 6140–6164. [Google Scholar] [CrossRef] [Green Version]

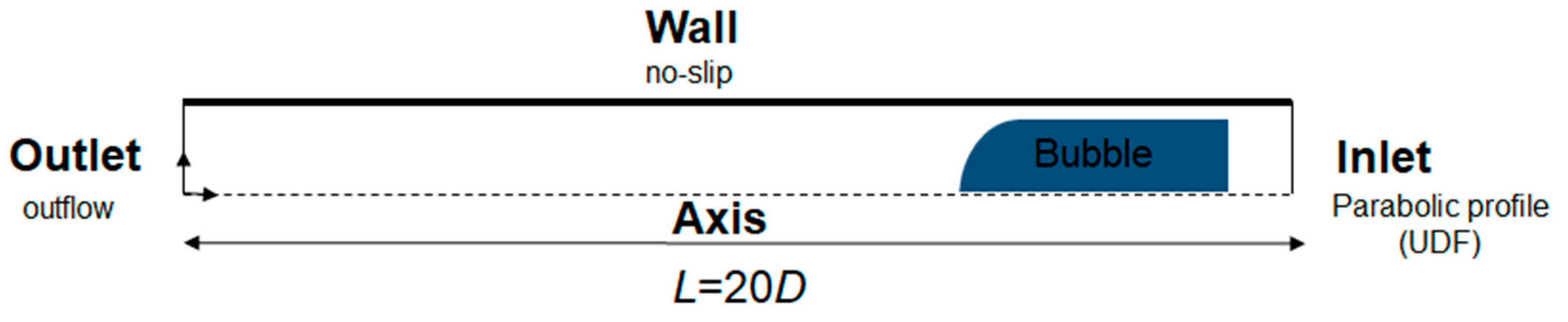


| interFoam | interFlow | |
|---|---|---|
| ddtSchemes | Euler | Euler |
| gradSchemes | Gauss linear | Gauss linear |
| divSchemes | ||
| div(rho*phi, u) | ---- | Gauss limitedLinearV 1; |
| div(rhoPhi, u) | Gauss linear Upwind grad (U); | Gauss limitedLinearV 1; |
| div(phi, alpha) | Gauss van Leer; | Gauss vanLeer; |
| div(phi, alpha1) | ---- | Gauss HRIC; |
| div(phirb, alpha) | Gauss linear; | Gauss interfaceCompression; |
| div((muEff*dev (T(grad(U))))) | ---- | Gauss linear; |
| div((rho*nuEff)*dev2(T(grad(U)))) | Gauss linear; | Gauss linear; |
| laplacianSchemes | Gauss Linear corrected | Gauss Linear corrected |
| interpolationSchemes | linear; | linear; |
| snGradSchemes | corrected; | corrected; |
| Physical Properties | Dimensionless Groups | Simulation Parameters | |
|---|---|---|---|
| Case A | ρ = 1000 kg·m−3 μ = 3.74 × 10−2 Pa·s | CaB = 10 ReB = 2.0 | Co = 0.25 Δt = 10−7 |
| Case B | ρ = 1000 kg·m−3 μ = 7.48 × 10−3 Pa·s | CaB = 100 ReB = 0.8 | Co = 0.25 Δt = 10−8 |
| Case C | ρ = 1000 kg·m−3 μ = 4.58 × 10−2 Pa·s | CaB = 0.1 ReB = 0.03 | Co = 0.25; 0.20 *; 0.10 * Δt =10−6; 10−7 *; 10−8 *; 10−9 * |
| Theoretical | VOF+PLIC | MULES | IsoAdvector | |
|---|---|---|---|---|
| 1.57 × 10−1 | 1.63 × 10−1 ± 3.78% | 1.55 × 10−1 ± 1.02% | 1.56 × 10−1 ± 0.78% | |
| (m·s−1) | 3.5 | 3.6 | 3.5 | 3.5 |
| Theoretical | VOF+PLIC | MULES | IsoAdvector | |
|---|---|---|---|---|
| 1.23 × 10−1 | 1.27 × 10−1 ± 3.47% | 1.33 × 10−1 ± 8.36% | 1.3 × 10−1 ± 5.91% | |
| (m·s−1) | 6.5 | 6.7 | 6.8 | 6.8 |
| Theoretical | VOF+PLIC | MULES | IsoAdvector | |
|---|---|---|---|---|
| 4.96 × 10−2 | 4.7 × 10−2 ± 5.15% | 1.15 × 10−1 + 132% | 1.11 × 10−1 + 122% | |
| (m·s−1) | 0.046 | 0.046 | 0.046 | 0.049 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, M.F.; Campos, J.B.L.M.; Miranda, J.M.; Araújo, J.D.P. Numerical Study of Single Taylor Bubble Movement Through a Microchannel Using Different CFD Packages. Processes 2020, 8, 1418. https://doi.org/10.3390/pr8111418
Silva MF, Campos JBLM, Miranda JM, Araújo JDP. Numerical Study of Single Taylor Bubble Movement Through a Microchannel Using Different CFD Packages. Processes. 2020; 8(11):1418. https://doi.org/10.3390/pr8111418
Chicago/Turabian StyleSilva, Mónica F., João B. L. M. Campos, João M. Miranda, and José D. P. Araújo. 2020. "Numerical Study of Single Taylor Bubble Movement Through a Microchannel Using Different CFD Packages" Processes 8, no. 11: 1418. https://doi.org/10.3390/pr8111418
APA StyleSilva, M. F., Campos, J. B. L. M., Miranda, J. M., & Araújo, J. D. P. (2020). Numerical Study of Single Taylor Bubble Movement Through a Microchannel Using Different CFD Packages. Processes, 8(11), 1418. https://doi.org/10.3390/pr8111418







