Heat Transfer Improvement in MHD Natural Convection Flow of Graphite Oxide/Carbon Nanotubes-Methanol Based Casson Nanofluids Past a Horizontal Circular Cylinder
Abstract
:1. Introduction
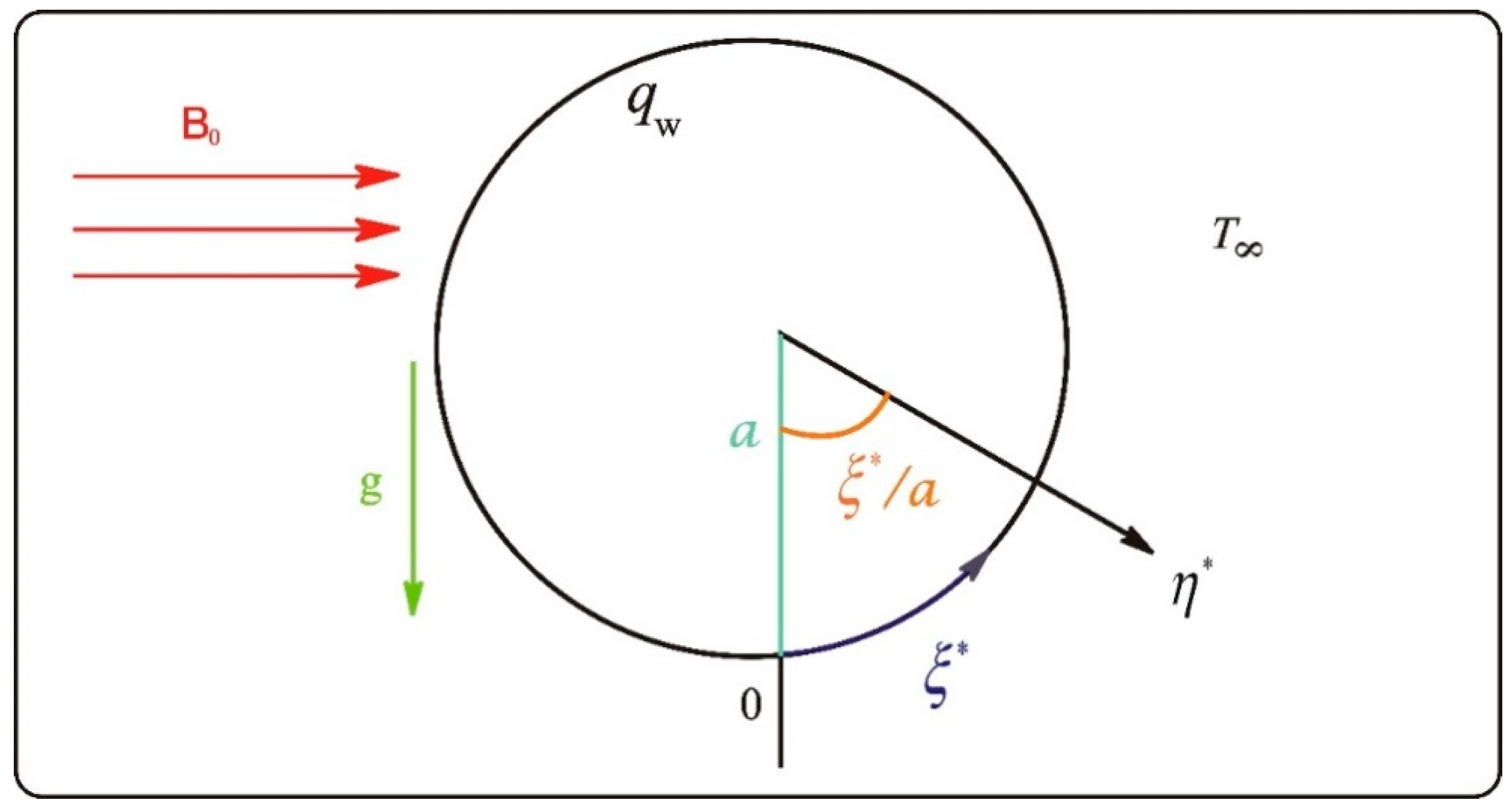
2. Problem Description
3. Numerical Solution
3.1. The Finite-Difference Method
3.2. Newton’s Method
3.3. The Block Tridiagonal Matrix
4. Results and Discussion
4.1. Validation of Results
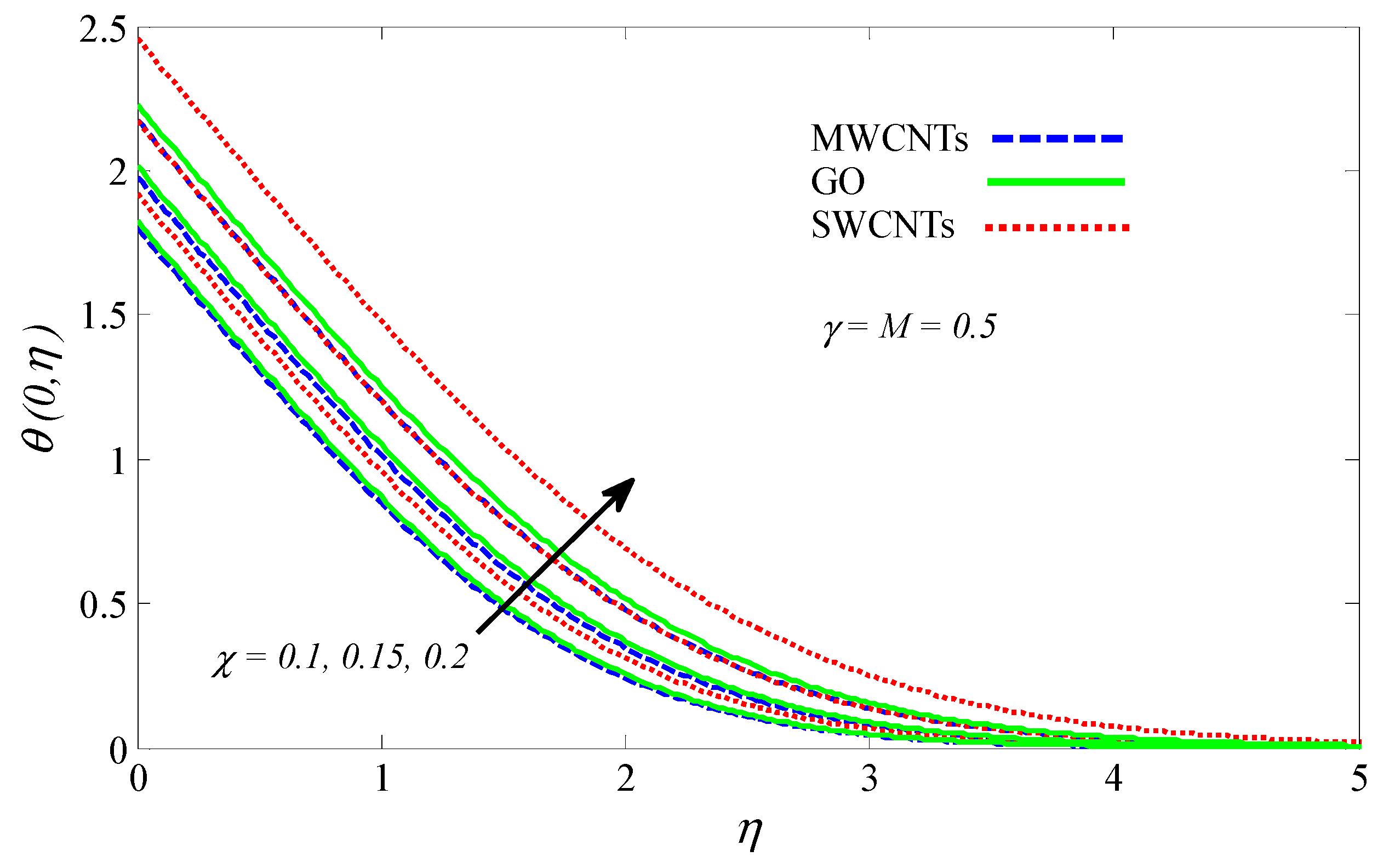
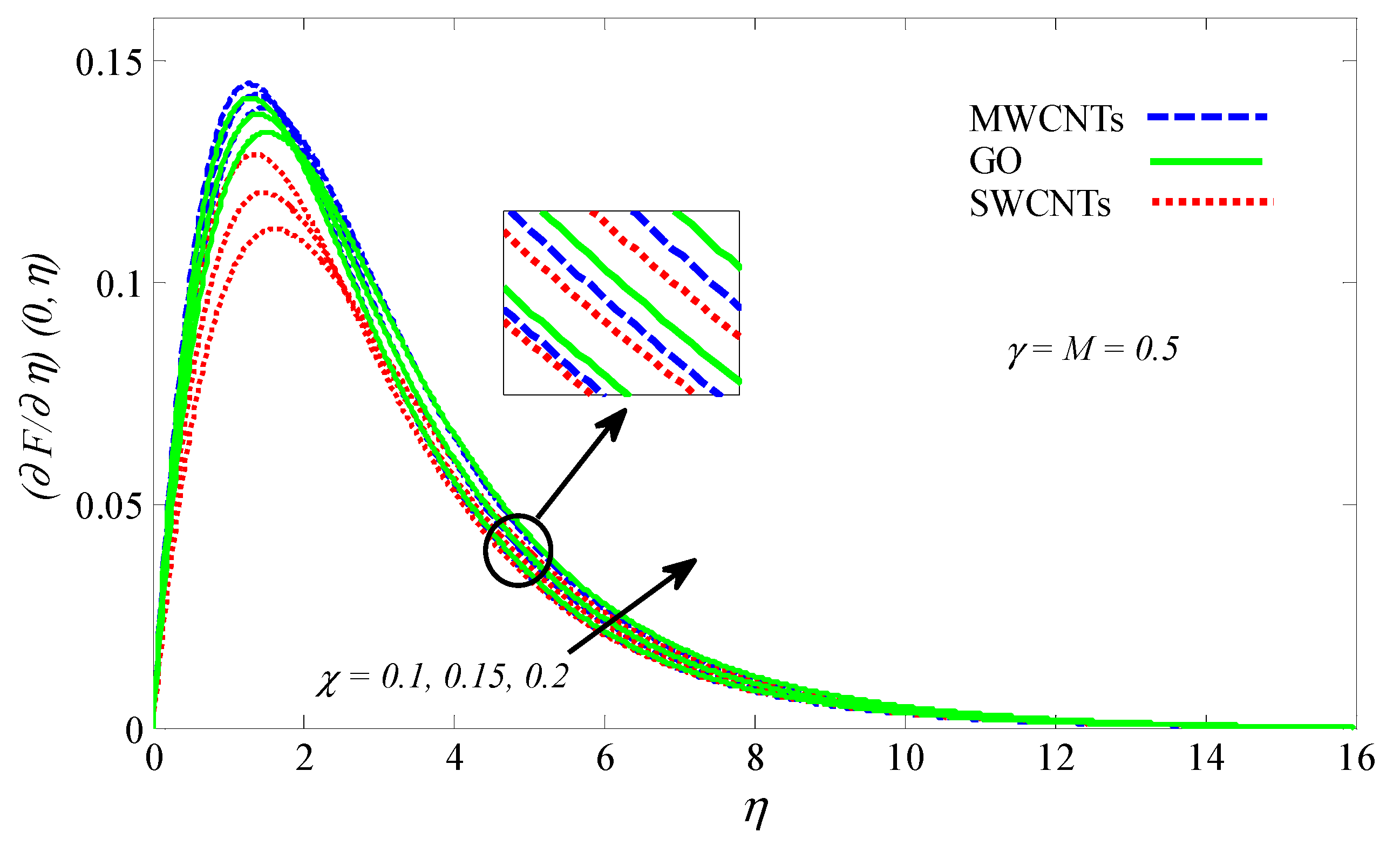
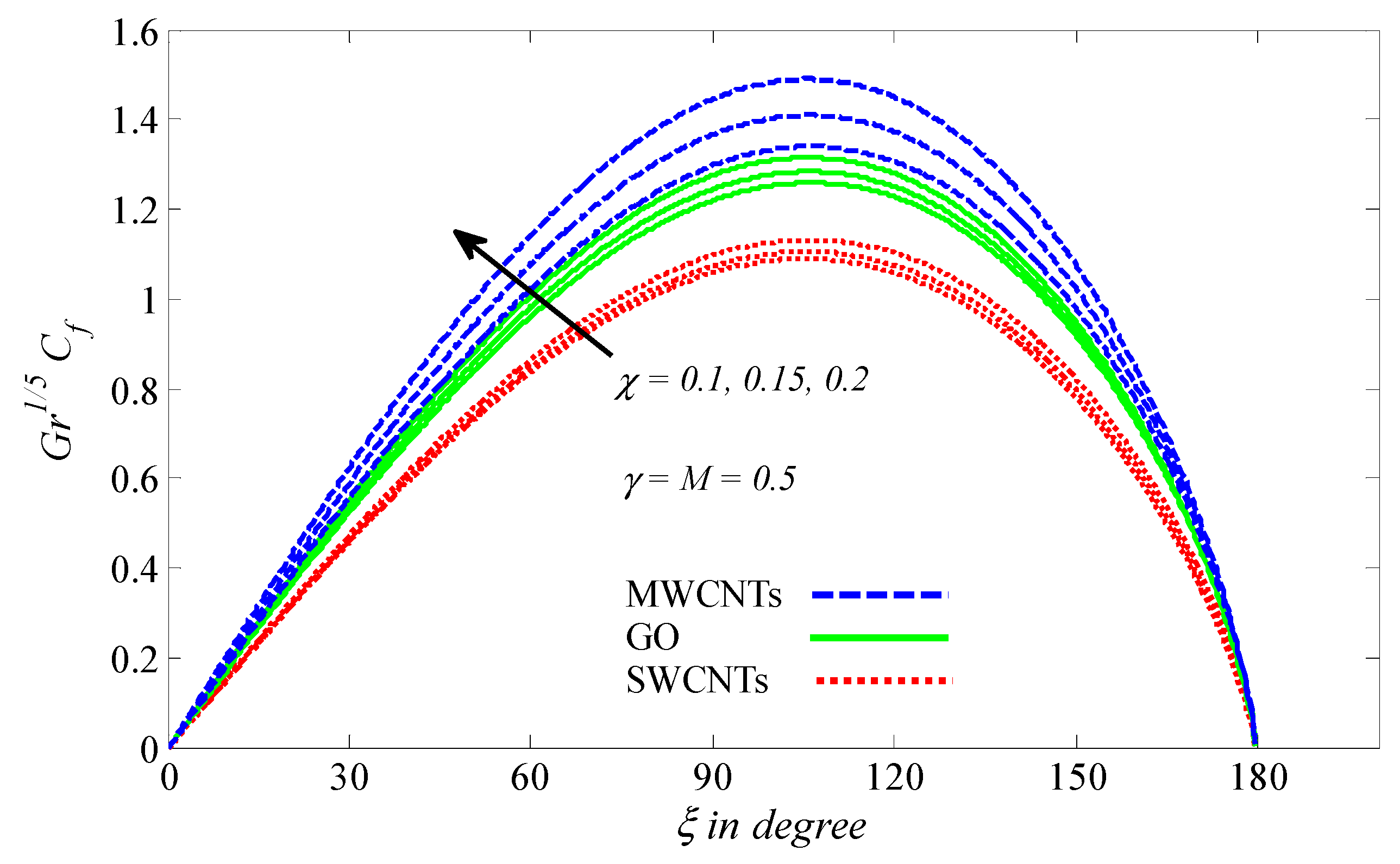
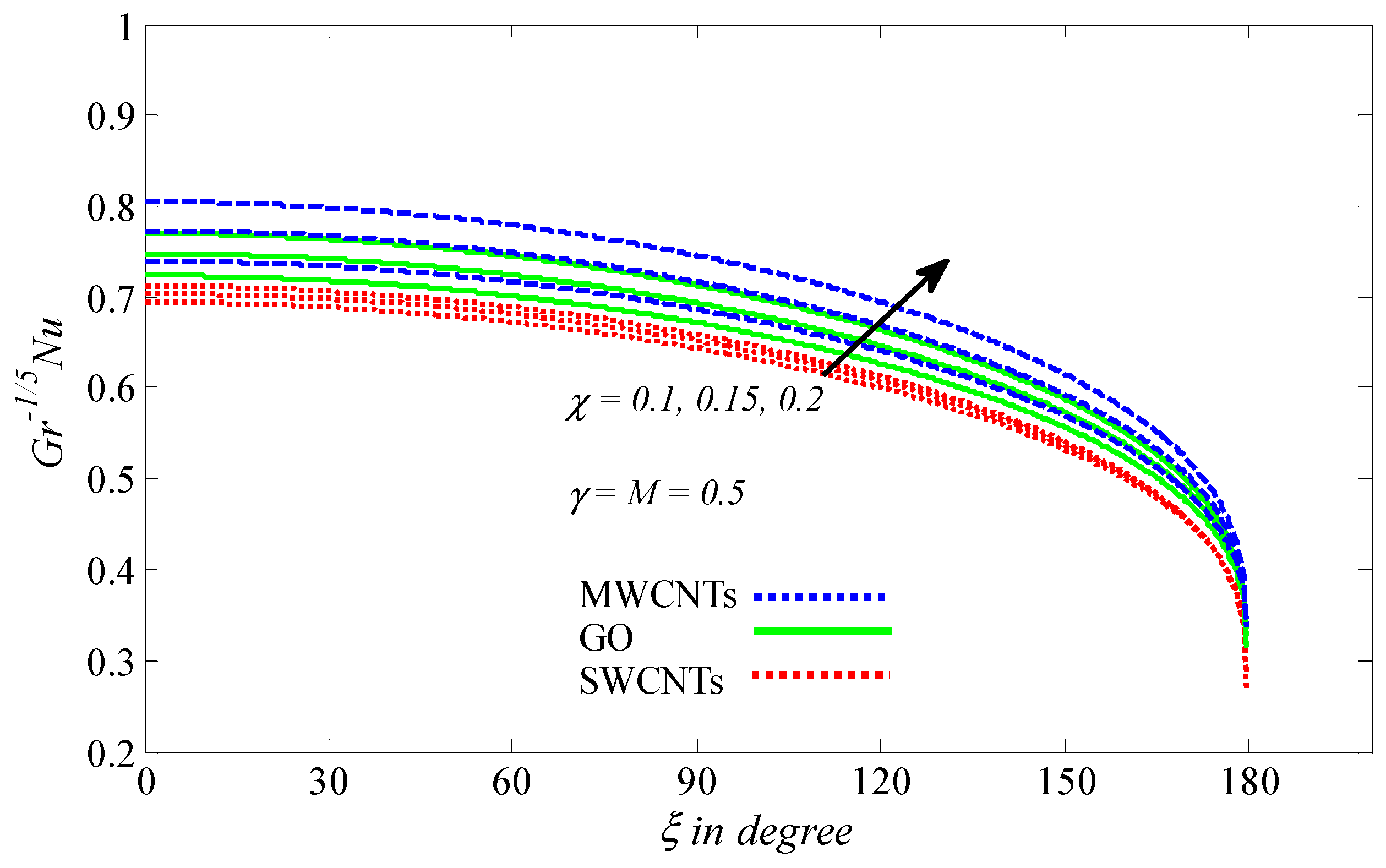
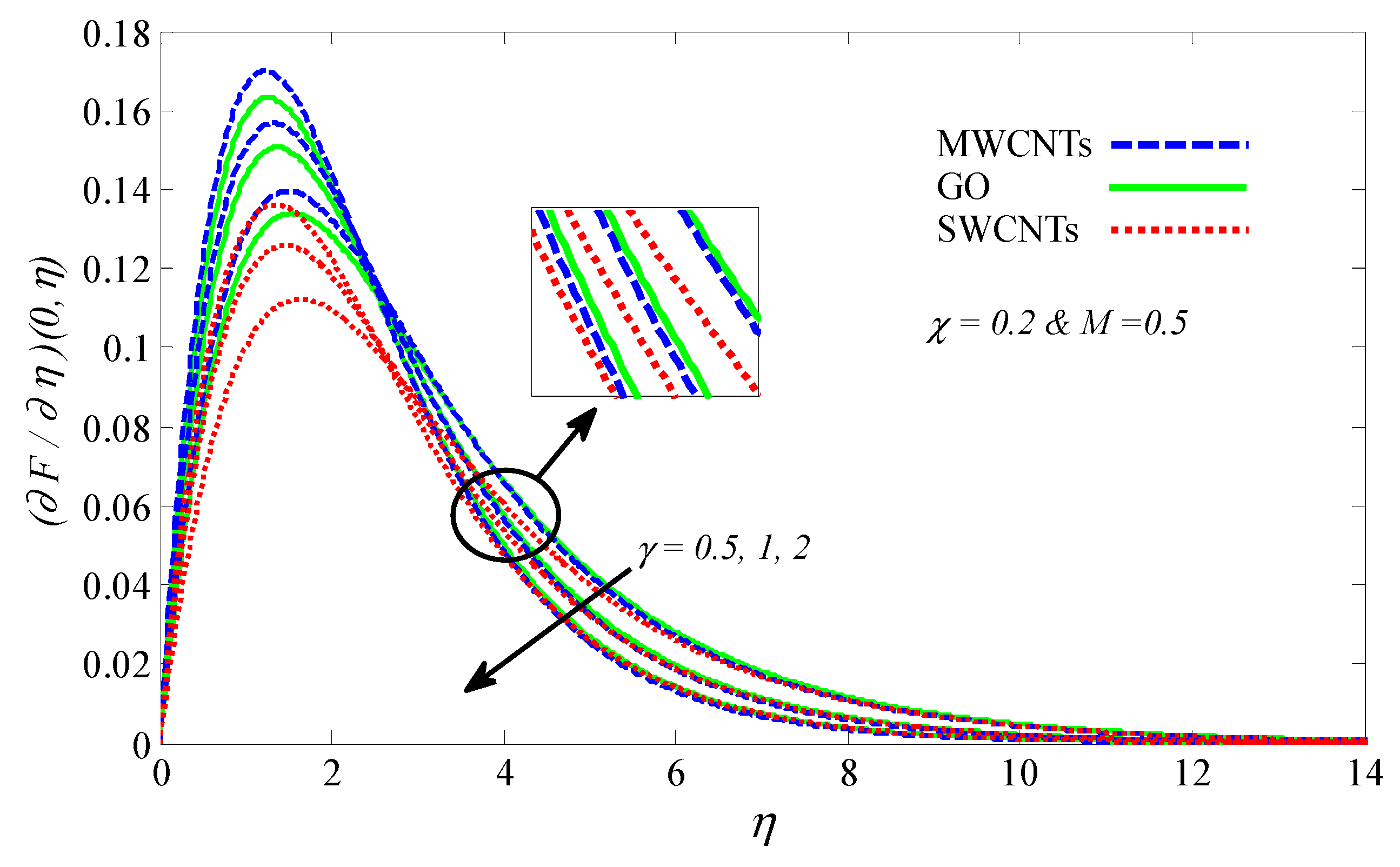
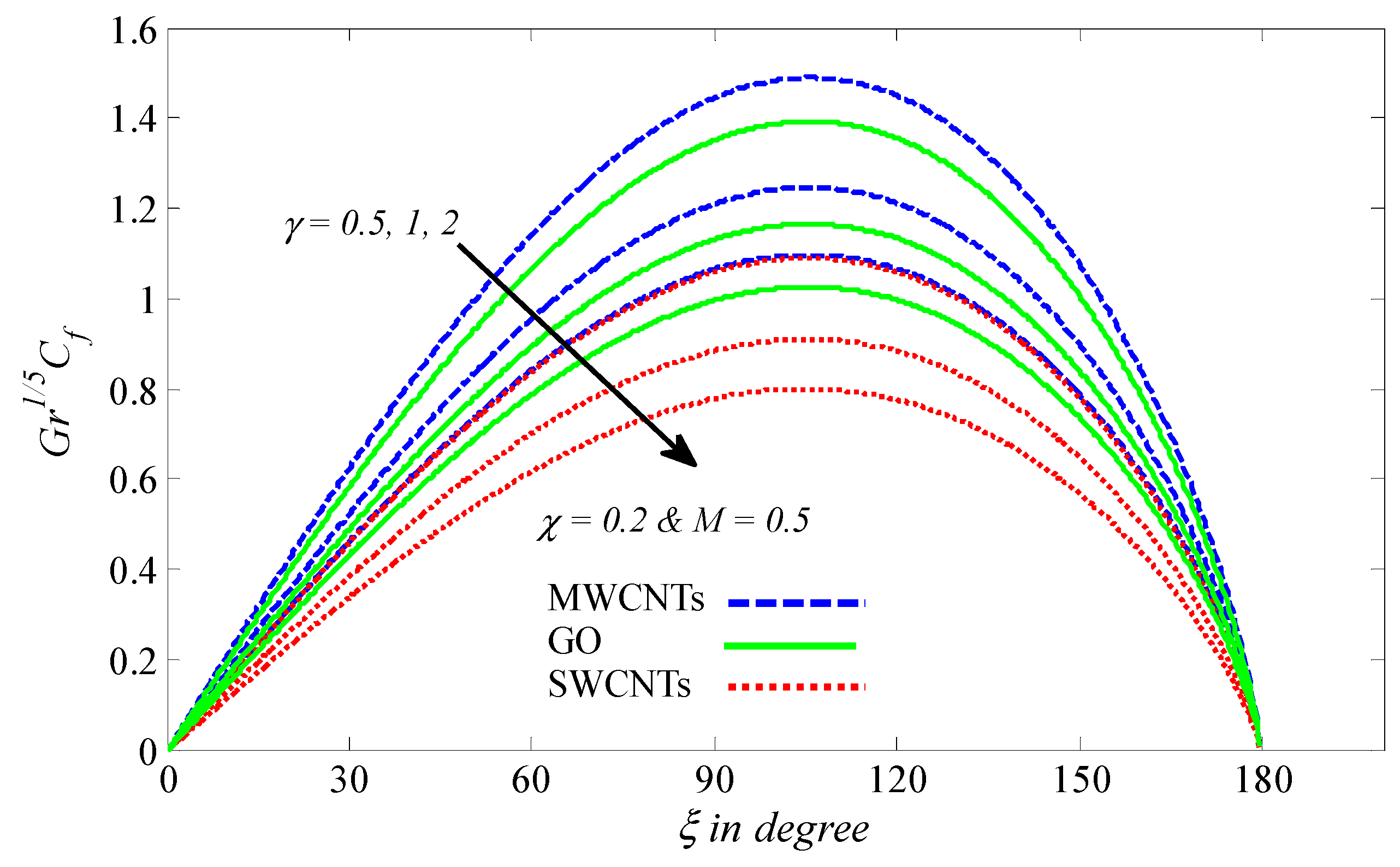
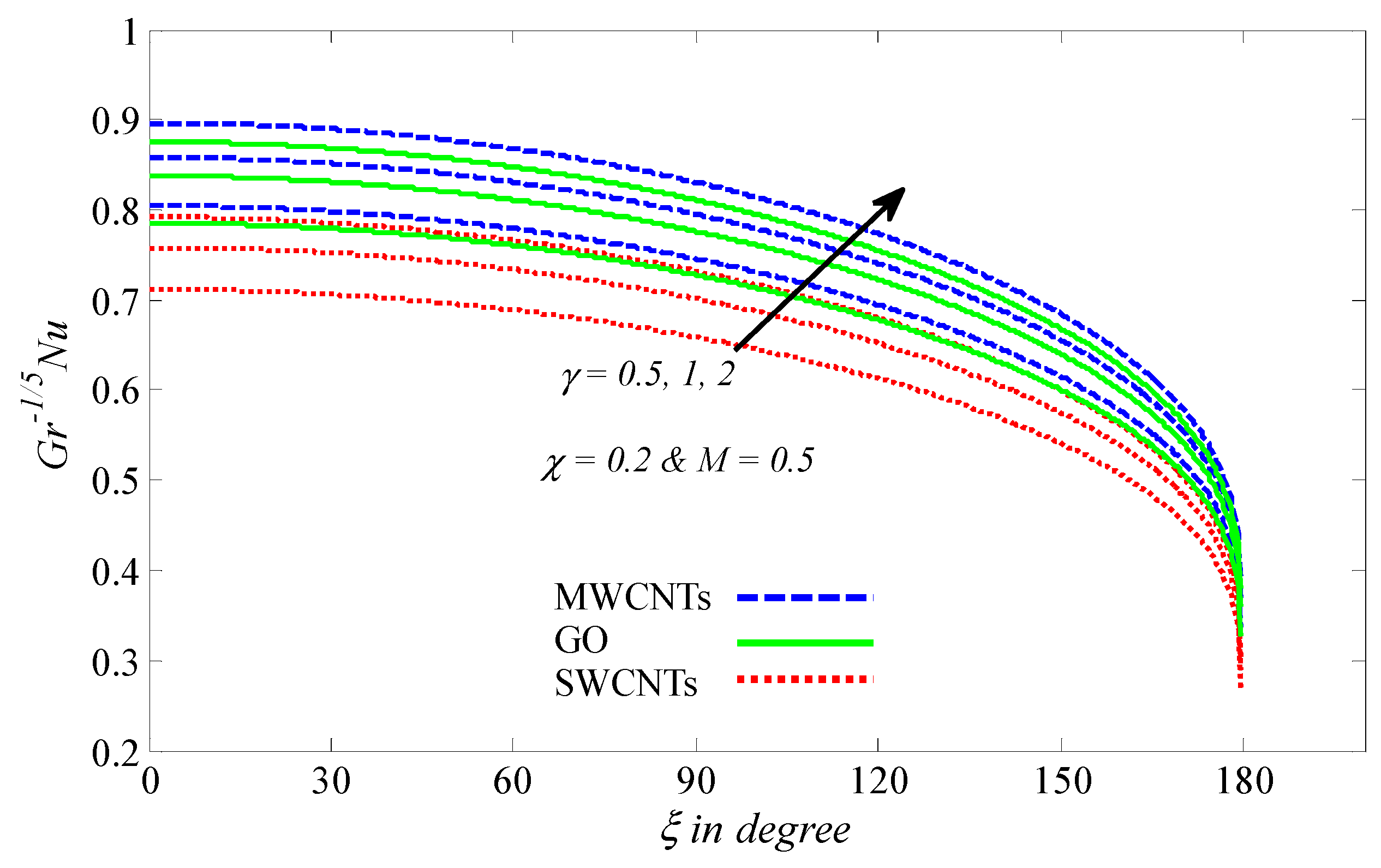
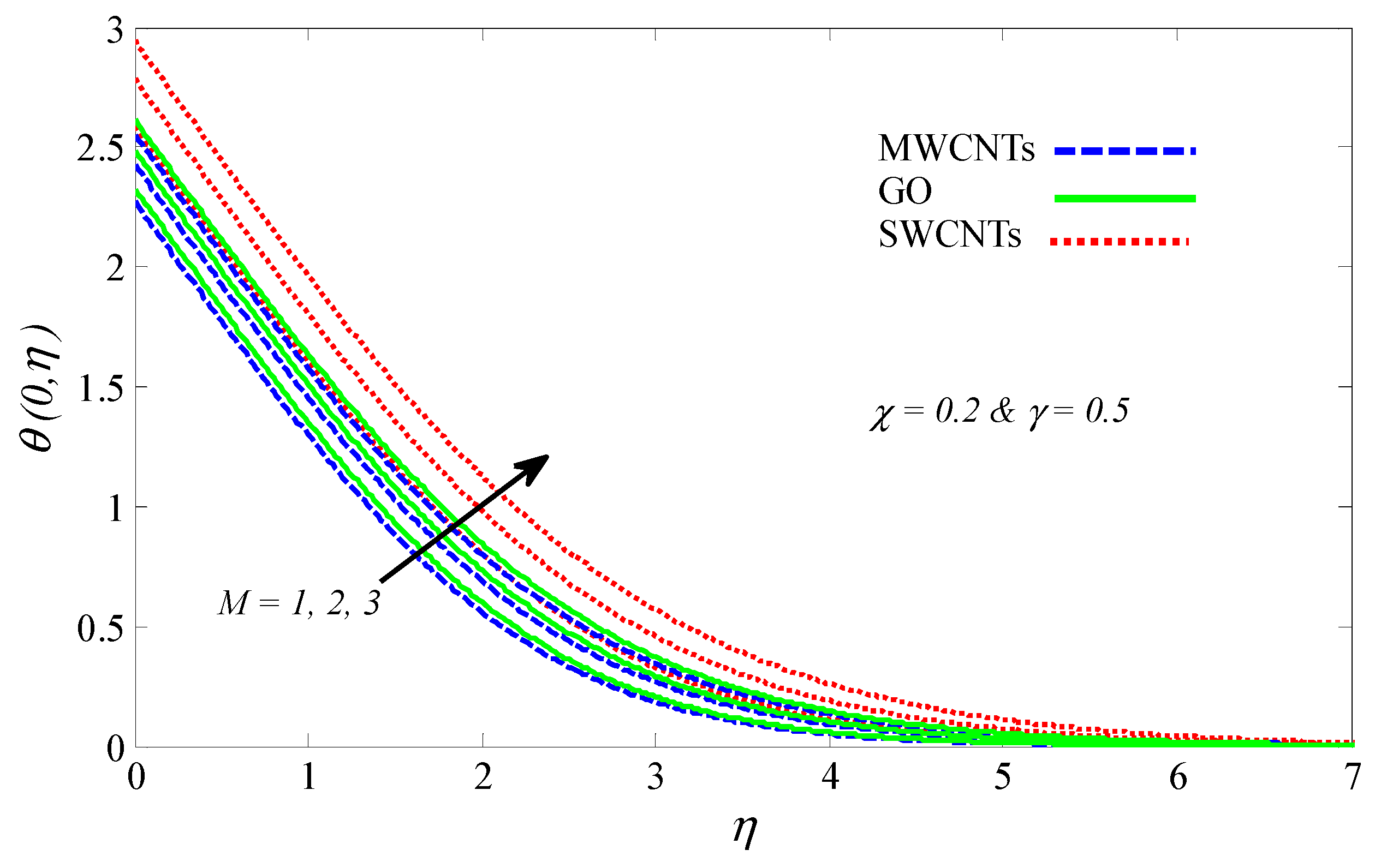
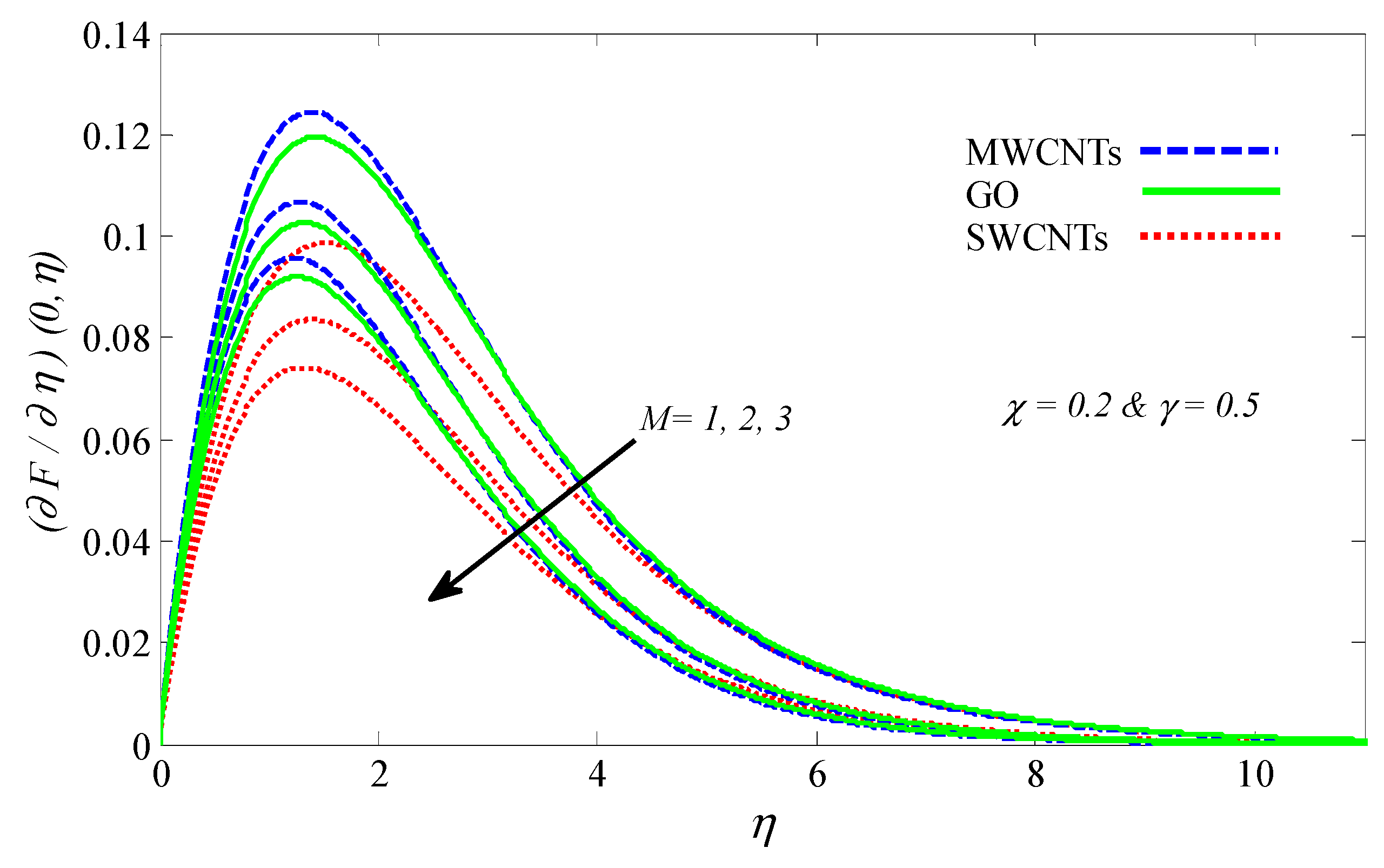
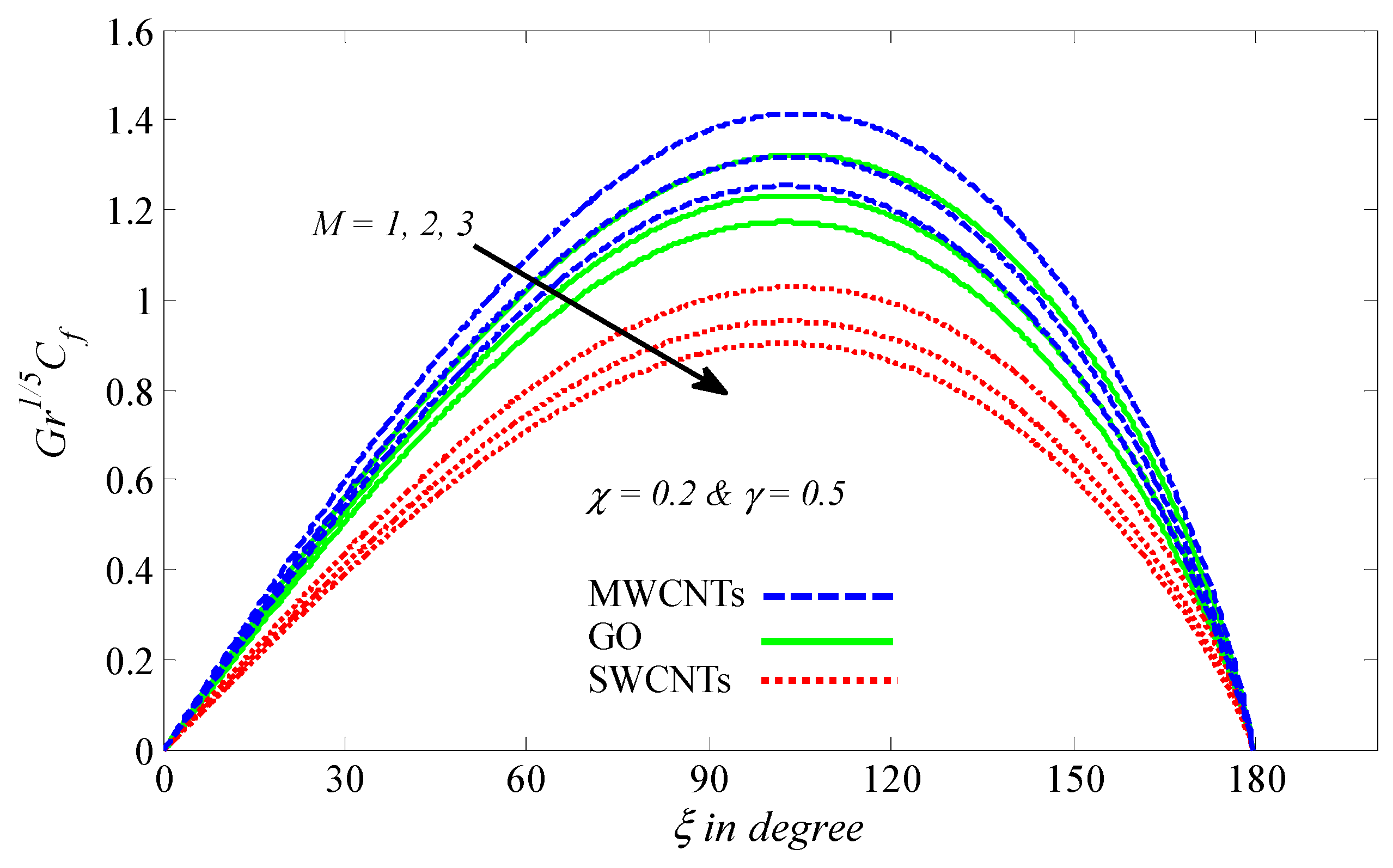
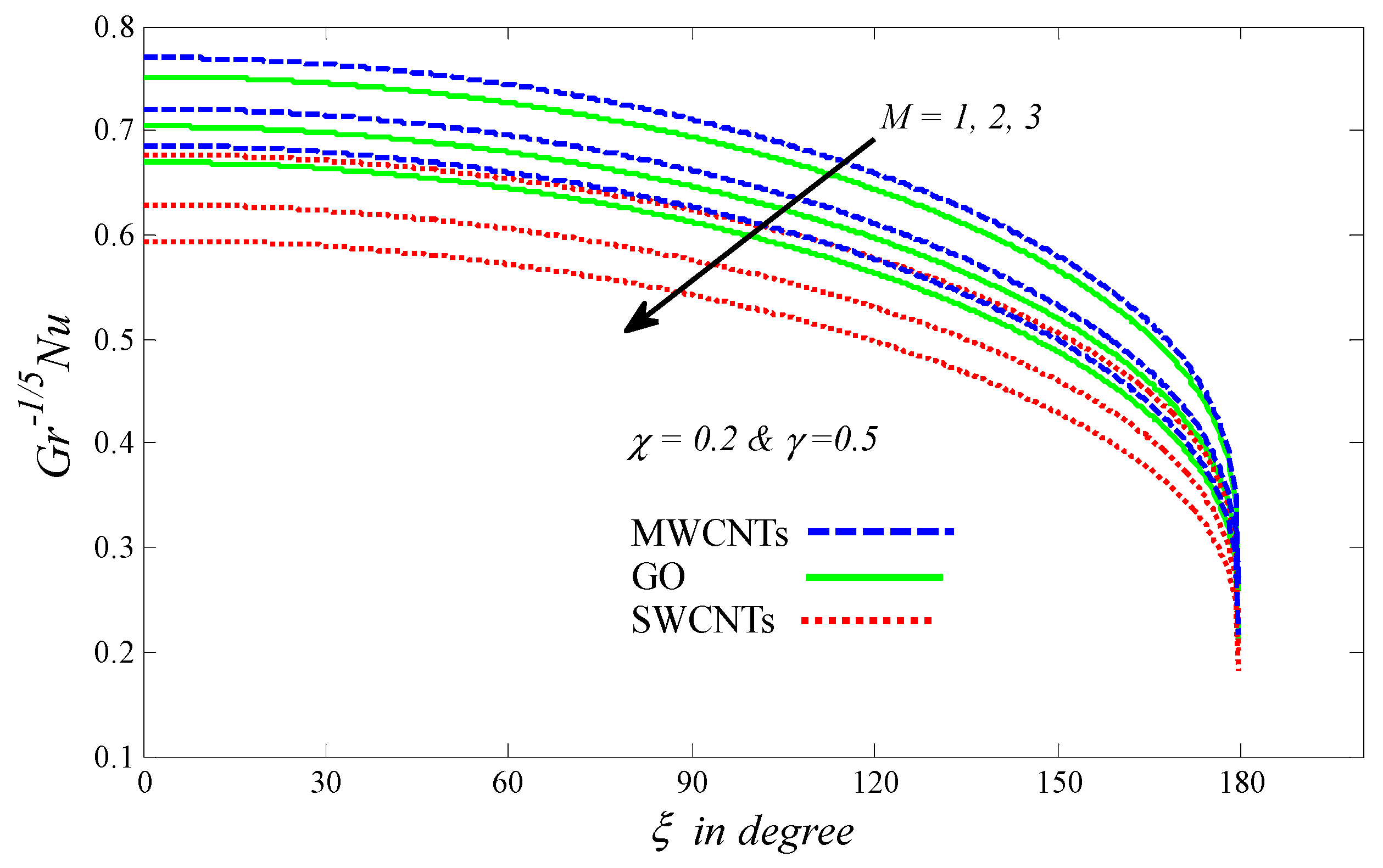
4.2. Graphical Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Radius of Cylinder | Thermal diffusivity | ||
| Magnetic field strength | Casson parameter | ||
| Skin friction coefficient | Thermal expansion of base fluid | ||
| Grashof number | Thermal expansion of nanoparticles | ||
| Gravity vector | Temperature of nanofluid | ||
| Thermal conductivity | Plastic Dynamic viscosity of base fluid | ||
| Magnetic parameter | Dynamic viscosity of base fluid | ||
| Nusselt Number | Density | ||
| Prandtl number | Heat capacity | ||
| Yield stress | Wall shear stress | ||
| Wall heat flux | Nanoparticle volume fraction | ||
| Temperature of the fluid | Stream function | ||
| Ambient temperature | Electrical conductivity | ||
| —component of velocity | Subscript | ||
| —component of velocity | nanoparticles | ||
| Kinematic viscosity | Nanofluid | ||
| Greek symbols | Base fluid | ||
References
- Blasius, H. Grenzschichten in Flumigkeiten Mit Kleiner Reibung. Z. Math. Phys. 1908, 56, 1–37. [Google Scholar]
- Frossling, N. Calculation by series expansion of the heat transfer in laminar, constant-property boundary layers at nonisothermal surfaces. Ark. Fys. 1958, 14. Available online: https://www.osti.gov/biblio/4314587 (accessed on 10 October 2020).
- Merkin, J. Free convection boundary layer on an isothermal horizontal cylinder. In Proceedings of the American Society of Mechanical Engineers and American Institute of Chemical Engineers, Heat Transfer Conference, St. Louis, MO, USA, 9–11 August 1976. [Google Scholar]
- Merkin, J. Mixed convection from a horizontal circular cylinder. Int. J. Heat Mass Transf. 1977, 20, 73–77. [Google Scholar] [CrossRef]
- Merkin, J.; Pop, I. A note on the free convection boundary layer on a horizontal circular cylinder with constant heat flux. Heat Mass Transf. 1988, 22, 79–81. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Pop, I. Mixed convection boundary-layer flow from a horizontal circular cylinder in micropolar fluids: Case of constant wall temperature. Int. J. Numer. Method H 2003, 13, 86–109. [Google Scholar] [CrossRef]
- Anwar, I.; Amin, N.; Pop, I. Mixed convection boundary layer flow of a viscoelastic fluid over a horizontal circular cylinder. Int. J. Nonlin. Mech. 2008, 43, 814–821. [Google Scholar] [CrossRef] [Green Version]
- Mabood, F.; Khan, W.; Yovanovich, M. Forced convection of nanofluid flow across horizontal circular cylinder with convective boundary condition. J. Mol. Liq. 2016, 222, 172–180. [Google Scholar] [CrossRef]
- Rao, A.S.; Amanulla, C.; Nagendra, N.; Beg, O.A.; Kadir, A. Hydromagnetic flow and heat transfer in a Williamson Non-Newtonian fluid from a Horizontal circular cylinder with Newtonian Heating. Int. J. Appl. Comput. Math. 2017, 3, 3389–3409. [Google Scholar]
- Ingham, D.; Pop, I. Natural convection about a heated horizontal cylinder in a porous medium. J. Fluid Mech. 1987, 184, 157–181. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Pop, I. Mixed convection boundary-layer flow from a horizontal circular cylinder with a constant surface heat flux. Heat Mass Transf. 2004, 40, 219–227. [Google Scholar] [CrossRef]
- Ibrahim, F.; Hamad, M. Group method analysis of mixed convection boundary-layer flow of a micropolar fluid near a stagnation point on a horizontal cylinder. Acta Mech. 2006, 181, 65–81. [Google Scholar] [CrossRef]
- Gorla, R.S.R.; El-Kabeir, S.; Rashad, A. Heat transfer in the boundary layer on a stretching circular cylinder in a nanofluid. J. Heat Transf. 2011, 25, 183–186. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.; Aly, A.M. Transient natural convection flow of a nanofluid over a vertical cylinder. Meccanica 2013, 48, 71–81. [Google Scholar] [CrossRef]
- Rashad, A.; Chamkha, A.; Modather, M. Mixed convection boundary-layer flow past a horizontal circular cylinder embedded in a porous medium filled with a nanofluid under convective boundary condition. Comput. Fluids 2013, 86, 380–388. [Google Scholar] [CrossRef]
- Tlili, I.; Khan, W.; Ramadan, K. MHD Flow of Nanofluid Flow Across Horizontal Circular Cylinder: Steady Forced Convection. J. Nanofluids 2019, 8, 179–186. [Google Scholar] [CrossRef]
- Rashad, A.; Nabwey, H.A. Gyrotactic mixed bioconvection flow of a nanofluid past a circular cylinder with convective boundary condition. J. Taiwan Inst. Chem. Eng. 2019, 99, 9–17. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Aly, A. MHD free convection flow of a nanofluid past a vertical plate in the presence of heat generation or absorption effects. Chem. Eng. Commun. 2010, 198, 425–441. [Google Scholar] [CrossRef]
- Hamad, M.; Pop, I.; Ismail, A.M. Magnetic field effects on free convection flow of a nanofluid past a vertical semi-infinite flat plate. Nonlinear Anal. Real World Appl. 2011, 12, 1338–1346. [Google Scholar] [CrossRef]
- Rana, P.; Dhanai, R.; Kumar, L. MHD slip flow and heat transfer of Al2O3-water nanofluid over a horizontal shrinking cylinder using Buongiorno’s model: Effect of nanolayer and nanoparticle diameter. Adv. Powder Technol. 2017, 28, 1727–1738. [Google Scholar] [CrossRef]
- Alwawi, F.A.; Alkasasbeh, H.T.; Rashad, A.M.; Idris, R. A numerical approach for the heat transfer flow of carboxymethyl cellulose-water based Casson nanofluid from a solid sphere generated by mixed convection under the influence of Lorentz force. Mathematics 2020, 8, 1094. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Laboratory: DuPage County, IL, USA, 1995. [Google Scholar]
- Akbar, N.S.; Nadeem, S.; Haq, R.U.; Khan, Z. Radiation effects on MHD stagnation point flow of nano fluid towards a stretching surface with convective boundary condition. Chin. J. Aeronaut. 2013, 26, 1389–1397. [Google Scholar] [CrossRef] [Green Version]
- Dhanai, R.; Rana, P.; Kumar, L. MHD mixed convection nanofluid flow and heat transfer over an inclined cylinder due to velocity and thermal slip effects: Buongiorno’s model. Powder Technol. 2016, 288, 140–150. [Google Scholar] [CrossRef]
- Besthapu, P.; Haq, R.U.; Bandari, S.; Al-Mdallal, Q.M. Thermal radiation and slip effects on MHD stagnation point flow of non-Newtonian nanofluid over a convective stretching surface. Neural Comput. Appl. 2019, 31, 207–217. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Mujumdar, A.S. Heat transfer characteristics of nanofluids: A review. Int. J. Sci. 2007, 46, 1–19. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Swalmeh, M.Z.; Alkasasbeh, H.T.; Hussanan, A.; Mamat, M. Heat transfer flow of Cu-water and Al2O3-water micropolar nanofluids about a solid sphere in the presence of natural convection using Keller-box method. Res. Phys. 2018, 9, 717–724. [Google Scholar] [CrossRef]
- Swalmeh, M.Z.; Alkasasbeh, H.T.; Hussanan, A.; Nguyen Thoi, T.; Mamat, M. Microstructure and inertial effects on natural convection micropolar nanofluid flow about a solid sphere. Int. J. Ambient. Energy 2019, 1–12. [Google Scholar] [CrossRef]
- Alwawi, F.A.; Alkasasbeh, H.T.; Rashad, A.; Idris, R. Heat transfer analysis of ethylene glycol-based Casson nanofluid around a horizontal circular cylinder with MHD effect. Proc. Inst. Mech. Eng. Part C 2020, 234, 2569–2580. [Google Scholar] [CrossRef]
- Casson, N. A flow equation for pigment-oil suspensions of the printing ink type. Rheol. Disperse Syst. 1959, 2, 84–102. [Google Scholar]
- Mustafa, M.; Hayat, T.; Pop, I.; Aziz, A. Unsteady boundary layer flow of a Casson fluid due to an impulsively started moving flat plate. Heat. Transf. Asian. Res. 2011, 40, 563–576. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Khan, A.; Shafie, S. Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium. Eng. Sci. Technol. Int. J. 2015, 18, 309–317. [Google Scholar] [CrossRef] [Green Version]
- EL-Kabeir, S.; El-Zahar, E.; Rashad, A. Effect of chemical reaction on heat and mass transfer by mixed convection flow of casson fluid about a sphere with partial slip. J Comput. Nanos. 2016, 13, 5218–5226. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Alkasasbeh, H.T.; Khan, I. MHD flow and heat transfer in a Casson fluid over a nonlinearly stretching sheet with Newtonian heating. Heat Transf. Res. 2018, 49, 1185–1198. [Google Scholar] [CrossRef]
- Alwawi, F.A.; Alkasasbeh, H.T.; Rashad, A.M.; Idris, R. Natural convection flow of Sodium Alginate based Casson nanofluid about a solid sphere in the presence of a magnetic field with constant surface heat flux. In Proceedings of the Journal of Physics, Conference Series, Kuantan, Malaysia, 23–25 July 2019; p. 012005. [Google Scholar]
- Haldar, S.; Mukhopadhyay, S.; Layek, G. Flow and heat transfer of Casson fluid over an exponentially shrinking permeable sheet in presence of exponentially moving free stream with convective boundary condition. Mech. Adv. Mater. Struct. 2019, 26, 1498–1504. [Google Scholar] [CrossRef]
- Alwawi, F.A.; Alkasasbeh, H.T.; Rashad, A.; Idris, R. MHD natural convection of Sodium Alginate Casson nanofluid over a solid sphere. Res. Phys. 2020, 16, 102818. [Google Scholar] [CrossRef]
- Haq, R.U.; Nadeem, S.; Khan, Z.H.; Noor, N.F.M. Convective heat transfer in MHD slip flow over a stretching surface in the presence of carbon nanotubes. Phys. B 2015, 457, 40–47. [Google Scholar] [CrossRef]
- Aman, S.; Khan, I.; Ismail, Z.; Salleh, M.Z.; Al-Mdallal, Q.M. Heat transfer enhancement in free convection flow of CNTs Maxwell nanofluids with four different types of molecular liquids. Sci. Rep. 2017, 7, 2445. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iqbal, Z.; Akbar, N.; Azhar, E.; Maraj, E. MHD rotating transport of CNTS in a vertical channel submerged with Hall current and oscillations. Eur. Phys. J. Plus 2017, 132, 143. [Google Scholar] [CrossRef]
- Molla, M.M.; Paul, S.C.; Hossain, M.A. Natural convection flow from a horizontal circular cylinder with uniform heat flux in presence of heat generation. Appl. Math. Model. 2009, 33, 3226–3236. [Google Scholar] [CrossRef]
- Alkasasbeh, H.T.; Swalmeh, M.Z.; Hussanan, A.; Mamat, M. Numerical Solution of Heat Transfer Flow in Micropolar Nanofluids with Oxide Nanoparticles in Water and Kerosene Oil about a Horizontal Circular Cylinder. IAENG Int. J. Appl. Math. 2019, 49, 1–8. [Google Scholar]
- Zangooee, M.; Hosseinzadeh, K.; Ganji, D. Hydrothermal analysis of MHD nanofluid (TiO2-GO) flow between two radiative stretchable rotating disks using AGM. Case Stud. Eng. 2019, 14, 100460. [Google Scholar] [CrossRef]
- Dero, S.; Mohd Rohni, A.; Saaban, A. Effects of the viscous dissipation and chemical reaction on Casson nanofluid flow over the permeable stretching/shrinking sheet. Heat Transf. 2020, 49, 1736–1755. [Google Scholar] [CrossRef]
- Keller, H.; Bramble, J. Numerical Solutions of Partial Differential Equations; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Jones, E. An asymptotic outer solution applied to the Keller box method. J. Comput. Phys. 1981, 40, 411–429. [Google Scholar] [CrossRef]
- Cebeci, T.; Bradshaw, P. Physical and Computational Aspects of Convective Heat Transfer; Springer Science & Business Media: New York, NY, USA, 2012; p. 487. [Google Scholar]
- Reddy, J.R.; Sugunamma, V.; Sandeep, N. Impact of nonlinear radiation on 3D magnetohydrodynamic flow of methanol and kerosene based ferrofluids with temperature dependent viscosity. J. Mol. Liq. 2017, 236, 93–100. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Khan, A.; Shafie, S.; Tlili, I. Case study of MHD blood flow in a porous medium with CNTS and thermal analysis. Case Stud. Eng. 2018, 12, 374–380. [Google Scholar] [CrossRef]

| Merkin and Pop [5] | Molla et al. [43] | Alkasasbeh et al. [44] | Present | |
|---|---|---|---|---|
| 0 | 0.000 | 0.000 | 0.0000 | 0.0000 |
| 0.2 | 0.274 | 0.272 | 0.2732 | 0.2727 |
| 0.6 | 0.795 | 0.789 | 0.7947 | 0.7924 |
| 1 | 1.241 | 1.226 | 1.2351 | 1.237 |
| 1.6 | 1.671 | 1.637 | 1.6679 | 1.6642 |
| 2 | 1.744 | 1.693 | 1.7394 | 1.7349 |
| 2.6 | 1.451 | 1.370 | 1.4447 | 1.4391 |
| 3 | 0.913 | 0.797 | 0.9046 | 0.8977 |
| π | 0.613 | 0.585 | 0.6068 | 0.5733 |
| Merkin and Pop [5] | Molla et al. [43] | Alkasasbeh et al. [44] | Present | |
|---|---|---|---|---|
| 0 | 1.996 | 1.996 | 1.9964 | 1.9966 |
| 0.2 | 1.999 | 1.999 | 1.9985 | 1.9984 |
| 0.6 | 2.014 | 2.015 | 2.0127 | 2.0127 |
| 1 | 2.043 | 2.047 | 2.0436 | 2.0422 |
| 1.6 | 2.120 | 2.129 | 2.1225 | 2.1207 |
| 2 | 2.202 | 2.216 | 2.2064 | 2.2035 |
| 2.6 | 2.403 | 2.430 | 2.4128 | 2.4069 |
| 3 | 2.660 | 2.716 | 2.6807 | 2.6680 |
| π | 2.824 | 2.841 | 2.8284 | 2.8519 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamarsheh, A.S.; Alwawi, F.A.; Alkasasbeh, H.T.; Rashad, A.M.; Idris, R. Heat Transfer Improvement in MHD Natural Convection Flow of Graphite Oxide/Carbon Nanotubes-Methanol Based Casson Nanofluids Past a Horizontal Circular Cylinder. Processes 2020, 8, 1444. https://doi.org/10.3390/pr8111444
Hamarsheh AS, Alwawi FA, Alkasasbeh HT, Rashad AM, Idris R. Heat Transfer Improvement in MHD Natural Convection Flow of Graphite Oxide/Carbon Nanotubes-Methanol Based Casson Nanofluids Past a Horizontal Circular Cylinder. Processes. 2020; 8(11):1444. https://doi.org/10.3390/pr8111444
Chicago/Turabian StyleHamarsheh, Abdulkareem Saleh, Firas A. Alwawi, Hamzeh T. Alkasasbeh, Ahmed M. Rashad, and Ruwaidiah Idris. 2020. "Heat Transfer Improvement in MHD Natural Convection Flow of Graphite Oxide/Carbon Nanotubes-Methanol Based Casson Nanofluids Past a Horizontal Circular Cylinder" Processes 8, no. 11: 1444. https://doi.org/10.3390/pr8111444
APA StyleHamarsheh, A. S., Alwawi, F. A., Alkasasbeh, H. T., Rashad, A. M., & Idris, R. (2020). Heat Transfer Improvement in MHD Natural Convection Flow of Graphite Oxide/Carbon Nanotubes-Methanol Based Casson Nanofluids Past a Horizontal Circular Cylinder. Processes, 8(11), 1444. https://doi.org/10.3390/pr8111444







