Challenges and Opportunities on Nonlinear State Estimation of Chemical and Biochemical Processes
Abstract
:1. Introduction
2. Nonlinear State Estimation Background and Design
2.1. State of the Art
2.2. Approach for Nonlinear State Estimation Design
3. Challenges on Nonlinear State Estimation
3.1. Covariance Estimation
3.2. Uncertainty Quantification
3.3. Time-Scale Multiplicity
3.4. Bioprocess Monitoring
3.5. Online Implementation
4. Case Study Highlighting Nonlinear Estimation Implementation Challenges
4.1. Background
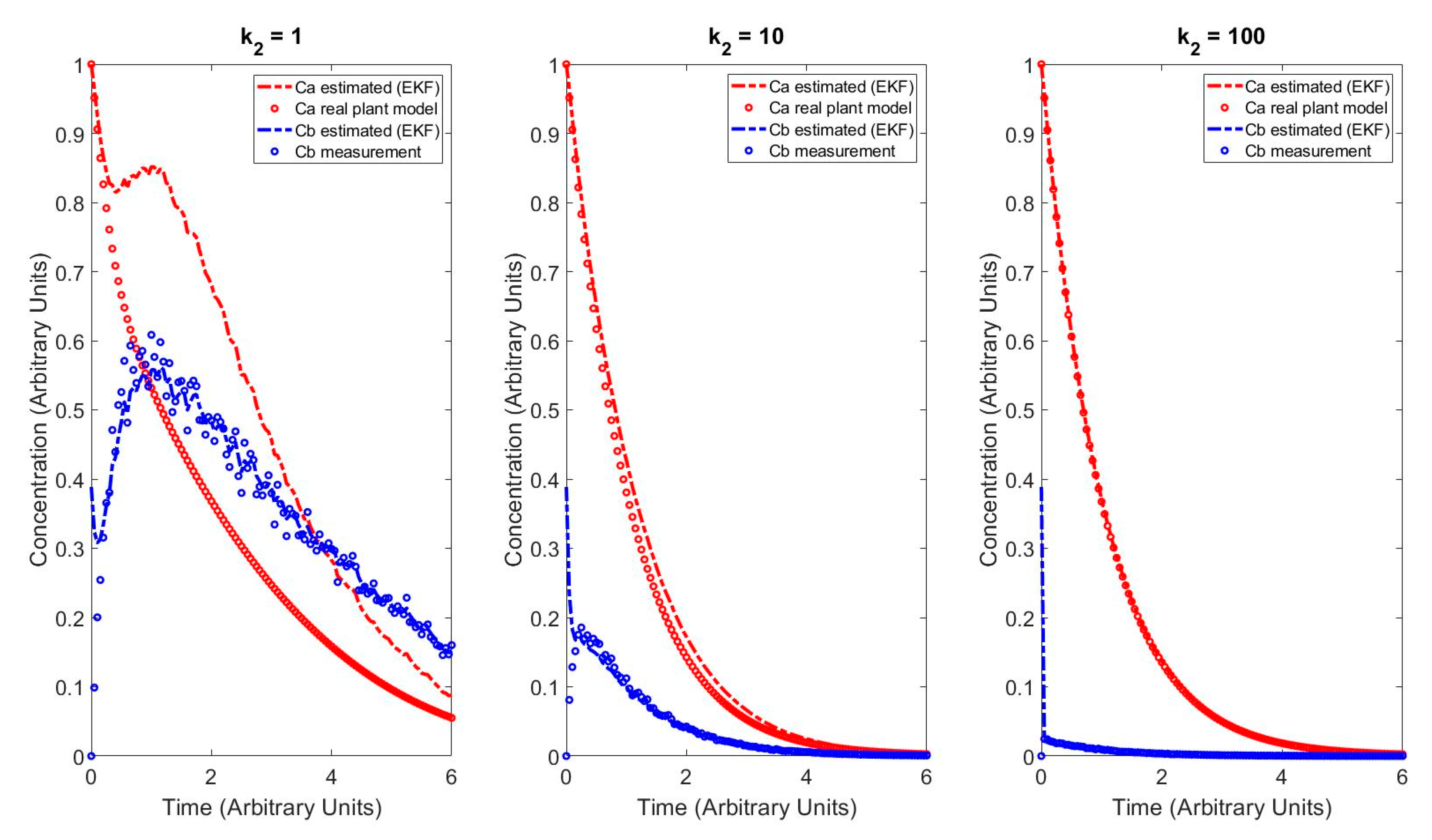
4.2. EKF Results
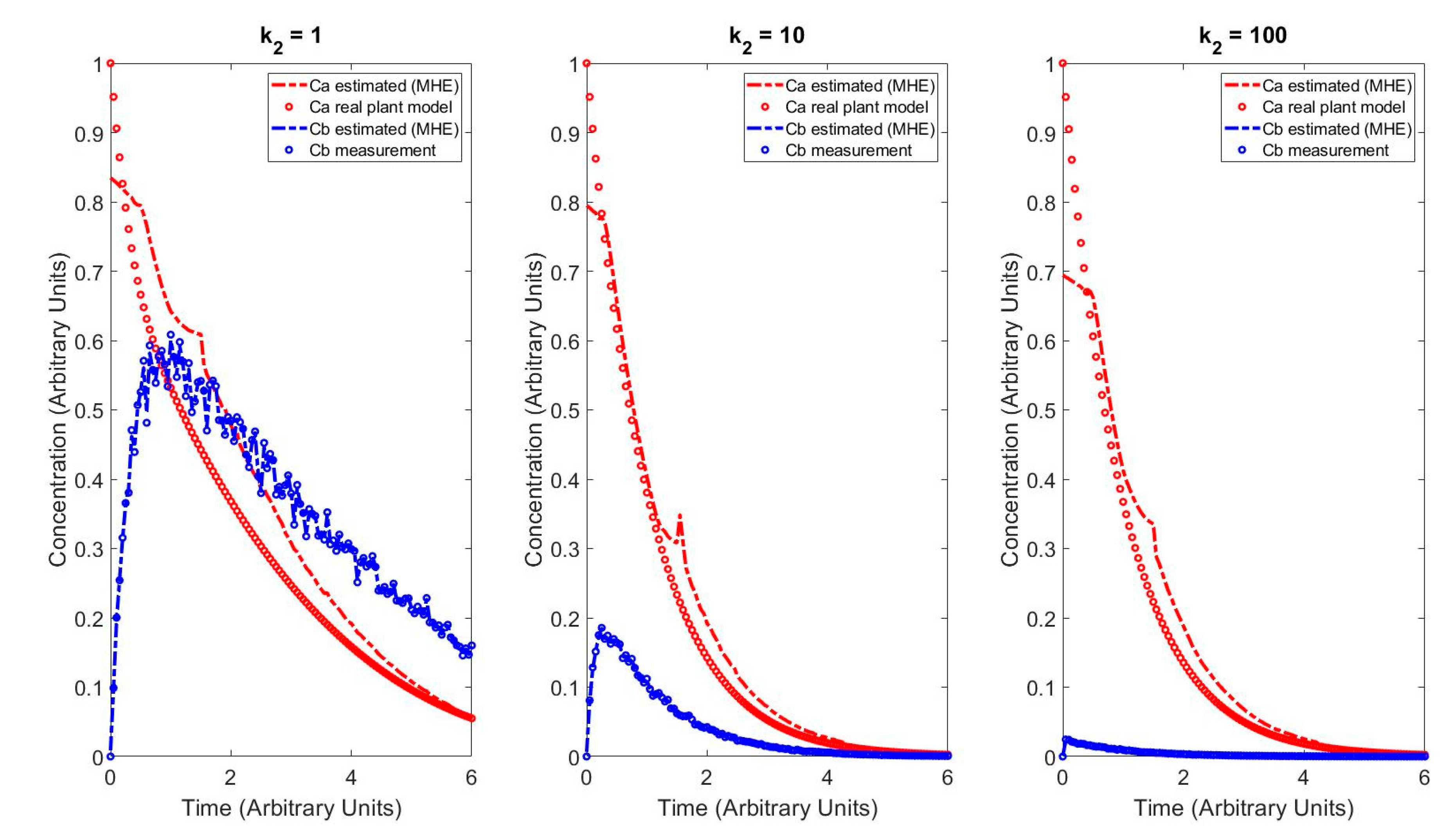
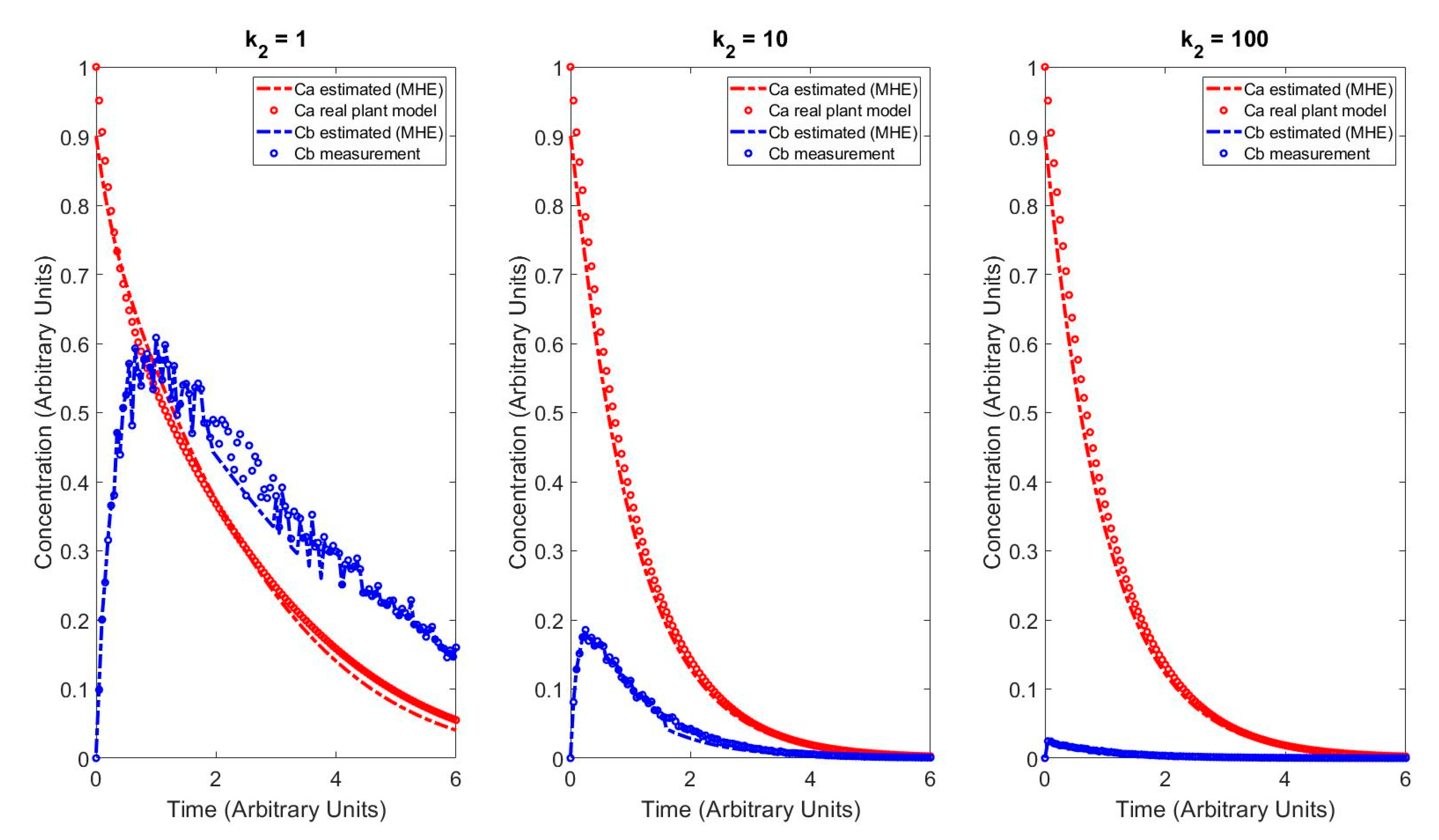
4.3. MHE Results
4.4. Computational Performance Analysis
5. Opportunities and Future Trends
5.1. Development of Fast Optimization Techniques
5.2. Heuristics for MHE Implementation
5.3. Integration of Estimators with Commercial Software
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mohd Ali, J.; Ha Hoang, N.; Hussain, M.A.; Dochain, D. Review and classification of recent observers applied in chemical process systems. Comput. Chem. Eng. 2015, 76, 27–41. [Google Scholar] [CrossRef] [Green Version]
- Seborg, D.E.; Edgar, T.F.; Mellichamp, D.A.; Doyle, F.J. Process Dynamics and Control, 4th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Mesbah, A.; Huesman, A.E.M.; Kramer, H.J.M.; Van den Hof, P.M.J. A comparison of nonlinear observers for output feedback model-based control of seeded batch crystallization processes. J. Process Control 2011, 21, 652–666. [Google Scholar] [CrossRef]
- Lima, F.V.; Rajamani, M.R.; Soderstrom, T.A.; Rawlings, J.B. Covariance and State Estimation of Weakly Observable Systems: Application to Polymerization Processes. IEEE Trans. Control Syst. Technol. 2013, 21, 1249–1257. [Google Scholar] [CrossRef]
- Rincón, F.D.; Le Roux, G.A.C.; Lima, F.V. The Autocovariance Least-Squares Method for Batch Processes: Application to Experimental Chemical Systems. Ind. Eng. Chem. Res. 2014, 53, 18005–18015. [Google Scholar] [CrossRef]
- Rincón, F.D.; Esposito, M.; de Araújo, P.H.H.; Lima, F.V.; Le Roux, G.A.C. Robust Calorimetric Estimation of Semi-Continuous and Batch Emulsion Polymerization Systems with Covariance Estimation. Macromol. React. Eng. 2014, 8, 456–466. [Google Scholar] [CrossRef]
- Yin, X.; Liu, J. Distributed moving horizon state estimation of two-time-scale nonlinear systems. Automatica 2017, 79, 152–161. [Google Scholar] [CrossRef]
- López-Negrete, R.; Biegler, L. A Moving Horizon Estimator for processes with multi-rate measurements: A Nonlinear Programming sensitivity approach. J. Process Control 2012, 65, 4548–4556. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Mayne, D.Q.; Diehl, M.M. State Estimation. In Model Predictive Control: Theory, Computation, and Design; Nob Hill Publishing: Santa Barbara, CA, USA, 2019; pp. 265–369. [Google Scholar]
- Varshney, D.; Bhushan, M.; Patwardhan, S.C. Robust State Estimation and Parameter Estimation for Linear and Nonlinear Direct Feed-through Systems with Correlated Disturbances. Ind. Eng. Chem. Res. 2019, 58, 11532–11552. [Google Scholar] [CrossRef]
- Raïssi, T.; Ramdani, N.; Candau, Y. Bounded error moving horizon state estimator for non-linear continuous-time systems: Application to a bioprocess system. J. Process Control 2005, 15, 537–545. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, L.; Yu, T. On-line Estimation in Fed-batch Fermentation Process Using State Space Model and Unscented Kalman Filter. Chin. J. Chem. Eng. 2010, 18, 258–264. [Google Scholar] [CrossRef]
- Campani, G.; Ribeiro, M.P.A.; Zangirolami, T.C.; Lima, F.V. A hierarchical state estimation and control framework for monitoring and dissolved oxygen regulation in bioprocesses. Bioprocess Biosyst. Eng. 2019, 42, 1467–1481. [Google Scholar] [CrossRef] [PubMed]
- Furlong, V.B.; Corrêa, L.J.; Lima, F.V.; Giordano, R.C.; Ribeiro, M.P.A. Estimation of Biomass Enzymatic Hydrolysis State in Stirred Tank Reactor through Moving Horizon Algorithms with Fixed and Dynamic Fuzzy Weights. Processes 2020, 8, 407. [Google Scholar] [CrossRef] [Green Version]
- Lima, F.V.; Rawlings, J.B. Nonlinear stochastic modeling to improve state estimation in process monitoring and control. AIChE J. 2011, 57, 996–1007. [Google Scholar] [CrossRef]
- Afshari, H.H.; Gadsden, S.A.; Habibi, S. Gaussian filters for parameter and state estimation: A general review of theory and recent trends. Signal Process. 2017, 135, 218–238. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Bakshi, B.R. Particle filtering and moving horizon estimation. Comput. Chem. Eng. 2006, 30, 1529–1541. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Ji, L. Optimization-based state estimation: Current status and some new results. J. Process Control 2012, 22, 1439–1444. [Google Scholar] [CrossRef]
- Patwardhan, S.C.; Narasimhan, S.; Jagadeesan, P.; Gopaluni, B.; Shah, S.L. Nonlinear Bayesian state estimation: A review of recent developments. Control Eng. Pract. 2012, 20, 933–953. [Google Scholar] [CrossRef]
- Li, T.; Su, J.; Liu, W.; Corchado, J.M. Approximate Gaussian conjugacy: Parametric recursive filtering under nonlinearity, multimodality, uncertainty, and constraint, and beyond. Front. Inf. Technol. Electron. Eng. 2017, 18, 1913–1939. [Google Scholar] [CrossRef]
- Bayes, T. LII. An essay towards solving a problem in the doctrine of chances. By the late Rev. Mr. Bayes, F.R.S. communicated by Mr. Price, in a letter to John Canton, A.M.F.R.S. Philos. Trans. R. Soc. Lond. 1763, 53, 370–418. [Google Scholar]
- Gauss, C.F. Theory of the Motion of the Heavenly Bodies: Moving about the Sun in Conic Sections: A Translation of Theoria Motus; Dover: Mineola, NY, USA, 2004. [Google Scholar]
- Fisher, R.A. On an absolute criterion for fitting frequency curves. Messenger Math. 1912, 41, 155–160. [Google Scholar]
- Kolmogorov, A.N. Interpolation and Extrapolation of Stationary Sequences. Ser. Math. 1941, 5, 3–14. [Google Scholar]
- Wiener, N. Extrapolation, Interpolation, and Smoothing of Stationary Time Series with Engineering Application; MIT Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Julier, S.J.; Uhlmann, J.K. Unscented Filtering and Nonlinear Estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef] [Green Version]
- Kolås, S.; Foss, B.A.; Schei, T.S. Constrained nonlinear state estimation based on the UKF approach. Comput. Chem. Eng. 2009, 33, 1386–1401. [Google Scholar] [CrossRef]
- Prakash, J.; Patwardhan, S.; Shah, S. Constrained Nonlinear State Estimation Using Ensemble Kalman Filters. Ind. Eng. Chem. Res. 2010, 49, 2242–2253. [Google Scholar] [CrossRef]
- Ungarala, S.; Dolence, E.; Li, K. Constrained extended Kalman filter for nonlinear state estimation. IFAC Proc. Vol. 2007, 40, 63–68. [Google Scholar] [CrossRef]
- Rao, C.V.; Rawlings, J.B. Constrained process monitoring: Moving-horizon approach. AIChE J. 2002, 48, 97–109. [Google Scholar] [CrossRef]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Morris, J.; Martin, E. Particle filters for state and parameter estimation in batch processes. J. Process Control 2005, 15, 665–673. [Google Scholar] [CrossRef] [Green Version]
- Imtiaz, S.A.; Roy, K.; Huang, B.; Shah, S.L.; Jampana, P. Estimation of States of Nonlinear Systems using a Particle Filter. In Proceedings of the 2006 IEEE International Conference on Industrial Technology, Mumbai, India, 15–17 December 2006; pp. 2432–2437. [Google Scholar]
- Shenoy, A.V.; Prakash, J.; Prasad, V.; Shah, S.L.; McAuley, K.B. Practical issues in state estimation using particle filters: Case studies with polymer reactors. J. Process Control 2013, 23, 120–131. [Google Scholar] [CrossRef]
- Rajamani, M.R.; Rawlings, J.B. Improved State Estimation using a Combination of Moving Horizon Estimator and Particle Filters. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 4443–4444. [Google Scholar]
- Markana, A.; Padhiyar, N.; Moudgalya, K. Multi-criterion control of a bioprocess in fed-batch reactor using EKF based economic model predictive control. Chem. Eng. Res. Des. 2018, 136, 282–294. [Google Scholar] [CrossRef]
- Vachhani, P.; Narasimhan, S.; Rengaswamy, R. Robust and reliable estimation via Unscented Recursive Nonlinear Dynamic Data Reconciliation. J. Process Control 2006, 16, 1075–1086. [Google Scholar] [CrossRef]
- Lang, L.; Chen, W.; Bakshi, B.R.; Goel, P.K.; Ungarala, S. Bayesian estimation via sequential Monte Carlo sampling—Constrained dynamic systems. Automatica 2007, 43, 1615–1622. [Google Scholar] [CrossRef] [Green Version]
- Chitralekha, S.B.; Prakash, J.; Raghavan, H.; Gopaluni, R.B.; Shah, S.L. A comparison of simultaneous state and parameter estimation schemes for a continuous fermentor reactor. J. Process Control 2010, 20, 934–943. [Google Scholar] [CrossRef]
- Abdollahi, J.; Dubljevic, S. Lipid production optimization and optimal control of heterotrophic microalgae fed-batch bioreactor. Chem. Eng. Sci. 2012, 84, 619–627. [Google Scholar] [CrossRef]
- Ellis, M.; Zhang, J.; Liu, J.; Christofides, P.D. Robust moving horizon estimation based output feedback economic model predictive control. Syst. Control Lett. 2014, 68, 101–109. [Google Scholar] [CrossRef]
- Bastin, D.; Dochain, G. State and Paramater Estimation with Known Yield Coefficients. In On-line Estimation and Adaptive Control of Bioreactors; Elsevier: Amsterdam, The Netherlands, 1990; pp. 101–200. [Google Scholar]
- Dochain, D. State and parameter estimation in chemical and biochemical processes: A tutorial. J. Process Control 2003, 13, 801–818. [Google Scholar] [CrossRef]
- Méndez-Acosta, H.O.; Palacios-Ruiz, B.; Alcaraz-González, V.; Steyer, J.-P.; González-Álvarez, V.; Latrille, E. Robust Control of Volatile Fatty Acids in Anaerobic Digestion Processes. Ind. Eng. Chem. Res. 2008, 47, 7715–7720. [Google Scholar] [CrossRef]
- Dochain, D. State observers for tubular reactors with unknown kinetics. J. Process Control 2000, 10, 259–268. [Google Scholar] [CrossRef]
- Dochain, D.; Couenne, F.; Jallut, C. Enthalpy based modelling and design of asymptotic observers for chemical reactors. Int. J. Control 2009, 82, 1389–1403. [Google Scholar] [CrossRef]
- Hadj-Sadok, M.Z.; Gouzé, J.L. Estimation of uncertain models of activated sludge processes with interval observers. J. Process Control 2001, 11, 299–310. [Google Scholar] [CrossRef]
- Aziz, N.; Hussain, M.A.; Mujtaba, I.M. Performance of different types of controllers in tracking optimal temperature profiles in batch reactors. Comput. Chem. Eng. 2000, 24, 1069–1075. [Google Scholar] [CrossRef]
- Kadlec, P.; Gabrys, B.; Strandt, S. Data-driven Soft Sensors in the process industry. Comput. Chem. Eng. 2009, 33, 795–814. [Google Scholar] [CrossRef] [Green Version]
- Horta, A.C.L.; da Silva, A.J.; Sargo, C.R.; Gonçalves, V.M.; Zangirolami, T.C.; de Campos Giordano, R. Robust artificial intelligence tool for automatic start-up of the supplementary medium feeding in recombinant E. coli cultivations. Bioprocess Biosyst. Eng. 2011, 34, 891–901. [Google Scholar] [CrossRef]
- Furlong, V.B.; Corrêa, L.J.; Giordano, R.C.; Ribeiro, M.P.A. Fuzzy-Enhanced Modeling of Lignocellulosic Biomass Enzymatic Saccharification. Energies 2019, 12, 2110. [Google Scholar] [CrossRef] [Green Version]
- Porru, G.; Aragonese, C.; Baratti, R.; Servida, A. Monitoring of a CO oxidation reactor through a grey model-based EKF observer. Chem. Eng. Sci. 2000, 55, 331–338. [Google Scholar] [CrossRef] [Green Version]
- Prakash, J.; Senthil, R. Design of observer based nonlinear model predictive controller for a continuous stirred tank reactor. J. Process Control 2008, 18, 504–514. [Google Scholar] [CrossRef]
- Vafamand, N.; Arefi, M.M.; Khayatian, A. Nonlinear system identification based on Takagi-Sugeno fuzzy modeling and unscented Kalman filter. ISA Trans. 2018, 74, 134–143. [Google Scholar] [CrossRef]
- Fang, H.; de Callafon, R.A.; Cortés, J. Simultaneous input and state estimation for nonlinear systems with applications to flow field estimation. Automatica 2013, 49, 2805–2812. [Google Scholar] [CrossRef]
- Tulsyan, A.; Huang, B.; Bhushan Gopaluni, R.; Fraser Forbes, J. On simultaneous on-line state and parameter estimation in non-linear state-space models. J. Process Control 2013, 23, 516–526. [Google Scholar] [CrossRef]
- Nelles, O. Nonlinear System Identification; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Ogata, K. Control Systems Analysis in State Space. In Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Muske, K.R.; Edgar, T.F. Nonlinear State Estimation. In Nonlinear Process Control; Henson, M.A., Seborg, D.E., Eds.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Reinschke, K. Multivariable Control a Graph-Theoretic Approach, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Sueur, C.; Dauphin-Tanguy, G. Bond-graph approach for structural analysis of MIMO linear systems. J. Frankl. Inst. 1991, 1, 55–70. [Google Scholar] [CrossRef]
- Spivey, B.J.; Hedengren, J.D.; Edgar, T.F. Constrained Nonlinear Estimation for Industrial Process Fouling. Ind. Eng. Chem. Res. 2010, 49, 7824–7831. [Google Scholar] [CrossRef]
- Heffes, H. The Effect of Erroneous Models on the Kalman Filter Response. IEEE Trans. Autom. Control 1966, 11, 541–543. [Google Scholar] [CrossRef]
- Nishimura, T. Error Bounds of Continuous Kalman Filters and the Application to Orbit Determination Problems. IEEE Trans. Autom. Control 1967, 12, 268–275. [Google Scholar] [CrossRef]
- Duník, J.; Kost, O.; Straka, O.; Blasch, E. State and Measurement Noise in Positioning and Tracking: Covariance Matrices Estimation and Gaussian Assessment. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018. [Google Scholar]
- Odelson, B.; Rajamani, M.; Rawlings, J. A New Autocovariance Least-Squares Method for Estimating Noise Covariances. Available online: https://sites.engineering.ucsb.edu/~jbraw/jbrweb-archives/tech-reports/twmcc-2003-04.pdf (accessed on 14 November 2020).
- Rajamani, M.; Rawlings, J. Estimation of the disturbance structure from data using semidefinite programming and optimal weighting. Automatica 2009, 45, 142–148. [Google Scholar] [CrossRef]
- Duník, J.; Kost, O.; Straka, O.; Blasch, E. Covariance Estimation and Gaussinity Assessment for State and Measurement Noise. J. Guid. Control Dyn. 2020, 43, 132–139. [Google Scholar] [CrossRef] [Green Version]
- Duník, J.; Straka, O.; Kost, O.; Havlík, J. Noise covariance matrices in state-space models: A survey and comparison of estimation methods—Part 1. Int. J. Adapt. Control Signal Process. 2017, 31, 1505–1543. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Gharamti, M.E.; Hoteit, I. Complex step-based low-rank extended Kalman filtering for state-parameter estimation in subsurface transport models. J. Hydrol. 2014, 509, 588–600. [Google Scholar] [CrossRef]
- Lü, H.; Yu, Z.; Drake, S.; Hao, Z.; Sudicky, E. Dual state-parameter estimation of root zone soil moisture by optimal parameter estimation and extended Kalman filter data assimilation. Adv. Water Resour. 2011, 34, 395–406. [Google Scholar] [CrossRef]
- Van der Merwe, R.; Wan, E.A. The square-root unscented Kalman filter for state and parameter-estimation. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001. [Google Scholar]
- Moradkhani, H.; Sorooshian, S.; Gupta, H.V.; Houser, P.R. Dual state–parameter estimation of hydrological models using ensemble Kalman filter. Adv. Water Resour. 2005, 28, 135–147. [Google Scholar] [CrossRef] [Green Version]
- Varshney, D.; Bhushan, M.; Patwardhan, S.C. State and parameter estimation using extended Kitanidis Kalman filter. J. Process Control 2019, 76, 98–111. [Google Scholar] [CrossRef]
- Kühl, P.; Diehl, M.; Kraus, T.; Schlöder, J.P.; Bock, H.G. A real-time algorithm for moving horizon state and parameter estimation. Comput. Chem. Eng. 2011, 35, 71–83. [Google Scholar] [CrossRef]
- Valluru, J.; Lakhmani, P.; Patwardhan, S.C.; Biegler, L.T. Development of moving window state and parameter estimators under maximum likelihood and Bayesian frameworks. J. Process Control 2017, 60, 48–67. [Google Scholar] [CrossRef]
- Wiener, N. The homogeneous chaos. Am. J. Math. 1938, 60, 897–936. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener–Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Bavdekar, V.; Mesbah, A. A Polynomial Chaos-Based Nonlinear Bayesian Approach for Estimating State and Parameter Probability Distribution Functions. In Proceedings of the 2016 American Control Conference, Boston, MA, USA, 6–8 July 2016; pp. 2047–2052. [Google Scholar]
- Dutta, P.; Bhattacharya, R. Nonlinear Estimation of Hypersonic State Trajectories in Bayesian Framework with Polynomial Chaos. J. Guid. Control Dyn. 2010, 33, 1765–1778. [Google Scholar] [CrossRef]
- Li, J.; Xiu, D. A generalized polynomial chaos based ensemble Kalman filter with high accuracy. J. Comput. Phys. 2009, 228, 5454–5469. [Google Scholar] [CrossRef]
- Blanchard, E.; Sandu, A.; Sandu, C. A Polynomial Chaos-Based Kalman Filter Approach for Parameter Estimation of Mechanical Systems. J. Dyn. Syst. Meas. Control 2010, 132, 061404. [Google Scholar] [CrossRef]
- Alspach, D.; Sorenson, H. Nonlinear Bayesian estimation using Gaussian sum approximations. IEEE Trans. Autom. Control 1972, 17, 439–448. [Google Scholar] [CrossRef]
- Ito, K.; Xiong, K. Gaussian filters for nonlinear filtering problems. IEEE Trans. Autom. Control 2000, 45, 910–927. [Google Scholar] [CrossRef] [Green Version]
- Terejanu, G.; Singla, P.; Singh, T.; Scott, P.D. Uncertainty Propagation for Nonlinear Dynamic Systems Using Gaussian Mixture Models. J. Guid. Control Dyn. 2008, 31, 1623–1633. [Google Scholar] [CrossRef]
- Gauvain, J.; Lee, C. Maximum a posteriori estimation for multivariate Gaussian mixture observations of Markov chains. IEEE Trans. Speech Audio Process. 1994, 2, 291–298. [Google Scholar] [CrossRef]
- Risken, H.; Frank, T. The Fokker-Planck Equation, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Muscolino, G.; Ricciardi, G.; Vasta, M. Stationary and non-stationary probability density function for non-linear oscillators. Int. J. Non-Linear Mech. 1997, 32, 1051–1064. [Google Scholar] [CrossRef]
- Paola, M.; Sofi, A. Approximate solution of the Fokker–Planck–Kolmogorov equation. Probabilistic Eng. Mech. 2002, 17, 369–384. [Google Scholar] [CrossRef]
- Kumar, M.; Singla, P.; Chakravorty, S.; Junkins, J. The Partition of Unity Finite Element Approach to the Stationary Fokker-Planck Equation. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar] [CrossRef] [Green Version]
- Becerra, V.; Roberts, P.; Griffiths, G. Dynamic data reconciliation for a class of nonlinear differential-algebraic equation models using the extended Kalman filter. IFAC Proc. Vol. 1999, 32, 5961–5966. [Google Scholar] [CrossRef]
- Becerra, V.; Roberts, P.; Griffiths, G. Applying the extended Kalman filter to systems described by nonlinear differential-algebraic equations. Control Eng. Pract. 2001, 9, 267–281. [Google Scholar] [CrossRef]
- Mandela, R.; Rengaswamy, R.; Narasimhan, S. Nonlinear State Estimation of Differential Equations. IFAC Proc. Vol. 2009, 42, 792–797. [Google Scholar] [CrossRef]
- Mandela, R.; Rengaswamy, R.; Narasimhan, S.; Sridhar, L. Recursive state estimation techniques for nonlinear differential algebraic systems. Chem. Eng. Sci. 2010, 65, 4548–4556. [Google Scholar] [CrossRef]
- Kraus, T.; Kühl, P.; Wirsching, L.; Bock, H.; Diehl, M. A Moving Horizon State Estimation algorithm applied to the Tennessee Eastman Benchmark Process. In Proceedings of the 2006 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, Heidelberg, Germany, 3–6 September 2006. [Google Scholar]
- Shuler, M.L.; Kargi, F.; DeLisa, M.P. Bioprocess Engineering: Basic Concepts, 3rd ed.; Prentice Hall: Boston, MA, USA, 2017. [Google Scholar]
- FDA. Guidance for Industry PAT—A Framework for Innovative Pharmaceutical Development, Manufacturing, and Quality Assurance; Food and Drug Administration: Rockville, MD, USA, 2004; p. 16.
- Simon, L.L.; Pataki, H.; Marosi, G.; Meemken, F.; Hungerbühler, K.; Baiker, A.; Tummala, S.; Glennon, B.; Kuentz, M.; Steele, G.; et al. Assessment of Recent Process Analytical Technology (PAT) Trends: A Multiauthor Review. Org. Process Res. Dev. 2015, 19, 3–62. [Google Scholar] [CrossRef]
- Zhao, L.; Fu, H.-Y.; Zhou, W.; Hu, W.-S. Advances in process monitoring tools for cell culture bioprocesses. Eng. Life Sci. 2015, 15, 459–468. [Google Scholar] [CrossRef]
- Pörtner, R.; Platas Barradas, O.; Frahm, B.; Hass, V.C. Advanced Process and Control Strategies for Bioreactors. In Current Developments in Biotechnology and Bioengineering; Elsevier: Amsterdam, The Netherlands, 2017; pp. 463–493. [Google Scholar]
- Komives, C.; Parker, R.S. Bioreactor state estimation and control. Curr. Opin. Biotechnol. 2003, 14, 468–474. [Google Scholar] [CrossRef] [PubMed]
- Venkateswarlu, C. Advances in monitoring and state estimation of bioreactors. J. Sci. Ind. Res. 2004, 63, 491–498. [Google Scholar]
- Cuthbertson, A.B.; Rodman, A.D.; Diab, S.; Gerogiorgis, D.I. Dynamic Modelling and Optimisation of the Batch Enzymatic Synthesis of Amoxicillin. Processes 2019, 7, 318. [Google Scholar] [CrossRef] [Green Version]
- Jabarivelisdeh, B.; Carius, L.; Findeisen, R.; Waldherr, S. Adaptive predictive control of bioprocesses with constraint-based modeling and estimation. Comput. Chem. Eng. 2020, 135, 106744. [Google Scholar] [CrossRef]
- Valdes-Gonzalez, H.; Flaus, J.-M. State estimation in a bioprocess described by a hybrid model. In Proceedings of the 2001 IEEE International Symposium on Intelligent Control (ISIC ’01) (Cat. No.01CH37206), Mexico City, Mexico, 5–7 September 2001; pp. 132–137. [Google Scholar]
- Morabito, B.; Kienle, A.; Findeisen, R.; Carius, L. Multi-mode Model Predictive Control and Estimation for Uncertain Biotechnological Processes. IFAC-PapersOnLine 2019, 52, 709–714. [Google Scholar] [CrossRef]
- Hulhoven, X.; Wouwer, A.V.; Bogaerts, P. Hybrid extended Luenberger-asymptotic observer for bioprocess state estimation. Chem. Eng. Sci. 2006, 61, 7151–7160. [Google Scholar] [CrossRef]
- Bogaerts, P.; Hanus, R. On-line state estimation of bioprocesses with full horizon observers. Math. Comput. Simul. 2001, 56, 425–441. [Google Scholar] [CrossRef]
- Simutis, R.; Lübbert, A. Bioreactor control improves bioprocess performance. Biotechnol. J. 2015, 10, 1115–1130. [Google Scholar] [CrossRef]
- Murtuza Baker, S.; Poskar, C.H.; Schreiber, F.; Junker, B.H. An improved constraint filtering technique for inferring hidden states and parameters of a biological model. Bioinformatics 2013, 29, 1052–1059. [Google Scholar] [CrossRef] [Green Version]
- Hyland, D.; Bernstein, D. The optimal projection equations for model reduction and the relationships among the methods of Wilson, Skelton, and Moore. IEEE Trans. Autom. Control 1985, 30, 1201–1211. [Google Scholar] [CrossRef] [Green Version]
- Bernstein, D.S.; Haddad, W.M. Steady-state Kalman filtering with an H∞ error bound. Syst. Control Lett. 1989, 12, 847–852. [Google Scholar] [CrossRef]
- Xu, S.; Chen, T. Reduced-order H/sub/spl infin//filtering for stochastic systems. IEEE Trans. Signal Process. 2002, 50, 2998–3007. [Google Scholar]
- Doucet, A.; Gordon, N.J.; Krishnamurthy, V. Particle filters for state estimation of jump Markov linear systems. IEEE Trans. Signal Process. 2001, 49, 613–624. [Google Scholar] [CrossRef]
- Tong, G.; Fang, Z.; Xu, X. A Particle Swarm Optimized Particle Filter for Nonlinear System State Estimation. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006. [Google Scholar]
- Thierry, D.; Nicholson, B.; Biegler, L. A General Framework for Sensitivity-Based Optimal Control and State Estimation. Comput. Aided Chem. Eng. 2018, 44, 787–792. [Google Scholar]
- Zavala, V.M.; Biegler, L.T. Nonlinear programming strategies for state estimation and model predictive control. In Nonlinear Model Predictive Control, 1st ed.; Magni, L., Raimondo, D.M., Allogöwer, F., Eds.; Springer: Berlin, Germany, 2009; Volume 384, pp. 419–432. [Google Scholar]
- Fatehi, A.; Huang, B. Kalman filtering approach to multi-rate information fusion in the presence of irregular sampling rate and variable measurement delay. J. Process Control 2017, 53, 15–25. [Google Scholar] [CrossRef]
- Gopalakrishnan, A.; Kaisare, N.; Narasimhan, S. Incorporating delayed and infrequent measurements in Extended Kalman Filter based nonlinear state estimation. J. Process Control 2011, 21, 119–129. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Emzir, M.F. State estimation with asynchronous multi-rate multi-smart sensors. Inf. Sci. 2012, 196, 15–27. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, R.; Wang, J.; Yu, T.; Su, A. Nonlinear state estimation with delayed measurements using data fusion technique and cubature Kalman filter for chemical processes. Chem. Eng. Res. Des. 2019, 141, 502–515. [Google Scholar] [CrossRef]
- Gu, Y.; Chou, Y.; Liu, J.; Ji, Y. Moving horizon estimation for multirate systems with time-varying time-delays. J. Frankl. Inst. 2019, 356, 2325–2345. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Kerrigan, E.C.; Wyk, E.J.; Falugi, P. Tube-based robust nonlinear model predictive control. Int. J. Robust Nonlinear Control 2011, 21, 1341–1353. [Google Scholar] [CrossRef]
- Lorenzen, M.; Allgöwer, F.; Cannon, M. Adaptive Model Predictive Control with Robust Constraint Satisfaction. IFAC-PapersOnLine 2017, 50, 3313–3318. [Google Scholar] [CrossRef]
- Paulson, J.; Mesbah, A. An efficient method for stochastic optimal control with joint chance constraints for nonlinear systems. Int. J. Robust Nonlinear Control 2017, 29, 5017–5037. [Google Scholar] [CrossRef]
- Pantea, C.; Gupta, A.; Rawlings, J.; Craciun, G. The QSSA in Chemical Kinetics: As Taught and as Practiced. In Discrete and Topological Models in Molecular Biology; Natural Computing Series; Springer: Berlin/Heidelberg, Germany, 2013; pp. 419–442. [Google Scholar]
- He, X.; Lima, F.V. A modified SQP-based model predictive control algorithm: Application to supercritical coal-fired power plant cycling. Ind. Eng. Chem. Res. 2020, 59, 15671–15681. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Andersson, J.; Gills, J.; Horn, G.; Rawlings, J.; Diehl, M. CasADi: A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2018, 11, 1–36. [Google Scholar] [CrossRef]
- Zhou, Y.; Tan, Y. GPU-based Parallel Particle Sawm Optimization. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 1493–1500. [Google Scholar]
- Kim, R.; Lima, F.V. A Tchebycheff-based multi-objective combined with a PSO-SQP dynamic real-time optimization framework for cycling energy systems. Chem. Eng. Res. Des. 2020, 156, 180–194. [Google Scholar] [CrossRef]
- Turton, R.; Shaeiwitz, J.; Bhattacharyya, D.; Whiting, W. Utilizin Experience-Based Principles to Confirm the Suitability of a Process Design. In Analysis, Synthesis and Design of Chemical Processes, 5th ed.; Pearson: Boston, MA, USA, 2018; pp. 347–368. [Google Scholar]
- Golightly, R. The Aspen DMC3TM Difference. Available online: https://www.aspentech.com/-/media/AspenTech/Home/Resources/White%20Papers/PDFs/11-8885-WP-DMC3%20Difference (accessed on 13 November 2020).
- Froisy, J. Model predictive control—Building a bridge between theory and practice. Comput. Chem. Eng. 2006, 30, 1426–1435. [Google Scholar] [CrossRef]
- Amrit, R.; Canney, W.; Carrette, P.; Linn, R.; Martinez, A.; Singh, A.; Skrovanek, T.; Valiquette, J.; Williamson, J.; Zhou, J.; et al. Platform for Advanced Control and Estimation (PACE): Shell’s and Yokogawa’s Next Generation Advanced Process Control Technology. IFAC-PapersOnLine. 2015, 48, 1–5. [Google Scholar] [CrossRef]
- Mayne, D.; Rawlings, J.; Rao, C.; Scokaert, P. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Latif, H.; Shao, G.; Starly, B. Integrating a Dynamic Simulator and Advanced Process Control using the OPC-UA Standard. Procedia Manuf. 2019, 34, 813–819. [Google Scholar] [CrossRef]


| k2 = 1 | k2 = 10 | k2 = 100 | |
|---|---|---|---|
| EKF, Linear Forecasting | 0.0440 | 0.00204 | 0.00125 |
| EKF, Nonlinear Forecasting | 0.00256 | 0.00161 | 0.00125 |
| k2 = 1 | k2 = 10 | k2 = 100 | |
|---|---|---|---|
| MHE, Linear Forecasting | 0.00701 | 0.00277 | 0.00408 |
| MHE, Nonlinear Forecasting | 0.00125 | 0.000732 | 0.000839 |
| Trial | k2 = 1 | k2 = 10 | k2 = 100 | Average Time Per Step |
|---|---|---|---|---|
| Linear Forecasting | 0.0181 s | 0.00816 s | 0.00572 s | 8.88∙10−5 s |
| Nonlinear Forecasting | 0.0642 s | 0.0676 s | 0.0778 s | 5.82∙10−4 s |
| Trial | k2 = 1 | k2 = 10 | k2 = 100 | Average Time Per Step |
|---|---|---|---|---|
| n = 30, linear forecasting, fmincon | 610 s | 400 s | 399 s | 5.22 s |
| n = 30, nonlinear forecasting, fmincon | 3966 s | 4499 s | 4027 s | 46.2 s |
| n = 30, nonlinear forecasting, modSQP | 458 s | 172 s | 159 s | 2.92 s |
| n = 20, nonlinear forecasting, modSQP | 193 s | 80.8 s | 67.7 s | 1.26 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexander, R.; Campani, G.; Dinh, S.; Lima, F.V. Challenges and Opportunities on Nonlinear State Estimation of Chemical and Biochemical Processes. Processes 2020, 8, 1462. https://doi.org/10.3390/pr8111462
Alexander R, Campani G, Dinh S, Lima FV. Challenges and Opportunities on Nonlinear State Estimation of Chemical and Biochemical Processes. Processes. 2020; 8(11):1462. https://doi.org/10.3390/pr8111462
Chicago/Turabian StyleAlexander, Ronald, Gilson Campani, San Dinh, and Fernando V. Lima. 2020. "Challenges and Opportunities on Nonlinear State Estimation of Chemical and Biochemical Processes" Processes 8, no. 11: 1462. https://doi.org/10.3390/pr8111462






