Theoretical Evaluation of the Melting Efficiency for the Single-Screw Micro-Extrusion Process: The Case of 3D Printing of ABS
Abstract
:1. Introduction
2. Modeling Details
2.1. Earlier Model Developments and Current Modeling Strategy
2.1.1. General Principles
2.1.2. Implementation for a Micro-Extruder with ABS Polymer
3. Results
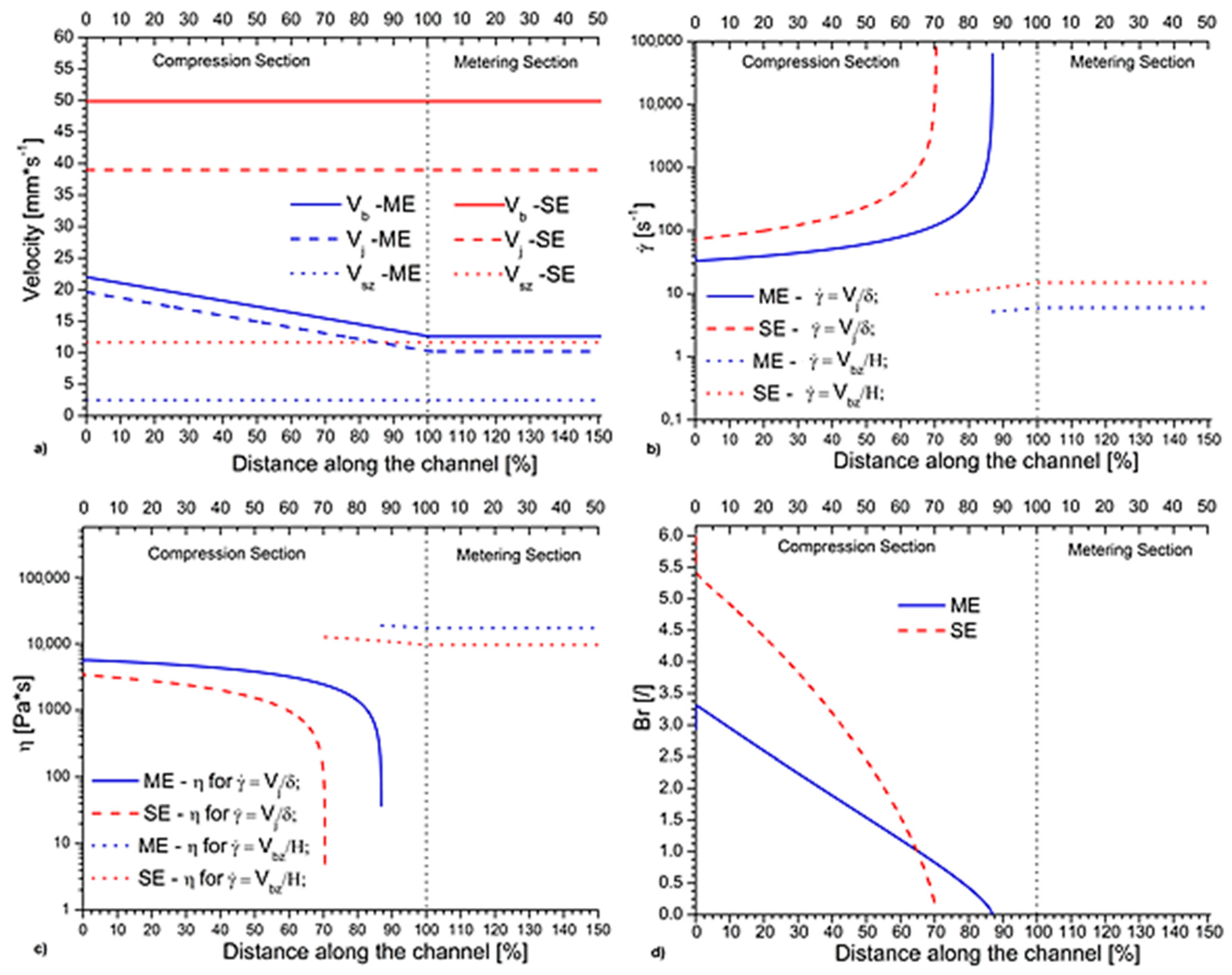
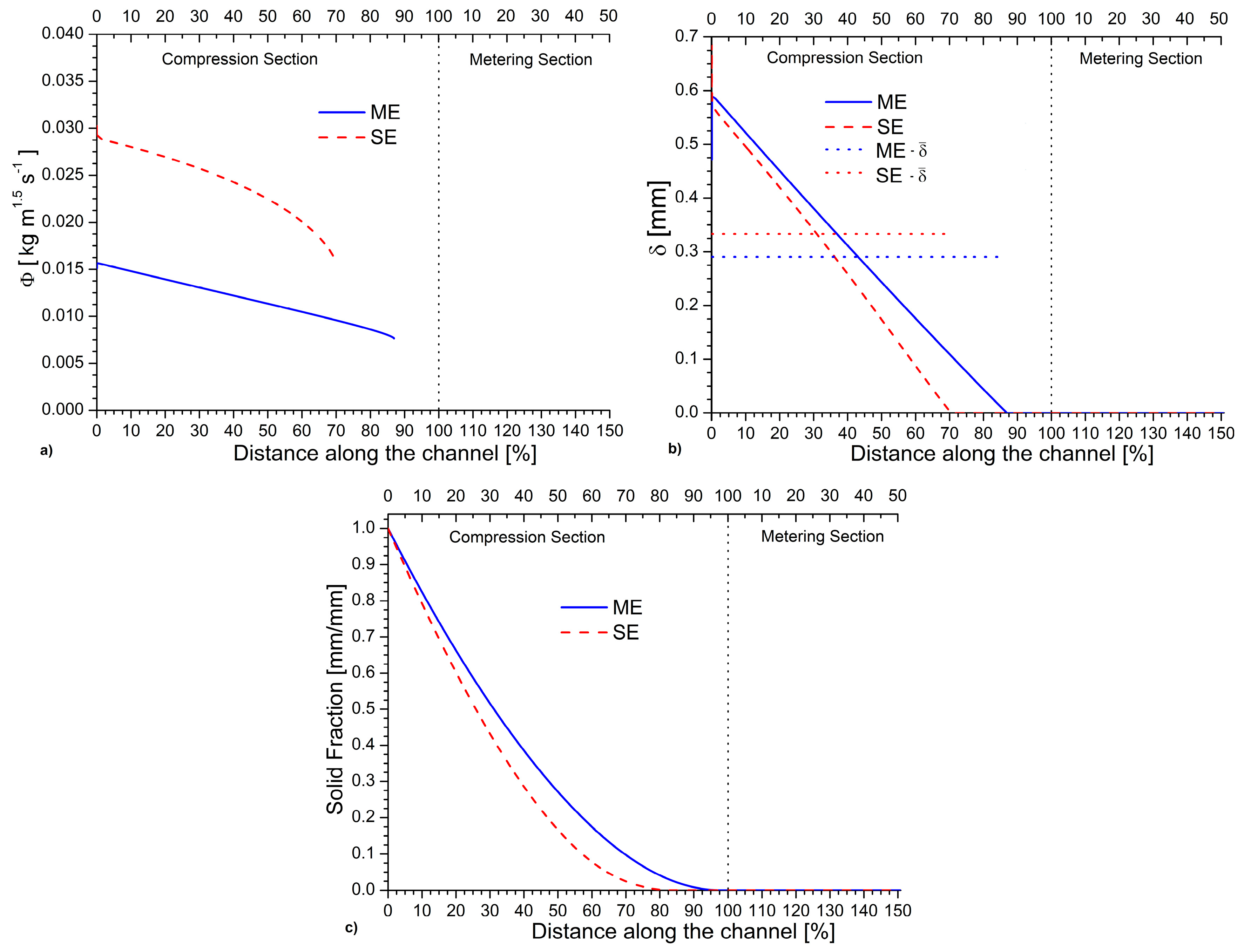
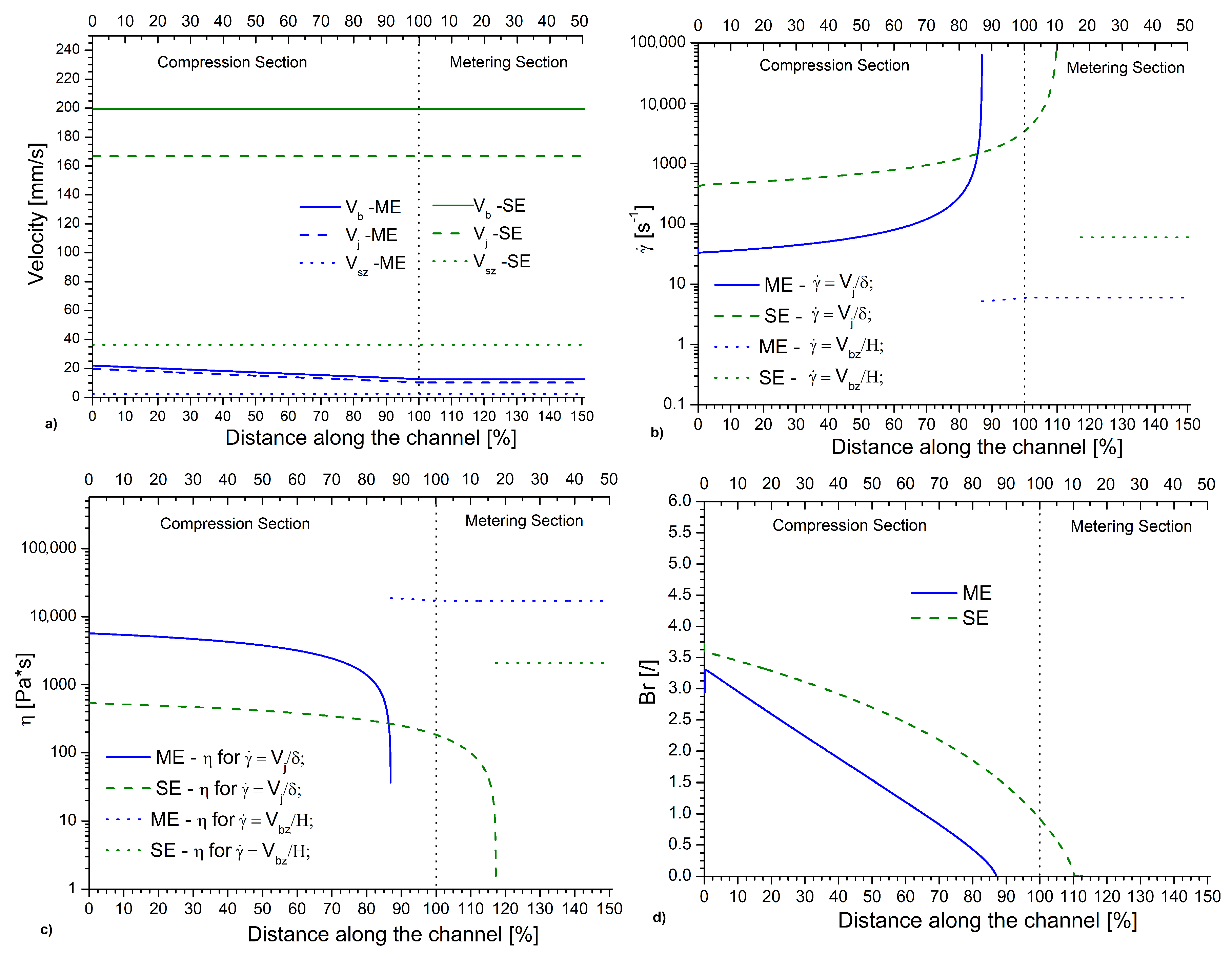
3.1. Melting Efficiency for Micro- vs. Conventional Extruder
3.2. Effect of Barrel Temperature
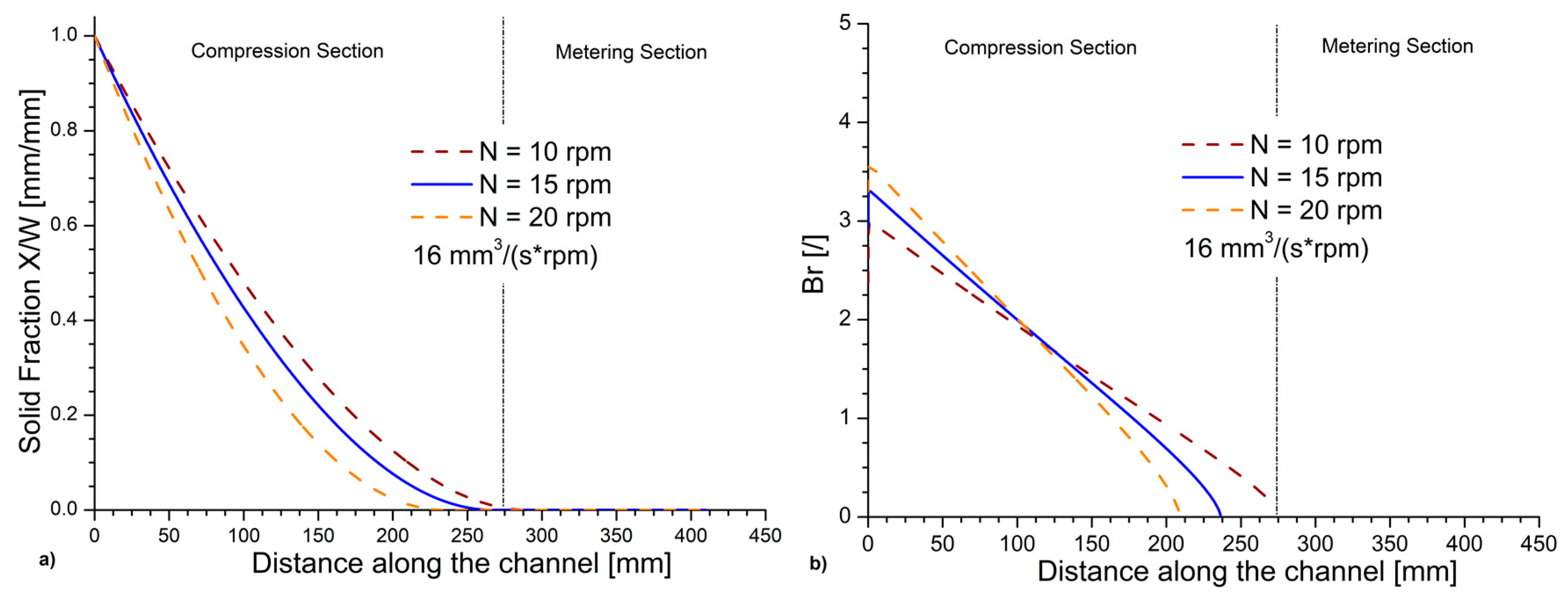
3.3. Effect of Screw Frequency under Flood Feeding
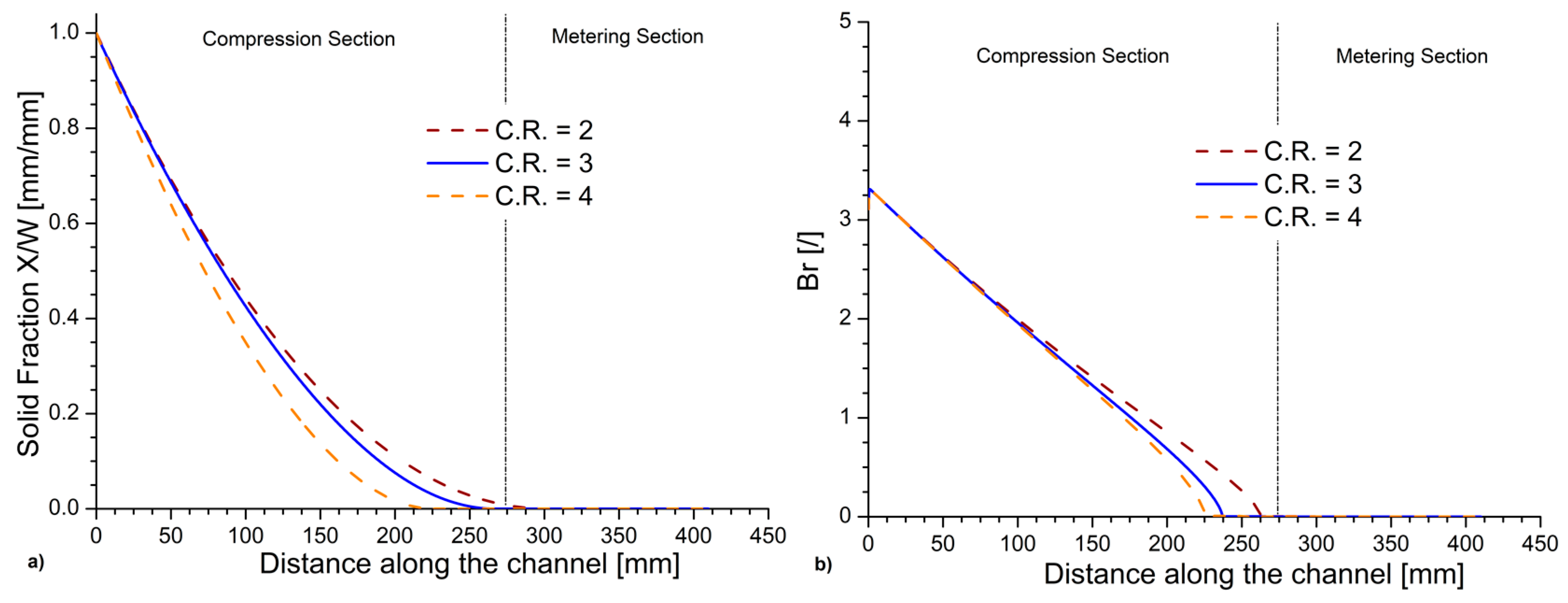
3.4. Effect of the Compression Ratio of the Screw
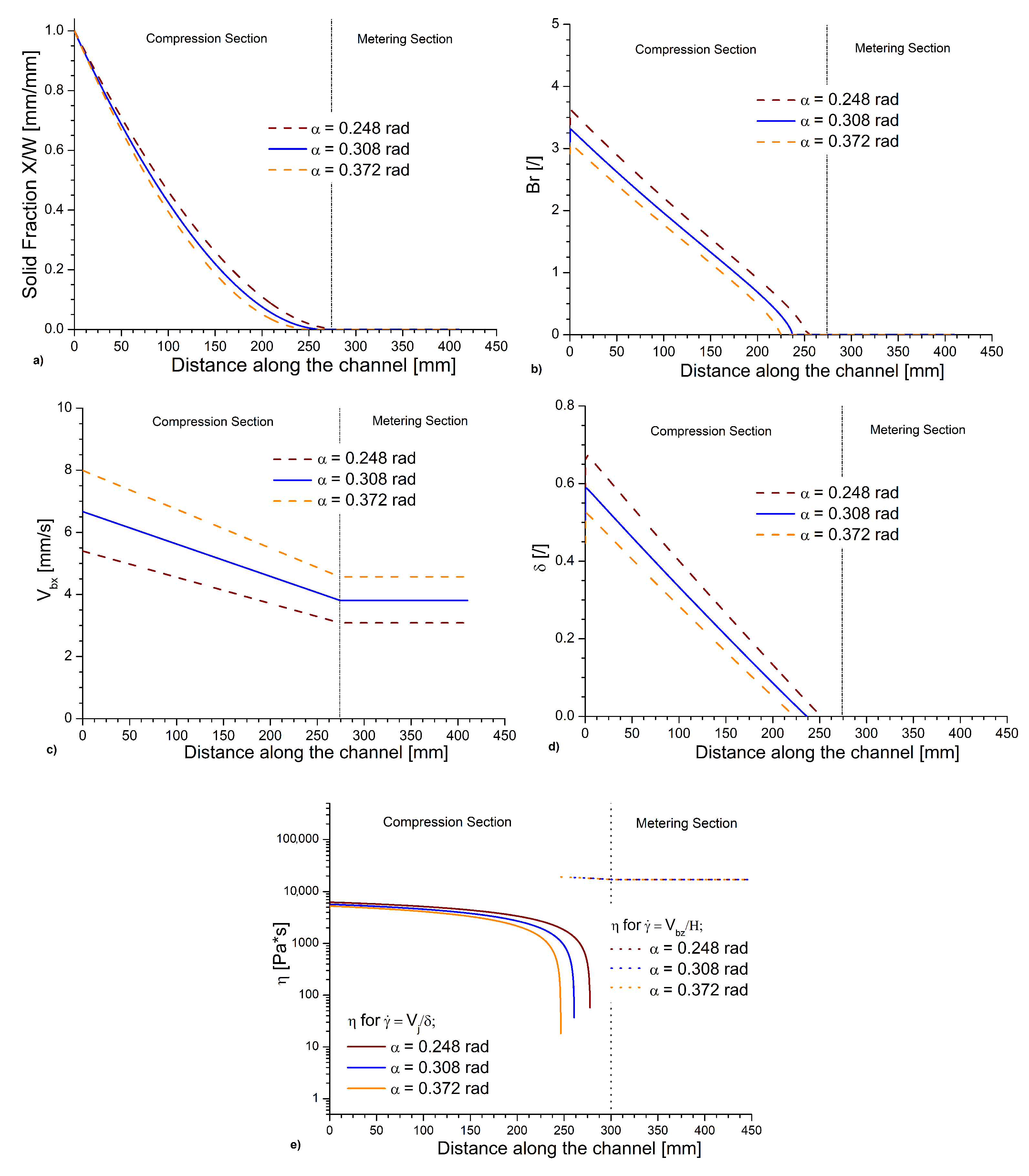
3.5. Effect of the Screw Pitch Angle
3.6. Effect of Volumetric Feeding Rate
3.7. Effect of Screw Channel Width
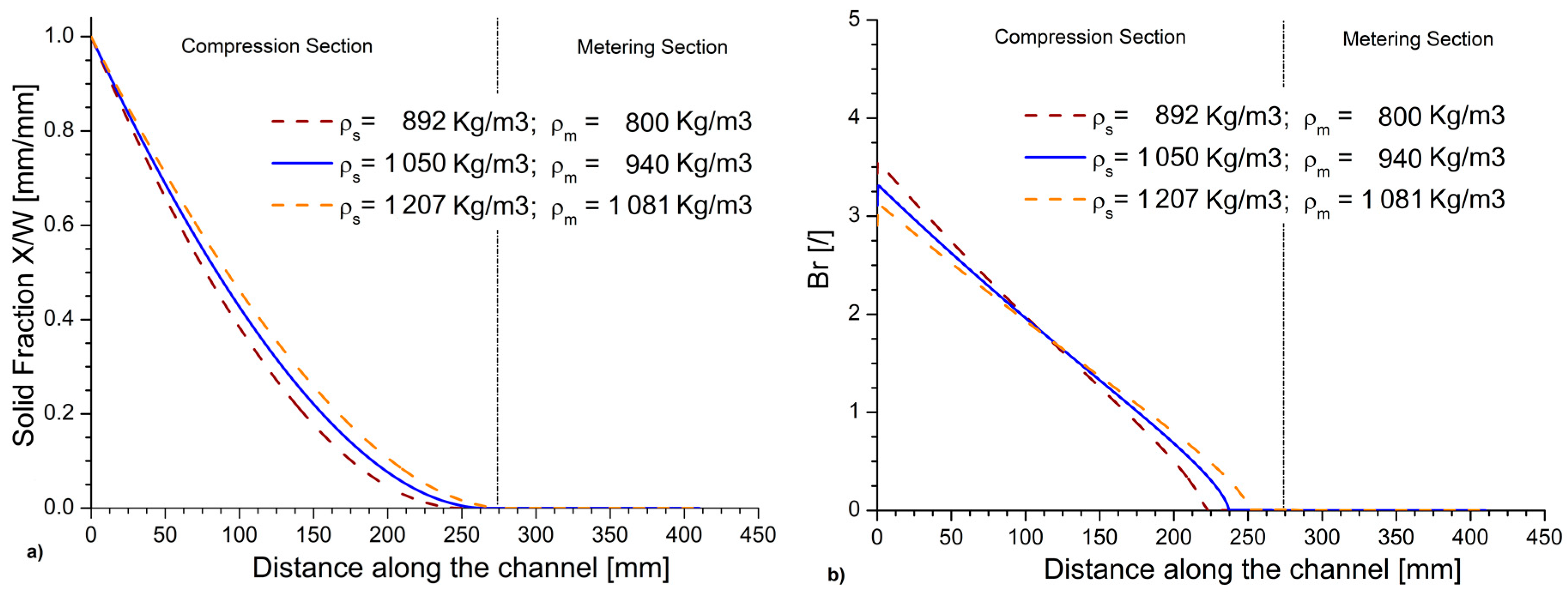
3.8. Effect of Polymer Density
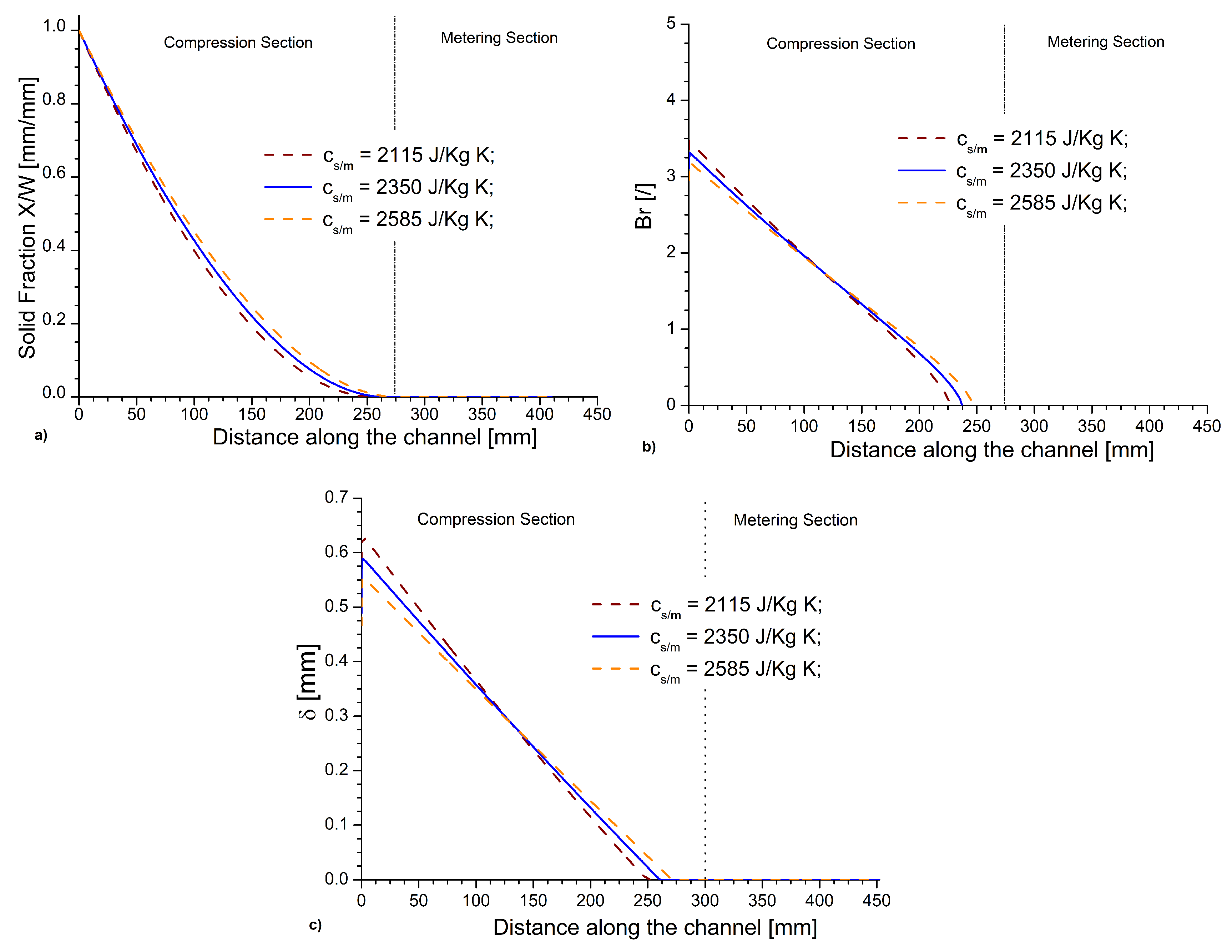
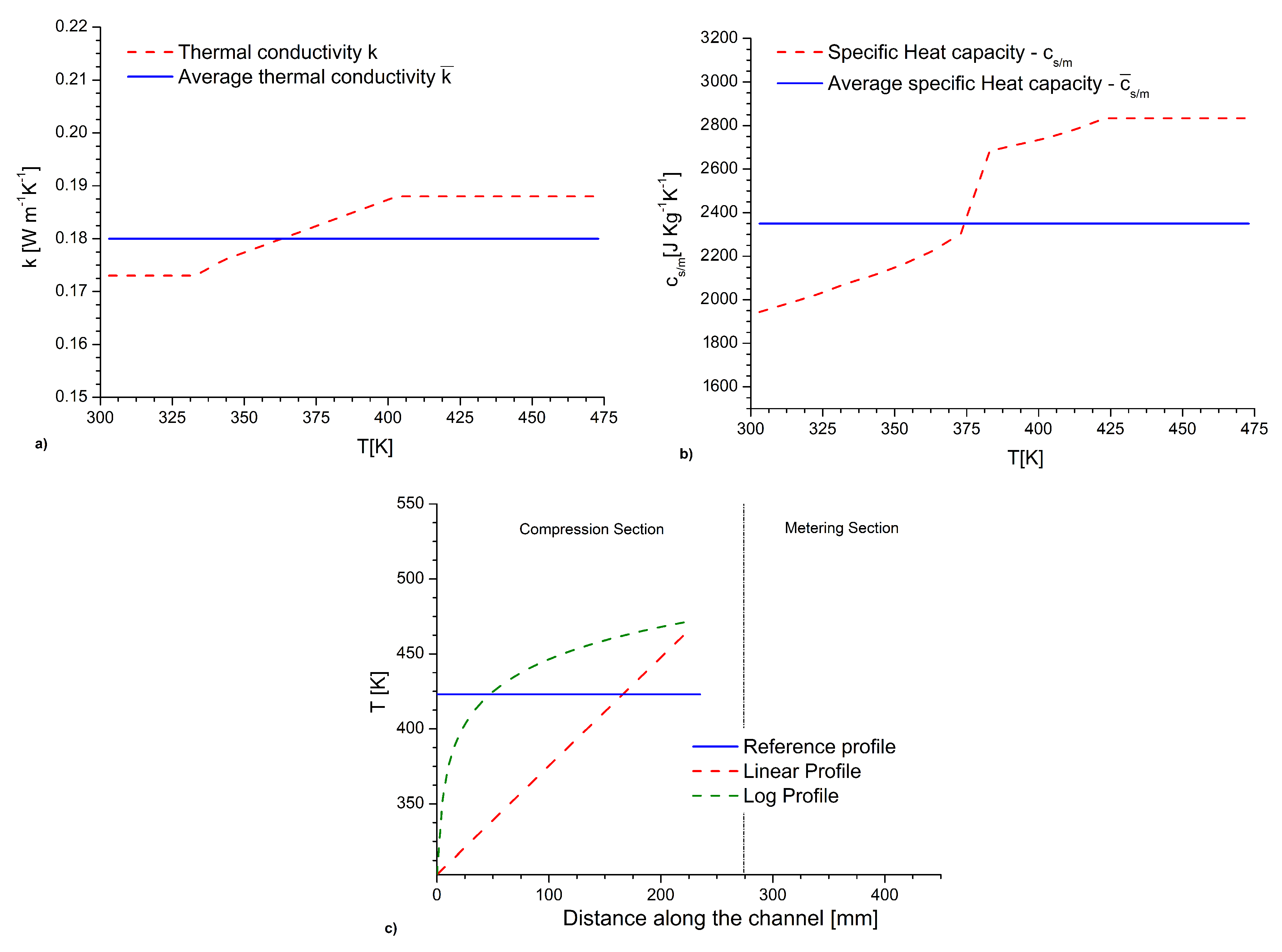
3.9. Effect of Specific Heat Capacity and Thermal Conductivity
3.10. Effect of Power-Law Index
3.11. Summary of Individual Variations
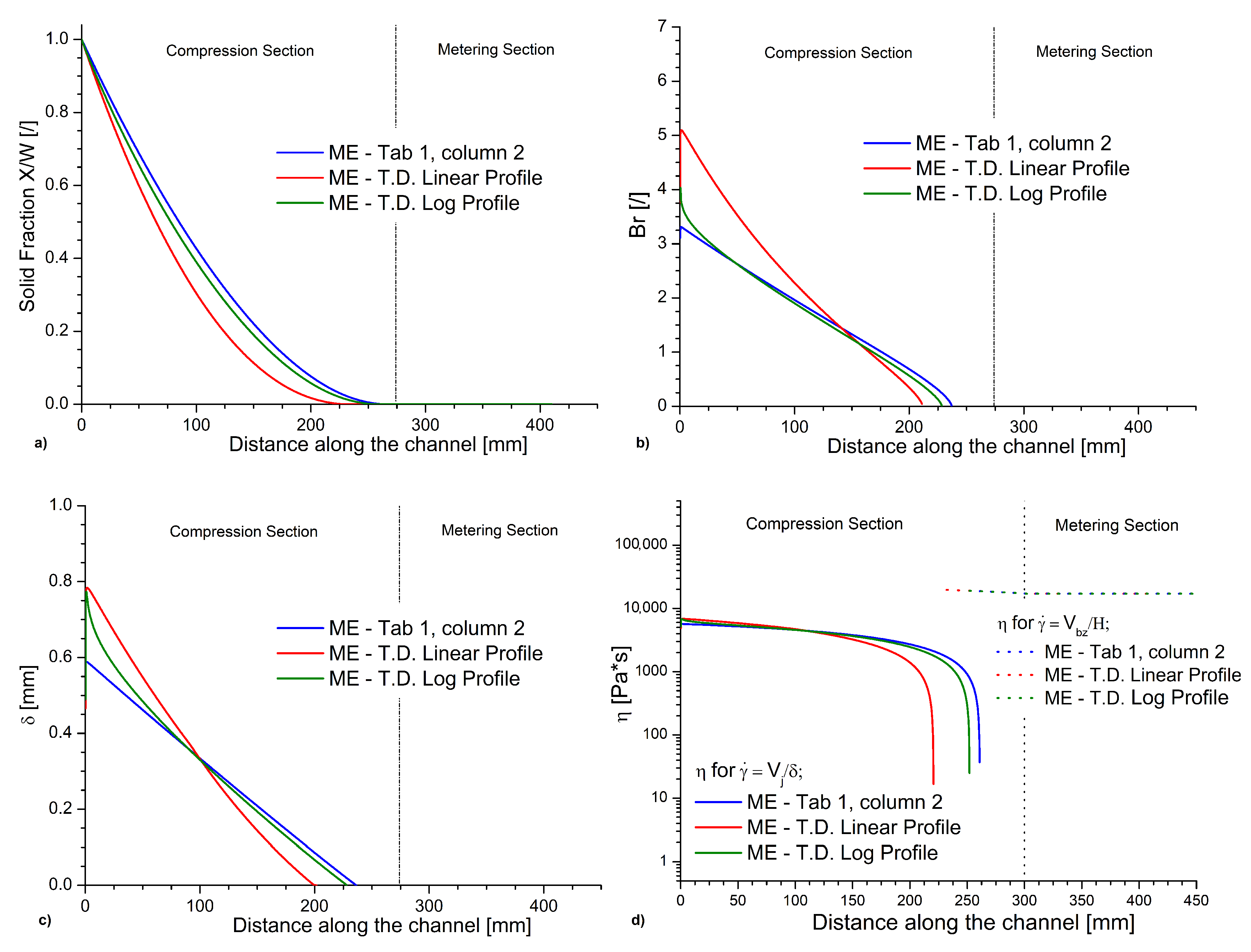
3.12. Extension for Varying Physicochemical Parameters
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Huang, S.; Liu, P.; Mokasdar, A.; Hou, L. Additive Manufacturing and Its Societal Impact: A Literature Review. Int. J. Adv. Manuf. Technol. 2013, 67, 1191–1203. [Google Scholar]
- Attaran, M. The rise of 3-D printing: The advantages of additive manufacturing over traditional manufacturing. Bus. Horiz. 2017, 60, 677–688. [Google Scholar]
- Ben-Ner, A.; Siemsen, E. Decentralization and Localization of Production: The Organizational and Economic Consequences of Additive Manufacturing (3D Printing). Calif. Manag. Rev. 2017, 59, 5–23. [Google Scholar] [CrossRef]
- Calignano, F.; Manfredi, D.; Ambrosio, E.P.; Biamino, S.; Lombardi, M.; Atzeni, E.; Salmi, A.; Minetola, P.; Iuliano, L.; Fino, P. Overview on Additive Manufacturing Technologies. Proc. IEEE 2017, 105, 593–612. [Google Scholar] [CrossRef]
- Peng, T.; Kellens, K.; Tang, R.; Chen, C.; Chen, G. Sustainability of additive manufacturing: An overview on its energy demand and environmental impact. Addit. Manuf. 2018, 21, 694–704. [Google Scholar]
- Majeed, A.; Zhang, Y.; Ren, S.; Lv, J.; Peng, T.; Waqar, S.; Yin, E. A Big Data-Driven Framework for Sustainable and Smart Additive Manufacturing. Robot. Comput. Integr. Manuf. 2021, 67, 102026. [Google Scholar]
- Dobrzański, L.; Dobrzański, L. Dentistry 4.0 Concept in the Design and Manufacturing of Prosthetic Dental Restorations. Processes 2020, 8, 525. [Google Scholar] [CrossRef]
- González-Henríquez, C.M.; Sarabia-Vallejos, M.A.; Rodriguez-Hernandez, J. Polymers for additive manufacturing and 4D-printing: Materials, methodologies, and biomedical applications. Prog. Polym. Sci. 2019, 94, 57–116. [Google Scholar]
- Franco, D.; Miller Devós Ganga, G.; de Santa-Eulalia, L.A.; Godinho Filho, M. Consolidated and inconclusive effects of additive manufacturing adoption: A systematic literature review. Comput. Ind. Eng. 2020, 148, 106713. [Google Scholar]
- Khosravani, M.; Reinicke, T. On the Environmental Impacts Of 3D Printing Technology. Appl. Mater. Today 2020, 20, 100689. [Google Scholar]
- Sun, Q.; Rizvi, G.M.; Bellehumeur, C.T.; Gu, P. Effect of processing conditions on the bonding quality of FDM polymer filaments. Rapid Prototyp. J. 2008, 14, 72–80. [Google Scholar]
- Wang, S.; Capoen, L.; D’hooge, D.R.; Cardon, L. Can the melt flow index be used to predict the success of fused deposition modelling of commercial poly(lactic acid) filaments into 3D printed materials? Plast. Rubber Compos. 2018, 47, 9–16. [Google Scholar] [CrossRef]
- Duty, C.; Ajinjeru, C.; Kishore, V.; Compton, B.; Hmeidat, N.; Chen, X.; Liu, P.; Hassen, A.; Lindahl, J.; Kunc, V. What Makes A Material Printable? A Viscoelastic Model for Extrusion-Based 3D Printing Of Polymers. J. Manuf. Process. 2018, 35, 526–537. [Google Scholar]
- Ajinjeru, C.; Kishore, V.; Liu, P.; Lindahl, J.; Hassen, A.; Kunc, V.; Post, B.; Love, L.; Duty, C. Determination of melt processing conditions for high performance amorphous thermoplastics for large format additive manufacturing. Addit. Manuf. 2018, 21, 125–132. [Google Scholar]
- Go, J.; Schiffres, S.N.; Stevens, A.G.; Hart, A.J. Rate limits of additive manufacturing by fused filament fabrication and guidelines for high-throughput system design. Addit. Manuf. 2017, 16, 1–11. [Google Scholar]
- Duty, C.E.; Kunc, V.; Compton, B.; Post, B.; Erdman, D.; Smith, R.; Lind, R.; Lloyd, P.; Love, L. Structure and mechanical behavior of big area additive manufacturing (BAAM) materials. Rapid Prototyp. J. 2017, 23, 181–189. [Google Scholar]
- Liu, X.; Chi, B.; Jiao, Z.; Tan, J.; Liu, F.; Yang, W. A large-scale double-stage-screw 3D printer for fused deposition of plastic pellets. J. Appl. Polym. Sci. 2017, 134, 45147. [Google Scholar] [CrossRef]
- Zhou, Z.; Salaoru, I.; Morris, P.; Gibbons, G.J. Additive manufacturing of heat-sensitive polymer melt using a pellet-fed material extrusion. Addit. Manuf. 2018, 24, 552–559. [Google Scholar]
- Whyman, S. Design and development of an extrusion system for 3D printing biopolymer pellets. Int. J. Adv. Manuf. Technol. 2018, 96, 3417–3428. [Google Scholar]
- Post, B.; Lind, R.F.; Lloyd, P.D.; Kunc, V.; Linhal, J.M.; Love, L.J. The Economics of Big Area Addtiive Manufacturing. In Proceedings of the Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference, Austin, TX, USA, 8–10 August 2016. [Google Scholar]
- Wang, Z.; Liu, R.; Sparks, T.; Liou, F. Large-Scale Deposition System by an Industrial Robot (I): Design of Fused Pellet Modeling System and Extrusion Process Analysis, 3D Print. Addit. Manuf. 2016, 3, 39–47. [Google Scholar]
- Wilczynski, K. SSEM: A computer model for a polymer single-screw extrusion. J. Mater. Process. Technol. 2001, 109, 308–313. [Google Scholar]
- Tadmor, Z.; Gogos, C.G. Principles of Polymer Processing, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Altınkaynak, A.; Gupta, M.; Spalding, M.A.; Crabtree, S.L. Melting in a Single Screw Extruder: Experiments and 3D Finite Element Simulations. Int. Polym. Process. 2011, 26, 182–196. [Google Scholar] [CrossRef]
- Razeghiyadaki, A.; Zhang, D.; Wei, D.; Perveen, A. Optimization of Polymer Extrusion Die Based on Response Surface Method. Processes 2020, 8, 1043. [Google Scholar] [CrossRef]
- Grimard, J.; Dewasme, L.; Vande Wouwer, A. A Review of Dynamic Models of Hot-Melt Extrusion. Processes 2016, 4, 19. [Google Scholar] [CrossRef] [Green Version]
- Vera-Sorroche, J.; Kelly, A.; Brown, E.; Coates, P.; Karnachi, N.; Harkin-Jones, E.; Li, K.; Deng, J. Thermal optimisation of polymer extrusion using in-process monitoring techniques. Appl. Therm. Eng. 2013, 53, 405–413. [Google Scholar]
- Abeykoon, C.; Kelly, A.; Vera-Sorroche, J.; Brown, E.; Coates, P.; Deng, J.; Li, K.; Harkin-Jones, E.; Price, M. Process efficiency in polymer extrusion: Correlation between the energy demand and melt thermal stability. Appl. Energy 2014, 135, 560–571. [Google Scholar]
- Jamarani, R.; Erythropel, H.; Burkat, D.; Nicell, J.; Leask, R.; Maric, M. Rheology of Green Plasticizer/Poly(vinyl chloride) Blends via Time–Temperature Superposition. Processes 2017, 5, 43. [Google Scholar] [CrossRef]
- Giles, H.F., Jr.; Wagner, J.R., Jr.; Mount, E.M., III. Extrusion: The Definitive Processing Guide and Handbook; William Andrew, Inc.: Norwich, NY, USA, 2005. [Google Scholar]
- Covas, J.A.; Costa, P. A miniature extrusion line for small scale processing studies. Polym. Test. 2004, 23, 763–773. [Google Scholar]
- Bruker, I.; Balch, G.S. Melting Mechanism in Single Screw Extrusion. Polym. Eng. Sci. 1989, 29, 258–267. [Google Scholar] [CrossRef]
- Rauwendaal, C. An improved analytical melting theory. Adv. Polym. Tech. 1989, 9, 331–336. [Google Scholar]
- Rauwendaal, C. Dispersed solids melting theory. In Proceedings of the Society of Plastics Engineers, Annual Technical Conference—ANTEC, New Orleans, LA, USA, 9–13 May 1993; pp. 2232–2237. [Google Scholar]
- Hyvärinen, M.; Jabeen, R.; Kärki, T. The Modelling of Extrusion Processes for Polymers—A Review. Polymers 2020, 12, 1306. [Google Scholar]
- Christiano, J.P.; Davis Standard, L.; Pawcatuck, C. Examination of the performance of a high-speed single screw extruder for several different extrusion applications. In Proceedings of the Annual Technical Conference—ANTEC, Orlando, FL, USA, 2–4 April 2012; pp. 1029–1034. [Google Scholar]
- Agur, E.E.; Vlachopoulos, J. Numerical Simulation of a Single-Screw Plasticating Extruder. Polym. Eng. Sci. 1982, 22, 1084–1094. [Google Scholar] [CrossRef]
- Edmondson, I.R.; Fenner, R.T. Melting of Thermoplastics in Single Screw Extruders. Polymer 1975, 16, 49–56. [Google Scholar] [CrossRef]
- Mount, E.M.; Chung, C.I. Melting Behavior of Solid Polymers on a Metal Surface at Processing Conditions. Polym. Eng. Sci. 1978, 18, 711–720. [Google Scholar] [CrossRef]
- Mount, E.M., III; Watson, J.G., III; Chung, C.I. Analytical Melting Model for Extrusion: Melting Rate of Fully Compacted Solid Polymers. Polym. Eng. Sci. 1982, 22, 729–737. [Google Scholar] [CrossRef]
- Mount, E.M. M. Impact of Rheological Properties on Melting Rate Calculations. In Proceedings of the Society of Plastics Engineers, Annual Technical Conference—ANTEC, Boston, MA, USA, 1–4 May 2005; Volume 1, pp. 328–334. [Google Scholar]
- Tadmor, Z. Fundamentals of Plasticating Extrusion. I. A Theoretical Model for Melting. Polym. Eng. Sci. 1966, 6, 185–190. [Google Scholar] [CrossRef]
- Tadmor, Z.; Duvdevani, I.; Klein, I. Melting in Plasticating Extruders–Theory and Experiments. Polym. Eng. Sci. 1967, 7, 198–217. [Google Scholar] [CrossRef]
- Shapiro, J.; Halmos, A.L.; Pearson, J.R.A. Melting in Single Screw Extruders. Polymer 1976, 17, 905–918. [Google Scholar] [CrossRef]
- Sundstrom, D.W.; Young, C.C. Melting Rates of Crystalline Polymers under Shear Conditions. Polym. Eng. Sci. 1972, 12, 59–63. [Google Scholar] [CrossRef]
- Maddock, B. A visual analysis of flow and mixing in extruder screws. SPE ANTEC Tech. Papers 1959, 15, 383–389. [Google Scholar]
- Vermeulen, J.R.; Gerson, P.M.; Beek, W.J. The Melting of a Bed of Polymer Granules on a Hot Moving Surface. Chem. Eng. Sci. 1971, 26, 1445–1455. [Google Scholar] [CrossRef]
- Vermeulen, J.R.; Scargo, P.G.; Beek, W.J. The Melting of a Crystalline Polymer in a Screw Extruder. Chem. Eng. Sci. 1971, 26, 1457–1465. [Google Scholar] [CrossRef]
- Syrjala, S. A New Approach for the Simulation of Melting in Extruders. Int. Comm. Heat Mass Transf. 2000, 27, 623–634. [Google Scholar] [CrossRef]
- Pearson, J.R.A. Heat transfer in flowing polymers Progress in Heat and Mass Transfer. In Selected Papers of the 1970 International Seminar; Elsevier: Amsterdam, The Netherlands, 1972; pp. 73–87. [Google Scholar] [CrossRef]
- Coelho, P.; Pinho, F. A generalized brinkman number for non-Newtonian duct flows. J. Nonnewton. Fluid Mech. 2009, 156, 202–206. [Google Scholar]
- Winter, H. Viscous Dissipation in Shear Flows of Molten Polymers. Adv. Heat Transf. 1977, 13, 205–267. [Google Scholar] [CrossRef]
- Tso, C.; Mahulikar, S. The role of the Brinkman number in analyzing flow transitions in microchannels. Int. J. Heat Mass Transf. 1999, 42, 1813–1833. [Google Scholar]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Cross, M.M. Rheology of non-Newtonian fluids: a new flow equation for pseudoplastic systems. J. Colloid Sci. 1965, 20, 417–437. [Google Scholar]
- Wilczynski, K. A computer model for single screw plasticating extrusion. Polym. Plast. Technol. Eng. 1996, 35, 449–477. [Google Scholar]
- Lewandowski, A.; Wilczynski, K.; Wilczynski, K.J.; Nastaj, A. A composite model for an intermeshing counter-rotating twin-screw extruder and its experimental verification. Polym. Eng. Sci. 2015, 55, 2838–2848. [Google Scholar]
- Tsukuda, R.; Sumimoto, S.; Ozawa, T. Thermal conductivity and heat capacity of ABS resin composites. J. Appl. Polym. Sci. 1997, 63, 1279–1286. [Google Scholar]

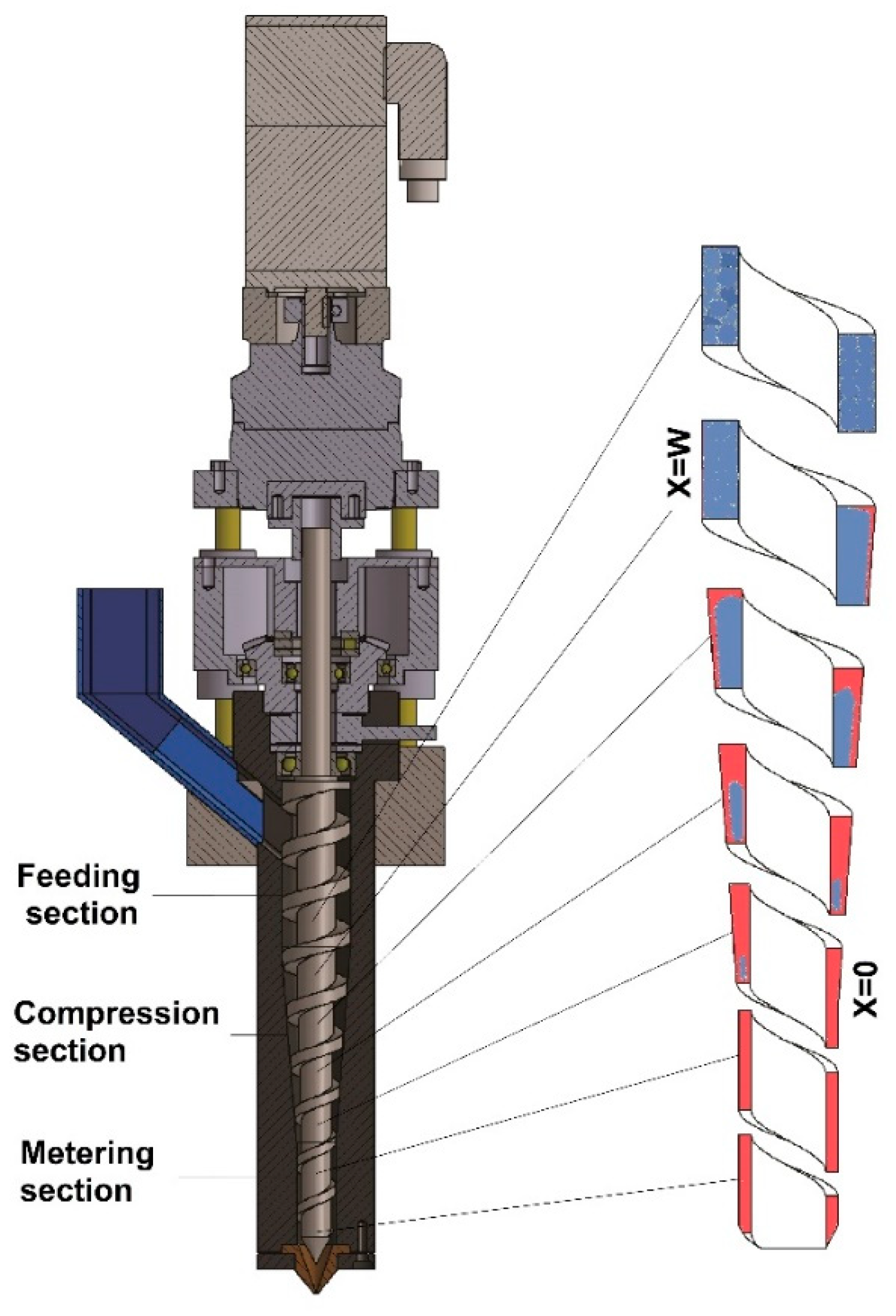


| Extruder Dimensions | Micro Extruder (This Work) | Standard Extruder SE I (This Work) | Standard Extruder SE II (Altınkaynak et al. 2011) | Unit |
|---|---|---|---|---|
| Axial length | 662 | 1333 | 1333 | (mm) |
| -Feeding (helical length) | 280 | 1245 | 1245 | (mm) |
| -Compression (helical length) | 274 | 1672 | 1672 | (mm) |
| -Metering (helical length) | 108 | 1463 | 1463 | (mm) |
| Screw diameter—initial | 28 | 63.5 | 63.5 | (mm) |
| Screw diameter—final | 16 | 63.5 | 63.5 | (mm) |
| Helical length | 690 | 4380 | 4380 | (mm) |
| H—Channel depth—initial | 6 | 8.89 | 8.89 | (mm) |
| H—Channel depth—final | 2 | 3.18 | 3.18 | (mm) |
| W—Channel width | 16 | 53 | 53 | (mm) |
| θ—Pitch angle | 0.308 | 0.308 | 0.308 | (rad) |
| Axial length | 662 | 1333 | 1333 | (mm) |
| -Feeding (helical length) | 280 | 1245 | 1245 | (mm) |
| Operational parameters | ||||
| Q—Volumetric Flow rate | 8.6 × 10−4 | 1.43 × 10−2 | 5.7 × 10−2 | (m 3 h−1) |
| N—Screw Speed | 15 | 15 | 60 | (rpm) |
| Tb—Barrel Temperature | 473 | 473 | 503 | (K) |
| Material parameters | ||||
| D1—Material parameter Cross-WLF | 3.6 × 1011 | 3.6 × 1011 | 3.6 × 1011 | (Pa s) |
| A1—Material parameter Cross-WLF | 27.2 | 27.2 | 27.2 | (-) |
| A2—Material parameter Cross-WLF | 92.6 | 92.6 | 92.6 | (-) |
| Ta—Material parameter Cross-WLF | 373 | 373 | 373 | (K) |
| —Critical stress at the transition to shear thinning | 29000 | 29000 | 29000 | (Pa) |
| —Critical shear rate | 1.1 × 10−1 | 1.1 × 10−1 | 3.8 × 10−1 | (s −1) |
| n—Power-law index | 0.33 | 0.33 | 0.33 | (-) |
| ρs—Density (solid) | 1050 | 1050 | 1050 | (kg m −3) |
| ρm—Density (melt) | 940 | 940 | 940 | (kg m −3) |
| cs—Specific heat capacity | 2350 | 2350 | 2350 | (J kg −1 K −1] |
| k—Thermal conductivity | 0.18 | 0.18 | 0.18 | (W m −1 K −1) |
| —Heat of fusion | 0 | 0 | 0 | (J kg −1) |
| Tm—Melt Temperature | 423 | 423 | 423 | (K) |
| T0—Initial polymer Temperature | 300 | 300 | 300 | (K) |
| Variable | Entity of the Variation [%] | Variation in the Complete Melting Point Position [%] | Variation in Br at the Beginning of the Compression Section [%] |
|---|---|---|---|
| Barrel temperature | +10 | +0.3 | −51.5 |
| −10 | −1.8 | +173.0 | |
| Screw frequency | +33 | −12.8 | +9.2 |
| −33 | +9.3 | −13.2 | |
| Compression ratio | +33 | −15.3 | 0 |
| −33 | +11.2 | 0 | |
| Pitch angle | +20 | −5.6 | −6.4 |
| −20 | +6.5 | +8.3 | |
| Volumetric feeding rate | +15 | +12.8 | +4.8 |
| −15 | −11.4 | −3.2 | |
| Channel width | +10 | +2.9 | +3.5 |
| −10 | −3.2 | −3.8 | |
| Density | +15 | +5.5 | −6.7 |
| −15 | −6.5 | +10.2 | |
| Specific heat capacity | +10 | +3.8 | −5.1 |
| −10 | −4.2 | +7.7 | |
| Thermal conductivity | +20 | −4.9 | −13.2 |
| −20 | +6.0 | +20.9 | |
| Power-law index | +20 | −15.3 | +74.6 |
| −20 | +11.2 | −37.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
La Gala, A.; Fiorio, R.; Erkoç, M.; Cardon, L.; D’hooge, D.R. Theoretical Evaluation of the Melting Efficiency for the Single-Screw Micro-Extrusion Process: The Case of 3D Printing of ABS. Processes 2020, 8, 1522. https://doi.org/10.3390/pr8111522
La Gala A, Fiorio R, Erkoç M, Cardon L, D’hooge DR. Theoretical Evaluation of the Melting Efficiency for the Single-Screw Micro-Extrusion Process: The Case of 3D Printing of ABS. Processes. 2020; 8(11):1522. https://doi.org/10.3390/pr8111522
Chicago/Turabian StyleLa Gala, Andrea, Rudinei Fiorio, Mustafa Erkoç, Ludwig Cardon, and Dagmar R. D’hooge. 2020. "Theoretical Evaluation of the Melting Efficiency for the Single-Screw Micro-Extrusion Process: The Case of 3D Printing of ABS" Processes 8, no. 11: 1522. https://doi.org/10.3390/pr8111522
APA StyleLa Gala, A., Fiorio, R., Erkoç, M., Cardon, L., & D’hooge, D. R. (2020). Theoretical Evaluation of the Melting Efficiency for the Single-Screw Micro-Extrusion Process: The Case of 3D Printing of ABS. Processes, 8(11), 1522. https://doi.org/10.3390/pr8111522







