Predicting By-Product Gradients of Baker’s Yeast Production at Industrial Scale: A Practical Simulation Approach
Abstract
1. Introduction
2. Materials and Methods
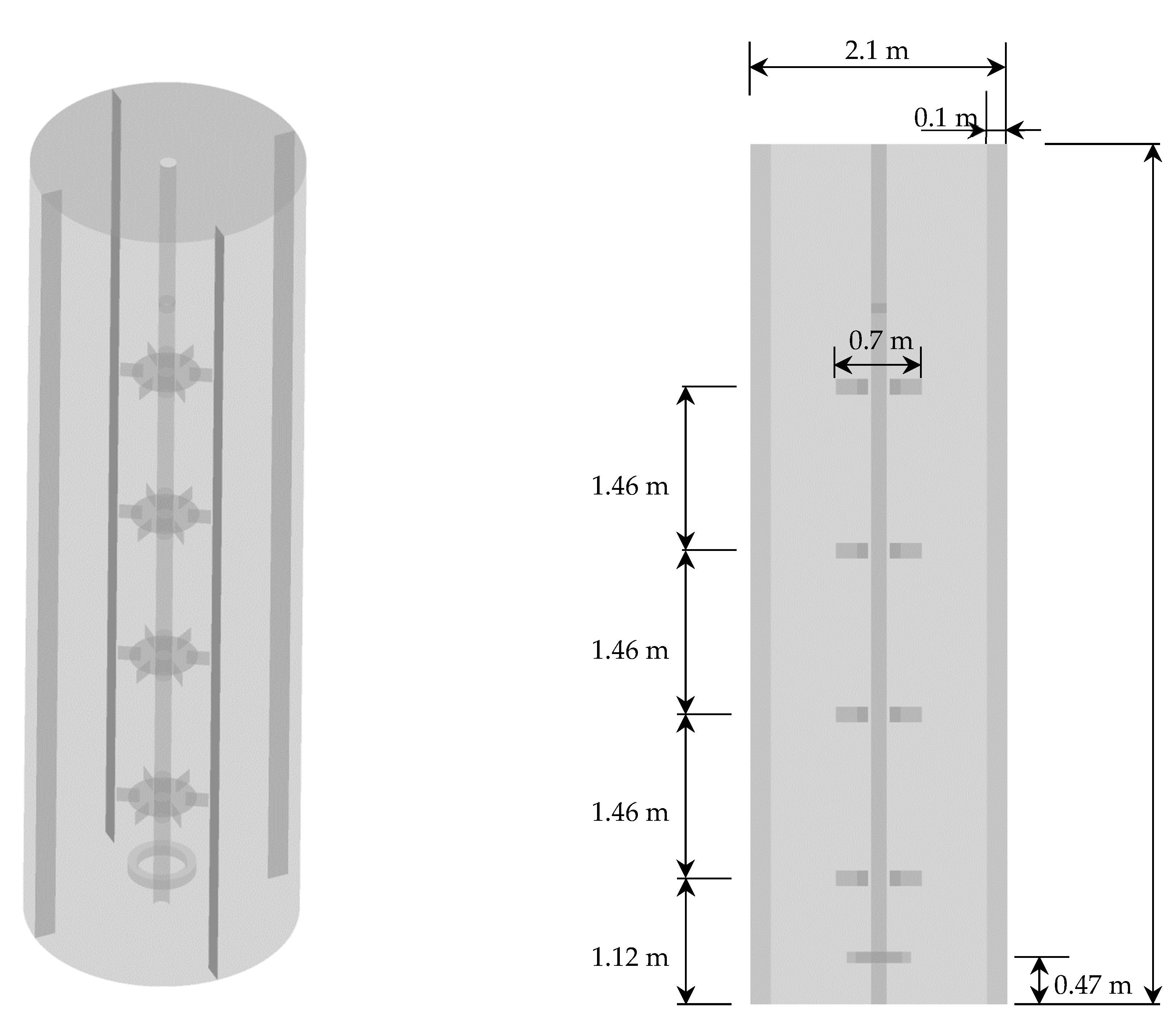
2.1. Geometry and Mesh
2.2. CFD Setup
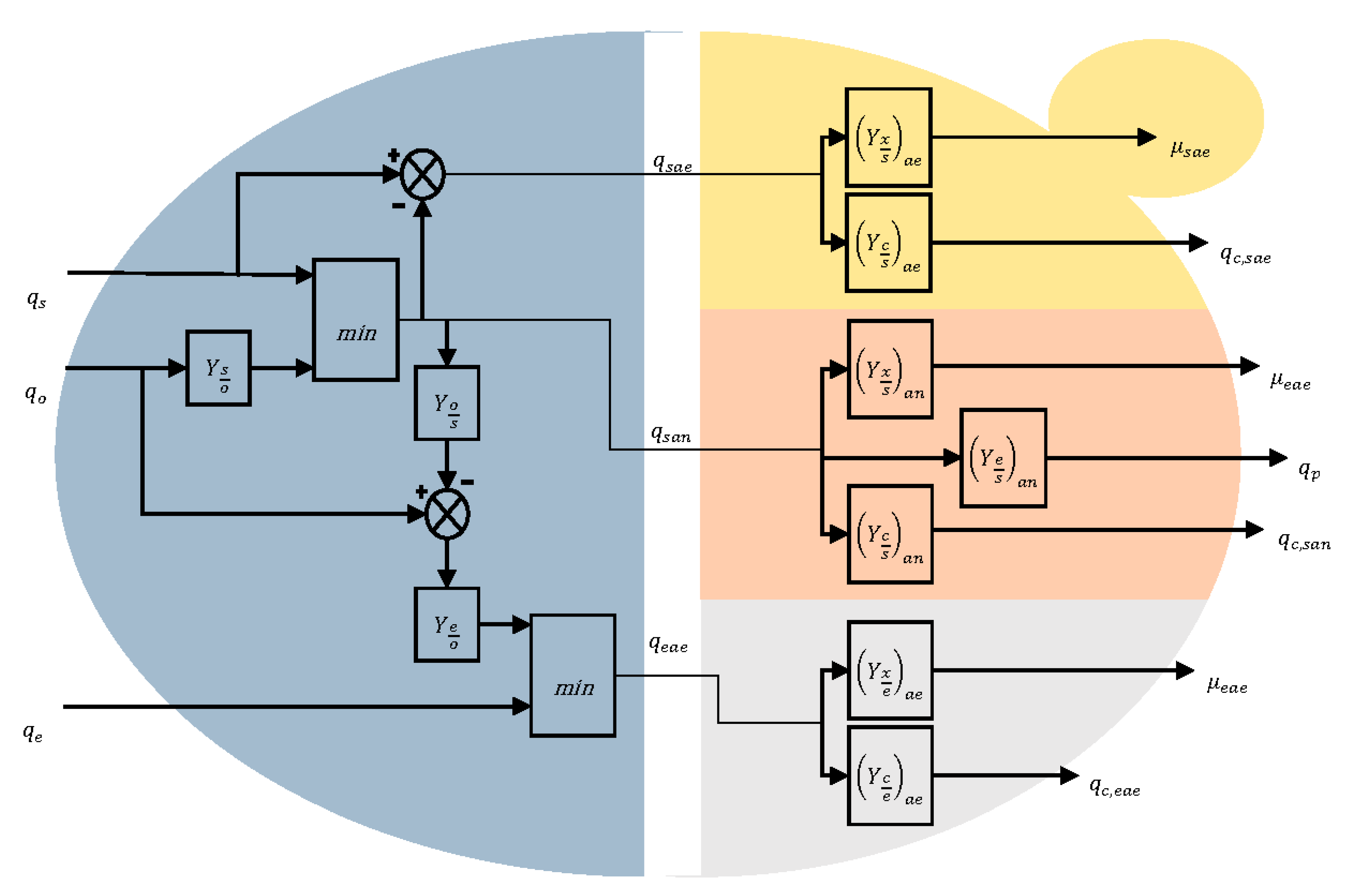
2.3. Biokinetics
- Aerobic growth on glucose (indexed sae)
- Anaerobic growth on glucose (indexed san)
- Aerobic growth on ethanol (indexed eae)
2.4. Mass Transfer
3. Results
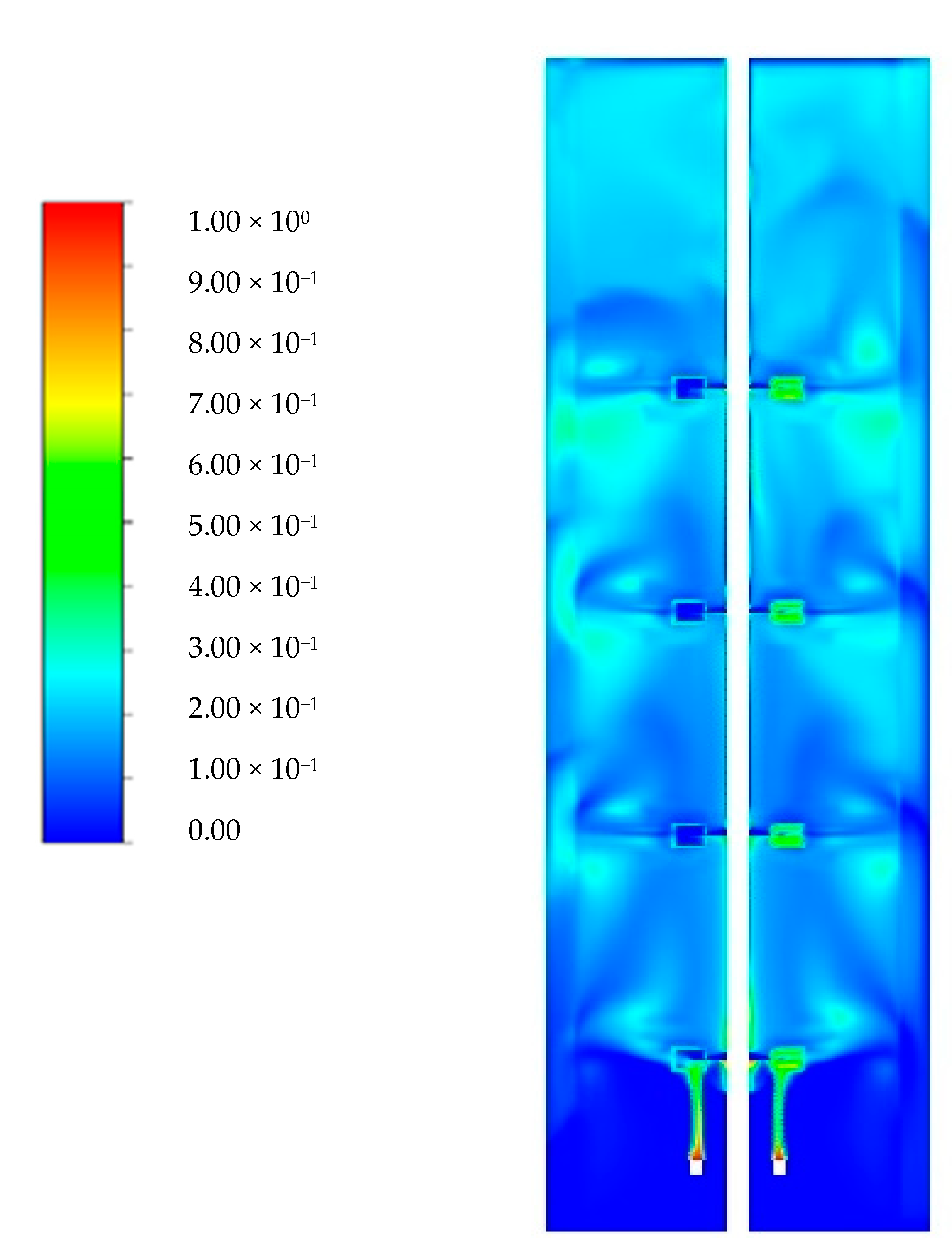
3.1. Flow Field Validation
3.2. Scenario I: Experimental Fermentation
3.3. Scenario II: Protein Production
4. Discussion
4.1. Glucose Gradient
4.2. Ethanol Gradient
4.3. Oxygen Gradient
4.4. Carbon Dioxide Gradient
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| C | Concentration matrix | |
| Concentration at the interface | mol/L | |
| Ethanol concentration | mol/L | |
| Concentration of component “i” in liquid phase | mol/L | |
| Oxygen concentration | mol/L | |
| Glucose concentration | mol/L | |
| Biomass concentration | g/L | |
| Bubble diameter | m | |
| Concentration of dissolved carbon dioxide | mol/L | |
| Concentration of dissolved oxygen | mol/L | |
| Critical concentration of dissolved oxygen | mol/L | |
| E | Elemental composition matrix | |
| H | Henry coefficient | l·atm/mol |
| k | Turbulent kinetic energy | m2/s2 |
| Partition coefficient | - | |
| Monod constant for ethanol | mol/L | |
| Mass transfer coefficient | 1/h | |
| Monod constant for oxygen | mol/L | |
| Monod constant for glucose | mol/L | |
| MTR | Mass transfer rate | mol/L/s |
| Partial pressure of the component “i” in gas phase | atm | |
| Specific ethanol uptake rate | mol/gx/s | |
| Specific ethanol uptake rate under aerobic conditions | mol/gx/s | |
| Maximum specific ethanol uptake rate | mol/gx/s | |
| Specific oxygen uptake rate | mol/gx/s | |
| Maximum specific oxygen uptake rate | mol/gx/s | |
| qs | Specific glucose uptake rate | mol/gx/s |
| Specific glucose uptake rate for aerobic metabolism | mol/gx/s | |
| Specific glucose uptake rate for anaerobic metabolism | mol/gx/s | |
| Maximum specific glucose uptake rate | mol/gx/s | |
| r | Reaction rate matrix | |
| Reaction rate of component “i” when growing aerobically on ethanol | mol/L/s | |
| Reaction rate of component “i” when growing aerobically on glucose | mol/L/s | |
| Reaction rate of component “i” when growing anaerobically on glucose | mol/L/s | |
| S.C. | Stoichiometry coefficients matrix | |
| Circulation time | s | |
| Mixing time | s | |
| Consumption timescale of component “i” | s | |
| Supply timescale of component “i” | s | |
| V | Volume | m3 |
| Carbon dioxide yield (aerobic) per mole substrate | mol/mol | |
| Carbon dioxide yield (aerobic) per mole ethanol | mol/mol | |
| Carbon dioxide yield (anaerobic) per mole substrate | mol/mol | |
| Ethanol yield (anaerobic) per mole substrate | mol/mol | |
| Oxygen yield per mole ethanol | mol/mol | |
| Oxygen yield per mole glucose | mol/mol | |
| Substrate yield per mole oxygen | mol/mol | |
| Biomass yield (aerobic) per mole ethanol | mol/mol | |
| Biomass yield (aerobic) per mole glucose | mol/mol | |
| Biomass yield (anaerobic) per mole glucose | mol/mol | |
| ΔC | concentration driving force | mol/L |
| ε | dissipation rate of turbulent kinetic energy | m2/s3 |
| ν | Kinematic viscosity | m2/s |
| ρ | Density | kg/m3 |
Abbreviations
| cAMP | Cyclic adenosine monophosphate |
| CFD | Computational fluid dynamics |
| MRF | Multiple reference frames |
| QUICK | Quadratic Upstream Interpolation for Convective Kinematics |
| RANS | Reynolds-averaged Navier–Stokes |
| RQ | Respiratory quotient |
| SIMPLE | Semi-Implicit Method for Pressure Linked Equations |
| TRY | Titer, rate, yield |
Appendix A. Glucose Gradients
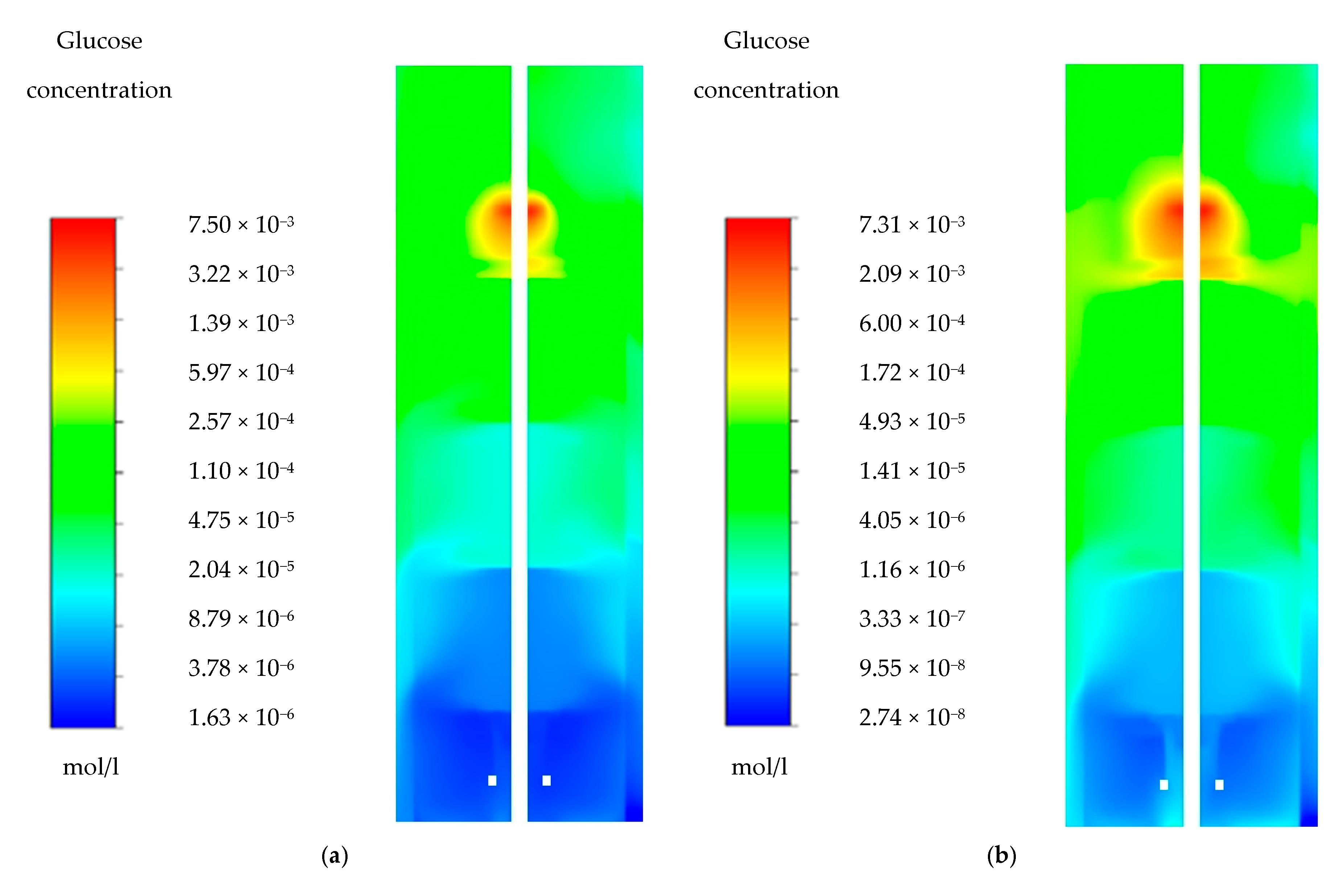
| Glucose Concentration (µmol/L) | ||||||
|---|---|---|---|---|---|---|
| [4] | [74] | [25] | This Work | |||
| Scenario I | Scenario II | |||||
| Probe location | Top | 199 | 222 | 455 | 356 | 250 |
| Mid. | 91.6 | 62.2 | 97 | 32.6 | 56 | |
| Bot. | 40 | 28.3 | 23.8 | 4.15 | 2.55 | |
References
- Suarez-Mendez, C.; Sousa, A.; Heijnen, J.; Wahl, A. Fast “Feast/Famine” Cycles for Studying Microbial Physiology Under Dynamic Conditions: A Case Study with Saccharomyces cerevisiae. Metabolites 2014, 4, 347–372. [Google Scholar] [CrossRef]
- Suarez-Mendez, C.A.; Ras, C.; Wahl, S.A. Metabolic adjustment upon repetitive substrate perturbations using dynamic 13C-tracing in yeast. Microb. Cell Fact. 2017, 16, 1–14. [Google Scholar] [CrossRef]
- Kresnowati, M.T.A.P.; Van Winden, W.A.; Van Gulik, W.M.; Heijnen, J.J. Energetic and metabolic transient response of Saccharomyces cerevisiae to benzoic acid. FEBS J. 2008, 275, 5527–5541. [Google Scholar] [CrossRef]
- Noorman, H. An industrial perspective on bioreactor scale-down: What we can learn from combined large-scale bioprocess and model fluid studies. Biotechnol. J. 2011, 6, 934–943. [Google Scholar] [CrossRef]
- Wang, G.; Haringa, C.; Noorman, H.; Chu, J.; Zhuang, Y. Developing a Computational Framework To Advance Bioprocess Scale-Up. Trends Biotechnol. 2020, 1–11. [Google Scholar] [CrossRef]
- Zieringer, J.; Wild, M.; Takors, R. Data-Driven In-silico Prediction of Regulation Heterogeneity and ATP Demands of Escherichia coli in Large-scale Bioreactors. Biotechnol. Bioeng. 2020, bit.27568. [Google Scholar] [CrossRef] [PubMed]
- Morchain, J.; Pigou, M.; Lebaz, N. A population balance model for bioreactors combining interdivision time distributions and micromixing concepts. Biochem. Eng. J. 2017, 126, 135–145. [Google Scholar] [CrossRef]
- Linkès, M.; Fede, P.; Morchain, J.Ô.; Schmitz, P. Numerical investigation of subgrid mixing effects on the calculation of biological reaction rates. Chem. Eng. Sci. 2014, 116, 473–485. [Google Scholar] [CrossRef]
- Haringa, C.; Tang, W.; Wang, G.; Deshmukh, A.T.; Van Winden, W.A.; Chu, J.; Van Gulik, W.M.; Heijnen, J.J.; Mudde, R.; Noorman, H. Computational fluid dynamics simulation of an industrial, P. chrysogenum fermentation with a coupled 9-pool metabolic model: Towards rational scale-down and design optimization. Chem. Eng. Sci. 2018, 175, 12–24. [Google Scholar] [CrossRef]
- Haringa, C.; Mudde, R.F.; Noorman, H.J. From industrial fermentor to CFD-guided downscaling: What have we learned? Biochem. Eng. J. 2018, 140, 57–71. [Google Scholar] [CrossRef]
- Lapin, A.; Müller, D.; Reuss, M. Dynamic behavior of microbial populations in stirred bioreactors simulated with Euler-Lagrange methods: Traveling along the lifelines of single cells. Ind. Eng. Chem. Res. 2004, 43, 4647–4656. [Google Scholar] [CrossRef]
- Wright, M.R.; Bach, C.; Gernaey, K.V.; Krühne, U. Investigation of the effect of uncertain growth kinetics on a CFD based model for the growth of, S. cerevisiae in an industrial bioreactor. Chem. Eng. Res. Des. 2018, 140, 12–22. [Google Scholar] [CrossRef]
- Wang, G.; Haringa, C.; Tang, W.; Noorman, H.; Chu, J.; Zhuang, Y.; Zhang, S. Coupled metabolic-hydrodynamic modeling enabling rational scale-up of industrial bioprocesses. Biotechnol. Bioeng. 2020, 117, 844–867. [Google Scholar] [CrossRef]
- Lara, A.R.; Galindo, E.; Ramírez, O.T.; Palomares, L.A. Living with heterogeneities in bioreactors: Understanding the effects of environmental gradients on cells. Mol. Biotechnol. 2006, 34, 355–381. [Google Scholar] [CrossRef]
- Wright, N.R.; Wulff, T.; Palmqvist, E.A.; Jørgensen, T.R.; Workman, C.T.; Sonnenschein, N.; Rønnest, N.P.; Herrgård, M.J. Fluctuations in glucose availability prevent global proteome changes and physiological transition during prolonged chemostat cultivations of Saccharomyces cerevisiae. Biotechnol. Bioeng. 2020, 117, 2074–2088. [Google Scholar] [CrossRef] [PubMed]
- Binai, N.A.; Bisschops, M.M.M.; Van Breukelen, B.; Mohammed, S.; Loeff, L.; Pronk, J.T.; Heck, A.J.R.; Daran-Lapujade, P.; Slijper, M. Proteome adaptation of Saccharomyces cerevisiae to severe calorie restriction in retentostat cultures. J. Proteome Res. 2014, 13, 3542–3553. [Google Scholar] [CrossRef] [PubMed]
- Kraakman, L.S.; Winderickx, J.; Thevelein, J.M.; De Winde, J.H. Structure-function analysis of yeast hexokinase: Structural requirements for triggering cAMP signalling and catabolite repression. Biochem. J. 1999, 343, 159–168. [Google Scholar] [PubMed]
- François, J.; Parrou, J.L. Reserve carbohydrates metabolism in the yeast Saccharomyces cerevisiae. FEMS Microbiol. Rev. 2001, 25, 125–145. [Google Scholar] [CrossRef]
- De Winde, J.H.; Crauwels, M.; Hohmann, S.; Thevelein, J.M.; Winderickx, J. Differential requirement of the yeast sugar kinases for sugar sensing in establishing the catabolite-repressed state. Eur. J. Biochem. 1996, 241, 633–643. [Google Scholar] [CrossRef]
- Mans, R.; Daran, J.M.G.; Pronk, J.T. Under pressure: Evolutionary engineering of yeast strains for improved performance in fuels and chemicals production. Curr. Opin. Biotechnol. 2018, 50, 47–56. [Google Scholar] [CrossRef]
- Zhang, J.; Martinez-Gomez, K.; Heinzle, E.; Wahl, S.A. Metabolic switches from quiescence to growth in synchronized Saccharomyces cerevisiae. Metabolomics 2019, 15, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Rizzi, M.; Baltes, M.; Theobald, U.; Reuss, M. In vivo analysis of metabolic dynamics in Saccharomyces cerevisiae: II. Mathematical model. Biotechnol. Bioeng. 1997, 55, 592–608. [Google Scholar] [CrossRef]
- Link, H.; Fuhrer, T.; Gerosa, L.; Zamboni, N.; Sauer, U. Real-time metabolome profiling of the metabolic switch between starvation and growth. Nat. Methods 2015, 12, 1091–1097. [Google Scholar] [CrossRef] [PubMed]
- Siebler, F.; Lapin, A.; Hermann, M.; Takors, R. The impact of CO gradients on, C. ljungdahlii in a 125 m3 bubble column: Mass transfer, circulation time and lifeline analysis. Chem. Eng. Sci. 2019, 207, 410–423. [Google Scholar] [CrossRef]
- Haringa, C.; Deshmukh, A.T.; Mudde, R.F.; Noorman, H.J. Euler-Lagrange analysis towards representative down-scaling of a 22 m3 aerobic, S. cerevisiae fermentation. Chem. Eng. Sci. 2017, 170, 653–669. [Google Scholar] [CrossRef]
- Kordas, M.; Konopacki, M.; Grygorcewicz, B.; Augustyniak, A.; Musik, D.; Wójcik, K.; Jędrzejczak-Silicka, M.; Rakoczy, R. Hydrodynamics and mass transfer analysis in bioflow® bioreactor systems. Processes 2020, 8, 1311. [Google Scholar] [CrossRef]
- Di Serio, M.; Aramo, P.; De Alteriis, E.; Tesser, R.; Santacesaria, E. Quantitative analysis of the key factors affecting yeast growth. Ind. Eng. Chem. Res. 2003, 42, 5109–5116. [Google Scholar] [CrossRef]
- Sweere, A.P.J.; Mesters, J.R.; Janse, L.; Luyben, K.C.A.M.; Kossen, N.W.F. Experimental simulation of oxygen profiles and their influence on baker’s yeast production: I. One-fermentor system. Biotechnol. Bioeng. 1988, 31, 567–578. [Google Scholar] [CrossRef]
- Sweere, A.P.J.; Matla, Y.A.; Zandvliet, J.; Luyben, K.C.A.M.; Kossen, N.W.F. Experimental simulation of glucose fluctuations—The influence of continually changing glucose concentrations on the fed-batch baker’s yeast production. Appl. Microbiol. Biotechnol. 1988, 28, 109–115. [Google Scholar] [CrossRef]
- Enfors, S.; Hedenberg, J.; Olsson, K. Bi0pr0cess Engineering Simulation of the dynamics in the Baker ’ s yeast process. Bioprocess Eng. 1990, 5, 191–198. [Google Scholar] [CrossRef]
- Sweere, A.P.J.; van Dalen, J.P.; Kishoni, E.; Luyben, K.C.A.M.; Kossen, N.W.F. Theoretical analysis of the baker’s yeast production: An experimental verification at a laboratory scale—Part 2: Fed-batch fermentations. Bioprocess Eng. 1989, 4, 11–17. [Google Scholar] [CrossRef]
- Raab, A.M.; Lang, C. Oxidative versus reductive succinic acid production in the yeast Saccharomyces cerevisiae. Bioeng. Bugs. 2011, 2, 120–123. [Google Scholar] [CrossRef] [PubMed]
- Arikawa, Y.; Kuroyanagi, T.; Shimosaka, M.; Muratsubaki, H.; Enomoto, K.; Kodaira, R.; Okazaki, M. Effect of gene disruptions of the TCA cycle on production of succinic acid in Saccharomyces cerevisiae. J. Biosci. Bioeng. 1999, 87, 28–36. [Google Scholar] [CrossRef]
- Otero, J.M.; Cimini, D.; Patil, K.R.; Poulsen, S.G.; Olsson, L.; Nielsen, J. Industrial Systems Biology of Saccharomyces cerevisiae Enables Novel Succinic Acid Cell Factory. PLoS ONE 2013, 8, e54144. [Google Scholar] [CrossRef] [PubMed]
- Yan, D.; Wang, C.; Zhou, J.; Liu, Y.; Yang, M.; Xing, J. Construction of reductive pathway in Saccharomyces cerevisiae for effective succinic acid fermentation at low pH value. Bioresour. Technol. 2014, 156, 232–239. [Google Scholar] [CrossRef]
- Nissen, T.L.; Schulze, U.; Nielsen, J.; Villadsen, J. Flux distributions in anaerobic, glucose-limited continuous cultures of Saccharomyces cerevisiae. Microbiology 1997, 143, 203–218. [Google Scholar] [CrossRef]
- Hakkaart, X.; Liu, Y.; Hulst, M.; El Masoudi, A.; Peuscher, E.; Pronk, J.; Van Gulik, W.M.; Daran-Lapujade, P. Physiological responses of Saccharomyces cerevisiae to industrially relevant conditions: Slow growth, low pH, and high CO2 levels. Biotechnol. Bioeng. 2020, 117, 721–735. [Google Scholar] [CrossRef]
- Pham, H.T.B.; Larsson, G.; Enfors, S.O. Growth and energy metabolism in aerobic fed-batch cultures of Saccharomyces cerevisiae: Simulation and model verification. Biotechnol. Bioeng. 1998, 60, 474–482. [Google Scholar] [CrossRef]
- Sonnleitner, B.; Käppeli, O. Growth of Saccharomyces cerevisiae is controlled by its limited respiratory capacity: Formulation and verification of a hypothesis. Biotechnol. Bioeng. 1986, 28, 927–937. [Google Scholar] [CrossRef]
- Postma, E.; Alexander Scheffers, W.; Van Dijken, J.P. Kinetics of growth and glucose transport in glucose-limited chemostat cultures of Saccharomyces cerevisiae CBS 8066. Yeast 1989, 5, 159–165. [Google Scholar] [CrossRef]
- De Deken, R.H. The Crabtree effect: A regulatory system in yeast. J. Gen. Microbiol. 1966, 44, 149–156. [Google Scholar] [CrossRef] [PubMed]
- Van Urk, H.; Voll, W.S.L.; Scheffers, W.A.; Van Dijken, J.P. Transient-state analysis of metabolic fluxes in Crabtree-positive and crabtree-negative yeasts. Appl. Environ. Microbiol. 1990, 56, 281–287. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, T.; Morley, A. An evolutionary perspective on the Crabtree effect. Front. Mol. Biosci. 2014, 1, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Hagman, A.; Piškur, J. A study on the fundamental mechanism and the evolutionary driving forces behind aerobic fermentation in yeast. PLoS ONE 2015, 10, e0116942. [Google Scholar] [CrossRef]
- Van Urk, H.; Postma, E.; Scheffers, W.A.; van Dijken, J.P. Glucose Transport in Crabtree-positive and Crabtree-negative. Yeasts 1989, 2399–2406. [Google Scholar] [CrossRef]
- Vrábel, P.; Van der Lans, R.G.J.M.; Van der Schot, F.N.; Luyben , K.C.A.M.; Xu, B.; Enfors, S.O. CMA: Integration of fluid dynamics and microbial kinetics in modelling of large-scale fermentations. Chem. Eng. J. 2001, 84, 463–474. [Google Scholar]
- Mazzoleni, S.; Landi, C.; Cartenì, F.; De Alteriis, E.; Giannino, F.; Paciello, L.; Parascandola, P. A novel process-based model of microbial growth: Self-inhibition in Saccharomyces cerevisiae aerobic fed-batch cultures. Microb. Cell Factories 2015, 14, 1–14. [Google Scholar] [CrossRef]
- Enfors, S.-O.; Jahic, M.; Rozkov, A.; Xu, B.; Hecker, M.; Jürgen, B.; Krüger, E.; Schweder, T.; Hamer, G.; O’Beirne, D.; et al. Physiological responses to mixing in large scale bioreactors. J. Biotechnol. 2001, 85, 175–185. [Google Scholar] [CrossRef]
- Kozak, B.U.; van Rossum, H.M.; Niemeijer, M.S.; van Dijk, M.; Benjamin, K.; Wu, L.; Daran, J.G.; Pronk, J.T.; van Maris, A.J.A. Replacement of the initial steps of ethanol metabolism in Saccharomyces cerevisiae by ATP-independent acetylating acetaldehyde dehydrogenase. FEMS Yeast Res. 2016, 16, fow006. [Google Scholar] [CrossRef][Green Version]
- Delafosse, A.; Collignon, M.-L.; Calvo, S.; Delvigne, F.; Crine, M.; Thonart, P.; Toye, D. CFD-based compartment model for description of mixing in bioreactors. Chem. Eng. Sci. 2014, 106, 76–85. [Google Scholar] [CrossRef]
- Nieß, A.; Löffler, M.; Simen, J.D.; Takors, R. Repetitive Short-Term Stimuli Imposed in Poor Mixing Zones Induce Long-Term Adaptation of E. coli Cultures in Large-Scale Bioreactors: Experimental Evidence and Mathematical Model. Front. Microbiol. 2017, 8, 1195. [Google Scholar] [CrossRef] [PubMed]
- Smets, B.; Ghillebert, R.; De Snijder, P.; Binda, M.; Swinnen, E.; De Virgilio, C.; Winderickx, J. Life in the midst of scarcity: Adaptations to nutrient availability in Saccharomyces cerevisiae. Curr. Genet. 2010, 56, 1–32. [Google Scholar] [CrossRef] [PubMed]
- Larsson, C.; Påhlman, I.L.; Gustafsson, L. The importance of ATP as a regulator of glycolytic flux in Saccharomyces cerevisiae. Yeast 2000, 16, 797–809. [Google Scholar] [CrossRef]
- Larsson, C.; Nilsson, A.; Blomberg, A.; Gustafsson, L. Glycolytic flux is conditionally correlated with ATP concentration in Saccharomyces cerevisiae: A chemostat study under carbon or nitrogen-limiting conditions. J. Bacteriol. 1997, 179, 7243–7250. [Google Scholar] [CrossRef] [PubMed]
- Somsen, O.J.G.; Hoeben, M.A.; Esgalhado, E.; Snoep, J.L.; Visser, D.; Van der Heijden, R.T.J.M.; Heijnen, J.J.; Westerhoff, H.V. Glucose and the ATP paradox in yeast. Biochem. J. 2000, 352, 593–599. [Google Scholar] [CrossRef]
- Verma, M.; Zakhartsev, M.; Reuss, M.; Westerhoff, H.V. ‘Domino’ systems biology and the ‘A’ of ATP. Biochim. Biophys. Acta (BBA) Gen. Subj. 2013, 1827, 19–29. [Google Scholar] [CrossRef]
- Kerkhoven, E.J.; Lahtvee, P.J.; Nielsen, J. Applications of computational modeling in metabolic engineering of yeast. FEMS Yeast Res. 2015, 15, 1–13. [Google Scholar] [CrossRef]
- Almquist, J.; Cvijovic, M.; Hatzimanikatis, V.; Nielsen, J.; Jirstrand, M. Kinetic models in industrial biotechnology—Improving cell factory performance. Metab. Eng. 2014, 24, 38–60. [Google Scholar] [CrossRef]
- Campbell, K.; Xia, J.; Nielsen, J. The Impact of Systems Biology on Bioprocessing. Trends Biotechnol. 2017, 35, 1156–1168. [Google Scholar] [CrossRef]
- Campbell, K.; Westholm, J.; Kasvandik, S.; Di Bartolomeo, F.; Mormino, M.; Nielsen, J. Building blocks are synthesized on demand during the yeast cell cycle. Proc. Natl. Acad. Sci. USA 2020, 117, 7575–7583. [Google Scholar] [CrossRef]
- Szatkowska, R.; Albornoz, M.G.; Roszkowska, K.; Holman, S.W.; Furmanek, E.; Hubbard, S.J.; Beynon, R.J.; Adamczyk, M. Glycolytic flux in Saccharomyces cerevisiae is dependent on RNA polymerase III and its negative regulator Maf1. Biochem. J. 2019, 476, 1053–1082. [Google Scholar] [CrossRef] [PubMed]
- Delvigne, F.; Takors, R.; Mudde, R.; van Gulik, W.; Noorman, H. Bioprocess scale-up/down as integrative enabling technology: From fluid mechanics to systems biology and beyond. Microb. Biotechnol. 2017, 10, 1267–1274. [Google Scholar] [CrossRef] [PubMed]
- Takors, R. Scale-up of microbial processes: Impacts, tools and open questions. J. Biotechnol. 2012, 160, 3–9. [Google Scholar] [CrossRef]
- Takors, R. Biochemical engineering provides mindset, tools and solutions for the driving questions of a sustainable future. Eng. Life Sci. 2020, 20, 5–6. [Google Scholar] [CrossRef] [PubMed]
- Noorman, H.J.; Heijnen, J.J. Biochemical engineering’s grand adventure. Chem. Eng. Sci. 2017, 170, 677–693. [Google Scholar] [CrossRef]
- Morchain, J.; Gabelle, J.C.; Cockx, A. A coupled population balance model and CFD approach for the simulation of mixing issues in lab-scale and industrial bioreactors. AIChE J. 2014, 60, 27–40. [Google Scholar] [CrossRef]
- Lemoine, A.; Delvigne, F.; Bockisch, A.; Neubauer, P.; Junne, S. Tools for the determination of population heterogeneity caused by inhomogeneous cultivation conditions. J. Biotechnol. 2017, 251, 84–93. [Google Scholar] [CrossRef]
- Murthy, B.N.; Joshi, J.B. Assessment of standard k-ε{lunate}, RSM and LES turbulence models in a baffled stirred vessel agitated by various impeller designs. Chem. Eng. Sci. 2008, 63, 5468–5495. [Google Scholar] [CrossRef]
- Derksen, J.J. Direct simulations of mixing of liquids with density and viscosity differences. Ind. Eng. Chem. Res. 2012, 51, 6948–6957. [Google Scholar] [CrossRef]
- Witz, C.; Treffer, D.; Hardiman, T.; Khinast, J. Local gas holdup simulation and validation of industrial-scale aerated bioreactors. Chem. Eng. Sci. 2016, 152, 636–648. [Google Scholar] [CrossRef]
- Pigou, M.; Morchain, J. Investigating the interactions between physical and biological heterogeneities in bioreactors using compartment, population balance and metabolic models. Chem. Eng. Sci. 2015, 126, 267–282. [Google Scholar] [CrossRef]
- Sarkizi Shams Hajian, C.; Zieringer, J.; Takors, R. Chapter 15: Euler-Lagrangian simulations – a proper tool for predicting cellular performance in industrial scale bioreactors. In Digital Twins—Applications to the Design and Optimization of Bioprocesses; Herwig, C., Möller, J., Pörtner, R., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2020. [Google Scholar]
- Eigenstetter, G.; Takors, R. Dynamic modeling reveals a three-step response of Saccharomyces cerevisiae to high CO2 levels accompanied by increasing ATP demands. FEMS Yeast Res. 2017, 17, 1–11. [Google Scholar] [CrossRef][Green Version]
- Larsson, G.; Törnkvist, M.; Ståhl Wernersson, E.; Trägårdh, C.; Noorman, H.; Enfors, S.O. Substrate gradients in bioreactors: Origin and consequences. Bioprocess Eng. 1996, 14, 281–289. [Google Scholar] [CrossRef]
- Marshall, E.M.; Bakker, A. Computational Fluid Mixing. In Handbook of Industrial Mixing; Atiemo-Obeng, V.A., Calabrese, R.V., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; pp. 257–343. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; (Dover Books on Engineering); Clift, R., Grace, J.R., Weber, M.E., Eds.; Dover Publ.: Mineola, NY, USA, 2005; Volume XIII, p. 381. [Google Scholar]
- Scargiali, F.; D’Orazio, A.; Grisafi, F.; Brucato, A. Modelling and simulation of gas—Liquid hydrodynamics in mechanically stirred tanks. Chem Eng Res Des. 2007, 85, 637–646. [Google Scholar] [CrossRef]
- Ansys® Academic Research Fluent, Release 2019 R1, Fluent user’s Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2019.
- Weusthuis, R.A.; Visser, W.; Pronk, J.T.; Scheffers, W.A.; Van Dijken, J.P. Effects of oxygen limitation on sugar metabolism in yeasts: A continuous-culture study of the Kluyver effect. Microbiology 1994, 140, 703–715. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sweere, A.P.J.; Giesselbach, J.; Barendse, R.; de Krieger, R.; Honderd, G.; Luyben, K.C.A.M. Modelling the dynamic behaviour of Saccharomyces cerevisiae and its application in control experiments. Appl. Microbiol. Biotechnol. 1988, 28, 116–127. [Google Scholar] [CrossRef]
- Kuschel, M.; Siebler, F.; Takors, R. Lagrangian Trajectories to Predict the Formation of Population Heterogeneity in Large-Scale Bioreactors. Bioengineering 2017, 4, 27. [Google Scholar] [CrossRef]
- Zieringer, J.; Takors, R. In Silico Prediction of Large-Scale Microbial Production Performance: Constraints for Getting Proper Data-Driven Models. Comput. Struct. Biotechnol. J. 2018, 16, 246–256. [Google Scholar] [CrossRef]
- Alves, S.S.; Vasconcelos, J.M.T.; Orvalho, S.P. Mass transfer to clean bubbles at low turbulent energy dissipation. Chem. Eng. Sci. 2006, 61, 1334–1337. [Google Scholar] [CrossRef]
- Sieblist, C.; Hägeholz, O.; Aehle, M.; Jenzsch, M.; Pohlscheidt, M.; Lübbert, A. Insights into large-scale cell-culture reactors: II. Gas-phase mixing and CO 2 stripping. Biotechnol. J. 2011, 6, 1547–1556. [Google Scholar] [CrossRef]
- Löser, C.; Schröder, A.; Deponte, S.; Bley, T. Balancing the ethanol formation in continuous bioreactors with ethanol stripping. Eng. Life Sci. 2005, 5, 325–332. [Google Scholar] [CrossRef]
- Vrábel, P.; Van Der Lans, R.G.J.M.; Cui, Y.Q.; Luyben, K.C.A.M. Compartment model approach: Mixing in large scale aerated reactors with multiple impellers. Chem. Eng. Res. Des. 1999, 77, 291–302. [Google Scholar] [CrossRef]
- Bailey, J.E.; Ollis, D.F. Biochemical Engineering Fundamentals. McGraw-Hill Chemical Engineering Series); McGraw-Hill. 1986. Available online: https://books.google.de/books?id=KM9TAAAAMAAJ (accessed on 26 September 2020).
- Blombach, B.; Takors, R. CO2—Intrinsic product, essential substrate, and regulatory trigger of microbial and mammalian production processes. Front. Bioeng. Biotechnol. 2015, 3, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Kuschel, M.; Takors, R. Simulated oxygen and glucose gradients as a prerequisite for predicting industrial scale performance a priori. Biotechnol. Bioeng. 2020, 117, 2760–2770. [Google Scholar] [CrossRef]
- Mancini, M.; Moresi, M. Rheological behaviour of baker’s yeast suspensions. J. Food Eng. 2000, 44, 225–231. [Google Scholar] [CrossRef]
- Delvigne, F.; Destain, J.; Thonart, P. A methodology for the design of scale-down bioreactors by the use of mixing and circulation stochastic models. Biochem. Eng. J. 2006, 28, 256–268. [Google Scholar] [CrossRef]
- Guijarro, J.M.; Lagunas, R. Saccharomyces cerevisiae does not accumulate ethanol against a concentration gradient. J. Bacteriol. 1984, 160, 874–878. [Google Scholar] [CrossRef] [PubMed]
- Piškur, J.; Rozpedowska, E.; Polakova, S.; Merico, A.; Compagno, C. How did Saccharomyces evolve to become a good brewer? Trends Genet. 2006, 22, 183–186. [Google Scholar] [CrossRef]
- Thomson, J.M.; A Gaucher, E.; Burgan, M.F.; De Kee, D.W.; Li, T.; Aris, J.P.; A Benner, S. Resurrecting ancestral alcohol dehydrogenases from yeast. Nat. Genet. 2005, 37, 630–635. [Google Scholar] [CrossRef]
- Tang, W.; Deshmukh, A.T.; Haringa, C.; Wang, G.; Van Gulik, W.; Van Winden, W.; Reuss, M.; Heijnen, J.J.; Xia, J.; Chu, J.; et al. A 9-pool metabolic structured kinetic model describing days to seconds dynamics of growth and product formation by Penicillium chrysogenum. Biotechnol. Bioeng. 2017, 114, 1733–1743. [Google Scholar] [CrossRef]
- La, A.; Du, H.; Taidi, B.; Perré, P. A predictive dynamic yeast model based on component, energy, and electron carrier balances. Biotechnol. Bioeng. 2020, 117, 2728–2740. [Google Scholar] [CrossRef] [PubMed]
- Orij, R.; Brul, S.; Smits, G.J. Intracellular pH is a tightly controlled signal in yeast. Biochim. Biophys. Acta (BBA) Gen. Subj. 2011, 1810, 933–944. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.H.; Mauvais, G.; Vergoignan, C.; De Coninck, J.; Dumont, F.; Lherminier, J.; Cachon, R.; Feron, G. Gaseous environments modify physiology in the brewing yeast Saccharomyces cerevisiae during batch alcoholic fermentation. J. Appl. Microbiol. 2008, 105, 858–874. [Google Scholar] [CrossRef] [PubMed]


| Operation Conditions | Description | Ref. |
|---|---|---|
| Primary phase | ~water
| [25] |
| Secondary phase | ~air
| [25] |
| Inter-phase forces | Drag
| [76,77] |
| Aeration rate | 0.231 kg/s | [74] |
| Headspace pressure | 130,710 Pa | [74] |
| Agitation rate | 2.22 s−1 | [74] |
| Glucose feed | 52 kg/h | [25] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarkizi Shams Hajian, C.; Haringa, C.; Noorman, H.; Takors, R. Predicting By-Product Gradients of Baker’s Yeast Production at Industrial Scale: A Practical Simulation Approach. Processes 2020, 8, 1554. https://doi.org/10.3390/pr8121554
Sarkizi Shams Hajian C, Haringa C, Noorman H, Takors R. Predicting By-Product Gradients of Baker’s Yeast Production at Industrial Scale: A Practical Simulation Approach. Processes. 2020; 8(12):1554. https://doi.org/10.3390/pr8121554
Chicago/Turabian StyleSarkizi Shams Hajian, Christopher, Cees Haringa, Henk Noorman, and Ralf Takors. 2020. "Predicting By-Product Gradients of Baker’s Yeast Production at Industrial Scale: A Practical Simulation Approach" Processes 8, no. 12: 1554. https://doi.org/10.3390/pr8121554
APA StyleSarkizi Shams Hajian, C., Haringa, C., Noorman, H., & Takors, R. (2020). Predicting By-Product Gradients of Baker’s Yeast Production at Industrial Scale: A Practical Simulation Approach. Processes, 8(12), 1554. https://doi.org/10.3390/pr8121554






