Prototype of the Runway Monitoring Process at Smaller Airports: Edvard Rusjan Airport Maribor
Abstract
:1. Introduction
2. Equipment and Methods
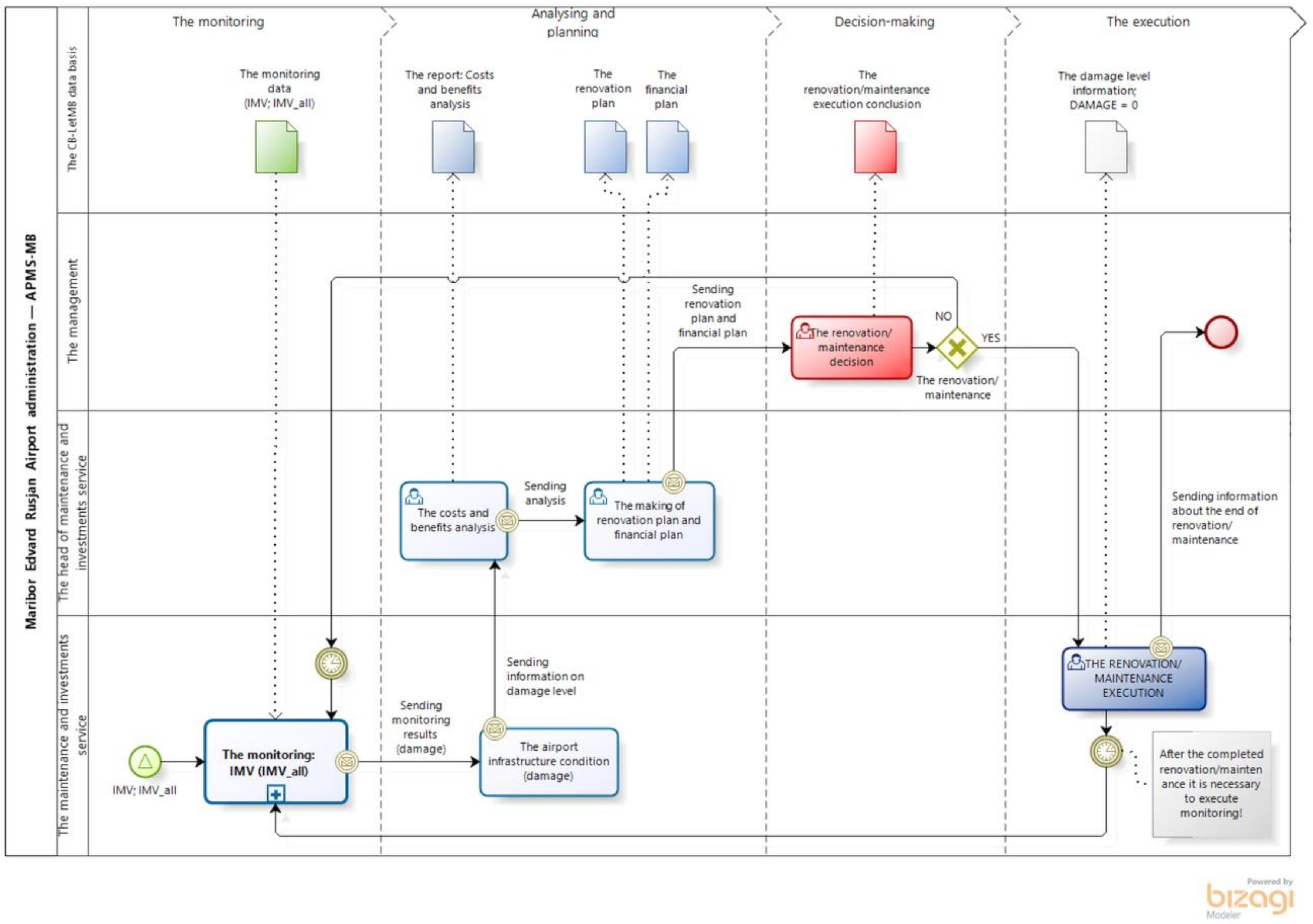
2.1. Process Model for Maintenance and Monitoring
2.2. Monitoring Methodology
2.2.1. Used Measurement Equipment
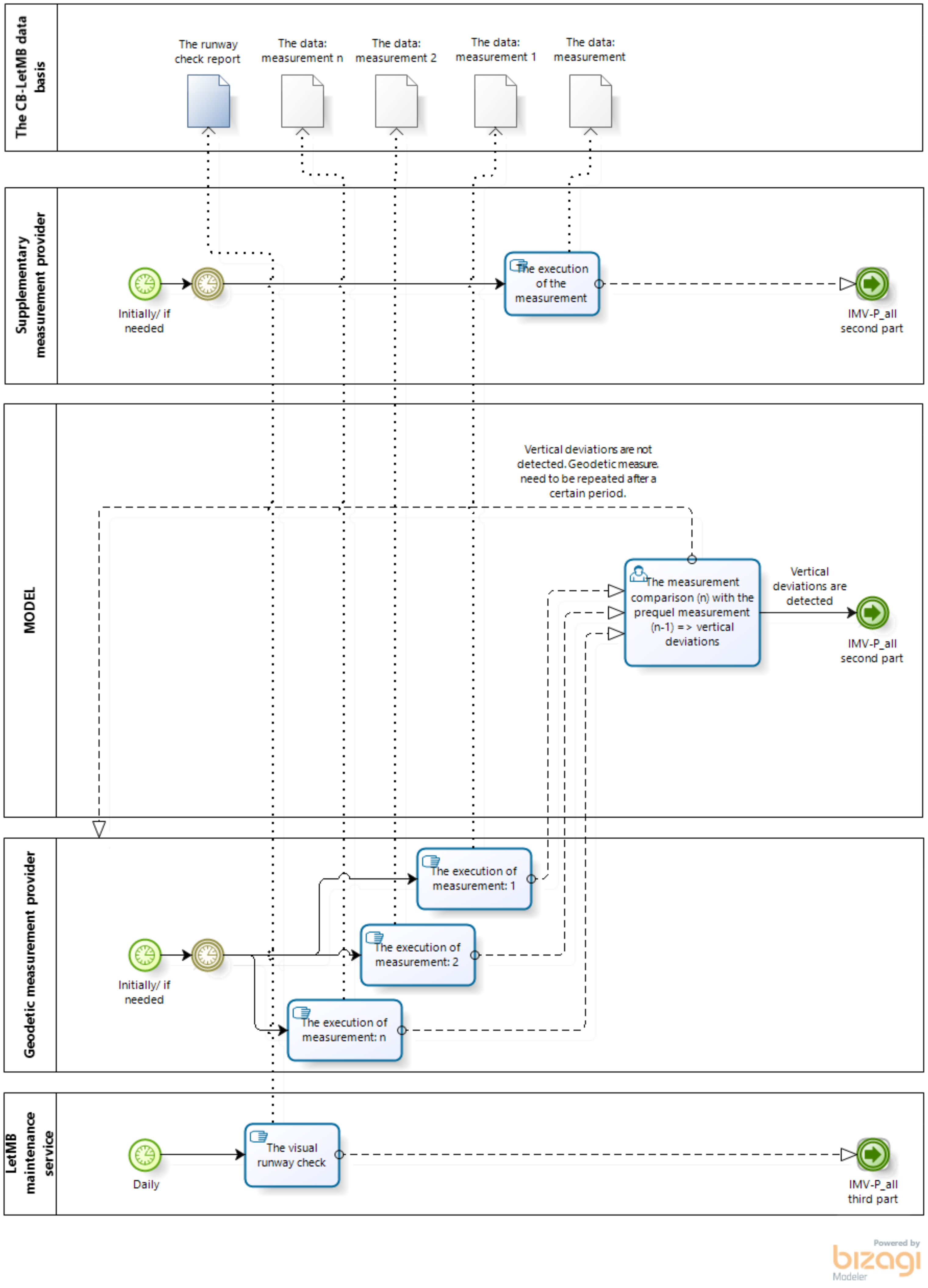
2.2.2. Methodology for Taking Geodetic Measurements
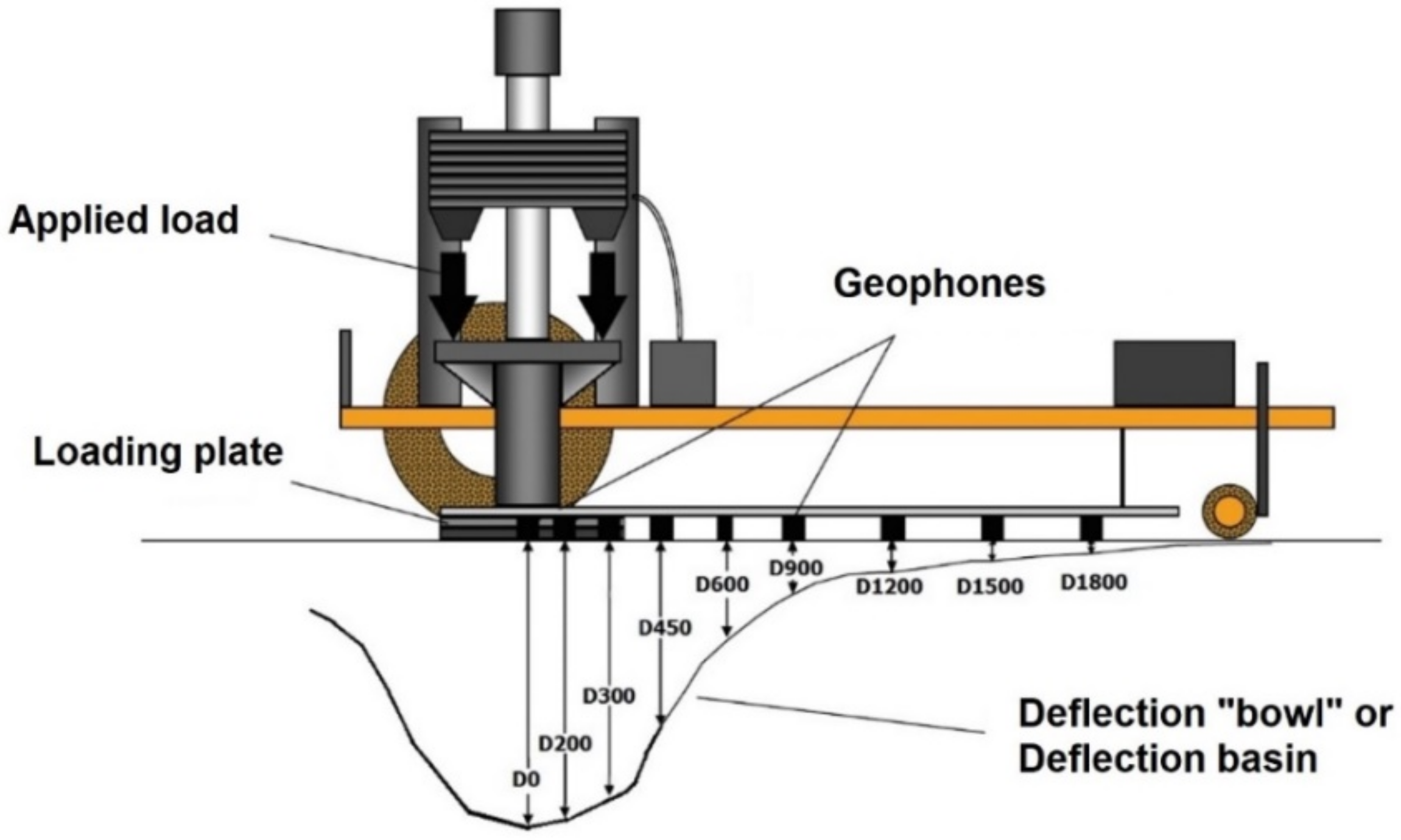
2.2.3. Methodology for FWD Measurement Execution
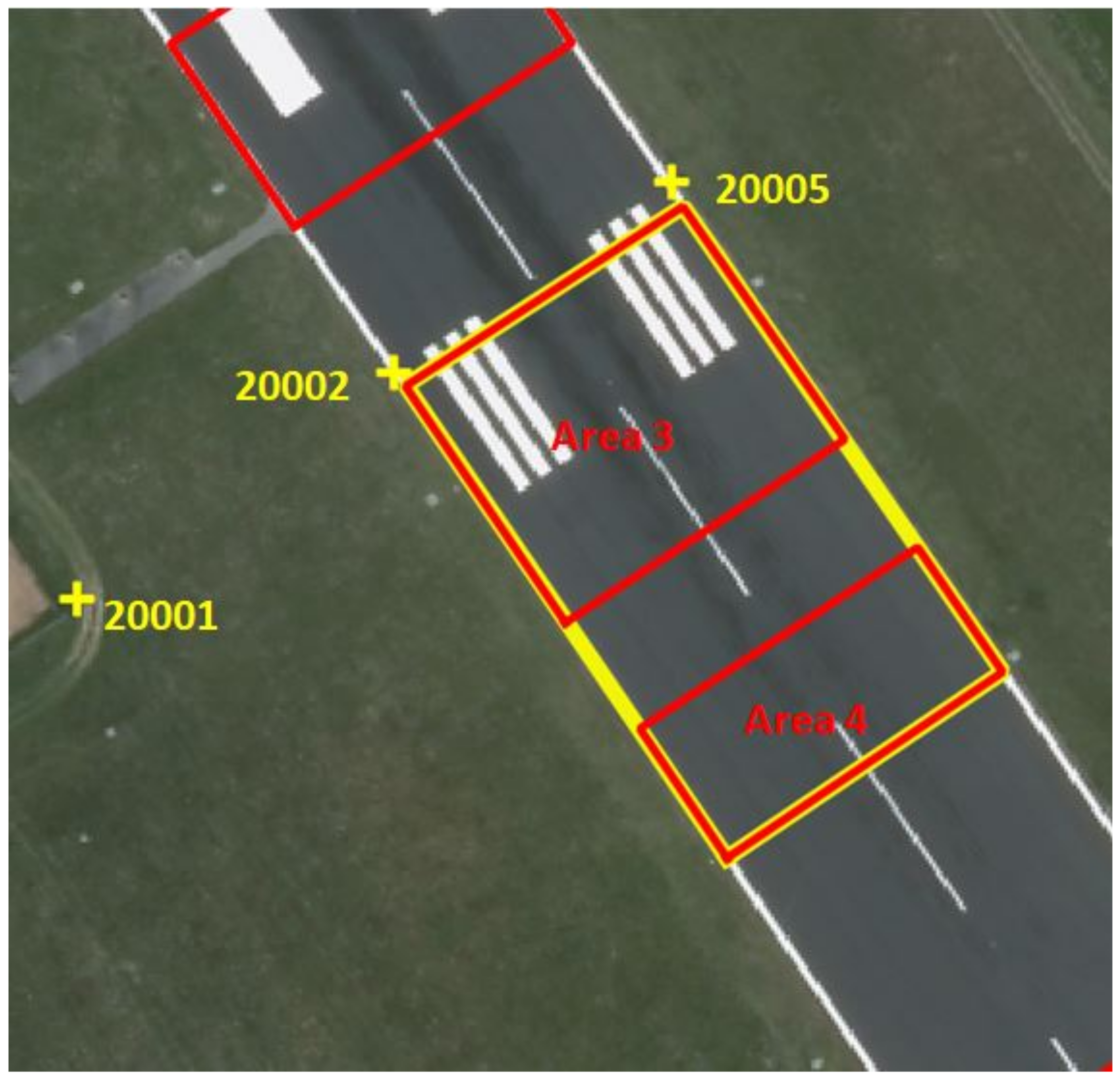
2.2.4. The Requirements of the Measurements
3. Measurement Results
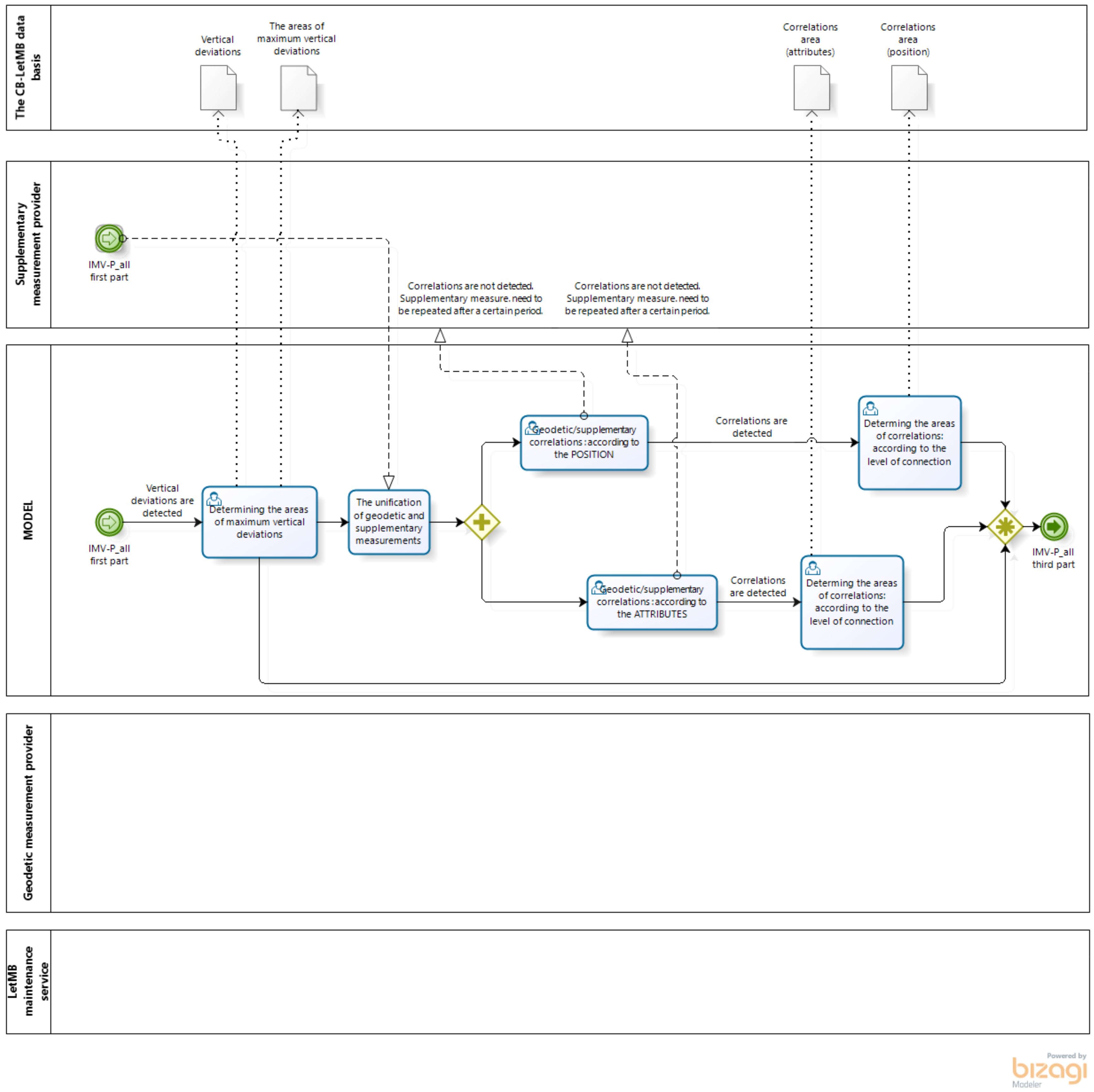
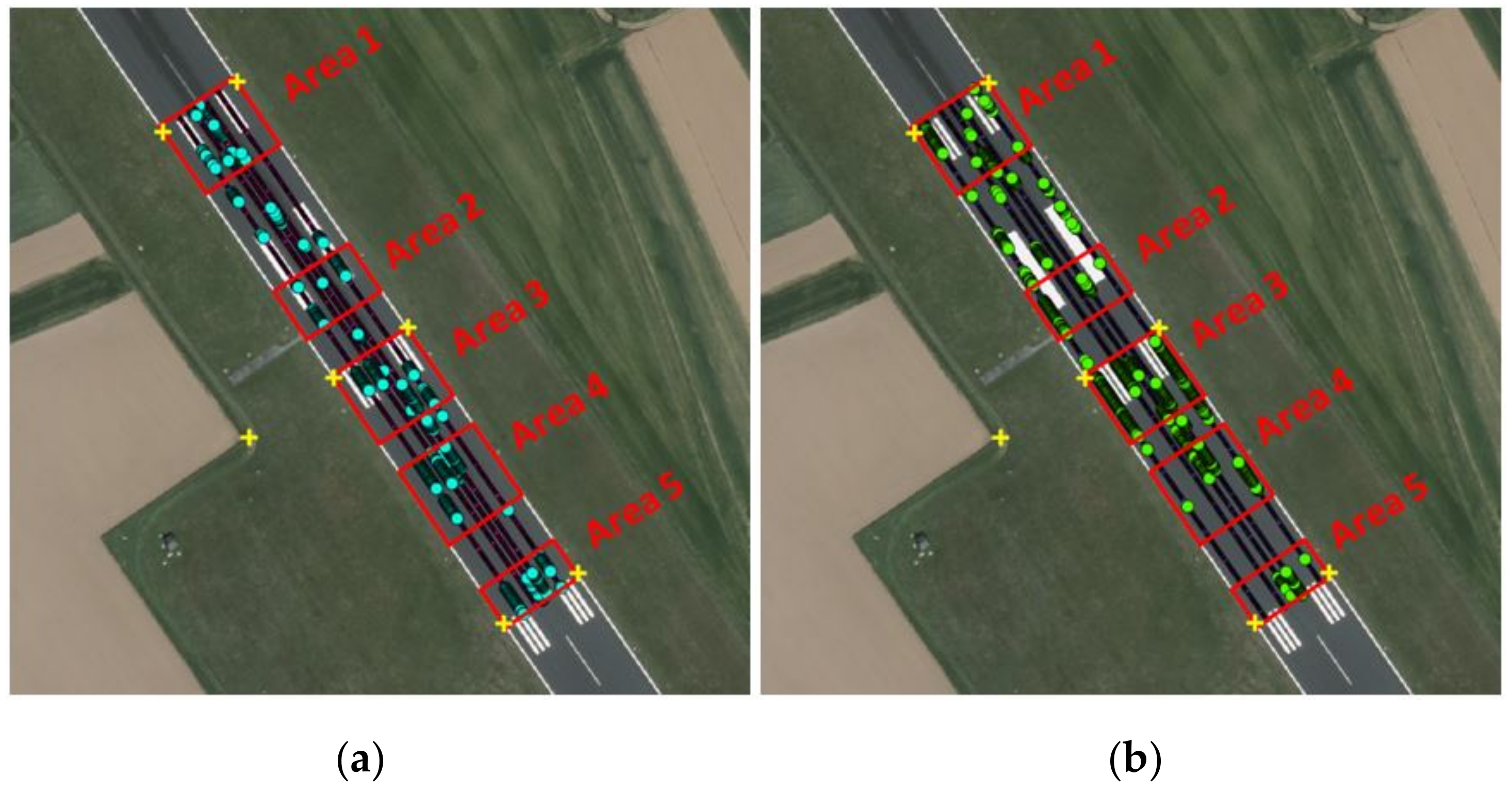
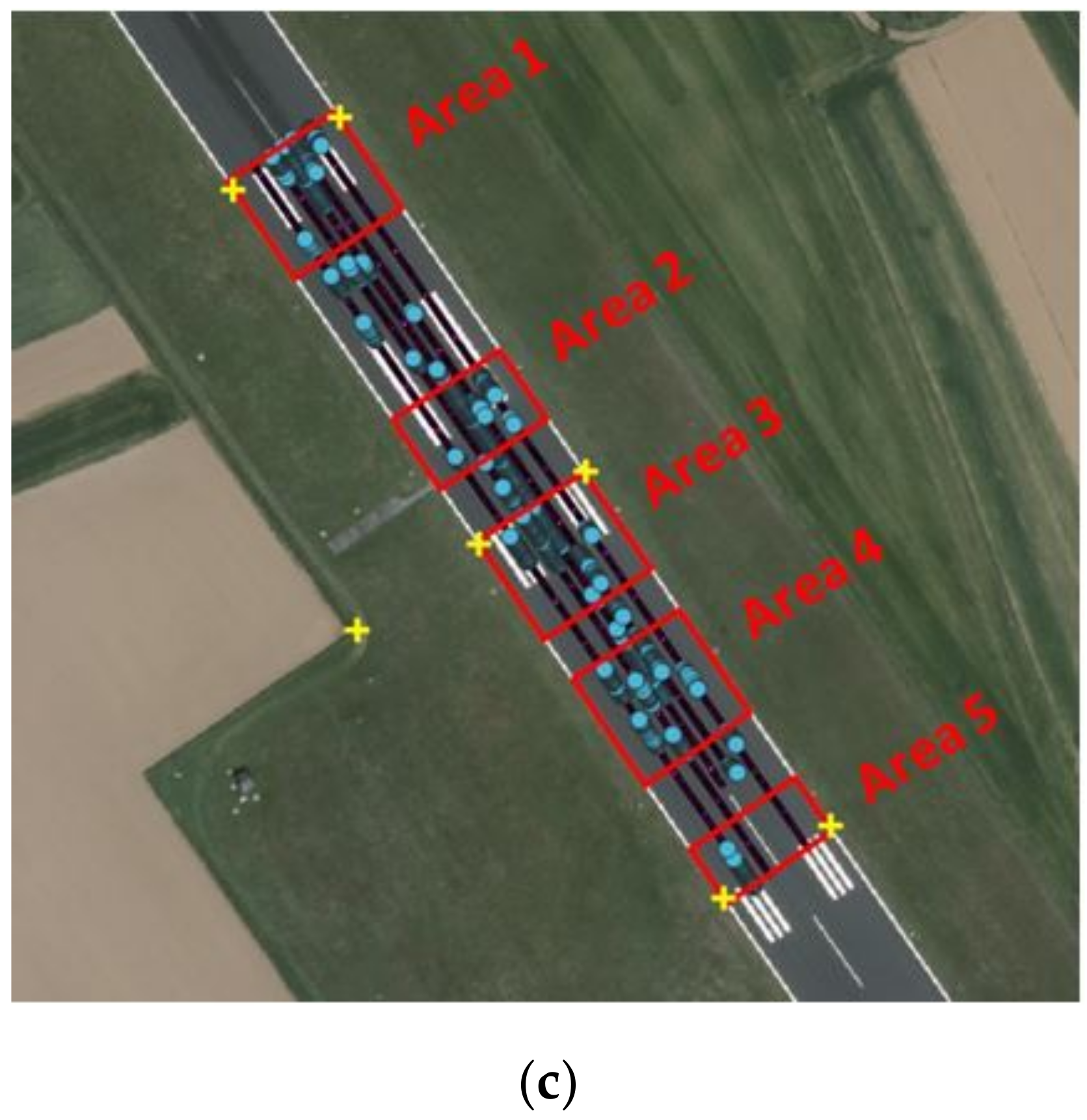
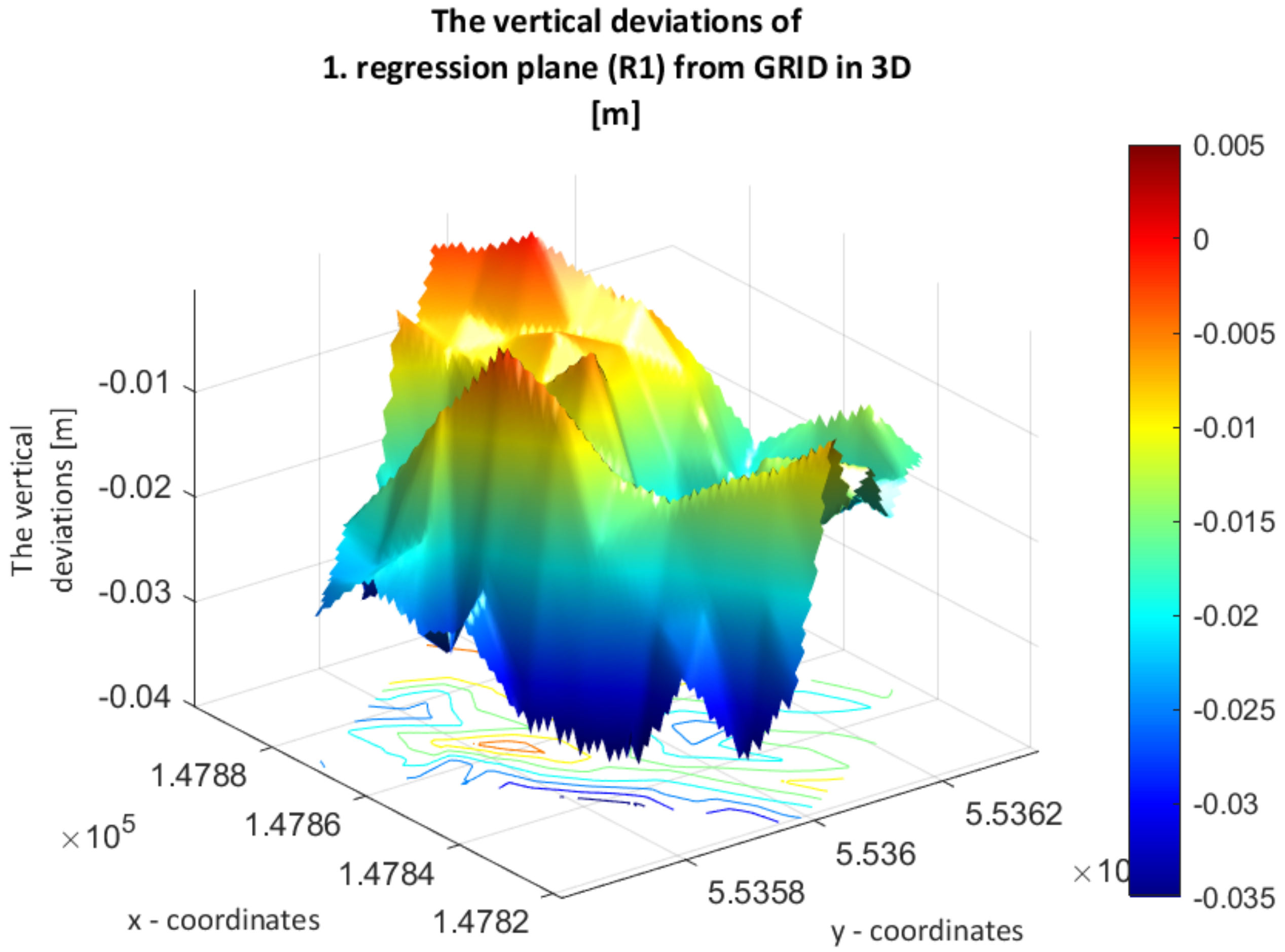
3.1. Results of Monitoring with Geodetic Measurements
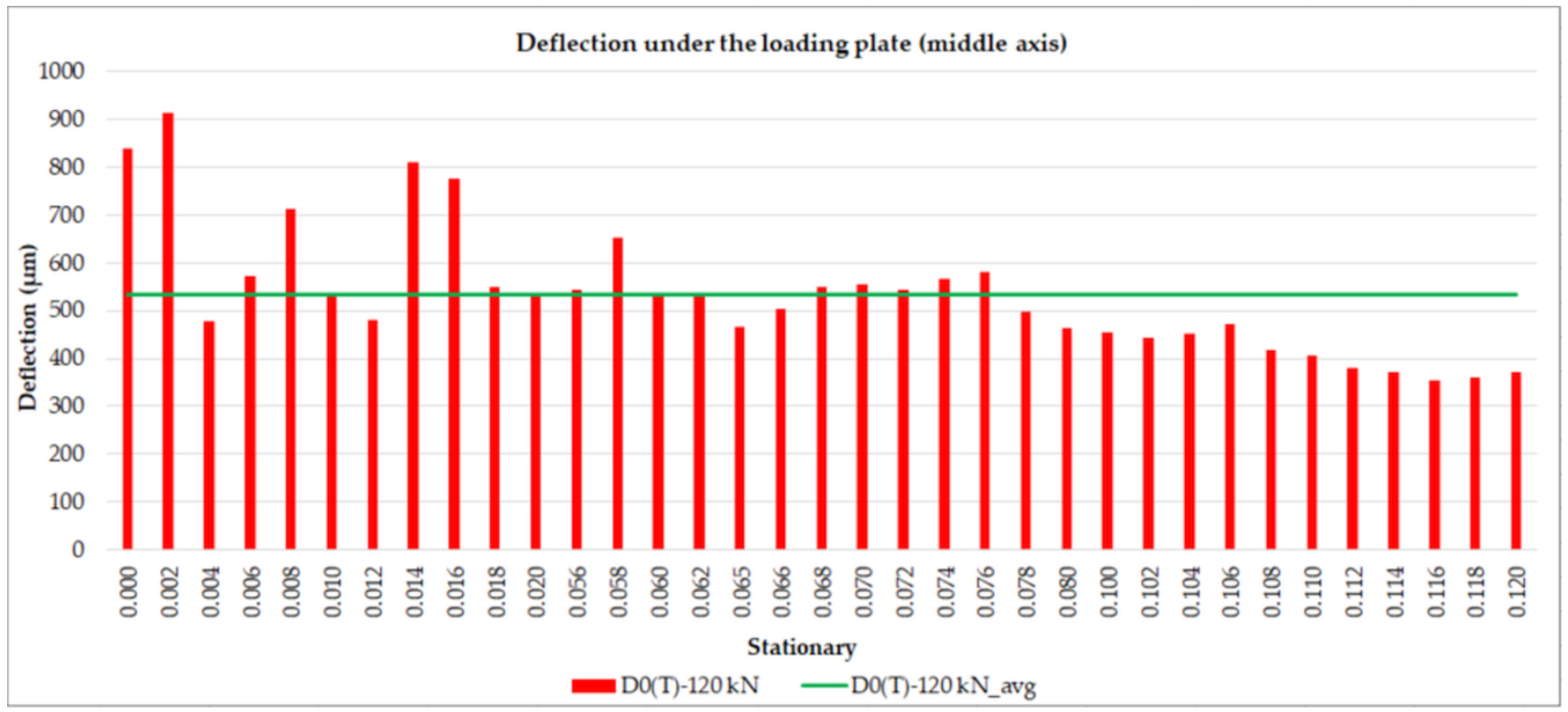
3.2. Results of Monitoring with FWD Measurements
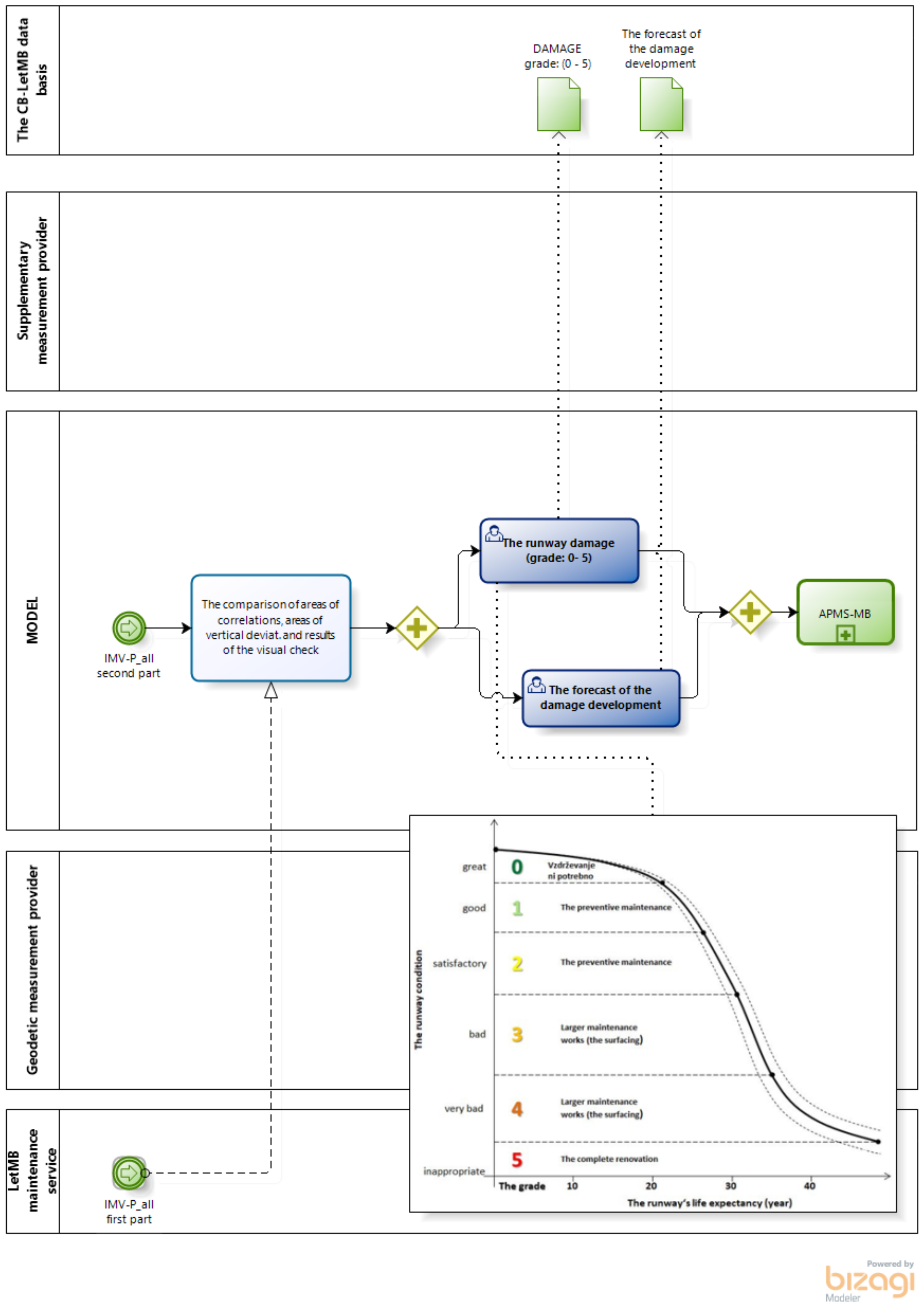
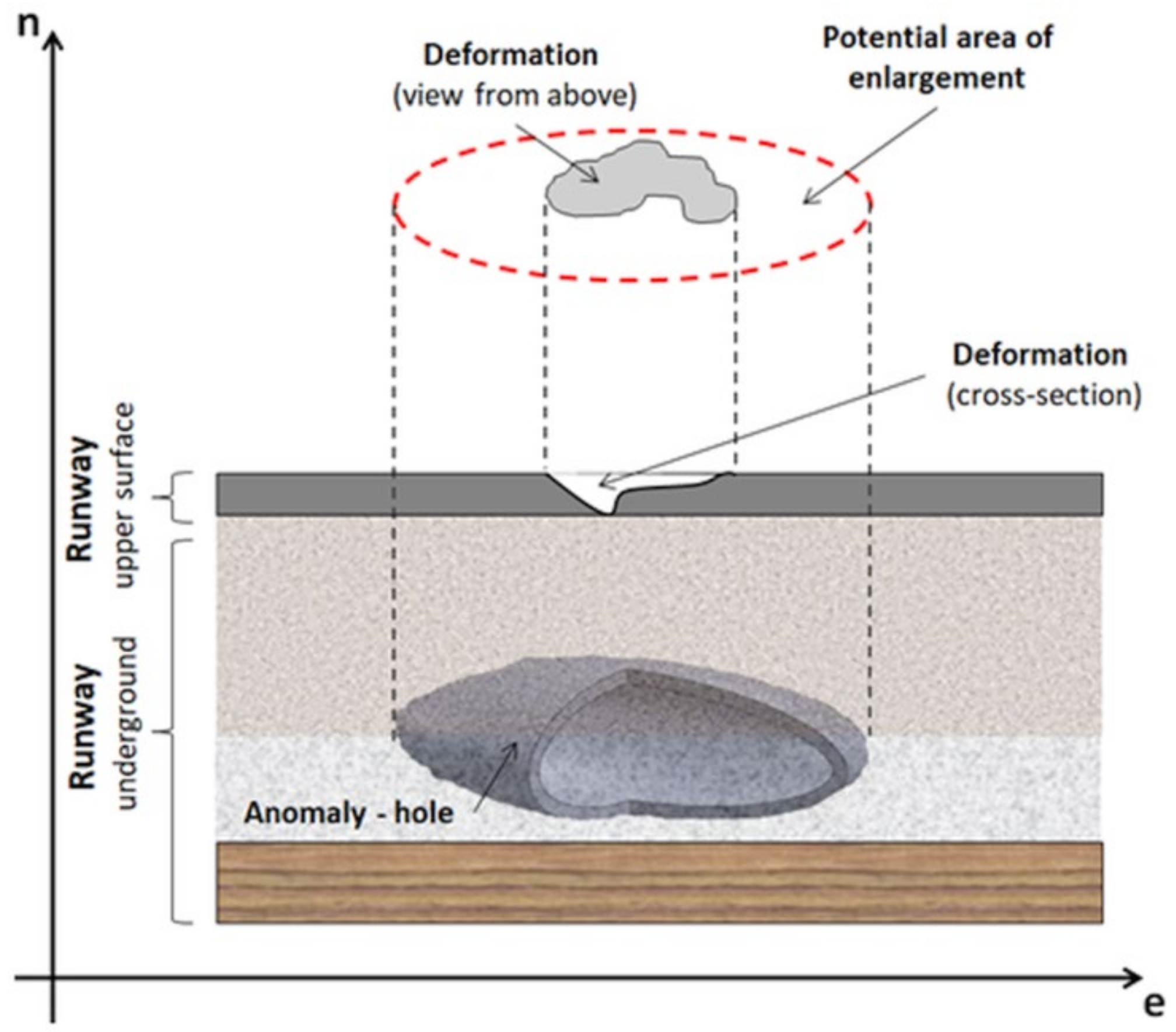
3.3. Results of the Monitoring Using Geodetic and FWD Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Orbanić, J.; Rosi, B. Razvoj Transporta, Logistike. In Mobilnosti v Sloveniji; Fakulteta za Logistiko: Celje, Slovenia, 2016. (In Slovenian) [Google Scholar]
- IATA—International Air Transports Association Air Passenger Forecasts Global Report. Available online: https://www.iata.org/publications/store/Pages/20-year-passenger-forecast.aspx (accessed on 13 October 2020).
- Wang, W.; Deng, S. Evaluation and analysis of the pavement roughness of airport runway. J. Chin. Civ. Aviat. Coll. 2006, 24, 10–15. [Google Scholar]
- D’Apuzzo, M.; Festa, B.; Giuliana, G.; Mancini, L.; Nicolosi, V. The Evaluation of Runway Surface Properties: A New Approach. Procedia Soc. Behav. Sci. 2012, 53, 1192–1201. [Google Scholar] [CrossRef]
- Jackson, P.T.; Nelson, C.J.; Schiefeley, J.; Obara, B.; Jackson, P.T.; Nelson, C.J.; Schiefeley, J.; Obara, B. Runway detection in High Resolution remote sensing data. In Proceedings of the 9th International Symposium on Image and Signal Processing and Analysis (ISPA), Zagreb, Croatia, 7–9 September 2015; pp. 170–175. [Google Scholar]
- Wang, W. Protocol Based Pavement Cracking Measurement with 1 Mm 3D Pavement Surface Model. Ph.D. Thesis, Oklahoma State University, Stillwater, OK, USA, 2015. [Google Scholar]
- Jamili, A. A robust mathematical model and heuristic algorithms for integrated aircraft routing and scheduling, with consideration of fleet assignment problem. J. Air Transp. Manag. 2017, 58, 21–30. [Google Scholar] [CrossRef]
- Oliveira, H.; Correia, P.L. Automatic Road Crack Detection and Characterization. IEEE Trans. Intell. Transp. Syst. 2013, 14, 155–168. [Google Scholar] [CrossRef]
- Mokhtari, S.; Wu, L.; Yun, H.-B. Comparison of Supervised Classification Techniques for Vision-Based Pavement Crack Detection. Transp. Res. Rec. J. Transp. Res. Board 2016, 2595, 119–127. [Google Scholar] [CrossRef]
- Shi, Y.; Cui, L.; Qi, Z.; Meng, F.; Chen, Z. Automatic Road Crack Detection Using Random Structured Forests. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3434–3445. [Google Scholar] [CrossRef]
- Wang, P.; Hu, Y.; Dai, Y.; Tian, M. Asphalt Pavement Pothole Detection and Segmentation Based on Wavelet Energy Field. Math. Probl. Eng. 2017, 2017, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Peng, L.; Chao, W.; Shuangmiao, L.; Baocai, F. Research on Crack Detection Method of Airport Runway Based on Twice-Threshold Segmentation. In Proceedings of the 5th International Conference on Instrumentation and Measurement, Computer, Communication and Control (IMCCC), Qinhuangdao, China, 18–20 September 2015; pp. 1716–1720. [Google Scholar]
- Fernández, A.C.; Rodriguez-Lozano, F.J.; Villatoro, R.; Olivares, J.; Palomares, J.M. Efficient pavement crack detection and classification. Eurasip J. Image Video Process. 2017, 2017, 39. [Google Scholar] [CrossRef]
- Li, W.; Huyan, J.; Tighe, S.L.; Ren, Q.-Q.; Sun, Z.-Y. Three-Dimensional Pavement Crack Detection Algorithm Based on Two-Dimensional Empirical Mode Decomposition. J. Transp. Eng. Part B Pavements 2017, 143, 04017005. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, J.; Lu, X.; Xie, R.; Li, L. DeepCrack: A deep hierarchical feature learning architecture for crack segmentation. Neurocomputing 2019, 338, 139–153. [Google Scholar] [CrossRef]
- Doler, D.; Kovačič, B. Improved decision-making geo-information system for continuous monitoring of deformations on airport infrastructure. ISPRS Int. J. Geo Inf. 2019, 8, 1. [Google Scholar] [CrossRef] [Green Version]
- Lalagüe, A. Use of Ground Penetrating Radar for Transportation Infrastructure Maintenance. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2015. [Google Scholar]
- Chapursky, V.; Ivashov, S.; Razevig, V.; Sheyko, A.; Vasilyev, I.; Pomozov, V.; Semeikin, N.; Desmond, D. Subsurface radar examination of an airstrip. In Proceedings of the 2002 IEEE Conference on Ultra Wideband Systems and Technologies (IEEE Cat. No.02EX580), Baltimore, MD, USA, 21–23 May 2002. [Google Scholar]
- Moropoulou, A.; Avdelidis, N.; Koui, M.; Aggelopoulos, A.; Karmis, P. Infrared thermography and ground penetrating radar for airport pavements assessment. Nondestruct. Test. Eval. 2002, 18, 37–42. [Google Scholar] [CrossRef]
- Berthelod, C.; Stuber, E.; Haichert, R.; Anthony, A.; Hansen, D.; Heal, P. Non Destructive Structural Asset Valuation of a Saskatchewan Rural Airfield before and after Structura Upgrade. In Proceedings of the Annual Conference of the Transportation Association of Canada, Vancouver, BC, Canada, 18–21 October 2009. [Google Scholar]
- Song, X.; Wu, R.; Liu, J. Underground diseases identification of airport runway using GPR. In Proceedings of the PIERS Proceedings, Xi’an, China, 22–26 March 2010. [Google Scholar]
- Celaya, M. Evaluation of Nondestructive Technologies to Assess Presence and Extent of Delamination of Hot Mix Asphalt Airfield Pavements. Ph.D. Thesis, The University of Texas, El Paso, TX, USA, 2011. [Google Scholar]
- Tsai, Y.; Jiang, C.; Wang, Z. Pavement Crack Detection Using High-Resolution 3D Line Laser Imaging Technology. In Proceedings of the 7th RILEM International Conference on Cracking in Pavements, Delft, The Netherlands, 22–22 June 2012; pp. 169–178. [Google Scholar] [CrossRef]
- Tsai, Y.; Wang, Z.; Jiang, C.; Mahfood, B.; Rone, J. Innovative Crack Sealing Analysis and Cost Estimation for Airport Runway Shoulders Using 3D Laser Technology and Automatic Crack Detection Algorithms. In Proceedings of the International Airfield and Highway Pavements Conference, Miami, FL, USA, 7–10 June 2015. [Google Scholar] [CrossRef]
- Sanchez Dominguez, F.; Ramos Garcia, J.A.; Salces Goni, C. Assessment of the structural condition of concrete runways and platforms in airports using 3D laser, HWD and 3D radar. In Proceedings of the International Symposium, Non-Destructive Testing in Civil Engineering (NDT-CE), Berlin, Germany, 15–17 September 2015. [Google Scholar]
- Slabej, M.; Grinč, M.; Kováč, M.; Decky, M.; Šedivý, Š. Non-invasive diagnostic methods for investigating the quality of Žilina airport’s runway. Contrib. Geophys. Geod. 2015, 45, 237–254. [Google Scholar] [CrossRef] [Green Version]
- Grinč, M. 3D GPR investigation of pavement using 1 GHz and 2 GHz horn type antenna—Comparison of the results. Contrib. Geophys. Geod. 2015, 45, 25–39. [Google Scholar] [CrossRef] [Green Version]
- Minasian, D.; Kayen, R.; Ashford, S.; Kawamata, Y.; Sugano, T. Ground Deformation Analysis of Blast-Induced Liquefaction at a Simulated Airport Infrastructure Using High Resolution 3D Laser Scanning. In Proceedings of the American Geophysical Union Fall Meeting, San Francisco, CA, USA, 25 November 2008. [Google Scholar]
- Barbarella, M.; De Blasiis, M.R.; Fiani, M.; Santoni, M. A LiDAR application to the study of taxiway surface evenness and slope. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 65–72. [Google Scholar] [CrossRef] [Green Version]
- Riesner, E. Modern Airfield Pavement Management Strategies. In Proceedings of the Airports Conference, Hershey, PA, USA, 12 March 2014. [Google Scholar]
- Schwarz, K.P.; El-Sheimy, N. Mobile Mapping Systems—State of The Art and Future Trends. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 759–768. [Google Scholar]
- Barbarella, M.; Fiani, M.; Lugli, A. Landslide monitoring using multitemporal terrestrial laser scanning for ground displacement analysis. Geomat. Nat. Hazards Risk 2013, 6, 398–418. [Google Scholar] [CrossRef]
- Hooper, A. A Statistical-Cost Approach to Unwrapping the Phase of InSAR Time Series. In Proceedings of the International Workshop on ERS SAR Interferometry, Frascati, Italy, 30 November–4 December 2009. [Google Scholar]
- Samsonov, S.V.; d’Oreye, N.; González, P.J.; Tiampo, K.F.; Ertolahti, L.; Clague, J.J. Rapidly accelerating subsidence in the greater vancouver region from two decades of ERS-ENVISAT-RADARSET-2 DInSAR measurements. Remote Sens. Environ. 2014, 143, 180–191. [Google Scholar] [CrossRef] [Green Version]
- Crosetto, M.; Monserrat, O.; Cuevas-Gonzalez, M.; Devanthéry, N.; Crippa, B. Analysis Of X-Band Very High Resolution Persistent Scatterer Interferometry Data Over Urban Areas. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 47–51. [Google Scholar] [CrossRef] [Green Version]
- Long, B.; Shatnawi, S. Structural evaluation of rigid pavement sections. Road Mater. Pavement Des. 2011, 1, 97–117. [Google Scholar] [CrossRef]
- García, J.A.R.; Castro, M. Analysis of the temperature influence on flexible pavement deflection. Constr. Build. Mater. 2011, 25, 3530–3539. [Google Scholar] [CrossRef]
- Djaha, S.I.K.; Prayuda, H. Quality Assessment of Road Pavement using Lightweight Deflectometer. In Proceedings of the 3rd International Conference on Sustainable Innovation 2019—Technology and Engineering (IcoSITE 2019), Yogyakarta, Indonesia, 30–31 July 2019. [Google Scholar]
- Kutay, M.E.; Chatti, K.; Lei, L. Backcalculation of Dynamic Modulus Mastercurve from Falling Weight Deflectometer Surface Deflections. Transp. Res. Rec. J. Transp. Res. Board 2011, 2227, 87–96. [Google Scholar] [CrossRef]
- Karballaeezadeh, N.S.; Mohammadzadeh, D.; Shamshirband, S.; Hajikhodaverdikhan, P.; Mosavi, A.; Ahmadi, M.H. Prediction of remaining service life of pavement using an optimized support vector machine (case study of Semnan–Firuzkuh road). Eng. Appl. Comput. Fluid Mech. 2019, 13, 188–198. [Google Scholar] [CrossRef] [Green Version]
- Karballaeezadeh, N.; Zaremotekhases, F.; Band, S.S.; Mosavi, A.; Nabipour, N.; Csiba, P.; Várkonyi-Kóczy, A.R. Intelligent Road Inspection with Advanced Machine Learning; Hybrid Prediction Models for Smart Mobility and Transportation Maintenance Systems. Energies 2020, 13, 1718. [Google Scholar] [CrossRef] [Green Version]
- Mihailović, K. Deformaciona Analiza Geodetskih Mreža; Institut za Geodeziju, Građevinski Fakultet, Univerzitet: Belgrade, Serbia, 1994. (In Slovenian) [Google Scholar]
- Penrose, R. A generalized inverse for matrices. In Proceedings of the Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press (CUP): Cambridge/London, UK, 1955; Volume 51, pp. 406–413. [Google Scholar]
- Jurgele, M.; Želodec, D. Falling Weight Deflectometer—Operation principles and examples of use in practice. In Proceedings of the 14th Slovenian Congress on Transport and Transport Infrastructure, Portorož, Slovenia, 24–26 October 2018. [Google Scholar]
- Jamnik, J.; Lipoglavšek, B.; Bajec, J.; Marinko, B.; Cezar, J.; Žmavc, J.; Podgoršek, F.; Stock, T.; Prosen, J. Meritve Nosilnosti Voziščnih Konstrukcij z Deflektometrom s Padajočo Utežjo (FWD—Falling Weight Deflectometer) kot Osnova za Dimenzioniranje Obstoječih Voziščnih Konstrukcij. Razvojno Raziskovalni Project; DDC Družba za Državne Ceste: Ljubljana, Slovenia, 2000. [Google Scholar]
- Burhani, A. Correlation Study on the Falling Weight Deflectometer and Light Weight Deflectometer for the Local Pavement Systems. Ph.D. Thesis, Ohio University, Athens, OH, USA, 2016. [Google Scholar]
- AASHTO Guide for Design of Pavement Structures. Available online: https://habib00ugm.files.wordpress.com/2010/05/aashto1993.pdf (accessed on 21 December 2020).
- Doler, D. Innovative model for continuous monitoring of runway deformations. Ph.D. Thesis, Fakulteta za logistiko, Celje, Slovenia, 2020. [Google Scholar]
- Kapović, Z. Prilog Određivanju I Analizi Pomaka i Deformacija Mostova s Posebnim Osvrtom na Temperaturne Utjecaje. Ph.D. Thesis, Geodetski Fakultet, Zagreb, Slovenia, 1993. (In Slovenian). [Google Scholar]
- Breznikar, A.; Koler, B. Inženirska Geodezija; Fakulteta za Gradbeništvo in Geodezijo: Ljubljana, Slovenia, 2009. (In Slovenian) [Google Scholar]
- Ong, G.P.R.; Nantung, T.E.; Sinha, K.C. Indiana Pavement Preservation Program 2011; Joint Transportation Research Program; Indiana Department of Transportation and Purdue University: West Lafayette, IN, USA, 2010. [Google Scholar]
- Liang, Z.; Xiao, F.; Qian, X.; Zhou, L.; Jin, X.; Lu, X.; Karichery, S. A column generation-based heuristic for aircraft recovery problem with airport capacity constraints and maintenance flexibility. Transp. Res. Part B Methodol. 2018, 113, 70–90. [Google Scholar] [CrossRef]
- Airlines for America. U. S. Passenger Carrier Delay Costs. 2018. Available online: https://www.airlines.org/dataset/per-minute-cost-of-delays-to-u-s-airlines/ (accessed on 28 October 2020).
- De Souza, N.M.; Filho, A.T.D.A. A systematic airport runway maintenance and inspection policy based on a delay time modeling approach. Autom. Constr. 2020, 110, 103039. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovačič, B.; Želodec, D.; Doler, D. Prototype of the Runway Monitoring Process at Smaller Airports: Edvard Rusjan Airport Maribor. Processes 2020, 8, 1689. https://doi.org/10.3390/pr8121689
Kovačič B, Želodec D, Doler D. Prototype of the Runway Monitoring Process at Smaller Airports: Edvard Rusjan Airport Maribor. Processes. 2020; 8(12):1689. https://doi.org/10.3390/pr8121689
Chicago/Turabian StyleKovačič, Boštjan, Damjan Želodec, and Damjan Doler. 2020. "Prototype of the Runway Monitoring Process at Smaller Airports: Edvard Rusjan Airport Maribor" Processes 8, no. 12: 1689. https://doi.org/10.3390/pr8121689
APA StyleKovačič, B., Želodec, D., & Doler, D. (2020). Prototype of the Runway Monitoring Process at Smaller Airports: Edvard Rusjan Airport Maribor. Processes, 8(12), 1689. https://doi.org/10.3390/pr8121689





