Model-Free Adaptive Direct Torque Control for the Speed Regulation of Asynchronous Motors
Abstract
:1. Introduction
2. Problem Formulation
2.1. Asynchronous Motor
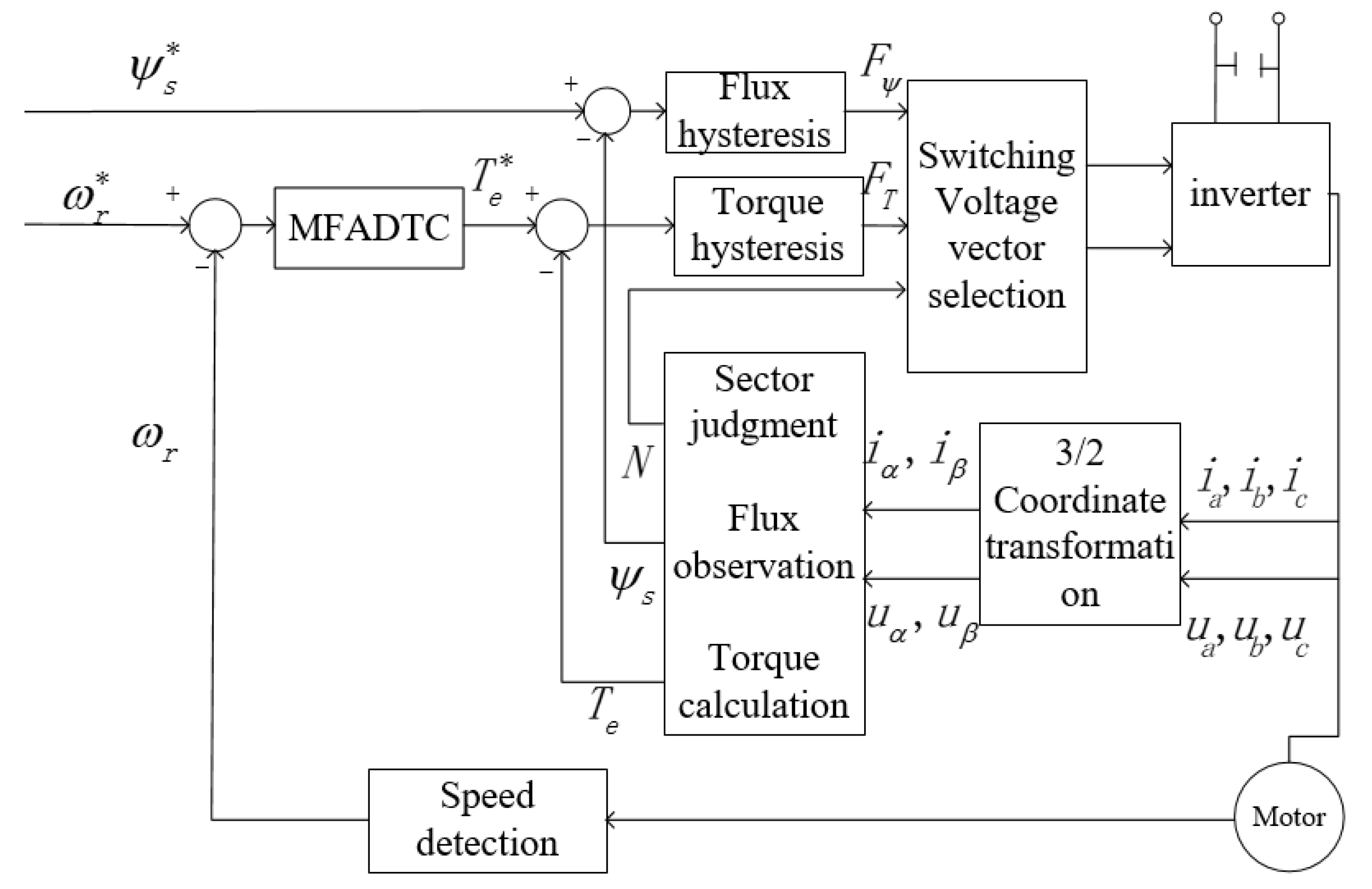
2.2. Direct Torque Control System for the Asynchronous Motor
3. Model-Free Adaptive Direct Torque Control Design
3.1. Full-Format Dynamic Linearization Method
3.2. Design of Model-Free Adaptive Direct Torque Controller
3.2.1. Control Algorithm
3.2.2. Pseudo-Gradient Estimation Algorithm
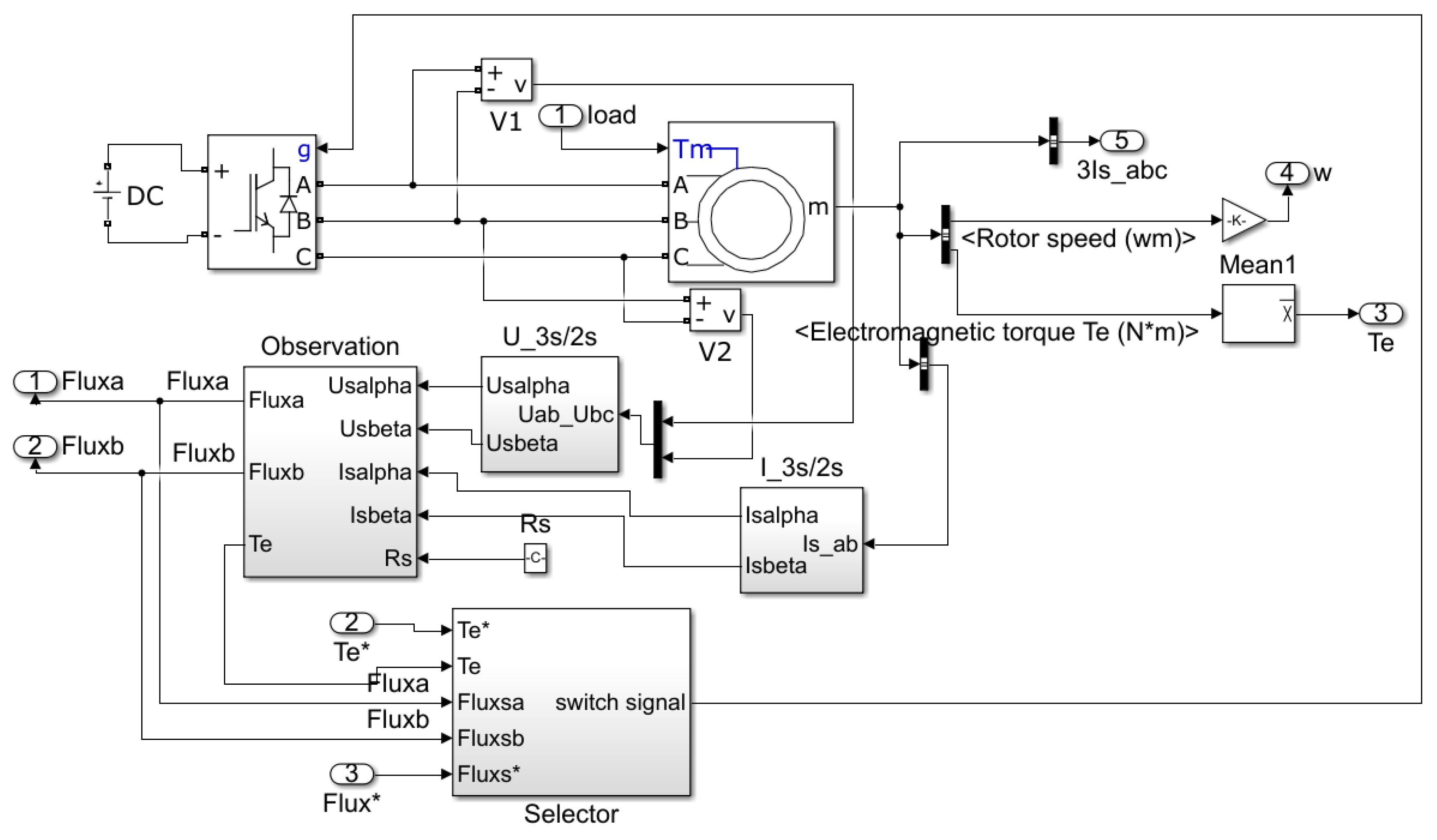
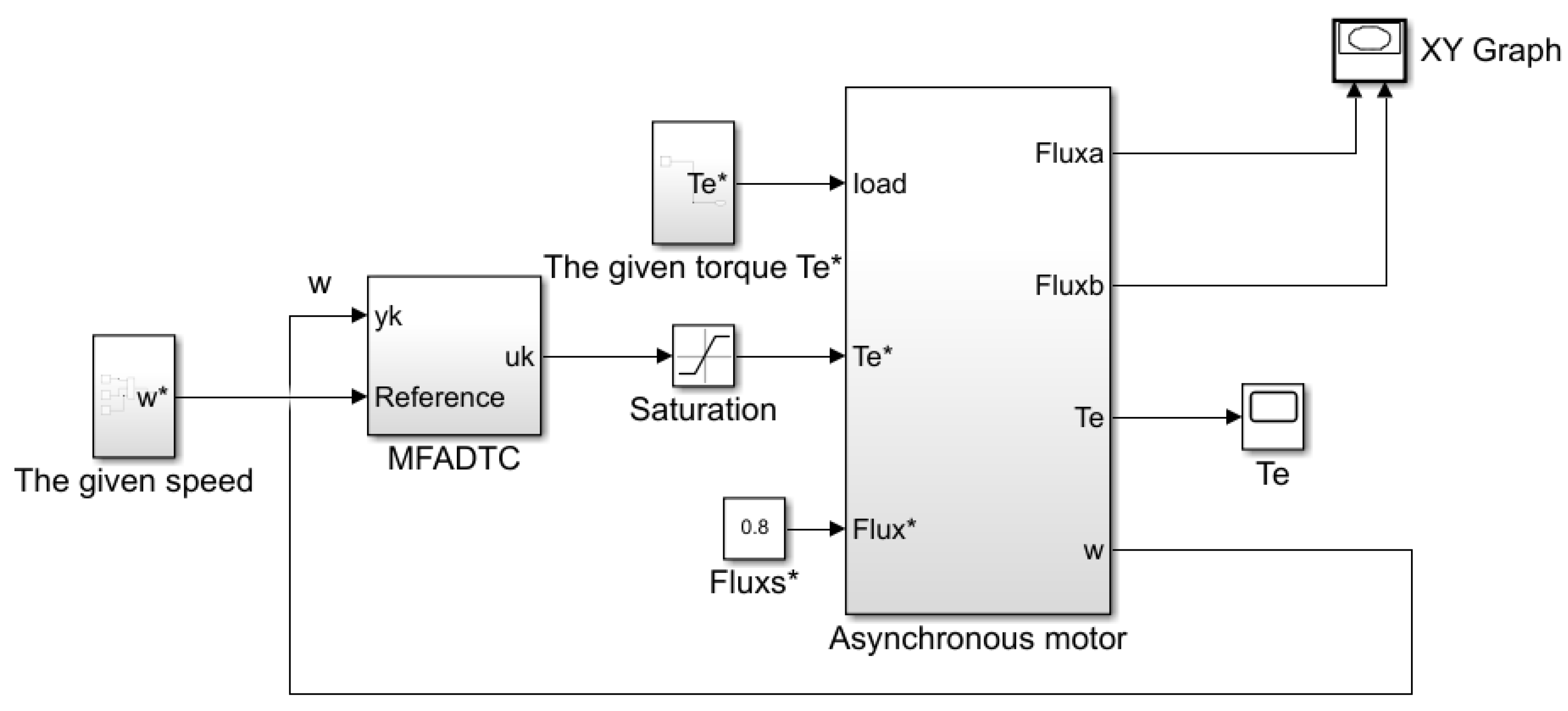
4. Simulation Studies
4.1. Simulation Result without Disturbance
4.2. Simulation Result with Disturbance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xin, X.N. Direct Torque Control and Vector Control of Three-phase Asynchronous Motors. In Proceedings of the 2018 International Conference on Power, Energy and Environmental Engineering, Wuhan, China, 7 February 2018; Volume 1, pp. 100–105. [Google Scholar]
- Li, J.H. Research on Direct Torque Control without Speed Sensor Based on MRAS. Electron. World 2013, 13, 88–89. [Google Scholar]
- Hu, J.; Dawson, D.M. Adaptive Control of Induction Motor Systems despite Rotor Resistance Uncertainty. Automatica 1996, 32, 1127–1143. [Google Scholar] [CrossRef]
- Açikgöz, H.; Yıldız, C.; Kale, G.; Kececio, F. Speed Control of Induction Motor Based on Model Reference Adaptive Control. In Proceedings of the 2015 9th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 26–28 November 2015; pp. 654–659. [Google Scholar]
- Xu, J.; Hu, Z.J.; Tian, G.Q. Model Reference Adaptive Vector Control of Asynchronous Motor without Speed Sensor. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 3195–3199. [Google Scholar]
- Lang, F.C.; Lin, Y. Design of Fuzzy PI Controller for Asynchronous Motor Direct Torque. In Proceedings of the Chinese Control and Decision Conference (CCDC), Liaoning, China, 9 June 2018; Volume 1, pp. 1116–1119. [Google Scholar]
- Liao, Y.H.; Feng, X.Y.; Wang, Z. Space Vector Modulation Direct Torque Control of Asynchronous Motor Based on Stator Flux Sliding-mode Observer. Proc. CSEE 2012, 32, 88–97. [Google Scholar]
- Li, Y. On Speed Regulation System of Asynchronous Motor Based on Tornambe Control. Master’s Thesis, North University of China, Taiyuan, China, 2018. [Google Scholar]
- Hou, Z.S.; Jin, S.T. Model Free Adaptive Control: Theory and Applications; CRC Press: Beijing, China, 2013. [Google Scholar]
- Zhang, X.F.; Ma, H.B. Data-Driven Model-Free Adaptive Control Based on Error Minimized Regularized Online Sequential Extreme Learning Machine. Energies 2019, 12, 3241. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Lai, H.; Gao, X. Modeling of Submersible Motor and Application of Model-free Adaptive Control. Control Eng. 2015, 22, 835–840. [Google Scholar]
- Guo, J.; Bao, W.; Yin, B. Simulation Study of Model-free Control Method in Asynchronous Motor Control. World Invert. 2012, 77–79. [Google Scholar]
- Zeng, Z.Q.; Cao, R.M.; Hou, Z.S. MIMO Model-Free Adaptive Contour Control for Two-dimensional Linear Motor. Control Theory Appl. 2019. [Google Scholar] [CrossRef]
- Song, D.L.; Lu, N. Simulation of Model-free Adaptive Control Algorithm in ROV Depth Determination Control. Ship Eng. 2019, 41, 87–92+103. [Google Scholar]
- Yu, W.; Bu, X.H. Design of Model-free Adaptive Anti-interference Attitude Controller for Quadrotor. J. Electron. Meas. Instrum. 2019, 33, 166–172. [Google Scholar]
- Zhang, X. Robustness of Model-Free Adaptive Control and Application in Four-rotor Aircraft. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2019. [Google Scholar]
- Hu, Y.; Jiang, F.C. Distributed Electric Vehicle Drive System MFAC Active Fault Tolerant Control. Automot. Eng. 2019, 41, 983–989+1005. [Google Scholar]
- Luo, Y.Y.; Chen, R.; Hu, Y. Distributed Electric Vehicle Steering System by Wire MFAC Active Fault Tolerant Control. Chin. J. Mech. Eng. 2019, 55, 131–139. [Google Scholar]
- Zhu, M.S.; Liu, J.M. Study on Model-free Adaptive Control of Boiler Water Circulation System. J. Chongqing Univ. Technol. 2019, 33, 214–220. [Google Scholar]
- Duan, J.M.; Ma, X.J.; Liu, X. A path Tracking Method Based on MFAPC for Driverless Vehicles. Comput. Eng. 2019, 45, 6–11+20. [Google Scholar]
- Lu, D. Application of Model-free Adaptive Control Method in Image Recognition. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2019. [Google Scholar]
- Zhang, S.; Zhou, P. Recursive Bilinear Subspace Modeling and Model-free Adaptive Control for Wastewater Treatment Process. Acta Automatica Sinica. 2019. [Google Scholar] [CrossRef]
- Hao, Y.; Bu, S.J. Design of Induction Motor Direct Torque Control Frequency Conversion Speed Regulation System. Autom. Instrum. 2015, 10, 30–32. [Google Scholar]
- Hou, Z.S.; Xiong, S.S. On Model-Free Adaptive Control and Its Stability Analysis. IEEE Trans. Autom. Control 2019, 64, 4555–4569. [Google Scholar] [CrossRef]




| Index | MSE-PID | MSE-MFADTC |
|---|---|---|
| Speed | 123376 | 122871 |
| Index | MSE-PID | MSE-MFADTC |
|---|---|---|
| Speed | 122126 | 119977 |
| Torque | 1751 | 1692 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Jin, S.; Liu, G.; Hou, Z.; Zheng, J. Model-Free Adaptive Direct Torque Control for the Speed Regulation of Asynchronous Motors. Processes 2020, 8, 333. https://doi.org/10.3390/pr8030333
Zhang Z, Jin S, Liu G, Hou Z, Zheng J. Model-Free Adaptive Direct Torque Control for the Speed Regulation of Asynchronous Motors. Processes. 2020; 8(3):333. https://doi.org/10.3390/pr8030333
Chicago/Turabian StyleZhang, Ziwei, Shangtai Jin, Genfeng Liu, Zhongsheng Hou, and Jianmin Zheng. 2020. "Model-Free Adaptive Direct Torque Control for the Speed Regulation of Asynchronous Motors" Processes 8, no. 3: 333. https://doi.org/10.3390/pr8030333
APA StyleZhang, Z., Jin, S., Liu, G., Hou, Z., & Zheng, J. (2020). Model-Free Adaptive Direct Torque Control for the Speed Regulation of Asynchronous Motors. Processes, 8(3), 333. https://doi.org/10.3390/pr8030333





