Kinetics, Isotherms, and Thermodynamic Modeling of the Adsorption of Phosphates from Model Wastewater Using Recycled Brick Waste
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Characterization of Adsorbent
2.3. Batch Adsorption Experiments
3. Results and Discussion
3.1. Characterization of Brick Particles
3.2. Effect of Contact Time
3.3. Effect of Adsorbent Dosage
3.4. Effect of Temperature
3.5. Adsorption Kinetics Modeling
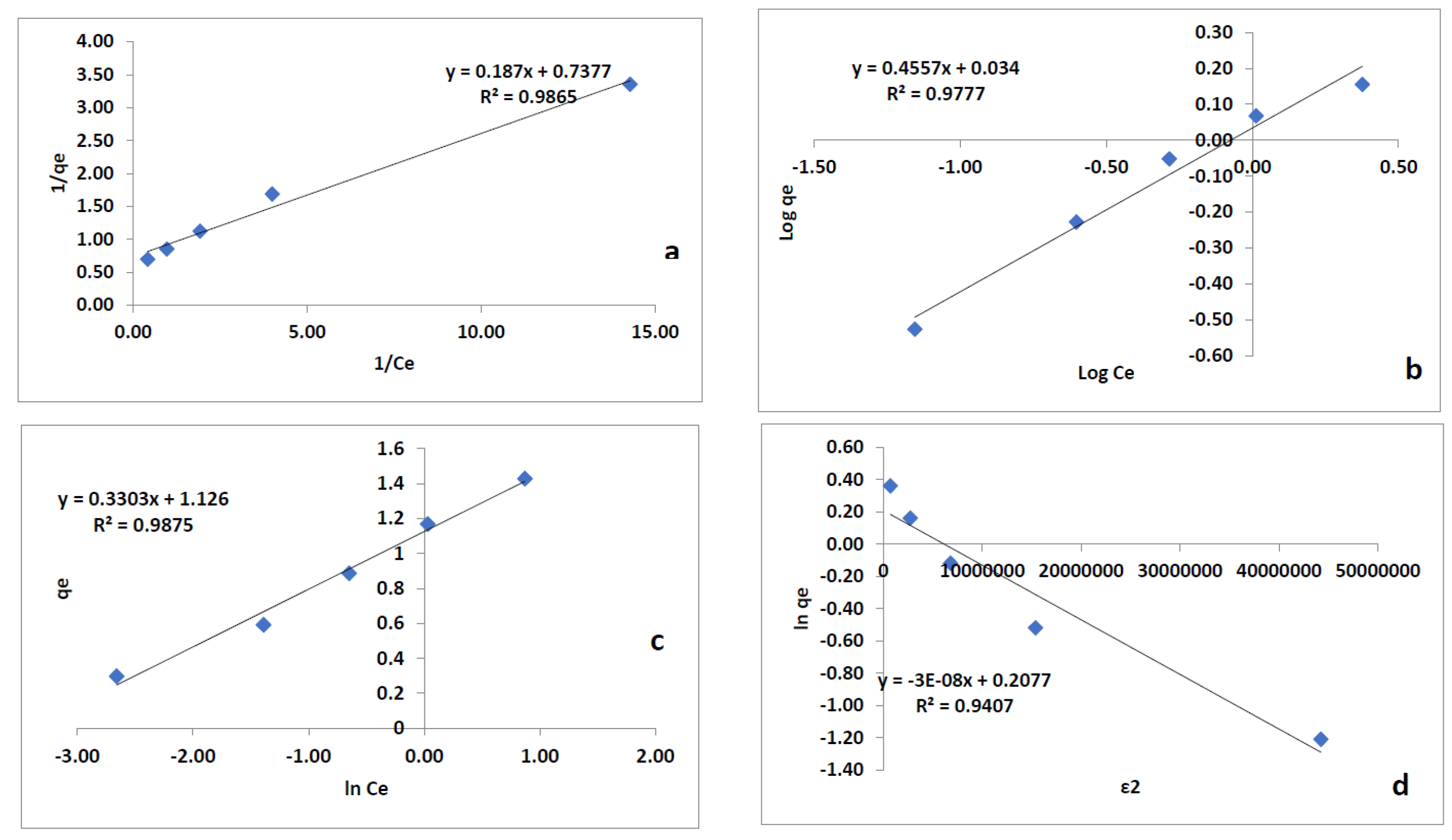
3.6. Adsorption Isotherm
3.6.1. Langmuir Isotherm
3.6.2. Freundlich Isotherm
3.6.3. Tempkin Adsorption Isotherm
3.6.4. Dubinin-Radushkevich Adsorption Isotherm
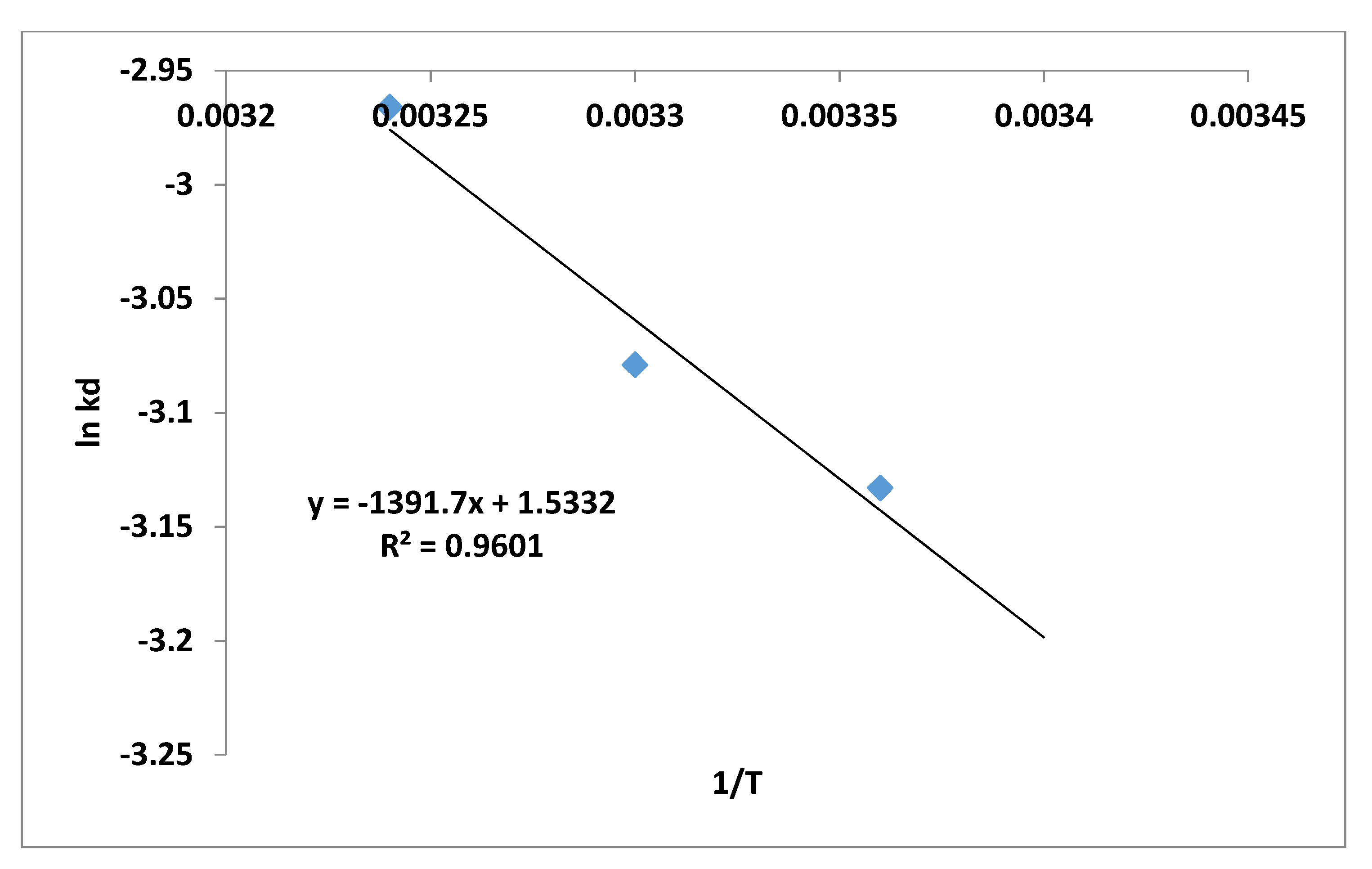
3.7. Thermodynamic of Adsorption
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Le Moal, M.; Gascuel-Odoux, C.; Ménesguen, A.; Souchon, Y.; Étrillard, C.; Levain, A.; Moatar, F.; Pannard, A.; Souchu, P.; Lefebvre, A.; et al. Eutrophication: A new wine in an old bottle? Sci. Total Environ. 2019, 651, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pawar, R.R.; Gupta, P.; Bajaj, L.H.; Lee, S.-M. Al-intercalated acid activated bentonite beads for the removal of aqueous phosphate. Sci. Total Environ. 2016, 572, 1222–1230. [Google Scholar] [CrossRef]
- Yoon, S.-Y.; Lee, C.-G.; Park, J.-A.; Kim, J.-H.; Kim, S.-B.; Lee, S.-H.; Choi, J.-W. Kinetic, equilibrium and thermodynamic studies for phosphate adsorption to magnetic iron oxide nanoparticles. Chem. Eng. J. 2014, 236, 341–347. [Google Scholar] [CrossRef]
- Ifelebuegu, A.O.; Ojo, P. Modelling the effects of ferric salt dosing for chemical phosphorus removal on the settleability of activated sludge. J. Environ. Chem. Eng. 2019, 7, 103256. [Google Scholar] [CrossRef]
- Xie, J.; Lin, Y.; Li, C.; Wu, D.; Kong, H. Removal and recovery of phosphate from water by activated aluminum oxide and lanthanum oxide. Powder Technol. 2015, 269, 351–357. [Google Scholar] [CrossRef]
- Ojo, P.; Ifelebuegu, A. The Impact of Aluminium Salt Dosing for Chemical Phosphorus Removal on the Settleability of Activated Sludge. Environments 2018, 5, 88. [Google Scholar] [CrossRef] [Green Version]
- Yan, Y.; Sun, X.; Ma, F.; Li, J.; Shen, J.; Han, W.; Liu, X.; Wang, L. Removal of phosphate from etching wastewater by calcined alkaline residue: Batch and column studies. J. Taiwan Inst. Chem. Eng. 2014, 45, 1709–1716. [Google Scholar] [CrossRef]
- Chen, W.-T.; Lin, C.-W.; Shih, P.-K.; Chang, W.-L. Adsorption of phosphate into waste oyster shell: Thermodynamic parameters and reaction kinetics. Desalin. Water Treat. 2012, 47, 86–95. [Google Scholar] [CrossRef]
- Babatunde, A.; Zhao, Y. Equilibrium and kinetic analysis of phosphorus adsorption from aqueous solution using waste alum sludge. J. Hazard. Mater. 2010, 184, 746–752. [Google Scholar] [CrossRef] [Green Version]
- Karaca, S.; Gurses, A.; Ejder, M.; Açıkyıldız, M. Kinetic modeling of liquid-phase adsorption of phosphate on dolomite. J. Colloid Interface Sci. 2004, 277, 257–263. [Google Scholar] [CrossRef]
- Zeng, L.; Li, X.; Liu, J. Adsorptive removal of phosphate from aqueous solutions using iron oxide tailings. Water Res. 2004, 38, 1318–1326. [Google Scholar] [CrossRef] [PubMed]
- Edet, U.A.; Ifelebuegu, A.; Wood, A.; Bateman, M. The Adsorptive Properties of Fired Clay Pellets for the Removal of Phosphate in Wastewater Treatment. In Proceedings of the Fourth International Conference on Advances in Bio-Informatics, Bio-Technology and Environmental Engineering (ABBE 2016), Birmingham, UK, 17–18 March 2016; pp. 15–21. [Google Scholar]
- Hamdi, N.; Srasra, E. Removal of phosphate ions from aqueous solution using Tunisian clays minerals and synthetic zeolite. J. Environ. Sci. 2012, 24, 617–623. [Google Scholar] [CrossRef]
- Kamiyango, M.; Masamba, W.R.L.; Sajidu, S.; Fabiano, E. Phosphate removal from aqueous solutions using kaolinite obtained from Linthipe, Malawi. Phys. Chem. Earth Parts A/B/C 2009, 34, 850–856. [Google Scholar] [CrossRef]
- Jia, C.; Dai, Y.; Chang, J.-J.; Wu, C.; Wu, Z.-B.; Liang, W. Adsorption characteristics of used brick for phosphorus removal from phosphate solution. Desalin. Water Treat. 2013, 51, 5886–5891. [Google Scholar] [CrossRef]
- Shanableh, A.; Enshasi, G.; Elsergany, M. Phosphorous Adsorption using Al3+/Fe3+-Modified Bentonite adsorbents—Effect of Al3+ and Fe3+ Combinations. Desalin. Water Treat. 2016, 57, 15628–15634. [Google Scholar] [CrossRef]
- CRWP. Overview of Demolition Waste in the UK. 2009. Available online: http://www.wrap.org.uk/sites/files/wrap/CRWP-Demolition-Report-2009.pdf (accessed on 16 June 2019).
- Zhu, L.; Hiltunen, E.; Shu, Q.; Zhou, W.; Li, Z.; Wang, Z. Biodiesel production from algae cultivated in winter with artificial wastewater through pH regulation by acetic acid. Appl. Energy 2014, 128, 103–110. [Google Scholar] [CrossRef]
- Sugashini, S.; Begum, K.M.M.S. Column Adsorption Studies for the Removal of Cr(VI) Ions by Ethylamine Modified Chitosan Carbonized Rice Husk Composite Beads with Modelling and Optimization. J. Chem. 2013, 2013, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Yaneva, Z.; Koumanova, B.; Allen, S. Applicability Comparison of Different kinetic/diffusion Models for 4-Nitrophenol Sorption on Rhizopus Oryzae Dead Biomass. Bulg. Chem. Commun. 2013, 45, 161–168. [Google Scholar]
- Mor, S.; Chhoden, K.; Ravindra, K.; Khaiwal, R. Application of agro-waste rice husk ash for the removal of phosphate from the wastewater. J. Clean. Prod. 2016, 129, 673–680. [Google Scholar] [CrossRef]
- Albadarin, A.B.; Mangwandi, C.; Al-Muhtaseb, A.; Walker, G.M.; Allen, S.J.; Ahmad, M. Kinetic and thermodynamics of chromium ions adsorption onto low-cost dolomite adsorbent. Chem. Eng. J. 2012, 179, 193–202. [Google Scholar] [CrossRef]
- Tian, S.; Jiang, P.; Ning, P.; Su, Y. Enhanced adsorption removal of phosphate from water by mixed lanthanum/aluminum pillared montmorillonite. Chem. Eng. J. 2009, 151, 141–148. [Google Scholar] [CrossRef]
- Ifelebuegu, A.; Salauh, H.T.; Zhang, Y.; Lynch, D.E. Adsorptive Properties of Poly(1-methylpyrrol-2-ylsquaraine) Particles for the Removal of Endocrine-Disrupting Chemicals from Aqueous Solutions: Batch and Fixed-Bed Column Studies. Processes 2018, 6, 155. [Google Scholar] [CrossRef] [Green Version]
- Mall, I.D.; Upadhyay, S.N.; Sharma, Y.C. A review on economical treatment of wastewaters and effluents by adsorption. Int. J. Environ. Stud. 1996, 51, 77–124. [Google Scholar] [CrossRef]
- Köse, T.E.; Kıvanç, B. Adsorption of phosphate from aqueous solutions using calcined waste eggshell. Chem. Eng. J. 2011, 178, 34–39. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, S.; Yu, J.; Shu, Z. Novel hollow microspheres of hierarchical zinc–aluminum layered double hydroxides and their enhanced adsorption capacity for phosphate in water. J. Hazard. Mater. 2011, 192, 1114–1121. [Google Scholar] [CrossRef]
- Yuan, X.; Xia, W.; An, J.; Yin, J.; Zhou, X.; Yang, W. Kinetic and Thermodynamic Studies on the Phosphate Adsorption Removal by Dolomite Mineral. J. Chem. 2015, 2015, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Mezenner, N.Y.; Bensmaili, A. Kinetics and thermodynamic study of phosphate adsorption on iron hydroxide-eggshell waste. Chem. Eng. J. 2009, 147, 87–96. [Google Scholar] [CrossRef]
- Qiu, H.; Lv, L.; Pan, B.; Zhang, Q.-J.; Zhang, W.-M.; Zhang, Q.-X. Critical review in adsorption kinetic models. J. Zhejiang Univ. A 2009, 10, 716–724. [Google Scholar] [CrossRef]
- Yakout, S.; Elsherif, E. Batch Kinetics, Isotherm and Thermodynamic Studies of Adsorption of Strontium from Aqueous Solutions onto Low Cost Rice-Straw Based Carbons. Carbon Sci. Technol. 2010, 1, 144–153. [Google Scholar]
- Subha, R.; Namasivayam, C. Modeling of Adsorption Isotherms and Kinetics of 2, 4, 6-Trichlorophenol Onto Microporous ZnCl2 Activated Coir Pith Carbon. J. Environ. Eng. Manag. 2008, 18, 275–280. [Google Scholar]
- Ho, Y.S.; McKay, G. Pseudo-second order model for sorption processes. Process Biochem. 1999, 34, 451–465. [Google Scholar] [CrossRef]
- Balouch, A.; Kolachi, M.; Talpur, F.N.; Khan, H.; Bhanger, M.I. Sorption Kinetics, Isotherm and Thermodynamic Modeling of Defluoridation of Ground Water Using Natural Adsorbents. Am. J. Anal. Chem. 2013, 4, 221–228. [Google Scholar] [CrossRef] [Green Version]
- Dada, A.; Olalekan, A.; Olatunya, A.; Dada, O. Langmuir, Freundlich, Temkin and Dubinin-Radushkevich Isotherms Studies of Equilibrium Sorption of Zn2+ Unto Phosphoric Acid Modified Rice Husk. J. Appl. Chem. 2012, 3, 38–45. [Google Scholar]
- Foo, K.Y.; Hameed, B. Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Boujelben, N.; Bouhamed, F.; Elouear, Z.; Bouzid, J.; Feki, M. Removal of phosphorus ions from aqueous solutions using manganese-oxide-coated sand and brick. Desalin. Water Treat. 2013, 52, 2282–2292. [Google Scholar] [CrossRef]
- Hutson, N.D.; Yang, R.T. Theoretical basis for the Dubinin-Radushkevitch (D-R) adsorption isotherm equation. Adsorption 1997, 3, 189–195. [Google Scholar] [CrossRef]
- Tempkin, M.; Pyzhev, V. Heavy Metals Removal and Isotherms Study. Acta Physiochim. URSS. 1940, 12, 217–222. [Google Scholar]
- Dąbrowski, A. Adsorption—From theory to practice. Adv. Colloid Interface Sci. 2001, 93, 135–224. [Google Scholar] [CrossRef]
- Al-Anber, M.A. Thermodynamics Approach in the Adsorption of Heavy Metals; Intech Open Access Publisher: London, UK, 2011. [Google Scholar]
- Huang, W.; Chen, J.; He, F.; Tang, J.; Li, D.; Zhu, Y.; Zhang, Y. Effective phosphate adsorption by Zr/Al-pillared montmorillonite: Insight into equilibrium, kinetics and thermodynamics. Appl. Clay Sci. 2015, 104, 252–260. [Google Scholar] [CrossRef]
- Ifelebuegu, A.O. Removal of Steriod Hormones by Activated Carbon adsorption—Kinetic and Thermodynamic Studies. J. Environ. Prot. 2012, 3, 469–475. [Google Scholar] [CrossRef] [Green Version]
- Ifelebuegu, A.O.; Ukpebor, J.E.; Obidiegwu, C.C.; Kwofi, B.C. Comparative potential of black tea leaves waste to granular activated carbon in adsorption of endocrine disrupting compounds from aqueous solution. Glob. J. Environ. Sci. Manag. 2015, 1, 205–214. [Google Scholar]




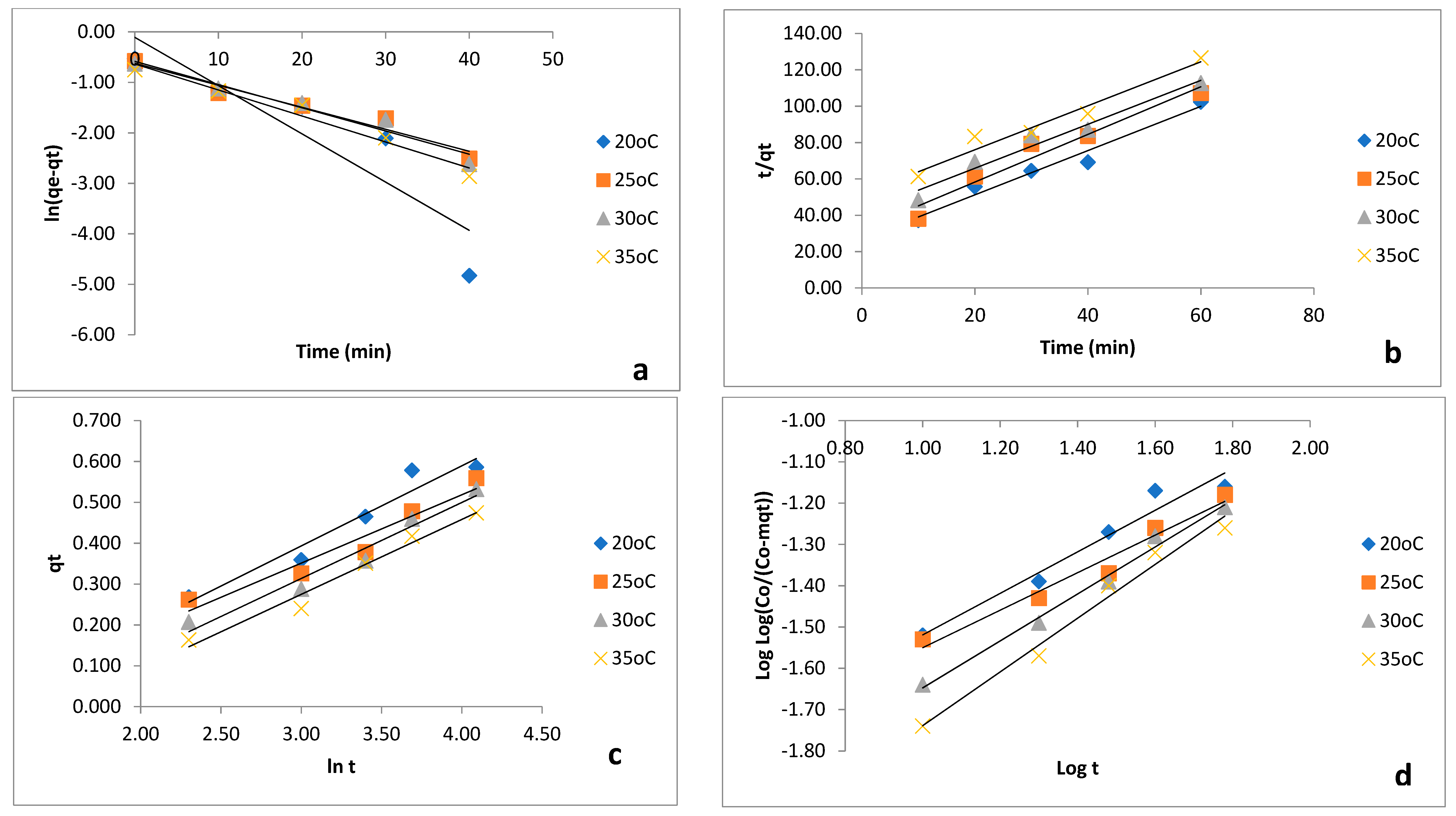
| Kinetic Model | Parameter | 20 °C | 25 °C | 30 °C | 35 °C |
|---|---|---|---|---|---|
| Pseudo-first-order | k1 (/min) | −0.05 | −0.03 | −0.03 | −0.03 |
| qe (mg/g) | 10.46 | 22.94 | 21.74 | 19.42 | |
| R2 | 0.818 | 0.9523 | 0.9526 | 0.966 | |
| Pseudo-second-order | k2 (g/mg/min) | 0.06 | 0.05 | 0.04 | 0.03 |
| h (mg/g/min) | 0.04 | 0.04 | 0.02 | 0.02 | |
| R2 | 0.9686 | 0.9498 | 0.9601 | 0.96 | |
| Elovich | α (mg/g/min) | 0.82 | 0.86 | 0.78 | 0.76 |
| b (g/mg) | 5.1 | 5.97 | 5.38 | 5.46 | |
| R2 | 0.9445 | 0.9326 | 0.9599 | 0.9731 | |
| Bangham’s | ko (mL/g/L | 44 | 39.35 | 51.20 | 61.84 |
| α | 9.50 × 10−3 | 9.90 × 10−3 | 6.07 × 10−3 | 4.07 × 10−3 | |
| R2 | 0.9587 | 0.965 | 0.9897 | 0.9803 |
| Adsorption Isotherm Model | Parameter | Brick Particles |
|---|---|---|
| Langmuir Isotherm | Qm (mg/g) | 5.35 |
| KL (L/mg) | 0.25 | |
| RL | 0.04 | |
| R2 | 0.9865 | |
| Freundlich Isotherm | kf (mg/g) | 1.08 |
| 0.4557 | ||
| n | 2.19 | |
| R2 | 0.9777 | |
| Temkin Isotherm | AT (L/mg) | 1.19 |
| b | 1287.51 | |
| B (J/mol) | 1.89 | |
| R2 | 0.9897 | |
| Dubinin-Radushkevich Isotherm | B (mol2/kJ2) | 2.84 × 10−7 |
| E (kJ/mol) | 1.35 | |
| R2 | 0.9351 |
| Parameter | Brick Particles |
|---|---|
| ΔGo | −0.595 |
| ΔHo (KJ/mol) | −0.139 |
| ΔSo (KJ/mol/K) | 1.53 × 10−3 |
| Ea (J/mol) | 0.012 |
| A | 0.572 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Edet, U.A.; Ifelebuegu, A.O. Kinetics, Isotherms, and Thermodynamic Modeling of the Adsorption of Phosphates from Model Wastewater Using Recycled Brick Waste. Processes 2020, 8, 665. https://doi.org/10.3390/pr8060665
Edet UA, Ifelebuegu AO. Kinetics, Isotherms, and Thermodynamic Modeling of the Adsorption of Phosphates from Model Wastewater Using Recycled Brick Waste. Processes. 2020; 8(6):665. https://doi.org/10.3390/pr8060665
Chicago/Turabian StyleEdet, Uduakobong A., and Augustine O. Ifelebuegu. 2020. "Kinetics, Isotherms, and Thermodynamic Modeling of the Adsorption of Phosphates from Model Wastewater Using Recycled Brick Waste" Processes 8, no. 6: 665. https://doi.org/10.3390/pr8060665
APA StyleEdet, U. A., & Ifelebuegu, A. O. (2020). Kinetics, Isotherms, and Thermodynamic Modeling of the Adsorption of Phosphates from Model Wastewater Using Recycled Brick Waste. Processes, 8(6), 665. https://doi.org/10.3390/pr8060665