Prediction of Cutting Material Durability by T = f(vc) Dependence for Turning Processes
Abstract
:1. Introduction
- cT—constant (derived from measured data or computed using the least squared method), (-)
- vc—cutting speed (m/min),
- m—index (dependence of cutting speed on tool-life).
- vcT—cutting speed (constant tool-life)
- ap—depth of cut (mm)
- f—feed (mm)
- xv—index (expression of depth of cut effect)
- yv—index (expression of feed rate).
2. Materials and Methods
- Standard provides the guide for this type of machine;
- Adequate swing diameter;
- Adequate stiffness of the machine;
- The adequate power output of the machine;
- Adequate turn range.
- Possibility to set the constant cutting speed;
- Adequate swing diameter;
- The adequate power output of the machine;
- Adequate turn range;
- Frequently used in practice.
- Tool-life of cutting materials (Equation (1));
- Tool-life of cutting materials (extended formula) (Equation (2));
- Correlation index [41]:
- y’i—calculated values according the selected function for i = 1, 2, …, n
- —arithmetic mean of the measured values
- yi—measured values.
- General equation of regression:
- —independent variable
- —parameters
- —error.
3. Carrying Out of the Experiments
- Limited area for recording the measured outputs of the resulting dependence;
- Common characteristics and its course for all defined cutting tools;
- Interpolation of the dependence into an unmeasured area of cutting speeds;
- Interpolation of a straight line through the measured points by estimation, or by eye.
4. Prediction of Cutting Material Durability
4.1. Design of Data Processing by the Least-Squares Method
4.2. Design of Data Processing by the Regression Analysis
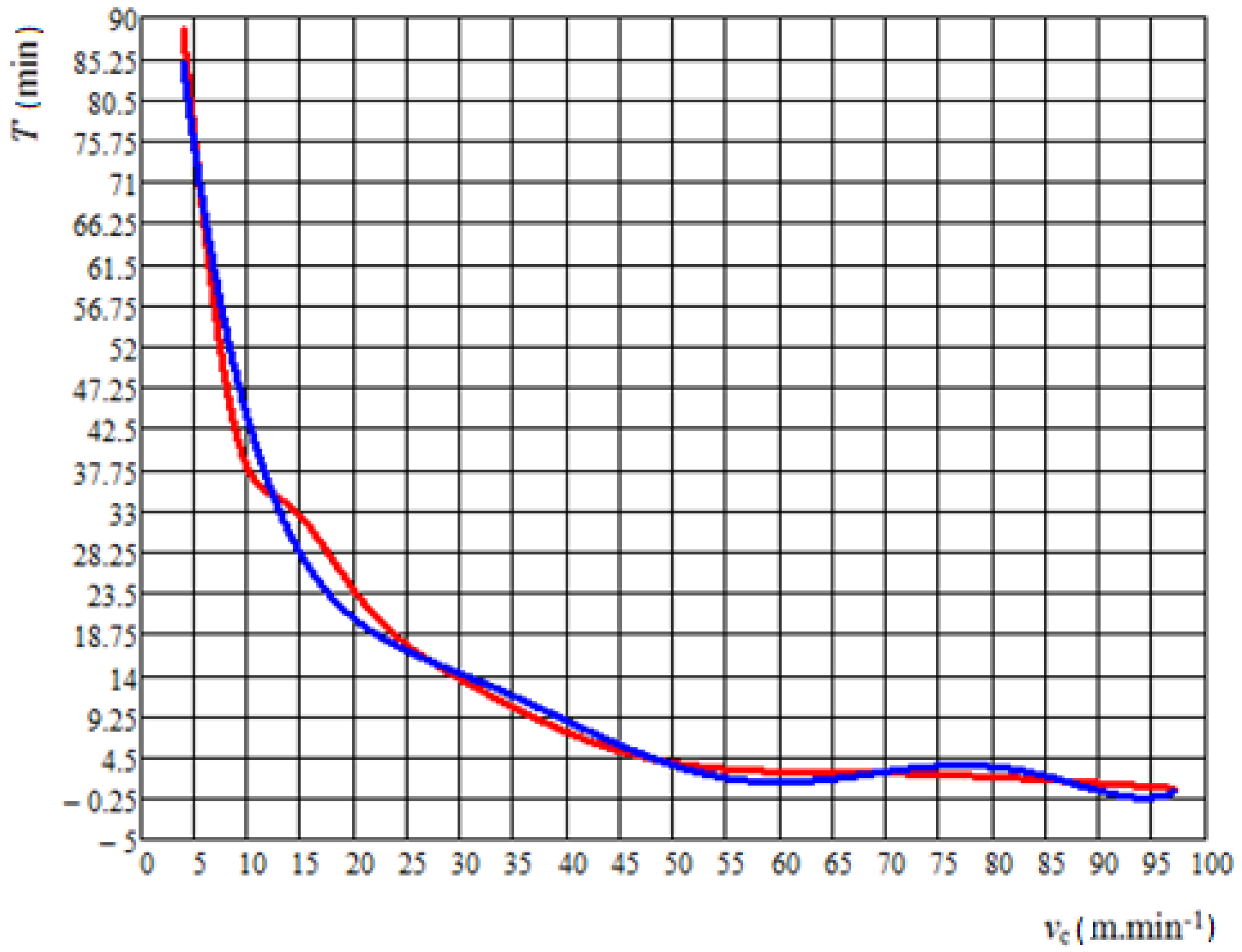
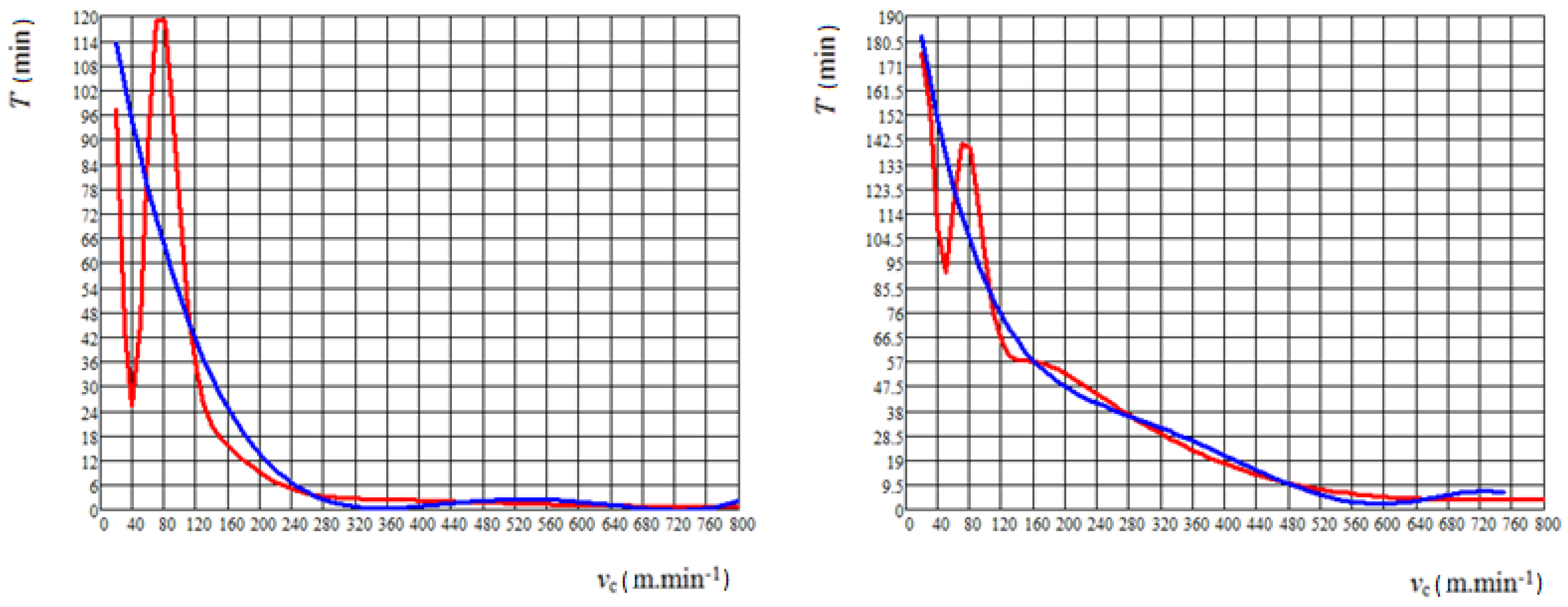
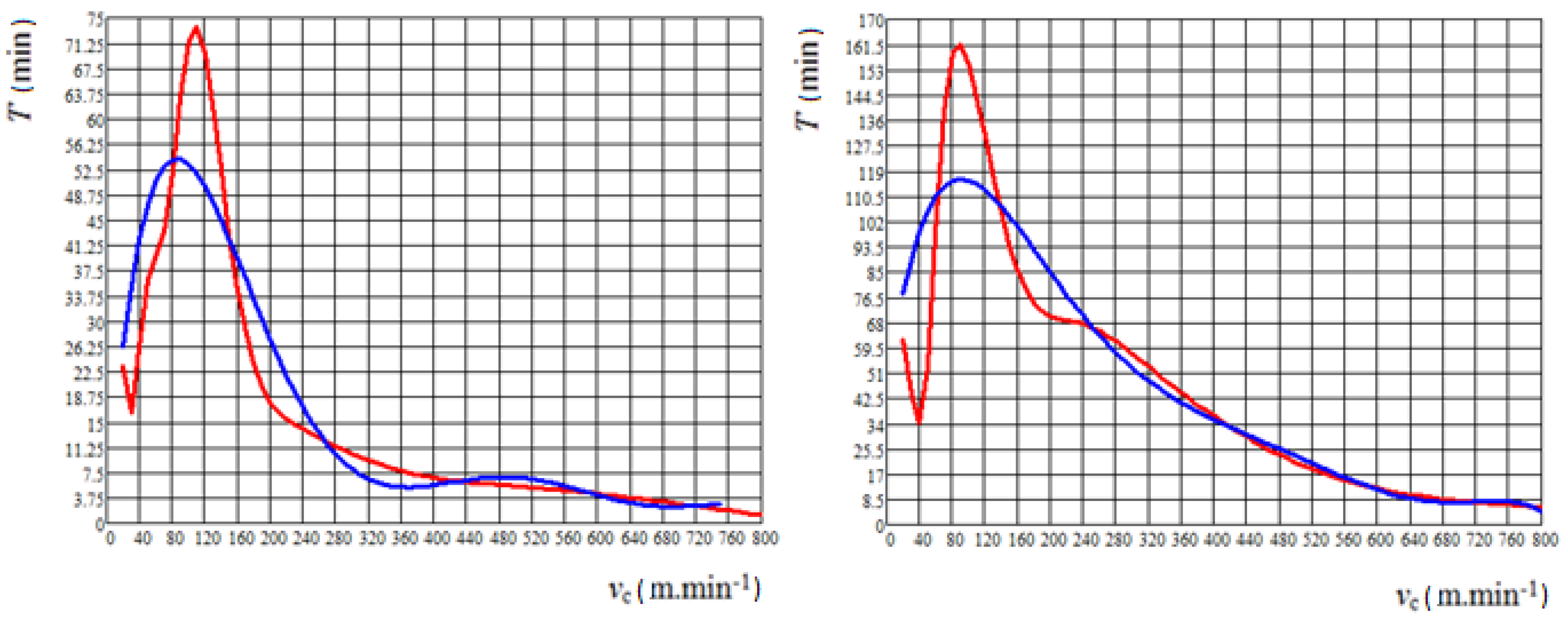
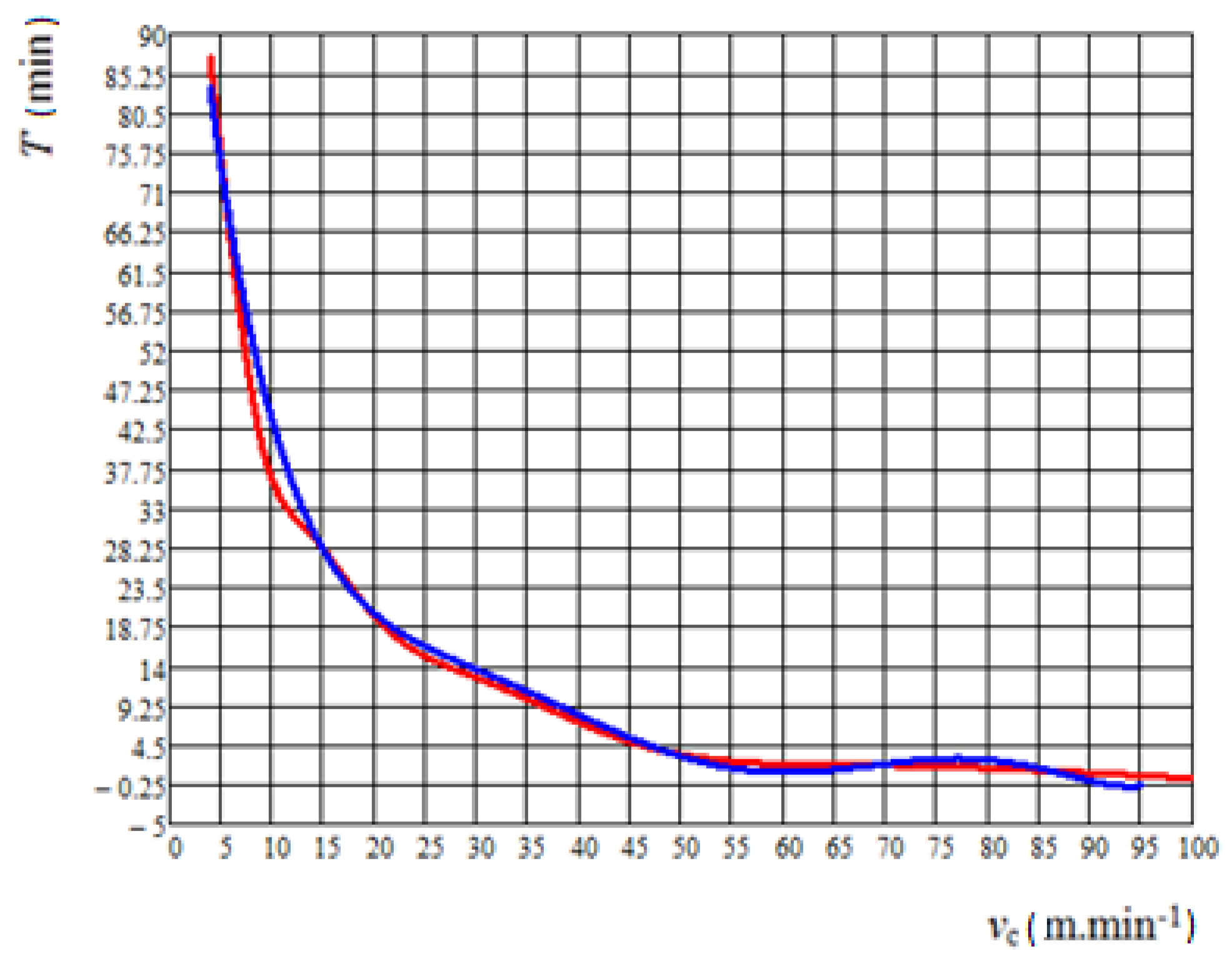
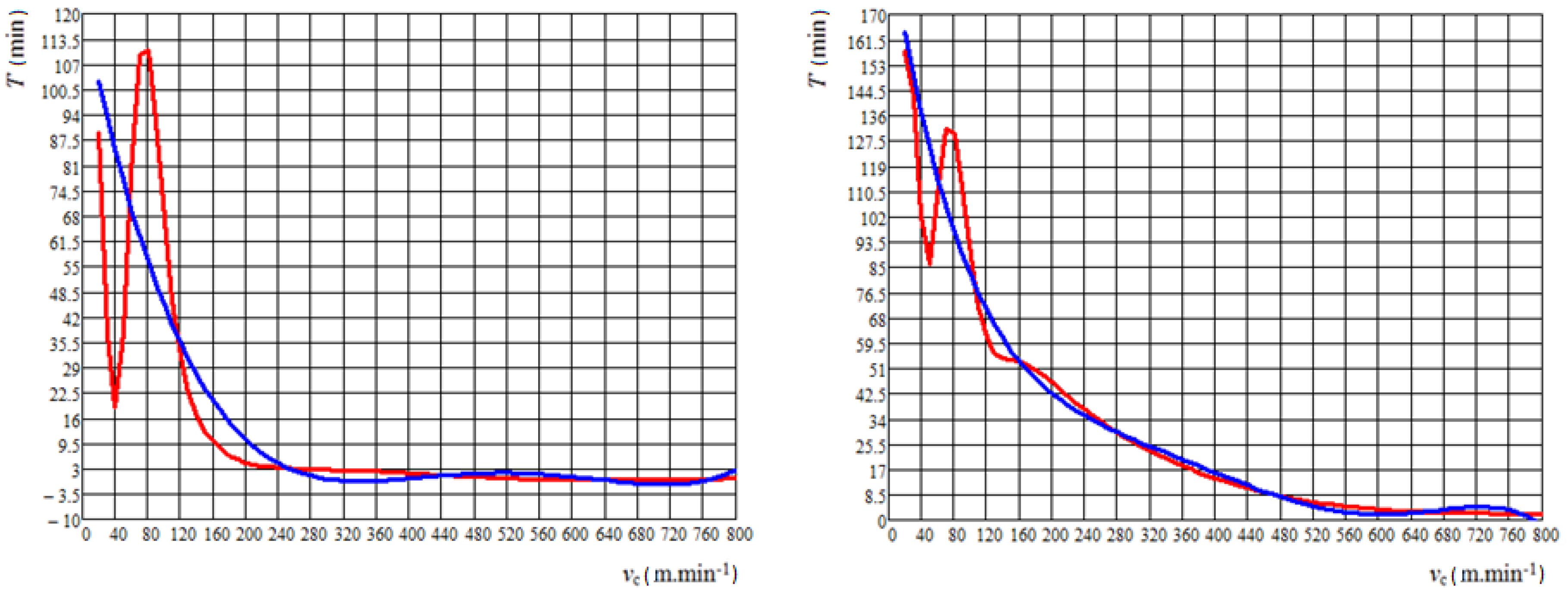
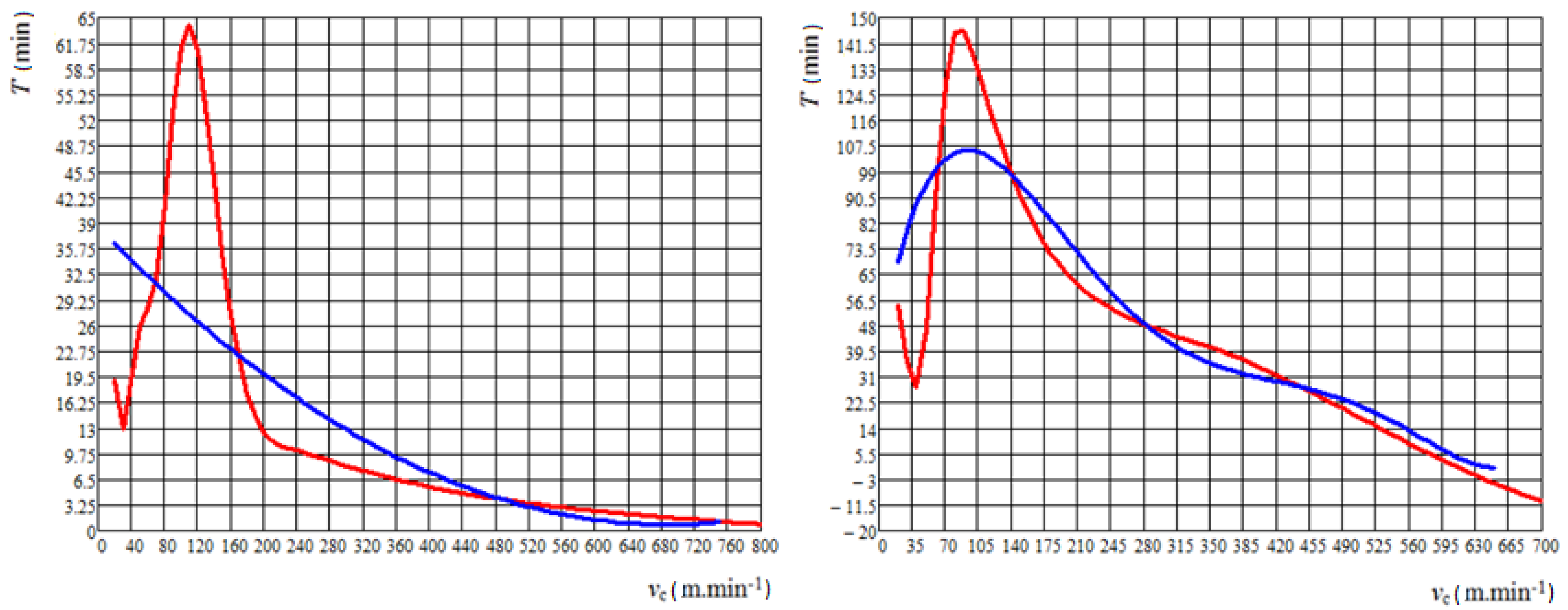
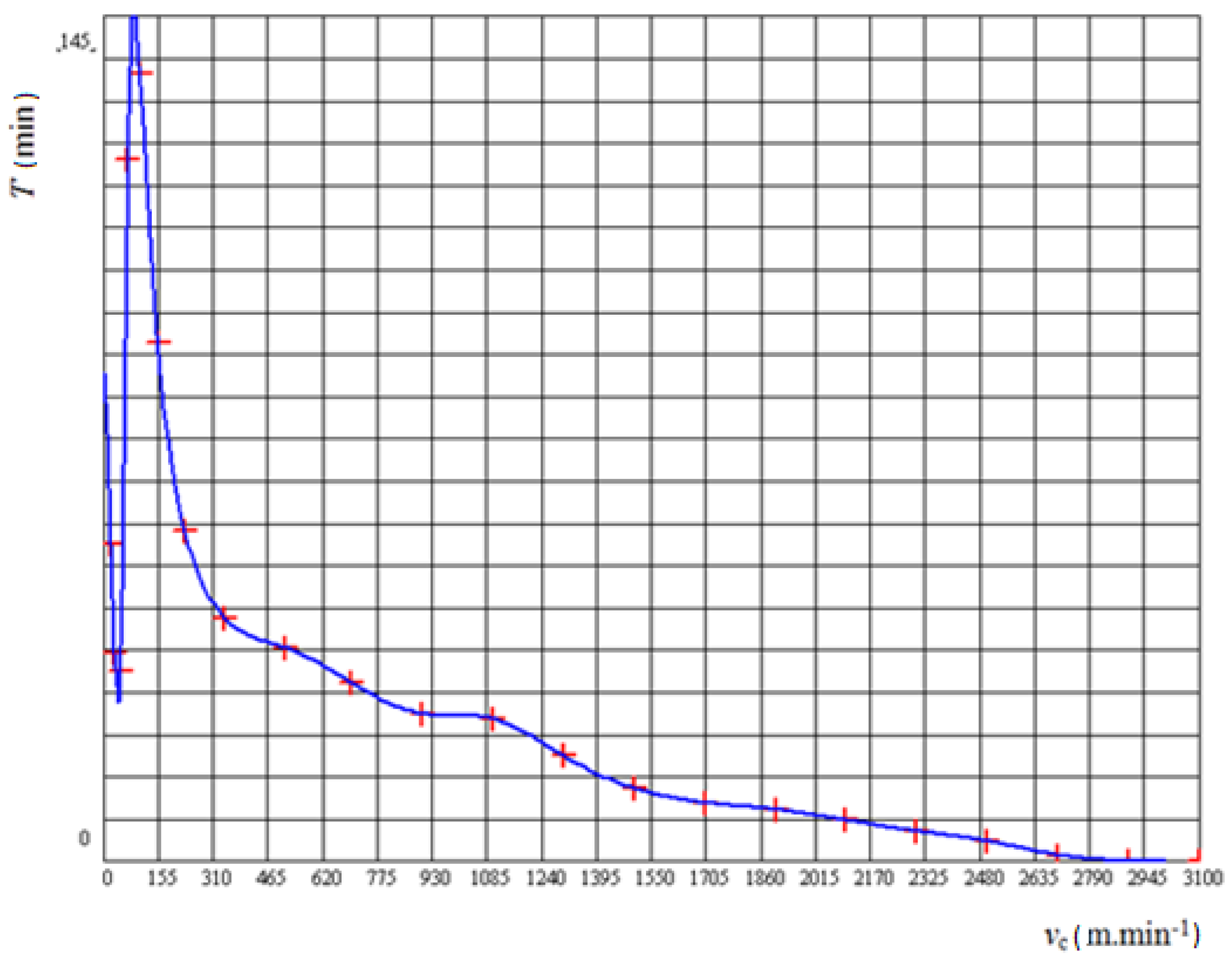
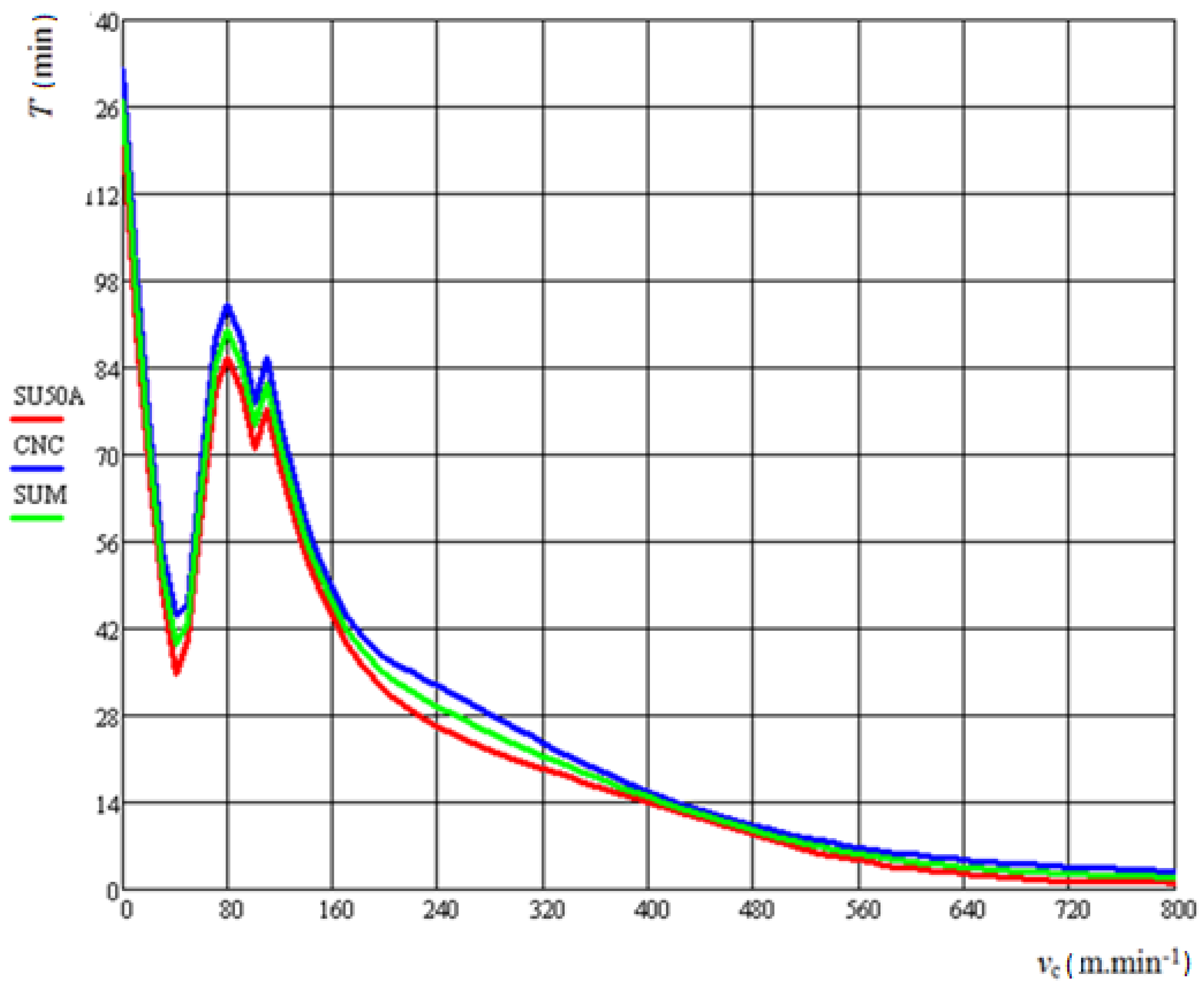
5. Results and Discussion
- The least-squares method:
- Regression analysis:
6. Conclusions
- Comprehensive knowledge of the T-vc dependence for the most commonly used cutting tools;
- Analytical description of experimental measurements;
- Experimental invalidity confirmation of ISO 3685;
- Through analytical expressions, it provides a proposal for correcting the standard used today by manufacturing companies;
- Identification of optimum cutting speed in terms of maximum tool life;
- Prediction of the behaviour of the cutting tool in the machining process.
Author Contributions
Funding
Conflicts of Interest
References
- Nicolich, M. Experimental Test for Tool-Life Prediction in Turning. CISM Cour. L 2002, 437, 185–192. [Google Scholar]
- Straka, Ľ.; Čorný, I.; Pite’, J. Prediction of the geometrical accuracy of the machined surface of the tool steel EN X30WCrV9-3 after electrical discharge machining with CuZn37 wire electrode. Metals 2017, 7, 462. [Google Scholar] [CrossRef] [Green Version]
- Valíček, J.; Harničárová, M.; Öchsner, A.; Hutyrová, Z.; Kušnerová, M.; Tozan, H.; Michenka, V.; Sepelak, V.; Mital, D.; Zajac, J. Quantifying the mechanical properties of materials and the process of elastic-plastic deformation under external stress on material. Materials 2015, 8, 7401–7422. [Google Scholar] [CrossRef] [Green Version]
- Knapčíková, L.; Dupláková, D.; Radchenko, S.; Hatala, M. Rheological behavior modelling of composite materials used in engineering industry. TEM J. 2017, 6, 242–245. [Google Scholar]
- Hutyrová, Z.; Harničarová, M.; Zajac, J.; Valíček, J.; Mihok, J. Experimental study of surface roughness of wood plastic composites after turning. Adv. Mater. Res. 2014, 856, 108–112. [Google Scholar] [CrossRef]
- Batista, M.; Davim, P.; Salguero, J.; Gomez-Parra, A.; Marcos, M. Taylor’s Model Based Analysis of Turning Inserts Tool-Life in the Dry Turning of UNS R56400 Alloy. In ASME 2014 International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Díaz, R.C.; Krahmer, D.M.; vila Rondón, R. Application of ISO 3685 in the evaluation of the machinability of steel SAE 1020 during the turning process. Rev. Tec. Fac. Ing. Univ. 2011, 34, 194–202. [Google Scholar]
- Dhabale, R.; Jatti, V.S.; Singh, T.P. Optimization of turning process during machining of AlMg1SiCu using Taguchi method and ANOVA. Int. J. Appl. Eng. Res. 2013, 8, 1273–1281. [Google Scholar]
- Chethan, Y.D.; Ravindra, H.V.; Krishnegowda, Y.T. Optimization of machining parameters in turning Nimonic-75 using machine vision and acoustic emission signals by Taguchi technique. Measurement 2019, 144, 144–154. [Google Scholar] [CrossRef]
- Dubovska, R.; Majerik, J.; Chochlikova, H. Investigation of Durability T = f (vc) in Turning of the AISI 304 Austenitic Stainless Steel using the CNMG 120408 Coated Carbide Insert. Adv. Mater. Res. 2014, 941, 1633–1643. [Google Scholar] [CrossRef]
- Iliescu, M. Cutting tool durability regression models in turning Inox 18-8 thermal sprayed coating. ACAD J. Manuf. Eng. 2011, 9, 61–66. [Google Scholar]
- Iliescu, M. Regression models of process parameters interdependence in turning S12Mn2Si metallized coatings. Wseas Trans. Syst. 2011, 10, 319–330. [Google Scholar]
- Miani, F.; Guseo, R.; Mortarino, C.; Meneghello, R. A new proposal for tool-life analysis: Response surface modelling of the flank wear progression. In Proceedings of the 2nd International Seminar on Improving Machine Tool Performance, La Baule, Nantes, France, 3–5 July 2000; pp. 3–5. [Google Scholar]
- Nath, C.; Brooks, Z.; Kurfess, T.R. Machinability study and process optimization in face milling of some super alloys with indexable copy face mill inserts. J. Manuf. Process. 2015, 20, 88–97. [Google Scholar] [CrossRef]
- Petru, J.; Schiffner, J.; Zlamal, T.; Cep, R.; Kratochvil, J.; Stancekova, D. Wear progress of exchangeable cutting inserts during Ti (6) Al (4) V alloy machining. In Proceedings of the 24th International Conference on Metallurgy and Materials, Brno, Czech Republic, 3–5 June 2015; pp. 1147–1155. [Google Scholar]
- Qehaja, N.; Kyçyku, A. Tool life modeling based on cutting parameters and work material hardness in turning process. Scientific proceedings XIV international congress. Mach. Technol. Mater. 2017, 11, 356–359. [Google Scholar]
- Sadílek, M.; Kratochvíl, J.; Petrů, J.; Čep, R.; Zlámal, T.; Stančeková, D. Cutting tool wear monitoring with the use of impedance layers. Vjesnik 2014, 21, 639–644. [Google Scholar]
- Čep, R.; Janásek, A.; Martinický, B.; Sadílek, M. Cutting tool life tests of ceramic inserts for car engine sleeves. Vjesnik 2011, 18, 203–209. [Google Scholar]
- Majernikova, J.; Spisak, E. Increasing durability of cutting tools. Adv. Sci. Technol. Res. J. 2017, 11, 141–146. [Google Scholar]
- Bakša, T.; Kroupa, T.; Hanzl, P.; Zetek, M. Durability of cutting tools during machining of very hard and solid materials. Procedia Eng. 2015, 100, 1414–1423. [Google Scholar] [CrossRef] [Green Version]
- Chaus, A.S.; Rudnitskii, F.I. Influence of cutting conditions of cast-metal cutting tools on their wear and durability: Analysis of cutting conditions of tools. J. Frict. Wear 2007, 28, 416–421. [Google Scholar] [CrossRef]
- Chaus, A.S.; Rudnitskii, F.I. Influence of cutting conditions of cast-metal cutting tools on their wear and durability. Part 2. Durability test results. J. Frict. Wear 2008, 29, 151–155. [Google Scholar] [CrossRef]
- Gill, S.S.; Singh, H.; Singh, R.; Singh, J. Flank wear and machining performance of cryogenically treated tungsten carbide inserts. Mater. Manuf. Process. 2011, 26, 1430–1441. [Google Scholar] [CrossRef]
- Gill, S.S.; Singh, J.; Singh, H.; Singh, R. Investigation on wear behaviour of cryogenically treated TiAlN coated tungsten carbide inserts in turning. Int. J. Mach. Tools Manuf. 2011, 51, 25–33. [Google Scholar] [CrossRef]
- Caballero, J.E.; V-Niño, E.D. Wear evaluation of flank in burins of high speed steel modified with titanium ions. J. Phys. Conf. Ser. 2017, 935, 1–5. [Google Scholar] [CrossRef]
- Hao, X.; Chen, X.; Xiao, S.; Li, L.; He, N. Cutting performance of carbide tools with hybrid texture. Int. J. Adv. Manuf. Technol. 2018, 97, 3547–3556. [Google Scholar] [CrossRef]
- Jaworski, J.; Trzepieciński, T. Research on durability of turning tools made of low-alloy high-speed steel. Met. Mater. 2016, 54, 17–25. [Google Scholar] [CrossRef] [Green Version]
- Lalbondre, R.; Krishna, P.; Mohankumar, G.C. Machinability studies of low alloy steels by face turning method: An experimental investigation. Procedia Eng. 2013, 64, 632–641. [Google Scholar] [CrossRef]
- Neshta, A.; Kryvoruchko, D.; Hatala, M.; Ivanov, V.; Botko, F.; Radchenko, S.; Mital, D. Technological Assurance of High-Efficiency Machining of Internal Rope Threads on Computer Numerical Control Milling Machines. J. Manuf. Sci. Eng. 2018, 140, 1–8. [Google Scholar] [CrossRef]
- Holub, M.; Jankovych, R.; Andrs, O.; Kolibal, Z. Capability assessment of CNC machining centres as measuring devices. Measurement 2018, 118, 52–60. [Google Scholar] [CrossRef]
- Che-Haron, C.H. Tool life and surface integrity in turning titanium alloy. J. Mater. Process. Technol. 2001, 118, 231–237. [Google Scholar] [CrossRef]
- Yip, W.S.; To, S. Tool life enhancement in dry diamond turning of titanium alloys using an eddy current damping and a magnetic field for sustainable manufacturing. J. Clean. Prod. 2017, 168, 929–939. [Google Scholar] [CrossRef]
- Ren, Z.; Qu, S.; Zhang, Y.; Sun, F.; Li, X.; Yang, C. Machining performance of PCD and PCBN tools in dry turning titanium alloy Ti-6Al-0.6 Cr-0.4 Fe-0.4 Si-0.01 B. Int. J. Adv. Manuf. Technol. 2019, 102, 2649–2661. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Rahman, S.S.; Ashraf, M.Z.I.; Dhar, N.R. Tool life and workpiece surface integrity when turning an RR1000nickel-based superalloy. Int. J. Adv. Manuf. Technol. 2018, 98, 2461–2468. [Google Scholar]
- Antonialli, A.Í.S.; Magri, A.; Diniz, A.E. Tool life and tool wear in taper turning of a nickel-based superalloy. Int. J. Adv. Manuf. Technol. 2016, 87, 2023–2032. [Google Scholar] [CrossRef]
- Priarone, P.C.; Klocke, F.; Faga, M.G.; Lung, D.; Settineri, L. Tool life and surface integrity when turning titanium aluminides with PCD tools under conventional wet cutting and cryogenic cooling. Int. J. Adv. Manuf. Technol. 2016, 85, 807–816. [Google Scholar] [CrossRef]
- Da Silva, R.B.; Sales, W.F.; Costa, E.S.; Ezugwu, E.O.; Bonney, J.; Da Silva, M.B.; Machado, Á.R. Surface integrity and tool life when turning of Ti-6Al-4V with coolant applied by different methods. Int. J. Adv. Manuf. Technol. 2017, 93, 1893–1902. [Google Scholar] [CrossRef]
- Bonfá, M.M.; Costa, É.S.; Sales, W.F.; Amorim, F.L.; Maia, L.H.A.; Machado, Á.R. Evaluation of tool life and workpiece surface roughness in turning of AISI D6 hardened steel using PCBN tools and minimum quantity of lubricant (MQL) applied at different directions. Int. J. Adv. Manuf. Technol. 2019, 103, 971–984. [Google Scholar] [CrossRef]
- Verma, J.K.; Bartarya, G.; Bhaskar, J. Effect of Minimum Quantity Lubrication on Tool Wear and Surface Integrity During Hard Turning of EN31 Steel. In Advances in Forming, Machining and Automation; Shunmugam, M., Kanthababu, M., Eds.; Lecture Notes on Multidisciplinary Industrial Engineering; Springer: Singapore, 2019. [Google Scholar]
- Sulaiman, M.A.; Asiyah, M.S.; Shahmi, R.; Mohamad, E.; Mohamad, N.A.; Ali, M.M.; Yuniawan, D.; Ito, T. Effect of cutting parameter on the tool life of the uncoated carbide tool during turning using minimum quantity lubrication (MQL). Int. J. Adv. Manuf. Technol. 2019, 12, 63–72. [Google Scholar]
- Straka, Ľ.; Čorný, I.; Piteľ, J.; Hašová, S. Statistical Approach to Optimize the Process Parameters of HAZ of Tool Steel EN X32CrMoV12-28 after Die-Sinking EDM with SF-Cu Electrode. Metals 2017, 7, 35. [Google Scholar] [CrossRef] [Green Version]











| CSRNR2020K-12 | SCLCR1616-H09 | |
|---|---|---|
| Rake angle (γ) | −6° | 0° |
| Flank angle (α) | 6° | 4° |
| The cutting edge inclination angle (λs) | −6° | 0° |
| Tool cutting edge angle (κr) | 75° | 95° |
| Wedge angle (εr) | 90 | 80° |
| C | Mn | Si | Cr | Ni | Cu | P | S |
|---|---|---|---|---|---|---|---|
| 0.42–0.50 | 0.50–0.80 | 0.37 | upper limit 0.25 | upper limit 0.30 | upper limit 0.30 | upper limit 0.040 | upper limit 0.040 |
| Yield Strength (MPa) | Tensile Strength (MPa) | Fracture Elongation (%) | Brinell Hardness | Youngs Module (GPa) | Shear Module (GPa) |
|---|---|---|---|---|---|
| lower limit 305 | lower limit 530 | 16 | max. 225 | 221 | 79 |
| Cutting Parameters | Cutting Inserts | |
|---|---|---|
| Tungsten Carbide, Tungsten Carbide + Coating, Cutting Ceramics, Cutting Ceramics + Coating | High-Speed Steel (Poldi—Marked as Radeco) | |
| Cutting speed (m/min) | 20–768.8 | 3.95–101.25 |
| Feed (mm) | 0.1 | 0.1 |
| Depth of cut (mm) | 0.5 | 0.5 |
| Wear (mm) | 0.3 | 0.3 |
| Diameter D (mm) | Spindle Speed n (min−1) | Feed Speed vf (mm/min) | Time τs (min) |
|---|---|---|---|
| 89.7 | 71 | 7.1 | 67.59 |
| 88.7 | 71.8 | 7.18 | 66.84 |
| 70.5 | 90.3 | 9.03 | 53.12 |
| 70.2 | 90.7 | 9.07 | 52.9 |
| 57.2 | 111.3 | 11.13 | 43.1 |
| 45.5 | 139.9 | 13.99 | 34.28 |
| D (mm) | n (min−1) | vf (mm/min) | τs (min) | Tool |
|---|---|---|---|---|
| 96.2 | 66.21 | 6.62 | 19.63 | tungsten carbide |
| 95.2 | 468.34 | 93.66 | tool for preparation of the surface (SCLCR1616-H09) | |
| 94.9 | 67.11 | 6.71 | 19.36 | tungsten carbide + coating |
| 93.9 | 474.82 | 94.96 | tool for preparation of the surface (SCLCR1616-H09) | |
| 93.6 | 68.04 | 6.80 | 19.1 | cutting ceramics |
| 92.6 | 481.49 | 96.29 | tool for preparation of the surface (SCLCR1616-H09) | |
| 92.3 | 69 | 6.9 | 18.83 | cutting ceramics + coating |
| 91.3 | 488.34 | 6.62 | tool for preparation of the surface (SCLCR1616-H09) |
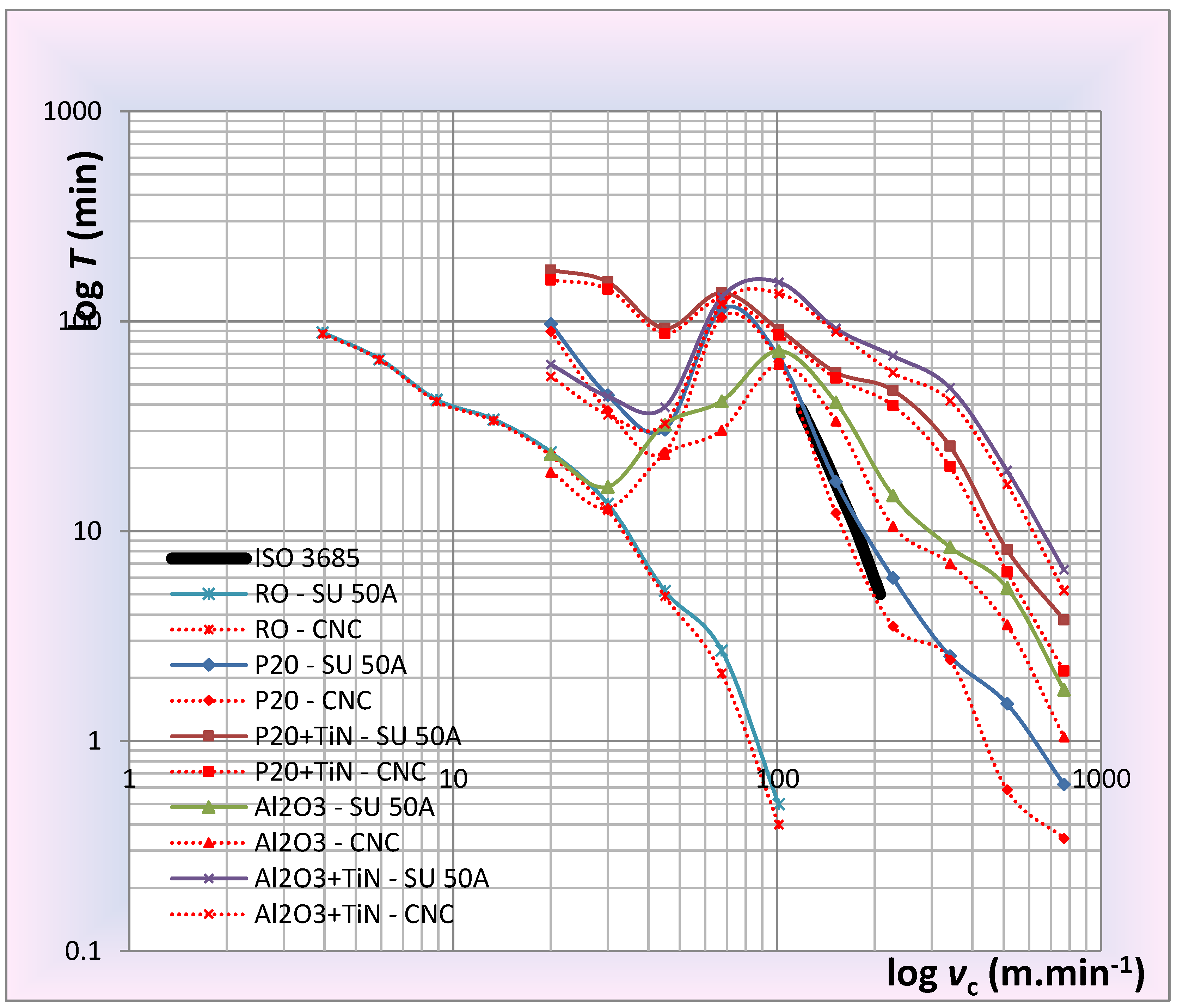
| SU 50 A | Cutting Materials | ||||
|---|---|---|---|---|---|
| vc (m/min) | HSS | P20 | P20 + TiN | Al2O3 | Al2O3 + TiN |
| T (min) | T (min) | T (min) | T (min) | T (min) | |
| 3.95 | 88.5 | ||||
| 5.93 | 66.1 | ||||
| 8.89 | 42.3 | ||||
| 13.33 | 34.1 | ||||
| 20 | 23.8 | 97.26 | 175.88 | 23.3 | 62.3 |
| 30 | 13.5 | 44.46 | 154.3 | 16.26 | 43.9 |
| 45 | 5.2 | 30.48 | 92.66 | 32.24 | 39.02 |
| 67.5 | 2.7 | 114.28 | 137.08 | 41.64 | 130.28 |
| 101.25 | 0.5 | 67.68 | 91.62 | 72.14 | 153.44 |
| 151.8 | 17.24 | 57.2 | 41.1 | 92.4 | |
| 227.8 | 6 | 46.92 | 14.82 | 68.46 | |
| 341.7 | 2.542 | 25.44 | 8.4 | 48.3 | |
| 512.5 | 1.508 | 8.16 | 5.38 | 19.48 | |
| 768.8 | 0.622 | 3.78 | 1.76 | 6.56 | |
| Cutting Material | The Least-Squares Method Equation | Correlation Index (%) |
|---|---|---|
| HSS | T = 0.086 vc2 − 5.03 KRM + 93.52 | 96.7 |
| P20 | T = 0.0008 vc2 – 0.47 KRM + 88.396 | 76.9 |
| P20 + TiN | T = 0.002 vc2 – 0.96 KRM + 174.5 | 95.6 |
| Al2O3 | T = –0.001 vc2 + 0.218 KRM + 25.48 | 71.4 |
| Al2O3 + TiN | T = –0.003 vc2 + 0.699 KRM + 50.43 | 74.6 |
| The final equation for all cutting materials—conventional lathe | ||
| T = −0.00054 vc2 + 0.009 KRM + 64.55 | 49.4 | |
| CNC. | Cutting Materials | ||||
|---|---|---|---|---|---|
| vc (m/min) | HSS | P20 | P20 + TiN | Al2O3 | Al2O3 + TiN |
| T (min) | T (min) | T (min) | T (min) | T (min) | |
| 3.95 | 87.2 | ||||
| 5.93 | 65.7 | ||||
| 8.89 | 41.5 | ||||
| 13.33 | 33.6 | ||||
| 20 | 22.9 | 89.46 | 157.71 | 19.148 | 54.63 |
| 30 | 12.6 | 37.5 | 142.426 | 12.846 | 35.798 |
| 45 | 4.9 | 23.84 | 87.664 | 23.252 | 32.556 |
| 67.5 | 2.1 | 104.44 | 127.974 | 30.298 | 120.7 |
| 101.25 | 0.4 | 64.22 | 86.238 | 62.148 | 135.59 |
| 151.8 | 12.2 | 53.69 | 33.524 | 89.28 | |
| 227.8 | 3.534 | 39.71 | 10.556 | 56.932 | |
| 341.7 | 2.438 | 20.32 | 7 | 41.756 | |
| 512.5 | 0.586 | 6.408 | 3.578 | 16.71 | |
| 768.8 | 0.344 | 2.156 | 1.048 | 5.21 | |
| Cutting Material | The Least-Squares Method Equation | Correlation Index (%) |
|---|---|---|
| HSS | T = 0.085 vc2 − 5.01 KRM + 92.58 | 96.8 |
| P20 | T = 0.0007 vc2 – 0.43 KRM + 79.43 | 74.5 |
| P20 + TiN | T = 0.002 vc2 – 0.88 KRM + 160.8 | 96.3 |
| Al2O3 | T = −0.0008 vc2 + 0.19 KRM + 19.39 | 68.7 |
| Al2O3 + TiN | T = −0.003 vc2 + 0.655 KRM + 43.32 | 73.7 |
| The final equation for all cutting materials—CNC machine | ||
| T = −0.0004 vc2 − 0.02 KRM + 59.67 | 49.3 | |
| Cutting Material | The Least-Squares Method Equation | Correlation Index (%) |
|---|---|---|
| HSS | T = 0.813 vc2 − 14.97 KRM + 132.45 | 99.7 |
| P20 | T = 0.003 vc2 − 1.109 KRM + 132.067 | 90.6 |
| P20 + TiN | T = 0.011 vc2 − 2.17 KRM + 221.402 | 97.7 |
| Al2O3 | T = −0.015 vc2 + 1.534 KRM + 0.919 | 93.1 |
| Al2O3 + TiN | T = −0.017 vc2 + 1.902 KRM + 46.087 | 91.6 |
| The final equation for all cutting materials—conventional lathe | ||
| T = 0.0004 vc2 − 0.345 KRM + 95.756 | 94.0 | |
| Cutting Material | The Least-Squares Method Equation | Correlation Index (%) |
|---|---|---|
| HSS | T = 0.779 vc2 − 14.558 KRM + 130.184 | 99.7 |
| P20 | T = 0.003 vc2 − 1.073 KRM + 122.908 | 90.6 |
| P20 + TiN | T = 0.008 vc2 − 1.765 KRM + 196.255 | 97.9 |
| Al2O3 | T = 0.00008 vc2 − 0.11 KRM + 38.588 | 91.9 |
| Al2O3 + TiN | T = −0.014 vc2 + 1.707 KRM + 40.034 | 90.7 |
| The final equation for all cutting materials—CNC machine | ||
| T = 0.003 vc2 − 0.31 KRM + 86.213 | 93.3 | |
| HSS | P20 | P20 + TiN | Al2O3 | Al2O3 + TiN |
|---|---|---|---|---|
| 3–4 | 2–3 | 1–2 | 3–4 | 1–2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zajac, J.; Duplak, J.; Duplakova, D.; Cizmar, P.; Olexa, I.; Bittner, A. Prediction of Cutting Material Durability by T = f(vc) Dependence for Turning Processes. Processes 2020, 8, 789. https://doi.org/10.3390/pr8070789
Zajac J, Duplak J, Duplakova D, Cizmar P, Olexa I, Bittner A. Prediction of Cutting Material Durability by T = f(vc) Dependence for Turning Processes. Processes. 2020; 8(7):789. https://doi.org/10.3390/pr8070789
Chicago/Turabian StyleZajac, Jozef, Jan Duplak, Darina Duplakova, Peter Cizmar, Igor Olexa, and Anton Bittner. 2020. "Prediction of Cutting Material Durability by T = f(vc) Dependence for Turning Processes" Processes 8, no. 7: 789. https://doi.org/10.3390/pr8070789
APA StyleZajac, J., Duplak, J., Duplakova, D., Cizmar, P., Olexa, I., & Bittner, A. (2020). Prediction of Cutting Material Durability by T = f(vc) Dependence for Turning Processes. Processes, 8(7), 789. https://doi.org/10.3390/pr8070789







