Comparative Study of a Compression–Absorption Cascade System Operating with NH3-LiNO3, NH3-NaSCN, NH3-H2O, and R134a as Working Fluids
Abstract
:1. Introduction
- The refrigerant that has been considered most frequently in the compression cycle is R134a, and less the NH3. Recently, models and designs have been reported that involve R410a, as in the work of Boyaghchi et al. [12]. Additionally, it proposes the use of H2O/Cu oxide (CuO) nanofluid as a fluid that transports energy from a solar collector to the generator.
- New configurations have been proposed, which involve double-effect absorption or the satisfaction of specific refrigeration applications as food conservation, cooling in naval ships, or solar energy coupled into the cascade system. These designs consider LiBr- H2O in the absorption cycle. An aspect that has caught our attention is the fact that the number of heat exchangers (also known as economizers) that the system must involve has not been identified. Additionally, the heat exchanger effectiveness changes from author to author, in ranges from 0.6 to 0.85.
- Thermodynamic analysis and simulation were presented by Cimsit et al. [7], Jain et al. [17], and Boyaghchi et al. [12] considering LiBr-H2O as the working fluid in the absorption cycle in several conditions, and the design consideration of solution heat exchanger. Then, Cimsit et al. [7] simulated the coefficient of the system performance considering NH3-H2O; while this work proposes an extension of the knowledge of Cimsit et al. [7] adding the evaluation of NH3-LiNO3, NH3-NaSCN in the absorption cycle.
- The works carried out by Karamangil et al. [24] can be compared with the present manuscript, developing a thermodynamic model of a visual software package to analyze the absorption single-stage refrigerant system. The solutions under study were H2O-LiBr, NH3-H2O, NH3-LiNO3, and acetone-ZnBr2, while this study presents a theoretical thermodynamic model to compute the energy efficiency parameters in the compression–absorption cascade system considering the influence of several economizers. The energy balance equation and the coefficient of performance were considered in both papers as comparison parameters.
- To the extent of our knowledge, the refrigerant–absorbent pair selected in this manuscript were NH3-LiNO3 and NH3-NaSCN for the first time for the compression–absorption system, the numerical results are compared with NH3-H2O performance; while R134a refrigerant remains in the compression cycle.
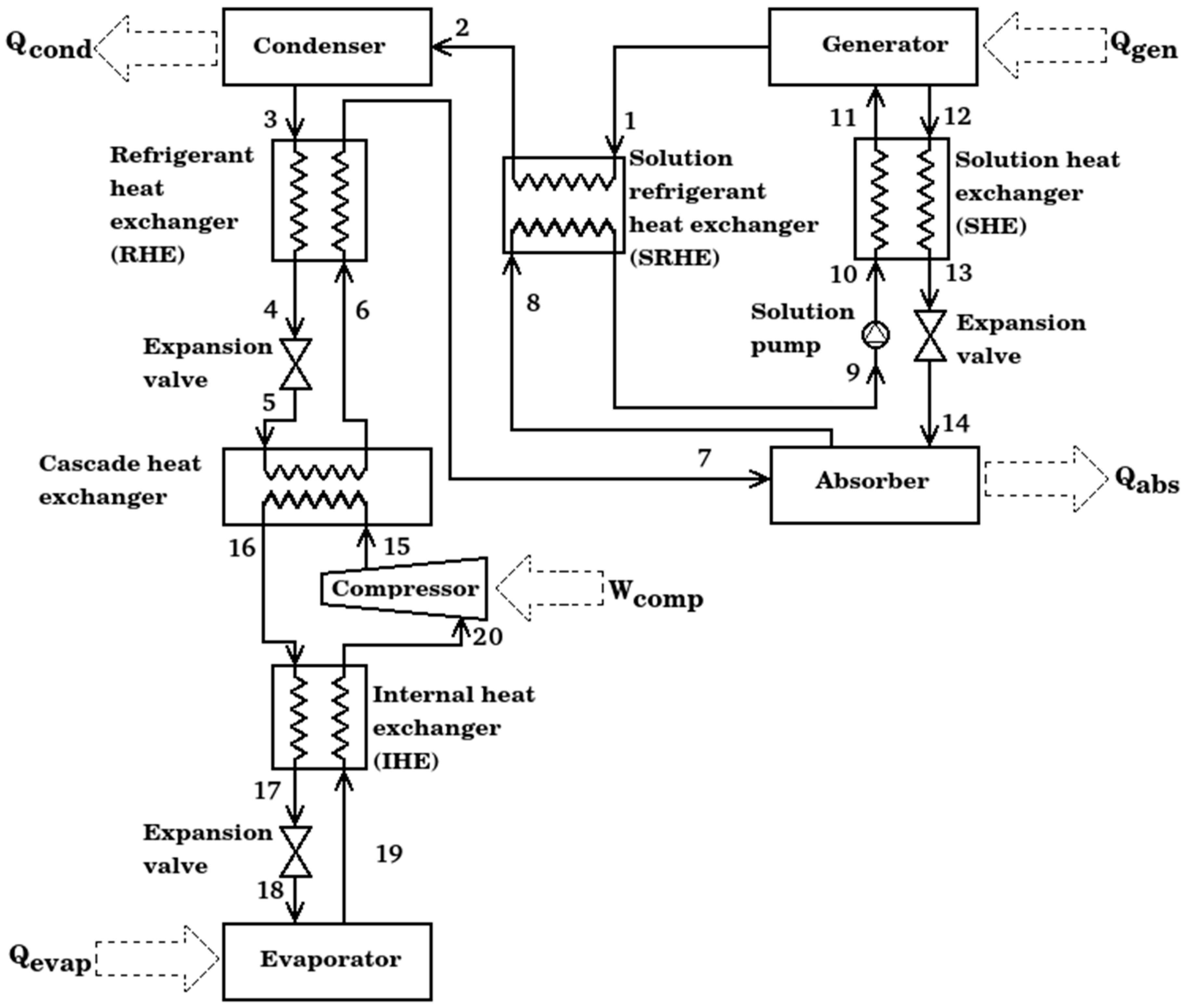
2. System Description
- Internal heat exchanger. Its objective is to reduce the work added by the compressor to the cycle, it exchanges the heat transfer from high pressure compressed liquid to saturated steam to low pressure; all previously in the compression cycle.
- Refrigerant heat exchanger. This heat exchanger was designed to increase the energy of the vapor stream at the cascade heat exchanger outlet, taking advantage of the condensed liquid obtained from the condenser.
- Solution refrigerant heat exchanger. This type of equipment is designed to operate between the two pressure levels of the absorption cycle, the strong LiBr solution and the refrigerant vapor are the working fluids that flow in the equipment. Solution heat exchanger. It is the heat exchanger commonly used in the literature for absorption cycles; its function is to preheat the solution from the absorber to the generator. Its use increases the use of the waste heat added in the generator.
3. Thermodynamic Modeling
- In the absorption cycle, the pump work necessary to circulate the solution is considered negligible [7].
- Pressure and temperature values could be worked with experimentally [9].
- Steady-state conditions are considered in this study.
- Thermodynamic equilibrium at the inlet and outlet of the components is assumed
- The heat losses from the equipment, the pressure drop in the piping, and the main components are considered negligible [20].
- The expansion process in the valve is considered isenthalpic.
- Solutions flowing out of the absorber and the generator are assumed to be saturated in equilibrium conditions at their respective temperatures and concentrations [24].
- The NH3-H2O thermophysical properties are obtained from the correlations provided by M. Conde Engineering [25].
- Infante Ferreira’s [28] correlation has been used to obtain the specific enthalpy of solution.
- For the NH3-NaSCN solution, vapor pressure and enthalpy correlation equation coefficients provided by D Cai et al. [29] and
- The correlation of density was provided by Chaudhari et al. [30]
4. Results and Discussion
4.1. Model Validation
4.2. Thermodynamic Results of Base-Case Exposed in This Work
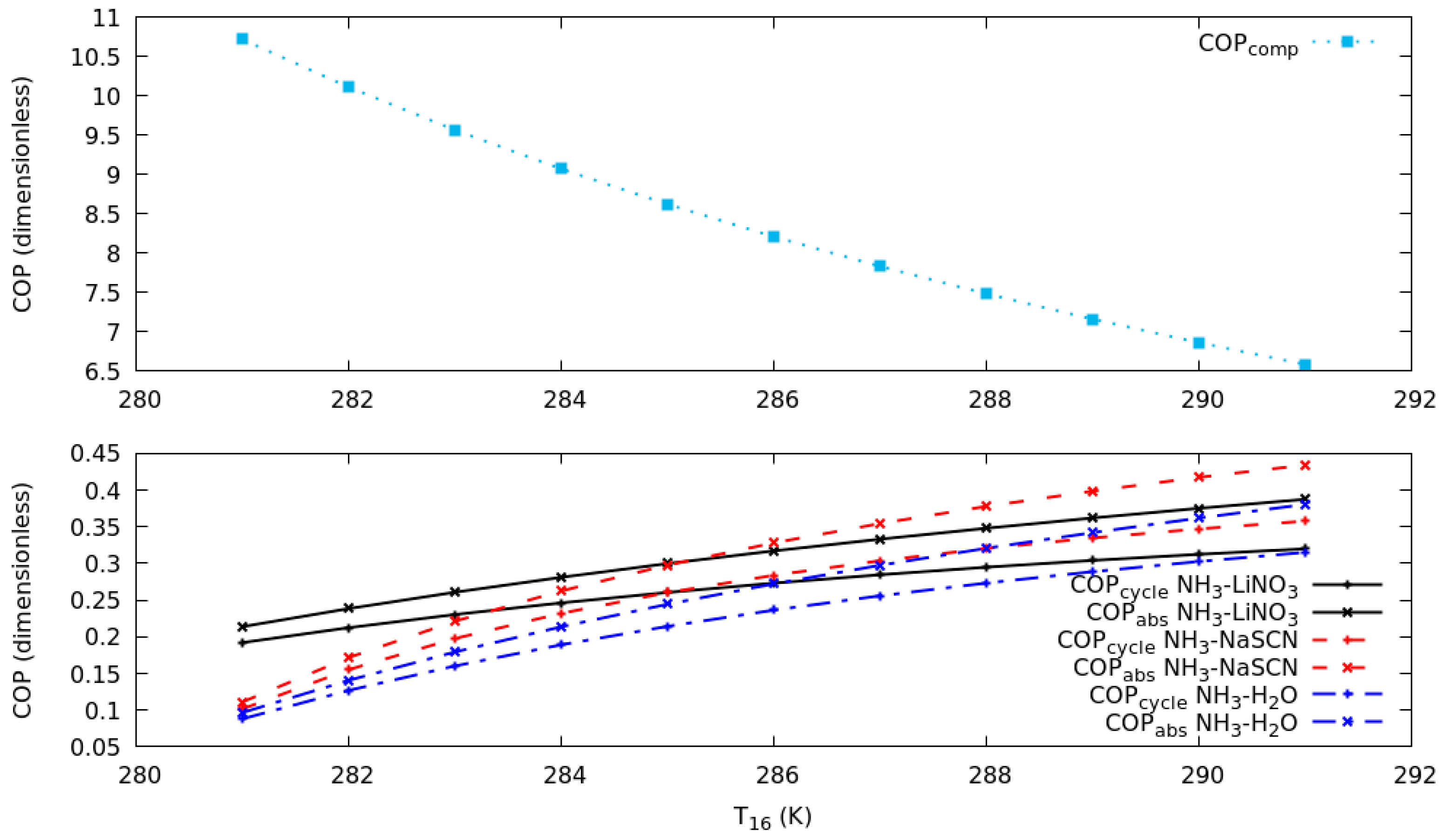
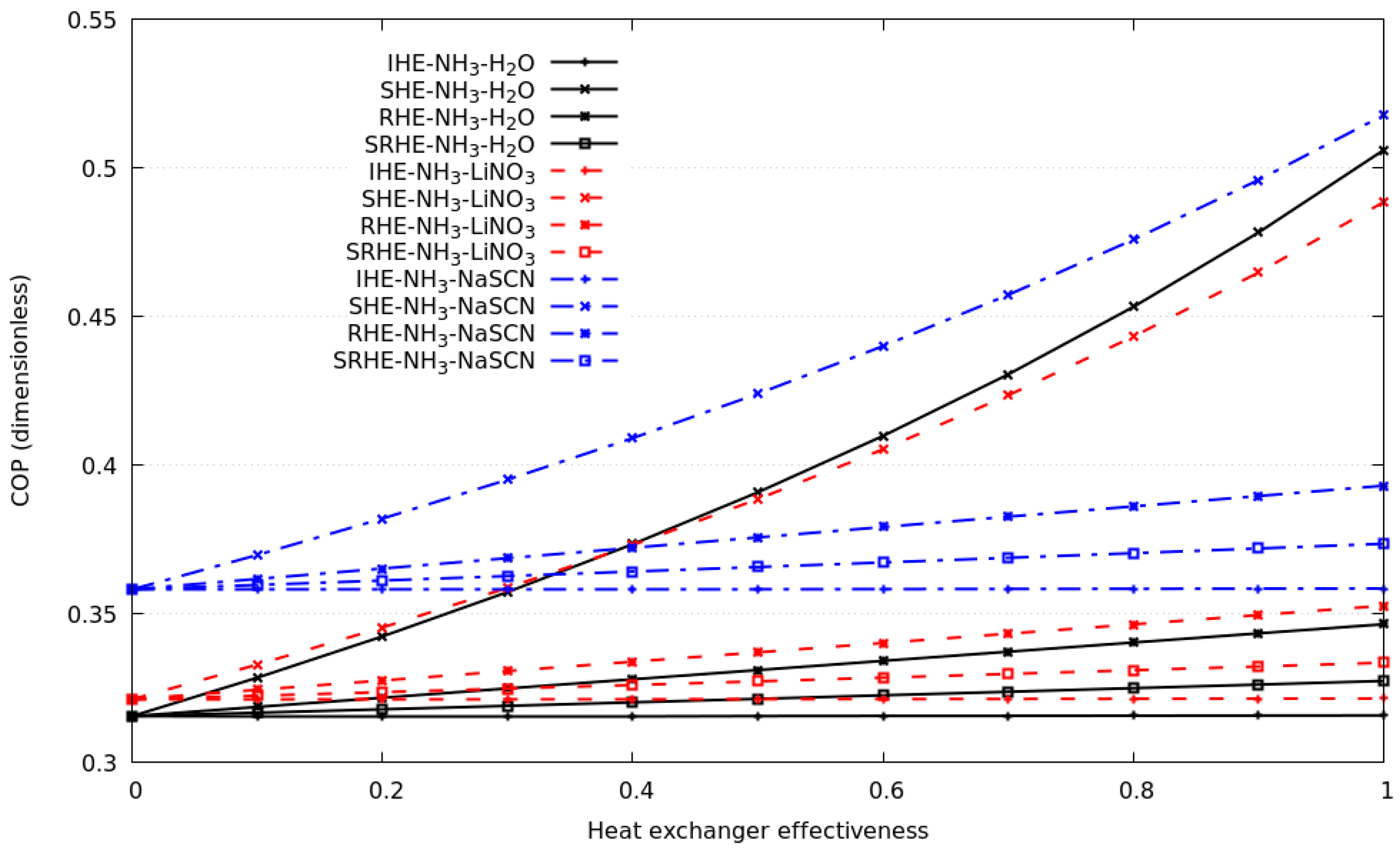
4.3. Effect of the Heat Source Temperature, Evaporation Temperature in the Compression Cycle and the Contribution of Each Economizer in the Cascade System
5. Conclusions
- For the refrigerant–absorbent pairs considered in this analysis, NH3-NaSCN in the absorption cycle and R134a in the compression cycle showed the highest coefficient of performances considering the heat source temperature and evaporator temperature conditions described in this work.
- Approximately 50% of the work consumed in the compressor can be reduced in a cascade system using NH3-NaSCN and R134a as working fluids, compared to a traditional vapor compression refrigeration system.
- The solution heat exchanger was the economizer that significantly benefits the coefficient of performance of the compression–absorption cascade system for all working fluids under study. The refrigerant heat exchanger is the economizer that secondly contributes a benefit to the performance of the entire system. The correct selection, cleaning, and maintenance of these economizers is suggested, to guarantee a greater heat exchanger effectiveness than 0.6.
- The contribution of a solution refrigerant and an internal heat exchanger was not theoretically significant in the coefficient of performance for all working fluids under study.
Author Contributions
Funding
Conflicts of Interest
References
- Srikhirin, P.; Aphornratana, S.; Chungpaibulpatana, S. A review of absorption refrigeration technologies. Renew. Sustain. Energy Rev. 2001, 5, 343–372. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Wang, R.Z. Absorption refrigeration cycles: Categorized based on the cycle construction. Int. J. Refrig. 2016, 62, 114–136. [Google Scholar] [CrossRef]
- She, X.; Cong, L.; Nie, B.; Leng, G.; Peng, H.; Chen, Y.; Zhang, X.; Wen, T.; Yang, H.; Luo, Y. Energy-efficient and-economic technologies for air conditioning with vapor compression refrigeration: A comprehensive review. Appl. Energy 2018, 232, 157–186. [Google Scholar] [CrossRef]
- Papadopoulos, A.I.; Kyriakides, A.S.; Seferlis, P.; Hassan, I. Absorption refrigeration processes with organic working fluid mixtures-a review. Renew. Sustain. Energy Rev. 2019, 109, 239–270. [Google Scholar] [CrossRef]
- Fernandez-Seara, J.; Sieres, J.; Vazquez, M. Compression–absorption cascade refrigeration system. Appl. Ther. Eng. 2006, 26, 502–512. [Google Scholar] [CrossRef]
- Garimella, S.; Brown, A.M.; Nagavarapu, A.K. Waste heat driven absorption/vapor-compression cascade refrigeration system for megawatt scale, high-flux, low-temperature cooling. Int. J. Refrig. 2011, 34, 1776–1785. [Google Scholar] [CrossRef]
- Cimsit, C.; Ozturk, I.T. Analysis of compression–absorption cascade refrigeration cycles. Appl. Ther. Eng. 2012, 40, 311–317. [Google Scholar] [CrossRef]
- Colorado, D.; Velazquez, V.M. Exergy analysis of a compression–absorption cascade system for refrigeration. Int. J. Energy Res. 2013, 37, 1851–1865. [Google Scholar] [CrossRef]
- Cimsit, C.; Ozturk, I.T.; Kincay, O. Thermoeconomic optimization of LiBr/H2O-R134a compression-absorption cascade refrigeration cycle. Appl. Ther. Eng. 2015, 76, 105–115. [Google Scholar] [CrossRef]
- Colorado, D.; Rivera, W. Performance comparison between a conventional vapor compression and compression-absorption single-stage and double-stage systems used for refrigeration. Appl. Ther. Eng. 2015, 87, 273–285. [Google Scholar] [CrossRef]
- Jain, V.; Sachdeva, G.; Kachhwaha, S.S.; Patel, B. Thermo-economic and environmental analyses based multi-objective optimization of vapor compression–absorption cascaded refrigeration system using NSGA-II technique. Energy Convers. Manag. 2016, 113, 230–242. [Google Scholar] [CrossRef]
- Boyaghchi, F.A.; Mahmoodnezhad, M.; Sabeti, V. Exergoeconomic analysis and optimization of a solar driven dual-evaporator vapor compression-absorption cascade refrigeration system using water/CuO nanofluid. J. Clean. Prod. 2016, 139, 970–985. [Google Scholar] [CrossRef]
- Dixit, M.; Arora, A.; Kaushik, S.C. Energy, exergy, environment and economic analyses and optimization of two-stage absorption–compression combined refrigeration system. Clean Technol. Environ. Policy 2017, 19, 2215–2229. [Google Scholar] [CrossRef]
- Cimsit, C. Thermodynamic performance analysis of the double effect absorption-vapour compression cascade refrigeration cycle. J. Therm. Sci. Technol. 2018, 13, JTST0007. [Google Scholar] [CrossRef] [Green Version]
- Salhi, K.; Korichi, M.; Ramadan, K.M. Thermodynamic and thermo-economic analysis of compression–absorption cascade refrigeration system using low-GWP HFO refrigerant powered by geothermal energy. Int. J. Refrig. 2018, 94, 214–229. [Google Scholar] [CrossRef]
- Vasta, S.; Palomba, V.; La Rosa, D.; Mittelbach, W. Adsorption-compression cascade cycles: An experimental study. Energy Convers. Manag. 2018, 156, 365–375. [Google Scholar] [CrossRef]
- Jain, V.; Sachdeva, G.; Kachhwaha, S.S. Comparative performance study and advanced exergy analysis of novel vapor compression-absorption integrated refrigeration system. Energy Convers. Manag. 2018, 172, 81–97. [Google Scholar] [CrossRef]
- Turgut, M.S.; Turgut, O.E. Comparative investigation and multi objective design optimization of a cascaded vapor compression absorption refrigeration system operating with different refrigerants in the vapor compression cycle. Heat Mass Transfer. 2019, 55, 467–488. [Google Scholar] [CrossRef]
- Mahalle, K.; Parab, P.; Bhagwat, S. Optimization of cooling load in the combined vapour absorption–vapour compression refrigeration cycle using exergy analysis. Indian Chem. Eng. 2019, 61, 52–66. [Google Scholar] [CrossRef]
- Colorado-Garrido, D. Advanced Exergy Analysis of a Compression–Absorption Cascade Refrigeration System. J. Energy Res. Technol. 2019, 141. [Google Scholar] [CrossRef]
- Jing, Y.; Li, Z.; Chen, H.; Lu, S.; Lv, S. Exergoeconomic design criterion of solar absorption-subcooled compression hybrid cooling system based on the variable working conditions. Energy Convers. Manag. 2019, 180, 889–903. [Google Scholar] [CrossRef]
- Zoghi, M.; Habibi, H.; Chitsaz, A.; Javaherdeh, K.; Ayazpour, M. Exergoeconomic analysis of a novel trigeneration system based on organic quadrilateral cycle integrated with cascade absorption-compression system for waste heat recovery. Energy Convers. Manag. 2019, 198, 111818. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, C.; Liang, Y.; Sun, H.; Liu, S.; Dai, B. Theoretical study on a novel CO2 Two-stage compression refrigeration system with parallel compression and solar absorption partial cascade refrigeration system. Energy Convers. Manag. 2020, 204, 112278. [Google Scholar] [CrossRef]
- Karamangil, M.I.; Coskun, S.; Kaynakli, O.; Yamankaradeniz, N. A simulation study of performance evaluation of single-stage absorption refrigeration system using conventional working fluids and alternatives. Renew. Sustain. Energy Rev. 2010, 14, 1969–1978. [Google Scholar] [CrossRef]
- M. Conde Engineering. Thermophysical Properties of {NH3 + H2O} Mixtures for Industrial Design of Absorption Refrigeration Equipment. Formulation for Industrial use. 2008. Available online: http://www.mrc-eng.com/Downloads/NH3&H2O%20%20Props%20English.pdf (accessed on 30 March 2020).
- Libotean, S.; Salavera, D.; Valles, M.; Esteve, X.; Coronas, A. Vapour-liquid equilibrium of ammonia + lithium nitrate + water and ammonia + lithium nitrate solutions from (293.15 to 353.15) K. J. Chem. Eng. Data 2007, 52, 1050–1055. [Google Scholar] [CrossRef]
- Libotean, S.; Martiín, A.; Salavera, D.; Valles, M.; Esteve, X.; Coronas, A. Densities, viscosities, and heat capacities of ammonia+ lithium nitrate and ammonia+ lithium nitrate+ water solutions between (293.15 and 353.15) K. J. Chem. Eng. Data 2008, 53, 2383–2388. [Google Scholar] [CrossRef]
- Ferreira, C.I. Thermodynamic and physical property data equations for ammonia-lithium nitrate and ammonia-sodium thiocyanate solutions. Sol. Energy 1984, 32, 231–236. [Google Scholar] [CrossRef]
- Cai, D.; He, G.; Tian, Q.; Tang, W. Exergy analysis of a novel air-cooled non-adiabatic absorption refrigeration cycle with NH3–NaSCN and NH3–LiNO3 refrigerant solutions. Energy Convers. Manag. 2014, 88, 66–78. [Google Scholar] [CrossRef]
- Chaudhari, S.K.; Salavera, D.; Coronas, A. Densities, viscosities, heat capacities, and vapor–liquid equilibria of ammonia+ sodium thiocyanate solutions at several temperatures. J. Chem. Eng. Data 2011, 56, 2861–2869. [Google Scholar] [CrossRef]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [Green Version]


| Year | Author | Working Fluid | Design Parameters | Heat Exchanger and Efficiency | Methodologies Used by the Authors | |
|---|---|---|---|---|---|---|
| Compression | Absorption | |||||
| 2006 | José Fernández-Seara, Jaime Sieres, Manuel Vázquez [5] | CO2 and NH3 | NH3-H2O Single stage | Qeva = 1 kW Teva = 228 K Tcond = 271 K | ɛSHX = 0.8 ɛRHE = 0.8 | The exhaust gases are assumed to feed the generator. A rectification column is considered. |
| 2011 | Srinivas Garimella, Ashlie M. Brown, Ananda Krishna Nagauarapu [6] | CO2 | LiBr-H2O Single stage | Teva = 233 K Tmedium = 278 K Qeva = 82 MW Wcompressor = 23 MW | ɛSHX = 0.9 ɛRHE = 0.9 | Theoretical first law of thermodynamics analysis, heat load and lithium bromide concentration results were carried out. |
| 2012 | Canan Cimsit, Ilhan Tekin Ozturk [7] | R134a, R410A, NH3 | LiBr-H2O and NH3- H2O Single stage | Teva = 263 K Qeva = 50 kW Wcompressor = 8.30 kW | ɛSHX = 0.6 | Theoretical first law of thermodynamics analysis is developed by the authors |
| 2013 | D. Colorado and Velázquez [8] | NH3, CO2, R134a | LiBr-H2O Single stage | Teva = 258 K Qeva = 50 kW | ɛSHX = 0.6 ɛIHE = 0.6 | Theoretical first and second laws of thermodynamics analysis are formulated, and numerical results are presented. |
| 2014 | Canan Cimsit, Ilhan Tekin Ozturk, Olcay Kincay [9] | R134a | LiBr-H2O Single stage | Qeva = 50 kW COP = 0.61 Wcompressor = 9.64 kW | ɛSHX = 0.5 (optimum case) | Thermodynamic, exergy and economic analysis are carried out. |
| 2015 | D. Colorado, W. Rivera [10] | R134a, CO2 | LiBr-H2O Double stage | Qeva = 50 kW Teva = 263 K Wcompre = 5.49 kW (R134a) Wcompre = 11.31 kW (CO2) | ɛSHX = 0.7 ɛIHX = 0.7 | The authors proposed that, the COP for the compression–double absorption systems were higher than those obtained with compression–single absorption systems. The results suggest the use of advanced cycles in the absorption process for cascade systems. |
| 2016 | Vaibhav Jain, Gulshan Sachdeva, Surendra Singh Kachhwaha, Bhavesh Patel [11] | R410a | LiBr-H2O Single stage | Qeva = 170 kW Teva = 273 K Tcond = 313 K ɛHX = 0.6 | ɛSHX = 0.6 | Thermodynamic, exergy, economic and environmental theoretical results were developed. Multi-objective optimization method is provided to show a feasible solution |
| 2016 | Fateme Ahmadi Boyaghchi, Motahare Mahmoodnezhad, Vajiheh Sabeti [12] | R134a, R1234ze, R1234yf, R407C, R22 | LiBr-H2O Single stage | Qgen = 104.9 kW COP = 4.60 (case base) Tgen = 363 K | ɛHX = 0.6 | Exergo-economic analysis considering an ejector in the compression vapor cycle is analyzed. |
| 2017 | Manoj Dixit, Akhilesh Arora, S.C. Kaushik [13] | R134a | LiBr-H2O Double stage | Qeva = 100 kW | ɛHPSHX = 0.6 ɛLPSHX = 0.6 | Energy, exergy, environmental and economic analysis are presented together with NSGA-II method to find the optimal solution. |
| 2018 | Canan Cimsit [14] | R134a | LiBr-H2O Double-stage | Qeva = 300 kW Teva = 275 K COP = 1.12 | ɛHPSHX = 0.6 ɛLPSHX = 0.6 | According to the author, the theoretical results indicate that the electrical energy consumption in the cycle is 73% lower than the one stage vapor compression refrigeration cycle. |
| 2018 | Khelifa Salhi, Mourad Korichi, Khaled M. Ramadan [15] | R1234yf, R1234ze(E) and R1233zd (E) | LiBr-H2O and LiCl-H2O single-stage | Qeva = 50 kW Tgethermal = 367 K Wcompre = 4.45 kW | ɛSHX = 0.6 | Energy, exergy and economic aspect for entire cycle were considered for air-cooling applications. Geothermal energy was considered for feed the generator in absorption cycle. |
| 2018 | Salvatore Vasta, Valeria Palomba, Davide La Rosa, Walter Mittelbach [16] | R410a | Silica gel- H2O Two-units | Qeva = 13.5 kW nominal cooling absorption cycle Qeva = 10 kW nominal cooling compression cycle COP = 0.54 | None | Experimental results such as: coefficient of performance, power and the temperature in different points of the system were analyzed by the authors. It is interesting to note that, the authors present enough experimental information to say that cascade chiller allows savings of about 50% with respect of the application of a vapor compression unit only. |
| 2018 | Vaidhav Jain, Gulshan Sachdeva, SS Kachhwaha [17] | R717 | LiBr-H2O Single stage | Qeva = 100 kW Teva = 243 K | ɛSHE = 0.7 | The authors propose a novel configuration of a compression–absorption cascade system; it includes the addition of intermediate compressor in the absorption cycle and a second solution heat exchanger. |
| 2019 | Mert Sinan Turgut, Oguz Emrah Turgut [18] | R1234yf, R134a, R717 and R290 | LiBr-H2O Single stage | Qeva = 80.7 kW Teva = 272.6 K Tgen = 363 K | ɛRHE = 0.6 ɛSHE = 0.6 | Regenerative and solution heat exchanger are considered in the analysis. Heat exchanger design, size, configuration, first and second law of thermodynamic and economic analysis were carried out. |
| 2019 | Kalpana Mahalle, Pallavi Parab, Sunil Bhagwat [19] | NH3 | LiBr-H2O Double stage | Qeva = 352 kW Teva = 271 K COP = 1.45 | ɛHPSHX = 0.7 ɛLPSHX = 0.7 | Evaporators connected in series; the external flow connects to the two systems are considered in the configuration of the compression–absorption cycles. |
| 2019 | D. Colorado [20] | R134a | LiBr-H2O Single stage | Qeva = 50 kW Teva = 258 K Tgen = 352 K | ɛSHX = 0.7 ɛIHX = 0.7 | Advanced exergy analysis of entire system was carried out; it means that energy and exergy analysis were formulated, and thermodynamic model computed to obtain the nature of irreversibility for each one of the pieces of equipment. |
| 2019 | Yue Jing, Zeyu Li, Hongkai Chen, Shengzi Lu, Shiliang Lv [21] | R410a | LiBr-H2O Single stage | Qeva = 160 kW Acollector = 270 m2 Wcompre = 4.22 kW | The heat exchangers were not considered | Exergy and economic analysis are considered; the evacuated tube collectors (ETC), a hot water storage tank, a single-effect absorption chiller, a vapor compression chiller with sub-cooler, a wet cooling tower, water pumps, liquid pipelines and valves were considered in the configuration. |
| 2019 | Mohammad Zoghi, Hamed Habibi, Ata Chitsaz, Koroush Javaherdeh, Mojtaba Ayazpour [22] | R410a | LiBr-H2O Single stage | Wcompre = 8.599 kW Qeva = 30.7 kW | ɛSHX = 0.7 | The performance of the integration of absorption–compression system with an organic Rankine cycle using cyclohexane as working fluid was calculated. |
| 2020 | Zhili Sun, Caiyun Wang, Youcai Liang, Huan Sun, Shengchun Liu, Baomin Dai [23] | CO2 Two-stage compression cycle | LiBr-H2O Single stage | Qeva = 35 kW Teva = 245 K | DTSHX = 288 K | A cascade system that involves a single-stage absorption, solar energy and two-stage compression cycle was proposed and theoretical evaluated using meteorological data of China. |
| Parameters: Tgen = 363 K, Tevap = 263 K, Tabs = Tcon = 313 K, εSHX = 0.6, 50 kW Load | |||
|---|---|---|---|
| Components | Energy Flow (kW) | ε | |
| Cimsit and Ozturk [7] | Present Study | ||
| Qgen | 117.64 | 115.44 | 1.87 |
| Qevap2 | 57.30 | 58.06 | 1.33 |
| Qabs | 109.03 | 104.02 | 4.60 |
| Qcon2 | 65.87 | 69.83 | 6.01 |
| Wcomp | 8.08 | 8.06 | 0.25 |
| Qevap1 | 50 | 50 | 0.00 |
| Qcon1 | 57.30 | 58.06 | 1.33 |
| Performance parameters | |||
| COPabs | 0.487 | 0.501 | 2.87 |
| COPvapour-comp | 6.188 | 6.207 | 0.31 |
| COPcycle | 0.398 | 0.404 | 1.51 |
| State | T (K) | P (kPa) | X | (kg/s) | h (kJ/kg) |
|---|---|---|---|---|---|
| 1 | 363.00 | 1548.96 | 1.00 | 0.0491 | 1691.60 |
| 2 | 363.00 | 1548.96 | 1.00 | 0.0491 | 1605.40 |
| 3 | 313.00 | 1548.96 | 1.00 | 0.0491 | 389.90 |
| 4 | 294.51 | 1548.96 | 1.00 | 0.0491 | 300.40 |
| 5 | 283.00 | 611.87 | 1.00 | 0.0491 | 300.40 |
| 6 | 283.00 | 611.87 | 1.00 | 0.0491 | 1471.98 |
| 7 | 317.17 | 611.87 | 1.00 | 0.0491 | 1561.48 |
| 8 | 313.00 | 611.87 | 0.53 | 0.3769 | −88.94 |
| 9 | 313.00 | 611.87 | 0.53 | 0.3769 | −77.71 |
| 10 | 316.79 | 1548.96 | 0.53 | 0.3769 | −76.74 |
| 11 | 346.62 | 1548.96 | 0.53 | 0.3769 | 20.88 |
| 12 | 363.00 | 1548.96 | 0.45 | 0.3278 | 62.43 |
| 13 | 326.03 | 1548.96 | 0.45 | 0.3278 | −49.80 |
| 14 | 326.03 | 611.87 | 0.45 | 0.3278 | −49.80 |
| 15 | 323.50 | 534.65 | 1.00 | 0.2671 | 439.87 |
| 16 | 291.00 | 534.65 | 1.00 | 0.2671 | 224.45 |
| 17 | 277.09 | 534.65 | 1.00 | 0.2671 | 205.36 |
| 18 | 263.00 | 199.42 | 1.00 | 0.2671 | 205.36 |
| 19 | 263.00 | 199.42 | 1.00 | 0.2671 | 392.57 |
| 20 | 285.40 | 199.42 | 1.00 | 0.2671 | 411.67 |
| State | T (K) | P (kPa) | X | (kg/s) | h (kJ/kg) |
|---|---|---|---|---|---|
| 1 | 363.00 | 1548.96 | 1.00 | 0.0491 | 1691.60 |
| 2 | 363.00 | 1548.96 | 1.00 | 0.0491 | 1605.40 |
| 3 | 313.00 | 1548.96 | 1.00 | 0.0491 | 389.90 |
| 4 | 294.53 | 1548.96 | 1.00 | 0.0491 | 300.40 |
| 5 | 283.00 | 611.87 | 1.00 | 0.0491 | 300.40 |
| 6 | 283.00 | 611.87 | 1.00 | 0.0491 | 1471.98 |
| 7 | 317.17 | 611.87 | 1.00 | 0.0491 | 1561.48 |
| 8 | 313.00 | 611.87 | 0.50 | 0.4505 | −82.48 |
| 9 | 313.00 | 611.87 | 0.50 | 0.4505 | −73.08 |
| 10 | 317.49 | 1548.96 | 0.50 | 0.4505 | −72.11 |
| 11 | 345.29 | 1548.96 | 0.50 | 0.4505 | −7.18 |
| 12 | 363.00 | 1548.96 | 0.43 | 0.4014 | 5.21 |
| 13 | 326.60 | 1548.96 | 0.43 | 0.4014 | −67.65 |
| 14 | 326.60 | 611.87 | 0.43 | 0.4014 | −67.65 |
| 15 | 323.50 | 534.65 | 1.00 | 0.2671 | 439.87 |
| 16 | 291.00 | 534.65 | 1.00 | 0.2671 | 224.45 |
| 17 | 277.09 | 534.65 | 1.00 | 0.2671 | 205.36 |
| 18 | 263.00 | 199.42 | 1.00 | 0.2671 | 205.36 |
| 19 | 263.00 | 199.42 | 1.00 | 0.2671 | 392.57 |
| 20 | 285.40 | 199.42 | 1.00 | 0.2671 | 411.67 |
| State | T (K) | P (kPa) | X | (kg/s) | h (kJ/kg) |
|---|---|---|---|---|---|
| 1 | 363.00 | 1548.96 | 1.00 | 0.0491 | 1691.60 |
| 2 | 363.00 | 1548.96 | 1.00 | 0.0491 | 1605.40 |
| 3 | 313.00 | 1548.96 | 1.00 | 0.0491 | 389.90 |
| 4 | 294.51 | 1548.96 | 1.00 | 0.0491 | 300.40 |
| 5 | 283.00 | 611.87 | 1.00 | 0.0491 | 300.40 |
| 6 | 283.00 | 611.87 | 1.00 | 0.0491 | 1471.98 |
| 7 | 317.17 | 611.87 | 1.00 | 0.0491 | 1561.48 |
| 8 | 313.00 | 611.87 | 0.55 | 0.2814 | −69.04 |
| 9 | 313.00 | 611.87 | 0.55 | 0.2814 | −53.99 |
| 10 | 316.48 | 1548.96 | 0.55 | 0.2814 | −52.81 |
| 11 | 347.25 | 1548.96 | 0.55 | 0.2814 | 95.08 |
| 12 | 363.00 | 1548.96 | 0.45 | 0.2323 | 159.79 |
| 13 | 325.79 | 1548.96 | 0.45 | 0.2323 | −19.36 |
| 14 | 325.79 | 611.87 | 0.45 | 0.2323 | −19.36 |
| 15 | 323.50 | 534.65 | 1.00 | 0.2671 | 439.87 |
| 16 | 291.00 | 534.65 | 1.00 | 0.2671 | 224.45 |
| 17 | 277.09 | 534.65 | 1.00 | 0.2671 | 205.36 |
| 18 | 263.00 | 199.42 | 1.00 | 0.2671 | 205.36 |
| 19 | 263.00 | 199.42 | 1.00 | 0.2671 | 392.57 |
| 20 | 285.40 | 199.42 | 1.00 | 0.2671 | 411.67 |
| ηHX’s = 0 | ηHX’s = 0.8 | Only Compression Cycle | |||||
|---|---|---|---|---|---|---|---|
| NH3-LiNO3 | NH3-H2O | NH3-NaSCN | NH3-LiNO3 | NH3-H2O | NH3-NaSCN | ||
| Qgen | 148.05 | 150.85 | 161.30 | 95.66 | 93.43 | 88.40 | |
| Qcon2 | 69.23 | 69.23 | 69.23 | 59.69 | 59.69 | 59.69 | |
| Qevap₂ | 57.55 | 57.55 | 57.55 | 57.53 | 57.53 | 57.53 | |
| Qabs | 136.76 | 139.53 | 150.09 | 93.87 | 91.61 | 86.68 | |
| Wpump | 0.40 | 0.36 | 0.47 | 0.37 | 0.33 | 0.44 | |
| COPabs | 0.39 | 0.38 | 0.36 | 0.60 | 0.61 | 0.65 | |
| Wcomp | 7.55 | 7.55 | 7.55 | 7.53 | 7.53 | 7.53 | 15.51 |
| Qcond1 | 57.55 | 57.55 | 57.55 | 57.53 | 57.53 | 57.53 | 65.51 |
| Qevap1 | 50.00 | 50.00 | 50.00 | 50.00 | 50.00 | 50.00 | 50.00 |
| COPcomp | 6.62 | 6.62 | 6.62 | 6.64 | 6.64 | 6.64 | 3.22 |
| COPcycle | 0.32 | 0.32 | 0.30 | 0.48 | 0.50 | 0.52 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herrera-Romero, J.; Colorado-Garrido, D. Comparative Study of a Compression–Absorption Cascade System Operating with NH3-LiNO3, NH3-NaSCN, NH3-H2O, and R134a as Working Fluids. Processes 2020, 8, 816. https://doi.org/10.3390/pr8070816
Herrera-Romero J, Colorado-Garrido D. Comparative Study of a Compression–Absorption Cascade System Operating with NH3-LiNO3, NH3-NaSCN, NH3-H2O, and R134a as Working Fluids. Processes. 2020; 8(7):816. https://doi.org/10.3390/pr8070816
Chicago/Turabian StyleHerrera-Romero, JV, and Dario Colorado-Garrido. 2020. "Comparative Study of a Compression–Absorption Cascade System Operating with NH3-LiNO3, NH3-NaSCN, NH3-H2O, and R134a as Working Fluids" Processes 8, no. 7: 816. https://doi.org/10.3390/pr8070816
APA StyleHerrera-Romero, J., & Colorado-Garrido, D. (2020). Comparative Study of a Compression–Absorption Cascade System Operating with NH3-LiNO3, NH3-NaSCN, NH3-H2O, and R134a as Working Fluids. Processes, 8(7), 816. https://doi.org/10.3390/pr8070816





