Adaptive Feedback Control for a Pasteurization Process
Abstract
:1. Introduction
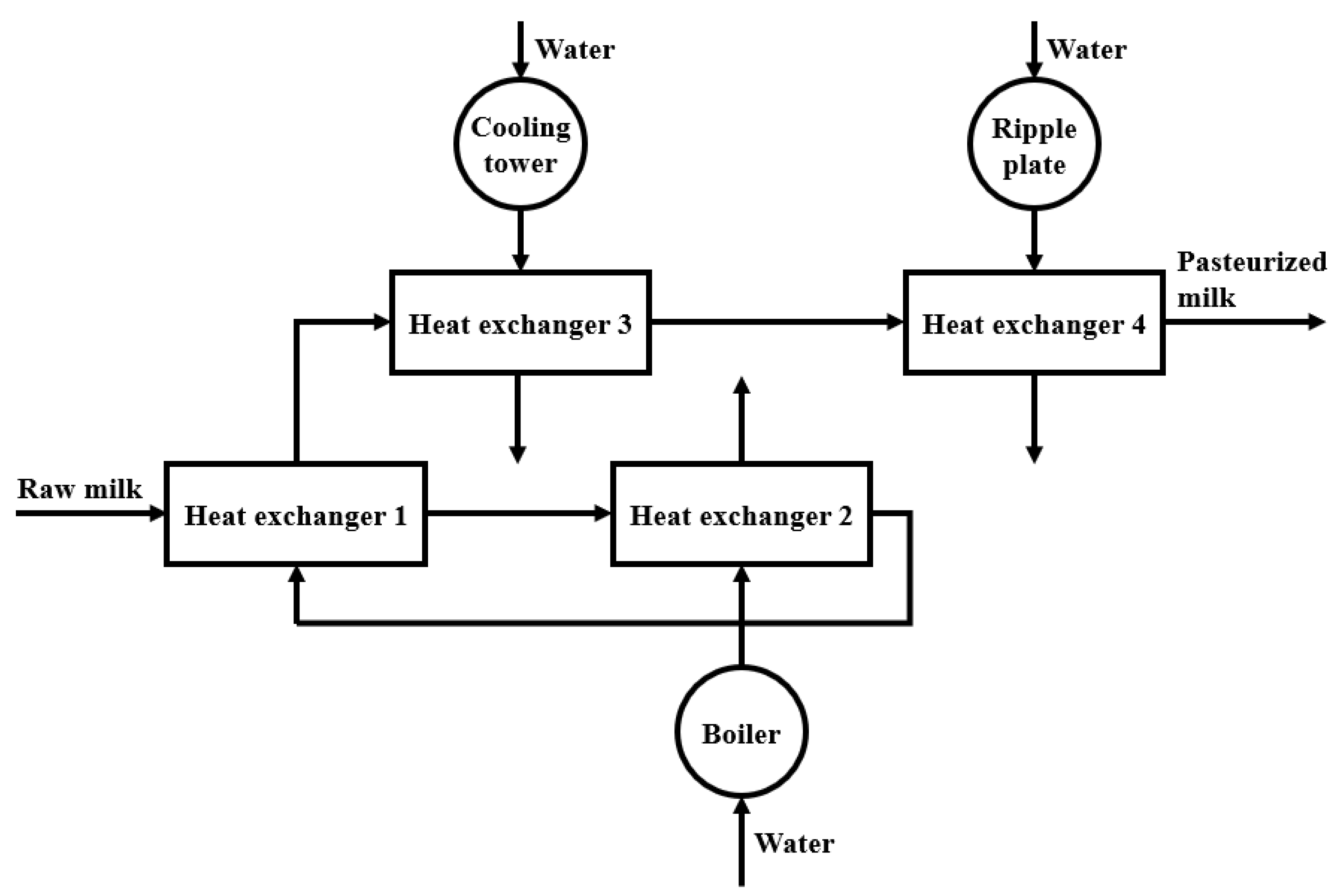
2. Process Model
- Perfectly mixed conditions;
- Physical and chemical properties of liquids, such as density and heat capacity, are constant, apart from the properties of milk, which are modeled as function of temperature and milk composition;
- Negligible variation of volume on both sides of the plate heat exchanger, the heating coil of the water tank, the boiler, the ripple plate, and the cooling tower;
- Well-insulated piping for hot and iced water of the boiler and ripple plate, meaning omitted temperature drop at the piping surface throughout the length of the piping.
3. Impact of Process Disturbances and Control Strategy
4. Control Design
4.1. Observer-Based Control
4.2. Adaptive Scheme
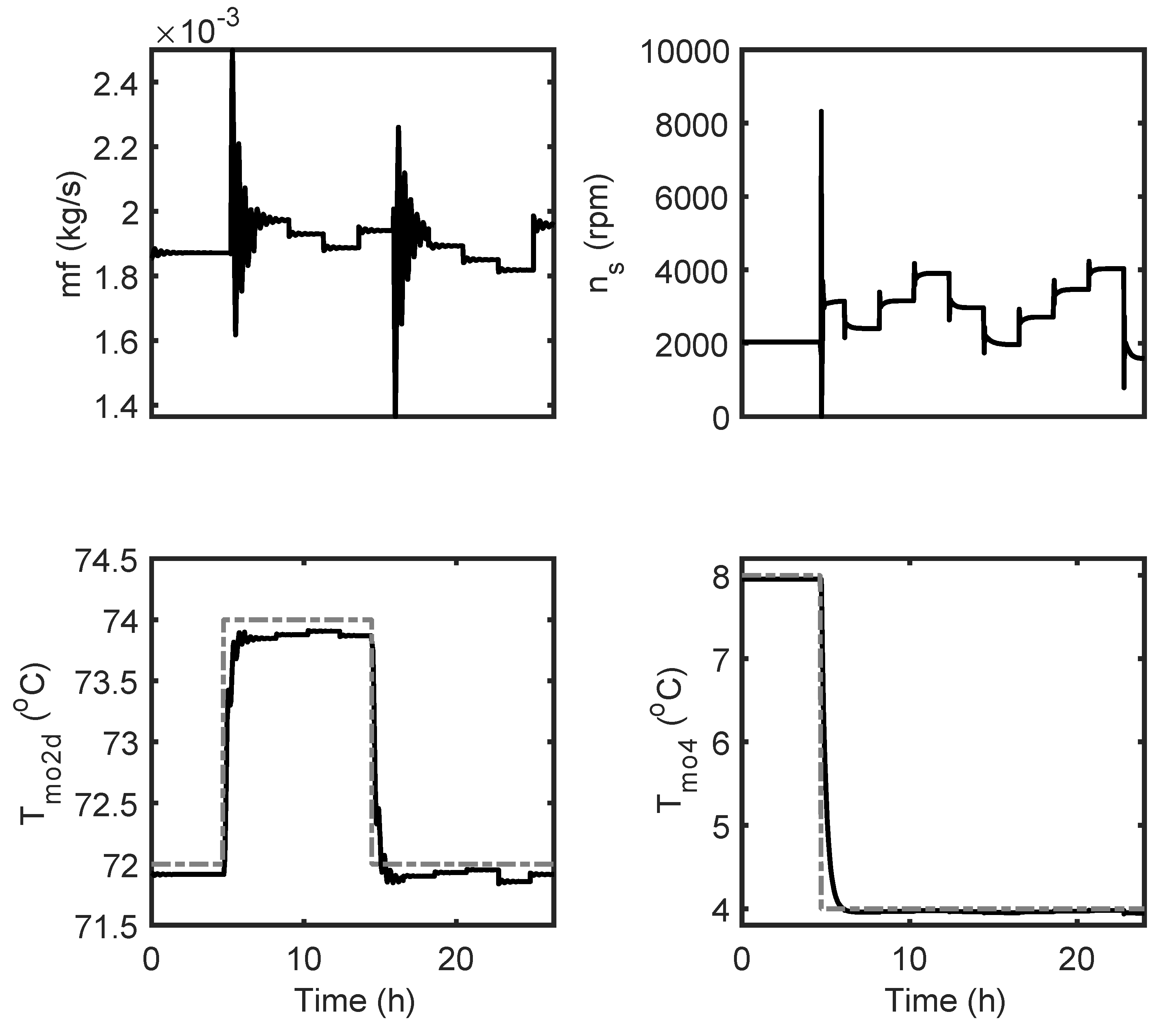
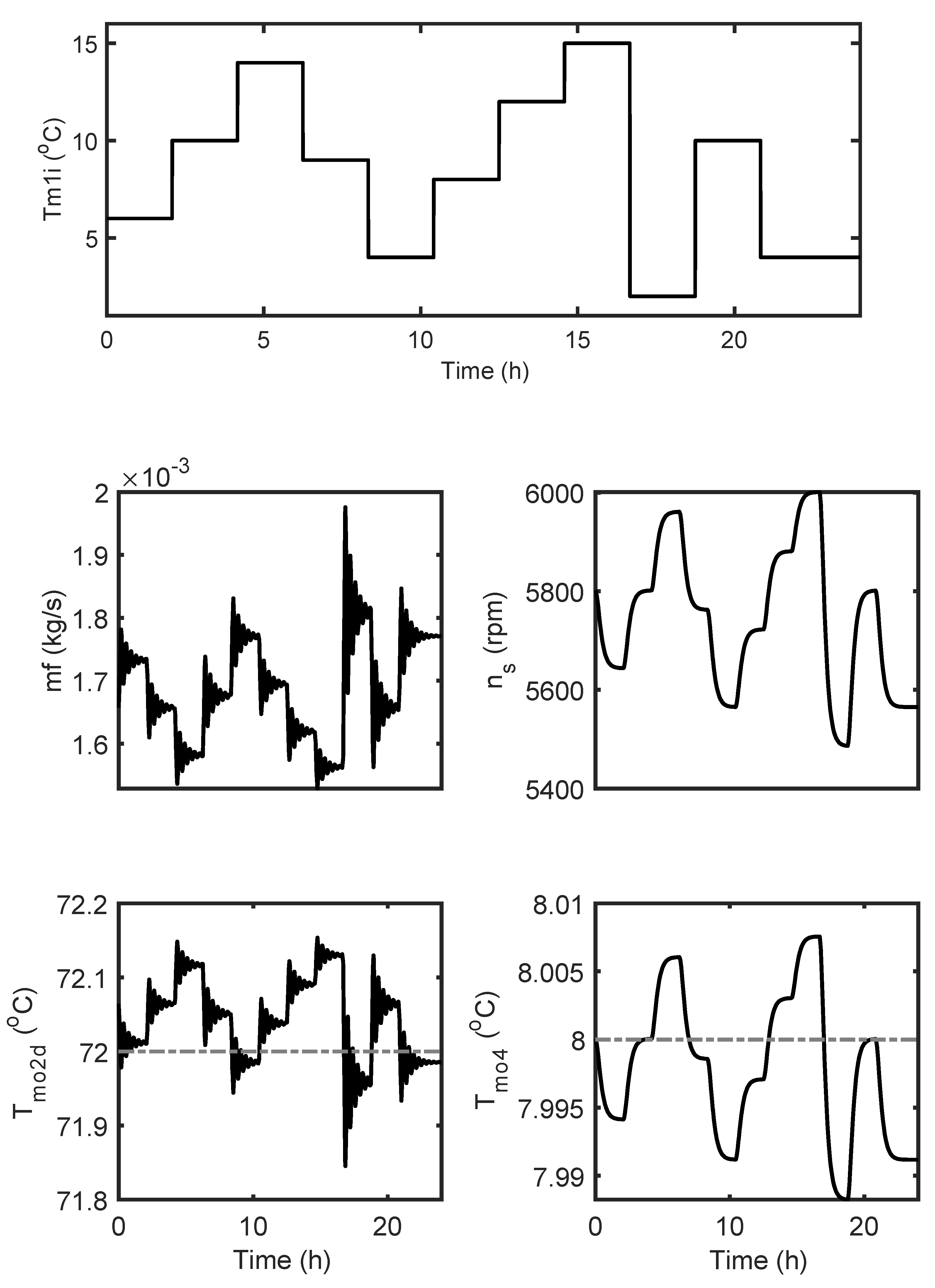
5. Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Heat exchanger area (plate pasteurizer), boiler, peripheral flow area of ripple plate compressor and ripple plate [m2] | |
| , , , , | Heat capacity at constant pressure of milk, hot water, tap water and ice water [J kg−1 °C−1] |
| df | Impeller diameter at ripple plate compressor [m] |
| dp | Diameter of holding tube [m] |
| E | Evaporation rate for cooling tower [m3 s−1] |
| Fm, Fh, Ft, Fi, Fw, Fc | Volumetric flow of milk, hot water, tap water, ice water, make-up water and circulation water [m3 s−1] |
| Hf | Heating value of fuel [kJ kg−1] |
| hv | Latent heat of vaporization of water [kJ kg−1] |
| hA | Heat transfer coefficient at water surface [W K−1] |
| hfg | Latent heat of vaporization of refrigerant at ripple plate [kJ kg−1] |
| Ld | Mechanical drift loss at cooling tower [%] |
| Lp | Length of holding tube [m] |
| Fueling rate at boiler [kg s−1] | |
| ns | Impeller rotational speed at ripple plate compressor [rpm] |
| , | Temperature of milk at inlet or outlet of heat exchanger [°C] |
| , | Temperature of hot water at inlet or outlet of heat exchanger [°C] |
| , | Temperature of hot water at inlet or outlet of heat exchanger [°C] |
| , | Temperature of hot water at inlet or outlet of heat exchanger [°C] |
| Temperature of make-up water [°C] | |
| Ta | Ambient temperature [°C] |
| t | Time [s] |
| Logarithmic mean temperature difference [°C] | |
| Upp, Ub, Urp, Up | Overall heat transfer coefficient of heat exchanger, boiler, ripple plate and holding tube [W m−2 K−1] |
| Water volume for heat exchanger, boiler, cooling tower and ripple plate [m3] | |
| , , , , | Density of milk, hot water, tap water, ice water and make-up water [kg m−3] |
References
- Early, R. Dairy products and milk-based food ingredients. In Natural Food Additives, Ingredients and Flavourings; Woodhead Publishing Series in Food Science; Technology and Nutrition: Sawston, UK, 2012; pp. 417–445. [Google Scholar]
- Rankin, S.A.; Bradley, R.L.; Miller, G.; Mildenhall, K.B. A 100-year review: A century of dairy processing advancements-pasteurization, cleaning and sanitation, and sanitary equipment design. J. Dairy Sci. 2017, 100, 9903–9915. [Google Scholar] [CrossRef]
- Westhoff, D.C. Heating milk for microbial destruction: A historical outline and update. J. Food Prot. 1978, 41, 122–130. [Google Scholar] [CrossRef] [PubMed]
- Stancl, J.; Zitny, R. Milk fouling at direct ohmic heating. J. Food Eng. 2010, 99, 437–444. [Google Scholar] [CrossRef]
- Valero, E.; Villamiel, M.; Sanz, J.; Martinez-Castro, I. Chemical and sensorial changes in milk pasteurized by microwave and conventional systems during cold storage. Food Chem. 2000, 70, 77–81. [Google Scholar] [CrossRef]
- McAuley, C.M.; Singh, T.K.; Haro-Maza, J.F.; Williams, R.; Buckow, R. Microbiological and physicochemical stability of raw, pasteurized or pulsed electric field-treated milk. Innov. Food Sci. Emerg. Technol. 2016, 38, 365–373. [Google Scholar] [CrossRef]
- Monteiro, S.H.M.C.; Silva, E.K.; Alvarenga, V.O.; Morares, J.; Freitas, M.Q.; Silva, M.C.; Raices, R.S.L.; Sant’Anna, A.S.; Meireles, M.A.A.; Cruz, A.G. Effects of ultrasounds energy density on the non-thermal pasteurization of chocolate milk beverage. Ultrason. Sonochem. 2018, 42, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Lim, S.-Y.; Benner, L.C.; Clark, S. Neither thermosonication nor cold sonication is better than pasteurization for milk shelf life. J. Diary Sci. 2019, 102, 3965–3977. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Sunden, B.; Manglik, R.M. Plate Heat Exchangers: Design, Applications and Performance, 1st ed.; WIT Press: Southampton, UK, 2007. [Google Scholar]
- Kanade, P.; Subramani, A. Hygienic design aspects of pasteurizer to assure effective pasteurization of milk. J. Hyg. Eng. Des. 2014, 8, 19–29. [Google Scholar]
- Bon, J.; Clemente, G.; Vaquiro, H.; Mulet, A. Simulation and optimization of milk pasteurization processes using a general process simulator (ProSimPlus). Comput. Chem. Eng. 2010, 34, 414–420. [Google Scholar] [CrossRef]
- Arteaga, G.E.; Vazquez-Arteaga, M.C.; Nakai, S. Dynamic optimization of the heat treatment of milk. Food Res. Int. 1994, 27, 77–82. [Google Scholar] [CrossRef]
- EUROSTAT. 2020. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Milk_and_milk_product_statistics (accessed on 15 June 2020).
- Niamsuwan, S.; Kittisupakorn, P.; Mujtaba, I.M. Control of milk pasteurization process using model predictive approach. Comput. Chem. Eng. 2014, 66, 2–11. [Google Scholar] [CrossRef] [Green Version]
- Khadir, M.T.; Ringwood, J. Linear and nonlinear model predictive control design for a milk pasteurization plant. Control Intell. Syst. 2003, 31, 1–8. [Google Scholar]
- Niamsuwan, S.; Kittisupakorn, P.; Mujtaba, I.M. Optimization approach to minimize energy consumption in pasteurized milk process. In International Proceedings of Chemical, Biological & Environmental Engineering, Bangkok, Thailand; IACSIT Press: Singapore, 2011; pp. 35–39. [Google Scholar]
- Kayalvizhi, M.; Manamalli, D.; Bhuvanithaa, K. Cascade control of HTST milk pasteurization process with and without pre-cooling stage. In Proceedings of the International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS), Chennai, India, 1–2 August 2017; pp. 1807–1812. [Google Scholar] [CrossRef]
- Pour, F.K.; Puig, V.; Ocampo-Martinez, C. Comparative assessment of LPV-based predictive control strategies for a pasteurization plant. In Proceedings of the 4th International Conference on Control, Decision and Information Technologies (CoDIT), Barcelona, Spain, 5–7 April 2017; pp. 0821–0826. [Google Scholar] [CrossRef]
- Pour, F.K.; Puig, V.; Ocampo-Martinez, C. Multi-layer health-aware economic predictive control of a pasteurization pilot plant. Int. J. Appl. Math. Comput. Sci. 2018, 28, 97–110. [Google Scholar] [CrossRef] [Green Version]
- Munir, M.T.; Zhang, Y.; Yu, W.; Wilson, D.I.; Young, B.R. Virtual milk for modelling and simulation of dairy processes. J. Dairy Sci. 2015, 99, 3380–3395. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castellanos-Sahagún, E.; Alvarez-Ramírez, J.; Alvarez, J. Two-point temperature control structure and algorithm design for binary distillation columns. Ind. Eng. Chem. Res. 2005, 44, 142–152. [Google Scholar] [CrossRef]
- Siguemoto, E.S.; Purgatto, E.; Hassimotto, N.M.A.; Gut, J.A.W. Comparative evaluation of flavor and nutritional quality after conventional and microwave assisted pasteurization of cloudy apple juice. LWT Food Sci. Technol. 2019, 11, 853–860. [Google Scholar] [CrossRef]
- Morison, K.R. Steady-state control of plate pasteurisers. Food Control 2005, 16, 23–30. [Google Scholar] [CrossRef]
- Tronci, S.; Baratti, R. A Gain-Scheduling PI Control Based on Neural Networks. Complexity 2017. [Google Scholar] [CrossRef] [Green Version]
- Tronci, S.; Grosso, M.; Alvarez, J.; Baratti, R. On the global nonlinear stochastic dynamical behavior of a class of exothermic CSTRs. J. Process Control 2011, 21, 1250–1264. [Google Scholar] [CrossRef]


| Boiler Characteristics | |||
|---|---|---|---|
| Regenerative stage; | 2 | Fuel rate ; | |
| Heating stage; | 2.2 | Fuel heating value ; | |
| Precooling stage; | 1 | Heat transfer area ; | 2.3 |
| Cooling stage; | 5.0 | ||
| Regenerative stage; | 940 | Cooling tower characteristics | |
| Heating stage; | 940 | Heat transfer coefficient ; | 2000 |
| Precooling stage; | 950 | Heat of vaporization [; | 2410 |
| Cooling stage; | 1000 | Circulation water ; | |
| Boiler; | 227 | Drift loss [%]; | 2 |
| 27 | |||
| Milk; | Evaporation rate [; E | ||
| Hot water; | |||
| Tap water; | Specifications for ripple plate compressor | ||
| Ice water; | Rotating speed [rpm]; | 5000 | |
| 0.4 | |||
| Regenerative stage; | 0.3803 | Peripheral flow area [; | 0.002 |
| Heating stage; | 0.4079 | Heat transfer area ; | 2.5 |
| Precooling stage; | 0.2873 | ||
| Cooling stage; | 0.4565 | Specifications for refrigerant | |
| Boiler; | 1.2 | Heat of vaporization ; | 217 |
| Cooling tower; | 0.05 | Specific volume at the exit; | 0.5 |
| Ripple plate; | 0.5 | Overall heat transfer ; | 1120 |
| Ambient air temperature [°C]; | 30 | ||
| Disturbance Variable | Disturbance Amount | Change in Temperature at the Exit of Holding Tube | Change in Temperature at the Exit of Fourth Heat Exchanger |
|---|---|---|---|
| Milk feed temperature | +4 °C | +2.6 °C | +0.94 °C |
| −4 °C | −2.6 °C | −0.92 °C | |
| Environment temperature | +4 °C | +1.48 °C | 3.05 °C |
| −4 °C | −1.47 °C | −3.04 °C |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasmussen, E.D.J.; Errico, M.; Tronci, S. Adaptive Feedback Control for a Pasteurization Process. Processes 2020, 8, 930. https://doi.org/10.3390/pr8080930
Rasmussen EDJ, Errico M, Tronci S. Adaptive Feedback Control for a Pasteurization Process. Processes. 2020; 8(8):930. https://doi.org/10.3390/pr8080930
Chicago/Turabian StyleRasmussen, Emil D.J., Massimiliano Errico, and Stefania Tronci. 2020. "Adaptive Feedback Control for a Pasteurization Process" Processes 8, no. 8: 930. https://doi.org/10.3390/pr8080930
APA StyleRasmussen, E. D. J., Errico, M., & Tronci, S. (2020). Adaptive Feedback Control for a Pasteurization Process. Processes, 8(8), 930. https://doi.org/10.3390/pr8080930







