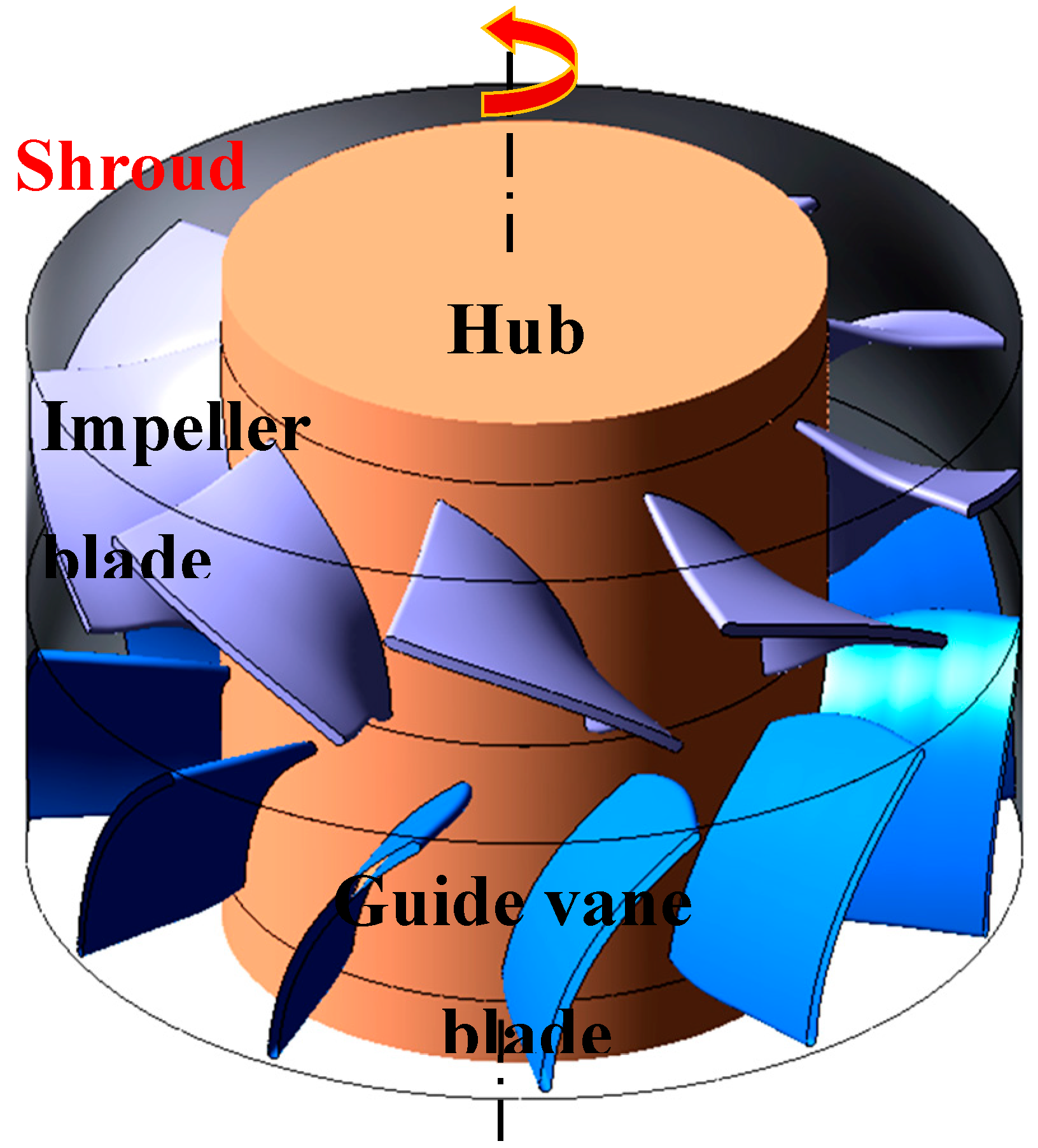
4.1. Pressure Fluctuation Characteristics of Axial-Flow Fan under Stall Conditions
The pressure coefficient
Cp is used for dimensionless treatment of dynamic pressure to express the intensity of pressure fluctuation. The equation is as follows:
where
p is the dynamic pressure of the monitoring points;
is the average pressure in the rotation period of the monitoring points; and
u2 is the peripheral speed of the impeller outlet; 1
t* represents the time required for impeller to rotate one revolution in the circumferential direction.
Figure 8 shows the location of monitoring points, and
Figure 9 shows the pressure fluctuation characteristics of axial flow fan under different flow coefficients. In order to clearly show the rotating stall characteristics, the working conditions near the hump point are selected for research. As the main influence region of rotating stall is the rim region, so the monitoring points are located in the middle section of rotor, and located at 0.8 span. The definition of each stage under the stall conditions is as follows. The term “stall-inception” will be used to describe the time period during which a rotating disturbance grows into a fully developed stall cell and the term “pre-stall” will be used to describe the time period prior to stall-inception; the term “post-stall” will be used to describe the time period which the axial-flow fan is fully controlled by rotating stall (RS).
The pressure fluctuation curves of operation point A (OP-A) in different flow channels are consistent, showing large-scale and low-amplitude transient characteristics. Meanwhile, OP-A is located on the right side of the hump point. Due to the above reasons, the axial-flow fan is only disturbed by the modal wave under this flow coefficient, with a period of 8.75 t*, so the circumferential propagation speed of modal disturbance is about 1/10 of the rotor speed. Compared with OP-A, the pressure fluctuation characteristics of the hump point (OP-B) have changed greatly. After experiencing a 10 t* weak disturbance of LLSD, the axial flow fan will show the signal singularity. The strong disturbance from the spike wave will gradually replace the modal wave as the main disturbance form. With the impeller rotating, the strong disturbance effect will gradually increase, and it will evolve into a circumferential propagation of the stable stall cell. The period of SLSD and rotating stall is the same, and their circumferential propagating speed is about 1/3 rotor speed. With the further reduction of the flow coefficient (OP-C–OP-E), the emerging time of signal singularity (spike) will gradually advance, the control time of fan system disturbed by modal wave will further reduce, and each path will step into the stall state in advance, while the propagating speed of SLSD and stall cell will remain unchanged. Under the point of OP-G, the fan system will be subject to strong disturbance from rotating stall at the initial time, and the modal disturbance will disappear basically.
As rotating stall is a transient evolution process from signal singularity to a developed stall cell, the traditional Fast Fourier transform (FFT) is unable to capture the time and frequency information of the signal at the same time, and continuous wavelet transform (CWT) has been proven useful in uncovering mechanisms of spike or modal type stall.
In this paper, the Morlet wavelet, which is representative of nonorthogonal wavelet bases, is used in continuous wavelet transform. The Morlet wavelet is the real part and imaginary part of the amplitude are harmonic vibration signals; Meanwhile, as a nonorthogonal wavelet, the Morlet wavelet as the wavelet base for CWT. In addition, its scale changes continuously, and can adjust the time and frequency domain resolution as required.
The mathematical equation of Morlet wavelet
ψ(
t) is as follows:
In Equation (4), t represents time, fb represents wavelet bandwidth, and fc represents center frequency.
In practical application, complex wavelet can easily lead to phase distortion. Therefore, the real part of Morlet wavelet is often used as wavelet function, and the mathematical equation is as follows:
Its Fourier transform
ϕ(
t) can be expressed as follows:
In this paper, the sine function signal is used to verify the applicability of continuous wavelet transform. The equation is shown as follows
At different times, the equation of the sine function signal is
y = sin(2π
x) and
y = sin(4π
x), the frequency of the two signal is 1 Hz and 2 Hz partly, and the sampling frequency of the signal is 10 Hz. The time domain generated is also shown in
Figure 10. After adjusting the appropriate center frequency and frequency bandwidth, the spectrum distribution obtained by Morlet wavelet is shown in
Figure 11. The frequency spectrum shows that when 0 <
x < 5π, the main frequency of the signal is 1 Hz; when 5π <
x < 10π, the main frequency of the signal is 2 Hz. Hence, the accuracy of CWT can be verified.
For the pressure fluctuation signal of axial-flow fan under different working conditions, it belongs to one-dimensional signal, the general form of one-dimensional CWT is shown in Equation (8).
where
x(
t) is the time domain information, and
ψ(
t) is the wavelet function. The symbol
ψ* represents complex conjugate.
s is the scaling parameter, and
b is the translation parameter.
Based on CWT,
Figure 12 shows the time-frequency distribution characteristics of dynamic pressure signals at different flow rates, and discusses the differences of time-frequency distribution in pre-stall stage, stall-inception stage and post-stall stage.
Before the hump point, all paths of rotor are occupied by LLSD, so the frequency band of 8–12 Hz appears in the time-frequency diagram. Among them, the maximum pressure fluctuation energy (main frequency) is appears near 10 Hz. Under OP-A condition, the monitoring points are only disturbed by LLSD and will not be affected by RS, modal disturbance is a harmonic type disturbance formed before the formation of stall cell, so the frequency and amplitude of LLSD remain unchanged. The amplitude caused by modal disturbance is relatively low, and the circumferential propagation speed is very slow.
At the hump point, the rotor will experience pre-stall, stall-inception and post-stall stage successively. Different from the pre-stall stage, the flow path is only disturbed by the low amplitude and long period disturbance mode from modal wave. In the stall-inception stage, after experiencing spike emerging, the stall cell with higher amplitude and faster circumferential rotation speed gradually form in the flow path. Although the low amplitude disturbance brought by modal wave still exists, but the spike disturbance of higher amplitude replaces it and becomes the dominant frequency. Each path of impeller will not only be disturbed by LLSD, but also by rotating stall with higher amplitude and faster propagation period. As can be seen from
Figure 8, the propagation speed of SLSD is the same as the propagation speed of the stall cell which is 1/3 of the rotor speed, so the visual reflection of SLSD and rotating stall disturbance in the frequency spectrum is
fRS = 33.3 Hz.
With the decrease of the flow coefficient, the difference of time-frequency distribution begins to appear, which is mainly reflected in the changes of frequency and amplitude of
fLLSD and
fRS. First of all, with the decrease of flow coefficient, the occurrence time of rotating stall is a little earlier, and the stall effect is gradually enhanced, but the propagation period of a single stall cell remains unchanged, so the frequency of
fRS reflected in the time-frequency diagram remains unchanged, but the appearance time and amplitude of
fRS increase significantly with the decrease of flow coefficient. In contrast, with the decrease of flow coefficient, the frequency band range of
fLLSD increases from 4.17 Hz to 16.7 Hz. From the FFT results in
Figure 13, it can be seen that with the decrease of flow coefficient, the pressure fluctuation energy caused by LLSD gradually decreases, so the amplitude of
fLLSD also decreases. While in the deep stall point (OP-F), the pulsation induced by the weak disruption from LLSD is reduced to the pole, and each path is always controlled by the stall cell from the initial time period, and the stall effect is always throughout the transient flow process of axial-flow fan, so
fRS does not show the trend of gradually enhancing with the impeller rotation like the hump point (OP-B), its amplitude basically remains unchanged, and the induced pressure fluctuation energy is higher than OP-B.
4.2. Analysis of Transient Flow Characteristics under Hump Point
As the hump point is the initial condition of rotating stall, so it is necessary to further study the transient flow characteristics at hump point, and explore the transient distortion process generated by emerging spike.
Figure 14 shows the pressure and velocity fluctuation characteristics of the hump point, and the monitoring points are Y1, Y4 and Y7 respectively. The velocity fluctuation waveform is consistent with that of static pressure. After the emerging spike, the flow velocity decays with the flow separation at LE, and finally decreases to 0 m/s. At this moment, the air flow cannot be discharged from the flow path smoothly, and the whole rim region of the stall path is seriously blocked. According to the disturbance mode and pressure fluctuation waveform of spike stall, the characteristic time a–g is selected, and the selected time is as shown in
Figure 14.
The meridional velocity reflects the flow capacity of the axial-flow fan. Based on the assumption that the cylinder layer is independent, the velocity gradient equation of the axial-flow fan is taken as the basis, and the equation of the meridional velocity is as follows:
where,
ω is the angular velocity, rad/s; and Γ(
r) is the airfoil blade circulation. The calculation formula is as follows:
where:
W∞(
r) represents the relative velocity of each blade;
l(
r) represents the chord length of each blade.
Since the meridional velocity Vm is the velocity vector, its value is always positive, and its flow direction cannot be displayed. Therefore, this paper divides the meridional velocity according to the XYZ direction, and counts the data of the axial component of the meridional velocity (Vm_aixal).
As can be seen from
Figure 15, in different cross-sections of the rotor,
Vm_axial keeps the trend of increasing first and then decreasing gradually from hub to rim side in each time period. Among them, the maximum value of
Vm_axial is existing in 0.25–0.4 span. In this region, the axial flow fan has the strongest overcurrent capacity. However, in the rim region, the whole surface has negative values. The disturbance and countercurrent phenomenon of tip leakage flow under part-loading conditions are still the main factors that affect the flow capacity and blade construction of the axial flow fan, especially the inverse flow at LE. As the axial-flow fan changes from a weak disturbance of LLSD to a strong disturbance of SLSD and further evolves into rotating stall, the flow pattern and overcurrent capacity of the fan change greatly. After experiencing emerging spike, the velocity of the whole rim flow surface is attenuated, and the rim region disturbed by SLSD and rotating stall was blocked, so the air flow could not be smoothly discharged, and then flow into the hub region. Therefore, the axial velocity of the hub region was further increased in the stall state, and the vortex on the hub side under the stall path was also disappeared, and the flow capacity was enhanced. In the process from pre-stall stage to post-stall stage, with the increase of chord length coefficient, the position of span where meridional velocity attenuation decreases. At the intake surface, the stall disturbance effect is mainly concentrated in the rim region; while in the outlet surface, the velocity decays at 0.34 span, the stall blocking effect is the most obvious at this span.
Figure 16 shows the transient distribution characteristics of the incidence angle in the inlet surface of the rotor under the hump point. The equation of the incidence angle is as follows:
where:
vaxial is the axial velocity, m/s;
v is the local speed, m/s; and
θ is the blade inlet setting angle, °.
As the stall cell is located in the rim region and the distortion induced by rotating stall is the most significant in rim region, the transient distribution characteristics of incidence angle at 0.8 span are counted.
In the pre-stall stage, the axial-flow fan is not affected by rotation stall, but only by LLSD’s weak disturbance. Therefore, the distribution of incidence angle of each path is basically the same, and the incidence angle basically keeps periodic oscillation in the range of 16.7–17.5°. At this time, the incidence angle has not reached the critical value, and the internal flow characteristics of fan are relatively stable. Due to the reason of impeller rotation, there is a certain phase difference in the distribution characteristics of the incidence angle at different time. However, with the sudden appearance of spike emerging, SLSD replaces LLSD as the main disturbance, the incidence angle of one path is slightly higher than that of the earlier stage, and gradually reaches the critical value, and a small amount of flow separation phenomenon occurs in the rim region. Therefore, when t = b, the signal in one path appears a sharp shock wave, and the pressure shows a small sharp drop, so the critical value is about 18°.
As the impeller rotates, the sharp increase of the incidence angle induced by SLSD becomes worse. In the stall-inception stage (b–d), with the impeller rotating, the incidence angle of one passage is gradually increasing, and the flow separation phenomenon on the suction side is gradually intensified. However, as the stall cell is in the developing stage, the surge of the incidence angle is relatively small, and the rise range is about 1°. However, in the post-stall stage, the sharp increase of incidence angle is further intensified, which is far higher than the critical incidence angle. The inflow angle has been reduced to nearly 0°. In the stall path, a large amount of air flows close to the suction surface in LE, and a large area of boundary layer flow separation phenomenon occurs, and many vortices are formed. Meanwhile, as the propagation period of rotating stall is lower than the rotor speed, there is a certain phase difference in the range of the sharp increase of incidence angle at different times.
With the emergence of spike disturbance, the incidence angle increases sharply as well as the flow pattern of the inlet surface changes.
Figure 17 shows the transient flow characteristics of the inlet surface at the hump point. In order to show the difference of flow distribution in each path more clearly, the space rectangular coordinate system is transformed into the cylindrical coordinate system. As shown in
Figure 16, Path 1 is in the range of 0–40°, Path 2 is in the range of 40–80°, and so on.
At the moment of the emerging spike, similar to the change of incidence angle, the inflow pattern does not show obvious distortion. The distribution of the inlet flow pattern is uniform, and the flow pattern of each path is basically the same. The low-velocity flow region only appears on the hub and rim side, while the flow velocity on the hub side is relatively lower. However, with the continuous disturbance of spike, the low-velocity flow region on the rim side gradually extends to the lower span side, the flow paths gradually show the difference of inflow quality, and the inflow pattern presents a circumferential uneven distribution, such as the moment of t = d. After the spike disturbance mode is further transformed into the developed rotating stall, the difference of inflow is further intensified. At this moment, the low-velocity region near the rim side has spread to 0.5 span, and interferes with several adjacent paths. The phenomenon of distorted flow in the rim region is intensified, which directly affects the sharp deterioration of the flow pattern. In the post-stall stage, the low-velocity region of the inlet surface also propagates in the circumferential direction of the flow path, its propagation speed is the same as the stall propagation speed, and opposite to the rotation direction of the rotor.
Figure 18 shows the transient flow characteristics in the middle section of the rotor to show the evolution and development of rotating stall. In the pre-stall stage, the axial flow fan is only disturbed by modal wave, and the flow in the rim region is relatively stable without flow distortion. In the hub region, as the blade angle of the hub side is larger than the inlet flow angle, the formation of negative incidence angle causes the flow separation near the pressure surface of each path. With the emergence of spike, the inlet flow angle of the rim region gradually breaks through the critical value, and the flow distortion spreads to multiple passages, accompanied by the decrease of the air velocity and flow capacity in the rim region. In the stall-inception and post-stall stage, flow distortion in the rim region is gradually intensified, and the stall vortex is formed gradually. In the flow path disturbed by rotating stall, the flow in the rim region is distorted, and the flow is squeezed to the flow surface of the hub. Therefore, the flow angle of the hub surface gradually increases, and the flow separation phenomenon in the hub region gradually disappears. However, the flow in the rim region is relatively stable in the flow path which is not disturbed by rotating stall, and there is still a large area of separated flow in its hub side.
Figure 19 shows the transient flow characteristics of the rotor outlet surface at the hump point. Like the flow characteristics of the inlet surface and the middle section of the rotor, the flow in the rim region is gradually distorted and the low-velocity airflow region is gradually formed after experiencing the emerging spike. Then, the fully developed stall cell propagates counter-clockwise on the outlet surface, and the circumferential velocity is far lower than the rotor rotation speed.
The emerging spike and rotating stall will not only affect the flow pattern of different cross-sections, but also directly change the flow pattern and trajectory of TLF.
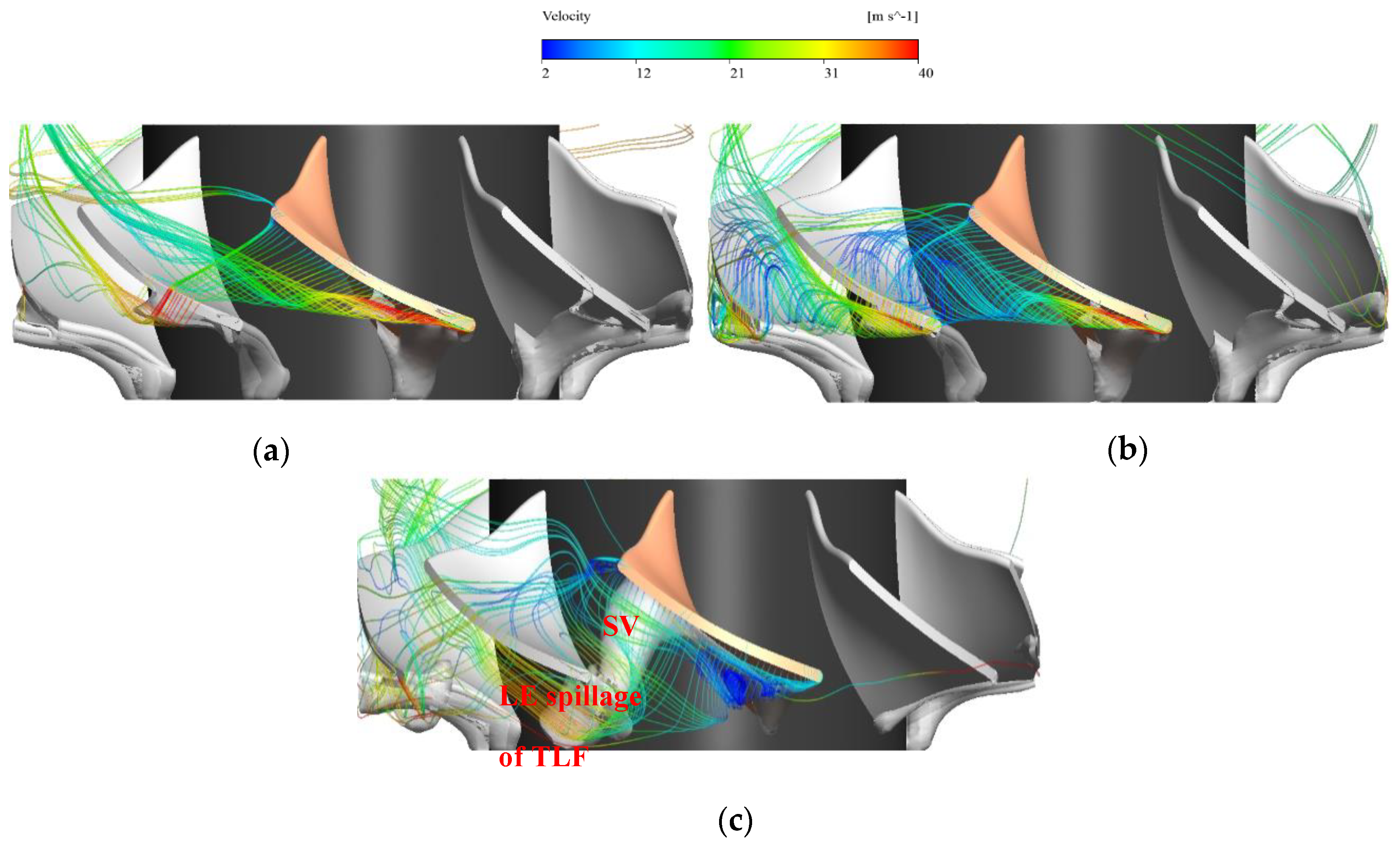
Figure 20 shows the transient process of tip leakage flow from the pre-stall stage to post-stall stage, and iso-surface is used to characterize the low-pressure flow region in the rotor to better show the stall vortex.
In the pre-stall stage, the flow pattern of TLF is relatively stable, most of TLF can flow smoothly out of the rotor from leading edge (LE) to trailing edge (TE), while a small amount of TLF from TE flows into the next path along the rotor shroud through the tip clearance, and there is no obvious distortion in the TLF. In the stall-inception stage, TLF deteriorated rapidly after expiring emerging spike. With the distortion caused by the surge of incidence angle, the leakage flow pattern changed greatly. TLF has been unable to flow out of the rotor smoothly. Due to the phenomenon of flow separation, the airflow velocity of TLF has been attenuated. A large amount of TLF flows into the next path through the tip clearance, seriously interferes with the downstream flow field, and there is a tendency of condensation to form in the vortex in the downstream path. In the post-stall stage, the trajectory of TLF changed again. Due to the blocking effect of the stall vortex, TLF is unable to smoothly discharge the flow path. Meanwhile, the phenomenon of tip overflow through the tip clearance also decreased. The trajectory of most TLF is distorted due to the blockage effect, part of TLF forms a vortex under the stall interference effect, and presents the inverse flow situation. After TLF flows back to LE, it flows close to the suction surface of the downstream blade and overflows into the downstream path, gradually changes the flow pattern of the downstream path, and triggers the surge of the incidence angle, which causes the flow separation and promotes the counter-clockwise circumferential propagation of rotating stall. The fundamental reason for the circumferential propagation of rotating stall is that the blocking effect of the stall vortex leads to the distortion of the trajectory of TLF. The distorted TLF flows into the next flow path in the form of LE spillage, and then changes the flow pattern of the downstream flow path.